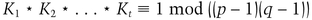
This is a generalization of RSA (see Section 19.3) [217,212]. The modulus, n, is the product of two primes, p and q. However, instead of choosing e and d such that ed ≡ 1 mod ((p − 1)(q − 1)), choose t keys, Ki, such that
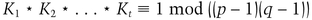
Since
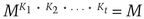
this is a multiple-key scheme as described in Section 3.5.
If, for example, there are five keys, a message encrypted with K3 and K5 can be decrypted with K1, K2, and K4:
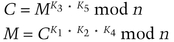
One use for this is multisignatures. Imagine a situation where both Alice and Bob have to sign a document for it to be valid. Use three keys: K1, K2, and K3. The first two are issued one each to Alice and Bob, and the third is made public.
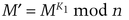
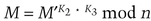
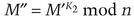
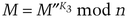
Note that a trusted party is needed to set this system up and distribute the keys to Alice and Bob. Another scheme with the same problem is [484]. Yet a third scheme is [695,830,700], but the effort in verification is proportional to the number of signers. Newer schemes [220,1200] based on zero-knowledge identification schemes solve both shortcomings of the previous systems.
Back in Section 3.7 I discussed the idea behind secret-sharing schemes. The four different algorithms that follow are all particular cases of a general theoretical framework [883].
Adi Shamir uses polynomial equations in a finite field to construct a threshold scheme [1414]. Choose a prime, p, which is both larger than the number of possible shadows and larger than the largest possible secret. To share a secret, generate an arbitrary polynomial of degree m − 1. For example, if you want to create a (3,n)-threshold scheme (three shadows are necessary to reconstruct M), generate a quadratic polynomial
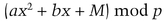
where p is a random prime larger than any of the coefficients. The coefficients a and b are chosen randomly; they are kept secret and discarded after the shadows are handed out. M is the message. The prime must be made public.
The shadows are obtained by evaluating the polynomial at n different points:
In other words, the first shadow could be the polynomial evaluated at x = 1, the second shadow could be the polynomial evaluated at x = 2, and so forth.
Since the quadratic polynomial has three unknown coefficients, a, b, and M, any three shadows can be used to create three equations. Two shadows cannot. One shadow cannot. Four or five shadows are redundant.
For example, let M be 11. To construct a (3, 5)-threshold scheme, where any three of five people can reconstruct M, first generate a quadratic equation (7 and 8 were chosen randomly):
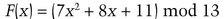
The five shadows are:
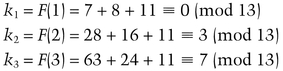
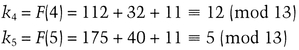
To reconstruct M from three of the shadows, for example k2, k3, and k5, solve the set of linear equations:
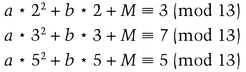
The solution will be a = 7, b = 8, and M = 11. So M is recovered.
This sharing scheme can be easily implemented for larger numbers. If you want to divide the message into 30 equal parts such that any six can get together and reproduce the message, give each of the 30 people the evaluation of a polynomial of degree 6.
Six people can solve for the six unknowns (including M); five people cannot learn anything about M.
The most mind-boggling aspect of secret sharing is that if the coefficients are picked randomly, five people with infinite computing power can’t learn anything more than the length of the message (which each of them knows anyway). This is as secure as a one-time pad; an attempt at exhaustive search (that is, trying all possible sixth shadows) will reveal that any conceivable message could be the secret. This is true for all the secret-sharing schemes presented here.
George Blakley invented a scheme using points in space [182]. The message is defined as a point in m-dimensional space. Each shadow is the equation of an (m − 1)-dimensional hyperplane that includes the point. The intersection of any m of the hyperplanes exactly determines the point.
For example, if three shadows are required to reconstruct the message, then it is a point in three-dimensional space. Each shadow is a different plane. With one shadow, you know the point is somewhere on the plane. With two shadows, you know the point is somewhere on the line formed where the two planes intersect. With three shadows, you can determine the point exactly: the intersection of the three planes.
This scheme uses prime numbers [65]. For an (m, n)-threshold scheme, choose a large prime, p, greater than M. Then choose n numbers less than p, d1, d2, …, dn, such that:
To distribute the shadows, first choose a random value r and compute
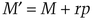
The shadows, ki, are
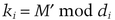
Any m shadows can get together and reconstruct M using the Chinese remainder theorem, but any m − 1 cannot. See [65] for details.
This scheme uses matrix multiplication [818]. Choose n + 1 m-dimensional vectors, V0, V1, …, Vn, such that any possible m * m matrix formed out of those vectors has rank m. The vector U is a row vector of dimension m + 1.
M is the matrix product U·V0. The shadows are the products U·Vi, where i is a number from 1 to n.
Any m shadows can be used to solve the m * m system of linear equations, where the unknowns are the coefficients of U. UV0 can be computed from U. Any m − 1 shadows cannot solve the system of linear equations and therefore cannot recover the secret.
The previous examples illustrate only the simplest threshold schemes: Divide a secret into n shadows such that any m can be used to recover the secret. These algorithms can be used to create far more complicated schemes. The following examples will use Shamir’s algorithm, although any of the others will work.
To create a scheme in which one person is more important than another, give that person more shadows. If it takes five shadows to recreate a secret and one person has three shadows while everyone else has only one, then that person and two other people can recreate the secret. Without that person, it takes five to recreate the secret.
Two or more people could get multiple shadows. Each person could have a different number of shadows. No matter how the shadows are distributed, any m of them can be used to reconstruct the secret. Someone with m − 1 shadows, be it one person or a roomful of people, cannot do it.
In other types of schemes, imagine a scenario with two hostile delegations. You can share the secret so that two people from the 7 in Delegation A and 3 people from the 12 in Delegation B are required to reconstruct the secret. Make a polynomial of degree 3 that is the product of a linear expression and a quadratic expression. Give everyone from Delegation A a shadow that is the result of an evaluation of the linear equation; give everyone from Delegation B a shadow that is the evaluation of the quadratic equation.
Any two shadows from Delegation A can be used to reconstruct the linear equation, but no matter how many other shadows the group has, they cannot get any information about the secret. The same is true for Delegation B: They can get three shadows together to reconstruct the quadratic equation, but they cannot get any more information necessary to reconstruct the secret. Only when the two delegations share their equations can they be multiplied to reconstruct the secret.
In general, any type of sharing scheme that can be imagined can be implemented. All you have to do is to envision a system of equations that corresponds to the particular scheme. Some excellent papers on generalized secret-sharing schemes are [1462,1463,1464].
This algorithm modifies the standard (m, n)-threshold scheme to detect cheaters [1529]. I demonstrate this using the LaGrange scheme, although it works with the others as well.
Choose a prime, p, that is both larger than n and larger than
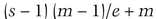
where s is the largest possible secret and e is the probability of successful cheating. You can make e as small as you want; it just makes the computation more complex. Construct your shadows as before, except instead of using 1, 2, 3, …, n for xi, choose random numbers between 1 and p − 1 for xi.
Now, when Mallory sneaks into the secret reconstruction meeting with his false share, his share has a high probability of not being possible. An impossible secret is, of course, a fake secret. See [1529] for the math.
Unfortunately, while Mallory is exposed as a cheater, he still learns the secret (assuming that there are m other valid shares). Another protocol, from [1529,975], prevents that. The basic idea is to have a series of k secrets, such that none of the participants knows beforehand which is correct. Each secret is larger than the one before, except for the real secret. The participants combine their shadows to generate one secret after the other, until they create a secret that is less than the previous secret. That’s the correct one.
This scheme will expose cheaters early, before the secret is generated. There are complications when the participants deliver their shadows one at a time; refer to the papers for details. Other papers on the detection and prevention of cheaters in threshold schemes are [355,114,270].
This subliminal channel (see Section 4.2), designed by Gustavus Simmons [1458,1459,1460], uses the Ong-Schnorr-Shamir identification scheme (see Section 20.5). As in the original scheme, the sender (Alice) chooses a public modulus, n, and a private key, k, such that n and k are relatively prime. Unlike the original scheme, k is shared between Alice and Bob, the recipient of the subliminal message.
The public key is calculated:
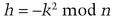
If Alice wants to send the subliminal message M by means of the innocuous message M′, she first confirms that M′ and n are relatively prime, and that M and n art relatively prime.
Alice calculates
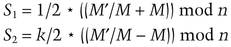
Together, the pair, S1 and S2, is the signature under the traditional Ong-Schnorr-Shamir scheme and the carrier of the subliminal message.
Walter the warden (remember him?) can authenticate the message as described by the Ong-Schnorr-Shamir signature scheme, but Bob can do better. He can authenticate the message (it is always possible that Walter can make his own messages). He confirms that
If the message is authentic, the receiver can recover the subliminal message using this formula:
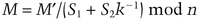
This works, but remember that the basic Ong-Schnorr-Shamir has been broken.
Simmons’s second subliminal channel [1459], described in [1407,1473], is based on the ElGamal signature scheme (see Section 19.6).
Key generation is the same as the basic ElGamal signature scheme. First choose a prime, p, and two random numbers, g and r, such that both g and r are less than p. Then calculate
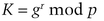
The public key is K, g, and p. The private key is r. Besides Alice, Bob also knows r; it is the key that is used to send and read the subliminal message in addition to being the key used to sign the innocuous message.
To send a subliminal message M using the innocuous message M′, M and p must be all relatively prime to each other, and M and p − 1 must be relatively prime. Alice calculates
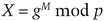
and solves the following equation for Y (using the extended Euclidean algorithm):
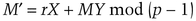
As in the basic ElGamal scheme, the signature is the pair: X and Y.
Walter can verify the ElGamal signature. He confirms that
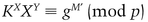
Bob can recover the subliminal message. First he confirms that
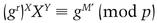
If it does, he accepts the message as genuine (not from Walter).
Then, to recover M, he computes
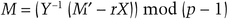
For example, let p = 11 and g = 2. The private key, r, is chosen to be 8. This means the public key, which Walter can use to verify the signature, is gr mod p = 28 mod 11=3.
To send the subliminal message M = 9, using innocuous message M′ = 5, Alice confirms that 9 and 11 are relatively prime and that 5 and 11 are relatively prime. She also confirms that 9 and 11 – 1 = 10 are relatively prime. They are, so she calculates
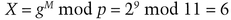
Then, she solves the following equation for Y:
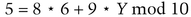
Y = 3, so the signature is the pair, X and Y: 6 and 3.
Bob confirms that
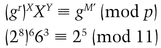
It does (do the math yourself if you don’t trust me), so he then recovers the subliminal message by calculating
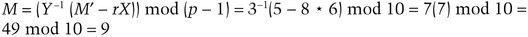
A subliminal channel can be added to ESIGN [1460] (see Section 20.6).
In ESIGN, the secret key is a pair of large prime numbers, p and q, and the public key is n = p2q. With a subliminal channel, the private key is three primes, p, q, and r, and the public key is n, such that
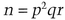
The variable, r, is the extra piece of information that Bob needs to read the subliminal message.
To sign a normal message, Alice first picks a random number, x, such that x is less than pqr and computes:
w, the least integer that is larger than (H(m) − xk mod n)/pqr)
s = x + ((w/kxk − 1) mod p)pqr
H(m) is the hash of the message; k is a security parameter. The value s is the signature.
To verify the signature, Bob computes sk mod n. He also computes a, which is the least integer larger than the number of bits of n divided by 3. If H(m) is less than or equal to sk mod n, and if sk mod n is less than H(m) + 2a, then the signature is considered valid.
To send a subliminal message, M, using the innocuous message, M′, Alice calculates s using M in place of H(m). This means that the message must be smaller than p2qr. She then chooses a random value, u, and calculates
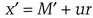
Then, use this x′ value as the “random number” x to sign M′. This second s value is sent as a signature.
Walter can verify that s (the second s) is a valid signature of M′.
Bob can also authenticate the message in the same way. But, since he also knows r, he can calculate
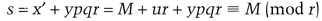
This implementation of a subliminal channel is far better than the previous two. In the Ong-Schnorr-Shamir and ElGamal implementations, Bob has Alice’s private key. Besides being able to read subliminal messages from Alice, Bob can impersonate Alice and sign normal documents. Alice can do nothing about this; she must trust Bob to set up this subliminal channel.
The ESIGN scheme doesn’t suffer from this problem. Alice’s private key is the set of three primes: p, q, and r. Bob’s secret key is just r. He knows n = p2qr, but to recover p and q he has to factor that number. If the primes are large enough, Bob has just as much trouble impersonating Alice as would Walter or anyone else.
There is also a subliminal channel in DSA (see Section 20.1) [1468,1469,1473]. In fact, there are several. The simplest subliminal channel involves the choice of k. It is supposed to be a 160-bit random number. However, if Alice chooses a particular k, then Bob, who also knows Alice’s private key, can recover it. Alice can send Bob a 160-bit subliminal message in each DSA signature; everyone else simply verifies Alice’s signature. Another complication: Since k should be random, Alice and Bob need to share a one-time pad and encrypt the subliminal message with the one-time pad to generate a k.
DSA has subliminal channels that do not require Bob to know Alice’s private key. These also involve choosing particular values of k, but cannot be used to send 160 bits of information. This scheme, presented in [1468,1469], allows Alice and Bob to exchange one bit of subliminal information per signed message.
Sending multiple bits via this method involves making r either a quadratic residue or a quadratic nonresidue modulo a variety of parameters. See [1468,1469] for details.
This scheme can be easily extended to send multiple subliminal bits per signature. If Alice and Bob agree on two random primes, P and Q, Alice can send two bits by choosing a random k such that r is either a quadratic residue mod P or a quadratic nonresidue mod P, and either a quadratic residue mod Q or a quadratic nonresidue mod Q. A random value of k has a 25 percent chance of producing an r of the correct form.
Here’s how Mallory, an unscrupulous implementer of DSA, can have the algorithm leak 10 bits of Alice’s private key every time she signs a document.
It’s scary that even if Alice knows what is happening, she cannot prove it. As long as those 14 secret primes stay secret, Mallory is safe.
The subliminal channel relies on the fact that Alice can choose k to transmit subliminal information. To foil the subliminal channel, Alice cannot be allowed to choose k. However, neither can anyone else; if someone else were allowed to choose k, it would allow that person to forge Alice’s signature. The only solution is for Alice to jointly generate k with another party, call him Bob, in such a way that Alice cannot control a single bit of k and Bob cannot know a single bit of k. At the end of the protocol, Bob should be able to verify that Alice used the k that they jointly generated.
Here’s the protocol [1470,1472,1473]:
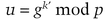
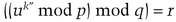
If it does, he knows that k was used to sign M.
After step (4), Bob knows that no subliminal information can be embedded in r. If he is a trusted party, he can certify that Alice’s signature is subliminal-free. Others will have to trust his certification; Bob cannot prove this fact to a third party with a transcript of the protocol.
A surprising result is that if Bob wants to, he can use this protocol to create his own subliminal channel. Bob can embed a subliminal message in one of Alice’s signatures by choosing k″ with certain characteristics. When Simmons discovered this, he dubbed it the “Cuckoo’s Channel.” Details on how the Cuckoo’s Channel works, and a three-pass protocol for generating k that prevents it, are discussed in [1471,1473].
Any signature scheme can be converted into a subliminal channel [1458,1460,1406]. A protocol for embedding a subliminal channel in the Fiat-Shamir and Feige-Fiat-Shamir protocols, as well as possible abuses of the subliminal channel, can be found in [485].
This undeniable signature algorithm (see Section 4.3) is by David Chaum [343,327]. First, a large prime, p, and a primitive element, g, are made public, and used by a group of signers. Alice has a private key, x, and a public key, gx mod p.
To sign a message, Alice computes z = mx mod p. That’s all she has to do. Verification is a little more complicated.
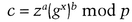
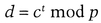
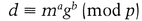
If it is, he accepts the signature as genuine.
Imagine that Alice and Bob went through this protocol, and Bob is now convinced that Alice signed the message. Bob wants to convince Carol, so he shows her a transcript of the protocol. Dave, however, wants to convince Carol that some other person signed the document. He creates a fake transcript of the protocol. First he generates the message in step (1). Then in step (3) he generates d and the fake transmission from this other person in step (2). Finally, he creates the message in step (2). To Carol, both Bob’s and Dave’s transcripts are identical. She cannot be convinced of the signature’s validity unless she goes through the protocol herself.
Of course, if she were watching over Bob’s shoulder as he completed the protocol, she would be convinced. Carol has to see the steps done in order, just as Bob does.
There may be a problem with this signature scheme, but I know of no details. Please pay attention to the literature before you use it.
Another protocol not only has a confirmation protocol—Alice can convince Bob that her signature is valid—but it also has a disavowal protocol; Alice can use a zero-knowledge interactive protocol to convince him that the signature is not valid, if it is not [329].
Like the previous protocol, a group of signers use a shared public large prime, p, and a primitive element, g. Alice has a unique private key, x, and a public key, gx mod p. To sign a message, Alice computes z = mx mod p.
To verify a signature:
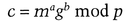
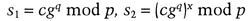
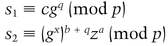
then the signature is valid.
Alice can also disavow a signature, z, for a message, m. See [329] for details.
Additional protocols for undeniable signatures can be found in [584,344]. Lein Harn and Shoubao Yang proposed a group undeniable signature scheme [700].
An algorithm for a convertible undeniable signature, which can be verified, disavowed, and also converted to a conventional digital signature is given in [213]. It’s based on the ElGamal digital signature algorithm.
Like ElGamal, first choose two primes, p and q, such that q divides p − 1. Now you have to create a number, g, less than q. First choose a random number, h, between 2 and p − 1. Calculate
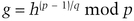
If g equals the 1, choose another random h. If it doesn’t, stick with the g you have.
The private keys are two different random numbers, x and z, both less than q. The public keys are p, q, g, y, and u, where
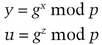
To compute the convertible undeniable signature of message m (which is actually the hash of a message), first choose a random number, t, between 1 and q − 1. Then compute
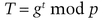
and
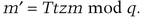
Now, compute the standard ElGamal signature on m′. Choose a random number, R, such that R is less than and relatively prime to p − 1. Then compute r = gR mod p, and use the extended Euclidean algorithm to compute s, such that
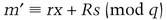
The signature is the ElGamal signature (r, s), and T..
Here’s how Alice verifies her signature to Bob:
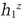mod p, and sends both of those numbers to Bob.Alice can convert all of her undeniable signatures to normal signatures by publishing z. Now, anyone can verify her signature without her help.
Undeniable signature schemes can be combined with secret-sharing schemes to create distributed convertible undeniable signatures [1235]. Someone can sign a message, then distribute the ability to confirm that the signature is valid. He might, for example, require three out of five people to participate in the protocol in order to convince Bob that the signature is valid. Improvements on this notion deleted the requirement for a trusted dealer [700,1369].
Here’s how Alice can sign a message and Bob can verify it, such that Carol can verify Alice’s signature at some later time to Dave (see Section 4.4) [333].
First, a large prime, p, and a primitive element, g, are made public and used by a group of users. The product of two primes, n, is also public. Carol has a private key, z, and a public key is h = gx mod p.
In this protocol Alice can sign m such that Bob is convinced that the signature is valid, but cannot convince a third party.
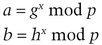
She computes the hash of m, H(m), and the hash of a and b concatenated, H(a,b). She then computes
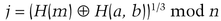
and sends a, b, and j to Bob.
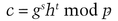
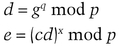
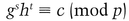
Then she sends Bob q.
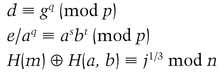
If they all check out, he accepts the signature as genuine.
Bob cannot use a transcript of this proof to convince Dave that the signature is genuine, but Dave can conduct a protocol with Alice’s designated confirmer, Carol. Here’s how Carol convinces Dave that a and b constitute a valid signature.
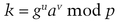
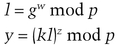
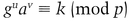
Then she sends Dave w.
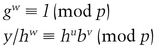
If they both check out, he accepts the signature as genuine.
In another protocol Carol can convert the designated-confirmer protocol into a conventional digital signature. See [333] for details.
There is a large prime, p, and a generator, g. Alice has a particular value for x, and wants to know e, such that
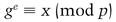
This is a hard problem, and Alice lacks the computational power to compute the result. Bob has the power to solve the problem—he represents the government, or a large computing organization, or whatever. Here’s how Bob can do it without Alice revealing x [547,4]:
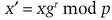
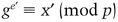
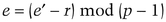
Similar protocols for the quadratic residuosity problem and for the primitive root problem are in [3,4]. (See also Section 4.8.)
The following protocols allow Alice and Bob to flip a fair coin over a data network (see Section 4.9) [194]. This is an example of flipping a coin into a well (see Section 4.10). At first, only Bob knows the result of the coin toss and tells it to Alice. Later, Alice may check to make sure that Bob told her the correct outcome of the toss.
Coin-flip subprotocol:
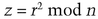
and sends z to Alice.
Similarly, call y′ the smaller of these two numbers:
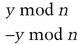
Note that r is equal either to x′ or y′.
Verification subprotocol:
Alice has no way of knowing r, so her guess is real. She only tells Bob one bit of her guess in step (4) to prevent Bob from getting both x′ and y′. If Bob has both of those numbers, he can change r after step (4).
Exponentiation modulo a prime number, p, is used as a one-way function in this protocol [1306]:
Coin-flip subprotocol:
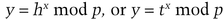
She sends y to Bob.
Verification subprotocol:
For Alice to cheat, she has to know two integers, x and x′, such that hx ≡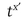 
(mod p). If she knew those values, she would be able to calculate:
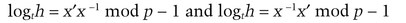
These are hard problems.
Alice would be able to do this if she knew logth, but Bob chooses h and t in step (2). Alice has no other recourse except to try to compute the discrete logarithm. Alice could also attempt to cheat by choosing an x that is not relatively prime to p − 1, but Bob will detect that in step (6).
Bob can cheat if h and t are not primitive in GF(p), but Alice can easily check that after step (2) because she knows the prime factorization of p − 1.
One nice thing about this protocol is that if Alice and Bob want to flip multiple coins, they can use the same values for p, h, and t. Alice just generates a new x, and the protocol continues from step (3).
Blum integers can be used in a coin-flipping protocol.
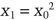mod n. She sends n and X1 to Bob.
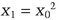mod n. If all this checks out, Bob wins the flip if he guessed correctly.It is crucial that n be a Blum integer. Otherwise, Alice may be able to find an x′0 such that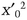 
mod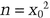 
mod n = x1, where x′0 is also a quadratic residue. If x0 were even and x′0 were odd (or vice versa), Alice could freely cheat.
There is a simple one-way accumulator function [116] (see Section 4.12):
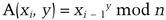
The numbers n (n is the product of two primes) and x0 must be agreed upon in advance. Then, the accumulation of y1, y2, and y3 would be
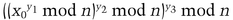
This computation is independent of the order of y1, y2, and y3.
This protocol allows multiple parties (at least two are required for the protocol to work) to buy individual secrets from a single seller (see Section 4.13) [1374,1175]. First, here’s a definition. Take two bit strings, x and y. The fixed bit index (FBI) of x and y are the bits where the ith bit of x equals the ith bit of y.
For example:
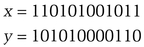
FBI(x, y) = {1, 4, 5, 11}
(We’re reading the bits from right to left, with the right-most bit as zero.)
Now, here’s the protocol. Alice is the seller. Bob and Carol are buyers. Alice has k n-bit secrets: S1, S2, …, Sk. Bob wants to buy secret Sb; Carol wants to buy secret Sc.
Carol encrypts Bc (remember, Sc is the secret she wants to buy) with the public key from Alice. She computes the FBI of Bc and the result she just encrypted. She sends this FBI to Bob.
Carol takes each of the n-bit numbers C1 C2, …, Ck, and replaces every bit whose index is not in the FBI she received from Bob with its complement. She sends this new list of n-bit numbers, C′1, C′2, …, C′k, to Alice.
Alice decrypts all B′i with Carol’s private key, giving her k n-bit numbers: B″1, B″2, …, B″k. She computes Si ⊕ B″i, for i = 1 to k, and sends the results to Carol.
Carol computes Sc by XORing Bc and the cth number she received from Alice.
This is complicated. An example will go a long way to help.
Alice has the following eight 12-bit secrets for sale: S1 = 1990, S2 = 471, S3 = 3860, S4 = 1487, S5 = 2235, S6 = 3751, S7 = 2546, and S8 = 4043. Bob wants to buy S7. Carol wants to buy S2.
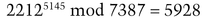
Now:
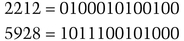
So, the FBI of those two numbers is {0, 1, 4, 5, 6). He sends this to Carol.
Carol wants to buy S2, so she encrypts B2 with the public key that Alice gave her and computes the FBI of B2 with the result of her encryption. She sends {0, 1, 2, 6, 9, 10} to Bob.
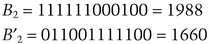
He sends B′1, B′2, … B′8, to Alice.
Carol takes C1 C2, …, C8, and replaces every bit whose index is not in the set {0, 1, 4, 5, 6} with its complement. For example:
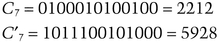
She sends C′1, C′1, … C′8, to Alice.
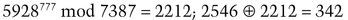
She sends the results to Bob.
Alice decrypts all B′i with Carol’s private key and XORs the results with Si. For example, for i = 2:
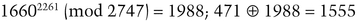
She sends the results to Carol.
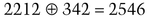
Carol computes S2 by XORing B2 and the second number she received from Alice.
The protocol works for any number of buyers. If Bob, Carol, and Dave want to buy secrets, Alice gives each buyer two public keys, one for each of the others. Each buyer gets a set of numbers from each other buyer. Then, they complete the protocol with Alice for each of their sets of numbers and XOR all of their final results from Alice to get their secret. More details are in [1374,1175].
Unfortunately, a pair of dishonest parties can cheat. Alice and Carol, working together, can easily find out what secret Bob is getting: If they know the FBI of Cb and Bob’s encryption algorithm, they can find b such that Cb has the right FBI. And Bob and Carol, working together, can easily get all the secrets from Alice.
If you assume honest parties, there’s an easier protocol [389].
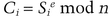
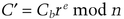
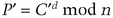
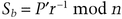
If the parties may be dishonest, Bob can prove in zero-knowledge that he knows some r such that C′= Cbre mod n and keep b secret until Alice gives him P′ in step (3) [246].
Fair cryptosystems are a way to do key escrowing in software (see Section 4.14). This example is from Silvio Micali [1084,1085]. It is patented [1086,1087].
In the basic Diffie-Hellman scheme, a group of users share a prime, p, and a generator, g. Alice’s private key is s, and her public key is t = gs mod p.
Here’s how to make Diffie-Hellman fair (this example uses five trustees).
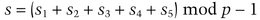
and her public key is
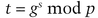
Alice also computes
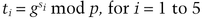
Alice’s public shares are ti, and her private shares are si.
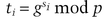
If it does, the trustee signs ti and sends it to the KDC. The trustee stores si in a secure place.
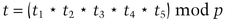
If it does, the KDC approves the public key.
At this point, the KDC knows that the trustees each have a valid piece, and that they can reconstruct the private key if required. However, neither the KDC nor any four of the trustees working together can reconstruct Alice’s private key.
Micali’s papers [1084,1085] also contain a procedure for making RSA fair and for combining a threshold scheme with the fair cryptosystem, so that m out of n trustees can reconstruct the private key.
Like the previous protocol, a group of users share a prime, p, and a generator, g. Alice’s private key is s, and her public key is t = gs mod p.
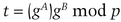
She sets her private key as
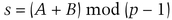
The trustees can reconstruct A. Since the KDC knows B, this is enough to reconstruct s. And Alice cannot make use of any subliminal channels to send unauthorized information. This protocol, discussed in [946,833] is being patented.
Peggy wants to prove to Victor that she knows an x that satisfies
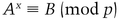
where p is a prime, and x is a random number relatively prime to p − 1. The numbers A, B, and p are public, and x is secret. Here’s how Peggy can prove she knows x without revealing it (see Section 5.1) [338,337].
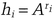mod p, for all values of i, and sends them to Victor.
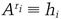(mod p)
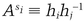(mod p)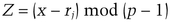
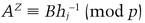
Peggy’s probability of successfully cheating is 2−t.
Alice knows Carol’s private key. Maybe she has broken RSA; maybe she has broken into Carol’s house and stolen the key. Alice wants to convince Bob that she knows Carol’s key. However, she doesn’t want to tell Bob the key or even decrypt one of Carol’s messages for Bob. Here’s a zero-knowledge protocol by which Alice convinces Bob that she knows Carol’s private key [888].
Carol’s public key is e, her private key is d, and the RSA modulus is n.
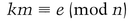
They should choose the numbers randomly, using a coin-flip protocol to generate k and then computing m. If both k and m are greater than 3, the protocol continues. Otherwise, they choose again.
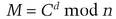
She then computes
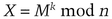
and sends X to Bob.
A similar protocol can be used to demonstrate the ability to break a discrete logarithm problem [888].
There are no known truly practical zero-knowledge proofs that n=pq, where p and q are primes congruent to 3 modulo 4. However, if you allow n to be of the form prqs, where r and s are odd, then the properties which make Blum integers useful in cryptography still hold. And there exists a zero-knowledge proof that n is of that form.
Assume Alice knows the factorization of the Blum integer n, where n is of the form previously discussed. Here’s how she can prove to Bob that n is of that form [660].
The odds of Alice successfully cheating are one in 2k.
The notion of blind signatures (see Section 5.3) was invented by David Chaum [317,323], who also invented their first implementation [318]. It uses the RSA algorithm.
Bob has a public key, e, a private key, d, and a public modulus, n. Alice wants Bob to sign message m blindly.
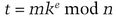
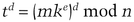
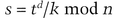
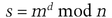
This can easily be shown
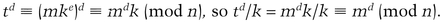
Chaum invented a family of more complicated blind signature algorithms in [320,324], called blind unanticipated signatures. These signatures are more complex in construction, but more flexible.
In this protocol by Michael Rabin [1286], Alice has a 50 percent chance of sending Bob two primes, p, and q. Alice will not know whether the transfer is successful. (See Section 5.5.) (This protocol can be used to send Bob any message with a 50 percent success rate if p and q reveal an RSA private key.)
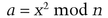
If Bob receives x or n − x, he can’t compute anything.
This protocol may have a weakness: It might be the case that Bob can compute a number a such that given the square root of a you can calculate a factor of n all the time.
This protocol is from [1373]. Alice knows the integer i; Bob knows the integer j. Alice and Bob together wish to know whether i ≤ j or if i ≥ j, but neither Alice nor Bob wish to reveal the integer each knows. This special case of secure multiparty computation (see Section 6.2) is sometimes known as Yao’s millionaire problem [1627].
For this example, assume that i and j range from 1 to 100. Bob has a public key and a private key.
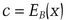
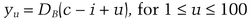
DB is the decryption algorithm with Bob’s private key.
He chooses a large random prime, p. (The size of p should be somewhat smaller than x. Bob doesn’t know x, but Alice could easily tell him the size of x.) He then computes the following 100 numbers:
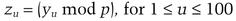
He then verifies that, for all u ≠ v
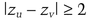
and that for all u
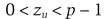
If this is not true, Bob chooses another prime and tries again.
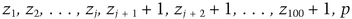
All the verification that Bob goes through in step (3) is to guarantee that no number appears twice in the sequence generated in step (4). Otherwise, if za = zb, Alice knows that a ≤ j < b.
The one drawback to this protocol is that Alice learns the result of the computation before Bob does. Nothing stops her from completing the protocol up to step (5) and then refusing to tell Bob the results in step (6). She could even lie to Bob in step (6).
Assume they’re using RSA. Bob’s public key is 7 and his private key is 23; n = 55. Alice’s secret value, i, is 4; Bob’s secret value, j, is 2. (Assume that only the values 1, 2, 3, and 4 are possible for i and j.)
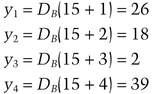
He chooses p = 31 and calculates:
He does all the verifications and confirms that the sequence is fine.
This protocol can be used to create far more complicated protocols. A group of people can conduct a secret auction over a computer network. They arrange themselves in a logical circle, and through individual pairwise comparisons, determine which is offering the highest price. In order to prevent people from changing their bids in mid-auction, some sort of bit-commitment protocol could also be used. If the auction is a Dutch auction, then the highest bidder gets the item for his highest price. If it is an English auction, then he gets the item for the second-highest price. (This can be determined by a second round of pairwise comparisons.) Similar ideas have applications in bargaining, negotiations, and arbitration.
The notion of probabilistic encryption was invented by Shafi Goldwasser and Silvio Micali [624]. Although its theory makes it the most secure cryptosystem invented, its early implementation was impractical [625]. More recent implementations have changed that.
The point behind probabilistic encryption is to eliminate any information leaked with public-key cryptography. Because a cryptanalyst can always encrypt random messages with a public key, he can get some information. Assuming he has ciphertext C = EK(M) and is trying to recover plaintext message M, he can pick a random message M′ and encrypt it: C′ = EK(M′). If C′ = C, then he guessed the correct plaintext. If it’s wrong, he just guesses again.
Also, no partial information is leaked about the original message. With public-key cryptography, sometimes a cryptanalyst can learn things about the bits: The XOR of bits 5, 17, and 39 is 1, and so on. With probabilistic encryption, even this type of information remains hidden.
Not a whole lot of information is to be gained here, but there are potential problems with allowing a cryptanalyst to encrypt random messages with your public key. Some information is being leaked to the cryptanalyst every time he encrypts a message. No one really knows how much.
Probabilistic encryption tries to eliminate that leakage. The goal is that no computation on the ciphertext, or on any other trial plaintexts, can give the cryptanalyst any information about the corresponding plaintext.
In probabilistic encryption, the encrypting algorithm is probabilistic rather than deterministic. In other words, a large number of ciphertexts will decrypt to a given plaintext, and the particular ciphertext used in any given encryption is randomly chosen.
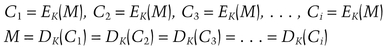
With probabilistic encryption, a cryptanalyst can no longer encrypt random plaintexts looking for the correct ciphertext. To illustrate, assume the cryptanalyst has ciphertext Ci = EK(M). Even if he guesses M correctly, when he encrypts EK(M), the result will be a completely different C: Cj. He cannot compare Ci and Cj, and so cannot know that he has guessed the message correctly.
This is amazingly cool stuff. Even if a cryptanalyst has the public encryption key, the plaintext, and the ciphertext, he cannot prove that the ciphertext is the encryption of the plaintext without the private decryption key. Even if he tries exhaustive search, he can only prove that every conceivable plaintext is a possible plaintext.
Under this scheme, the ciphertext will always be larger than the plaintext. You can’t get around this; it’s a result of the fact that many ciphertexts decrypt to the same plaintexts. The first probabilistic encryption scheme [625] resulted in a cipher-text so much larger than the plaintext that it was unusable.
However, Manual Blum and Goldwasser have an efficient implementation of probabilistic encryption using the Blum Blum Shub (BBS) random-bit generator described in Section 17.9 [199].
The BBS generator is based on the theory of quadratic residues. In English, there are two primes, p and q, that are congruent to 3 modulo 4. That’s the private key. Their product, pq = n, is the public key. (Mind your ps and qs; the security of this scheme rests in the difficulty of factoring n.)
To encrypt a message, M, first choose some random x, relatively prime to n. Then compute
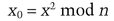
Use x0 as the seed of the BBS pseudo-random-bit generator and use the output of the generator as a stream cipher. XOR M, one bit at a time, with the output of the generator. The generator spits out bits bi (the least-significant bit of xi, where xi =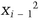 
mod n), so
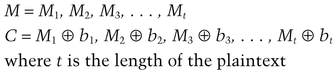
Append the last computed value, xt, to the end of the message and you’re done.
The only way to decrypt this message is to recover x0 and then set up the same BBS generator to XOR with the ciphertext. Because the BBS generator is secure to the left, the value xt is of no use to the cryptanalyst. Only someone who knows p and q can decrypt the message.
In C, the algorithm to recover x0 from xt is:
Once you have x0, decryption is easy. Just set up the BBS generator and XOR the output with the ciphertext.
You can make this scheme go even faster by using all the known secure bits of xi, not just the least significant bit. With this improvement, Blum-Goldwasser probabilistic encryption is faster than RSA while leaking no partial information about the plaintext. You can also prove that the difficulty of breaking this scheme is the same as the difficulty of factoring n.
On the other hand, this scheme is totally insecure against a chosen-ciphertext attack. From the least significant bits of the right quadratic residues, it is possible to calculate the square root of any quadratic residue. If you can do this, then you can factor. For details, consult [1570,1571,35,36].
Quantum cryptography taps the natural uncertainty of the quantum world. With it, you can create a communications channel where it is impossible to eavesdrop without disturbing the transmission. The laws of physics secure this quantum channel: even if the eavesdropper can do whatever he wants, even if the eavesdropper has unlimited computing power, even if P = NP. Charles Bennett, Gilles Brassard, Claude Crépeau, and others have expanded on this idea, describing quantum key distribution, quantum coin flipping, quantum bit commitment, quantum oblivious transfer, and quantum secure multiparty computation. Their work is described in [128,129,123,124,125,133,126,394,134,392,243,517,132,130,244,393,396]. The best overview of quantum cryptography can be found in [131]; [1651] is another good nontechnical overview. A complete bibliography of quantum cryptography is [237].
This would still be on the lunatic fringe of cryptography, but Bennett and Brassard actually went and built a working model of the thing [127,121,122]. Now we have experimental quantum cryptography.
So sit back, get yourself something to drink, and relax. I’m going to explain what this is all about.
According to quantum mechanics, particles don’t actually exist in any single place. They exist in several places at once, with probabilities of being in different places if someone looks. However, it isn’t until a scientist comes along and measures the particle that it “collapses” into a single location. But you can’t measure every aspect (for example, position and velocity) of a particle at the same time. If you measure one of those two quantities, the very act of measuring it destroys any possibility of measuring the other quantity. The quantum world has a fundamental uncertainty and there’s no way to avoid it.
That uncertainty can be used to generate a secret key. As they travel, photons vibrate in some direction; up and down, left to right, or more likely at some angle. Normal sunlight is unpolarized; the photons vibrate every which way. When a large group of photons vibrate in the same direction they are polarized. Polarization filters allow only photons that are polarized in a certain direction through; the rest are blocked. For example, a horizontal polarization filter only allows horizontally polarized photons through. Turn that filter 90 degrees, and only vertically polarized photons can come through.
Let’s say you have a pulse of horizontally polarized photons. If they try to pass through a horizontally polarized filter, they all get through. Slowly turn that filter 90 degrees; the number of photons getting through gets smaller and smaller, until none get through. This is counterintuitive. You’d think that turning the filter just a little will block all the photons, since the photons are horizontally polarized. But in quantum mechanics, each particle has a probability of suddenly switching its polarization to match the filter. If the angle is a little bit off, it has a high probability. If the angle is 90 degrees off. it has zero probability. And if the angle is 45 degrees off, it has a 50 percent probability of passing through the filter.
Polarization can be measured in any basis: two directions at right angles. An example basis is rectilinear: horizontal and vertical. Another is diagonal: left-diagonal and right-diagonal. If a photon pulse is polarized in a given basis and you measure it in the same basis, you learn the polarization. If you measure it in the wrong basis, you get a random result. We’re going to use this property to generate a secret key:
For example, Alice sends Bob:
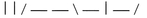
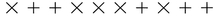
Now, when Bob sets his detector correctly, he will record the correct polarization. If he sets his detector to measure rectilinear polarization and the pulse is polarized rectilinearly, he will learn which way Alice polarized the photon. If he sets his detector to measure diagonal polarization and the pulse is polarized rectilinearly, he will get a random measurement. He won’t know the difference. In this example, he might get the result:
Using a prearranged code, Alice and Bob each translate those polarization measurements into bits. For example, horizontal and left-diagonal might equal one, and vertical and right-diagonal might equal zero. In our example, they both have:
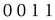
So, Alice and Bob have generated four bits. They can generate as many as they like using this system. On the average, Bob will guess the correct setting 50 percent of the time, so Alice has to send 2n photon pulses to generate n bits. They can use these bits as a secret key for a symmetric algorithm or they can guarantee perfect secrecy and generate enough bits for a one-time pad.
The really cool thing is that Eve cannot eavesdrop. Just like Bob, she has to guess which type of polarization to measure; and like Bob, half of her guesses will be wrong. Since wrong guesses change the polarization of the photons, she can’t help introducing errors in the pulses as she eavesdrops. If she does, Alice and Bob will end up with different bit strings. So, Alice and Bob finish the protocol like this:
Enhancements to this protocol allow Alice and Bob to use their bits even in the presence of Eve [133,134,192]. They could compare only the parity of subsets of the bits. Then, if no discrepancies are found, they only have to discard one bit of the subset. This detects eavesdropping with only a 50 percent probability, but if they do this with n different subsets Eve’s probability of eavesdropping without detection is only 1 in 2n.
There’s no such thing as passive eavesdropping in the quantum world. If Eve tries to recover all the bits, she will necessarily disrupt the communications.
Bennett and Brassard built a working model of quantum key distribution and have exchanged secure bits on a laser table. The latest I heard, some folks at British Telecom were sending bits over a 10-kilometer fiber-optic link [276,1245,1533]. They figure 50 kilometers is feasible. The mind boggles.