Algebraic Structures
B.1 Introduction
We define here algebraic structures that occur in almost all branches of mathematics. In particular, we will define a field that appears in the definition of a vector space. We begin with the definition of a group, which is a relatively simple algebraic structure with only one operation and is used as a building block for many other algebraic systems.
B.2 Groups
Let G be a nonempty set with a binary operation; that is, to each pair of elements a; b ∈ G there is assigned an element ab ∈ G. Then G is called a group if the following axioms hold:
[G1] For any a; b; c ∈ G, we have (ab) c = a (bc) (the associative law).
[G2] There exists an element e ∈ G, called the identity element, such that ae = ea = a for every a ∈ G.
[G3] For each a ∈ G there exists an element a– ∈ G called the inverse of a, such that aa–1 = a–1a = e.
A group G is said to be abelian (or: commutative) if the commutative law holds—that is, if ab = ba for every a; b ∈ G.
When the binary operation is denoted by juxtaposition as above, the group G is said to be written multiplicatively. Sometimes, when G is abelian, the binary operation is denoted by + and G is said to be written additively. In such a case, the identity element is denoted by 0 and is called the zero element; the inverse is denoted by –a and it is called the negative of a.
If A and B are subsets of a group G, then we write
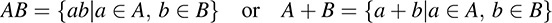
We also write a for {a}.
A subset H of a group G is called a subgroup of G if H forms a group under the operation of G. If H is a subgroup of G and a ∈ G, then the set Ha is called a right coset of H and the set aH is called a left coset of H.
DEFINITION: A subgroup H of G is called a normal subgroup if a– 1Ha ⊆ H for every a ∈ G. Equivalently, H is normal if aH = Ha for every a ∈ G—that is, if the right and left cosets of H coincide.
Note that every subgroup of an abelian group is normal.
THEOREM B.1: Let H be a normal subgroup of G. Then the cosets of H in G form a group under coset multiplication. This group is called the quotient group and is denoted by G/H.
EXAMPLE B.1 The set Z of integers forms an abelian group under addition. (We remark that the even integers form a subgroup of Z but the odd integers do not.) Let H denote the set of multiples of 5; that is, H = {… ; 10; 5; 0; 5; 10; …}. Then H is a subgroup (necessarily normal) of Z. The cosets of H in Z follow:
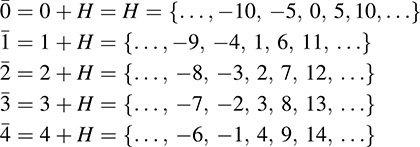
For any other integer n ∊ 
coincides with one of the above cosets. Thus, by the above theorem, 
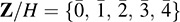forms a group under coset addition; its addition table follows:
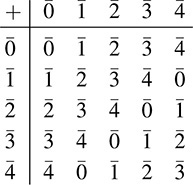
This quotient group Z/H is referred to as the integers modulo 5 and is frequently denoted by Z5. Analogeusly, for any positive integer n, there exists the quotient group Zn called the integers modulo n.
EXAMPLE B.2 The permutations of n symbols (see page 269) form a group under composition of mappings; it is called the symmetric group of degree n and is denoted by Sn. We investigate S3 here; its elements are
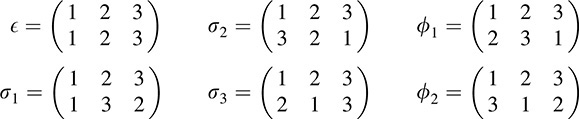
Here 
is the permutation that maps 1 ↣ i; ∈ ↣ j; 3 ↣ k. The multiplication table of S3 is
(The element in the ath row and bth column is ab.) The set H = {Ψ; s1} is a subgroup of S3, its right and left cosets are Right Cosets are
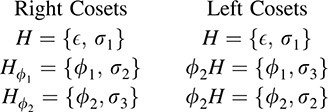
Observe that the right cosets and the left cosets are distinct; hence, H is not a normal subgroup of S3.
A mapping f from a group G into a group G′ is called a homomorphism if f(ab) = f(a)f(b). For every a, b ∈ G. (If f is also bijective, i.e., one-to-one and onto, then f is called an isomorphism and G and G′ are said to be isomorphic.) If f : G → G′ is a homomorphism, then the kernel of f is the set of elements of G that map into the identity element e′ ∈ G′: kernel of f = a ∈ G j f a ( ) = e′
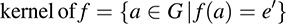
(As usual, f(G) is called the image of the mapping f : G → G′.) The following theorem applies.
THEOREM B.2: Let f: G → G be a homomorphism with kernel K. Then K is a normal subgroup of G, and the quotient group G/K is isomorphic to the image of f.
EXAMPLE B.3 Let G be the group of real numbers under addition, and let G′ be the group of positive real numbers under multiplication. The mapping f : G → G′ defined by f(a) = 2a is a homomorphism because
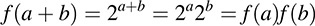
In particular, f is bijective, hence, G and G′ are isomorphic.
EXAMPLE B.4 Let G be the group of nonzero complex numbers under multiplication, and let G′ be the group of nonzero real numbers under multiplication. The mapping f : G → G′ defined by f(a) = 2a is a homomorphism because
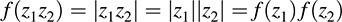
The kernel K of f consists of those complex numbers z on the unit circle—that is, for which |z| = 1. Thus, G/K is isomorphic to the image of f—that is, to the group of positive real numbers under multiplication.
B.3 Rings, Integral Domains, and Fields
Let R be a nonempty set with two binary operations, an operation of addition (denoted by +) and an operation of multiplication (denoted by juxtaposition). Then R is called a ring if the following axioms are satisfied:
[R1] For any a; b; c ∈ R, we have (a + b) + c = a + (b + c).
[R2] There exists an element 0 ∈ R; called the zero element, such that a + 0 = 0 + a = a for every a ∈ R.
[R4] For each a ∈ R there exists an element –a ∈ R, called the negative of a, such that a + (–a) = (–a) + a = 0.
[R5] For any a, b ∈ R, we have a + b = b + a.
[R5] For any a, b, c ∈ R we have (ab)c = a(bc).
[R6] For any a, b, c ∈ R; we have
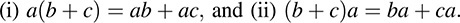
Observe that the axioms [R1] through [R4] may be summarized by saying that R is an abelian group under addition.
Subtraction is defined in R by a – b = a + (-b).
It can be shown (see Problem B.25) that a 0 = 0 a = 0 for every a ∈ R:
R is called a commutative ring if ab = ba for every a, b ∈ R: We also say that R is a ring with a unit element if there exists a nonzero element 1 ∈ R such that a · 1 = 1 a = a for every a ∈ R:
A nonempty subset S of R is called a subring of R if S forms a ring under the operations of R. We note that S is a subring of R if and only if a, b ∈ S implies a – b ∈ S and ab ∈ S.
A nonempty subset I of R is called a left ideal in R if (i) a – b ∈ I whenever a, b ∈ I; and (ii) ra ∈ I whenever r ∈ R; a ∈ I: Note that a left ideal I in R is also a subring of R. Similarly, we can define a right ideal and a two-sided ideal. Clearly all ideals in commutative rings are two sided. The term ideal shall mean two-sided ideal uniess otherwise specified.
THEOREM B.3: Let I be a (two-sided) ideal in a ring R. Then the cosets {a + I | a ∈ R } form a ring under coset addition and coset multiplication. This ring is denoted by R/I and is called the quotient ring.
Now let R be a commutative ring with a unit element. For any a ∈ R, the set (a) = {ra | r ∈ R} is an ideal; it is called the principal ideal generated by a. If every ideal in R is a principal ideal, then R is called a principal ideal ring.
DEFINITION: A commutative ring R with a unit element is called an integral domain if R has no zero divisors—that is, if ab = 0 implies a = 0 or b = 0.
DEFINITION: A commutative ring R with a unit element is called a field if every nonzero a ∈ R has a multiplicative inverse; that is, there exists an element a– ∈ R such that aa–1 = a–1 a = 1.
A field is necessarily an integral domain; for if ab = 0 and a ≦ 0; then
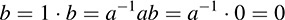
We remark that a field may also be viewed as a commutative ring in which the nonzero elements form a group under multiplication.
EXAMPLE B.5 The set Z of integers with the usual operations of addition and multiplication is the classical example of an integral domain with a unit element. Every ideal I in Z is a principal ideal; that is, I = (n) for some integer n. The quotient ring Zn = Zn is called the ring of integers module n. If n is prime, then Zn is a field. On the other hand, if n is not prime then Zn has zero divisors. For example, in the ring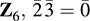 
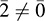and 
and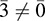 
.
EXAMPLE B.6 The rational numbers Q and the real numbers R each form a field with respect to the usual operations of addition and multiplication.
EXAMPLE B.7 Let C denote the set of ordered pairs of real numbers with addition and multiplication defined by
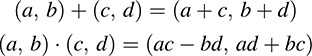
Then C satisfies all the required properties of a field. In fact, C is just the field of complex numbers (see page 4).
EXAMPLE B.8 The set M of all 2 × 2 matrices with real entries forms a noncommutative ring with zero divisors under the operations of matrix addition and matrix multiplication.
EXAMPLE B.9 Let R be any ring. Then the set R[x] of all polynomials over R forms a ring with respect to the usual operations of addition and multiplication of polynomials. Moreover, if R is an integral domain then R[x] is also an integral domain.
Now let D be an integral domain. We say that b divides a in D if a = bc for some c ∈ D. An element u ∈ D is called a unit if u divides 1—that is, if u has a multiplicative inverse. An element b ∈ D is called an associate of a ∈ D if b = ua for some unit u ∈ D. A nonunit p ∈ D is said to be irreducible if p = ab implies a or b is a unit.
An integral domain D is called a unique factorization domain if every nonunit a ∈ D can be written uniquely (up to associates and order) as a product of irreducible elements.
EXAMPLE B.10 The ring Z of integers is the classical example of a unique factorization domain. The units of Z are 1 and –1. The only associates of n ∈ Z are n and –n. The irreducible elements of Z are the prime numbers.
EXAMPLE B.11 The set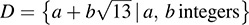 
is an integral domain. The units of D are ±1; 
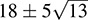and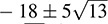 
. The elements 
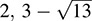and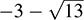 
are irreducible in D. Observe that 
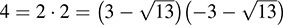Thus, D is not a unique factorization domain. (See Problem B.40.)
B.4 Modules
Let M be an additive abelian group and let R be a ring with a unit element. Then M is said to be a (left) R-module if there exists a mapping R → M → M that satisfies the following axioms:
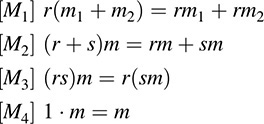
for any r, s ∈ R and any mi ∈ M.
We emphasize that an R-module is a generalization of a vector space where we allow the scalars to come from a ring rather than a field.
EXAMPLE B.12 Let G be any additive abelian group. We make G into a module over the ring Z of integers by defining
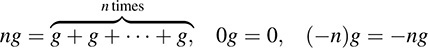
where n is any positive integer.
EXAMPLE B.13 Let R be a ring and let I be an ideal in R. Then I may be viewed as a module over R.
EXAMPLE B.14 Let V be a vector space over a field K and let T : V → V be a linear mapping. We make V into a module over the ring K[x] of polynomials over K by defining f(x) = f(T) ( v): The reader should check that a scalar multiplication has been defined.
Let M be a module over R. An additive subgroup N of M is called a submodule of M if u ∈ N and k ∈ R imply ku ∈ N: (Note that N is then a module over R.)
Let M and M′ be R-modules. A mapping T : M → M′ is called a homomorphism (or: R-homomorphism or R-linear) if
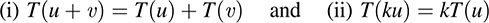
for every u; ν ∈ M and every k ∈ R.
PROBLEMS
Groups
B.1. Determine whether each of the following systems forms a group G:
(i) G = set of integers; operation subtraction;
(ii) G = {1, –1}, operation multiplication;
(iii) G = set of nonzero rational numbers, operation division;
(iv) G = set of nonsingular n × n matrices, operation matrix multiplication;
(v) G = {a + bi : a, b ∈ Z}, operation addition.
B.2. Show that in a group G:
(i) the identity element of G is unique;
(ii) each a ∈ G has a unique inverse a–1 ∈ G;
(iii) (a–)– = 11a; and (ab)– b– 1a–1;
(iv) ab = ac implies b = c, and ba = ca implies b = c.
B.3. In a group G, the powers of a ∈ G are defined by
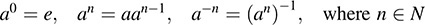
Show that the following formulas hold for any integers r, s, t ∈ Z: (i) aras = ar+s , (ii) (ar)s = ars
B.4. Show that if G is an abelian group, then (ab)n= anbn for any a, b ∈ G and any integer n ∈ Z:
B.5. Suppose G is a group such that (ab)2 = a2b2 for every a, b ∈ G. Show that G is abelian.
B.6. Suppose H is a subset of a group G. Show that H is a subgroup of G if and only if (i) H is nonempty, and (ii) a, b ∈ H implies ab–1 ∈ H.
B.7. Prove that the intersection of any number of subgroups of G is also a subgroup of G.
B.8. Show that the set of all powers of a ∈ G is a subgroup of G; it is called the cyclic group generated by a.
B.9. A group G is said to be cyclic if G is generated by some a ∈ G; that is, G = an : n ∈ (Z). Show that every subgroup of a cyclic group is cyclic.
B.10. Suppose G is a cyclic subgroup. Show that G is isomorphic to the set Z of integers under addition or to the set Zn (of the integers module n) under addition.
B.11. Let H be a subgroup of G. Show that the right (left) cosets of H partition G into mutually disjoint subsets.
B.12. The order of a group G, denoted by |G|; is the number of elements of G. Prove Lagrange’s theorem: If H is a subgroup of a finite group G, then |H| divides |G|.
B.13. Suppose |G| = p where p is prime. Show that G is cyclic.
B.14. Suppose H and N are subgroups of G with N normal. Show that (i) HN is a subgroup of G and (ii) H ∩ N is a normal subgroup of G.
B.15. Let H be a subgroup of G with only two right (left) cosets. Show that H is a normal subgroup of G.
B.16. Prove Theorem B.1: Let H be a normal subgroup of G. Then the cosets of H in G form a group G/H under coset multiplication.
B.17. Suppose G is an abelian group. Show that any factor group G/H is also abelian.
B.18. Let f : G → G′ be a group homomorphism. Show that
(i) f(e) = e0 where e′ and e′ are the identity elements of G and G′, respectively;
(ii) f(a-1) = f(a)- for any a ∈ G.
B.19. Prove Theorem B.2: Let f : G → G′ be a group homomorphism with kernel K. Then K is a normal subgroup of G, and the quotient group G/K is isomorphic to the image of f.
B.20. Let G be the multiplicative group of complex numbers z such that |z| = 1; and let R be the additive group of real numbers. Prove that G is isomorphic to R/Z:
B.21. For a fixed g ∈ G, let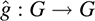 
be defined by 
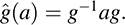. Show that G is an isomorphism of G onto G.
B.22. Let G be the multiplicative group of n × n nonsingular matrices over R. Show that the mapping A ↣ |A| is a homomorphism of G into the multiplicative group of nonzero real numbers.
B.23. Let G be an abelian group. For a fixed n ∈ Z, show that the map a ↣ an is a homomorphism of G into G.
B.24. Suppose H and N are subgroups of G with N normal. Prove that H ∩ N is normal in H and H/ (H ∩ N) is isomorphic to HN/N.
Rings
B.25. Show that in a ring R:
(i) a · 0 = 0 a = 0; (ii) a(–b) = (–a) = (–a)b, (iii) (–a)(–b) = ab
B.26. Show that in a ring R with a unit element: (i) (–1)a = a, (ii) (–1) (–1) = 1.
B.27. Let R be a ring. Suppose a2 = a for every a ∈ R: Prove that R is a commutative ring. (Such a ring is called a Boolean ring.)
B.28. Let R be a ring with a unit element. We make R into another ring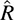 
by defining a ⊕ b = a + b + 1 and a · b = ab + a + b. (i) Verify that 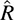is a ring. (ii) Determine the 0-element and 1-element of .
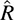B.29. Let G be any (additive) abelian group. Define a multiplication in G by a · b = 0. Show that this makes G into a ring.
B.30. Prove Theorem B.3: Let I be a (two-sided) ideal in a ring R. Then the cosets (a + I | a ∈ R) form a ring under coset addition and coset multiplication.
B.31. Let I1 and I2 be ideals in R. Prove that I1 + I2 and I1 ∩ I2 are also ideals in R.
B.32. Let R and R′ be rings. A mapping f : R → R′ is called a homomorphism (or: ring homomorphism) if
(i) f(a + b) = f(a) + f(b) and (ii) f(ab) = f(a) = f(a) f(b),
for every a, b ∈ R. Prove that if f : R → R′ is a homomorphism, then the set K = {r ∈ R | f (r) = 0} is an ideal in R. (The set K is called the kernel of f.)
Integral Domains and Fields
B.33. Prove that in an integral domain D, if ab = ac; a ≠ 0, then b = c.
B.34. Prove that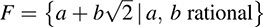 
is a field.
B.35. Prove that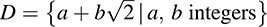 
is an integral domain but not a field.
B.36. Prove that a finite integral domain D is a field.
B.37. Show that the only ideals in a field K are {0} and K.
B.38. A complex number a + bi where a, b are integers is called a Gaussian integer. Show that the set G of Gaussian integers is an integral domain. Also show that the units in G are ±1 and ±i.
B.39. Let D be an integral domain and let I be an ideal in D. Prove that the factor ring D/I is an integral domain if and only if I is a prime ideal. (An ideal I is prime if ab ∈ I implies a ∈ I or b ∈ I.)
B.40. Consider the integral domain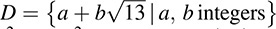 
(see Example B.11). If 
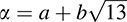we define N(α) = a2 – 13b2. Prove: (ii) N(αβ) = N(α)N(β); (ii) α is a unit if and only if N(α) = ±1; (iii) the units of D are 
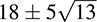and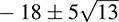 
; (iv) the numbers 
and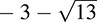 
are irreducible.
Modules
B.41. Let M be an R-module and let A and B be submodules of M. Show that A + B and A ∩ B are also submodules of M.
B.42. Let M be an R-module with submodule N. Show that the cosets {u + N : u ∈ M } form an R-module under coset addition and scalar multiplication defined by r(u + N) = ru + N. (This module is denoted by M/N and is called the quotient module.)
B.43. Let M and M′ be R-modules and let f : M→ M′ be an R-homomorphism. Show that the set K = {u ∈ M : f(u) = 0} is a submodule of f. (The set K is called the kernel of f.)
B.44. Let M be an R-module and let E(M) denote the set of all R-homomorphism of M into itself. Define the appropriate operations of addition and multiplication in E(M) so that E(M) becomes a ring.