Polynomials over a Field

C.1 Introduction

We will investigate polynomials over a field K and show that they have many properties that are analogous to properties of the integers. These results play an important role in obtaining canonical forms for a linear operator T on a vector space V over K.

C.2 Ring of Polynomials

Let K be a field. Formally, a polynomial of f over K is an infinite sequence of elements from K in which all except a finite number of them are 0:

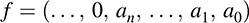
(We write the sequence so that it extends to the left instead of to the right.) The entry a_k is called the kth coefficient of f. If n is the largest integer for which a_n ≠ 0, then we say that the degree of f is n, written

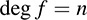
We also call a_n the leading coefficient of f, and if a_n = 1 we call f a monic polynomial. On the other hand, if every coefficient of f is 0 then f is called the zero polynomial, written f = 0. The degree of the zero polynomial is not defined.

Now if g is another polynomial over K, say

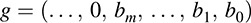
then the sum f + g is the polynomial obtained by adding corresponding coefficients. That is, if m ≥ n, then

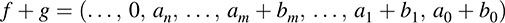
Furthermore, the product fg is the polynomial

that is, the kth coefficient c_k of fg is

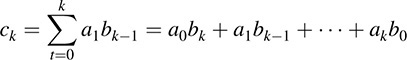
The following theorem applies.

THEOREM C.1:  The set P of polynomials over a field K under the above operations of addition and multiplication forms a commutative ring with a unit element and with no zero divisors—an integral domain. If f and g are nonzero polynomials in P, then deg (fg) = (deg f) (deg g).

Notation

We identify the scalar a₀ ∈ K with the polynomial

We also choose a symbol, say t, to denote the polynomial

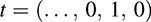
We call the symbol t an indeterminant. Multiplying t with itself, we obtain

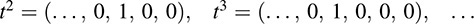
Thus, the above polynomial f can be written uniquely in the usual form

When the symbol t is selected as the indeterminant, the ring of polynomials over K is denoted by

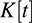
and a polynomial f is frequently denoted by f(t).

We also view the field K as a subset of K[t] under the above identification. This is possible because the operations of addition and multiplication of elements of K are preserved under this identification:

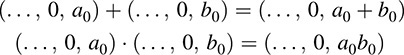
We remark that the nonzero elements of K are the units of the ring K[t].

We also remark that every nonzero polynomial is an associate of a unique monic polynomial. Hence, if d and d^′ are monic polynomials for which d divides d^′ and d^′ divides d, then d = d^′. (A polynomial g divides a polynomial f if there is a polynomial h such that f = hg:)

C.3 Divisibility

The following theorem formalizes the process known as “long division.”

THEOREM C.2  (Division Algorithm): Let f and g be polynomials over a field K with g ≠ 0. Then there exist polynomials q and r such that

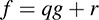
where either r = 0 or deg r < deg g.

Proof: If f = 0 or if deg f < deg g, then we have the required representation

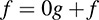
Now suppose deg f ≥ deg g, say

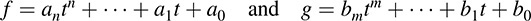
where a_n, b_m ≠ 0 and n ≠ m. We form the polynomial

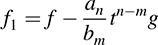
Then deg f₁ < deg f. By induction, there exist polynomials q₁ and r such that

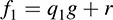
where either r = 0 or deg r < deg g. Substituting this into (1) and solving for f,

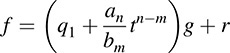
which is the desired representation.

THEOREM C.3:  The ring K[t] of polynomials over a field K is a principal ideal ring. If I is an ideal in K[t], then there exists a unique monic polynomial d that generates I, such that d divides every polynomial f ∈ I.

Proof. Let d be a polynomial of lowest degree in I. Because we can multiply d by a nonzero scalar and still remain in I, we can assume without loss in generality that d is a monic polynomial. Now suppose f ∈ I a_n b_m. By Theorem C.2 there exist polynomials q and r such that

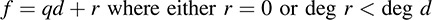
Now f, d ∈ I implies qd ∈ I; and hence, r = f qd ∈ I. But d is a polynomial of lowest degree in I. Accordingly, r = 0 and f = qd; that is, d divides f. It remains to show that d is unique. If d^′ is another monic polynomial that generates I, then d divides d^′ and d^′ divides d. This implies that d = d^′, because d and d^′ are monic. Thus, the theorem is proved.

THEOREM C.4:  Let f and g be nonzero polynomials in K[t]. Then there exists a unique monic polynomial d such that (i) d divides f and g; and (ii) d^′ divides f and g, then d^′ divides d.

DEFINITION: The above polynomial d is called the greatest common divisor of f and g. If d = 1, then f and g are said to be relatively prime.

Proof of Theorem C.4. The set I = {mf + ng | m, n ∈ K [t]} is an ideal. Let d be the monic polynomial that generates I. Note f, g ∈ I; hence, d divides f and g. Now suppose d^′ divides f and g. Let J be the ideal generated by d^′. Then f, g ∈ J, and hence, I ⊂ J. Accordingly, d ∈ J and so d^′ divides d as claimed. It remains to show that d is unique. If d₁ is another (monic) greatest common divisor of f and g, then d divides d₁ and d₁ divides d. This implies that d = d₁ because d and d₁ are monic. Thus, the theorem is proved.

COROLLARY C.5:  Let d be the greatest common divisor of the polynomials f and g. Then there exist polynomials m and n such that d = mf + ng. In particular, if f and g are relatively prime, then there exist polynomials m and n such that mf + ng = 1.

The corollary follows directly from the fact that d generates the ideal

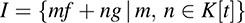
C.4 Factorization

A polynomial p ∈ K[t] of positive degree is said to be irreducible if p = fg implies f or g is a scalar.

LEMMA C.6:    Suppose p ∈ K[t] is irreducible. If p divides the product fg of polynomials f, g ∈ K[t], then p divides f or p divides g. More generally, if p divides the product of n polynomials f₁ f₂ … f_n, then p divides one of them.

Proof. Suppose p divides fg but not f. Because p is irreducible, the polynomials f and p must then be relatively prime. Thus, there exist polynomials m, n ∈ K[t such that mf + np = 1. Multiplying this equation by g, we obtain mfg + npg = g. But p divides fg and so mfg, and p divides npg; hence, p divides the sum g = mfg + npg.

Now suppose p divides f₁ f₂ f_n: If p divides f₁, then we are through. If not, then by the above result p divides the product f₂ f_n: By induction on n, p divides one of the polynomials f₂, … f_n: Thus, the lemma is proved.

THEOREM C.7:  (Unique Factorization Theorem) Let f be a nonzero polynomial in K[t] : Then f can be written uniquely (except for order) as a product

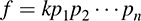
where k ∈ K and the p_i are monic irreducible polynomials in K[t].

Proof: We prove the existence of such a product first. If f is irreducible or if f ∈ K, then such a product clearly exists. On the other hand, suppose f = gh where f and g are nonscalars. Then g and h have degrees less than that of f. By induction, we can assume

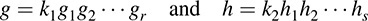
where k₁, k₂ ∈ K and the g_i and h_j are monic irreducible polynomials. Accordingly,

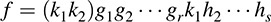
is our desired representation.

We next prove uniqueness (except for order) of such a product for f. Suppose

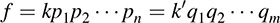
where k, k^′ ∈ K and the p₁, … , p_n, q_1; … ; q_m are monic irreducible polynomials. Now p₁ divides k^′q₁ … q_m: Because p₁ is irreducible, it must divide one of the q_i by the above lemma. Say p₁ divides q₁. Because p₁ and q₁ are both irreducible and monic, p₁ = q₁. Accordingly,

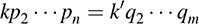
By induction, we have that n = m and p₂ = q₂, … ; p_n = q_m for some rearrangement of the q_i. We also have that k = k^′. Thus, the theorem is proved.

If the field K is the complex field C, then we have the following result that is known as the fundamental theorem of algebra; its proof lies beyond the scope of this text.

THEOREM C.8:  (Fundamental Theorem of Algebra) Let f(t) be a nonzero polynomial over the complex field C. Then f(t) can be written uniquely (except for order) as a product

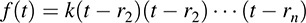
where k, r_i ∈ C—as a product of linear polynomials.

In the case of the real field R we have the following result.

THEOREM C.9:  Let f(t) be a nonzero polynomial over the real field R. Then f(t) can be written uniquely (except for order) as a product

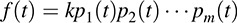
where k ∈ R and the p_i(t) are monic irreducible polynomials of degree one or two