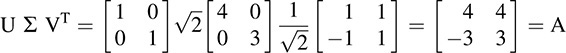Odds and Ends

D.1 Introduction

This appendix discusses various topics, such as equivalence relations and singular value decomposition.

D.2 Relations and Equivalence Relations

A binary relation or simply relation R from a set A to a set B assigns to each ordered pair (a, b) ∈ A × B exactly one of the following statements:

(i) “a is related to b,” written a R b, (ii) “a is not related to b” written a R = b.

A relation from a set A to the same set A is called a relation on A.

Observe that any relation R from A to B uniquely defines a subset 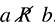of A × B as follows:

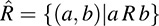
Conversely, any subset 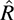of A × B defines a relation from A to B as follows:

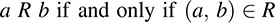
In view of the above correspondence between relations from A to B and subsets of A × B, we redefine a relation from A to B as follows:

DEFINITION D.1:   A relation R from A to B is a subset of A × B.

Equivalence Relations

Consider a nonempty set S. A relation R on S is called an equivalence relation if R is reflexive, symmetric, and transitive; that is, if R satisfied the following three axioms:

[E₁] (Reflexivity) Every a ∈ A is related to itself. That is, for every a ∈ A, a R a.

[E₂] (Symmetry) If a is related to b, then b is related to a. That is,

if a R b, then b R a.

[E₃] (Transitivity) If a is related to b and b is related to c, then a is related to c. That is, if a R b and b R c, then a R c:

The general idea behind an equivalence relation is that it is a classification of objects that are in some way “alike.” Clearly, the relation of equality is an equivalence relation. For this reason, one frequently uses or to denote an equivalence relation.

EXAMPLE D.1

(a) In Euclidean geometry, similarity of triangles is an equivalence relation. Specifically, suppose α, β, γ are triangles. Then (i) α is similar to itself. (ii). If α is similar to β, then β is similar to α. (iii) If α is similar to β and β is similar to γ, then α is similar to γ.

(b) The relation ⊆ of set inclusion is not an equivalence relation. It is reflexive and transitive, but it is not symmetric because A ⊆ B does not imply B ⊆ A.

Equivalence Relations and Partitions

Let S be a nonempty set. Recall first that a partition P of S is a subdivision of S into nonempty, nonoverlapping subsets; that is, a collection P = {A_j} of nonempty subsets of S such that (i) Each a ∈ S belong to one of the A_j, (ii) The sets {A_j} are mutually disjoint.

The subsets in a partition P are called cells. Thus, each a ∈ S belongs to exactly one of the cells. Also, any element b ∈ A_j is called a representative of the cell A_j, and a subset B of S is called a system of representatives if B contains exactly one element in each of the cells in {A_j}.

Now suppose R is an equivalence relation on the nonempty set S. For each a ∈ S, the equivalence class of a, denoted by [a], is the set of elements of S to which a is related:

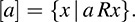
The collection of equivalence classes, denoted by S/R, is called the quotient of S by R:

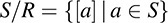
The fundamental property of an equivalence relation and its quotient set is contained in the following theorem:

THEOREM D.1:   Let R be an equivalence relation on a nonempty set S. Then the quotient set S/R is a partition of S.

EXAMPLE D.2 Let be ≢ the relation on the set Z of integers defined by x ≡ y (mod 5) which reads “x is congruent to y modulus 5” and which means that the difference x – y is divisible by 5. Then ≡ is an equivalence relation on Z.

Then there are exactly five equivalence classes in the quotient set Z/ ≡ as follows:

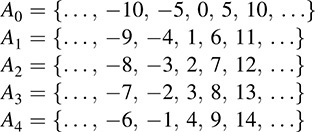
Note that any integer x, which can be expressed uniquely in the form x = 5q + r where 0 ≥ r < 5, is a member of the equivalence class A_r where r is the remainder. As expected, the equivalence classes are disjoint and their union is Z:

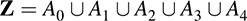
This quotient set Z/ ≡, called the integers modulo 5, is denoted

Z/5Z or simply Z₅:

Usually one chooses {0, 1, 2, 3, 4 } or {–2, –1, 0, 1, 2} as a system of representatives of the equivalence classes.

Analagously, for any positive integer m, there exists the congruence relation defined by

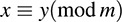
and the quotient set Z/ ≡, denoted by Z/mZ or simply Z_m, is called the integers modulo m.

D.3 Properties of AA^T and A^TA

Let A be any m × n matrix. Then A^TA and AA^T are both symmetric since

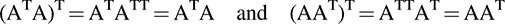
One can also show that A^TA and AA^T have the same nonzero eigenvalues.

Recall [Theorem 9.14] that a symmetric matrix M is orthogonally diagonalizable, that is, there exists an orthogonal matrix P and diagonal matrix D = [d_i] such that

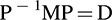
where the columns of P are the eigenvectors of M and the d_i are the eigenvalues of M.

In particular, the symmetric matrix M is called:

(i) positive definite if, for every nonzero u, <u, Mu> = u^TMu>0

(ii) positive semidefinite if, for every nonzero u, <u, Mu> = u^TMu 0]

In such a case, the diagonal elements in P^–1MP = D are: (i) positive, (ii) nonnegative.

A^TA is positive definite if A has full column rank since Au ≠ 0 when u ≠ 0; so

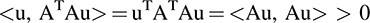
Similarly, AA^T is positive definite if A has full row rank. since A^Tu ≠ 0 when u ≠ 0; so

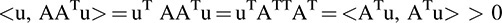
On the other hand, A^TA and AA^T are always both positive semidefinite.

D.4 Singular Value Decomposition

Let A be any m × n matrix of rank r. Then there exists a factorization of A of the form

A = U Σ V^T

where U is an m-square orthogonal matrix, V is an n-square orthogonal matrix, and Σ = [σ_ij] is an m × n generalized diagonal matrix, that is, σ_ij = 0 for i σ j. Such a factorization is called a singular value decomposition (SVD) of A, and the diagonal entries σ_i = σ_ii of Σ, usually listed in descending order, are called the singular values of A.

THEOREM D.2: Every matrix A with rank r>0 has a singular value decomposition.

We indicate how the entries U, V and Σ in the SVD of A are obtained.

Recall AA^T is symmetric and positive definite (or positive semidefinite). Accordingly, AA^T is orthogonally diagonalizable, that is, AA^T = P ⁷ 1DP = P^TDP where the columns of the orthogonal matrix P are eigenvectors of AA^T, and the entries of D are the eigenvalues of AA^T and they are nonnegative.

Assuming A = U Σ V^T, we have

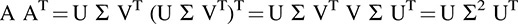
Thus the columns of U in the SVD of A are the normalized eigenvectors of AA^T and the entries σ_i in Σ are the square roots of the eigenvalues of A^TA.

Similarly, assuming A = U Σ V^T, we have

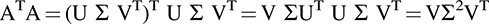
Thus the columns of V and the rows of V^T are the normalized eigenvectors of A^TA and the entries s_i in S are the square roots of the eigenvalues of AA^T (which are the same as the eigenvalues of A^TA).

EXAMPLE D.3. We find the singular value decomposition (SVD) of 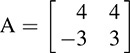. Note

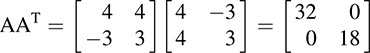
The eigenvalues are 32 and 18 with corresponding eigenvectors [1, 0]^T and [0,1]^T. Thus

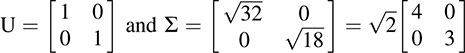
Also

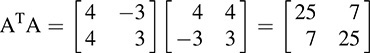
Hence Δ(t) = t² – 50t + 576 = (t – 32)(t – 18). Thus, again, the eigenvalues are 32 and 18.

The normalized corresponding eigenvectors are 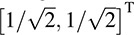and 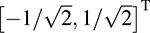. Thus

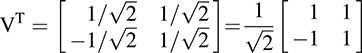
As expected,