4 / IV The decline and fall of the Roman numerals, II: Safety in numbers
Consider the following three fictional but familiar examples of decision-making processes:
- So many golfers are using Whackalot clubs these days. They must know something I don’t about the quality of those clubs. Anything that is so popular must be better than less popular alternatives, so I think I’ll pick myself some up Whackalots.
- Everyone is wearing zipper-pocket jeans this year. They are so cool! Why, just the other week, I saw ten people wearing them in my linguistics class. I want to fit in with the crowd and be cool, so I’m going to pick up some zipper-pocket jeans.
- Huge numbers of people use Headshot as a social networking website. If I use some other website instead, I won’t be able to chat with all my friends. Therefore, I’d better give in and start using Headshot.
In each of these cases, a decision-making process to adopt something is initiated or accelerated by the information that this thing is commonly used. The reasoning underlying each decision, however, differs considerably. In this chapter, I will analyze why a single characteristic—frequency of use—and a single outcome—the adoption of a novelty—should interact in these three radically different ways, and apply this to the particular case of the Roman numerals in late medieval and early modern Europe. As we saw in the previous chapter, explanations that are based on abstract consideration of the structure of the Roman versus the Western numerals aren’t sufficient to explain why people chose to abandon one system and prefer a new one. Decisions are cognitively motivated, but not in ways that can be predicted simply. Here we’ll look at what the actual process of the replacement of the Roman numerals looked like, not particularly at the individual scale (because, as previously noted, few people at the time explicitly compared the two systems or talked about their reasoning), but at an aggregate, social level, across the centuries when the transition was most rapid and evident. I will argue that it was the commonality and ubiquity of the Roman numerals that insulated them against replacement or even any real competition in Western Europe—right up until a set of interrelated disruptions around 1500 made their replacement inevitable.
Three kinds of frequency dependence
Frequency-dependent bias is the term coined by the evolutionary anthropologists Peter Richerson and Robert Boyd to describe cultural transmission in which the frequency of a cultural trait in some population of individuals influences the probability that additional individuals will adopt it (Richerson and Boyd 2005: 120–123). In other words, “a naïve individual uses the frequency of a variant among his models to evaluate the merit of the variant” (Boyd and Richerson 1985: 206). Conformity (a greater-than-expected propensity to conform to the majority) is one form of frequency dependence, but it is not the only form—the conscious choice not to conform is equally frequency-dependent. In frequency-dependent situations, the characteristics of the trait being replicated are potentially irrelevant to its transmission.
Another form of bias that is relevant here is prestige bias. While a frequency-dependent bias works on the basis of the popularity of some phenomenon, prestige biases work on the basis of their adoption by important, prestigious, or notable individuals in some context. When some important person—whether the King of France or the latest YouTube “content creator” sensation—adopts a phenomenon, it’s not the number of people who are using something but their importance that matters. Both frequency-dependent and prestige biases are thus kinds of indirect bias, as opposed to direct biases, in which the usefulness of the trait for some function(s) is the characteristic being evaluated. If Roman numerals and Western numerals were being directly compared with one another, we might expect a lot of metanotational comparison—people looking at the two systems and giving explicit comparisons. Because that sort of comparison is rare, we should suspect that indirect biases are at play.
Frequency-dependent and prestige biases are two of several important ways in which cultural transmission differs from biological transmission. Biological transmission of genetic material proceeds, metaphorically speaking, in a vertical fashion, from ancestors to descendants. In contrast, cultural transmission is both vertical and horizontal—we acquire culture, including (usually) our first language, from parents, but many other aspects of our lives are shaped through our interactions with non-kin, including particularly those of a similar age—our friends, allies, and even our rivals—and through media. When we choose, as youths or adults, to adopt or reject some new innovation, we are mostly talking about horizontal transmission. Western numerals were transmitted through arithmetic texts, in mercantile practice, and through everyday use in inscriptions, books, and manuscripts, and thus fit this model well.
Boyd and Richerson are writing from a perspective in which the adoption and transmission of culturally derived traits motivates long-term and large-scale cultural change. They are not, however, chiefly concerned with individual motivation. Yet, once we take motivation into account—in other words, by adopting specifically cognitive perspectives—it becomes clear that frequency dependence is not a unitary phenomenon. The three examples above illustrate the variety of decision-making processes underlying frequency-dependent outcomes.
In Case A, it may or may not be the case that Whackalot clubs are superior to other golf clubs. The perception that they have a positive utility for playing golf (longer drives, reduced hooks and slices, etc.) is based on the presumption that, if many people are using them, those people must have perceived something beneficial about them. Adopting these clubs is not merely a trend or fad, but reflects an assumption about how others are believed to make decisions about which golf club to adopt. Frequency in this case indexes perceived utility. This is related to the phenomenon identified by James Surowiecki as the “wisdom of crowds,” where, in a wide sample of a population, an average of individual choices is likely to approximate the best possible answer (Surowiecki 2004). But it draws on a tradition in the psychology of individual and group behavior that is much older—Charles Mackay’s 1841 study Extraordinary Popular Delusions and the Madness of Crowds showed that numerous hoaxes, follies, economic bubbles, and other trends were based on the same sort of reasoning (Mackay 1963). Surowiecki’s point, though, is that in many cases crowd wisdom is correct. Many contemporary systems on the internet, such as upvoting / downvoting on social media or search engine algorithms, depend on the frequency with which previous users have selected some alternative to determine what to show new users. The advantage of this process is that it provides some information to users about what they might prefer; the downside is that such algorithms sediment biases and prejudiced notions about preferences, making them seem neutral (O’Neil 2016; Seaver 2018). Regardless of their positive or negative effects, let’s call such cases where adopters assume that a frequent variant is useful by the name crowd wisdom.
Case B is similar, but adopters of such features as zipper-pocket jeans, or bell-bottoms, or Capri-length pants, may be fully aware that these items may not be better than what came before them in any absolute sense. They are a trend or a fad, but are nonetheless useful—their utility lies in conforming with that trend in order to acquire social status. Here, frequency measures an item’s stylishness. It is socially useful to adopt it: one may hope to achieve wider popularity in doing so. It may even increase one’s reproductive success. Nevertheless, there are potential costs. There is the cost of acquiring the trendy item, which may be expected to rise in price if demand outstrips supply. Also, like all trends, it is unlikely to be exceedingly long-lived, and the social advantage to be achieved through a frequency-dependent trait adoption in this case will be fleeting. But the utility is intricately linked to the popularity of the trend in a way that is not true of Whackalot clubs, which may actually be better than less popular alternatives. The study of these sorts of trends has a long history in anthropology, going back at least as far as A. L. Kroeber’s (1919) pioneering studies of changes in fashion such as skirt length and seen more recently in Greg Urban’s (2010) studies of cultural motion. This work influenced archaeologists who studied frequency seriation, including the famous “battleship curve” whereby new styles in ceramics, or projectile points, or tombstone decoration, or any other aspect of material culture start out as infrequent, growing rapidly to some maximum and then fading away (Dethlefsen and Deetz 1966; Lyman and Harpole 2002). The evaluation of the trait is always dependent on its current popularity, with adopters following the crowd, not because they think the crowd is eternally right, but because the crowd’s “rightness” is a social product evaluated at each moment. We might use the term “conformist” to describe this thought process, but terms like “conformity bias” are used in some literature to describe frequency dependence in general, which might be confusing. Bearing in mind that we’re really talking about fads and trends here, where what is going on is simply following some newly popular variant, let’s call this kind of frequency dependence faddish.
Case C has similarities with both A and B, but is substantially more complex. Because Headshot is a communication technology that is closed to nonusers, its perceived utility is not dependent solely on the assumption that anything popular is likely to be superior, nor on the perception that it is socially advantageous to conform to a trend. Rather, because it is used for communication among other users, its utility is actually dependent on its frequency. The larger the number of users, the more people any individual user can communicate with. A less popular, noncompatible but otherwise similar system would be simply less useful for the function for which it is designed: communication. In other words, this is a case where a frequency-dependent bias is also a direct bias. Let us call this kind of frequency dependence networked, because it is in the exchange of information within a network that it becomes useful.
What these three cases have in common is the feature that in each case, the frequency of something in the environment influences the probability that people will decide to adopt it. Where they differ is in the motivations underlying frequency dependence. But the fact that there are three distinct patterns of frequency-dependent bias is not simply typological trivia. This distinction has major implications for the retention and replacement of cultural phenomena, technologies, and, as we will see, numerical notations.
In crowd-wisdom frequency dependence, the expectation of utility of some cultural phenomenon for some function may be followed up with an evaluation of its utility. If it turns out that Whackalot clubs were popular for some other reason than their overwhelming superiority (perhaps due to a prestige bias—some famous golfer uses them), they may be abandoned once this becomes clear. Even if they are superior for golfing, unless these clubs are the best clubs conceivable, at some point a new set of clubs will be developed that are even better, at which point a new cycle of frequency-dependent bias, leading to adoption, leading to evaluation (and eventual abandonment) may arise. But remember that each new technology, no matter how good it is, starts from a frequency of zero—no one is using it when the product is first launched. Frequency dependence is something to be overcome by users perceiving the new technology to be better—in other words, it doesn’t merely need to “be” better; it needs to be recognized as such, indeed as sufficiently superior to warrant replacing the old technology. The frequency curves of three hypothetical technologies under crowd-wisdom frequency dependence might look a little bit like figure 4.1. The popularity of any one variant (on the graph, its maximum) lasts only as long as there is nothing that is perceived as sufficiently superior to replace it.
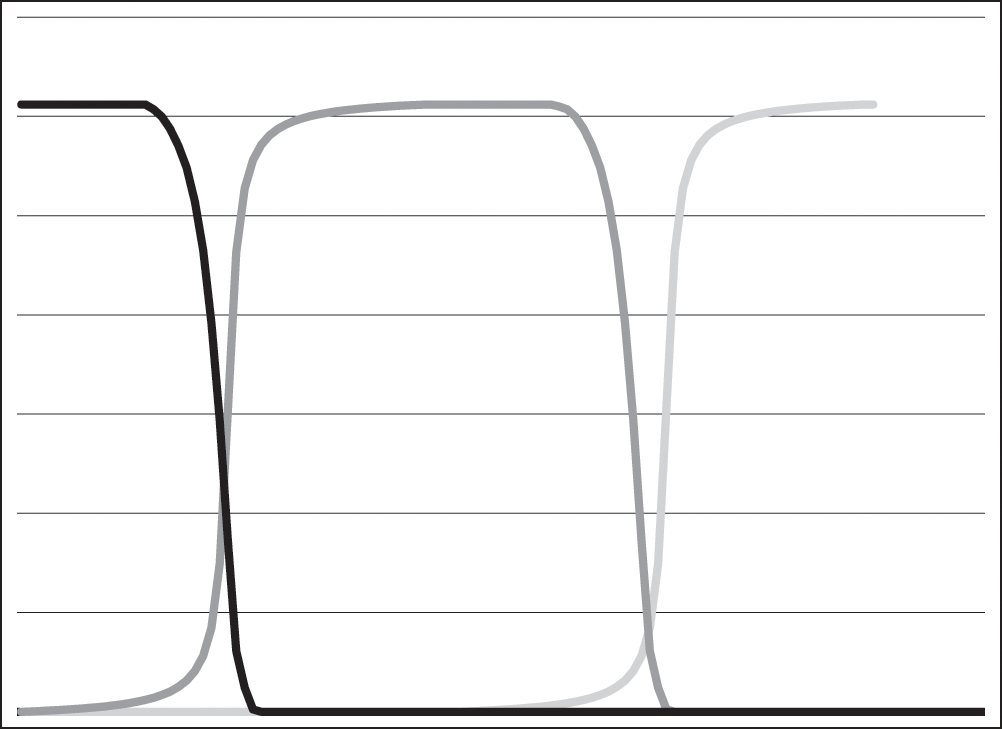
Crowd-wisdom frequency dependence
In faddish frequency dependence, however, the utility of a style of clothing cannot be evaluated adequately independently of its popularity. What makes a fashion fashionable is that it is in fashion. There may be other features than frequency dependence involved (prestige bias, cost, etc.), but because its popularity is a primary determinant of its perceived utility, when it fades as a trend, as it surely will, it is very likely to be replaced, sometimes quite rapidly. Nothing has to be “bad” about the old fashion—the mere presence of some new fashion may be enough to replace it. Some trends, like colors or skirt lengths or jean leg widths, may be cyclical and may fall in and out of fashion multiple times—this is what Kroeber found about many of the trends in women’s fashion he examined. Others, like the 1920s fad of pole sitting, may come into vogue once and then never be heard from again. But why do trends fade at all? Simply put, because people like new things, and old fashions lack appeal. So this is a case where frequency dependence may be counteracted by novelty-seeking behavior by individuals seeking to get ahead of trends. The frequency curve for three hypothetical phenomena under conditions of faddish frequency dependence might look a little bit like figure 4.2.
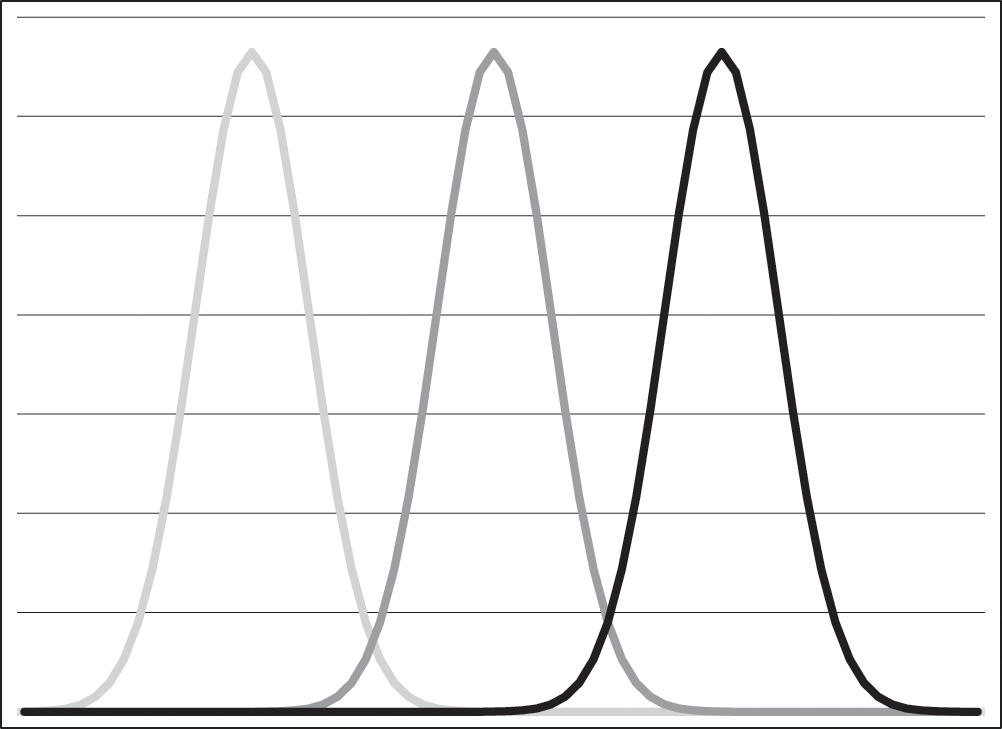
Faddish frequency dependence
Networked frequency dependence combines features of both of these. Like items favored by crowd wisdom, a communication technology can have intrinsic features that promote or limit its popularity. So, for instance, a social media platform may decide to start bombarding its users with unwanted advertising, or may introduce content restrictions that are seen as undesirable, leading to its abandonment. As with faddish frequency dependence, because one of the criteria that is used to evaluate a communication technology is its popularity, its utility cannot be evaluated fully independently of its popularity. But in this case there is an additional cost to abandoning the technology, namely that one will be cut off from communication with other users. Abandoning something popular means choosing to abandon the network still engaged with it. As a result, we might expect that such technologies will be longer-lived than fads, and will also be evaluated in terms of their utility for some function. We might also expect that in many circumstances, it becomes much more difficult for a competitor to break into some domain of activity—that it would be relatively rare for a new variant to take over from the old one completely, and that relative stasis would be the normal condition within any particular community or context. New innovations might arise but then be rapidly discarded, not because they are poor in some absolute sense, but because they are rare initially and are unable to overcome the inertia of an extremely popular system already in existence. This might look a bit like figure 4.3.
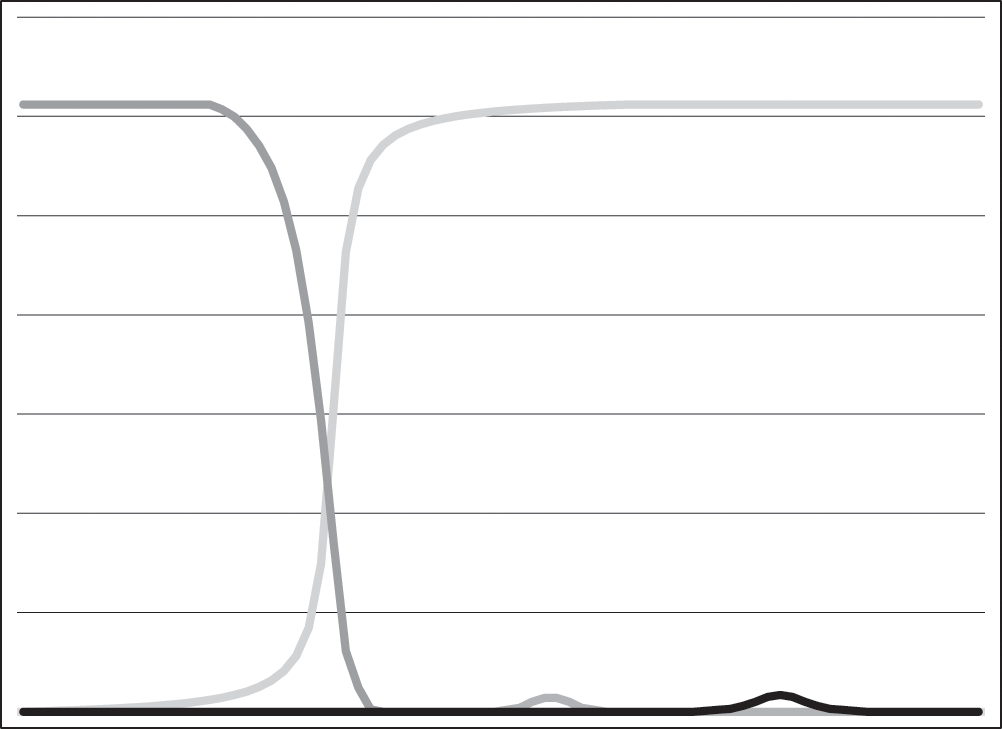
Networked frequency dependence
In addition to patterns of replacement, a further difference between these three types of frequency-dependent phenomena involves how faithful replication is likely to be. The characteristics of networked frequency dependence encourage extremely faithful phenotypic replication of traits being emulated. Because one must be understood for the trait to be of any value, one must communicate very similarly to one’s peers. Writing systems are good examples of communicative systems whose stability is encouraged by the need to communicate with others—stray far, and you will not be understood. Change does happen, but it is slow. With faddish cases, on the other hand, while some fidelity is necessary to enjoy the social benefits of conformity, there may also be some advantage to a slight but significant alteration of the phenotype in order to “get ahead of the curve” of the trend. With phenomena whose utility is partly independent of frequency (such as traits influenced by crowd wisdom), users might make adjustments to their behavior in order to gain an advantage over the many other users of the same trait. The first two types lead to further innovations (and in faddish frequency dependence, at least, this can lead to the trend failing), while networked frequency dependence tends to lead toward the long-term retention of a single variant within a social system.
The question we then need to ask is: In conditions where networked frequency dependence applies, why and how do new innovations come to replace old ones at all? If you’ve spent any time around social media and chat programs, you may have noticed that, far from being shaped by persistent, long-lived phenomena, interactive electronic communication over the past thirty years has transitioned from bulletin board systems and IRC chat to Usenet and AOL Instant Messenger to Livejournal, Myspace, Friendster, Facebook, Twitter, Instagram, Reddit, Tumblr, Snapchat, and more. How did each of these overcome the popularity of the preceding technology? In part, the development of new features made a difference—for instance, many users of chat programs appreciated the feature whereby the program tells you when your interlocutor is typing, prior to their message coming through (Machak 2014). But speak to nearly any user of Facebook today and you will not hear from them that they believe it to be technologically superior. The choice of technology is deeply influenced by the network of users with whom one can be put in contact through using it, and the factors influencing any particular network’s choice may be different (Kwon, Park, and Kim 2014).
In the early years, prior to the late 1990s, internet access was rare enough and diffused across numerous enough platforms (Usenet, AOL, IRC, etc.) that there was no “killer app.” Most people were becoming users of social media for the first time, and this was true right up until the middle 2000s, when many of the now-established platforms were founded. One might then expect that whichever site won out—in this case, perhaps Facebook and Twitter—would dominate all the others to such a degree that no competition would be possible. However, there is another important source of new users—young people, who as they mature into their teenage years pick social media not on the basis of the total number of users of some platform, but the number of users relevant to them—i.e., largely their peers (Hofstra, Corten, and Van Tubergen 2016). Adoption of Facebook among high school students is now substantially lower than it was ten years ago, because of the perception that it is now an adult-oriented medium where their parents and other adults can surveil their activities. In other words, its popularity among one set of users actively reduces the likelihood of its adoption among another—most teens do not have an overwhelming desire to communicate online with their elders. As a result, although the largest social media platforms do exercise some frequency-dependent dominance among some groups—it is unlikely that Facebook is going to collapse anytime soon—the constant infusion of new users of social media whose goals and interests may be very different from their predecessors’ ensures fluidity in this domain.
Networks and frequency in communication systems
Networked frequency dependence is extremely commonplace in communication systems. Many approaches, including several of those we saw earlier, presume that people are more likely to directly compare the utility of two technologies or phenomena than to depend on indirect biases, but this presumption must be tested in each case. Did VHS video technology succeed over Beta because it was cheaper (despite Beta’s higher image quality)—a selectionist argument? Alternatively, after achieving an initial level of success (frequency), did VHS win simply because once more video stores stocked VHS and more distributors produced VHS products, more viewers were inclined to purchase the most popular communication technology? Brian Arthur (1990) was among many favoring the latter explanation, although there is a complex relationship between these sorts of feedback effects, economic systems including pricing, and other social factors. To choose a more modern example, are Windows operating systems actually fitter than Mac or Linux ones, or is their success due to the fact that the choice of operating system can affect one’s ability to share files or to use a colleague’s computer while away from home? Movement in the direction of computers that can read or convert between formats may have mitigated the frequency-dependent effects in this case, allowing users to make choices based on personal preference rather than popularity.
In an interesting study, Alex Bentley (2006) uses data derived from keyword searches in the ISI Web of Knowledge database (one of the principal databases of scholarly articles) to critique sloppy language use in archaeology, using an evolutionary anthropological framework. Using data on the words “nuanced” and “agency” used in titles, abstracts, and keywords of articles, he suggests that these terms are used by humanistic archaeologists in a way analogous to faddish frequency dependence—as “buzzwords” intended to impress others. Under this theory, their increasing frequency reflects conformity to ongoing trends as a status-seeking mechanism, but otherwise lacks any intellectual purpose. In responding to Bentley, however, I have shown that the use of “agency” as a keyword is instead a social and communicative strategy adopted by authors who wish their work to be found and read by others (Chrisomalis 2007). When you write an abstract or title, or choose keywords, you are not merely signaling to gain status, but to be found and read. Thus this case is much more like networked frequency dependence; keywords become popular because authors and readers have an interest in using shared communicative conventions when using keyword searching in electronic databases like the Web of Knowledge. If authors used phrases like “the theory that individual action influences large-scale processes” in place of “agency,” their work would be less accessible, less widely read, and less frequently cited. Keyword searching is a communicative technology in which the use of common terminology allows author and reader to find one another more readily, and in which a frequency-dependent bias leads to certain keywords’ popularity increasing on that basis.
As early as the 1930s, linguists such as George Zipf noted frequency-dependent effects in linguistic transmission, as we saw in chapter 2 (Zipf 1935). This work was later fundamental to Joseph Greenberg’s development of the concept of markedness, establishing that unmarked linguistic forms were virtually always more frequent than marked ones (Greenberg 1966). These accounts differ significantly from that of Boyd and Richerson in that they adopt an explicitly structuralist model for the organization of knowledge, but like them assume a relatively naïve transmission process in which the cognition of the recipient is not necessarily relevant to cultural replication. They are also studies of outcomes, rather than of cognitive decision-making processes underlying those outcomes.
The study of frequency-dependent linguistic phenomena thus remains incipient, despite these early efforts. Lieberman et al.’s (2007) research linking lexical frequency to the regularization of English irregular verbs is a notable exception. This study argued that, among irregular verbs, those more commonly used were less likely to undergo regularization. Why should this be? From a purely efficiency-based perspective, the opposite should be true—people should seek to simplify that which is common, where the pressure would be greatest to make some improvement. The answer they provide is cognitive, relying on the limits of human memory for rarely encountered phenomena. For frequent irregular verbs like be and go, constant exposure to verb forms such as was and went continually reinforces their use. You use those verbs every day and are unlikely to say *goed unless you are a “new user”—e.g., a child, overregularizing based on a pattern not yet fully established in your mind. In contrast, for a rare irregular verb like stride, English speakers are less certain about strode vs. strided, which most of us use rarely if at all. Analogies with other, more common verbs don’t help us much here, because we have divide/divided, hide/hid, and ride/rode, any of which could be the model we choose. So, when in doubt, we turn to the regular morpheme -ed. Over time, *strided may be predicted to become more common and eventually replace strode.
In the domain of numerals, Coupland’s (2011) corpus-based analysis of the frequency of English numeral words in online usage, which I have discussed briefly earlier, shows how spoken and written number words may be affected by frequency dependence. Coupland starts with the recognition that lower numerals are more frequent than higher ones, although that fact is not in itself a product of frequency dependence. Some of the other factors he establishes, however, such as the greater frequency of certain round numbers, or of “geminated” numerals with repeated elements, like ninety-nine, might well be a product of long-established patterns of networked frequency dependence. His hypothesis that humans prefer scale marking using small quantities, for instance preferring ten minutes to six hundred seconds, is also amenable to a frequency-dependent interpretation. We are only at the beginning of this sort of study.
This is not to say that frequency dependence is the sole factor behind the adoption of communication technologies. Stephen Houston (2004) shows that, among writing systems in ancient states, the goal was frequently not to be understood by large numbers of nonelites, but rather to ideologically manipulate others by impressing the difference between those who possessed the skill and those who did not. In some cases, texts may not even have been intended for human eyes, but solely for those of the gods: here the production of such texts serves to highlight the writers’ rare ability to communicate with those entities. Similarly, writing can serve cryptographic or exclusionary functions, to be understood among a select group of individuals but no further. Literacy rates in most of the premodern world were extremely low, and literate communities were limited in size. This does not negate the general pattern that communication technologies are used for communication, and as such we ought to be aware of situations where utility for communication is evaluated by potential users in terms of the size of the networks involved.
Roman and Western numerals: A case study in frequency dependence
We saw in the previous chapter that many histories of mathematics presume that numerical notation systems are adopted on the basis of their (perceived or actual) superiority for performing arithmetic (Dehaene 1997:101; Ifrah 1998: 592)—that is, through a direct bias that does not involve considerations of frequency dependence. However, we also saw that written numerals historically have rarely been used directly for computation; written numerals are used primarily to record and transmit numerical information, while other techniques are used for performing computations. Numerical notation is thus primarily a communication technology rather than a computational technology. Because such notation is relatively easy to learn (low initial cost) and because it is translinguistic (thus not dependent on knowledge of an entirely different and complex symbol system, i.e., a language), it makes a useful case study in frequency dependence.
Over the past 1,500 years, a variety of historically related decimal, place value systems with signs for 1–9 and 0 have been used, first in India and spreading from there throughout the world. The Western numerals, which have several billion users, and the Tibetan numerals, which have a few hundred thousand users at best, are structurally identical notations. As communication systems, however, the Western numerals are generally preferred because they allow one to communicate with many more individuals than would be possible with any other system. Even though the cost of learning a new system is low—ten symbols are not particularly difficult to memorize—Western numerals persist in part because they are so popular. Tibetan numerals, on the other hand, are limited both by a frequency-dependent bias and by a prestige bias in favor of the Chinese numerals, which have hundreds of millions of users, as well as significant social and political constraints on their spread since the 1959 occupation of Tibet. For most of the less common ciphered-positional decimal systems—e.g., Tibetan, Lao, Khmer, Javanese, Bengali, Oriya—the main system replacing them is the Western numerals, a structurally identical system. Here, frequency-dependent and prestige biases can really be the only explanation.
But we need to start earlier, with the Roman numerals, which for over a millennium were the only system in use throughout much of Western Europe. They were the frequent variant, not the rarity. For the most part, the Roman numerals persisted in late antiquity and the early medieval period despite the presence of other systems that could have competed with them—Greek alphabetic numerals to the east, for instance. It would have been very easy for medieval scribes to replace the letters of the Greek alphabet with Roman letters, and in fact there are a handful of texts that use Latin alphabetic numerals (a = 1, b = 2, c = 3 … k = 10, l = 20 … t = 100, u = 200 …) (Lemay 2000; Burnett 2000). Such numerals show up in a handful of translations of astronomical texts that use some other alphabetic numeral system (like Greek or Arabic) starting in the twelfth century, then disappear entirely in the thirteenth. At the time, virtually everyone in Western Europe—even mathematicians—was using Roman numerals, and so the new system never caught on. The Western numerals were largely restricted to a set of mathematical texts, and even then to particular sorts of arithmetical work in those texts.
The frequency-dependent bias in favor of the Roman numerals involved not only the frequency of present users but also of past users, since the ability to use and read older texts depended on knowing them. In an era when the transmission of written knowledge was dependent on scribes reading and writing old texts, faithful replication of Roman numerals was actually quite important. Where the Roman numerals had changed, this could cause problems, as in the texts discussed by Shipley (1902) where the ninth-century scribes did not understand fifth-century manuscripts and thus made systematic errors. For instance, because XL was the most typical form for 40 in the ninth century whereas XXXX had been quite common in the fifth century, the later scribes often presumed that the fourth X was an error, and so deleted it. These and other errors are only minor blips in what is otherwise a highly persistent, extremely common notational practice across space and time. This motivation for retention, to be able to read old materials, is quite different from, say, motivations in connection with social media, where the ability to read and use decades-old material may not be socially valued. It does have a rough parallel with technologies like VHS—long supplanted by DVD, Blu-Ray, and now by streaming video—which is why many of us have a box full of old VHS tapes of holiday concerts from years gone by, and a dusty VCR hanging out in storage somewhere, probably never to be used again.
The Western numerals themselves were once a newfangled, foreign innovation used mainly by infidels—that is, there was every social reason imaginable to reject them in favor of the tried and tested Roman numerals (with the handy abacus for computation). Their eventual predominance was not a rapid and straightforward process of replacement; rather, the Roman numerals persisted for centuries as the notation of choice for scribes, merchants, and administrators. In some cases, the use of Western numerals was discouraged, ostensibly because their unpopularity led to the potential for obfuscation and fraud (an infrequency-dependent bias!) (Struik 1968).
In the late tenth century, Gerbert of Aurillac (who would later become Pope Sylvester II) introduced the use of the “abacus with apices” into Western Europe. Essentially this was a counting board on which counters or jetons were placed; not unmarked counters as on a Greco-Roman abacus, but instead notated with one of the nine apices—the Western digits 1 through 9 (Burnett and Ryan 1988). The user could then place these on a grid or table to manipulate numbers in a materialized form. This is not a cumulative-positional abacus using the repetition of objects (beads, pebbles, etc.), but a ciphered-positional abacus where the counters serve in lieu of writing down calculations. But this was a competitor for the abacus, not for the Roman numerals, which could have been written as apices on a token just as easily as Western ones could. As we see in figure 4.4, a manuscript depiction of the abacus with apices, the columns could readily be notated in Roman numerals, even as the Western numerals began to be used.

Abacus with apices (source: Bibliothèque nationale de France, Latin 8663, folio 49v)
As we saw in the previous chapter, the choice between the use of the reckoning board (medieval abacus) and the Western numerals and written arithmetic was complex and rarely a matter of selecting one notation over the other. Leonardo of Pisa’s Liber abaci promoted the use of written arithmetic with place value numerals but was never intended to supplant Roman numerals. Later medieval mathematicians advocating for what we can, in an overly blunt fashion, call the “algorist” position continued to use Roman numerals in all sorts of ordinary contexts, including when writing about mathematical subjects. Just as al-Uqlidisi recommended using Arabic numerals only for doing the computation but some other system (such as the abjad numerals) for writing down answers, Western Europeans were simply not concerned with possible deficiencies of the Roman numerals and were happy to keep using them as an everyday notation, even despite the availability of an alternative. At this point, the use of Western numerals was still extraordinarily rare outside of a narrow group of specialists. Only in the thirteenth century and more in the fourteenth did Western numerals show up among other users, and even then their appearance outside theological or astronomical matter is remarkable at this period. So, for instance, the Genoese notary Lanfranco used Western numerals in the margins of his cartularies between 1202 and 1226, but usually only to indicate the honoraria he received for his work (Krueger 1977). Some thirteenth-century sculpted figures at Wells Cathedral bear mason’s marks with Western numerals to indicate their correct position, but the cathedral accounts were notated using Roman numerals until the seventeenth century (Wardley and White 2003: 7). Pritchard (1967: 62–63) discusses an early fourteenth-century graffito at the church at Westley Waterless, in Cambridgeshire, enumerating grapevines in a series of rough-carved lines, and suggesting, on the basis of the rarity of Western numerals in England at the time, the presence of an Italian priest at the church. These represent thin, sporadic evidence, barely a trace in comparison to the thousands upon thousands of inscriptions and manuscripts with Roman numerals from this period.
The fifteenth century marks, roughly, the period when the Western numerals began, in large parts of Europe, to be well enough known that their appearance is no longer remarkable in most texts. Carvalho (1957) examined a variety of late medieval text genres in Portuguese, showing that it was not until around 1490 that the Western numerals became predominant in travel accounts and scientific documents, and still later for other contexts. Crossley’s (2013) examination of catalogues of dated manuscripts showed an increase from 7% of dates in Western numerals in the thirteenth century to 47% by the late fifteenth century. In the Catasto tax records and fiscal documents of Florence from 1427, Rebecca Emigh shows that Western numerals were used not only by central authorities but also by local households (Emigh 2002). Still, on the whole, the Roman numerals were substantially more common throughout the entire fifteenth century across all of Europe than the Western numerals.
The sixteenth century marks the major inflection point, the time at which the Western numerals became, if not ubiquitous yet, clearly preferred for most functions in most areas. England, which in many aspects was the slowest to adopt the change, certainly did so enthusiastically by the period from 1570 to 1630, as shown by two studies involving English probate inventories: Wardley and White’s “Arithmeticke Project” (2003) and Cheryl Periton’s recent doctoral dissertation (2017). Probate inventories are inventories of goods, money, and property owned by a person at the time of their death. They are particularly useful because they are so widespread. Wardley and White developed and used a taxonomy for identifying texts using Roman numerals alone, Western numerals alone, Roman numerals but Western totals, Western numerals but Roman totals, mixed notations, lexical (number words), and some miscellaneous categories. This fine-grained approach allows a year-by-year demonstration of the shift. Periton (2017), similarly, uses this model to discuss the prevalence of Roman numerals, Western numerals, and English number words in a small corpus of 92 probate inventories dating from 1590 to 1630, showing that while there are surely trends toward writing dates in Western numerals, lexical and Roman numeral representations continued throughout this period.
There were still holdouts—for instance, Sayce (1966) shows that Parisian bookbinders were still using Roman numerals internally, for markings on books designed for industrial practice, throughout the seventeenth century and even up until 1780! William Cecil, Lord Burghley (1520–1598), the Lord High Treasurer of England under Elizabeth I and the figure responsible for most English economic policy, is said to have translated documents written in Western numerals back into Roman numerals, with which he was more comfortable (Stone 1949: 31). At the level of individual choices, this is to be expected. As an aggregate, the Western numerals had secured their position by this time.
All of the above provides some evidence of a roughly S-shaped curve of the frequency of the Western numerals, starting out very slowly and rising rapidly until, by the late seventeenth century, writers such as John Aubrey could lament, and John Wallis could praise, the fact that no one really used Roman numerals any longer. But what this sort of data doesn’t tell us is the motivations of users for switching. And given how little metalinguistic or metanotational material directly bears on the evaluation of the Roman numerals, it’s hard to know whether and for what purposes anyone found the Western numerals to be useful. For this process to get started, the Western numerals had to come from a position of radical infrequency, and the process of replacing Roman numerals took centuries to complete. This was one of the reasons originally given by their detractors for not adopting them: they were obscure, no one knew them, so they were prone to falsification and fraud. How did the ubiquitous Roman numerals come to occupy the position they now have, as an archaism and a bogeyman of the middle-school classroom, after their medieval ubiquity?
The answer, I think, lies in another radical change in communication technology: the printing press. As Elizabeth Eisenstein (1979) and others have argued, the printing press was an enormous agent of social change, and one of the most important of its effects was to open up literacy to a much wider range of users—the burgeoning European middle class—than had ever been possible in a manuscript-based literary tradition. Printers became the vectors through which a centuries-old notation, the Western numerals, could become accessible to far broader audiences. Newly literate people, unencumbered by the tradition of Roman numeral use, and unconcerned with what system had been used in the past, adopted the Western numerals. These newly literate individuals, reading and writing outside the medieval manuscript tradition and engaging with printed texts, were the disruptive force that put an end to the dominance of the Roman numerals in Western Europe. Jessica Otis (2017) argues convincingly, based on textual analysis of English arithmetic books and their marginal notes, that the spread of printed arithmetic texts through the sixteenth and seventeenth centuries brought literacy and numeracy together for the first time, at least in England. We are used to thinking of literacy and numeracy as going hand in hand, linked to formal schooling and in fact to preschool activities, but this is a modern idea, a product of a particular historical moment.
This is not to say that the adoption of the Western numerals was instant upon the adoption of printing. One strategy for examining the transition in a more fine-grained way is to look at texts that use both Western and Roman numerals but for different purposes. Books that use only one system may indicate a printer’s preference for one system or another, or simply that the audience for a particular text was expected to know only one or the other. In contrast, books that use both systems suggest the functions for which each system was perceived as useful, and thus give us a window into the motivations of the printers relative to their audiences. The corpus of early English incunabula (the technical term for printed books published before 1501, during the earliest decades of European movable-type printing) as well as early sixteenth-century printed books provides a robust sample. Searching through the full-text Early English Books Online database, I found 55 books dating from between the beginning of the English printing tradition and 1534 that contain both Western and Roman numerals. If Western numerals were adopted in part because of their utility for foliation (page numbering), chapter headings, or indexing, then one might expect that they would most often serve organizational functions, while Roman numerals might be retained in colophons or title pages, perhaps for recording publication dates. If no such pattern exists, then the organization of texts for the convenience of readers was probably unrelated to the choice of numerical notation. This analysis will help us better understand how printers were thinking about the new notation, its advantages, and its weaknesses.
Table 4.1 lists the major organizational features of books that use numerals, along with the number of books in the corpus of 55 books that use a particular system for that function. For most functions, Roman numerals are preferred throughout this period, the exceptions being for title pages (a late development) and marginal notes (which are rare in the earliest decades of the period under study).
Roman numerals and Western numerals in early English printed books, 1470–1534
|
Feature |
Roman |
Western |
||
|---|---|---|---|---|
|
Colophon |
25 |
21 |
||
|
Title page |
0 |
6 |
||
|
Foliation |
26 |
17 |
||
|
Table of contents |
7 |
7 |
||
|
Marginal notes |
2 |
6 |
||
|
Chapter headings |
11 |
2 |
||
|
Signature marks |
29 |
14 |
Western numerals were rare in England before 1530, in both manuscripts and printed texts (Jenkinson 1926). William Caxton briefly experimented with Western numerals in six of his works printed at Westminster between 1481 and 1483 (Blades 1882: 47). However, Caxton used Western numerals only for signature marks: organizational features used by bookbinders to ensure that pages are placed in the correct order, but not really intended for the eventual reader at all. He printed all the other organizational features, such as chapter headings, in Roman numerals. This suggests that while he expected (or knew) that his bookbinders were familiar with the new system, it was still novel enough to his readership that he did not employ them in features intended for them. Figure 4.5 shows a leaf from Caxton’s Reynard of 1481 (STC 20919) containing the first Western numeral ever printed in an English book (the signature mark “a2,” bottom right), alongside the chapter headings in the table, numbered in Roman numerals. Caxton’s experiment was short-lived; from 1484 onward, he reverted to Roman numerals for signature marks and used no Western numerals anywhere else. Indeed, these were the only Western numerals in English incunabula.

Leaf from Caxton’s Reynard of 1481—with "a2," bottom right, the first printed Western numeral in an English book (STC 20919)
The use of Western numerals in books printed in England resumed only in 1505 with the printing of Hieronymus de Sancto Marco’s Opusculum (STC 13432), probably by Richard Pynson in London. The choice to use Western numerals was more than simply one of picking a notation, since, to use Western numerals in print, printers needed to develop fonts that included the new characters. Although the foliation (page numbers), signature marks, and table of contents all use Roman numerals, the date that appears in the bottom line of page xxix is in highly irregular Western numerals (figure 4.6). Each numeral comes from elsewhere in Pynson’s type set: the 1 from majuscule I, the 0 and 5 from black-letter o and h, and the 9 (in the day number) from the apostrophe used for the Latin syllabic ending -us. Very likely the printer lacked a set of Western numerals, which may explain why they were not used throughout the text. But in that case, why were they used at all? And note that the volume is still paginated in Roman numerals—how could it be otherwise, if the printer had no numerals in his type set? This is, bear in mind, at least three centuries after the Western numerals were first used in England, and five centuries after their first use in the Latin mathematical tradition.

Hieronymus de Sancto Marco, Opusculum, fol. xxix, printed by Richard Pynson in 1505 (STC 13432)
Throughout the corpus I examined, 16 of the 55 books examined are, like the Opusculum, dated in Western numerals (either in the colophon or on the title page) but have folio numbers in Roman numerals. Conversely, 13 books are dated in Roman numerals but foliated in Western numerals. This suggests that, far from presenting an obvious cognitive convenience for organizing books, both Western and Roman numerals were seen as perfectly adequate for either function. Even more remarkably, eight of the 55 books with both Western and Roman numerals use different notations for the foliation of leaves than for the folio numbers in the table or index of the book—four with the foliation in Roman, four in Western. In other words, the reader would look up the folio number in the index in one notation, and then find the correct folio in the book using the other one! While one interpretation of these irregularities is that printers expected readers to be so familiar with both systems that they could rapidly transliterate between them, this can hardly be correct, given the scarcity of Western numerals at this time. What we more likely have is a set of norms still in flux, developing along with its new audiences, with few settled production standards.
By the second quarter of the sixteenth century, the Western numerals were becoming more common in English printed books. Pynson’s 1523 edition of Villa Sancta’s Problema indulgentiarum (STC 24729) was the first book printed in England to contain only Western numerals—no Roman numerals at all. The London printer John Rastell was one of the earliest English advocates for the new system, and in the late 1520s he wrote and printed The Book of the New Cards (STC 3356.3), which survives only in a half-sheet quarto including the table, but whose contents indicated how “to rede all nom[bers] of algorysme” (Devereux 1999: 129). Yet Rastell (and his son William, who succeeded him in the early 1530s) never used Western numerals exclusively in any of his books, generally using them only in title pages and colophons, and only sporadically in signatures and elsewhere. Similarly, William Tyndale’s Bible of 1535 contains no Western numerals whatsoever—chapters, marginal notes, signatures, and the colophon are all in Roman numerals.
Over the course of the early English printing tradition, a sporadic and inconsistent increase is evident in the use of Western numerals, one that is more evident in colophons and title pages than in organizational features. Their placement in these visually prominent contexts illustrated the printer’s familiarity with the new system, without requiring readers to be fluent with the innovation. Ironically, then, the Western numerals served a prestige function in early English printed books for their novelty, just as Roman numerals would eventually serve a prestige function in title pages for their antiquity.
Even printers very favorable to the use of Western numerals in general made frequent use of Roman numerals in organizational contexts such as foliation, side notes, and chapter headings. Inconsistencies in printers’ practice suggest that, far from a cognitive revolution, the introduction of Western numerals resulted in some potential for awkwardness and confusion. Sixteenth-century Bibles and prayer books mixed Roman and Western numerals in ways that Williams (1997: 7) describes as “schizophrenic”—at the very least, unpredictably and without any clear underlying pattern. But the mixing of systems in different contexts need not be seen as a retrograde step. Rather, in some cases it served the very useful function of distinguishing parallel enumerated lists—just as even today prefatory material in books, or nested sublists, use Roman numerals alongside Western ones. The revolutionary idea that multiple notations can coexist in parallel for the benefit of the readers represents the most important insight to take from the tradition of early printed books from England. But this is hardly grounds for replacing Roman numerals, but rather, for retaining them.
This hodgepodge of different notations in the first century of the printing tradition puts to rest the claim that Western numeration was responsible for effecting significant cognitive changes in how people organize information. Elizabeth Eisenstein, the historian of printing, claimed:
Increasing familiarity with regularly numbered pages, punctuation marks, section breaks, running heads, indices, and so forth, helped to reorder the thought of all readers, whatever their profession or craft. Hence countless activities were subjected to a new “esprit de système.” The use of Arabic numbers for pagination suggests how the most inconspicuous innovation could have weighty consequences—in this case, more accurate indexing, annotation, and cross-referencing resulted. (Eisenstein 1979: 105–106)
In the same year, Rouse and Rouse made the comparison with Roman numerals more explicit:
Tools of reference required a system of symbols with which to designate either portions of the text (book, chapter) or portions of the codex (folio, opening, column, line). Toolmakers were nearly unanimous in their rejection of roman numerals as being too clumsy for this purpose. Before widespread acquaintance with Arabic numerals, the lack of a feasible sequence of symbols posed serious problems in the creation of a reference apparatus. (Rouse and Rouse 1979: 32)
If this were true, we would expect the data to look very different, with systematic replacements and consistent notation within particular volumes and the printers who published them. It would also imply that crowd-wisdom frequency dependence is more likely than networked frequency dependence as an explanation for the shift—in other words, that the Western numerals really were better, and their adoption was merely a confirmation that users found them useful for organizing information.
But this is not what we see at all. The place where readers would be most likely to encounter the numerals, printed books, was a new medium with only gradually evolving standards and norms for notations. Roman numerals remained common throughout the first decades of the printing tradition and, when abandoned, were abandoned sporadically and without apparent reason. Thus, just as the Western numerals were preferred for reasons other than their arithmetical efficiency, they equally were not the leading edge of a cognitive revolution in organizing and structuring knowledge. Rather, gradually, they developed a critical mass of use alongside a critical mass of new users in the sixteenth century especially (in France and Italy, a little earlier), until their frequency cemented their position as the dominant notation of the region.
Even so, both perceived utility (crowd wisdom) and conformity (faddishness) may still have played a role in the increasing prevalence of Western numerals. In contrast to the Roman numerals, Western numerals were used for pen-and-paper computation, and the perception that they were better for doing so must have played a role in their adoption in some cases (although abacus computation is quite rapid and error-free also, as we have seen). So, too, the novelty of the system may have appealed to a newly literate middle class interested in breaking away from older traditions. However, if either of these were the primary explanation for the adoption of Western numerals, we would expect a very different pattern of their retention. We also would not expect them, five hundred years later, to be nearly ubiquitous worldwide, unless they were actually the best system imaginable. That sort of teleological argument may be comforting to someone who prefers to think that we live in the best of all possible worlds, but there is no evidence, other than our own wishfulness, to suggest that it is true.
The most parsimonious explanation for the rise of the Western numerals to their present level of ubiquity is the combination of new technology (the printing press), new forms of information transmission (higher literacy, educational texts), and a set of social and political changes to go with it. At or around the same time as the Western numerals were adopted, the centrality of the Western European countries at the core of a system of domination, communication, and information was coming into place. This new network—the capitalist world system—starting around AD 1450–1600 established itself not just as one of many local networks, but as the principal vector through which information was transmitted and inequality sustained (Wallerstein 1974). Once this network had been established, communication systems whose utility was evaluated within that context became increasingly common and, thereby, increasingly difficult to replace. This is, again, very similar to the argument that Saxe (2012) raises about the transformations and importance of the Oksapmin body-counting practices discussed earlier. It is not the technique or the technology alone, but only taken in conjunction with social, economic, educational, and political systems, that makes the difference.
It is not a coincidence that the Western numerals came to predominate at the same time as the world system. There is no cognitive revolution associated with decimal place value notation. Rather, the confluence of economic, social, and communicative factors cemented both the Western numerals’ place as a notation and the economic system that would contribute to its spread. Their ubiquity, established by printers disseminating notations to a new group of literate users, was ensured. Only in such novel circumstances could a break from the Roman numeral tradition be permanently achieved.
Conclusion
In their treatment of frequency dependence, Efferson et al. (2008) show that even in experimental contexts where frequency dependence, particularly conformity, might be expected, many individuals are neither conformists nor passive nonconformists but mavericks. This is a valuable insight because it recognizes that the value of conformity for an individual rests on the presumption that some individuals do not conform to the majority. The authors are also very careful to distinguish conformity, as a disproportionate tendency to follow the majority, from frequency dependence in general. Yet it rests its theoretical focus on outcomes rather than the processes underlying those outcomes, and as such, like other recent work in the tradition of evolutionary studies of cultural transmission (e.g., Rendell et al. 2010), does not recognize important variability in the concept of frequency dependence. The very best work in this tradition, such as Mercier and Morin’s (2019) survey of experimental research on conformity and “majority rules” principles, highlights a real challenge to individual adopters, which is that communication is not always to be trusted and so individuals don’t always have a good guide as to how to proceed when considering some popular innovation. Frankly, most psychological studies of frequency dependence, being reliant on experimental, short-term conditions with research participants who are not invested in conforming to the majority for any reason—and surely not for networking purposes—are unlikely to shed light on situations like the decline of the Roman numerals and their replacement. I do not see any way to get undergraduates in a laboratory to think like a sixteenth-century printer, much less to recapitulate a centuries-long process of replacement. These experiments will provide insights and hypotheses that will be extraordinarily useful, but that can only be tested through the ethnographic and historical records.
Stephen Shennan (2002: 48) notes that evolutionary anthropologists’ and archaeologists’ knowledge of the psychological mechanisms behind cultural transmission is rudimentary. He suggests instead that “the way forward for archaeologists and anthropologists, if not for psychologists, seems to be to ignore the psychological mechanisms and accept that, whatever they may be, they lead to culture having the characteristics of an inheritance system with adaptive consequences.” Because prehistoric data are rarely amenable to “paleopsychology,” it is tempting to fall back on a position that neglects intentionality, or to assume that cultural differences will make it impossible to discern intentionality. If frequency-dependent biases are relatively common, however, then this assumption is not warranted. Many scholars of an earlier generation—sociologists such as Everett Rogers (1962), geographers such as Torsten Hagerstrand (1967), psychologists such as Solomon Asch (1955), and anthropologists such as Margaret Hodgen (1974) and Homer Barnett (1953)—used ethnographic, social, and historical data to conceptualize cultural transmission as the outcome of decision-making processes. This same sort of holistic approach, which does not hide from modeling, evolutionary thinking, or quantitative data but recognizes their limitations, is needed to understand the cognitive underpinnings of historical phenomena like these.
Linguists and scholars of communication have spent less energy than is needed on questions of motivation and decision making in the transmission of variants. Thus, the study of transmission may begin with a return to Zipfian principles—focusing on the adoption and retention of already-common forms—but must quickly move past it. Zipf’s analysis does not focus chiefly on the choice between two or more variants, but simply on the description of rank-ordered frequencies. But if we want to understand the choice between tsunami and tidal wave, sneaked and snuck, dozen and twelve, we must investigate how new variants emerge and are accepted in a population, bearing in mind that this is both a cultural and a psychological process as well as a linguistic one. We can also use the models described above to investigate choices between entire communicative systems, be they alphabets, computer operating systems, social networking websites, or numerical systems. Because the adoption of common communication systems becomes more useful as systems acquire more adopters, the communicative sciences constitute a special domain of inquiry relevant to cultural analyses of frequency-dependent phenomena.
The integrative and rigorous understanding of cultural transmission requires that we begin to move away from models that assume that we can know nothing about variation in decision-making processes. The three types of frequency-dependent bias do not merely reflect three different patterns of trait transmission, adoption, retention, and abandonment; they reflect the different decision-making processes described in the three cases above, and potentially in others. These processes remain undertheorized and incompletely demonstrated, but without asking these questions we are unlikely to get an adequate picture of the distinctions among these three types of frequency dependence, and potentially all sorts of other cultural evolutionary processes. We can know more about decision making than we are presently willing to admit, and we have the data at hand to ask useful questions about decision making that will aid in the understanding of evolutionary processes in cultural transmission.
Frequency-dependent biases, under conditions of massively increasing literacy rates and new technologies such as the printing press, structured, if not determined, the replacement of the Roman numerals by the Western numerals in Western Europe. Thus, simply comparing the structure of the Western numerals to the Roman numerals is of limited use, except in narrow contexts such as arithmetic textbooks. While this is an important subject in the history of mathematics, it is not nearly as important in the history of number systems, because most number systems were simply never used for arithmetic, and even those that are, like the Western numerals, are mostly used for representation, not computation. This should also imply that elsewhere in the world, the replacement of nonpositional systems by the Western numerals, or by other decimal, ciphered-positional systems like the Arabic, Indian, Lao, or Tibetan, will have a different trajectory. From a narrowly Western-centered point of view, it’s easy to forget that these other systems existed: alphabetic systems such as the Armenian, Georgian, Arabic, Hebrew, and Syriac numerals; alphasyllabic systems such as the katapayadi numerals of the Indian tradition; additive numerals of the southern Indian subcontinent such as the Tamil, Malayalam, and Sinhalese systems; the classical and other traditional numeral systems of China and East Asia. How were these replaced?
If the structure of systems were the most pertinent factor, then decimal ciphered-positional numerals should be equally potent as agents replacing nonpositional systems worldwide, but this is not the case. In China, mathematicians became aware of ciphered-positional numerals in the eighth century CE; Qutan Xida, a Buddhist astronomer of Indian descent working at the Tang Dynasty capital of Changan, wrote his Kaiyuan zhanjing between 718 and 729 and described positional numeration with the zero (Needham 1959: 12). But zero wasn’t used at all in Chinese arithmetic until the Shùshū Jiǔzhāng (Mathematical Treatise in Nine Sections) of 1247, half a millennium later (Libbrecht 1973: 69). Even then, zero didn’t serve as a general-purpose number in such texts, but simply to fill in empty medial positions in numbers like 105 or 12,007. The contemporary Chinese zero, ling (零), came into use in the late sixteenth century, sporadically at first, but the contemporary Chinese practice of using the traditional numerals 1–9 along with either ling or a circle did not become customary until the twentieth century, by which time Western mathematical practices and global mathematical transmission were predominant. As we saw with the Roman numerals, the fact that some innovation is known and might have some advantage does not automatically recommend it to new users.
In India, the homeland of positional numeration, where decimal ciphered-positional numerals were used by the sixth century and perhaps even earlier, nonpositional systems were retained, not just incidentally or for peripheral or prestige purposes but as part of core representational practices. In northern India the transition to ciphered-positional numeration was fairly rapid, with the older Brahmi ciphered-additive/multiplicative-additive system being replaced by the ninth or tenth century by simply retaining the old signs for 1 through 9 and adding a zero. But in southern India, although positional numeration was known very early, it did not replace older notations. The Tamil, Malayalam, and Sinhalese core numeral systems were all ciphered-additive or multiplicative-additive through the nineteenth century; the philologist Pihan (1860) reports all of these systems in use at the time he was writing. Babu (2007) provides an important historical analysis of the teaching of Tamil mathematics, including these numbers, in eighteenth- and nineteenth-century schools. These systems were only replaced in the nineteenth and early twentieth centuries, under British colonial rule (they are retained and used historically, like Roman numerals). A thousand years of contact with northern India did not displace them; a hundred years of colonialism, mass literacy, printing, and education were necessary.
As we saw in the previous chapter, the Arabic world was similarly divided; positional numeration was known there by the seventh century CE, but the ciphered-additive alphabetic numerals, finger reckoning, and other techniques survived far longer. The Arabic abjad numerals are like the Greek alphabetic numerals and other similar systems, in which the letters, in their order, are given the values 1–9, 10–90, and 100–900, with some variation. It seems that, following the advice of al-Uqlidisi which we saw in chapter 3, some Arabic writers may have been doing calculations on a dust board positionally, but permanent records were not common in that system until much later than might be expected. Until the thirteenth century, Arabic astrology and astronomy was conducted using the abjad numerals alone, and for centuries thereafter abjad numerals and positional numerals were used side by side (Lemay 1982: 385–386). The retention of abjad numeration for astronomical and astrological purposes, in which arithmetic is needed intensively, belies any easy functional explanation. Only around the seventeenth century, and especially after the French conquest of Egypt in 1798 and the beginnings of the Arabic printing tradition with movable type, did the abjad numerals come to occupy an auxiliary role similar to the Roman numerals in modern Europe and North America.
In each of these regions, positional numeration was known centuries before it was known in Western Europe, but in all of them, additive systems persisted, not just for a century or two but for a millennium or more in active, regular use by discourse communities. In these communities, the costs of switching from one system to another—the time to learn a new system, the loss of the ability to read older material, and the inaccessibility of new notations to old audiences—overwhelmed any advantage that might have accrued from the switch. Just as with the Roman numerals, it took a disruptive event in the history of those communities to lead to a permanent abandonment of additive systems. The advent of widespread literacy and the printing press, and the integration of local economies and social institutions into global systems, played that role. None of the older systems was forcibly extirpated by colonial officials or imperialist bureaucrats (in contrast to Mesoamerica and the Andes, where Aztec, Maya, and Inka practices were sharply criticized and forcibly curtailed). But the logic of worldwide networked economic and social systems does not always require such direct violence in order to disrupt longstanding systems. It didn’t need it in Western Europe, the very heart of the contemporary global world system, to displace the Roman numerals, so why should it have anywhere else?
The one remaining question is: What about new innovations? In figure 4.3, I hypothesized that once a networked frequency-dependent bias takes hold, new innovations that might compete with the dominant system will be developed, but normally quickly abandoned. In the following chapter, we will examine one such case study in detail, in the broader context of the development of numerical notation since the Western numerals achieved their present level of ubiquity.