During the last decade, the research on vehicular networks has led to the proposal of countless network solutions specifically designed for vehicular environments. Such solutions encompass all network paradigms, with original algorithms and architectures proposed for next-generation roadside cellular access networks, pure vehicular ad hoc networks and opportunistic disruption-tolerant vehicular networks.
When such vehicular network solutions target vast deployments that comprise tens, hundreds or even thousands of cars, simulation is the means of choice for their performance evaluation. Indeed, large-scale experimental test beds are too expensive and complex to scale to more than a few communication-enabled cars, while comprehensive analytical approaches are often untraceable from a mathematical viewpoint.
The reliability of simulative evaluations has thus emerged as a critical aspect to the performance analysis of vehicular networks. A major role in achieving such a reliability is played by the representation of car mobility in simulation. As a matter of fact, the road traffic dynamics are the most distinctive feature that tells vehicular environments apart from other mobile scenarios. The vehicular mobility determines the node (from an ad hoc perspective) or user (from the point of view of the cellular access infrastructure) movement, which, in turn, drives the topology of the network (ad hoc scenario) or the user demand (cellular scenario).
As repeatedly proven in the past [BAI 03, FIO 08, VIR 11], the movement of vehicles can dramatically affect the behavior of network protocols, and an incorrect representation of car traffic can lead to misleading performance results and wrong conclusions, even if the network-level simulation is flawless. As a result, it is today widely acknowledged that, for the results of a vehicular network simulative campaign to be credible, the latter must build on mobility traces that faithfully capture the unique macroscopic and microscopic dynamics of car movement patterns.
The safest approach to the generation of mobility traces for vehicular network simulation would then be to extract mobility patterns from a direct monitoring of real-world road traffic. Indeed, projects aiming at tracking and logging car traffic in the real world first appeared during the first half of the past decade [JET 03, BUR 06] and have since then grown in number and scale [HUA 07, SED 08, DOE 10, ZHA 10, YUA 11]. However, the resulting traces are today limited to subsets of specific vehicles, for example, buses or taxis, and typically exhibit reduced temporal detail, that is order-of-minute position information updates. As a result, these traces are mainly employed for the performance evaluation of applications based on delay-tolerant or opportunistic networking paradigms. However, it is clear that significantly higher penetration rates and time granularity are needed for more general use cases. An interesting breakthrough in the collection of real-world vehicular movement data could be provided by the diffusion of recent navigation systems [TOM 10, MEI 11], which periodically communicate car position information to traffic management centers. Although this may greatly help real-world traffic tracking to scale up, it is easy to foresee that market rules and privacy concerns will hinder the public disclosure of such data, similarly to what happens today with the mobile access network logs of telecom operators.
As a result, synthetic vehicular mobility traces have emerged as the most viable solution to represent node or user dynamics in network simulation. The generation process of such synthetic traces has drastically improved over the last few years. The simplistic stochastic models employed in early works [DAV 00, BAI 03] have been replaced by random mobility over realistic road topologies [SAH 04], at first, and by microscopic vehicular models borrowed from transportation research [JAA 05] later on. These features were then included in dedicated simulation environments and integrated with road signalization [KRA 02, HÄR 11]. Since then, vehicular mobility simulators have been increasing their complexity and features, allowing us to accurately simulate the individual movement of vehicles over realistic road topologies [HÄR 09].
In this chapter, we will provide a comprehensive survey on the generation of vehicular mobility traces for network simulation. An introduction to the process of generating synthetic mobility traces is presented in section 6.2, where we also briefly outline the history of synthetic vehicular mobility generation. Section 6.3 then provides a taxonomy of the most important tools employed in the process above, that is the microscopic-level simulators that are available today for the generation of vehicular mobility traces. The outcome of the process, that is the mobility traces that are publicly available for the simulation of vehicular networks, are then presented in section 6.4.
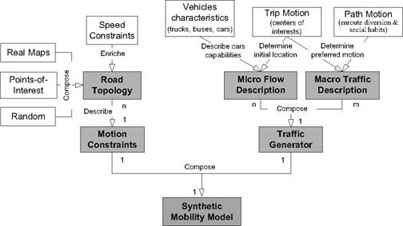
When simulating intervehicular applications, the crucial role of synthetic vehicular mobility traces has been illustrated by multiple studies [FIO 08, SOM 11]. As illustrated in Figure 6.1, the generation of realistic synthetic traces of vehicular mobility builds on three major components mutually influencing each others, that is the road topology information composing motion constraints, and the microscopic flow description and the macroscopic traffic description, composing traffic demands. Traffic demands provide a description of the desired mobility, whereas motion constraints limit them. In this section, we introduce such components, outlining their importance to the realism of the resulting movement trace. Discussing the different components in the order above also gives us the opportunity to review the evolution that the simulation of road traffic for vehicular networking has undergone during the last decade.
Early works on vehicular networks used to employ very intuitive representations of car mobility. The very first simulations of vehicular networks constrained the car movement over simplistic graphs, so as to mimic traffic dynamics over a street layout. These graphs were typically regular grids [DAV 00, BAI 03], also referred to as Manhattan scenarios and depicted in Figure 6.2(a), or simple user-defined layouts [TIA 02], as shown in Figure 6.2(b). Automatic road topology generation was also explored, by leveraging clustered Voronoi tessellation [HÄR 11], which led to layouts as shown in Figure 6.2(c). However, all these approaches did not yield a sufficient level of realism and were soon abandoned.
Figure 6.1. Concept map for synthetic vehicular traces, where the two main blocks are enriched with added blocks and features providing an increased accuracy

Real-world maps then started to be used to model the movement-constraining graph. The U.S. Census Bureau TIGER database [BUR 12], providing complete topological information on the whole US road network and being freely accessible, became especially popular to that end. Notable works that used the TIGER database include [SAH 04, NAN 06], while an example of TIGER road layout is shown in Figure 6.2(d). Another source of road topology information that became quite popular was Ertico’s geographic data file (GDF) database [ERT 12]. The GDF format was more complete than the TIGER format, but the two databases were complementary, as the Ertico database provided topology information of European cities. The GDF format was employed, for example, in [HÄR 11]. A sample road topology is shown in Figure 6.2(e).
Figure 6.2. Road topology database examples
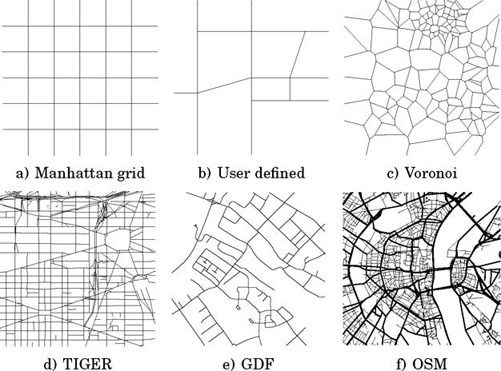
More recently, the success of the OpenStreetMap (OSM) [OPE 12] initiative has granted to the OSM format a de facto standard status. The OSM initiative applies the open-source concept to road cartography, and thus provides freely exportable maps of cities worldwide, which are contributed and updated by a vast user community. Map information includes roads, railways, buildings and points of interests (PoI) such as parks, commercial centers, leisure centers and commercial activities. The OSM road information is generated and validated by the user community through satellite imagery and GPS traces, and is commonly regarded as the highest-quality road data publicly available today. Indeed, the accuracy of OSM street layouts, comprising highways, major urban arteries and minor roads, often matches that of proprietary ones such as Google Maps or Mappy, especially for large cities. An example of OSM topology is provided in Figure 6.2(f).
The second key component in the generation of vehicular movement traces is the microscopic-level mobility model. This model controls the acceleration (possibly deceleration) of an individual car at each time instant, thus determining its speed over time. Diverse microscopic mobility models can have very different levels of detail. In the following, we provide an overview of the evolution of microscopic mobility modeling for vehicular network simulation over the last few years. For a more complete discussion, we refer the reader to [FIO 09].
Early works on the simulation of vehicular networks employed stochastic microscopic mobility models that, in their simplest implementation, assigned to each vehicle a random speed in a predetermined speed range. The vehicle then traveled at a constant speed during its whole trip. Basic stochastic models were employed, for example, in [DAV 00, TIA 02, SAH 04]. In the latter work, the speed range was made road dependent, and obtained as [vmax − δ, vmax + δ], where vmax was the maximum speed allowed on the current road, and δ was a tunable value.
These models are clearly not representative of a real-world driver behavior, since they completely disregard the fact that the speed of each vehicle depends on the presence of other vehicles nearby at least. As a result, vehicles can, for example, travel over one another and cross an intersection at the same time. A more complex stochastic model was introduced in [BAI 03], so as to avoid the possibility of vehicles traveling over each other. The proposed model, called the Freeway model, still employed random speed decision, but forced each driver to maintain a speed lower than that of the preceding vehicle. However, the Freeway model was proven to yield properties very far from the minimum requirements demanded for a realistic microscopic mobility simulation [FIO 08].
A few microscopic mobility models were proposed by leveraging traffic stream properties of road traffic. These models looked at vehicular mobility as a hydrodynamic phenomenon and related the three fundamental variables of velocity v (in km/h), density ρ (vehicles/km) and flow q (in vehicles/h), according to the fundamental equation:
As a result, the speed of a vehicle was determined according to the road traffic intensity over the road segment it was travelling on. Examples of traffic stream models employed in the vehicular networking literature can be found in [SES 92, RUD 02]. Although they represent an improvement with respect to stochastic models, traffic stream models yield a limited level of detail, for example forcing all the vehicles on the same road segment to travel at the exact same speed. As such, traffic stream models were also proven not to be a solution for the simulation of vehicular networks [FIO 08].
A significantly higher level of realism is provided by car-following models that describe the behavior of a driver depending on the state of its neighboring vehicles. Most car-following models determine the acceleration of a vehicle in relation to the state of the car in front. A general expression for a car-following model is:
where vi(t) and xi(t) are the speed and position of vehicle i at time t. The equation allows us to compute the acceleration of i, depending on the absolute and relative speed of both vehicles, as well as their distance xj(t) − xi(t). Examples of car-following models employed in the simulations of vehicular networks abound, and include the intelligent driver model (IDM) [TRE 00] employed, for example, in [JAA 05, HÄR 11, BAU 08], the Krauss model [KRA 97] adopted, for example, by [BRE 01, KAR 07] or the Gipps model [GIP 81] used in [FRA 06]. All these models have been validated through standard tests proposed by the transportation research community.
An alternative to car-following modeling, that is equivalently valid, is represented by cellular automata models. These models discretize time (by assuming a fixed-length time step), space (by fragmenting roads into cells each hosting a single car at most) and speed (by considering a finite state of instantaneous speeds). The movement of cars is then described, at each time step, as a shift of finite states (i.e. vehicles with an associate speed) along a one-dimensional lattice of cells. Different cellular automata models implement different rules to realize the shift: a widely adopted model is the Nagel-Schreckenberg model [NAG 92], which is used for the simulation of vehicular networks in [FRA 06].
All the models discussed to this point deal with intraflow microscopic mobility, that is they can be used to determine the movement of vehicles over a single unidirectional lane. However, in most real-world scenarios, interflow interactions must be modeled as well. The latter occur in highway traffic, when, for example, one vehicle overtakes the other in front (and thus changes lane, merging into a new flow) or joins the traffic from a ramp. Similarly, when simulating urban traffic, flows constantly merge at intersections or roundabouts. Thus, modeling intraflow mobility is critical to achieve a complete road traffic representation in vehicular network simulation.
Models have thus been proposed that complement the intraflow descriptions presented above, by adding rules to manage the movement of a vehicles from one flow to another. These interflow models are typically built over realistic car-following or cellular automata models, and extend them so as to mimic lane changing and ramp in-flow [TRE 02, KRA 98, NAG 98], as well as intersection management in the presence of road signalization (e.g. traffic lights, stop or yield signs) [HÄR 11]. A detailed presentation of all these interflow models is out of the scope of this chapter, and we once again point the interested reader to [FIO 09] and references therein for a thorough discussion.
A detailed representation of the road topology and a faithful driver behavior model are not sufficient to the generation of a realistic synthetic trace of road traffic. Indeed, the first two components discussed above allow vehicles to move on a real-world street layout with an accurate microscopic behavior, that is stopping at red traffic lights, respecting speed limits, performing overtakings and avoiding accidents. However, an important question remains unanswered: where should vehicles go? In other words, the missing component is the macroscopic description of road traffic that determines when vehicles start their trips and from which location, which route they choose, and where they finally stop.
The macroscopic description is critical to the realism of the resulting trace, since it is easy to understand that it determines the volume of traffic in the scenario, as well as its evolution over time. In addition, the start and stop locations of trips and the routes followed by each vehicle in the real world guide the planning of the road topology, which, as a consequence, is designed to accommodate the real-life traffic flows. Therefore, injecting unrealistic (e.g. random) flows in the road topology risks leading to large traffic jams in some areas and road underutilization in others.
In fact, the availability of accurate road topology information, discussed in section 6.2.1, and of detailed intra- and interflow mobility models, as from section 6.2.2, makes the description of macroscopic traffic the real challenge on the path toward realistic synthetic traces of vehicular mobility. To faithfully mimic macroscopic traffic flows along highway networks and across metropolitan areas, we must correctly identify the traffic demand, that is the start time, the origin and the destination of each car trip in the simulated region, represented as a so-called Origin/Destination (O/D) matrix. Then, an appropriate traffic assignment algorithm needs to be run on the O/D matrix, so as to identify the realistic route followed by each driver to reach his/her destination.
Most of the simulative evaluations in the vehicular networking literature neglect the importance of the macroscopic traffic description, and assume random traffic demands, that is O/D matrices that contain random locations and times, or fixed probabilistic turns at each intersection. Also, the shortest path is the common solution to the traffic assignment problem. Such an approach easily leads to unrealistic flows and thus strongly biased simulation results.
However, as the awareness on the importance of macroscopic modeling grows, solutions start to be proposed and adopted in order to generate traces that are also realistic from the viewpoint of large-scale traffic flows. In section 6.4, we will thus classify the datasets currently available for the simulation of vehicular networks according to the macroscopic description they employ.
We describe in this section different tools available to the community to extract synthetic mobility traces for vehicular networking. A larger coverage on vehicular mobility simulators may be found in [HÄR 10, HÄR 09].
Mostly developed for urban traffic engineering, microscopic traffic simulators such as PARAMICS [PAR 12], CORSIM [TSI 12], VISSIM [VIS 12a], TRANSIMS [TRA 12], AIMSUN [AIM 12], VanetMobiSim [VAN 12] or SUMO [SUM 12] are able to model individual urban traffic at a microscopic level. Yet, not all of these simulators can be used straightaway for vehicular networking, as either synthetic traces cannot be exported or open Application Programming Interface (API) are not available to interconnect them with a network simulator. The semicommercial simulators VISSIM and AIMSUN provide support for trace extractions and interconnection. In the interest of comparability of research results, it is however more beneficial to use readily available free and open source software simulators, such as SUMO. SUMO is capable of extracting synthetic traces in the shape of data files and provides external control through an open API called TraCI.
From a macroscopic road traffic level (topological maps and traffic models), they mostly all support similar features, but it is at the microscopic level that they differ. For instance, TRANSIMS and AIMSUN are based on an extension of the Gipps microscopic flow equations [GIP 81], whereas VISSIM is based on a psychophysical flow model from Wiedemann [WIE 74]. SUMO initially supported only the Krau flow model [KRA 97] and its extensions, but has been recently been extended to include the same complex Gibbs model called IDM from Treiber et al. [TRE 00] as VanetMobiSim.
Microscopic traffic simulators represent the most used simulators to simulate vehicular networks, as they are capable of modeling individual mobility at a high level of precision. It is also this feature that made microscopic traffic simulators popular for the design and evaluation of traffic safety applications based on vehicular communications. The scale is their limitation, as modeling individual and strongly correlated mobility at a microscopic level requires a significant computational capability. Nevertheless, simulators such as SUMO or VISSIM are capable of simulating up to 10,000 vehicles faster than or equal to real-time, and SUMO has been the preferred choice for the open-source intelligent transportation system (ITS) simulation platform iTETRIS [ITE 11].
One typical approach to simulate traffic at a mesoscopic level is to model road elements as a queue and intersections as nodes. The vehicular dynamics are represented by queue parameters, such as the queue capacity (the maximum bumper-to-bumper vehicles allowed on a road element) and the maximum flow of the queue. The node parameters represent the intersection scheduling policy, such as the intersection type, level of priority and access control to connecting queues. The simulators Matsim [MAT 12] and FastTrans [FAS 11] are two popular tools in this category. Both simulators support the import of detailed topological maps and detailed added features, and also include efficient traffic models (macroscopic) such as advanced Dijikstra routing and origin-destination matrices. Both are capable of simulating and extracting synthetic traces of individual cars up to a city-wide scale. FastTrans also provides parallelization on multiprocessors for a higher scalability.
The mesoscopic traffic simulators represent the best trade-off between granularity and scalability, as they can simulate very large scenarios, but still provide the detailed mobility values of each vehicle. For instance, mesoscopic simulators are a preferred choice to simulate large-scale impacts of vehicular communication to improve traffic efficiency. Mesoscopic simulators are yet not recommended for the evaluation of vehicular networking for traffic safety applications, as they do not provide a sufficient granularity, in particular, between vehicles located in the same mesoscopic queue.
Traffic simulated at a macroscopic flow level does not consider the mobility parameters of a specific car but instead quantities of macroscopic meanings such as flow, speed or density. Inspired by fluid theory, macroscopic flows have the advantage of a reduced computational complexity compared to the microscopic flows but they can still realistically model macroscopic quantities. The most well-known simulator capable of simulating vehicular traffic at a macroscopic scale is VISUM from PTV [VIS 12b]. As other simulators, it is capable of importing precise topological maps and can configure the traffic light policies at a very precise level. It is typically used by urban planners and traffic departments at the city and regional level to evaluate traffic congestions.
The synthetic traces obtained by macroscopic simulators cannot be used for vehicular networking directly, as they do not provide detailed mobility values of single entities, but instead aggregated measures such as density and speed. Macroscopic simulators are also unable to model mobility changes or personalized navigation of single vehicles that is typically found in ITS applications for traffic efficiency. Yet, aggregated mobility values are crucial for the design of efficient vehicular networking solutions, for instance, considering that aggregated vehicular density in various streets are indicators of vehicular connectivity. Also, macroscopic synthetic traces are often used to calibrate the microscopic traffic simulators, such as SUMO. Within the iTETRIS project [ITE 11], for instance, traffic in the city of Bologna has been simulated using SUMO, but during the calibration step, synthetic traffic flows extracted from VISUM have been used.
Obtaining close-to-reality synthetic traffic traces and using it for vehicular networking requires using multiple simulators. Traffic calibration first requires multiple sources of data that come from external sources. Second, vehicular networking needs to be able to use the mobility information from the simulators. For the sake of clarity in this chapter, we will differentiate between the use of multiple traffic simulators to calibrate one or multiple simulators to obtain synthetic traces, and the use of multiple types of simulators for vehicular networking. However, conceptually speaking, both categories fall into the same domain relating the interactions between simulators.
The first step to design and obtain synthetic traffic traces is to select the traffic simulator fitting best. Yet, as any tool, a simulator needs to be fed with parameters, such as topological map, traffic demand, traffic lights policy or driver models. Such data may either be obtained from statistical behaviors or extracted from dedicated simulators. Considering the case of the calibration of the city of Bologna, as conducted during the iTETRIS project [ITE 11], the selected traffic simulator was SUMO. Yet, multiple various other simulators have been used to be able to calibrate the synthetic traces. Conceptually speaking, calibrating a simulator may be represented as in Figure 6.3. First, the macroscopic simulator VISUM has been configured with the topological map of the city of Bologna and from vehicular flow interactions measured at intersections. The output of VISUM took the shape of traffic volumes at each road segment that have later been imported by SUMO to calibrate its traffic demand. Second, a traffic light control simulator has been used to be able to provide a close-to-reality traffic light policy in the city of Bologna. This policy has then been integrated into SUMO. The output has been a calibrated synthetic trace of the typical traffic in the city of Bologna for 1 hour.
Figure 6.3. The microscopic simulator SUMO calibrated by external simulators

We previously described the different methods required to obtain close-to-reality synthetic vehicular traces. Yet, in order to be used by the vehicular networking community, these traces need to be made available to network simulators. The description of network simulators available to vehicular research is out of the scope of this chapter, but we may still cite ns-3 [NS3 12] and OMNET++ [OMN 12] as two popular simulators that are often used in research, as cited in [JOE 12].
The interaction between traffic and network simulators may be categorized into two groups as illustrated in Figure 6.4 isolated and federated. In the former case, synthetic traces are extracted from traffic simulators in the shape of mobility files that may later be integrated into the network simulator using a dedicated parser. In the latter case, a bidirectional interaction is created between two (or more) simulators to be able to exchange mobility data or to influence the control of one or the other. This approach is more complex, as an interface has to be developed to synchronize and exchange data.
Figure 6.4. Interactions between network and traffic simulators

The isolated case was initially the preferred choice for network design based on small-scale random mobility, but nowadays, network simulators are able to integrate large-scale realistic mobility data files from various sources. This approach also remains a favorite choice when mobility does not need to be influenced by vehicular communication or networking. Considering applications for ITSs, mobility shall be influenced, either to avoid an accident, or to reduce congestion. So, the federated case is mostly used in that case. Several integrated tools have been created and made available to the community. The iTETRIS platform interlinks the simulator SUMO and ns-3 [NS3 12], the VEINS platform [VEI 12] interlinks SUMO and OMNET++ [OMN 12], and VSIMRTI [VSI 12] provides APIs to interlink jist/swans [SWA 12] and VISSIM. iTETIS and VEINS are both open source, but VsimRTI only provides open APIs without releasing the code of its core.
Figure 6.5. Turin scenario: city center, sparse traffic

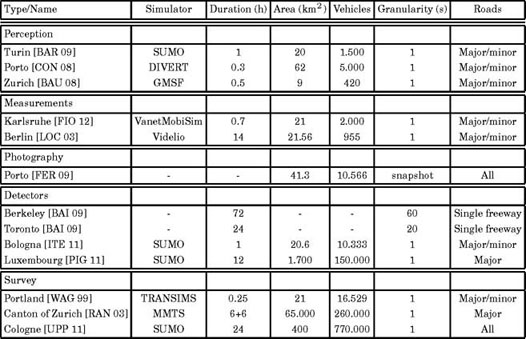
In this section, we will overview the body of work on vehicular mobility traces for network simulation. We categorize the datasets based on the nature of their macroscopic traffic data, that is the sources employed to determine the time and routes of trips traveled by individual vehicles in the dataset. The most relevant features of the different mobility traces we discuss in the following are summarized in Table 6.1.
Table 6.1. Major features of publicly available vehicular mobility traces
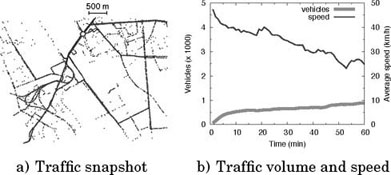
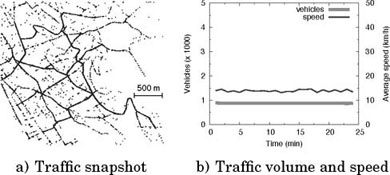
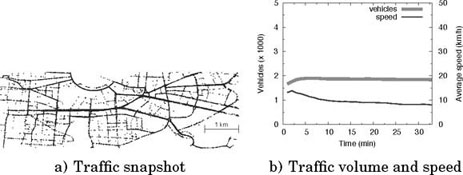
A simple way to fill the O/D matrix and determine the traffic assignment is to employ one’s perception of the road traffic. The authors [BAR 09] leveraged their knowledge of the traffic in Turin, Italy, so as to determine the macroscopic demand injected in different areas of the city. The traces were generated using OSM as the road topology database and SUMO as the microscopic traffic simulator. Figures 6.5 and 6.6 refer to the Turin city center and Turin outskirts scenarios, respectively. In both figures, the left plots portray a snapshot of the vehicular mobility, so as to provide an intuitive glimpse of the mobility reproduced by each trace. Also, dot brightness is used to distinguish fluid traffic conditions from traffic congestion: light dots denote high average speeds, whereas dark ones indicate speeds close to zero. We can observe heavy localized traffic jams in Figure 6.5(a): given the sparse traffic conditions assumed in this scenario, congestion is an artifact of the incorrect traffic demand modeling rather than a representation of a real-world phenomenon. The snapshot in Figure 6.6(a) depicts instead a much simpler road topology, where traffic is fluid along the few major roads and absent elsewhere. Congestion is only recorded around the main roundabout in the northern region of the scenario. Figure 6.5(b) and Figure 6.6(b) show instead the time evolution of the traffic volume and average speed, for the same two scenarios. We can observe that, notwithstanding the limited duration of the traces, none of them is in a stationary condition. In both cases, the number of vehicles in the region tends to grow, while speeds decrease. The significant difference between the traffic conditions at the beginning and at the end of the traces is another evidence of the difficulty of calibrating the traffic demand based on pure perception. As an example, in Figure 6.5(b), the average speed starts at 30 km/h (that, considering the presence of traffic lights, denotes a completely empty road network) and progressively drops to 10 km/h (that is instead a symptom of major congestion) in less than 1 hour. Such a phenomenon would be hardly observed in the real world, in the presence of the sparse traffic assumed in the trace.
Figure 6.6. Turin scenario: city outskirts, dense traffic
We remark that a similar macroscopic approach is also adopted in [CON 08], although a different microscopic simulator framework, named DIVERT, is employed. The city concerned is in this case Porto, in Portugal.
The technique used to generate mobility traces of the region of Zurich, Switzerland, in [BAU 08], is instead slightly different. Apart from the microscopic simulation environment adopted, that is this time Generic Mobility Simulation Framework (GMSF), and the road topology information, retrieved from the Swiss Geographic Information System (GIS), the macroscopic traffic flows are injected assuming that larger roads attract more traffic. The features of the resulting mobility are reported in Figure 6.7, for one of the scenarios in [BAU 08], namely that representing the city center (the others refer instead to suburban and rural areas). From the traffic snapshot, in Figure 6.7(a), we can observe that, in the small region compassed by the simulation (less than 10 km2), the traffic tends to be consistently slow over the whole street layout. Such a uniformity is also present in time, as the number of vehicles in the region and the average speed are constant over the 20 min of duration of the trace. Overall, the Zurich city center trace exhibits speeds exceedingly low with respect to the traffic volume considered. More importantly, the mobility description appears significantly limited in terms of size and temporal duration.
Figure 6.7. Zurich scenario: city center
In fact, a common weakness of traces built on simplistic macroscopic traffic descriptions is that they show limited extension, in both space and time. As a matter of fact, they only cover a few tens of square kilometers, and have durations ranging between 20 min and 1 hour. This limitation is a by-product of the macroscopic description: the perception approach can be applied on small areas for short time periods. However, the lack of real-world data behind the traffic demand and assignment leads to significant problems when large regions or long time periods are taken into account. Manually assigning large-scale flows so that the road topology can accommodate them is a prohibitive task. Similarly, the introduction of realistic variations of road traffic over time is hard to accomplish, if no realistic data are available to support it.
Several works have exploited small-scale measurements, typically conducted by the authors themselves, so as to provide some simple validation to the authors’ perception or to complement the latter. This is the case of the mobility trace presented in [LOC 03] that reproduces the vehicular traffic in the center of Berlin, Germany. The trace, generated with a dedicated microscopic simulator named Videlio, covers a small area of around 20 km2 for a quite long period of 14 hours. However, the small number of vehicles (less than 1,000) present in the trace over such a long time interval raises questions on the realism of the macroscopic traffic demand employed.
Small-scale measurements are also at the base of the macroscopic modeling in the trace of downtown Karlsruhe, Germany, employed in [FIO 12]. The dataset, generated by feeding a OSM map to the VanetMobiSim microscopic mobility simulator, mimics the movement of 2,000 vehicles for approximately 40 min. The plots in Figure 6.8 show that, similarly to what observed for the Zurich traces before, the number of vehicles is quite stable, while the vehicular mobility is characterized by a generalized low speed. In fact, the average velocity recorded in the trace shows a slow but constantly decreasing trend with a steady traffic volume, a symptom of potential problems when extending the simulation duration.
Figure 6.8. Karlsruhe scenario: city downtown
Overall, approaches based on small-scale measurement represent an appreciable effort toward the simulation of more realistic traffic demands. However, it is clear that they lack the statistical rigor needed for a realistic representation of the macroscopic traffic distribution, and, as such, can hardly capture the complexity of traffic flows in urban areas or their evolution over long time periods. For these reasons, these traces only cover modest geographical surfaces, constrained to a few tens of square kilometers, or have limited time duration, in the order of tens of minutes.
An original solution to the derivation of the macroscopic traffic information was adopted in [FER 09], where the authors leveraged stereoscopic aerial photography in order to capture the vehicle distribution in the city of Porto, Portugal. A private aircraft was flown over the city for 2 hours in the early afternoon of a weekday, and photographs were shot from the plane every 5 s. The flight followed a parallel row pattern so as to cover the whole geographical area of 41.3 km2 corresponding to the surface of Porto. By studying the aerial imagery, the authors were able to reconstruct a single snapshot of the positions of 10.566 vehicles in the urban area. The time error in the snapshot, due to the fact that pictures of different locations were taken at different moments, is of 23 min between two cars, on average. Although this appears as an interesting way to derive static macroscopic data, its applicability to the generation of mobility traces is not clear, due to the complexity and cost of running a large-scale aerial photography campaign for a significant period of time.
Another interesting attempt at using imagery to estimate the macroscopic behavior of car traffic has recently been presented in [THA 11]. There, the authors exploit the pervasiveness of road surveillance cameras to infer traffic densities in two large urban areas, namely London and Sydney. Although promising, this approach has not yet been used for the generation of traffic demands in mobility traces.
Induction loops, infrared counters and roadside sensors represent the traditional way to measure vehicular traffic flows in both freeways and urban road networks. The authors [BAI 09] use two sets of empirical data obtained from dual-loop and metal detectors from sections of the I-80 Freeway in Berkeley, CA, USA, and of the Gardiner Expressway in Toronto, Canada. The detector information covers a span of 24 hours and allows us to determine the per-lane intervehicle arrival time and spacing. Although the data could be fed to a microscopic simulator to derive the position of individual vehicles over time, their validity is limited to highway environments.
Roadside detectors have been employed in a urban environment within the iTetris project [ITE 11]. Vehicular mobility traces of several areas of the city of Bologna were generated accounting for macroscopic traffic data acquired through 636 induction loops spread over the road network, and complemented by user surveys on usual commuting trips. The main trace covers 20.6 km2 in the city center for a period of 1 hour, featuring the movement of 10,333 vehicles. Because of the real-world nature of the macroscopic data they are built upon, these traces reach an unprecedented level of realism. Unfortunately, they do not cover large surfaces or long time periods.
A similar approach has been discussed in [PIG 11], where the authors calibrate the microscopic mobility simulation of the city of Luxembourg through traffic flow information gathered by the local Ministry of Transport. As such real-world data only covers major traffic arteries, it is complemented by driver routes inferred from the different nature of geographical zones in the area under study, and used to define traffic flows on medium- and small-sized roads. The resulting mobility trace covers a very large area of 1,700 km2 and features 150,000 car trips. Although a very interesting dataset, the Luxembourg trace focuses on highway and major roads traffic, as depicted in Figure 6.9(a), and only accounts for inbound flows, that is traffic moving toward the city center. Furthermore, the dataset is limited to the morning period and yields clearly unstable traffic conditions toward the end of the simulated period, as shown in Figure 6.9(b).
Sociodemographic surveys represent a significant source of information for the derivation of vehicular traffic data. Seminal work in that direction was performed in [WAG 99], where the authors generated a mobility trace whose macroscopic traffic description is obtained from knowledge of driver activity in downtown Portland, OR, USA. The resulting mobility dataset is acknowledged to be very realistic, but it only covers 15 min of vehicular movements in an small area of 21 km2, for a total of 16.529 simulated cars. Moreover, the trace is not publicly available.
Figure 6.9. Luxembourg scenario: Luxembourg city and surroundings

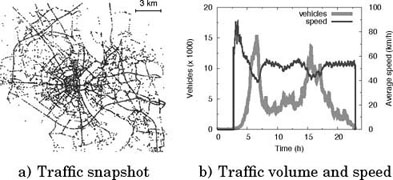
The largest vehicular mobility trace generated to date is the trace reproducing the road traffic in the whole Canton of Zurich, a 65.000 km2 region of Switzerland [RAN 03]. The mobility dataset is said to cover 24 hours, through traffic demand data obtained from the Swiss Regional Planning Authority and complemented using the 1994 Swiss National Travel Survey. The resulting trace, as well as subsets of the same, is widely employed in the vehicular networking literature. However, the size of the road topology forced the authors to limit the detail of the microscopic-level simulation. Thus, they resorted to a queue-based multi-agent microscopic traffic simulator (MMTS), significantly less accurate than standard fine-grained vehicular mobility simulators based on car-following models. Moreover, once again due to scalability reasons, the road topology was pruned down to major traffic arteries, as observable in Figure 6.10(a), that portrays a snapshot of the vehicular mobility in the most significant 400 km2 portion of the simulated region. The selected area represents the city of Zurich and its surroundings: the low topological detail is striking, especially when comparing the figure with Figure 6.7(a), that represents that city center only, but at a much higher detail level. The light color that dominates the plot also indicates a high average speed: this is normal, since only major roads, that is highways and freeways, are represented. However, the lack of minor urban and rural roads clearly affects the completeness of the mobility description provided by the trace.
Figure 6.10. Canton of Zurich scenario: Zurich city and surroundings

Elevated average speeds are also observed in Figure 6.10(b), where, however, the more interesting aspect is the limited detail of the traffic demand. As a matter of fact, the plot evidences how the trace only considers vehicular mobility during the morning and afternoon traffic peaks, while the off-peak hours are neglected, with the traffic volume dropping to zero. The Canton of Zurich trace is therefore a clear example of the trade-off between complexity and scale in the generation of synthetic vehicular mobility traces: in order to be able to reproduce road traffic on a very large scale, we have to accept low road topology detail, low microscopic precision and approximate macroscopic description.
The vehicular mobility dataset in [UPP 11] reproduces the road traffic in the greater urban area of the city of Cologne, in Germany. The trace was generated by extracting OSM data about 4,500 km of roads in an area of more than 400 km2 around the urban agglomeration of Cologne. The OSM information was then fed to SUMO, and coupled with a macroscopic traffic demand provided by the TAPASCologne project, an initiative by the Institute of Transportation Systems at the German Aerospace Center (ITS-DLR). More precisely, the O/D matrix was generated though the Travel and Activity Patterns Simulation (TAPAS) methodology [VAR 06], a technique that exploits information on (1) the population, that is home locations and sociodemographic characteristics, (2) the PoI in the urban area, that is places where working and free-time activities take place, and (3) the time use patterns, that is habits of the local residents in organizing their daily schedule [HER 04]. The TAPAS methodology was applied on real-world data collected in the Cologne region by the German Federal Statistical Office, including 30,700 daily activity reports from more than 7,000 households [RIN 02, EHL 96].
The resulting TAPASCologne O/D matrix faithfully mimics the daily movements of inhabitants of the area for a period of 24 hours, for a total of 1.2 million individual trips.
The assignment of the vehicular traffic flows described by the TAPASCologne O/D matrix over the road topology was then performed by means of the Gawron algorithm [GAW 98]. This traffic assignment technique calculates the fastest route for each vehicle, and then assigns to each road segment a cost reflecting the intensity of traffic over it. By iteratively moving part of the traffic to alternate, less congested paths, and recomputing the road costs, the scheme finally achieves a so-called user equilibrium. Additionally, since the intensity of the traffic demand varies over time, the traffic assignment model must also be able to adapt to the time-varying traffic conditions. Indeed, Gawron’s algorithm satisfies such a requirement, thus attaining a so-called dynamic user equilibrium. Gawron’s is one the most popular traffic assignment techniques developed within the transportation research community and allows us to reach a road capacity utilization close to reality and significantly higher than that obtained with, for example, a simple weighted Dijkstra algorithm.
The resulting vehicular mobility trace is shown in Figure 6.11. Figure 6.11(a) show the large scale as well as the high level of detail of the dataset that comprises at the same time highways, rural roadways, major roads and small streets in the urban center. In addition, speeds match the expectations, since highways and peripheral roads are characterized by high velocities, while the average speed is reduced when closing down on the city center. However, no unrealistic congestion (i.e. widespread dark color) can be noticed, even if the snapshot is taken at 7.30 am, that is during the morning traffic peak. Figure 6.11(b) proves how the traffic volume is representative of the typical daily activity, with morning and afternoon traffic peaks, but a non-zero activity otherwise, including a minor peak around noon.
Figure 6.11. Cologne scenario: Cologne city and surroundings
Overall, the ultimate vehicular mobility trace for network simulation should feature all of the following: (1) representation of the completeness of the road traffic; (2) a high time granularity, the position of each vehicle being traced with at least an order-of-second precision; (3) compass very large regions (i.e. whole urban areas), with a faithful description of the road layout and signalization; (4) provide a realistic representation of the microscopic behavior of individual drivers in everyday traffic, accounting for their interactions with other drivers and their behavior with respect to road regulations; (5) be also realistic from a macroscopic point of view, by faithfully mimicking the movement of large-scale traffic flows across a metropolitan area, over long time periods.
The first two requirements rule out traces obtained though real-world tracking, as they are limited to subsets of the vehicles, that is buses or taxis, and exhibit reduced temporal detail, that is order-of-minute position information updates. These traces are today mainly employed for the performance evaluation delay-tolerant or opportunistic data exchanges, and remain interesting for applications that fit such transfer paradigms.
By then resorting to synthetic mobility traces, the third constraint can also be easily met, thanks to the availability of accurate real-world road map services. Similarly, recent vehicular mobility simulators allow us to satisfy the fourth requirement, as they implement realistic microscopic vehicular mobility models, borrowed from transportation theory and validated through comparison with real-world measurements. Today’s challenge lies in fact in the last aspect, that is attaining macroscopic-level realism in the simulation of road traffic. As previously discussed, the problem is separated into two phases, that is the identification of the traffic demand and the iteration of an appropriate traffic assignment algorithm on the O/D matrix.
The synthetic traces presented in this chapter address the issue of macroscopic realism by using different data sources, as clearly outlined by the classification we proposed. Some sources are hardly credible by their own nature (e.g. perception or small-scale measurements) or not scalable due to their complexity (e.g. aerial photography). Finally, and quite unsurprisingly, the most reliable and scalable sources are those commonly employed by transportation engineering (e.g. road traffic detectors and population surveys).
However, none of the traces making use of such macroscopic traffic data sources cover large urban regions for long periods of time, and provide at the same time high microscopic-level accuracy. The Berkely and Toronto traces [BAI 09] are limited to one freeway segment. The Bologna [ITE 11] and Portland [WAG 99] datasets focus on small urban areas of a few tens of square kilometer. The Luxembourg [PIG 11] and Canton of Zurich [RAN 03] traces are closer to compassing all of the desirable features we outlined above. However, their limit lies in that they mainly model traffic on major roads, as also testified by the relatively low number of vehicles per square kilometer they comprise. The only dataset that seems to meet all the requirements is the Cologne dataset [UPP 11], which couples a large scale with a high level of detail and an accurate macroscopic traffic description.
We stress, however, that the road to the generation of ultimate synthetic vehicular mobility traces is still long. More precisely, aspects that are still to be addressed concern at the same time the scalability of microscopic simulation and the increased detail of the same. In terms of scalability, it would be desirable to obtain traces that cover whole regions, and, why not, even countries. As far as the level of detail is concerned, a highly desirable feature that is missing today is instead the timing of traffic lights in the simulation environment so that it matches the real-world configuration.
Moreover, the macroscopic traffic description remains an open problem. Apart from isolated initiatives, such as TAPASCologne, realistic road traffic demand information on vast regions is hard to retrieve. To that end, the growing trend of government bodies and local administrations making urban-related data publicly available can provide a significant breakthrough. Open access data initiatives such as Vancouver’s VanMap, OpenBaltimore, London DataStore and ParisData, just to cite a few significant examples, could indeed lead to the public disclosure of road counter collections or traffic flow datasets. Such information would, in turn, grant the possibility to extract new macroscopic O/D matrices as well as validate traffic assignments.
Finally, it is important to note that random models, both at the motion constraint and traffic demand sides, have lost momentum over the past few years. Yet, they should not be ignored, as they still represent a very powerful approach for fast configuration of motion patterns, where statistical evaluations over multiple different configurations are more important than on a specific dataset. The challenge in that case is to provide random models, yet ones that are statistically representative of realistic vehicular motion patterns, such as random graphs providing statistically similar motion constraints or random traffic demands providing statistically similar macroscopic traffic patterns.
[AIM 12] AIMSUN, http://www.aimsun.com/wp/, 2012.
[BAI 03] BAI F., SADAGOPAN N., HELMY A., “The IMPORTANT framework for analyzing the Impact of Mobility on Performance Of RouTing protocols for Adhoc NeTworks”, Elsevier Ad Hoc Networks, vol. 1, pp. 383–403, 2003.
[BAI 09] BAI F., KRISHNAMACHARI B., “Spatio-temporal variations of vehicle traffic in VANETs: facts and implications”, ACM VANET, Beijing, PRC, 2009.
[BAR 09] BARBERIS C., G.M., “Large-scale simulation of V2V environments”, IEEE ICUMT, St. Petersburg, Russia, 2009.
[BAU 08] BAUMANN R., LEGENDRE F., P.S., “Generic mobility simulation framework (GMSF)”, ACM MobilityModels, Hong Kong, PRC, 2008.
[BRE 01] BREISEMEISTER L., Group Membership and communication in highly mobile ad hoc networks, PhD thesis, Tecnhical University of Berlin, 2001.
[BUR 06] BURGESS J., GALLAGHER B., JENSEN D., et al., “MaxProp: routing for vehicle-based disruption-tolerant networks”, IEEE INFOCOM, Barcelona, Spain, 2006.
[BUR 12] BUREAU U.C., “Topologically integrated geographic encoding and referencing (TIGER) system”, http://www.census.gov/geo/www/tiger, 2012.
[CON 08] CONCEIÇÃO H., DAMAS L., FERREIRA M., et al., “Large-Scale Simulation of V2V Environments”, ACM SAC, Fortaleza, Brazil, 2008.
[DAV 00] DAVIES V., Evaluating mobility models within an ad hoc network, Master’s thesis, Colorado School of Mines, 2000.
[ERT 12] ERTICO, Geographic Data Files, http://www.ertico.com/gdf-geographic-data-files, 2012.
[FAS 11] FASTTRANS, http://www.lanl.gov/programs/nisac/fasttrans.shtml, 2011.
[FER 09] FERREIRA M., CONCEIÇÃO H., FERNANDES R., et al., “Stereoscopic aerial photography: an alternative to model-based urban mobility approaches”, ACM VANET, Beijing, PRC, 2009.
[FIO 08] FIORE M., HÄRRI J., “The networking shape of vehicular mobility”, ACM MobiHoc, Hong Kong, PRC, 2008.
[FIO 09] FIORE M., “Vehicular mobility models”, Vehicular Networks from Theory to Practice, Chapman & Hall/CRC, 2009.
[FIO 12] FIORE M., CASETTI C., CHIASSERINI C.-F., et al., “Discovery and verification of neighbor positions in mobile ad hoc networks”, IEEE Transactions on Mobile Computing.
[FRA 06] FRACCHIA R., MEO M., ROSSI D., “VANETs: to beacon or not to beacon”, IEEE Globecom Autonet, San Francisco, CA, USA, 2006.
[GAW 98] GAWRON C., “An iterative algorithm to determine the dynamic user equilibrium in a traffic simulation model”, International Journal of Modern Physics C, vol. 9, no. 3, pp. 393–407, 1998.
[GIP 81] GIPPS P., “A behavioural car following model for computer simulation”, Transportation Research B, vol. 15, pp. 105–111, 1981.
[HÄR 09] HÄRRI J., FILALI F., C.B., “Mobility models for vehicular ad hoc networks: a survey and taxonomy”, IEEE Communications Surveys and Tutorials, vol. 11, no. 4, pp. 19–41, 2009.
[HÄR 10] HÄRRI J., “Vehicular mobility modeling for VANET”, VANET Vehicular Applications and Inter-Networking Technologies, pp. 107-156, 2010.
[HÄR 11] HÄRRI J., FIORE M., FILALI F., et al., “Vehicular mobility simulation with VanetMobiSim”, Transactions of The Society for Modeling and Simulation International, vol. 87, no. 4, 2011.
[HER 04] HERTKORN G., WAGNER P., “The application of microscopic activity based travel demand modelling in large scale simulations”, World Conference on Transport Research, Istanbul, Turkey, 2004.
[ITE 11] ITETRIS, An integrated wireless and traffic platform for real-time road traffic management solutions, http://ict-itetris.eu/10-10-10-community/, 2011.
[JAA 05] JAAP S., BECHLER M., L.W., “Evaluation of routing protocols for vehicular ad hoc networks in city traffic scenarios”, IEEE ITSC, Vienna, Austria, 2005.
[JET 03] JETCHEVA J., HU Y.-C., PALCHAUDHURI S., et al., “Design and evaluation of a metropolitan area multitier wireless ad hoc network architecture”, IEEE WMCSA, Monterey, CA, USA, 2003.
[JOE 12] JOERER S., DRESSLER F., SOMMER C., “Comparing apples and oranges? Trends in IVC simulations”, 9th ACM International Workshop on Vehicular Internetworking (VANET 2012), Low Wood Bay, Lake District, UK, June 2012.
[KAR 07] KARNADI F., MO Z., LAN K.-C., “Rapid Generation of realistic mobility models for VANET”, IEEE WCNC, Hong Kong, 2007.
[KRA 97] KRAUSS S., WAGNER P., GAWRON C., “Metastable states in a microscopic model of traffic flow”, Physical Review E, vol. 55, no. 304, pp. 55–97, 1997.
[KRA 98] KRAUSS S., Microscopic modeling of traffic flow: Investigation of collision free vehicle dynamics, PhD thesis, University of Cologne, 1998.
[KRA 02] KRAJZEWICZ D., HERTKORN G., ROSSEL C., et al., “SUMO (Simulation of Urban MObility): an open-source traffic simulation”, SCS MESM, Sharjah, United Arab Emirates, 2002.
[LOC 03] LOCHERT C., HARTENSTEIN H., TIAN J., et al. “A routing strategy for vehicular ad hoc networks in city environments”, IEEE IV, Columbus, OH, USA, 2003.
[MAT 12] MATSIM, http://matsim.org, 2012.
[MEI 11] MEIHUISOFTWARE, http://www.meihuichina.com, 2011.
[NAG 92] NAGEL K., SCHRECKENBERG M., “A cellular automaton model for freeway traffic”, Journal de Physique I, vol. 2, no. 12, pp. 2221-2229, 1992.
[NAG 98] NAGEL K., WOLF D., WAGNER P., et al. “Two-lane traffic rules for cellular automata: a systematic approach”, Physical Review E, vol. 58, pp. 1425–1437, 1998.
[NAN 06] NANDAN A., TEWARI S., DAS S., et al., “AdTorrent: delivering location cognizant advertisements to car networks”, WONS, Les Ménuires, France, 2006.
[OMN 12] OMNET++, http://www.omnetpp.org/, 2012.
[OPE 12] OPENSTREETMAP, The free wiki world map, http://www.openstreetmap.org, 2012.
[PAR 12] PARAMICS, http://www.paramics.com/, 2012.
[PIG 11] PIGNE Y., DANOY G., P. B., “A vehicular mobility model based on real traffic counting data”, Nets4Cars, Oberpfaffenhofen, Germany, 2011.
[RAN 03] RANEY B., CETIN N., VÖLLMY A., et al., “An agent-based microsimulation model of Swiss travel: first results”, Networks and Spatial Economics, vol. 3, no. 1, pp. 23-41, 2003.
[RUD 02] RUDACK M., MEINCKE M., LOTT M., “On the dynamics of ad hoc networks for inter-vehicle communications (IVC)”, ICWN, Las Vegas, NV, USA, 2002.
[SAH 04] SAHA A., JOHNSON D., “Modeling mobility for vehicular ad hoc networks”, ACM VANET, Philadelphia, PA, USA, 2004.
[SES 92] SESKAR I., MARIE S., HOLTZMAN J., et al., “Rate of location area updates in cellular systems”, IEEE VTC, Denver, CO, USA, 1992.
[SOM 11] SOMMER C., GERMAN R., DRESSLER F., “Bidirectionally coupled network and road traffic simulation for improved IVC analysis”, IEEE Transactions on Mobile Computing, vol. 10, no. 1, pp. 3-15, January 2011.
[SUM 12] SUMO, Simulator of urban mobility, http://sumo.sourceforge.net/, 2012.
[SWA 12] SWANS, Scalable wireless ad hoc network simulator, http://jist.ece.cornell.edu/, 2012.
[THA 11] THAKUR G., HUI P., KETABDAR H., et al., “Towards realistic vehicular network modeling using planet-scale public webcams”, Computing Research Repository (CoRR), 2011.
[TIA 02] TIAN J., HAEHNER J., BECKER C., et al., “Graph-based mobility model for mobile ad hoc network simulation”, SCS ANSS, San Diego, CA, USA, 2002.
[TOM 10] TOMTOM, How TomTom’s HD TrafficTM and IQ RoutesTM data provides the very best routing, White paper, 2010.
[TRA 12] TRANSIMS, Transportation analysis and simulation system, http://code.google.com/p/transims, 2012.
[TRE 00] TREIBER M., HENNECKE A., HELBING D., “Congested traffic states in empirical observations and microscopic simulations”, Physical Review E, vol. 62, no. 2, pp. 1805–1824, 2000.
[TRE 02] TREIBER M., HELBING D., “Realistische mikrosimulation von strassenverkehr mit einem einfachen modell”, ASIM, Rostock, Germany, 2002.
[TSI 12] TSIS-CORSIM, http://mctrans.ce.ufl.edu/featured/tsis/, 2012.
[UPP 11] UPPOOR S., FIORE M., “Large-scale urban vehicular mobility for networking research”, IEEE VNC, Amsterdam, The Netherlands, 2011.
[VAN 12] VANETMOBISIM, The vehicular mobility simulator, http://sourceforge.net/projects/vanetmobisim/, 2012.
[VAR 06] VARSCHEN C., WAGNER P., “Mikroskopische Modellierung der Personenverkehrsnachfrage auf Basis von Zeitverwendungstagebüchern”, Stadt Region Land, vol. 81, pp. 63–69, 2006.
[VEI 12] VEINS, http://veins.car2x.org/, 2012.
[VIR 11] VIRIYASITAVAT W., BAI F., TONGUZ O., “Dynamics of network connectivity in urban vehicular networks”, IEEE Journal on Selected Areas in Communications, vol. 29, no. 3, pp. 515–533, 2011.
[VIS 12a] VISSIM, http://www.ptv-vision.com/en-uk/products/vision-traffic-suite/ptv-vissim/overview/, 2012.
[VIS 12b] VISUM, http://www.ptv-vision.com/en-uk/products/vision-traffic-suite/ptv-visum/overview/, 2012.
[VSI 12] VSIMRTI, http://www.dcaiti.tu-berlin.de/research/simulation/, 2012.
[WAG 99] WAGNER P., K.N., “Microscopic modeling of travel-deman: Approaching the home-to-work problem”, Transportation Research Board Annual Meeting, Washington, DC, USA, 1999.
[WIE 74] WIEDEMANN R., “Simulation des straenverkehrsflusses”, Schriftenreihe Heft 8, Institute for Transportation Science, University of Karlsruhe, 1974.