15
Mathematics 101
In this chapter, you will learn the proper pronunciation and terminology for:
- Basic mathematical operations: addition, subtraction, multiplication, division, square (a2) versus cube (a3) roots, etc.
- Numerals, factors and factors with exponents, fractions, time and words of succession (ranking or order).
- Geometric patterns (triangle, square, rectangle, pentagon, etc.).
- Velocity or speed
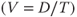 versus acceleration.
versus acceleration. - Density
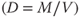 , mass versus weight.
, mass versus weight. - Exponents (Scientific Notation) for equations such as:
- Pythagorean Theory:

- Avogadro's number:
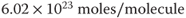 .
.
- Pythagorean Theory:
15.1 Basic Math Operations and Terminology
| Math operation | Example, definition, symbol, and so on | Deutsches Wort |
| Addv, additionn. | 2 + 2 = 4 (addition ≠ subtraction) | Addition |
| Subtractv., subtractionn. | 2 − 1 = 1 (subtraction ≠ addition) | Subtraktion |
| Dividev., divisionn. | 4 ÷ 2 = 2 (multiplication is the reciprocal of division) | Division |
| Multiplyv., multiplicationn. | 2 × 3 = 6 (division is the reciprocal of multiplication) | Multiplikation |
| Cubed | 33 | hoch drei |
| Cube root | 3√x | Kubikwurzel |
| Equal | = (equal sign) | gleich |
| Even ≠ odd (uneven) numbers |
|
|
| Equation, formula | E = mc2,  |
Gleichung, Formel |
| Fraction | ⅕, 7/8, 9/16 | Bruch |
| Greater than or equal to | a ≥ b | größer gleich oder größer als |
| Infinite (∞) | There seems to be an infinite number of stars in our universe! | unendlich |
| Less than or equal to | a ≤ b | gleich oder kleiner als |
| Measurement | A meter stick measures distance | Messung |
| Minus vs. plus | (−) vs. (+) | Minus, Plus |
| Ratio | 3 : 5 (60%), 40/100 (40%) | Verhältnis (zwischen gleichartigen Größen) |
| Squared | 82, M2, cm2 | Quadrat |
| Square root | 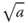 |
Quadratwurzel |
15.2 Numerals, Factors, and Words of Succession (Ranking or Order)
Counting numbers in English is certainly different than counting in German language.
- 21 (twenty-one) is pronounced in German as einundzwanzig
- 57 (fifty-seven); siebenundfünfzig
- 121 (one hundred and twenty-one); einhunderteinundzwanzig… and so on.
15.2.1 Numerals
For anyone working in the laboratory, numbers are critical in their line of work, so below is a list of numerals spelled out in English.
15.2.2 Factor Numbers
| Factor number | Spelling and pronouncing factors, some with exponents |
| 1 000 000 000 000 (one trillion) |  : nine trillion (nine times ten to the twelfth power or exponent) : nine trillion (nine times ten to the twelfth power or exponent) |
| 1 000 000 000 (one billion) | 3 465 000 000: three billion, four-hundred and sixty-five million |
| 1 000 000 (one million) | 47 928 867: forty-seven million, nine hundred and twenty-eight thousand, eight-hundred and sixty-seven |
| 100 000 (hundred thousand) | 600 201: six hundred thousand, two hundred and one |
| 1000 (thousand) | 5986.76: Five thousand, nine-hundred and eighty-six, point seven-six |
| 100 (hundred) | 438: four hundred and thirty-eight |
| 10 (ten) | 17: seventeen |
| 0.1 | One-tenth |
| 0.01 | One-hundredth |
| 0.001 | One-thousandth |
| 0.000001 | One-millionth |
| 0.000000001 | One-billionth |
| 0.000000000001 | One-trillionth |
15.2.3 Numbers of Succession
| Numbers of succession | Ordnungszahlen |
| First, 1st | Erste(r) |
| Second, 2nd | Zweite(r) |
| Third, 3rd | Dritte(r) |
| Fourth, 4th | |
| Fifth, 5th | |
| Sixth, 6th | |
| Seventh, 7th | |
| Eighth, 8th | |
| Ninth, 9th | |
| Tenth, 10th | |
| Eleventh, 11th | |
| Twelfth, 12th | |
| Thirteenth, 13th | |
| Fourteenth, 14th | |
| Fifteenth, 15th |
15.2.4 Fractions
| Fractions | Brüche |
| One-half, ⅕ | ein Halbes |
| One-third, 1/3 | ein Drittel |
| Two-thirds, 2/3 | ein Viertel |
| One-fourth, ¼ | |
| One-fifth, 1/5 | |
| One-sixth, 1/6 | |
| Four-sixths, 4/6 | |
| One-seventh, 1/7 | |
| One-eighth, 1/8 | |
| Three-eighths, 3/8 | |
| One-ninth, 1/9 | |
| One-tenth, 1/10 | |
| Three-tenths, 3/10 | |
| One-eleventh, 1/11 | |
| One-twelfth, 1/12 | |
| Five-twelfths, 5/12 | |
| One and a half | eineinhalb |
15.2.5 Time and Frequency
| Time and words of succession (calendar related) | Wörter der Nachfolge |
| Daily | Täglich |
| Weekly, bi-weekly | Wöchentlich, 14-tägig |
| Monthly, bi-monthly | Monatlich |
| Quarterly, 3 months | Quartalsmäßig; vierteljährlich |
| Annual, 1 year | Jährlich |
| Bi-annual – 2×/year | |
| Biennial – 2 years | |
| Triennial – 3 years | |
| Quadrennial – 4 years | |
| Quinquennial – 5 years | |
| Sexennial – 6 years | |
| Septennial – 7 years | |
| Octennial – 8 years | |
| Novennial – 9 years | |
| Decennial – 10 years |
15.2.6 Words of Succession (Rank or Order)
| Primary | primär |
| Secondary | sekundär |
| Tertiary | tertiär |
| Quaternary | quartär |

(© Mopic – fotolia.com.)
Examples:
- 1. Primary
- For some people, BBC or CNN remains their primary TV news source.
- When I was 5 years old, I attended Plaza Elementary School in Baldwin, New York. Although Plaza School was called an elementary school, many also considered it a primary school (Grundschule).
- 2. Secondary
- For me, “The New York Times” newspaper is my primary source for daily news; however, since I'm living and working in Germany, “ZDF-Heute” remains my secondary news source.
- When I was 15 years old, I attended South Side Senior High School, which is in New York. Although titled a high school, South Side was also considered a secondary school (Oberschule, weiterführende Schule).
- 3. Tertiary
- Tertiary is the term for a geologic period between 65 and 2.6 million years ago.
Last, but not least… Her primary goal was to win the election, but if she didn't win, her secondary goal was to show that she could put up a good fight!
15.3 Geometry and Geometric Shapes
15.4 Velocity (Speed)
Speed is a synonym for velocity, and it's understood as a function of the distance covered at a certain rate or speed.
Using a practical or realistic situation, when driving in an auto to work, most likely in what units would you use to calculate your auto's velocity?
- s km−1, km s−1, or km h−1
- miles s−1 or miles h−1?
You will most likely use km h−1, because if you were traveling at 50–55 km s−1, you most likely would have missed your exit (Ausfahrt) on the Autobahn!
However, If you answered in miles h−1, well that might have been due to the fact that America still uses English units to measure distance (inches, feet, yards, miles). The Metric System will be further discussed in the Chapter 16 – “Measurements and the Metric System”

| Velocity's (speed) equation | |
| Velocity = |  |
Speed vs. Acceleration: Speed (velocity) remains constant, but, when you increase your speed on an Autobahn (MotorwayUK, AutorouteBelg. or F, SnellwegNL, Interstate HighwayUSA) to pass a slower driver or truck (LKW), that is ACCELERATION.
According to the Merriam-Webster dictionary, “Acceleration is the rate of change of velocity with respect to time.”
15.5 Density
Mass vs. Weight – Probably, you have already recognized that density is calculated with the mass of a certain object or body, and not weight. So what is the actual difference between Mass and Weight? After all, has any English-speaking person to date ever asked you, “What is your mass?”
Mass is a measurement of the amount of matter contained within an object or body and its amount is not affected by the force of gravity. As an example, your mass on Earth will be the same as it is on the moon. But what will be your weight on the Sun?
Weight is a measurement determined by the pull or force of gravity on an object or body. As an example, your weight on Earth will be different than on the Moon, and that is a result of less gravity on the Moon! So what will happen to your weight on Earth's Sun?
15.5.1 Calculating Density
Take a look at the two boxes below. Each box has the same volume.
If each ball has the same mass, which box has a greater density of balls? Why?
The box that has more balls has more mass per unit of volume. This property of matter is called density. The density of a material helps to distinguish it from other materials. Either as a student or while working in the laboratory, most likely you have already calculated the density of an object in experiments and have expressed mass in grams (g) and volume in cubic centimetres (cm3). Thus, you would have expressed density in g cm−3.

15.5.2 Calculating a Three-Dimensional Object's Volume
Starting simply, let's suppose the object (cube below) that you wish to calculate is a solid, three-dimensional block with unequal sides. But before performing a practical application, you need to learn the following keywords:

QUIZ YOURSELF
Suppose the cube above has the following dimensions? What is the cube's volume?
- Length: 5 cm
- Height: 4 cm
- Width (depth): 2 cm
Answer: Cube's volume = 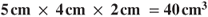
Now the real test for you to pronounce in English correctly, 40 cm3
If you were calculating only in two dimensions, length × height, how would you pronounce, 40 cm2? Did you say forty square centimetres…GREAT!
What laboratory instrument would you use to measure a liquid? Did you answer, a graduated cylinder … GREAT!

(© defun – fotolia.com.)
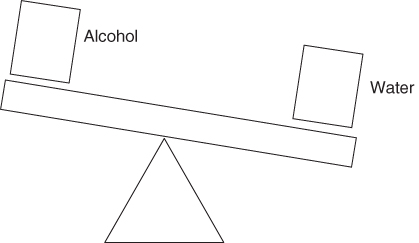
Using a simple balance or measuring scale, suppose we pour equal amounts (50 ml) of H2O + isopropyl alcohol (70% conc.), both measured with a graduated cylinder into two cups. The densities of the two liquids is different, but the volume is the same.
QUIZ YOURSELF
Considering both cups weigh the same and contain 50 ml of each substance (alcohol and water), why is the cup of H2O tilting the balance in its favor?
With reference to the following densities below of of these substances (solid, liquid, or gas states of existence) at 1 atm (760 mm Hg), what conclusions can you draw or determine?
- 1. Why at 0°C is Mercury (Hg) denser than H2O (water ice)?
- 2. Why at −253°C is Hydrogen (H) more dense than when it is in a gaseous state at 0°C?
- 3. At 20°C, what accounts for Aluminum (Al) being less dense than Copper (Cu) at this temperature?
| Substance | Temperature (°C) | Density (g cm−3) |
| Solids | ||
| Aluminum (Al) | 20 | 2.7 |
| Bone (human) | 20 | 1.6 |
| Copper (Cu) | 20 | 8.8 |
| Glass | 20 | 2.6 |
| H2O (ice) | 0 | 0.917 |
| Lead (Pb) | 20 | 11.3 |
| Steel | 20 | 7.7 |
| Liquids | ||
| Blood (human) | 37 | 1.05 |
| Ethanol (ethyl alcohol) | 20 | 0.791 |
| Glycerine | 0 | 1.26 |
| Hydrogen (H1 – liquid) | −253 | 0.07 |
| Mercury (Hg) | 0 | 13.6 |
| Oxygen (O2 – liquid) | −183 | 1.14 |
| Gases | ||
| Air | 0 | 0.0013 |
| Air | 20 | 0.0012 |
| Argon (Ar) | 0 | 0.0018 |
| CO2 | 0 | 0.0012 |
| Hydrogen (H1 – gas) | 0 | 0.00009 |
| Nitrogen (N2) | 0 | 0.0013 |
| Oxygen (O2 – gas) | 0 | 0.0014 |
| H2O (gas, steam) | 100 | 0.0006 |
15.6 Exponents (Scientific Notation)
The Pythagorean theory's definition: “In any right triangle, the area of the square whose side is the hypotenuse (the side opposite the right angle) is equal to the sum of the areas of the squares whose sides are the two legs (the two sides that meet at a right angle).”
The Pythagorean equation, 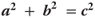 represents a geometric relation among the three sides of a right triangle (triangle with a 90° angle).
represents a geometric relation among the three sides of a right triangle (triangle with a 90° angle).
However, the purpose of this lesson is not so much to test you on the theorem or equation, but to help you pronounce the exponents. So how would you pronounce a2 or c2? Did you say, “A-squared (a2)” “C-squared (c2)?”…Great!
Now, let's get further onto the proper pronunciation of the exponents.

(© WavebreakMediaMicro – fotolia.com.)
How do you properly pronounce these two well known numbers with their exponents?
- Avogadro's number =
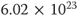 mol/molecule
mol/molecule - Planck's constant =
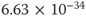 J s−1
J s−1
Answers
- Avogadro's number (
 ): Two possibilities may be…“six point zero-two times ten to the twenty-third power” or “six point zero-two to the twenty-third.”
): Two possibilities may be…“six point zero-two times ten to the twenty-third power” or “six point zero-two to the twenty-third.” - Planck's constant (
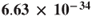 ): Two possibilities may be…“six point six-three times ten to the negative thirty-fourth power” or “six point six-three to the negative thirty-fourth.”
): Two possibilities may be…“six point six-three times ten to the negative thirty-fourth power” or “six point six-three to the negative thirty-fourth.”
In the space provided, write how you would pronounce the following exponents in English:
- 0.0005 =
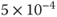 __________________________________________
__________________________________________ - 1000.00 =
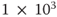 __________________________________________
__________________________________________ - 4.0 =
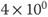 __________________________________________
__________________________________________ 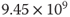 __________________________________________
__________________________________________
QUIZ YOURSELF: Vocabulary Matching Quiz
Place the letter from Column “B” with its correct answer from Column “A” in the “Answer” column
| Answer | Column A | Column B |
| (1) X | (a) 3000 m3 | |
| (2) Distance from a circle's center to its outermost surface | (b) Line from one end of a circle to its other end, and through (thru) its center | |
(3) 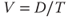 |
(c) Decimals | |
(4) 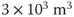 |
(d) Example (ex.) of a fraction | |
| (5) Example of a ratio | (e) 0.003 m | |
(6) 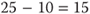 |
(f) Example of an addition equation | |
| (7) Numbers based on 10 | (g) Avogadro's number (equation) | |
| (8) Circumference | (h) Example of a percentage | |
| (9) 3/10 (three-tenths) | (i) Formula or equation for speed | |
(10) 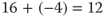 |
(j) The distance around a sphere or circle | |
(11) 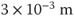 |
(k) Numbers based on powers of 10 | |
(12) 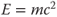 |
(l) Example of a subtraction equation | |
| (13) 55% | (m) Einstein's equation:  |
|
| (14) Formula for density | (n) Radius | |
| (15) Exponents | (o) ÷ | |
| (16) Symbol for division (dividing) | (p) Multiplication sign | |
(17)  particles/mol particles/mol |
(q) 3 : 5 | |
| (18) Diameter | (r)  |