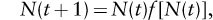
1. Fluctuations in populations
2. Brief guide to dynamic systems
3. Chaotic dynamics in models in ecology and population biology
5. Resolution as noisy clockwork
The cause of fluctuations in ecological populations has long been the subject of study, with the goal of understanding the relative importance of exogenous versus endogenous forces in explaining observed dynamics. The discovery of the likelihood of chaotic dynamics in simple discrete-time models that could be used to describe single-species population dynamics spurred much research focused on understanding chaos and its importance and likelihood in ecological systems. To understand the importance of chaos, we consider the role of fluctuations in ecological systems, the generation of chaotic dynamics in models, and the determination of chaos from time series. This naturally leads to more general questions on the role of complex dynamics in ecology and to a more synthetic view of the causes of observed fluctuations.
asymptotically stable solution. A solution that is approached by all nearby solutions is asymptotically stable. This is also known as an attractor.
chaos. Chaos is a property of an attractor in a dynamic system that can be roughly characterized as sensitive dependence on initial conditions and can be detected by the presence of a positive Lyapunov exponent.
cycle. A cycle is a solution that repeats at regular intervals.
equilibrium. An equilibrium of a model is a solution that does not change in time.
Lyapunov exponent. A Lyapunov exponent represents the exponential rate of divergence (if positive) or convergence (if negative) of (two) solutions started on or near an attractor.
A key observation that is central in ecology is that populations fluctuate in time. These fluctuations can exhibit some regularity or can be irregular. Periodical cicadas emerge with great regularity, whereas outbreaks of other insects such as locusts are both dramatic and irregular. The cause of fluctuations in populations in ecology has been a central question in ecology for many years. Early in the history of ecology, Volterra and Lotka focused on the regular oscillations produced by interactions between predator and prey in their models. Shortly thereafter, Gause attempted to reproduce these oscillations in laboratory systems using microorganisms and found that sustained oscillations were difficult to reproduce. In the simple laboratory systems, either the predator ate up all the prey and then starved or the predator could not find enough food and starved with only the prey surviving. This set up a problem that remains until today, namely, what allows predator and prey to coexist. Also, many of the mechanisms that might allow coexistence of species might lead to more complex dynamics, and more often coexisting species fluctuate.
In any examination of natural populations, fluctuations in numbers have been found to be the almost universal outcome. These fluctuations could range from relatively regular cycles, such as those observed in small mammal populations, or more dramatic changes, such as outbreaks of insect populations. A classic debate in ecology has focused on the causes of these fluctuations. One potential source of fluctuations could be external influences, such as changes in weather or climate. These exogenous forces could be responsible for changes in the dynamics of populations, producing cycles that were either regular or irregular. Another cause of changes in the numbers of populations would be endogenous forces within the population that would lead to cycles or more complex dynamics. Enlarging the question to look at fluctuations not just in time but also over space was thought of as one way to decide. Population fluctuations that are synchronous over space would either have to be caused by exogenous forces that were synchronous over space (the Moran effect) or endogenous forces such as dispersal that would synchronize populations.
One particular kind of fluctuating population that we will return to later that deserves special attention is the incidence of disease. In particular, the numbers of individuals with various childhood diseases (measles, mumps, rubella, and others) in the prevaccination era have been intensely studied. These particular fluctuations have played a special role for several reasons. The data are of much higher quality, with more, and more accurate, observations than for the numbers of many organisms. Another important aspect is that the underlying interactions producing the dynamics of diseases are relatively simple and relatively easily described. Finally, because data are known for multiple diseases in multiple locations, deeper understanding is possible.
The idea I now consider is that the primary cause of the fluctuations in ecological systems is interactions within and between populations rather than primarily external influences. The role of internal dynamics should be carefully examined in model systems using ideas from the mathematical theory of dynamics. This theory has undergone long development and can be traced back to attempts by physical scientists to understand the motion of the planets and other systems. A brief review of the theory of dynamic systems can elucidate many implicit assumptions ecologists make when using models framed in differential or difference equations or partial difference equations in attempts to understand what drives dynamics of ecological systems.
First, dynamic systems are systems that incorporate changes through time. In many engineering or physical examples, the systems, initial conditions, and parameters controlling the systems are well defined. However, in ecology, this is rarely the case. Ecological systems are so complex that only rough descriptions are often possible, the measurements of population sizes are notoriously difficult, and parameters such as birth and death rates are known only imprecisely. Thus, the way to understand the behavior of ecological systems is not to look for exact solutions of fully specified dynamic systems through either numerical or analytic means. An understanding of what is known as the qualitative behavior is much more appropriate and important.
Fortunately for ecologists, advances in understanding dynamic systems have focused primarily on the qualitative behavior of these systems. One focus is on long-term or asymptotic behavior of dynamic systems. Several definitions are needed. The simplest long-term dynamic is an equilibrium, or a solution that remains constant in time. The next most complex dynamic behavior is a cycle, or a solution that repeats regularly in time, so x(t + T) = x(t) for some cycle period T for all times t. Before we turn to other more complex asymptotic behaviors, we need a definition of stability.
I use heuristic, rather than mathematically rigorous, definitions. An asymptotic solution to a dynamic system is stable if it is approached from all nearby initial conditions. Such a solution is also known as an attractor. Attractors can be as simple as equilibrium points but can also be more complex. Cyclic attractors are also known as limit cycles. Quasicyclic attractors oscillate but with two (superimposed) incommensurate periods so the solutions do not exactly repeat. Attractors can also be chaotic.
A chaotic attractor is a solution that is still stable in the sense that it is approached by nearby solutions. A chaotic attractor has the property that even solutions that start on the chaotic attractor diverge from each other at an exponential rate, so all solutions have very sensitive dependence on initial conditions. The understanding and appreciation of the concept of chaotic dynamics can be traced back to work by Lorenz over 40 years ago and further back to work of Poincaré and Andronov and others more than a century ago. The importance of chaotic dynamics is that it challenges notions of predictability. However, note that even solutions that exhibit chaotic dynamics are predictable over short time scales, even if prediction is not possible over long time scales.
Within ecology, the first appreciation of chaotic dynamics arose in studies of single-species models with overcompensatory density dependence and nonoverlapping generations. The key idea of overcompensatory density dependence refers to the fact that not only does the per capita production of individuals in the next generation decline as the number of individuals in the current generation goes up, but additionally, the total population size of the next generation eventually declines as the number of individuals in the current generation is increased. These models take the general form
where N(t) is the population size of a single species at time t, and f[N(t)] is the mean number of individuals in the next generation left by an individual in the current generation. The dependence of the function f on the population size N(t) is used to describe the action of density-dependent factors in determining the population size of the following generation. Thus, if f[N(t)] is a declining function of the population size, the model exhibits density dependence. And if N(t)f[N(t)] eventually declines, then the system is said to incorporate overcompensatory density dependence. Classic density-dependent terms used in fisheries can be incorporated this way, with the Ricker function exhibiting overcompensatory density dependence, and the Beverton-Holt form not exhibiting this property. It is the functional forms that include overcompensatory density dependence that can lead to complex dynamics and chaos.
One important observation is that chaotic dynamics is essentially a generic property of discrete-time models with strong enough overcompensatory density dependence, so it makes sense to study simple models. Some of the first investigations of chaotic dynamics used an idealized form to describe the population dynamics, namely,
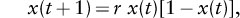
where x(t) is a scaled (between 0 and 1) measure of population size at time t, and r (between 0 and 4) is a measure both of the growth rate when rare and degree of overcompensation in the density dependence. This seemingly simple model, the quadratic or logistic population model, was extensively investigated by Robert May (1974b) and others in the 1970s and since.
A description of the dependence of the dynamic behavior of the quadratic model as a function of the parameter r provides insight into the possible aspects of chaotic dynamics in populations, and similar behavior is found in other models. For small values of r, the population cannot survive. For larger values of r, the population inevitably approaches a stable equilibrium. As the parameter r is increased, the asymptotic behavior of the model is a two-point cycle with the population alternating between two values. This period-doubling behavior continues as r increases, with asymptotic behavior of four-point cycles, then eight-point cycles, then 16, and so on. The ranges of values of the parameter r over which the cycles of period 2n occur get smaller and smaller as n gets bigger. A limit is reached at a critical value of r, beyond which the dynamics is much more complex, and chaotic solutions are found. The presence of this period-doubling sequence is one of several “routes to chaos.”
Although an emphasis on the study of the discrete-time model for a single species seemed to imply that chaos was strictly a property of ecological systems with nonoverlapping generations, this is not the case. In continuous-time models, there need to be at least three interacting quantities (e.g., species) for the system to exhibit chaotic dynamics. Since the discovery of chaos in discrete-time models, studies have emphasized that chaotic dynamics is likely to be found in simple models of food webs (or food chains) with three or more species with nonlinearities as would arise from functional responses used to describe predation. Essentially, chaos seems to arise when dynamics is characterized by interactions among oscillating systems with different periods as is the case with predator–prey systems. Even systems with enough competitive relationships can produce chaos.
Chaos and other forms of complex dynamics also arise very naturally in descriptions of ecological systems that include different population levels at different spatial locations. Chaotic behavior can arise in models as simple as those describing two coupled predator–prey oscillators.
One additional class of models that can exhibit chaotic dynamics comes from epidemiology. Among the simplest epidemiological models are those phrased in terms of susceptible, infectives, and removed individuals, the SIR model first discussed by Kermack and McKendrick in the 1920s. Because this is a continuous-time model that can be reduced to two quantities, it cannot produce chaos. However, if the contact rate describing the transition from susceptible to infective varies seasonally (periodically), the model does have chaotic solutions.
The behavior of the simplest population models that could exhibit chaotic dynamics, the single-species discrete-time models, seemed to provide a possible way of explaining irregular fluctuations in natural populations. However, the possibility of chaotic dynamics is not the same as the existence of chaotic dynamics. Thus, great efforts have been made to uncover evidence for chaotic dynamics in ecological systems, both natural and in the laboratory.
One procedure for uncovering chaotic dynamics begins with the collection of a time series of population abundances or disease incidence or similar data. At first, the possibility of uncovering chaotic dynamics would seem to be doomed because typical time series of natural populations in ecology or population biology focus on only a single species or the incidence of a single disease. Here a powerful idea that shows how to study a system with many dimensions (e.g., many species) from a single dimension (time series for a single species) comes to the rescue. The idea is based on a powerful mathematical argument (though the conditions that justify the procedure are almost never checked) that says that the full dynamic behavior of a system can be understood and replicated by a reconstruction procedure beginning with a single time series. Instead of focusing on the time series itself, say x(t), consider representing the data with lags and plotting x(t) versus x(t – T) and x(t – 2T). The actual number of lags chosen (which may often be more than two) and the length of the lag (T) can be critical, and unfortunately there is no well-established procedure for their choice. However, by using this procedure, one can clearly focus on the search for chaos.
At this point, there is still the problem of looking for a signature of chaos, such as a positive Lyapunov exponent. For data sets much larger than any found in ecology, there would be direct procedures for estimating this Lyapunov exponent. In ecology, given the limited data sets, an approach based on choosing a model and fitting this model to the data and then looking at properties of the best-fitting model must be used. There are relatively standard approaches for estimating a Lyapunov exponent from a model. There are, however, two different kinds of approaches for making models fit, based either on choosing a very general functional form, which is purely phenomenological, or on choosing from among a set of much more mechanistic descriptions of the biological processes. The former approach has the advantage of flexibility while perhaps ignoring important biological constraints. The latter approach has the advantage of biological realism but can be difficult to apply to data from a single time series of a more complex system. The latter approach also depends critically on choosing a good set of candidate models that can exhibit an appropriate range of dynamic behavior.
The general approach of using time series to look for chaos has been applied to a variety of data sets, including childhood diseases (Finkenstadt and Gren-fell, 2000) and laboratory systems such as flour beetles (Costantino et al., 1997). The evidence for chaos in childhood diseases such as measles is not completely clear-cut, but there at least seems to be a very strong possibility of chaotic dynamics.
For the flour beetle system studied by Costantino and collaborators (1997), the evidence for chaos in this highly controlled system is clearer. The calculations of the Lyapunov exponent for a model that fits the system well yield a positive Lyapunov exponent, one hallmark of chaos. Moreover, both the model (clearly) and experimental results (somewhat less clearly) also exhibit the period-doubling behavior that is one of the signatures of chaos.
For systems outside the laboratory other than childhood diseases, the evidence for chaotic dynamics is much weaker. This may be because natural systems are not chaotic, but part of this may be a result of the difficulty of obtaining high-quality data. One point that clearly is important is that stochastic forces must play a role, as environmental fluctuations and demographic heterogeneity inevitably influence all populations. Stochasticity clearly plays an important role.
To some extent, so far we have focused on the causes of observed fluctuations in population levels as a dichotomy: either endogenous or exogenous. It is clear that stochastic forces must be important for the dynamics of natural populations, and it is equally clear that there are strong interactions within and between species affecting population dynamics. This sets up what is essentially a false dichotomy between two forces. Instead, it is much more realistic to consider the interplay between endogenous and exogenous forces.
This idea that the dynamics of natural populations must depend on both stochastic and deterministic forces has been referred to as “noisy clockwork” (Bjornstad and Grenfell, 2001), although the idea has a longer history. One important aspect is that the stochastic aspects of population dynamics cannot be thought of as small perturbations of a deterministic population trajectory. Instead, the complex endogenous aspects of population dynamics and the exogenous forces are inexorably intertwined. These two aspects together produce the complex population trajectories we observe.
One can study populations from this point of view and obtain new insights. One can define a Lyapunov exponent for a stochastic system in terms of expectations and therefore sensibly ask whether chaotic dynamics exist in natural systems. However, difficulties of limited data still make detection of chaos a challenge.
There is one other way that the emphasis on chaotic dynamics in ecology may have led investigators away from important ecological behavior. Although it is possible to sensibly define chaotic behavior on shorter time scales, much of the study of chaotic behavior, especially in model systems, has emphasized asymptotic behavior. However, many ecological systems may best be understood by studying transient dynamics rather than asymptotic behavior.
The modern approaches to understanding dynamic systems and new statistical approaches for understanding time series that have been used in the study of chaos in ecology can also be used to shed light on other dynamic behavior. Transient dynamics can be studied using ideas from dynamic systems. There are mathematical tools for understanding spatial systems and, in particular, systems of coupled oscillators (e.g., predator–prey systems and epidemiological systems) and synchrony, even in the presence of stochasticity.
New and novel statistical approaches will also likely prove useful in understanding the forces producing observed population fluctuations. Model-based frequentist approaches and Bayesian methods that truly incorporate different kinds of stochasticity will both contribute to a deeper understanding of population dynamics.
Bjornstad, O. N., and B. T. Grenfell. 2001. Noisy clockwork: Time series analysis of population fluctuations in animals. Science 293: 638–643.
Costantino, R. F., R. A. Desharnais, J. M. Cushing, and B. Dennis. 1997. Chaotic dynamics in an insect population. Science 275: 389–391.
Finkenstadt, B. F., and B. T. Grenfell. 2000. Time series modelling of childhood diseases: A dynamical systems approach. Journal of the Royal Statistical Society Series C–Applied Statistics 49: 187–205.
Hastings, A. 2004. Transients: The key to long-term ecological understanding? Trends in Ecology and Evolution 19: 39–45.
Hastings, A., C. Hom, S. Ellner, P. Turchin, and H.C.J. Godfray. 1993. Chaos in ecology: Is mother nature a strange attractor? Annual Reviews of Ecology and Systematics 24: 1–33.
Huisman, J., and F. J. Weissing. 2001. Fundamental unpredictability in multispecies competition. American Naturalist 157: 488–494.
May, R. M. 1974a. Stability and Complexity in Model Ecosystems. Princeton, NJ: Princeton University Press.
May, R. M. 1974b. Biological populations with nonover-lapping generations: Stable points, stable cycles, and chaos. Science 186: 645–647.