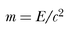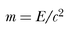Lightness of Being

Finding New Laws, Made Simple

Now for anyone who’s had experience with elementary algebra, it’s so immediately obvious that those three laws are all equivalent to each other that this story becomes a joke. But there’s a deep point to it. (There’s also a shallow point, which I think is the one Sam wanted me to absorb. When teaching beginners, you should try to say the same thing several times in slightly different ways. Connections that are obvious to a pro might not come automatically to the beginner. And those students who see you belaboring the obvious won’t mind. Very few people get offended when you make them feel clever.)

The deep point connects with a statement made by the great theoretical physicist Paul Dirac. When asked how he discovered new laws of nature, Dirac responded, “I play with equations.” The deep point is that different ways of writing the same equation can suggest very different things, even if they are logically equivalent.

Einstein’s Second Law

Einstein’s second law is

Einstein’s first law is of course E = mc². Famously, that first law suggests the possibility of getting large amounts of energy from small amounts of mass. It calls to mind nuclear reactors and nuclear bombs.

Einstein’s second law suggests something quite different. It suggests the possibility of explaining how mass arises from energy. “Second law” is a misnomer, actually. In Einstein’s original 1905 paper, you do not find the equation E = mc². What you find is m = E/c². (So maybe we should call that Einstein’s zeroth law.) In fact, the title of that paper is a question: “Does the Inertia of a Body Depend on Its Energy Content?” In other words: can some of a body’s mass arise from the energy of the stuff it contains? Right from the start Einstein was thinking about the conceptual foundations of physics, not about the possibility of making bombs or reactors.

The concept of energy is much more central to modern physics than the concept of mass. This shows up in many ways. It is energy, not mass, that is truly conserved. It is energy that appears in our fundamental equations, such as Boltzmann’s equation for statistical mechanics, Schrödinger’s equation for quantum mechanics, and Einstein’s equation for gravity. Mass appears in a more technical way, as a label for irreducible representations of the Poincaré group. (I won’t even try to explain that statement—fortunately, just the act of stating it conveys the point.)

Einstein’s question, therefore, lays down a challenge. If we can explain mass in terms of energy, we’ll be improving our description of the world. We’ll need fewer ingredients in our world-recipe.

With Einstein’s second law, it becomes possible to think of a good answer to the question we earlier debunked. What is the origin of mass? It could be energy. In fact, as we’ll see, it mostly is.

FAQ

Here are two excellent questions that people frequently ask me when I give public lectures about the origin of mass. If they occurred to you, congratulations! These questions raise basic issues about the possibility of explaining mass in terms of energy.

Question 1: If E = mc², then mass is proportional to energy. So if energy is conserved, doesn’t that mean that mass will be conserved, too?

Answer 1: The short answer is that E = mc² really applies only to isolated bodies at rest. It’s a pity that this equation, the equation of physics that is best known to the general public, is actually a little cheesy. In general, when you have moving bodies, or interacting bodies, energy and mass aren’t proportional. E = mc² simply doesn’t apply.

For a more detailed answer, take a look at Appendix A: “Particles have Mass, the World has Energy.”

Question 2: How can something made from massless building blocks feel gravitational forces? Didn’t Newton tell us that the gravitational force a body feels is proportional to its mass?

Answer 2: In his law of gravitation, Newton indeed told us that the gravitational force felt by a body is proportional to its mass. But Einstein, in his more accurate theory of gravity, general relativity, tells us something different. The complete story is quite complicated to describe, and I won’t try to do it here. Very roughly speaking, what happens is that where Newton would say the force is proportional to m, Einstein’s more accurate theory says it’s proportional to E/c². As we discussed in the previous question and answer, those aren’t the same thing. They are almost equal for isolated, slowly moving bodies, but they can be very different for interacting systems of bodies, or for bodies moving at close to the speed of light.

In fact, light itself is the most dramatic example. The particles of light, photons, have zero mass. Nevertheless light is deflected by gravity, because photons have nonzero energy, and gravity pulls energy. Indeed, one of the most famous tests of general relativity involves the bending of light by the Sun. In that situation, the gravity of the Sun is deflecting massless photons.

Carrying that thought a step further, one of the most dramatic consequences of general relativity is that you can imagine an object whose gravity is so powerful that it bends photons so drastically as to turn them completely around, even if they’re moving straight out at the start. Such an object traps photons. No light can escape it. It is a black hole.