Among other obscured parts of iOS and macOS SDK, there is one interesting library called SIMD. It is an interface for direct access to vector instructions and vector types, which are mapped directly to the vector unit in the CPU, without the need to write an assembly code. You can reference vector and matrix types as well as linear algebra operators defined in this header right from your Swift code, starting from 2.0 version.
To get access to those goodies, you need to import simd in Swift files, or #include <simd/simd.h> in C/C++/Objective-C files. GPU also has SIMD units in it, so you can import SIMD into your metal shader code as well.
The part I like the most about the SIMD is that all vectors and matrices in it have size explicitly mentioned as a part of their type. For example, function float 4() returns the matrix of size 4 x 4. But it also makes SIMD inflexible because only matrices of sizes from 2 up to 4 are available.
Take a look at the SIMD playground for some examples of SIMD usage:
let firstVector = float4(1.0, 2.0, 3.0, 4.0) let secondVector = firstVector let dotProduct = dot(firstVector, secondVector)
The result is as follows:
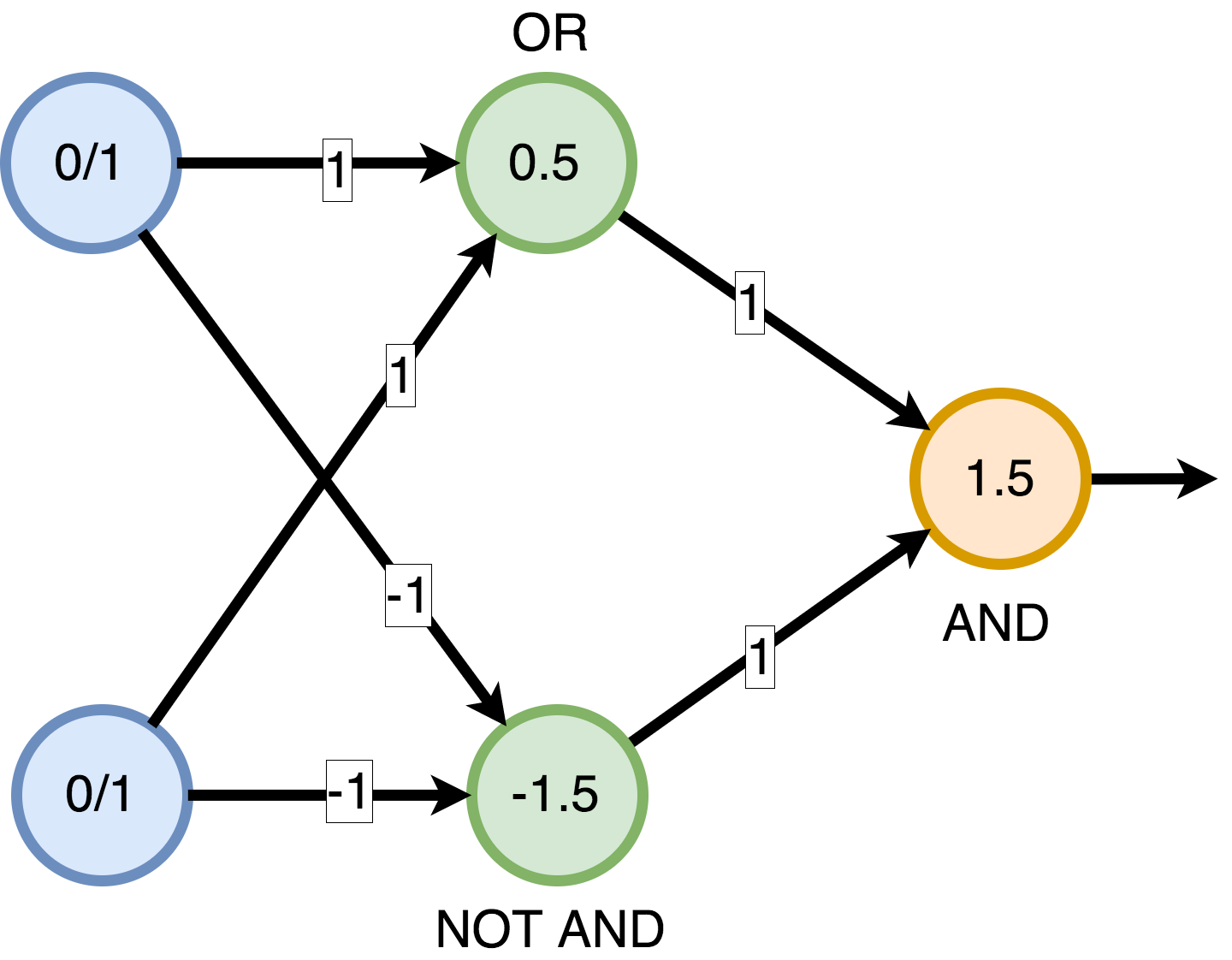
To illustrate that SIMD can be used for ML algorithms, let's implement a simple XOR NN in SIMD:
func xor(_ a: Bool, _ b: Bool) -> Bool {
let input = float2(Float(a), Float(b))
let weights1 = float2(1.0, 1.0)
let weights2 = float2(-1.0, -1.0)
let matrixOfWeights1 = float2x2([weights1, weights2])
let weightedSums = input * matrixOfWeights1
let stepLayer = float2(0.5, -1.5)
let secondLayerOutput = step(weightedSums, edge: stepLayer)
let weights3 = float2(1.0, 1.0)
let outputStep: Float = 1.5
let weightedSum3 = reduce_add(secondLayerOutput * weights3)
let result = weightedSum3 > outputStep
return result
}
The good thing about SIMD is that it explicitly says to the CPU to calculate the dot product in one step, without looping over the vector but rather utilizing SIMD instructions.