CHAPTER 5

Early Numerical Experiments

Polar Amplification

The use of GCMs to study changes in climate began at GFDL in the late 1960s and early 1970s. The results of this work were described in two companion papers published in the mid-1970s (Manabe and Wetherald, 1975; Wetherald and Manabe, 1975). In the former study, the total response of climate to a hypothetical doubling of the atmospheric CO₂ concentration was investigated. The response to a 2% change in solar irradiance was evaluated in the latter study. Although the model used for these studies was similar to the annual mean model described in the preceding chapter, there was one important difference. To incorporate the positive feedback effect of water vapor, the model used the distribution of water vapor determined by the model for the computation of radiative transfer—in contrast to the original annual mean model, which used the observed distribution.

Because of limited computing power available at that time, it was desirable to minimize the computational requirements of each numerical experiment. To achieve this goal, the spatial domain of the model was reduced from one hemisphere to a single sector that covered only one-sixth of the globe. This sector was bounded by two meridians separated by 120° of longitude and extended from the equator to 81.7°, as shown in figure 5.1. In the atmosphere, cyclic continuity was imposed at the eastern and western boundaries such that atmospheric disturbances that exited through one of the north–south boundaries would re-enter the domain through the other boundary. Insulated free-slip walls were placed at the equator and at 81.7°. Despite the reduced spatial domain, the sector was designed to be wide enough to maintain the planetary waves that play a critically important role in controlling the dynamics of the atmospheric circulation.

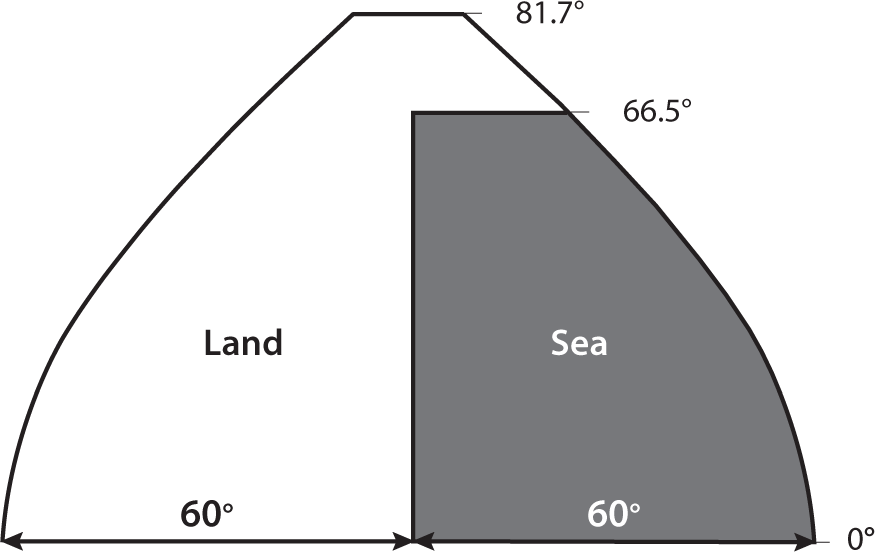
FIGURE 5.1 Computational domain of the general circulation model used by Manabe and Wetherald (1975).

This sector domain was subdivided further into land and sea, each of which had a longitudinal span of 60°. In contrast to previous models, which prescribed sea surface temperatures based on observations, the temperatures of both the oceanic and continental surfaces were determined by a heat balance requirement, implicitly assuming that the heat capacity of the sea surface is zero, as it is at the continental surface. This assumption enabled temperatures in the model to respond to the changes in top-of-atmosphere energy balance that result from the imposed changes in CO₂ concentration or solar irradiance. When the sea surface temperature dipped below the freezing point of seawater (−2°C), the sea surface was assumed to be covered by sea ice with a higher albedo. Although the oceanic surface of the model was prescribed to be always wet with an unlimited availability of water, soil moisture and snow depth were computed at the continental surface as in the annual mean model described in chapter 4. By allowing the model to predict the coverage of highly reflective sea ice and snow, the model was able to simulate the albedo feedback that enhances the sensitivity of climate.

The CO₂-Doubling Experiment

To estimate the equilibrium response of temperature to a doubling of the CO₂ concentration in the atmosphere, two sets of numerical time integrations of the model were performed. In the first set of integrations, the atmospheric CO₂ concentration was prescribed at 300 ppmv. Two 800-day integrations were run, differing only in their initial conditions. Although both started from an isothermal and dry atmosphere at rest, one initial condition was very warm and the other was very cold. Despite these large differences in temperature at the start of the two runs, the temperature of the atmosphere was practically identical toward the end of the time integrations. A quasi-equilibrium state was obtained, averaging the two 100-day mean states at the end of the two runs. An analogous set of simulations was made with the atmospheric CO₂ concentration prescribed at 600 ppmv, and a quasi-equilibrium state obtained in the same manner. The equilibrium response to CO₂ doubling was then determined from the difference between these two quasi-equilibrium states.

Figure 5.2a illustrates the equilibrium response of zonal mean temperature to the imposed CO₂ doubling. In agreement with the results from the 1-D radiative-convective model described in chapter 3, temperature increased not only at the Earth’s surface but also in the troposphere, whereas it decreased in the stratosphere. In the lower troposphere below a height of ~5 km, the magnitude of the warming increased with increasing latitude and was particularly large in the near-surface layer of the atmosphere, owing mainly to the poleward retreat of snow and sea ice that reflects a large fraction of incoming solar radiation. A close inspection of figure 5.2 reveals, however, that the large warming in high latitudes was not confined to the near-surface layer of the atmosphere. Instead, it extended upward to the mid-troposphere. This underscores the possibility that the polar amplification of the warming is attributable not only to the positive albedo feedback but also to a reduction of tropospheric static stability in high latitudes due to the change in the large-scale atmospheric circulation, as pointed out, for example, by Held (1978).

In contrast to high latitudes, where the magnitude of the warming decreased with increasing height in the troposphere, it increased with increasing height in low latitudes. This is attributable mainly to deep moist convection that often develops in the tropics, which keeps the vertical temperature gradient near the moist adiabatic lapse rate. Because the moist adiabatic lapse rate decreases with increasing temperature, the magnitude of the warming is larger in the upper troposphere than in the lower troposphere, as shown in figure 5.2. According to microwave soundings from satellites (Fu et al., 2004; Fu and Johanson, 2005), the temperature of the tropics has increased more in the upper troposphere than at the Earth’s surface during the past several decades, in agreement with the results presented here. It is interesting to note that the area-mean static stability of the model troposphere hardly changed in response to CO₂ doubling because of the compensation between high and low latitudes. Thus, the assumption of invariant static stability of the troposphere that was employed in the globally averaged radiative-convective model of the atmosphere introduced in chapter 3 appears to have been justified.

FIGURE 5.2 Latitude-height profile of the equilibrium response of zonal mean temperature (°C) in the atmosphere. (a) Response to a doubling of the atmospheric concentration of carbon dioxide (Manabe and Wetherald, 1975); (b) response to a 2% increase in the solar irradiance (Wetherald and Manabe, 1975). P, pressure; P*, surface pressure.

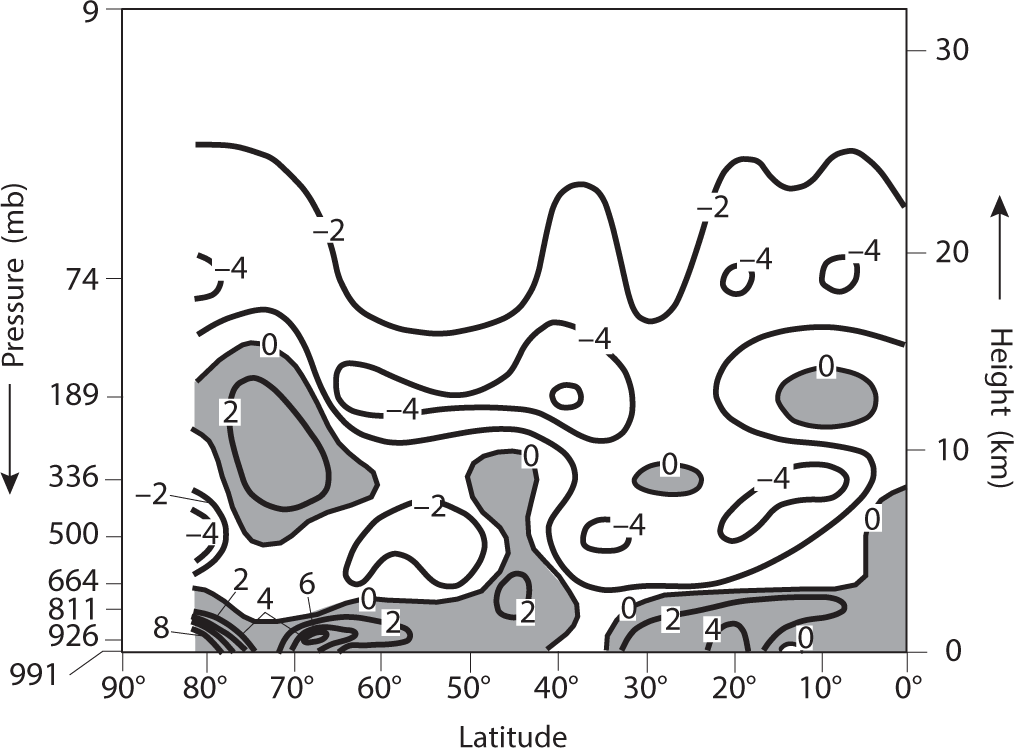
FIGURE 5.3 Latitude-height profile of the change in zonal mean relative humidity in response to the doubling of the atmospheric concentration of carbon dioxide. Zonal mean relative humidity is the percentage of the change in zonal mean vapor pressure relative to the zonal mean saturation vapor pressure. From Manabe and Wetherald (1975).

Averaged over the entire model domain, temperature increased by 2.9°C at the Earth’s surface, which is somewhat larger than the 2.4°C obtained from the radiative-convective model with water vapor feedback activated. The 3-D model described here incorporated not only the water vapor feedback but also the albedo feedback of snow and sea ice. It is therefore likely that the difference in the magnitude of the warming between the two models is mainly attributable to the albedo feedback.

To examine how the water vapor feedback operates in the model, figure 5.3 illustrates the change in zonal mean relative humidity in response to the doubling of the CO₂ concentration in the atmosphere. As this figure shows, the distribution is very patchy because the magnitude of the systematic change of relative humidity is much smaller than that of its natural variability. Nevertheless, one can identify some systematic changes in the distribution of relative humidity. For example, relative humidity increases by a few percent in the lower troposphere below 700 hPa, whereas it decreases by a few percent in the upper troposphere between 300 and 700 hPa. Referring to the study of Manabe and Wetherald (1967) that evaluated the relationship between the relative humidity of the troposphere and mean surface temperature, one can estimate crudely the contribution of this change in relative humidity to the change in surface temperature. Our estimate suggests that it is no more than 0.1°C because of the partial cancellation between the contributions from the upper and lower troposphere. In short, the strength of the water vapor feedback in this 3-D model is likely to be similar to that in the 1-D radiative-convective model with fixed relative humidity described in chapter 3.

FIGURE 5.4 Time series of the mean surface temperature anomaly relative to the reference period 1880–1960 in (a) the Northern Hemisphere (0°–85° N) and (b) the Arctic region (65°–85° N). The time series obtained by Kelly et al. (1982) are extended to 2010 using data updated by Brohan et al. (2006).

The polar amplification of global warming has been confirmed through climate observations conducted over the past 130 years. In figure 5.4, the time series of the annual mean surface temperature anomaly averaged over the Arctic region and the entire Northern Hemisphere are compared. This figure shows that both time series exhibit systematic warming trends with fluctuations on interannual, decadal, and multidecadal time scales. The average rate of the warming, however, is much larger in the Arctic than in the Northern Hemisphere as a whole, providing convincing evidence for the polar amplification of global warming. Although it is not shown here, the polar amplification of surface warming is not so evident in the Southern Hemisphere. This is because the deep vertical mixing of heat that predominates in the Southern Ocean has kept the magnitude of warming at the oceanic surface very small. This mechanism will be explored further in chapter 8, using a model that couples the atmosphere with the full oceans.

Change in Solar Irradiance

So far, we have presented results from a numerical experiment in which the atmospheric CO₂ concentration was doubled. Similar numerical experiments were also performed in which the solar irradiance (i.e., the average incoming solar radiation at the top of the atmosphere) was changed by +2%, −2%, and −4%, respectively. Figure 5.2b shows the latitude-height profile of the equilibrium response of zonal mean temperature to the +2% change in irradiance. Comparing it with the response to CO₂ doubling depicted in figure 5.2a, one finds that the responses of zonal mean temperature are quite similar in the troposphere below 15 km. For example, in the near-surface layer of the troposphere, the magnitude of the warming increases with increasing latitude and is at a maximum in high latitudes. On the other hand, in the upper troposphere around a height of 10 km, the warming decreases slightly with increasing latitude. This similarity is noteworthy when one considers the differences in thermal forcing between the +2%-solar-irradiance and doubled-CO₂ cases. Although both thermal forcings are positive, the former decreases with increasing latitude at a much larger rate than the latter. In view of the difference in the latitudinal gradient of the thermal forcing, it is surprising that the latitudinal profile of zonal mean temperature change is quite similar between the two types of thermal forcing.

The similarity between the responses to increased solar irradiance and increased CO₂ has been found in experiments using a different climate model. Hansen et al. (1984) conducted a similar pair of experiments using a GCM developed at the Goddard Institute for Space Studies (GISS) of the National Aeronautics and Space Administration (NASA). They found that latitude-height profile of the zonal mean response was practically identical between the +2%-solar-irradiance and CO₂-doubling experiments, in agreement with the results presented here. These studies suggest that, in the troposphere and at the Earth’s surface, the latitudinal profile of temperature change has little dependence upon the profile of the thermal forcing. Instead, it depends essentially upon the magnitude of the total thermal forcing that controls the polar amplification of near-surface temperature. These results also suggest that, in the troposphere and at the Earth’s surface, not only the +2% irradiance, but also the −2% and −4% experiments may be used as surrogates for the CO₂-doubling, CO₂-halving, and CO₂-quartering experiments, respectively.

The similarity between the CO₂-doubling and +2%-irradiance profiles suggests the possible existence of a dynamical mechanism that prevents the meridional temperature gradient from exceeding a certain critical value in the troposphere, where the static stability hardly changes. Such a mechanism has been proposed, for example, by Smagorinsky (1963), based upon the analysis of the long-term integration of his two-layer model mentioned in chapter 4. Here we describe briefly his hypothesis, which has been discussed further by Stone (1978). Suppose that the meridional temperature gradient exceeds the critical value for the instability of the midlatitude westerlies (i.e., baroclinic instability). As a result, planetary waves would be expected to amplify, enhancing the poleward transport of heat and preventing a further increase in the meridional temperature gradient in the troposphere. One can speculate that a similar mechanism is in operation in the model troposphere in both the CO₂-doubling and +2% experiments. This may be an important reason why the latitudinal distribution of zonal mean temperature change is similar between the two experiments, even though the distribution of zonal mean thermal forcing is quite different.

The latitudinal profiles of zonal mean surface temperature for four different values of solar irradiance are shown in figure 5.5. In addition to the profile from the control run, using a solar irradiance value of 340 W m⁻², the figure includes the profiles from three additional runs in which the solar constant is changed by +2%, −2%, and −4%, respectively. This figure shows that the meridional temperature gradient increases from the +2% run to the −4% run as the temperature decreases and the albedo feedback of snow and sea ice intensifies. Table 5.1 tabulates the equilibrium responses of the area-mean surface temperature to +2%, −2%, and −4% changes in the irradiance. For the sake of comparison, it also lists the responses obtained from the radiative-convective model introduced in chapter 3. Compared with the control run, the model warms by 3.04°C in response to a 2% increase in solar irradiance. This warming is substantially smaller than the 4.37°C cooling in response to a 2% reduction in irradiance and the 5.71°C cooling that occurs when the irradiance is further reduced from −2% to −4%. In other words, the magnitude of the response to each 2% reduction in the solar constant increases with decreasing solar irradiance.

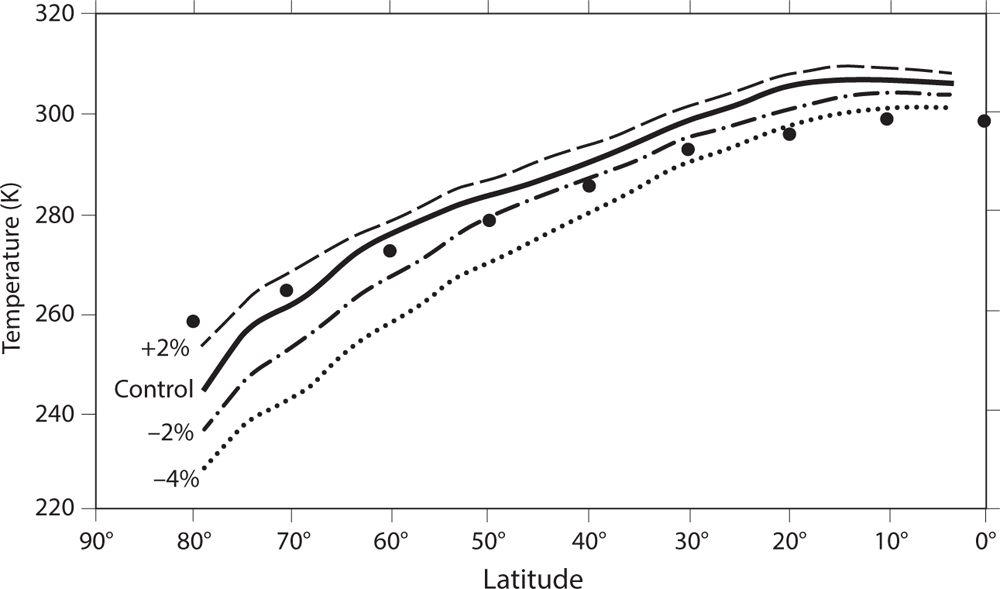
FIGURE 5.5 Latitudinal profiles of the zonal mean surface air temperature (K) obtained for four values of total solar irradiance: standard value (control; 1395.6 W m⁻²), +2%, −2%, and −4%. The observed annually averaged zonal mean surface temperature is indicated by black dots. From Wetherald and Manabe (1975).

TABLE 5.1 Equilibrium response of mean surface air temperature to change in solar irradiance
Change in Solar Irradiance	Change in Surface Temperature
	GC Model	RC Model
From control to +2%	+3.04°C	+2.57°C
From control to −2%	−4.37°C	−2.55°C
From −2% to −4%	−5.71°C	−2.54°C
GC model, general circulation model introduced here; RC model, radiative-convective model described in chapter 3. From Wetherald and Manabe (1975).

This dependence of the magnitude of the thermal response on global mean temperature in the GCM is dramatically different from the behavior of the radiative-convective model, where the responses to each 2% increment in solar irradiance are nearly identical at 2.57°C, 2.55°C, and 2.54°C. The difference in behavior between the two models is attributable mainly to the albedo feedback of snow and sea ice. In short, the response to a given thermal forcing increases with decreasing surface temperature as the areal coverage of the polar cap of snow and sea ice increases. In other words, if an increment of decreased thermal forcing moves the snow and sea ice boundaries equatorward by a given distance, the area of additional high-albedo surface is proportional to the length of latitude circle that defines those boundaries. Thus, each increment of cooling produces a greater amount of ice albedo feedback.

Energy balance models are powerful tools for understanding the role of ice-albedo feedback. In their simplest form, such models are 1-D, with temperature varying only with latitude. The components of the energy balance in these models are outgoing longwave radiation, absorption and reflection of incoming solar radiation, and meridional heat transport by large-scale atmospheric circulation, all of which are assumed to depend upon the perturbations of zonal mean surface temperature. Budyko (1969) and Sellers (1969) pioneered the construction of such models and used them to study the response of the polar ice caps to changes in solar irradiance. Held and Suarez (1974) and North (1975a, b, 1981) built upon these pioneering studies by conducting mathematically rigorous analyses of model behavior that yielded valuable insights into the response of ice caps and surface temperature to changes in solar irradiance.

Despite their simplicity, 1-D energy balance models (EBMs) anticipated many of the findings from the GCMs introduced here. For example, EBMs indicated that the response of global mean surface temperature to a given change in incoming solar radiation increases with decreasing solar irradiance, as the albedo feedback intensifies owing to the expansion of ice cover from the polar regions toward middle latitudes. They also indicated that ice cover becomes unstable when the solar irradiance dips below a threshold and the polar ice cap grows beyond a critical latitude (the so-called “large-ice-cap instability”). Under such circumstances, the positive ice albedo feedback overwhelms the negative feedback due to the temperature dependence of the emission of longwave radiation and the meridional diffusion of heat. Thus, ice cover can extend all the way to the equator, yielding an ice-covered planet reminiscent of the “Snowball Earth” that appeared intermittently approximately 750 to 550 million years ago (Harland, 1964; Hoffman et al., 1998; Pierrehumbert et al., 2011). According to the EBM studies of Budyko and Sellers, a reduction in solar radiation of less than 2% would be enough to induce such ice-cap instability. This conclusion differed from the study of Wetherald and Manabe described earlier in this chapter (1975), which indicated that a reduction of solar irradiance by much more than 2% (or a reduction in CO₂ concentration of more than a factor of two) would be required for the ice-cap instability to occur.

The sensitivity of the ice caps to solar irradiance was the subject of an in-depth analysis, which used a two-level GCM of the atmosphere (Held et al., 1981). The model was simplified such that a large number of numerical experiments could be performed with minimal computational cost and a quasi-equilibrium state could be obtained with relative ease. Held et al. found that the response of their model to changes in solar irradiance differed substantially from the response of the diffusive energy balance model. When solar irradiance is decreased by a few percent, pushing the albedo gradient at the ice-cap boundary to a position equatorward of 60° latitude, the model climate becomes very sensitive to the solar irradiance value, but this sensitivity is not a sign that ice-cap instability is close at hand. Instead, as the solar irradiance is lowered further, the model climate becomes less rather than more sensitive. These relatively stable large-ice-cap states exist for a range of ~5% of solar irradiance, while the ice cap extends all the way to 20° latitude. For still lower values of the solar constant, large-ice-cap instability develops and ice covers the entire planet.

Similar results were produced in a two-level diffusive EBM, closely patterned after the GCM, by making the diffusion coefficient for heat vary with latitude. Choosing diffusivity with a pronounced meridional structure resembling that of the effective diffusivity of the GCM, these authors found that the ice-cap boundary is less sensitive to solar irradiance when it is in the region in which effective diffusivity of the atmosphere increases with decreasing latitudes. On the other hand, greater sensitivity is seen when the ice-cap boundary enters the region in which the diffusivity decreases with decreasing latitude. The results from these experiments indicate that the large-ice-cap instability found in the EBM with constant diffusivity would require a much larger decrease in solar irradiance to occur in the GCM. The dependence of effective diffusivity on latitude is responsible for this difference in response, indicating that the transport of energy by transient eddies cannot be adequately represented by diffusivity that is independent of latitude. Thus, some caution is required in interpreting the quantitative aspects of results obtained from EBMs in which the thermal diffusivity does not depend upon latitude.

Seasonal Variation

So far, we have presented a series of studies of climate change that used highly idealized models with annually averaged insolation. By the 1970s, when increasingly powerful computers became available at GFDL, the GCMs used for studies of climate change were made to resemble the real world more closely by including realistic geography and seasonally varying insolation. One such model was used by Manabe and Stouffer (1979, 1980) and revealed how the polar amplification of global warming depends upon season. We will briefly describe the structure of this model before discussing the results that were obtained from it.

The model covers the entire globe and has a realistic geographic distribution of oceans and continents. As with the seasonal model described in chapter 4, it consists of a GCM of the atmosphere and a heat- and water-balance model of the continental surface. In contrast to the earlier model, sea surface temperature is not prescribed according to observations. Instead, the ocean is represented as a vertically isothermal layer with a thickness of ~70 m. The temperature of this “mixed layer” is determined such that it satisfies the surface heat budget; no horizontal transport of heat occurs within the model ocean. The heat exchange between the ocean mixed layer and the deeper ocean is neglected. Although this exchange is not very important over short time scales, it substantially affects changes in surface temperature over multidecadal and centennial time scales. The role of the deep ocean in climate change will be the subject of discussion in chapters 8 and 9.

An important factor that affects the heat budget of mixed-layer ocean is sea ice. It often covers the oceanic surface in high latitudes, reflecting a major fraction of incoming solar radiation. It also reduces the heat exchange between the mixed-layer ocean and the overlying atmosphere, substantially affecting the heat balance of the mixed layer. In the model, the change in sea ice thickness is computed from the budget of sea ice that involves snowfall, sublimation and melting at the top of the sea ice, and freezing (or melting) at the bottom of the sea ice, as illustrated in figure 5.6. Here the rate of freezing (or melting) at the bottom of the sea ice is determined such that the temperature of the mixed layer of ocean remains at its freezing point (−2°C) despite the heat conduction through the sea ice. The temperature at the top surface of the sea ice is determined such that the requirement of heat balance is satisfied among solar radiation, longwave radiation, sensible heat flux, sublimation, and heat conduction through the sea ice. When the temperature thus computed exceeds the melting point of sea ice (0°C), melting occurs, keeping the temperature at the melting point of sea ice.

Using the atmosphere/mixed-layer-ocean model described above, Manabe and Stouffer attempted to simulate the seasonal variation of climate. Starting from an isothermal initial condition at rest, they numerically integrated the model over 10 annual cycles. Initially, the global mean surface temperature of the model changed very rapidly. Toward the end of the integration, however, it closely approached the state of thermal equilibrium, in which the global mean flux of outgoing longwave radiation is practically identical to that of the net incoming solar radiation at the top of the atmosphere.

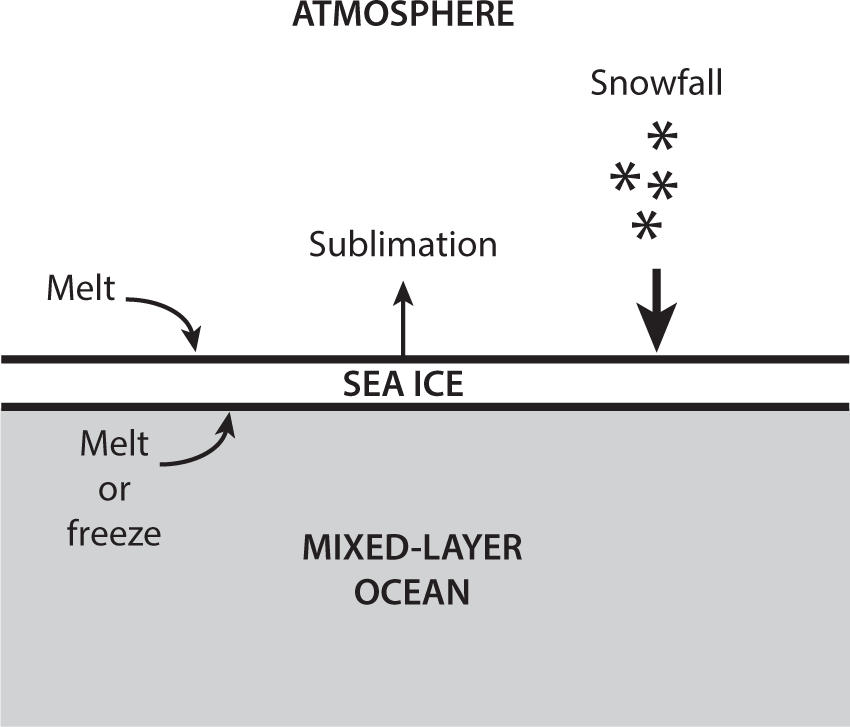
FIGURE 5.6 Components of the sea ice budget in the atmosphere/mixed-layer-ocean model constructed by Manabe and Stouffer (1979, 1980).

To evaluate the ability of the model to simulate the seasonal variation of surface temperature, maps of the difference in surface air temperature between August and February for the model were compared with observations (figure 5.7). Keeping in mind that the sign of the difference is opposite between the two hemispheres, one can use the magnitude of the difference as a rough indicator of the annual range of surface temperature variation.

Comparing figure 5.7a and b, one can see that the geographic distribution of the surface air temperature difference between August and February simulated by the model agrees well with observations. For example, the annual range of surface air temperature over oceanic regions is substantially smaller than the range over the continents, owing mainly to the thermal inertia of the mixed-layer ocean. It was encouraging to find that this relatively simple treatment of the ocean mixed layer allowed the model to simulate reasonably well the geographic distribution of the annual range of surface air temperature.

Using the atmosphere/mixed-layer-ocean model, Manabe and Stouffer performed a numerical experiment to investigate the climatic effect of increasing the atmospheric CO₂ concentration. The simulation described above, in which the atmospheric CO₂ concentration was held fixed at a value of 300 ppmv, was used as a control run (1×C). To simulate a high-CO₂ climate, another run was made with the CO₂ concentration held fixed at four times the standard value (1200 ppmv; 4×C). This large change in CO₂ was used to magnify the response of climate that would be determined by comparing the simulated 4×C and 1×C climates. Because the radiative forcing of climate is proportional to the ratio of CO₂ concentration before and after the change, as explained in chapter 3, the climate change due to CO₂ quadrupling is approximately twice as large as the change due to CO₂ doubling.

FIGURE 5.7 Geographic distribution of the difference in monthly mean surface air temperature (°C) between August and February: (a) simulated distribution; (b) observed distribution based upon data compiled by Crutcher and Meserve (1970) and Taljaad et al. (1969) for the Northern and Southern Hemispheres, respectively. Note that the contour interval is 2°C when the magnitude of the difference is less than 10°C, and is 10°C when the difference is more than 10°C. The area of negative difference is shaded. From Manabe and Stouffer (1980).

FIGURE 5.8 Simulated change in monthly averaged zonal mean surface temperature (°C) in response to the quadrupling of atmospheric CO₂ as a function of latitude and calendar month. From Manabe and Stouffer (1979, 1980).

The simulated change in zonal mean surface air temperature in response to CO₂ quadrupling is displayed as a function of latitude and calendar month, to illustrate the seasonal dependence of polar amplification of global warming, in figure 5.8. In high latitudes of the Northern Hemisphere, the magnitude of warming at the Earth’s surface varies greatly with season. It is very large from fall to late spring, but is small in summer with no polar amplification. Although similar seasonal variation also appears near the Antarctic coast around 70° S, its amplitude is much smaller. Sea ice plays a key role in modulating the heat exchange between the water beneath sea ice and the overlying air, thereby controlling the seasonal dependence of the warming over the Arctic Ocean and its immediate vicinity.

FIGURE 5.9 Simulated change in monthly averaged zonal mean sea ice thickness (m) as a function of latitude and calendar month: (a) control 1×C run; (b) 4×C run. Shading indicates the region where sea ice thickness exceeds 0.1 m. From Manabe and Stouffer (1980).

Figure 5.9a shows how the zonal mean thickness of sea ice in the control experiment (1×C) varies with season in the high latitudes of the two hemispheres. Poleward of 60° N, sea ice is thin and at a minimum during the three-month period of August–October. Sea ice thickness begins to increase in October and this increase continues until April, when it is at a maximum. While simulated surface air temperature decreases rapidly from summer to early winter as shown in figure 5.8, the temperature of the water beneath the sea ice remains at −2°C, the freezing point of seawater. Thus, the magnitude of the temperature gradient from the bottom to the top of the sea ice increases, enhancing the upward heat conduction that freezes water at the bottom of the sea ice. This process is responsible for the increase in sea ice thickness from September to April. Ice thickness begins to decrease rapidly during late spring owing to surface melting under increasing sunshine and warm air advected from the surrounding continents. Although similar seasonal variations of sea ice thickness occur near the Antarctic coast, their amplitude is small as compared with the Arctic Ocean.

Figure 5.9 indicates that the areal coverage of sea ice in the atmosphere/mixed-layer-ocean model is small in summer, when insolation is relatively strong, whereas it is large in winter, when insolation is relatively weak. This negative covariance between sea ice and insolation causes the total amount of reflected solar radiation during the annual cycle to be reduced owing to the seasonal variation of sea ice area. The consequent increase in absorbed solar radiation is one of the reasons why the mean surface air temperature was higher in the model with seasonal variation than in the model without such variation, as discussed by Wetherald and Manabe (1981). Comparing these simulations with and without annual variation, their results imply that the smaller the seasonal variation of incoming solar radiation, the stronger the albedo feedback and the lower the mean temperature at the Earth’s surface. This relationship would lend support for the so-called astronomical theory of the ice ages, in which the growth of Northern Hemisphere ice sheets is facilitated by reduced summer insolation. For further discussion of this subject, see Hays et al. (1976) and Imbrie and Imbrie (1979, 1980).

Comparing the latitude/calendar-month distributions of zonal mean sea ice thickness obtained from the 4×C and 1×C runs (figure 5.9), one can see that the coverage and thickness of sea ice are reduced markedly in the 4×C run. The reduction of sea ice thickness is attributable in no small part to the increase in the absorption of incoming solar radiation by the mixed-layer ocean in summer, when sea ice coverage is at a minimum and is reduced markedly from the 1×C run. The increase in the absorption of solar energy during summer delays the growth of sea ice during the cold season and contributes to a reduction of sea ice thickness throughout a year.

This overall reduction of sea ice thickness contributes strongly to the large seasonal contrast in the magnitude of Arctic warming depicted in figure 5.8. In winter, for example, temperature is much colder at the top of the sea ice than at the bottom, where it remains at the freezing point of seawater. Because the rate of heat conduction is inversely proportional to sea ice thickness, the heat conducted through the ice increases as sea ice thins. This is the main reason why surface temperature increases over the Arctic Ocean in response to the increase to CO₂ concentration. The magnitude of the warming is particularly large in winter, when the temperature difference between the top and bottom of the sea ice is very large. On the other hand, it is small in summer, when the temperature difference is small.

There is observational evidence that the magnitude of Arctic warming has varied with season. Chapman and Walsh (1993) examined the seasonal behavior of Arctic land station temperatures observed between 1961 and 1990. Their analysis shows that the median rates of warming in winter and spring are about 0.25°C and 0.5°C per decade, respectively. In summer the trend was near zero, and in autumn the trend was either neutral or showed slight cooling. The contrast between little or no observed warming in summer and substantial warming in winter and spring appears to be broadly consistent with the seasonal dependence of Arctic warming simulated by the model. Screen and Simonds (2010) used a state-of-the-art reanalysis product to estimate the seasonal variation of the trend of surface air temperature in high northern latitudes during the period 1989–2008. They found a pronounced near-surface warming trend over the Arctic Ocean in most seasons, but a much more modest near-surface warming in summer. They suggested that the large seasonal dependence of the warming was attributable mostly to the reduction of sea ice thickness.

Manabe et al. (2011) evaluated the seasonal dependence of the surface temperature trend during the past several decades, using a historical surface temperature data set compiled by the Climatic Research Unit of the University of East Anglia and the Hadley Centre for Climate Prediction and Research of the UK Meteorological Office. The result of their analysis is shown in figure 5.10, which illustrates the latitude/calendar-month distribution of the zonal mean surface air temperature anomaly for the period 1991–2009 relative to the 30-year base period of 1961–90. The anomalies over 1991–2009 can be regarded as indicative of the trend of zonal mean temperature during the past half-century. Zonal mean surface temperature increases at practically all latitudes and seasons. In the Northern Hemisphere, the warming trend increases with increasing latitude. The warming is particularly large over and around the Arctic Ocean during much of the year, with the notable exception of summer, when it is at its seasonal minimum. This is in good qualitative agreement with the model result shown in figure 5.8.

In sharp contrast with the Northern Hemisphere, polar amplification is not evident in the Southern Hemisphere. As a matter of fact, the temperature trend is small around 55° S in the Southern Ocean during much of the year, although the temperature anomalies are not shown poleward of 60° S in the figure because of the paucity of monthly mean temperature data in winter. The absence of significant warming in the Southern Ocean is attributable mainly to the exchange of heat between the mixed-layer and deep ocean, which cannot be captured by the atmosphere/mixed-layer model discussed here. We shall explore this subject further in chapter 8, using a coupled model in which a GCM of the atmosphere is combined with an ocean GCM.

FIGURE 5.10 Observed zonal mean surface air temperature anomaly averaged over the period 1991–2009 as a function of latitude and calendar month. The anomaly represents the deviation from the average over the 30-year base period 1961–90. Because of poor data coverage, the anomaly is not shown poleward of 80° N or 60° S. From Manabe et al. (2011).

Remote sensing of sea ice by microwave sounding instruments on satellites has made it possible to observe trends in areal coverage. Figure 5.11 illustrates the temporal variation of sea ice extent (%) in the Northern Hemisphere for September and March, when sea ice coverage is at a maximum and at a minimum, respectively (Perovich et al., 2010). Over the period 1979–2009, the extent of sea ice in the Arctic Ocean decreased at a rate of 8.9% per decade in September, whereas it decreased at much slower rate of 2.5% per decade in March. The observed difference in the rate of change in sea ice coverage between September and March in the Arctic Ocean is consistent with the result obtained from the model. As shown in figure 5.9, the poleward retreat of the southern margin of sea ice in response to CO₂ quadrupling is much larger in September than in March.

FIGURE 5.11 Time series of the difference (%) of observed sea ice extent from the mean value over the period 1979–2009 over the Arctic Ocean. Time series shown for September (the month of ice extent minimum) and March (the month of ice extent maximum). From Arndt et al. (2010).

The type of atmosphere/mixed-layer-ocean model described here was developed not only at GFDL but also at NASA/GISS by Hansen et al. (1983, 1984). The similarity of the latitude/calendar-month pattern of CO₂-induced warming from the GFDL model with that of the GISS model suggests that polar amplification is a robust result and not model dependent, at least in a qualitative sense. But although the basic structures of the GISS and GFDL atmosphere/mixed-layer models are similar, there are important differences between the two models.

The global mean surface temperature in the version of the GFDL model described above increased by about 4.1°C in response to the quadrupling of atmospheric CO₂. The log-linear relationship between CO₂ concentration and radiative forcing implies that the temperature change for CO₂ doubling would be slightly more than 2°C. In contrast, the model of Hansen et al. (1984) simulated a warming of 4°C for CO₂ doubling, meaning that it was almost twice as sensitive as the GFDL model presented here. The large difference between the sensitivities of the two models is indicative of the large uncertainty in the sensitivity of climate that still remains. The causes of this uncertainty will be the subject of discussion in the following chapter.