1. Embracing exponential thinking is unnatural at first.
There’s an old riddle about a beautiful, pristine pond that has become invaded by an exotic species of lily pads. This breed of lily pads doubles in number each day, quickly spreading to cover the entire surface of the pond. A scientist lives in a little house next to the pond, and she carefully tracks the invasive plant species growth each day with particular concern for the water life that is becoming choked of sunlight in the shadow of the lily pads.
By the thirtieth day of the invasion, the pond is completely covered, with a total of 536,870,912 lily pads. So the riddle goes: “On the fifteenth day, roughly how many lily pads covered the pond?” I know when I first heard this riddle, I thought it was going to be half of 536,870,912, or 268,435,456 lily pads. Wrong.
It’s easier to come to the answer when asked, “On what day is the pond half covered with lily pads?” The answer is the twenty-ninth day. Why? Because the lily pads double in number each day, so it’s logical that the day prior to the thirtieth is when the pond was half covered. In case you got that wrong, it’s fairly natural to want to think it was half covered on the fifteenth day, since that is halfway through the thirty days.
Let’s think about what really happens by the fifteenth day if we double the number of lily pads, starting with one lily pad on the first day.
Day 1 = 1 lily pad
Day 2 = 2 lily pads
Day 3 = 4 lily pads
Day 4 = 8 lily pads
Day 5 = 16 lily pads
Day 6 = 32 lily pads
Day 7 = 64 lily pads
Day 8 = 128 lily pads
Day 9 = 256 lily pads
Day 10 = 512 lily pads
Day 11 = 1,024 lily pads
Day 12 = 2,048 lily pads
Day 13 = 4,096 lily pads
Day 14 = 8,192 lily pads
Day 15 = 16,384 lily pads
Given that the Excel formula looks like = POWER(2, DAY−1) we can verify the number of lily pads on the thirtieth day as:
Day 30 = POWER(2, 30−1) = POWER(2, 29) = 536,870,912 lily pads
On the fifteenth day, we’re at 16,384 lily pads, so that’s still only 0.003 percent of the way to 536,870,912 lily pads—nowhere near the 50 percent mark. Running the formula further, past the fifteenth day, we find that we finally break 1 percent of the total number (5 million lily pads) between the twenty-third and twenty-fourth day:
Day 23 = POWER(2, 22) = 4,194,304
Day 24 = POWER(2, 23) = 8,388,608
If all this feels a bit difficult to conceptualize, it’s because it illustrates the difference between exponential thinking and linear thinking—linear thinking is how we’re wired.
When people mistakenly answer the riddle by saying the pond is 50 percent covered on the fifteenth day, they’re using linear thinking. We’re used to working with linear thinking because it’s how we know to make sense of our world. Think of how a seedling you plant, then water daily, is going to grow gradually each day. The only thing that might make it grow faster would be some fertilizer. But if left alone, it’s going to grow in an incremental manner. Steady, linear growth of course doesn’t have to mean slow growth—for instance, when children learn how to count by tens instead of ones, they get excited when they blaze past a hundred. But even when you count by millions, you’re still living in the commons of linear thinking by taking even steps of equal amounts.
Exponential thinking, as illustrated by the actual answer to the riddle, is what you become accustomed to in the computational world, not only because it governs the doubling power of Moore’s law, but also because of the way that loops are often crafted. I like to think of the difference between linear thinking and exponential thinking as akin to the difference between additive effects and multiplicative effects. Addition makes a number get bigger by a set increment; multiplication makes a number bigger by a set “leap.” For example, when I count by tens like an eager elementary schooler who has just discovered this superpower, I start with 1, add 10 each time, and in just ten steps I can leap to 101. But if I instead multiply by tens starting from 1, I’m already at 10 billion after ten iterations—which feels akin to a super-superpower for any budding mathlete that discovers this twist. We’re using the same old boring number 10 in both instances, but just rotating that plus sign (+) by 45 degrees into a times symbol (×) puts us in a whole different dimension. That’s because multiplication “hides” a bunch of additions inside itself.
Consider how 5 × 10 means taking the number 5 and adding it to itself a total of nine times: 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5. Or consider taking this further and calculating 5 × 1,000. It would look like this:
5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5.
So multiplying a number by 1,000 packs a punch and grows the number 5 at Jack and the Beanstalk speed, where one tiny bean grows into a giant stalk extending into the sky the morning right after it’s planted. To further cement this point, let your mind scan the “+ 5s” above and feel the incredible distance afforded by a multiplicative “leap” whereby you are shown the hidden power embodied in the × that a regular + doesn’t have.
Exponential growth is native to how the computer works. This is how the amount of computing memory available has evolved. The same can be said about processing power. So when you hear people in Silicon Valley talk about the future, it’s important to remember that they’re not talking about a future that is incrementally different year after year. They’re constantly on the lookout for exponential leaps—knowing exactly how to take advantage of them because of their fluency in speaking machine. Let’s next dip into how something so seemingly boring as speaking loops can make exponential sorcery happen within the computer.
2. Loops wrapped inside loops open new dimensions.
Recall how you first learned to draw a three-dimensional cube on paper back in elementary school. You start with two squares slightly offset. Then you connect the corners of each square to the other. The plane of the paper is flat, but your brain sees the line drawing of the cube and can’t help but imagine that there’s more space now available to you on the page. At first that seems impossible, because there’s been no net addition of any new space and all you have is the optical illusion of it. Consider, though, how you technically do have more space available to you with the cube as drawn—because now you can place points within the cube and tap into an entirely new dimension. For this to “click” for you, you need to activate your imagination a bit: consider how before you drew the cube you didn’t have access to a three-dimensional space of any size, and depending on how you draw it you can make it bigger than the plane of paper itself.
Let’s do this again using a different formulation that mathematicians use as a kind of gateway to the fourth dimension. Start off by drawing a point. This signifies zero dimensions.

Then extend that point in space and connect the two points. You get a line. This signifies one dimension.

Then extend that line in space and connect the four points. You get a plane. This signifies two dimensions.

Then extend that plane in space and connect the eight points. You get the cube you already know. It signifies three dimensions.
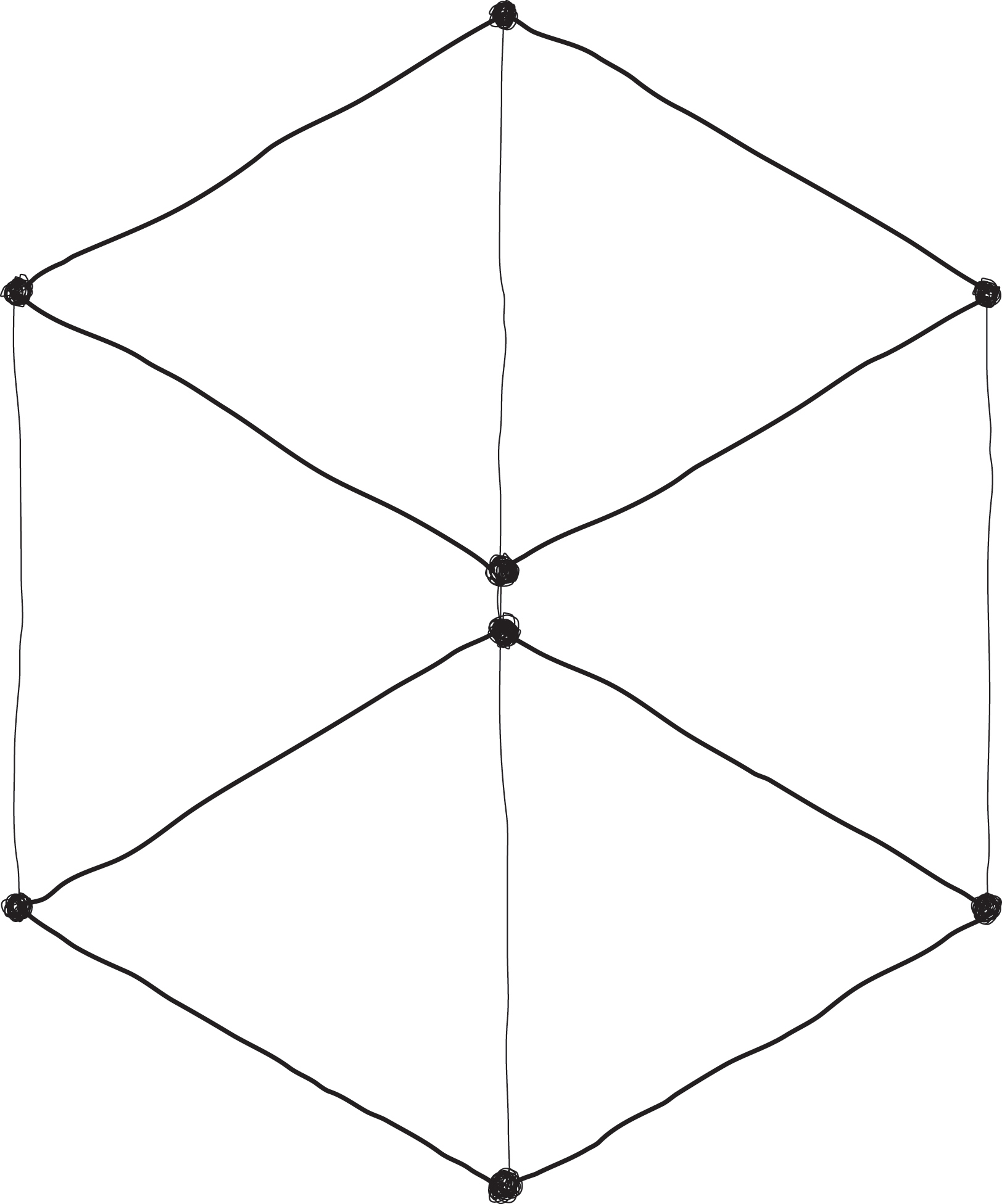
So how do you think you can depict the fourth dimension? Right! Take the cube, extend it in space, and connect the sixteen points. You get a hypercube, which signifies four dimensions.

With each dimensional addition, I want you to feel what is a typical exponential shift. For example, when we move from one dimension to two dimensions with, say, a 10-millimeter line projected to a 10-millimeter square, our new space coverage is 100 square millimeters. That’s a big jump in amount of space, and when we move to three dimensions that’s an even larger space—and it isn’t merely an incremental increase, but an extradimensional increase.
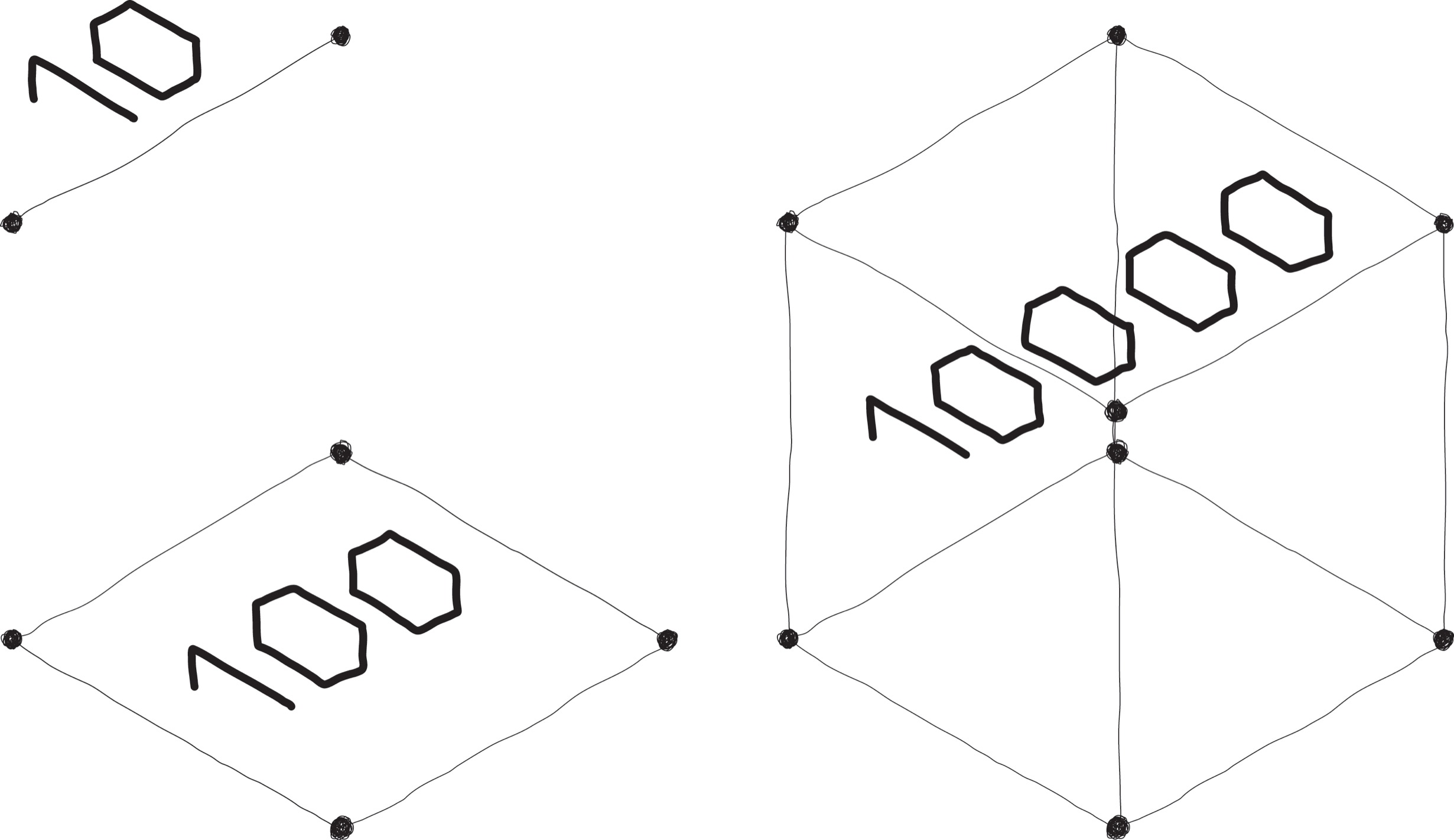
We move from 100 square millimeters to covering 10,000 cubic millimeters in three dimensions. With each dimensional shift, our growth in space is literally exponential. I know this is all pretty abstract, and although I would love to give you an easy-to-digest physical metaphor, I only have an invisible one: loops. Are you ready?
Let’s start by considering how a decade is ten years, and how a year is divided into twelve months. We traverse a decade by looping through ten years:
for( year = 1; year <= 10; year = year+1 ) { }
This piece of code starts at year = 1, increments itself by 1, and terminates when year is greater than 10. It currently does nothing important because it’s applied to a block of code that has nothing inside it. The { } can be thought of as giving a tight, squeezing “hug” so that the code inside sticks together as if it were one entity. Count it out.
1. 2. 3. 4. 5. 6. 7. 8. 9. 10.
Next, let’s consider looping over the twelve months in a year by reusing the first snippet of code with “year” replaced with “month” and stopping at 12 instead of 10:
for( month = 1; month <= 12; month = month+1 ) { }
Count it out.
1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12.
Now let’s put the month loop into the year loop.
for( year = 1; year <= 10; year = year+1 ) {
for( month = 1; month <= 12; month = month+1 ) { }
}
What happens is the years are stepped over for ten times, and for each year the months are stepped over for twelve times too. If you were to count it out, it would look something like:
1.
1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12.
2.
1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12.
3.
1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12.
4.
1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12.
5.
1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12.
6.
1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12.
7.
1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12.
8.
1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12.
9.
1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12.
10.
1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12.
Did you notice how that felt? By simply placing one loop inside another loop, something happened that shouldn’t feel natural at all to you. Now, if you were to assume that each month contained exactly thirty days—to make this example easier to understand—then you’d use a piece of code like:
for( day = 1; day <= 30; day = day+1 ) { }
Let’s count it out:
1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. 20. 21. 22. 23. 24. 25. 26. 27. 28. 29. 30.
Can you imagine what will happen if you place this loop inside the innermost loop that walks over months?
for( year = 1; year <= 10; year = year+1 ) {
for( month = 1; month <= 12; month = month+1 ) {
for( day = 1; day <= 30; day = day+1 ) { }
}
}
I prefer not to waste all the paper that would go into tracing out this case, but if you want to do so yourself, you’d start off with:
1.
1.
1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. 20. 21. 22. 23. 24. 25. 26. 27. 28. 29. 30.
2.
1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. 20. 21. 22. 23. 24. 25. 26. 27. 28. 29. 30.
3.
1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. 20. 21. 22. 23. 24. 25. 26. 27. 28. 29. 30.
. . .
and just keep going through the rest of the 3,600 numbers that you’ve generated from working in three dimensions by tracing ten years, with twelve months apiece, each containing thirty days. That’s a lot like taking your line, extending it out as a plane, and then extending that plane out as a rectangular solid. What all this means in practical terms is that when loops go inside of loops, it’s like an electric spark that triggers a turbo boost for whatever gets dropped into the lovingly hugged { block }.
Anything can be dropped into a { block }. Say, for instance, you’ve rented ten computing machines on the network somewhere. It would be easy to get all ten of them to do your task of stepping through ten years by looping over all your available machines.
for( machine = 1; machine <= 10; machine = machine+1 ) {
for( year = 1; year <= 10; year = year+1 ) {
for( month = 1; month <= 12; month = month+1 ) {
for( day = 1; day <= 30; day = day+1 ) { }
}
}
}
Or else you could flip that logic and instead do something on all ten machines for each day counted over a ten-year span:
for( year = 1; year <= 10; year = year+1 ) {
for( month = 1; month <= 12; month = month+1 ) {
for( day = 1; day <= 30; day = day+1 ) {
for( machine = 1; machine <=10; machine = machine+1 ) { }
}
}
}
A few thoughts might come to mind:
-
There’s nothing stopping you from changing the limit of year <= 10 to year <= 100,000.
-
You can continue counting all the way down to the hours, minutes, and seconds this way.
-
If we rented a few thousand machines, it would be as easy as changing machine <= 10 to as many machines that you can access.
Each successive loop introduces a new dimension, much in the same way that we made a point into a line, and a line into a plane, and then a plane into a cube. With each successively hugged or “nested” loop, another dimension of possibilities opened up. Space that didn’t exist prior to nesting a loop suddenly existed, and tweaking the start and end limits of each dimension made the additional space bigger or smaller. In short, it’s a means to open up spaces that are much larger than the ones that sit in front of us or surround us at the physical scale of our neighborhoods or entire cities. There are literally no limits to how far each dimension can extend, and no limits to how many dimensions can be conjured up with further nesting of loops. This should feel unnatural to those of us who live in the analog world, but it’s just another day inside the computational universe.
3. Be open to both directions of the powers of ten.
One of the best ways to translate the powerful feeling of transcending our limited perspective of the spaces around and inside us is to view the short film Powers of Ten by the late designers Ray and Charles Eames. The Eames duo are better known for their expensive chairs that you can find in many a fancy home, but their lesser-known film work gives the clearest glimpse of what was really going on in their dynamic minds. Powers of Ten is available to view online for free, and I’ve found that it’s the fastest way to understand the disturbing yet powerful feeling of omniscience that emerges when you work deeply in the computational medium.
The nine-minute film begins with a close-up overhead shot just one meter above the ground aimed at a couple napping on a picnic blanket in a Chicago park. The camera then begins to zoom out by one power of ten to get to 10 meters with the couple getting relatively smaller, and then to 100 meters with the entire park visible from the air, and then to 10,000,000 meters with the whole earth in view, and then to 10,000 million meters as we pass the orbit of Venus, and then we keep going all the way out past our galaxy to 10,000 light-years. We then zoom in all the way back to 1 meter away from the couple in the park and then down to 10 centimeters, where we can see the man’s skin up close, and then to 1 millimeter, where we start to enter the pores of his skin, and then all the way down to 0.00001 angstroms (one angstrom is one ten-billionth of a meter). It’s more compelling when seen animated, but you can imagine how it aptly illustrates both the grand scale of the universe and the miniscule scale at which atoms exist.
With your imagination fluidly tracing every zoomed-in or zoomed-out increment, you can feel like you’ve transcended the operating scale of your default existence. If you were born before the year 2000, when the pinch-to-zoom gesture on touch screens was still new, you might still remember the feeling of “wow” when, just with your fingertips, you could intuitively summon an extra magnification power of ten. But unlike the film Powers of Ten, there’s a limit you quickly run into as you zoom in or out of a picture, because the subresolution of your screen pixels starts to run out. At some point, all you can see are the underlying rectangular pixels instead of the micro-crinkly surface of someone’s face. In addition, when you zoom out of a photo, you eventually reach the edges of the frame, at which point there’s no reason to keep zooming out.
I know these limits well because much of my time as a visual designer in the early nineties involved crafting images that pushed beyond the edges of a normal photograph at the scale of buildings. Meanwhile, I paid attention to extremely fine details that could be rendered only with special computerized printing methods that required a magnifying glass to appreciate. A set of those experiments, the Morisawa 10 posters, made it into the permanent collection of the Museum of Modern Art (MoMA)—which you can likely recognize are simply the product of loops and more loops with repeating elements and sub-elements.

But all of those works were in print, so at some point they had to end at the edges of the paper on which they were printed. Also, a print is ultimately made out of ink dots, so when you zoom into the image you’ll end up at the dots. A more appropriate means to represent computational thinking at the infinite scale is to graduate from the surface of a printed page and to examine the power of recursion, and to go beyond the twist of the Möbius strip. Let’s take the famous mathematical example of a class of geometric figures called “fractals,” which demonstrates recursion. We start by considering a set of four lines arranged as such:

Go ahead and draw this in pencil on a surface near you. Now replace each of the line segments (all four of them) with an exact replica of that sequence of four shorter lines you originally drew. You can see it quickly becomes jagged and spiky, like the back of a seahorse:

This is called a Koch curve, named after Swedish mathematician Niels Fabian Helge von Koch, and dates to the turn of the last century. When you take three equisized Koch curves and attach them end to end to form a triangle at the endpoints, you get a six-sided star. Go ahead and draw it on paper to verify for yourself. This is what it will look like:

It starts off as a star, but when you replace each line with a Koch curve, you get what’s called a Koch snowflake, for obvious reasons as you can see below. This becomes immediately apparent as you successively continue each new cycle of line replacement. The details will get finer and finer as you progress—no matter how close you zoom into a Koch snowflake. The details are just repeated, of course, and they’re repeated forever. You ask yourself, When does it stop? And the answer is, simply, Never.

A fun, truly magical aspect of the Koch snowflake is that its perimeter is infinite but its area is finite. The former makes sense, because you can imagine replacing every _ with _/\_, increasing the length of the outline. But the actual area covered by this snowflake is mathematically proven to hit a limit, even though its perimeter keeps on growing. This makes no sense in the physical world. It’s as if I told you there was a pond that you can cover with an exact number of lily pads, but it will take you an infinite amount of time to circumnavigate. But such wonders are par for the course in the unusual world of computation.
Computation has a unique affinity for infinity, and for things that can be allowed to continue forever, which take our normal ideas of scale—big or small—and easily mess with our mind. You may think you are not in control, but you are in complete control when you write the codes and construct the loops to your liking. There is a certain comfort as you come to realize that, with eventual ease, you can craft infinitely large systems with also infinitely fine details. It’s trivial to define a computational means to traverse across a billion users and analyze their individual minutiae using a couple of well-crafted loops. It will look something vaguely like:
for( user = 1; user <= 1000000000; user = user+1 ) {
user_data = get_data(user);
for( data = 1; data <= length(user_data); data = data+1 ) {
analyze_user_data(data);
}
}
where we inspect every individual data item in a billion users, which could correspond to photos, keystrokes, or GPS locations. There’s no real upper bound, nor is there any limit to how fine-grained any computational process can be implemented by whoever constructs the codes. There’s no need to choose “how broad” or “how deep,” because the answer can simply be “both.” And if there’s any concern that the code might take too long to run, just wait for a few cycles of Moore’s law to tick away, and you can expect to eventually have enough processing power in just a few more years.
So think of this all as a kind of superpower where you can jump as high into outer space as you desire to gain vast and broad perspective by scaling the positive powers of ten: 1, 10, 100, 1,000, 10,000, 100,000, 1,000,000, 10,000,000, 100,000,000, and even larger. You also possess the flip opposite of this superpower, where you can shrink as small as you need to gain fine and precise perspective by scaling the negative powers of ten: 1, 0.1, 0.01, 0.001, 0.0001, 0.00001, 0.000001, 0.0000001, 0.00000001, 0.000000001, 1 angstrom, and even smaller. Pretty cool, huh? Unnatural, right? Almost . . . alien. You got it. Cue Bowie’s “Life on Mars” . . .
4. Losing touch with human scale can make you toxic.
“Complicated” means something that is knowable, and although it may take time, it’s wholly possible to understand. You might just need some good old-fashioned brute force to do it—you’ll get tired in the process, but it’s doable. A complicated machine (think of the printing press or digital delivery service that brought you this book) is understandable.
“Complex” means something that is not knowable, and even brute force can’t easily tackle it. I say easily because in the twenty-first century the computing power we have access to is absurdly amazing, but it still can’t solve complex problems—yet. A complex machine (think of any human being you have a relationship with) is not understandable.
I always find it necessary to keep this distinction in the foreground, because how we make systems out of computation is generally complicated, but how we humans relate to the computational systems we make has complex effects that we’re still figuring out. If you think back to the Powers of Ten and loops within loops and the infinite depth of fractals, and the ability to control time and space at the scale of infinity within the precision of fractions of an angstrom, you can see how a person who lives and breathes this invisible world of absolute power and who controls every minute of the day might lose their connection with reality. Or, as the late artificial intelligence (AI) pioneer Joseph Weizenbaum presciently wrote:
The computer programmer is a creator of universes for which they alone are the lawgiver. No playwright, no stage director, no emperor, however powerful, has ever exercised such absolute authority to arrange a stage or field of battle and to command such unswervingly dutiful actors or troops.
For that reason, I don’t find it surprising at all when folks who write code start to develop an unusual relationship with reality, or even veer into the zone of becoming slightly mad, considering the level of power and control that coding gives them. Playing a video game might seem to grant an analogous amount of power to a gamer—but writing the video game code itself kicks the power way up to being akin to godlike status. I’m not saying that every coder ends up with some kind of god complex. However, when other destructive personality traits get mixed in, the result is the archetypal “brogrammer”—a male coder who can impose his delusions and sense of entitlement on others to a terribly uncomfortable level. Keep in mind that coding does not causally create this outcome and is only correlative—there are plenty of friendly programmers out there. And even absent the fluency of coding, we can see a related behavior when despots and other powermongers use social media to impact millions of minds, and their moods, with just a few destructive keystrokes from anywhere on earth. The actual machinery of computing is complicated yet understandable; the social impact of this complicated machinery becomes complex when it involves as many humans as it does today. Complicated situations are ultimately resolvable, but complex situations are entirely different—though we should still try to understand them because they impact ourselves and our fellow human beings.
Wielding billions of bits and traveling at speeds of millions of cycles per second, with everything moving, behaving, working according to your exact instructions, with no complaints or dissent, is the definition of dictatorial control. So it’s not hard to imagine why some coders who have been operating gigantic systems at once unimaginable scales (but now imaginable to you) for a few decades might start feeling a bit powerful and trivialize the human beings around them who do not obey their keystroked commands. When I look at the snarky, annoyed, nasty behavior online by some of the technologically fluent men who literally grew up in cyberspace, I partially attribute it to the fact that coding can become extremely intoxicating—so it’s not a surprise to me when I occasionally encounter discomforting behavior among the most technically fluent. Keep in mind that composing lines of code is an extremely creative task that intrinsically involves generosity through sharing skills with others—it does not make you a bad person. But it definitely can change your perspective on the world around you if you aren’t careful.
I’m the first to admit that, in my early years of personal development, coding negatively affected me and all of my relationships. In my midforties, I was fortunate to have a close colleague at work, Jessie Shefrin, notice how easily I had soldiered through what could have been a career catastrophe. Jessie asked me how I could get so easily detached from the real world around me—which as an artist she found impossible to do—and wondered if something was wrong with me. This moment had the effect of sticking a moth in my brain that jostled about until the bug finally broke me. Today I believe that spending too much time in the computational world is especially unhealthy for human relationships—because the people around you will start to seem trivial and literally living in a lower dimension. People are unresponsive when you command them to do boring things over and over, whereas in the computational universe there is absolute compliance and infinite scale (large or small). In many ways, the world of art is what has saved me, at different points in my life, from living in this heady world of cybernetic superpowers.
My first encounter with the reframing power of art was when learning foundational arts in my pen-and-ink illustration class. I had drawn a line a little too long. So my left hand moved instinctively with my thumb and pinky raised to valiantly chord the keyboard sequence for “undo”—only then to realize that there was no “undo” in the physical world. This phantom reflex is something I had to reprogram myself around. I also needed to recalibrate my relation to physical materials—something I only fully learned after countless cuts and calluses that make me feel lucky I still have all of my fingers. My favorite moment was discovering the hard way how much more difficult aluminum is to grind by hand than wood whilst willing an intricate shape manually over three months. Until then I’d dismissed aluminum as a wimpy “second-class” metal, but I learned to profoundly respect its coefficient of stiffness.
A similar series of aha moments came later in life, after art school, with my experiences in leading people. Having had the fortunate misfortune of experiencing more than a few intense failures in that realm, I’ve carried with me the accruing gift of knowing how little I really know about the noncomputational world. My ability to take apart and understand complicated machinery as an engineer has been a useful skill, but what I learned later in life about appreciating the enigma as an artist and the craft of collaborating with people as a leader has served as an important counterbalance. For that reason, when I encounter software developers who have made their path to becoming leaders, or artists, I’m especially excited to meet them—they are my family. Meanwhile, I’ve still snuck in a few hours of coding here and there to stay close to that world, because there’s nothing else like working in its infinite spaces and feeling its magic—maybe as a form of therapy. If by chance I meet you someday and you see me acting like a machine, try to send a moth my way, please, and I’ll hopefully break from my loop.
There’s good and evil to be done with any technology. Consider how today we associate the name Nobel with peace, but we forget that Alfred Nobel invented dynamite, which has contributed to more wartime deaths than any other kind of weapon. On the other hand, dynamite also made it easier and safer for miners to clear tunnels. Or consider the Manhattan Project scientists who spent the rest of their lives weighing the balance between having invented nuclear weapons to destroy lives versus nuclear medicine to save lives. Today we can see a similar tension in the technology industry as it weighs the capability of educating anyone in the world with interactive videos versus manipulating people’s lives by constantly tracking their whereabouts and influencing how they behave and act.
We can use our knowledge of computation to make complicated systems that sometimes have complex implications. Our brains can be trained to tackle the complicated pieces, but our values need to drive the questions around how we take on the complex aspects. If the work of developers and tech companies impacted only a few thousand people like back in the early days of computing, perhaps we could more easily leave those who speak machine to themselves in their nerdy basement studios or garages. But now that computing impacts virtually everyone at the ultrafine level of their daily micromovements and at the scale of the entire world, it is more urgent than ever to know how to speak both machine and to speak humanism.
5. Computers team up with each other way better than we do.
If you examine a personal computer from a few decades ago, you will notice that there’s no place to plug in the internet. At first you might think, Well, then it must have been using Wi-Fi or some other wireless technology back in the day. Nope. Computers back in the day were islands mostly unconnected to each other. They were much less powerful, and much less useful. But over time we taught them how to connect to things like keyboards and printers and mice. And then we taught them how to connect to each other via networks that were “local”—near each other. The advent of the modem made it possible to connect via phone line to a computer that was much farther away. So a small, less powerful computer could talk to a bigger, more powerful computer, thus overcoming the limitations of its speed and memory. The small computer could become as powerful as the bigger one.
At MIT in the 1980s, I experienced this for the first time while sitting in the dorm room of an upperclassman friend of mine who was a computer whiz. He always made fun of my Mac computer as a kind of worthless toy, and so he wanted to show me what a “real man’s computer” could do. So late one cold-pizza night I watched him as he deftly hopped from an MIT computer to a computer at Columbia University, and then over to one at Stanford. My response was one of wonder: how weird it was that we were in Cambridge, Massachusetts, but somehow also in New York and California at the same time. I soon learned the craft of jumping anywhere in the world where there were computers—but, mind you, back then there weren’t that many machines out there to visit.
Hopping over to another computer started getting easier with AOL (America Online), but it didn’t really get easy until the internet was fully democratized with the advent of the World Wide Web. The Web enabled computers to connect with each other and easily share files in ways that made sense to human beings. Access to every obscure thing, from a live image feed of a coffeepot at the University of Cambridge to a niche magazine called Wired, had soon become available on the Web. In 1994, there were 2,738 websites up by the middle of the year, jumping to 10,000 by the end of the year. In 2019, it’s estimated that there are well over a billion websites, with that number continuing to grow. Say someone out there was seeking omniscience by learning about everything available on the internet—they would need extremely fast typing and clicking skills in order to visit all billion-plus sites in the world. Which is impossible, of course. But not impossible for—you got it—a computational system.
That’s how Google is able to find what you’re looking for on the internet—it simply crawls over all the websites in the world and compares what it finds out there with what you’re looking for. It would of course be impossible for a human to do that, but it’s as simple as writing code that looks something like:
for( website = 1; website <= all_the_websites; website = website+1 ){ < visit every page on the website and see if you get a match > }
This is an oversimplification of what actually happens, but you see how computation works at a scale and speed that make the proverbial needle in a haystack as simple to find as examining each individual strand of hay one strand at a time. What would be unthinkable for a human being to do—like searching the entire internet for the best “confused cat” article—is relatively easy to run as computer code. Making that search run quickly is the art and science of it all—and that’s part of the reason why Google is worth so much money as a company—but the logic should make sense to you. So now is a good time to supersize our thinking by comparing a single person accessing the Web versus a single computer accessing the Web on our behalf versus the sum total of computers in the world accessing each other’s processing capabilities. That’s right. If all the computers in the world are talking with each other at computational speeds and scales, then there’s no comparison to be made.
Computers on the network are always cooperating with each other on our behalf, and on their own behalf as well, because there is value in having neighbors from whom you can borrow a proverbial cup of sugar. Similarly, computers are always talking with each other because when one doesn’t know something, another one might. For example, when you ask your browser to bring you to the website howtospeakmachine.com, if it doesn’t know where that server exists, it will ask another computer; and if that computer doesn’t know either, it will just pass the buck on to the rest of the computers out there until a match is found. These communications and exchanges happen at speeds that far surpass our ability to type messages to each other human to human—they happen without delay and without resistance. Computers are always looking to collaborate in a way that is the ideal example of teamwork.
Smaller computers ask bigger computers to do favors for them all the time, like when you try to do something on your mobile device or from a home assistant appliance. If the computer doesn’t have enough horsepower, it can simply kick it off to the network of computers living out there that we now refer to nebulously as “the cloud.” It’s important to remember that there’s not just one cloud out there—most of the major technology companies like Google, Amazon, Apple, Alibaba, and Microsoft have clouds that consist of hundreds of thousands to millions of computers that are fully interconnected. These clouds require so much electrical power that they are often located near hydroelectric dams or solar farms in nondescript, windowless buildings with row upon row of computers placed densely in racks. With the cloud, the computer you have access to isn’t just doubled in capability à la Moore—it’s multiplicatively increased with each computer that’s been added to the network.
Consider how networks of computers made of many machines—billions of them, if you add in smartphones—can all talk and connect with each other. They can all run loops singly, doubly, and in multiple dimensions, and they can text each other (and ask each other for help) millions of times per second. We like our computers to grow infinitely in their skill level and capabilities, and the cloud lets us do just that. Today we’re at a point when holding any digital device is like grasping the tiny tentacle of an infinitely large cybermachine floating in the cloud that can do unnaturally powerful things. The useless computer that sat innocently on your desk for many years as an exotic replacement for your typewriter is now a gateway to billions of other computers in the cloud. Once this fact settles in, the power of the cloud services companies will start to excite you for the possibilities they can bring and frighten you for the scale they operate at.
For example, the primary engine of computational power for Netflix, a video streaming service, is Amazon’s cloud, because it is prohibitively expensive for Netflix to build its own and it is cheaper to rent the power in a competitive market. It doesn’t make sense for a company like Netflix to own its own massive computing infrastructure when that is not a kind of expertise they currently need to own and control. Putting the issue of costs and expertise aside, the core advantage Netflix gains is the fluid scalability of computing resources and the ability to dial up or dial down their need to flexibly meet their consumers’ demands. But when you note that Amazon controls half the cloud market and can easily change its prices at leisure, it only makes sense that Netflix would also want to shop the competitor Google’s cloud for insurance. It also means that every cloud company in the world is working overtime to make their individual computing servers dramatically better at collaborating with each other to garner greater speed and power for their customers.
It’s a relatively new thing that an entire tech company doesn’t need to be built on top of its own computing power but can instead wholly rent it in a fully flexible, on-demand capacity. The cloud model represents a fundamental shift in how companies can get built, where the raw materials are all completely ethereal, virtual, and invisible. But that doesn’t mean it’s not comprehensible—it’s just complicated. It’s knowable and learnable. And in the back of our minds we need to be wondering what the future implications might be for servicing an entire race of machines to become better collaborators with each other than we ourselves could ever be. I know that my own uneasiness on this matter has made me resolved to devote the remainder of my life to foster teamwork and to partner with fellow human colleagues, because our computational brethren are beating us, exponentially.