Chapter 8: Harmony and Chords
“Music, to create harmony, must investigate discord.”
Plutarch
In music, when two or more notes are played simultaneously, whether the same note on different instruments, different notes on the same instrument, or different notes on different instruments, that is harmony. When we hear the playful blend of the voices in a barbershop quartet, or the majestic brilliance of a symphony orchestra with multiple sections of instruments playing at the same time, or the soothing and intricate blend of human voices in an a cappella choir, we get a true sense of the beauty of harmony in music. The richness of the sound generated by the unison of the different instruments or voices — a sound that none of them could have created individually—is the essence harmony.
Of course, music does not require harmony. You can have music that is just rhythm, e.g., drum solos, with no notes played at all and so no harmony. Similarly, you can have music that plays notes but never simultaneously, and so never creates harmony. Nevertheless, music theorists consider harmony to be one of the key elements of music, along with rhythm and melody.
Moreover, the word harmony can also be a bit misleading. When notes are being played simultaneously, they do not have to be particularly "harmonious" or consonant; they may instead be quite dissonant. So, the important fact for defining harmony is that the notes are sounding at the same time.
Chords
Harmonies with three or more notes are called chords and
chords are derived from scales. In fact, each scale contains multiple possible chords, and it is usually quite easy to identify chords that are contained in any scale.
Chords, like scales, are also characterized by a set of intervals relative to the root note. For instance, a Major chord, which is derived from the Major scale, is a chord containing three notes. It is defined by the root and another note a major third above the root, and then another note a major third above the second note (and a perfect fifth above the root).
The way the notes in the chord relate back to its root note — is called the “spelling” of that chord, and this spelling is independent of the actual root note. So, if you know the name of the chord then you can easily determine the notes that are contained in it, regardless of what root note is used as the starting point. This spelling is often expressed as a series of numbers, e.g., 1 3 5, which actually corresponds to the degree numbers for the intervals in the scale from which the chord is derived.
As is the case with scales, degree numbers designate the intervals in a chord and how those intervals are arranged regardless of the root note. They do not correspond directly to notes until a root note is chosen, and the chord spelling then defines the chord.
For example, a “1 3 5 7” chord spelling, which is the formula for a Major 7th chord (more on this later) simply means that this chord consists of the Root (first scale degree), and the 3rd, 5th and 7th scale degree. If we take a Major scale, and assign it a key, let’s say key of C, we can then simply apply this formula to determine the actual notes of the C Major 7th chord.
Also, because of variations in enharmonic spelling, it is important to remember that the same note can have differently names in different chords. For example, the chord B Major contains the note D#, taken from the B Major scale, while the same note is called E♭
when it appears in the A♭
Major chord, derived from the A♭
Major scale.
The notes of the chord are usually played at the same time (stacked chords) and this can be done on one polyphonic instrument, such as a piano or guitar, or they may be played simultaneously on multiple instruments, e.g., three woodwind instruments. However, they may also be played separately with some overlap, or played separately, but in a quick enough succession, that they will be "heard" as a chord (arpeggios). Moreover, some of the notes may be left out completely and only "implied" by the other two notes of the chord.
For example, instruments like the flute, trumpet, and obviously a single human voice, can sound only one note at once. Thus, they are monophonic instruments. Clearly then, these instruments cannot play a stacked chord where the notes are sounded simultaneously. Nevertheless, chords can still be implied. For example, since it is difficult to play three strings simultaneously on a violin (a not totally monophonic instrument), the two lower notes of the chord (sonority) are played in such a way that they resonate for a longer period of time, and the third note is then played with that resonance as the background sound, thus simulating the harmony of the chord. This technique is called a broken chord.
Also, the third note may not be played at all and instead just implied by the playing of the other two notes. Nevertheless, the listener “hears” a three-note harmonic structure. For example, in the key of C Major, if the music comes to rest on the two notes G and B, most listeners will hear this as a G major chord even when the third note is not sounded at all.
Finally, harmonization in chords usually sounds pleasant to the ear when there is a balance between the consonant and dissonant
sounds. In simple words, that occurs when there is a balance between "tense" and "relaxed" moments (more on that later).
Chord Names
Since chords are derived from scales, the naming and notation conventions for chords are similar to those for scales. More specifically, different chords can be named by their “root note”, e.g. C♯, and their characteristic “quality.” For example, the chord Cmaj (or simply C) is a chord of the quality Major built on the root note C.
Minor chords are typically identified by a lowercase min, whereas chord quality is usually omitted for major chords. Similarly, + or aug is used for augmented chords, ° or dim (not -) for diminished chords, ø for half diminished chords, and dom for dominant chords. Additional symbols may also be added to the chord name to indicate if the chord is a triad, or some type of extended chord, e.g., a seventh (Δ7). Finally, any altered notes will also be identified (e.g. sharp five, or ♯5), as well as any added tones (e.g. add2) and the bass note if it is not the root (e.g. a slash chord).
For instance, for the chord name “C augmented seventh,” the corresponding symbols could be Caug7, or C+7. Both are composed of three parts: 1 (letter 'C'), 2(‘aug' or '+'), and 3 (digit '7'). The three parts of the symbol (C, aug, and 7) refer to the root note C, the augmented (fifth) interval from C to G♯, and the (minor) seventh interval from C to B♭
, respectively. These would then imply a chord formed by the notes C–E–G♯–B♭
.
Types of Chords
Triads
. Triads are the most commonly used type of chords and form the basis for most harmony in modern music. They are called triads called because they consist of three distinct notes, built from intervals of thirds, and with three relevant intervals total. In other
words, they consist of a root note and two other notes above that root that ascend in thirds. So, starting with the root note, count up by a third (which means up two degrees in the scale) to get the next chord note, and then count up by another third to get the final chord note. And of course, don’t forget that there is also an interval between the root and the top note, which is a perfect fifth.
The second note of a triad is called “the third” because it is an interval of a third away from the root of the chord. The “third” is especially important in constructing chords, as it is the quality of the “third” that determines whether you’re dealing with a major or minor chord. A chord is called a minor triad if there’s a minor third interval between the root and the third. A chord is called a major triad if there’s a major third interval between the root and the third.
Also, the third and last note of a triad is of course called “the fifth,” because it is a fifth interval from the root.
In fact, the most common triad chords are the Major and minor triads. But there are also augmented, diminished, and dominant triads.
A Major chord, as noted earlier, is made up of a root, a major third above the root, and a perfect fifth above the root. One way to see this is to start at the root, move up 4 half steps to the next note, then 3 half steps (or 7 total half steps above root) for the final note. The spelling of this chord is therefore “1 3 5.” And, as mentioned before, the pattern is the same no matter the root note.
In contrast, a minor chord is made up of a root, a minor (or flattened) third above the root, and then a perfect fifth. In other words, starting at the root, go up 3 half steps to find the next note, and then another 4 half steps (7 half steps total above root). The spelling would thus be “min 1 3 5.
In an augmented triad chord, one note is actually raised a half step (sharpened) above where it is normally. So the formula you
want to remember for building an augmented chord is: “1, 3, sharp 5.” For example, for a Major chord, just take the first major scale degree, then the third major scale degree, and then the fifth major scale degree but raised by a half step.
It’s also important to note here that “sharp 5” does not necessarily mean that the note will be a sharp, but rather that the “fifth” note will be raised, or sharpened, by a half step. Depending on the root you begin with, the result may in fact be a natural note.
A diminished triad chord consists of a root note, a minor third, and a diminished/flattened fifth. In a sense then, diminished triads are minor chords that have had both of the intervals between the third and fifth lowered by a half step. That means: first major scale degree, third major scale degree lowered one half step, and fifth major scale degree lowered one half step. Thus, the formula for building a diminished triad chords is: 1, flat 3, flat 5
Again, it’s important to note here that flat 3 and flat 5 do not mean that these notes will necessarily be flats, but are only the third and fifth notes occurring in the scale degree lowered by a half step.
Another way of looking at a diminished triad is as a stack of minor intervals, with three half steps between each interval. So, for example, to build a C diminished triad (written as Cdim), you could build it by counting out the half steps between intervals, like this: Root position + 3 half steps + 3 half steps (6 half steps above root).
Diminished chords are not common, because they have a distinctive timbre: tense, dark, and unstable. However, one common use for the diminished chord is as a transition point between two other chords in a chord progression (more about this later). The diminished chord contains a high amount of tension, which is then can be released once the progression arrives on its finishing chord. Moreover, with the diminished chord as a transition, this also creates a stepwise motion in the root notes of the chords in the
progression—they move up in half-step increments —which adds a powerful sense of movement to the music.
For example, in George Harrison’s classic, “My Sweet Lord”, the song starts on the key of E Major, and so the tonic chord is E maj, but there is also a brief alternation with C# min. Then this gives way to an F dim (diminished) chord, which serves as as transition that then gradually works its way to an F# min chord which becomes the finishing and resolving chord.
In summary, the major triad is very consonant; the minor triad is a bit less consonant but still enough so for most purposes. On the other hand, the augmented triad is very dissonant, and the diminished triad is extremely dissonant.
|
Figure 8.1. Common Triads
|
|
Component Intervals
|
|
|
|
Type
|
Third
|
Fifth
|
Chord Symbols
|
Notes
|
|
|
|
|
|
|
Major Triad
|
major
|
Perfect
|
C, CM, Cmaj, CΔ, Cma
|
C E G
|
|
|
|
|
|
|
Minor Triad
|
minor
|
Perfect
|
Cm, Cmin, C−, Cmi
|
C Eb G
|
|
|
|
|
|
|
Augmented Triad
|
major
|
Augmented
|
Caug, C
+
, C+
|
C E G#
|
|
|
|
|
|
|
Diminished Triad
|
minor
|
Diminished
|
Cdim, C
o
, Cm
(
♭
5)
|
C
E♭
G
♭
|
|
|
|
|
|
Quadads
. In many types of music, particularly contemporary instrumental and jazz, chords are often augmented with "tension". The tension is created by adding an additional note to the top of a
triad chord that creates a relatively dissonant interval in relation to the root. Typically, this dissonant chord then “resolves" to a more consonant chord. When triads are augmented in this way, the result is usually obtained by adding a 7th of some kind (e.g., 1 3 5 7). That’s why they’re also often called 7th chords.
One of the most common 7th chords is the Major 7th. These chords have a major 3rd interval, followed by a minor 3rd, which is then followed by another major 3rd on top. This means that they have a Root, a Major 3rd, a Perfect 5th and a Major 7th and so the chord formula is: 1 3 5 7. In C, for example, the notes of C Major7 chord, or just CMaj7, or even CM7, would be: C E G B.
In contrast, a minor 7th chord is composed of a minor 3rd, followed by a major 3rd, followed by another minor 3rd. So, they have the following notes: Root, minor 3rd, Perfect 5th and a minor 7th. The chord formula is then: 1 flat3 5 flat7. So, in C, for example, the notes of the C minor 7, or Cm7, would be: C Eb G Bb.
Another common type of quadad is called the Dominant 7th. They have a Root, a Major 3rd, a Perfect 5th and then a minor 7th. So, a major 3rd interval is followed by two minor 3rd intervals. Thus, these chords are positioned somewhat in the middle between the Maj7 and min7 chords. However, the sound is quite different, with clear tension that is best resolved as part of a chord progression. The Chord formula for a dominant 7 is: 1 3 5 b7. For the C dominant 7, or just C7 (as it’s usually written), the notes are then: C E G Bb.
The Minor 7 flat 5 chord just a minor 7th chord with a flattened 5th. It is composed of a: Root, a minor 3rd, a diminished 5th (a Tritone), and a minor 7th. This means that they have a minor 3rd interval followed by another minor 3rd, which is followed by a major 3rd (the opposite of Dominant 7). These very unique sounding chords are commonly used in jazz, sometimes in blues. The chord
formula then is: 1 b3 b5 b7. So, for C minor 7b5, or Cm7b5, the notes would be: C Eb Gb Bb.
The Diminished 7 or Full Diminished chord is composed of stacked minor 3rd intervals, which is why they are also often called symmetrical chords. Any chords that have the same intervals across all their notes are symmetrical. Their interval structure is always the same, no matter if you’re ascending or descending in pitch. In practice, this means that you can move these chords up or down by a minor 3rd interval (3 semitones) as much as you want, and the notes would remain the same, only in different order. The sound of diminished 7 chord can be described as jarring, dark and unstable, but also interesting and is often used in music to add a dramatic effect.
Diminished 7 chords should not be mistaken with diminished triads, which are typically just called ‘diminished’ chords. Specifically, diminished 7ths consist of a Root, minor 3rd, diminished 5th, and Major 6th. Chord formula is: 1 b3 b5 bb7. Of course, the bb7 simply means a double flatted 7th, which is in effect the same as the 6th scale degree. For example, for the C diminished 7, or Cdim7 for short, the notes are then: C Eb Gb Bbb.
These of course are not all of the possible combinations of intervals from which quadads can be constructed. There are quite a few more, e.g., Major and minor 6ths, or a Dominant 7 chord with a flat 5th (1 3 b5 b7), etc. But if you know what types of intervals you want to build the chord from, and then create the appropriate chord formula, and choose a root note, you can then quickly determine the chord notes. If course, the real test will be in then hearing the chord sounded out. At that point you will know better how the chord might best be used, if at all.
|
Figure 8.2. Common Quadads
|
|
Component Intervals
|
|
|
|
Type
|
Third
|
Fifth
|
Seventh
|
Chord Symbols
|
Notes
|
|
|
|
|
|
|
|
Diminished Seventh
|
minor
|
Diminished
|
Diminished
|
C
o
7
, Cdim
7
|
C
E♭G♭
B
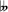
|
|
|
|
|
|
|
|
Half Diminished Seventh
|
minor
|
Diminished
|
minor
|
C
ø7
, Cm
7
♭
5
, C−
(
♭
5)
|
C
E♭G♭B
♭
|
|
|
|
|
|
|
|
Minor Seventh
|
minor
|
Perfect
|
minor
|
Cm
7
, Cmin
7
, C−
7
|
C
E♭
G
B
♭
|
|
|
|
|
|
|
|
Minor Major Seventh
|
Minor
|
Perfect
|
Major
|
Cm
M7
, Cm
maj7
, C−
(j7)
, C−
Δ7
, C−
M7
|
C
E♭
G B
|
|
|
|
|
|
|
|
Dominant Seventh
|
Major
|
Perfect
|
Minor
|
C
7
, Cdom
7
|
C E G
B
♭
|
|
|
|
|
|
|
|
Major Seventh
|
Major
|
Perfect
|
Major
|
CM
7
, C
M7
, C
maj7
, C
Δ
7
, C
j7
|
C E G B
|
|
|
|
|
|
|
|
Augmented Seventh
|
Major
|
Augmented
|
Minor
|
C+
7
, Caug
7
, C
7+
, C
7+5
, C
7
♯
5
|
C E G♯
B
♭
|
|
|
|
|
|
|
|
Augmented Major Seventh
|
Major
|
Augmented
|
Major
|
C+
M7
, C
M7+5
, C
M7
♯
5
, C+
j7
, C+
Δ
7
|
C E G♯B
|
|
|
|
|
|
|
Open and Closed Voicing
When all the notes of a chord are in the same octave, the chord is considered to be in a closed voicing. However, sometimes the notes of a triad may be spread out over two or more octaves, or with the different notes rearranged so that, for example, the root may carry the highest sounding note, or the third, or the fifth can carry the lowest sounding note. The notes are still the same (C, E, G, for example) — they’re just located an octave or even octaves above or below where you would expect them in a normal triad. This is called open voicing.
Inversion
Chords may also be inverted, changing the order in which the notes are stacked. If the third of a chord is the lowest-sounding note, then it is said that the chord is in “first inversion.” When the fifth of a chord is the lowest-sounding note, the chord is in “second inversion.” When a seventh of a chord is the lowest-sounding note, then that chord is in “third inversion.”
Chord Notation
For the benefit of performers, chords can be represented in various ways on a musical staff. However, some of these methods are more commonly used than others. One common method is to simply represent the notes of the chord on the staff in their normal relative
positions.
|
Figure 8.3. Chords on Musical Staff
|
|
|
Another approach is to write the chord names (letter and quality) above the staff. This tells the performer what chord should be played until the next name appears. Chord names also may be used even when the chord notes are written out on the staff, so that performers can read either the chord names or the notated music, as they prefer.
|
Figure 8.4. Chords on Musical Staff With Chord Names Above
|
|
|
Chord Charts
In an effort to simplify things for musicians, various other approaches to notating relevant chords for a piece of music have been developed over the years and are commonly used. One of these is the chord chart.
A chord chart describes the basic harmonic and rhythmic information for a piece of music and is intended to quickly lay out a rough outline so that the musician may improvise around it. Consequently, it is most commonly used by professional session musicians playing jazz or popular music where improvisation is expected. The chord chart is usually intended for the rhythm section (e.g., piano, guitar, drums and bass) to provide them with the minimal amount of information necessary to create the acoustic and rhythmic foundation for the music. The other musicians are then expected to improvise the individual notes used for the chords (the "voicing") and the appropriate ornamentation, counter melody or bass line.
In some chord charts, the harmony is provided as a series of chord symbols above a traditional musical staff. The rhythmic information is usually written using a special form of “rhythmic notation” and it can be very specific.