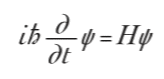
Chapter 6

1535, the year Jerome and his family leave the workhouse and begin to rise in Milanese society, is the year William Tyndale is arrested in Antwerp for heresy. All across Europe, religious disputes are boiling over. Sir Thomas More is soon to be executed for refusing to recognise King Henry VIII as head of the Church of England. In Holland, the Anabaptists attempt to take control of Amsterdam — and fail. In Germany, they succeed, ruling the city of Münster for five months. Six French Protestants are burned in front of Notre Dame Cathedral for distributing printed condemnations of the Catholic Church. They are only the thin end of the wedge, so King Francis I has decided to ban use of the printing press.

None of this bothers Nicolo Tartaglia, who is just trying to keep his head down and earn a living. It hasn’t been easy. Perhaps through circumstances, perhaps through bad luck, The Stammerer is not blessed with an amiable personality. Since growing up to become an intelligent, scholarly young man, he has been driven out of his hometown of Brescia not once, but twice for being avaricious, morose, and, above all, rude to everybody.

Biting his thumb at the Brescians, he has settled in Venice, where he writes down ideas in his own crude version of the Venetian dialect. Though it is far from the erudite language of scholarship, these ideas are clever and innovative enough to pass muster. A local nobleman has recognised his talent and helped him with money to study at the University of Padua. Tartaglia has become a teacher of Euclid’s theorems. It is a solid enough career for any self-taught man and one that Tartaglia is pleased to call his own. No wonder, then, that he is so incensed when Antonio Maria Fior arrives in town, his eye firmly fixed on Tartaglia’s hard-won job.

Fior is an inferior mathematician with a superior mathematical lineage. His teacher was a celebrated scholar, Scipio Ferreus, a professor at Bologna. And here Fior was in the right place at the right time. In 1505, Ferreus worked out a way to solve a particular type of equation known as a cubic. Cubic equations are those that include x raised to the power of three. That is, x multiplied by x multiplied by x. A simple way to visualise it is as the volume of a cube, whose sides are of lengthThe volume is its length multiplied by its breadth multiplied by its height: x3. If x is two, say, the cubic power is 2 x 2 x 2 = 8.

In Jerome’s time, however, there is no mathematical notation, so all problems are laid out in convoluted sentences such as ‘cubus6. rebus aequalis 20’. In modern notation, we would write that as x3 + 6x = 20. This makes it significantly easier to solve. The idea is to find a numerical value for x, but at this point some cubic equations were thought to be impossible to solve.

In 1494, the Franciscan friar Luca Pacioli had published a book, expansively illustrated by Leonardo da Vinci, in which he explained why there would never be a general solution to the cubic equation. Ferreus didn’t have a general solution, but he could solve an equation of the form x3 + bx =It was an impressive innovation, involving many complicated routines of substituting one variable for another, and making a variety of assumptions that allow a solution to emerge. However, it was still not the long-sought general solution. Give Ferreus something like 3x3 + 8x2 - 7x = 15 and he would be undone. A new solution was necessary.

To a medieval mathematician, a new solution to an equation is a precious thing. It is a stick with which to beat your enemies, a dagger by which to slay them and take their jobs. That’s because no one publishes their solutions then waits for their peers to give them acclaim. The modus operandi is to humiliate your rivals by challenging them to mathematical duels.

The public relish these occasions. This is Renaissance sport, featuring intellectual heavyweights sparring in the mathematical ring. It isn’t just about mathematics, either. In February 1498, for instance, Leonardo da Vinci joined a public battle with various mathematicians, astronomers, astrologers, and physicians. This was a contest designed to establish the pecking order of all the arts and sciences. It’s not clear who won the battle, but the occasion did lead da Vinci to write that painting — because it is based on observation, mathematics, and geometry — should be considered a science. ‘No human investigation may claim to be a true science,’ he says, ‘and if you would say that those sciences which begin and end in the mind possess truth, this is not conceded, but denied for many reasons. The foremost [reason] is that such mental discourses do not involve experience, and nothing renders certainty of itself without experience.’

Battles between mathematicians, though, bring entire populations to the city square. This is about more than who can make an argument for their intellectual superiority. Here, there are concrete problems to solve, points to score, answers that are definitively right, wrong, or unachievable. There is cheering and catcalling, a referee, champions, and underdogs — all accompanied, of course, by drinks and snacks. Once the contest is over, the winner takes all. In theory, the loser is supposed to buy his conqueror a dinner for each of the unsolved problems. In reality, he often has to cede fame, money, and sometimes even a job. No wonder Tartaglia is worried.

A battle starts with the competitors giving each other thirty problems to solve. They must be able to solve their own puzzles, so anyone with a solution that others don’t have is at a distinct advantage — they can set problems that their rival simply cannot figure out in the allotted time.

It is not clear whether Ferreus ever used his solution to the cubic equation in a public mathematical battle. But he knew its value and only passed it forward from his deathbed. The recipients were Fior, his pupil, and Ferreus’s son-in-law, Annibale della Nave. The son-in-law did nothing with it, but Fior had no qualms about putting his teacher’s skill to work.

Fior was a lazy student and an unskilled mathematician. Ferreus’s solution was his only card and he knew it. For two decades, he guarded it jealously and used it to great advantage in public duels. But then, in challenging Tartaglia, he pushed his luck too far. Fior wanted Tartaglia’s job and Tartaglia needed it to live. So when Fior challenged The Stammerer to an algebraic duel, Tartaglia took it as seriously as an assault on his life. What Fior didn’t know was that Tartaglia had already been working on cubic equations. Moreover, unlike Fior, he was born to the task. In many ways, Fior’s rising fame had worked against him. Tartaglia had discussed Fior’s wielding of cubic equations with a Brescian schoolteacher called Zuanne da Coi, a tall, lean, hollow-eyed man, with a strange, slow gait. Da Coi had then encouraged Tartaglia to think about the possible solutions and so he had — with some success. Tartaglia now possessed a solution for equations of the type x3 + ax2 = b, and x3 = ax2 + c.

Following the usual protocol, Tartaglia and Fior exchanged problems two weeks prior to the duel. Tartaglia evidently knew — perhaps from da Coi — about Fior’s weak grasp of mathematics and exploited it by setting him a range of mathematical tasks, including some that involved the new cubic solutions.

Predictably, Fior’s problems were only of the type for which he alone had a cast-iron schema that would generate solutions. The Stammerer took them to bed with him and rattled the equations around in his mind. It worked. Almost certainly because he had already worked out solutions to equations of a similar kind, Tartaglia worked out Ferreus’s method a full eight nights before the contest was to take place. He then went on to work out the solution to yet another form of the equation. By 13 February 1535, the night before the public duel, Tartaglia knew he would win.

Tartaglia was impressive. Fior’s face must have worn a look of pure horror when, in less than two hours, Tartaglia solved all the problems that had made Fior’s living for the last thirty years. Fior, for his part, couldn’t solve any of the equations Tartaglia had set. There was a clear winner. Fior asked Tartaglia to demonstrate his methods, but The Stammerer walked away. He didn’t even claim his thirty dinners. For him, a burnished reputation was enough.

ψ

‘Tartaglia was good, wasn’t he?’

The sun is almost up. Jerome’s skinny student, Rudolf Silvestri, has just delivered a bowl of boiled vegetables, setting it down on the floor at my feet. When he stood up and seemed to look right through me, I took offence, until I remembered that I am not sure whether I am actually, physically present. Jerome has picked up the bowl and set it on the table. Now he is fixing it with an intense stare, as if it contains the secrets of the universe.

‘Fior was hardly a great opponent,’ he says, eventually.

I smirk at Jerome’s withering snark, but decide not to pursue the point. ‘So, at this point, Tartaglia is riding high in mathematics and you are riding high in medicine, thanks to the job at the Priory. What went wrong?’

‘It wasn’t enough, I suppose,’ Jerome says into the bowl. He picks out a piece of turnip and brings it to his lips. ‘I didn’t want to just cure the sick. I wanted to move things forward — to understand.’

‘Understand what?’

‘Everything.’ He takes a bite of the turnip. It is soft and he barely chews it before swallowing. ‘Life. The cosmos. Everything. This is my calling, my only task.’

In this regard, Jerome reminds me of Erwin Schrödinger, the most famous quantum mechanic of them all. Schrödinger once said that to understand ourselves is the only task of science.

Fittingly, it is Jerome’s mathematical innovations that made Schrödinger’s work possible.

Remember the glowing horseshoe? The radiation comes from atoms of iron. More precisely, it comes from an electron that surrounds the nucleus of those atoms. As the electron loses energy, it effectively falls between these different orbits. The properties of that radiation are determined by the wave that fits onto the orbit. But that wave is no ordinary wave: it is psi, the wave function.

The wave function has a phase, which — as de Broglie pointed out — must exist outside of the pure physical reality of the time and space that we know. And the only way to fully describe that phase is to use mathematics that involve the imaginary numbers, written as i.

i is the square root of -1. I know I haven’t explained exactly what Jerome did to discover it yet (and that discovery is almost a decade away still), but trust me for now: the fact that Jerome did anything with such an oddity is extraordinary. In his day, negative numbers were themselves suspect. People understood what it meant to have two apples. They did not understand (and perhaps we don’t, really) what minus two apples could possibly be. How, then, to take a square root of a negative number? After all, you know that the opposite process — squaring a number — never gives a negative? We know that 2 x 2 = 4. We know that -2 x -2 = 4. We know that the square root of four is therefore two and minus two. But what is the square root of minus four?

Where we call such solutions ‘imaginary’, Jerome termed them ‘sophistry’. If you came across imaginary numbers at school, you probably hated them. Who knew they were hated for centuries prior?

If mathematical conundrums like this leave you floundering, you are in good company. They left Jerome floundering, too. But he was the first to face up to them. When the geometer Heron of Alexandria was working out the volume of a truncated pyramid in the first century AD, he found he had to deal with the square root of minus sixty-three. Heron just fudged his calculation, quietly dropping the negative number. In 250 AD, the Greek mathematician Diophantus derived a square root of a negative number in his calculations. He assumed he had made a mistake. That was also Jerome’s first thought when he discovered he had to deal with the square root of a negative number. But he checked, and there was no mistake. He gave the notion a name: ‘impossible quantities’. And then he went on to put them to use in solving fiendishly difficult equations. It was, he said, ‘impossible’ to find numbers that solved these equations, but there are certain ‘objects’ — his ‘impossible quantities’ — that get the job done.

Translators argue about the proper way to interpret Jerome’s Latin in this passage of his 1545 book on the art of algebra and arithmetic. Some believe he regarded the imaginary numbers as ‘mental tortures’ that had to be ignored before you could complete the calculation. Others infer that he was simply saying that the ‘imaginary parts’ become lost in the process, making all things work out in the end. One translation contends that Jerome said this mathematics is ‘truly sophisticated’, another that he thinks it ‘truly imaginary’. Still others have translated it as ‘truly sophistic’ — that is, something of an elegant fudge. And yet we see him demonstrating a difference between ‘pure negative’ numbers (minus two, for example) and ‘sophistic negative’ numbers, such as the square root of minus two:

Note that √9 is either +3 or -3, for a plus [times a plus] or a minus times a minus yields a plus. Therefore, √-9 is neither +3 or 3 but is some recondite third sort of thing.

That ‘recondite third sort of thing’ is central to our very existence, as it turns out. It is not only used in engineering bridges, aeroplanes, and mobile phones (and truncated pyramids, of course), but it is central to the most fundamental theory of physics. Without Jerome’s imaginary numbers we cannot explain how the universe works or even the most basic processes of atomic physics. It was Schrödinger, an Austrian, who worked that out over the Christmas holiday of 1925.

Schrödinger is the Pablo Picasso of physics. He was a genius, who represented reality in a way that defied all previous conventions and was also unrepentantly uninterested in living a ‘conventional’ life. Schrödinger’s lifestyle gave no quarter to the morals of his contemporaries and he left tragedy and a trail of shocked bystanders in his wake. Early in his professional life he became maths tutor to a thirteen-year-old girl called Itha Junger. In his diaries he admits he groomed Itha by writing her poems and engaging her in grown-up conversations about religion and science. Their maths lessons included petting, cuddling, and fondling her until she was seventeen, when he finally felt able to seduce her. Their secret relationship continued on and off for years. In 1932, she fell pregnant and sought an abortion because Schrödinger would not leave Anny, his wife. The procedure went badly and left Itha unable to have children.

Anny tolerated Schrödinger’s insistence that their relationship be ‘open’, commenting that ‘it would be easier to live with a canary than a racehorse, but I prefer the racehorse’. In 1934, Schrödinger took up a position at the University of Oxford and brought both his wife and a new mistress, setting up their household in a ménage à trois that the Oxford dons could barely tolerate — especially as his mistress was pregnant.

None of this detracts in any way from his genius — perhaps it even stimulated it. He was certainly stimulated at Christmas 1925, when he left his wife behind, picked up a different mistress — this one’s identity remains unknown — and a copy of Louis de Broglie’s work, and went on a trip to the Swiss Alps.

By the time he returned home, he had a world-changing equation that would win him a Nobel Prize. We now call it the Schrödinger equation, and we write it like this:

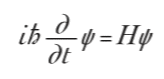
I have filled in the gaps on the wall with my stone scrawl.

Jerome shakes his head. ‘I don’t understand your notation,’ he says. Of course he doesn’t. The notation is a product of the centuries that are to follow.

‘The h with a bar through it is Planck’s constant divided by two times pi. Two things placed next to each other means multiply them together. d divided by dt means the rate of change of the thing it precedes.’

‘H?’

‘H is something called the Hamiltonian operator. It contains information about the energy in the system and varies from system to system — you just plug it into the formula.’

‘Hamiltonian?’

‘It’s named after a William Hamilton.’

Jerome raises his eyebrows at the name. ‘The Archbishop?’ he says. There is hope in his voice.

‘I’m afraid not. He was an Irish mathematician. Or he will be.’

Jerome looks disappointed. ‘Perhaps a descendant, then?’

‘Perhaps. William Hamilton had Scottish ancestors, I know that.’

It seems enough to satisfy him. ‘And this Hamiltonian,’ he points a finger at the wall. ‘What does it do?’

Now there is a question.

Schrödinger’s equation is a means to predict the physical properties of a system — not just an electron in an iron atom that might emit radiation, but anything that follows quantum laws. Because psi has a phase that exists outside of our ordinary three dimensions of space, we know that psi must itself inhabit another realm, something like Jerome’s aevum. Physicists call it Hilbert space, after David Hilbert, the mathematician who came up with the concept. Hilbert space has an infinite number of dimensions. It is generally described as an ‘abstract’ space, rather than a physical one, but there is an ongoing argument as to whether the wave function is physical or abstract. We’ll get to that. First we have to deal with a slightly more accepted oddity associated with the wave function’s behaviour within Hilbert space: it relies on Jerome’s probability theory.

Physicists use the Schrödinger equation to make predictions of what to expect from quantum experiments and processes. Very early on, they realised that — although the equation officially depends on the wave function, which describes the unfolding events — all we can actually do is work out the square of the wave function, Ψ2. The square of psi gives you a probability associated with anything you want to know. And the right choice of Hamiltonian operator, which depends on the physical system you’re working with, tunes the equation to each particular thing.

Understandably, Jerome looks confused. I don’t know if I can make it any easier. ‘Psi squared is linked to the probability of the atom’s position, say. You specify a position, and it will tell you how likely you are to find it in that position if you carry out a measurement.’

‘So it is like a bet?’

‘Worse. It’s like a bet that depends on imaginary numbers.’

‘And the equation won’t guarantee that you win?’

‘All it will do is give you the odds of winning.’

‘So the atom might be somewhere else when you look for it.’

I take a deep breath. ‘It’s not somewhere else. It’s everywhere else. And nowhere. Until you make a measurement.’

I stare at Jerome to see how he reacts to this. It baffles me. It baffles everyone I know.

Clearly, it doesn’t baffle Jerome. He looks intrigued. And rather pleased.

‘So you call it into existence with this measurement?’ he says. ‘Like a magus summoning a demon?’

My brow furrows. Is that right? I hesitate, then decide it’s as good as anything I’ve heard. I nod, as sagely as I can.

ψ

This is not quite the whole truth. This understanding of what the Schrödinger equation tells us is known as the Copenhagen interpretation of quantum mechanics because it was invented and promulgated — quite forcefully, at times — by the great Dane, Niels Bohr. It is the most popular of the interpretations among physicists — but not the physicists who think particularly deeply because it is actually bankrupt as an explanation of what happens in the quantum world.

Niels Bohr is widely considered the father of quantum theory. His research centre in Copenhagen, which was sponsored by the Carlsberg brewery for a time, was certainly the hub for the theory’s development. Bohr was well liked by most of his contemporaries. Although he was frustrating to argue with, since he gave no quarter and generally considered himself right about everything, he was far from dull. There were times when he engaged his colleagues in mock gun fights because he had developed a theory — drawn from watching American cowboy movies — that the person who draws second will always win.

For a highly intelligent man, Bohr was astoundingly slow to understand anything going on around him. From movie plots to presentations at physics conferences, he tended to need everything explained to him several times from several different angles. That didn’t prevent him from being a Nobel Prize–winning genius, however.

Here’s how Bohr’s explanation of the quantum world works. Go back to the double slit experiment, where a single photon has two apertures to pass through in order to reach a detector on the other side. Think of the photon as an arrow and the detector as two archery targets placed side by side. If the bullseyes are lined up with the two slits, you’d expect the arrows to hit only the bullseyes. That would be the everyday, ‘classical’ outcome. But after you watch the quantum archer fire one arrow at a time for a few hours, you go and look at the target. You find the arrows are clumped around a few particular points, with no arrows at the points between.

Now let’s change the spectator’s view. Instead of looking at the archer, look at the slits to see which one the arrow goes through. After a few hours, go and look at the targets. You’ll now find that the arrows are only in the bullseyes. The act of watching the arrow pass through the slits has changed the outcome.

Going back to the photon in the double slit experiment, what does this mean? According to Bohr’s Copenhagen interpretation, the photon — faced with two possibilities given by the two slits that it can pass through — exists as a wave. That means it is in a region of space, but not definable at one particular point, much like a wave on the sea. So we can’t say anything about the photon’s specific position. All we can do is talk about its wave function — the mathematical description that Schrödinger gives us. But remember, the wave function’s only purpose is to describe what the outcome of a measurement might be. Its square gives the probabilities of the various outcomes occurring. It says nothing about the photon’s life story, only its final outcome. In fact, Bohr would say there is no life story — there is no photon to talk about, effectively — until that measurement happens.

However … nowhere in the Copenhagen interpretation is the ‘measurement’ defined. Instead, Copenhagenists talk about the ‘collapse’ of the wave function from a wide array — a ‘superposition’ — of many possible states into just one definite state.

So, what is the measurement? How does it cause this ‘collapse’? There have been lots of attempts to find out. One group of researchers based in Vienna are working particularly hard at this and are convinced that it is something to do with information carried by the photon.

Think of the photon as Tartaglia’s father, Micheletto, the postman. His job is to carry letters from one place to another. He doesn’t know what is in the letters, but we do know they contain information. Whoever reads the information is carrying out a measurement. While the letters are sealed, only the sender knows what is in them. To everyone else, all possibilities are open, which is to say that they are in a superposition of all possible pieces of information. Maybe it’s a bill? Maybe it’s a love letter? Maybe it’s an order for unicorn’s horn? Once they are opened and read, however, the information is suddenly defined. That is a measurement.

What the Viennese researchers did was, effectively, to try melting the seal on those letters. At first just a little bit. They heated up the photons, and then they looked at the pattern on the detector. I know I’m conflating letters, photons, and arrows here, but what they saw was that the arrows were less clumped. The pattern was less stark. As they heated the photons more, so the distribution of the arrows became more and more like you’d expect in the everyday world — focussed on the bullseyes, with just a few strays elsewhere.

The act of heating, they suggested, tells us something about measurement. As anything gets hot, it radiates energy. That’s how we began this whole tale, if you remember. And the different wavelengths — the colours of that light energy — can contain different quantities of information. The result of heating was that some of the information about the photon — the contents of the letter — became readable. It’s as if the yielding wax allowed a corner of a page to roll up and be read. Only a few words became visible, but it was enough to allow the reader to see that it was probably a love letter. Perhaps the words ‘your lips’ came into view. Now it was definitely not a bill, nor an order for unicorn horn. It might still have been something other than a love letter. It could have been an instruction to keep silent: a threat, for instance, to a witness of a crime not to let a single word about the incident pass their lips. Whatever the truth, not all possibilities about the nature of that information are open any more. And so the weird quantum pattern is less stark. The Viennese researchers think that the information radiating away from the hotter photons is enough to read their location as they pass through the slits — in other words, that it could betray which slit the photon passed through.

This leaking of information is known as ‘decoherence’ and that’s about as much as we understand about it. There seems to be, according to the Copenhagenists, a threshold beyond which information leakage will cause the wave function’s superposition to ‘collapse’.

Niels Bohr first presented what came to be known as the Copenhagen interpretation of quantum physics in 1927, at a conference in Como, Italy. His presentation came after what was almost a two year silence about quantum theory, during which he had wrestled with the idea that a photon was both a wave and a particle, and — simultaneously — neither. In the end, his view was that we could say nothing about what it actually was. All we could say is what we see. In that way, the observer becomes an integral part of the system.

‘There is no quantum world,’ he once said. ‘There is only an abstract physical description.’ And later, ‘an independent reality in the ordinary physical sense can neither be ascribed to the phenomena nor to the agencies of observation’.

The reception to Bohr’s talk was mixed, with most people rather underwhelmed. One of the physicists in the audience, Eugene Wigner, was entirely unimpressed by Bohr’s Como lecture. It would change no one’s mind about their own take on the meaning of quantum physics, he said. But, in the end, Wigner was wrong. Louis de Broglie, for instance, changed his mind, coming over to Bohr’s point of view. There are many who wish he hadn’t. But to understand why de Broglie came round, we have to pursue Jerome’s story, too.