

I sing the body electric,
The armies of those I love engirth me and I engirth them,
They will not let me off till I go with them, respond to them,
And discorrupt them, and charge them full with the charge of the soul.
Was it doubted that those who corrupt their own bodies conceal themselves?
And if those who defile the living are as bad as they who defile the dead?
And if the body does not do fully as much as the soul?
And if the body were not the soul, what is the soul?
No one had told Alan that Christopher Morcom had contracted bovine tuberculosis from drinking infected cows’ milk as a small boy; it had set up a pattern of internal damage, and his life had been constantly in danger. The Morcom family had gone to Yorkshire in 1927 to observe the total eclipse of the sun on 29 June, and Christopher had been taken terribly ill in the train coming back. He had undergone an operation, and that was why Alan had been struck by his thin features when he returned to school late that autumn.
‘Poor old Turing is nearly knocked out by the shock,’ a friend wrote from Sherborne to Matthew Blamey next day. ‘They must have been awfully good friends.’ It was both less and more than that. On his side, Christopher had at last been becoming friendly, rather than polite. But on Alan’s side – he had surrendered half his mind, only to have it drop into a void. No one at Sherborne could have understood. But on the Thursday that Christopher died, ‘Ben’ Davis, the junior housemaster, did send to Alan a note telling him to prepare for the worst. Alan immediately wrote1 to his mother, asking her to send flowers to the funeral, which was held on the Saturday, at dawn. Mrs Turing wrote back at once and suggested that Alan himself write to Mrs Morcom. This he did on the Saturday.
15/2/30
Dear Mrs Morcom,
I want to say how sorry I am about Chris. During the last year I worked with him continually and I am sure I could not have found anywhere another companion so brilliant and yet so charming and unconceited. I regarded my interest in my work, and in such things as astronomy (to which he introduced me) as something to be shared with him and I think he felt a little the same about me. Although that interest is partly gone, I know I must put as much energy if not as much interest into my work as if he were alive, because that is what he would like me to do. I feel sure that you could not possibly have had a greater loss.
Yours sincerely, Alan Turing
I should be extremely grateful if you could find me sometime a little snapshot of Chris, to remind me of his example and of his efforts to make me careful and neat. I shall miss his face so, and the way he used to smile at me sideways. Fortunately I have kept all his letters.
Alan had awoken at dawn, at the time of the funeral:
I am so glad the stars were shining on Saturday morning, to pay their tribute as it were to Chris. Mr O’Hanlon had told me when it was to take place so that I was able to follow him with my thoughts.
Next day, Sunday, he wrote again, perhaps in more composed form, to his mother:
16/2/30
Dear Mother,
I wrote to Mrs Morcom as you suggested and it has given me a certain relief.…
… I feel sure that I shall meet Morcom again somewhere and that there will be some work for us to do together, and as I believed there was for us to do here. Now that I am left to do it alone I must not let him down but put as much energy into it, if not as much interest, as if he were still here. If I succeed I shall be more fit to enjoy his company than I am now. I remember what G O’H said to me once ‘Be not weary of well doing for in due season ye shall reap if ye faint not’ and Bennett* who is very kind on these occasions ‘Heaviness may endure for a night but joy cometh in the morning’. Rather Plymouth brotherish perhaps. I am sorry he is leaving. It never seems to have occurred to me to try and make any other friends besides Morcom, he made everyone seem so ordinary, so that I am afraid I did not really appreciate our ‘worthy’ Blamey and his efforts with me for instance.…
On receiving Alan’s letter, Mrs Turing wrote to Mrs Morcom:
Feb. 17 30
Dear Mrs Morcom,
Our boys were such great friends that I want to tell you how much I feel for you, as one mother for another. It must be terribly lonely for you, and so hard not to see here the fulfilment, that I am sure there will be, of all the promise of Christopher’s exceptional brains and lovable character. Alan told me one couldn’t help liking Morcom and he was himself so devoted to him that I too shared in his devotion and admiration: during exams he always reported Christopher’s successes. He was feeling very desolate when he wrote asking me to send flowers on his behalf and in case he feels he cannot write to you himself I know he would wish me to send his sympathy with mine.
Yours sincerely, Ethel S. Turing
Mrs Morcom immediately invited Alan to stay at the Clock House in the Easter holiday. Her sister Mollie Swan sent him a photograph of Christopher. Sadly, the Morcoms had very few pictures of him, and this was a poor likeness, taken on an automatic machine with a reversed image. Alan replied:
20/2/30
Dear Mrs Morcom,
Thank you very much for your letter. I should enjoy coming to the Clockhouse immensely. Thank you so much. We actually break up on April 1, but I am going to Cornwall with Mr O’Hanlon my housemaster until the 11th – so that I could come any time that suits you between then and the beginning of May. I have heard so much about the Clockhouse – Rupert, the telescope, the goats, the Lab and everything.
Please thank Miss Swan very much for the photograph. He is on my table now, encouraging me to work hard.
Apart from the photograph, Alan had to keep his emotions to himself. He was allowed no mourning period, but had to go through Corps and Chapel like everyone else. Alan’s devotion to Christopher’s memory had come as a surprise to the Morcoms. Christopher had always been reticent at home about his school friends, and had a way of referring to ‘a person called’ so-and-so as though he had never been mentioned before. ‘A person called Turing’ had featured in a few of his remarks about experiments, but no more than that, and the Morcom parents had only very briefly met Alan in December. They knew him only from his letters. At the beginning of March they changed their plans and decided to take the holiday in Spain which had been planned before Christopher died. So it was testimony to Alan’s letters that on 6 March they invited him to take Christopher’s place on the journey, instead of coming to their home. Alan wrote to his mother the next day:
… I am half sorry it is not to be the Clockhouse as I should like very much to see it and everything that Morcom has told me about there – but I don’t get invited to go to Gibraltar every day of the week.
On 21 March the Morcoms paid their farewell visit to Sherborne and Alan was allowed into Ross’s house to see them in the evening. Term ended a week later and Alan went to Rock, on the north coast of Cornwall, with O’Hanlon, whose private income allowed him to treat groups of boys in this way. The party included the tough Ben Davis and three Westcott House boys, Hogg and Bennett and Carse. Alan wrote later to Blamey that he ‘had a very good time there – plenty to eat and a pint of beer after lots of exercise.’
While he was away, Mrs Turing called on Mrs Morcom in her London flat. Mrs Morcom recorded in her diary (6 April):
Mrs Turing came to see me at flat tonight. Had not met her before. We talked nearly all the time about Chris and she told me how much he had influenced Alan and how Alan thought he was still working with him and helping him. She stayed till nearly 11 and had to get back to Guildford. She had been to Bach Concert at Queens Hall.
After ten days in Cornwall, Alan made a quick stop-over at Guildford, where Mrs Turing hastily tried to put him in order (extracting the usual quota of old handkerchieves from the lining of his overcoat), and on 11 April he arrived at Tilbury, joining the Morcom party on the Kaisar-i-Hind. Besides Colonel and Mrs Morcom, and Rupert, this included a director of Lloyds Bank and a Mr Evan Williams, chairman of Powell Dyffryn, the Welsh mining company. Mrs Morcom wrote in her diary:
… Sailed about noon. Wonderful day with bright sunshine until 3.30 when we began to come into mist and slowed down. Before tea we dropped anchor and remained just outside the mouth of the Thames until midnight. Ships all around us blowing fog-horns and sounding bells.… Rupert and Alan very excited about the fog and it really is rather alarming.
Alan shared a cabin with Rupert, who did his best to draw him out on Jeans and Eddington, but found Alan very shy and hesitant. Each night before going to sleep, Alan spent a long time looking at the photograph. On the first morning of the voyage, Alan began to talk to Mrs Morcom about Christopher, releasing his feelings in speech for the first time. The next day, after deck tennis with Rupert, was spent the same way, telling her how he had felt attracted to Christopher before getting to know him, about his presentiments of catastrophe and the moon setting. (‘It is not difficult to explain these things away – but, I wonder!’) On Monday, as they rounded Cape Vincent, Alan showed her the last letters he had received from Christopher.
They only spent four days on the Peninsula, driving over the hairpin bends to Granada where, it being Holy Week, they saw a religious procession in the starlight. On Good Friday they were back in Gibraltar and embarked on a homebound liner the next day. Alan and Rupert took early Communion on board ship on Easter Sunday.
Rupert was by now impressed with Alan’s originality of thought, but he did not think of Alan as in a different class from the Trinity mathematicians and scientists he had known. Alan’s future seemed unsure. Should he read science or mathematics at Cambridge? Was he sure of a scholarship at all? Somewhat in terms of a last resort, he spoke to Evan Williams about scientific careers in industry. Williams explained the problems of the coal industry, for instance the analysis of coal-dust for toxicity, but Alan was suspicious of this and remarked to Rupert that it might be used to cheat the miners by flourishing a scientific certificate at them.
They had done the trip in style, staying at the best hotels, but what Alan wanted most was to visit the Clock House. Mrs Morcom sensed this and gracefully asked him to ‘help’ her look through Christopher’s papers and sort them. So on the Wednesday, Alan went to her studio in London, and then after a visit to the British Museum joined her on the Bromsgrove train. For two days he saw the laboratory, the uncompleted telescope, the goats (they had replaced the guilty cow) and everything Christopher had told him about. He had to go home on Friday, 25 April, but surprised Mrs Morcom by coming up to London the next day, presenting her with a parcel of Christopher’s letters. On the Monday he wrote:
28/4/30
Dear Mrs Morcom,
I am only just writing to thank you for having me on your trip and to tell you how much I enjoyed it. I really don’t think I have had such a jolly time before, except that wonderful week at Cambridge with Chris. I must thank you too for all the little things belonging to Chris that you have let me have. It means a great deal to me to have them.…
Yours affectionately, Alan
I was so glad you let me come on to the Clockhouse. I was very much impressed with the house and everything connected with it, and was very pleased to be able to help putting Chris’ things in order.
Mrs Turing had also written:
27/4/30
Dear Mrs Morcom,
Alan got home last night looking so well and happy – He loved his time with you but specially precious to him was the visit to the Clockhouse: he went off to Town today to see someone but he said he would tell me of that part another day – and I knew he meant that it was an experience quite apart. We’ve had no real talk yet but I am sure it has helped him to exchange memories with you and he is treasuring with the tenderness of a woman the pencils and the beautiful star map and other souvenirs you gave him.…
I hope you won’t think it an impertinence – but after our talk and your telling me how true to his name Chris was – and I believe is – in helping the weak – I thought how beautiful it would be to have a panel in his memory of S. Christopher in the School Chapel – a panel of your doing, and what an inspiration it would be for the boys who are so reminded that there are the followers of S. Christopher today and that genius and humble service can go hand in hand as in Chris.…
Mrs Morcom had already put into effect a similar idea. She had commissioned a stained-glass window of St Christopher – not however for Sherborne, but for their parish church at Catshill. Nor was it the ‘humble service’ of Mrs Turing that it was to express, but the life that went on. Back at school, Alan wrote to Mrs Morcom:
3/5/30
… I am hoping to do as well as Chris in the Higher Certificate this term. I often think about how like I am to Chris in a few ways through which we became real friends, and wonder if I am left to do something that he has been called away from.
Mrs Morcom had also called upon Alan to help choose books for the school prizes that Christopher was posthumously to receive:
I think Chris would almost certainly have got The Nature of the Physical World (Eddington) and The Universe around us (Jeans) for the Digby prize and possibly one of The Internal Constitution of the Stars (Eddington), Astronomy and Cosmogony (Jeans). I think you would like The Nature of the Physical World.
The Morcom family endowed a new prize at Sherborne, a science prize to be awarded for work which included an element of originality. Alan had plodded on with the iodate experiment, and now he undertook to write it up for the prize. Christopher it was, even from the grave, who induced him to communicate and to compete. He wrote to his mother:
18 May 1930
… I have just written to a Mellor the author of a Chemistry book to see if he can give me a reference about the experiment I was doing in the summer last year. Rupert said he would look it up in Zurich if I could get him a reference. It’s annoying I couldn’t get hold of anything before.
Alan was also interested in perspective drawing:
This week’s efforts in drawing are not on any better paper … I don’t think much really of Miss Gillet’s efforts. I remember she did once or twice say something in a vague sort of way about parallel lines being drawn concurrent, but she usually had the slogan ‘vertical lines remain vertical’ on the tip of her tongue. I wonder how she managed drawing things below her. I have not been doing much by way of drawing bluebells and things like that but mostly perspective.
Mrs Turing wrote to Mrs Morcom:
May 21 1930
… Alan has taken up drawing which I was anxious for him to do long ago: I think this is quite likely an inspiration from you. He is quite devoted to you and I think he was just wishing for an excuse to pay you a call when he went up to Town the day after saying ‘Goodbye’ to you! You were all most awfully good to him, and in many ways opened up a new world to him.… Whenever we were alone he wanted to talk just of Chris and you and Col. Morcom and Rupert.
Alan hoped this summer to gain an improved mark in the Higher Certificate. His name was put down for Pembroke College, Cambridge, which awarded a number of scholarships on Higher Certificate marks alone, although he half-hoped to fail, so that he would have a chance of trying for Trinity. He did fail for he found the mathematics paper much more difficult than in the previous year, and his marks showed no improvement. But Eperson reported:
… I think he has succeeded in improving his style of written work, which is more convincing and less sketchy than last year…
and Gervis:
He is doing much better work than this time last year partly because he knows more but chiefly because he is getting a more mature style.
Andrews was presented with Alan’s submission for the new Morcom science prize, and later said:2
I first realised what an unusual brain Alan had when he presented me with a paper on the reaction between iodic acid and sulphur dioxide. I had used the experiment as a ‘pretty’ demonstration – but he had worked out the mathematics of it in a way that astonished me …
The iodates won him the prize. ‘Mrs Morcom is extraordinarily nice and the whole family is extremely interesting,’ Alan wrote to Blamey, ‘They have founded a prize in Chris’ memory which I very appropriately won this year.’ He also wrote:
I have started learning German. It is possible that I may be made to go to Germany sometime during next year but I don’t much want to. I am afraid I would much rather stay and hibernate in Sherborne. The worst of it is that most of the people left in Group III nauseate me rather. The only respectable person in it since February has been Mermagen and he doesn’t do Physics seriously or Chemistry at all.
The master who taught him German wrote: ‘He does not seem to have any aptitude for languages.’ It was not what he wanted to think about in his hibernation.
One Sunday that summer, the boys of Westcott House arrived back from their afternoon walks to find Alan, who was by now accorded a certain awed respect, engaged upon an experiment. He had set up a long pendulum in the stairwell, and was checking that, as the day went on, the plane of its motion would remain fixed while the Earth rotated beneath it. It was only the elementary Foucault pendulum experiment, such as he might have seen in the Science Museum in London. But it caused great astonishment at Sherborne, and made an impression second only to his arrival by bicycle in 1926. Alan also told Peter Hogg that it had to do with the theory of relativity, which ultimately it did: one problem that concerned Einstein was how the pendulum kept its place fixed relative to the distant stars. How did the pendulum know about the stars? Why should there be an absolute standard of rotation, and why should it agree with the disposition of the heavens?
But if the stars still exerted their attraction, Alan also had to work out his thoughts about Christopher. Mrs Morcom had asked him in April to write his recollections of her son for an anthology. Alan found this task very hard to fulfil:
My impressions of Chris that I have been writing for you seem to have become more a description of our friendship than anything else so I thought I would write it as such for you and write something less to do with me that you could print with the others.
In the end he would make three attempts but every one of them strayed from manly detachment, too honest to disguise his feelings. The first pages were sent off on 18 June, and explained:
My most vivid recollections of Chris are almost entirely of the kind things he said to me sometimes. Of course I simply worshipped the ground he trod on – a thing which I did not make much attempt to disguise, I am sorry to say.
Mrs Morcom asked for more, and Alan promised to try again when he was on holiday:
20/6/30
… I think I know what you mean about those little points of which you want a record. I shall have a lot of quiet time in Ireland to think them out for you. I couldn’t do it before that because there is not much longer this term and camp is not a very suitable atmosphere. A lot of the things I cut out were things which were to me typical of Chris but when I read them through later I realized that to anyone who did not know both Chris and myself a little bit at least, they would not mean much. I tried to get over that just to shew a little bit what Chris was to me. Of course you know.…
The OTC camp, in the first week of the summer holiday, also obstructed the invitation to stay at the Clock House which Mrs Morcom had extended to both Alan and his mother. Fortunately there was an outbreak of infectious illness at Sherborne and camp was cancelled.
Alan arrived at the Clock House on Monday 4 August. Mrs Morcom recorded ‘… Have just been along to tuck him up. He has my room but is sleeping in sleeping pack where Chris slept last autumn…’ Next day Mrs Turing joined them. Colonel Morcom gave Alan permission to work in the laboratory on an experiment that he and Chris together had begun. There was a day out to the county show and a visit to Christopher’s grave. On the Sunday evening, Mrs Morcom wrote:
… I went with Mrs Turing and Alan in Lanchester. They were leaving soon after 7 pm for Ireland. Stayed until 7 talking to them … Alan came in to talk to me this morning and said how he loves being here. He says he feels Chris’ blessing here.
The Turings crossed over to Ireland and holidayed in Donegal. Alan fished with John and his father, climbed the hills with his mother, and kept his thoughts to himself.
At the end of the summer term O’Hanlon had conferred the accolade: ‘A good term. With some obvious minor failings, he has character.’ Alan had become more prepared to go along with the system. It was not that he had ever rebelled, for he had only withdrawn; nor was it now a reconciliation, for he was still withdrawn. But he would take the ‘obvious duties’ as conventions rather than impositions, as long as they interfered with nothing important. In the autumn term of 1930 his contemporary Peter Hogg became head of house and, as the other third year sixth former, Alan was made a prefect. O’Hanlon wrote to Mrs Turing: ‘That he will be loyal I am well assured: and he has brains: also a sense of humour. These should carry him through…’ He did his share of disciplining the younger boys of the house. One new boy was David Harris, brother of the Arthur Harris who had been head of house four years before. As duty prefect, Alan caught him having left his football clothes off the peg for the second time. Alan said, ‘I’m afraid I shall have to beat you,’ and so he did, rendering Harris a hero among his peers for being the first of the new boys thus to suffer. Harris held on to the gas ring and Alan launched the strokes. However, without the right shoes on he slid all over the shiny washroom floor and the strokes landed at random, one on Harris’s spine, one on his leg. It was not the way to win respect. Alan Turing was a kindly but ‘weak’ prefect, one whom the younger boys could chafe, blowing out his candle in the dormitory or putting sodium bicarbonate in his chamberpot. (There were no lavatories attached to the house dormitories.) Old Turog, he was called, after the Turog loaf, and was always good for having his leg pulled. A similar incident, which took place in ‘Hall’ was witnessed3 by Knoop, one of the older boys who saw Alan as ‘brain where I was brawn’:
During this period of 11/2 hours punishment was normally carried out by pupils. Our studies at Westcott House were down a long corridor with studies on either side shared by from 2 to 4 boys. On this particular evening during this silent period, we heard footsteps come up the corridor, a knock on a door, a mumble of voices and then two lots of footsteps come up the corridor to the locker/washroom, then we heard the swish of a cane, a crash of crockery and a loaf as cane connected with bottom, this was stroke one, exactly the same happened on the second stroke, by that time me and my companions were splitting our sides with laughter. What happened was Turing on his back stroke had knocked down some tea making crockery belonging to prefects, he did this on two consecutive strokes and from the noise we could all tell what was going on in the washroom, the third and final stroke did not connect with crockery as by that time it was lying shattered on the floor.
Much more upsetting, his diary,4 which he kept under lock, was taken and damaged by another boy. There was, however, a limit to what Alan would take:5
Turing … was quite a lovable creature but rather sloppy in appearance. He was a year or more older than me, but we were quite good friends.
One day I saw him shaving in the washroom, with his sleeves loose and his general apearance rather execrable. I said, in a friendly way, ‘Turing, you look a disgusting sight.’ He seemed to take it not amiss, but I tactlessly said it a second time. He took offence and told me to stay there and wait for him. I was a bit surprised, but (as the house washroom was the place for beatings) I knew what to expect. He duly re-appeared with a cane, told me to bend over and gave me four. After that he put the cane back and resumed his shaving. Nothing more was said; but I realised that it was my fault and we remained good friends. That subject was never mentioned again.
But apart from the important matters of ‘Discipline, self-control, the sense of duty and responsibility’, there was Cambridge to think about:
2/11/30
Dear Mrs Morcom,
I have been waiting to hear from Pembroke to write to you. I heard indirectly a few days ago that they will not be able to give me a scholarship. I was rather afraid so; my marks were spread too evenly amongst the three subjects.… I am full of hope for the December exam. I like the papers they give us there so much better than the Higher Certificate ones. I don’t seem though to be looking forward to it like I was last year. If only Chris were there and we were to be up there for another week together.
Two of my books for the ‘Christopher Morcom’ prize have come. I had great fun yesterday evening learning some of the string figures out of ‘Mathematical Recreations’ … I have been made a school prefect this term, to my great surprise as I wasn’t even a house-prefect last term. Last term they started having at least two in each house which rather accounts for it.
I have just joined a Society here called the Duffers. We go (if we feel inclined) every other Sunday to the house of some master or other and after tea someone reads a paper he has written on some subject. They are always very interesting. I have agreed to read a paper on ‘Other Worlds’. It is now about half written. It is great fun. I don’t know why Chris never joined.
Mother has been out to Oberammergau. I think she enjoyed it very much but she has not told me much about it yet…
Yours affectionately, A.M. Turing
Alan’s elevation to School Prefect was a great comfort to his mother. But much more significant was a new friendship in his life.
There was a boy three years younger than Alan in the house, Victor Beuttell, who was also one who neither conformed, nor rebelled, but dodged the system. He also, like Alan, was labouring under a grief that no one knew about, for his mother was dying of bovine tuberculosis. Alan saw her when she came to visit Victor, himself in great peril with double pneumonia, and asked what was wrong. It struck a terrible chord. Alan also learnt something else that few knew, which was that Victor had been caned so severely by a prefect in another house that his spine had been damaged. This turned him against the beating system, and he never caned Victor (who was frequently in trouble), but passed him on to another prefect. The link between them was one of compassion, but it developed into friendship. Though at odds with the axioms of the public school, which normally would forbid boys of different ages from spending time together, a special dispensation from O’Hanlon, who kept a card index on the boys’ activities and watched closely over them, allowed it to continue.
They spent a good deal of time playing with codes and ciphers. One source of ideas might have been the Mathematical Recreations and Essays,6 which Alan had chosen as Christopher Morcom Prize, and which indeed had served a generation of school prize-winners since it appeared in 1892. The last chapter dealt with simple forms of cryptography. The scheme that Alan liked was not a very mathematical one. He would punch holes in a strip of paper, and supply Victor with a book. Poor Victor had to plod through the pages until he found one where through the holes in the strip appeared letters that spelt out a message such as HAS ORION GOT A BELT. By this time, Alan had passed on his enthusiasm for astronomy to Victor, and had explained the constellations to him. Alan also showed him a way to construct Magic Squares (also from Mathematical Recreations), and they played a lot of chess.
As it happened, Victor’s family was also linked with the Swan electric light industry, for his father, Alfred Beuttell, had made a small fortune by inventing and patenting the Linolite electric strip reflector lamp in 1901. The lamp was manufactured by Swan and Edison, while Mr Beuttell, who had broken away from his own father’s business in carpet wholesaling, acquired further experience as an electrical engineer. He had also enjoyed a fine life until the First World War, flying, motor racing, sailing, and gambling successfully at Monte Carlo.7
A very tall, patriarchal figure, Alfred Beuttell dominated his two sons, of whom Victor was the elder. In his character Victor took more after his mother, who in 1926 had published a curious pacifist, spiritualist book. He combined her bright-eyed, rather magical charm, with his father’s strong good looks. In the 1920s Alfred Beuttell had gone back into research into lighting, and in 1927 had taken out patents on a new invention, the ‘K-ray Lighting System’. It was designed to allow uniform illumination of pictures or posters. The idea was to frame a poster in a glass box, whose front surface would be curved in such a way that it reflected light from a strip light at the top exactly evenly over the poster. (Without such a reflection, the poster would be much brighter at the top than at the bottom.) The problem was to find the right formula for the curvature of the glass. Alan was introduced to the problem by Victor, and suddenly produced the formula, without being able to explain it, which agreed with Alfred Beuttell’s calculation. But Alan went further, and pointed out the complication which arose through the thickness of the glass, which would cause a second reflection at the front surface. This made necessary a change in the curve of the K-ray System, which was soon put into application for exterior hanging signs, the first contract being with J. Lyons and Co. Ltd., the catering chain.
It was characteristic. As with the iodate and sulphite calculation, it always delighted Alan that a mathematical formula could actually work in the physical world. He had always liked practical demonstrations, even though he was not good at them, and although pushed into the corner as the intellectual ‘maths brain’, did not make the error of considering thought as sullied or lowered by having a concrete manifestation.
There was a parallel development, in that he did not permit the Sherborne ‘games’ religion to instil in him a contempt for the body. He would have liked to have been as successful with corpus as with mens, and found the same difficulties with both: a lack of coordination and ease of expression. But he had discovered by now that he could run rather well. He would come in first place on the house runs, when rainy weather obliged the cancellation of all important Footer. Victor would go out with him for runs, but after two miles or so would say ‘It’s no good, Turing, I shall have to go back’, only to find Alan overtaking him on the return from a much longer course.
Running suited him, for it was a self-sufficient exercise, without equipment or social connotations. It was not that he had sprinting speed, nor indeed much grace, for he was rather flat-footed, but he developed great staying power by forcing himself on. It was not important to Sherborne, where what mattered was that (to Peter Hogg’s surprise) he became a ‘useful forward’ in the house team. But it was noticed with admiration by Knoop, and it was certainly important to Alan himself: He was not the first intellectual to impose this kind of physical training upon himself, and to derive lasting satisfaction from proving his stamina in running, walking, cycling, climbing, and enduring the elements. It was part of his ‘back to nature’ yearnings. But necessarily there were other elements involved; he perceived tiring himself out by running as an alternative to masturbation. It would probably be hard to overestimate the importance to his life of the conflicts surrounding his sexuality from this time onwards – both in controlling the demands of his body, and in a growing consciousness of emotional identity.
In December it was the same arrival at Waterloo, on the way to Cambridge, but no trip to Mrs Morcom’s studio. Instead his mother and John (now an articled clerk in the City) were there to meet him, and Alan said he would go and see Howard Hughes’ aerial film Hell’s Angels. At Cambridge he failed again to win a Trinity scholarship. But his greater confidence was not entirely misplaced, for he was elected to a scholarship at the college of his second choice, King’s. He was placed eighth in order of the Major Scholars, with £80 per annum.*
Everyone congratulated him. But he had set himself to do something, something that Christopher had been ‘called away from’. For a person with a mathematical mind, an ability to deal with very abstract relations and symbols as though with tangible everyday objects, a King’s scholarship was a demonstration like sight-reading a sonata or repairing a car – clever and satisfying, but no more. Many had won better scholarships, and at an earlier age. More to the point than the word ‘brilliant’ which now came to schoolmasters’ lips was the couplet that Peter Hogg sang at the house supper:
Our Mathematician comes next in our lines
With his mind deep in Einstein – and study light fines.
For he had thought deeply about Einstein and had broken the rules to do so.
Alan hibernated for two more terms – it was the usual thing. There was not much in the way of temporary employment in the conditions of 1931. By now he had settled upon mathematics rather than science as his future course at Cambridge. In February 1931 he acquired G.H. Hardy’s Pure Mathematics, the classic work with which university mathematics began. He took the Higher Certificate for a third time, this time with mathematics as major subject, and at last gained a distinction. He also entered again for the Morcom prize and won it. This time it came with a Prize Record Book, which Alan wrote ‘was most fascinatingly done and bears such a spirit of Chris in the clear bright illumination.’ The Morcoms had commissioned it in a contemporary neo-mediaeval style, which stood out sharply from the fusty Sherborne background.
In the Easter holiday, on 25 March, he went on a walking and hitchhiking trip with Peter Hogg (a keen ornithologist) and an older boy, George Maclure. On their way from Guildford to Norfolk they spent one night in a working men’s hostel, which suited Alan, indifferent to anything more fancy (though it shocked his mother). One day, rather typically, he walked on by himself while the other two accepted a lift. He also spent five days on the OTC course at Knightsbridge barracks, qualifying in drill and tactics. This rather amazed John, who detected an unwonted enthusiasm in Alan for dressing up as a soldier. Perhaps he found this rare contact with men from outside the upper-middle-class cocoon to be strangely exciting.
David Harris became his fag, and found him well-meaning but absent-minded as a master. One of Boughey’s revolutionary innovations was that prefects were allowed to have prefects from other houses to tea on Sunday afternoons, and occasionally Harris had to cook baked beans on toast when Alan availed himself of the concession. Alan had reached the summit of privilege. He continued with perspective drawing, stimulated by Victor’s interest and considerable artistic talent. They had many discussions on perspective and geometry. Alan entered a line drawing of the Abbey for a school art competition in July, and gave it to Peter Hogg. (Victor won a prize for his water-colour painting.) And then Valete, A. M. Turing, School Prefect, Sergeant in the OTC, Member of Duffers! Alan collected a number of prizes and a £50 per annum Cambridge subsidy from the Sherborne endowments. He was also awarded a King Edward VI gold medal for mathematics. At the Commemoration, he received the faint praise which was to be his only mention while at school in the Sherborne magazine8, marking out his proper place in the scheme of things. The scholarship winners were:
G.C. Laws, who had been extraordinarily helpful to him (the Headmaster), a real mainstay to the tone of the place and a perpetually genial and cheerful and thoroughly best type of Shirburnian. (Applause.) The other open scholarship, mathematics, was gained by A.M. Turing who, in his sphere, was one of the most distinguished boys they had had recently.
O’Hanlon described this as ‘a very successful close’ to ‘an interesting career, with varied experiences’, expressing gratitude for Alan’s ‘essentially loyal help’.
Mrs Morcom had invited Alan and Mrs Turing to stay again in the summer. A letter from Alan of 14 August, answering some more of Mrs Morcom’s questions, and enclosing all of Christopher’s letters, said that his mother should have written to make the arrangements. But, for some reason, no visit was made. Instead, for the first two weeks of September, Alan went with O’Hanlon to Sark. Peter Hogg, Arthur Harris, and two old friends of O’Hanlon made up the party. They stayed at an eighteenth-century farmhouse, and spent the days on the rocky shores of the island, where Alan bathed naked. Arthur Harris was sketching in water colours, when Alan came up behind him, pointing to a heap of horse manure that lay on the road ahead. ‘I hope you’re going to put that in,’ he said.
Few new students crossed the threshold of King’s College without some trepidation induced by its grandeur. Yet the translation to Cambridge was by no means a plunge into an entirely new environment, for in many ways the university resembled a very large public school – without its violence, but inheriting many of its attitudes. Anyone familiar with the subtle relationship of loyalties to house and school would find nothing perplexing in the system of college and university. The 11 pm curfew, the obligation to wear a gown after sunset, the prohibition on unchaperoned visits by the other sex, were lightly borne by the great majority of those in statu pupillari. They felt newly free, to drink and smoke and spend the day as they chose.
Cambridge was positively feudal in its arrangements. The majority of the undergraduates came from public schools, and the minority who came from a lower-middle-class background, having won scholarships from grammar schools, had to adapt to the peculiar relationship between ‘gentlemen’ and ‘servants’. As for ladies, they were supposed to be content with their two colleges.
As with public schools, there was a great deal about the ancient universities which had less to do with learning than with social status, with courses in geography and estate management for those of a less academic turn of mind. But the jolly raggings, debaggings and destruction of earnest students’ rooms had ended with the Twenties. With the depression, the Thirties had begun, stringent and serious. And nothing could interfere with that precious freedom – a room of one’s own. Cambridge rooms had double doors, and the convention was that the occupant who ‘sported his oak’ by locking the outer door was not at home. At last Alan could work, or think, or just be miserable – for he was far from happy – however and whenever he chose. His room could be as muddled and as untidy as he liked, so long as he made his peace with the college servants. He might be disturbed by Mrs Turing, who would scold him for the dangerous way he cooked breakfast on the gas ring. But these interruptions were very occasional, and after this first year, Alan saw his parents only on fleeting visits to Guildford. He had gained his independence, and was at last left alone.
But there were also the university lectures, which on the whole were of a high standard; the Cambridge tradition was to cover the entire mathematics course with lectures which were in effect definitive textbooks, by lecturers who were themselves world authorities. One of these was G.H. Hardy, the most distinguished British mathematician of his time, who returned in 1931 from Oxford to take up the Sadleirian Chair at Cambridge.
Alan was now at the centre of scientific life, where there were people such as Hardy and Eddington who at school had been only names. Besides himself, there were eighty-five students who thus embarked upon the mathematics degree course, or ‘Tripos’ as Cambridge had it, in 1931. But these fell into two distinct groups: those who would offer Schedule A, and those who would sit for Schedule B as well. The former was the standard honours degree, taken like all Cambridge degrees in two Parts, Part I after one year, and Part II two years later. The Schedule B candidates would do the same, but in the final year they would also offer for examination an additional number – up to five or six – of more advanced courses. It was a cumbersome system, which was changed the following year, the Schedule B becoming ‘Part III’. But for Alan Turing’s year it meant neglecting study for Part I, which was something of a historical relic, hard questions on school mathematics, and instead beginning immediately on the Part II courses, leaving the third year free to study for the advanced Schedule B papers.
The scholars and exhibitioners would be expected to offer Schedule B, and Alan par excellence was among them, one of those who could feel themselves entering another country, in which social rank, money, and politics were insignificant, and in which the greatest figures, Gauss and Newton, had both been born farm boys. David Hilbert, the towering mathematical intellect of the previous thirty years, had put it thus:9 ‘Mathematics knows no races … for mathematics, the whole cultural world is a single country,’ by which he meant no idle platitude, for he spoke as the leader of the German delegation at the 1928 international congress. The Germans had been excluded in 1924 and many refused to attend in 1928.
Alan responded with joy to the absolute quality of mathematics, its apparent independence of human affairs, which G.H. Hardy expressed another way:10
317 is a prime, not because we think so, or because our minds are shaped in one way rather than another, but because it is so, because mathematical reality is built that way.
Hardy was himself a ‘pure’ mathematician, meaning that he worked in those branches of the subject independent not only of human life, but of the physical world itself. The prime numbers, in particular, had this immaterial character. The emphasis of pure mathematics also lay upon absolutely logical deduction.
On the other hand, Cambridge also laid emphasis on what it called ‘applied’ mathematics. This did not mean the application of mathematics to industry, economics, or the useful arts, there being in English universities no tradition of combining high academic status with practical benefits. It referred instead to the interface of mathematics and physics, generally physics of the most fundamental and theoretical kind. Newton had developed the calculus and the theory of gravitation together, and in the 1920s there had been a similar fertile period, when it was discovered that the quantum theory demanded techniques which were miraculously to be found in some of the newer developments of pure mathematics. In this area the work of Eddington, and of others such as P.A.M. Dirac, placed Cambridge second only to Göttingen, where much of the new theory of quantum mechanics had been forged.
Alan was no foreigner to an interest in the physical world. But at this point, what he needed most was a grip on rigour, on intellectual toughness, on something that was absolutely right. While the Cambridge Tripos – half ‘pure’ and half ‘applied’ – kept him in touch with science, it was to pure mathematics that he turned as to a friend, to stand against the disappointments of the world.
Alan did not have many other friends – particularly in this first year, in which he still mentally belonged to Sherborne. The King’s scholars mostly formed a self-consciously élite group, but he was one of the exceptions. He was a shy boy of nineteen, who had had an education more to do with learning silly poems by rote, or writing formal letters, than with ideas or self-expression. His first friend, and link with the others of the group, was David Champernowne, one of the other two mathematical scholars. He came from the mathematical sixth form of Winchester College, where he had been a scholar, and was more confident socially then Alan. But the two shared a similar ‘sense of humour’, being alike unimpressed by institutions or traditions. They also shared a hesitancy in speech, although David Champernowne’s was more slight than Alan’s. It was and remained a rather detached, public school kind of friendship, but important to Alan was that ‘Champ’ was not shocked by unconventionality. Alan told him about Christopher, showing him a diary that he had kept of his feelings since the death.
They would go to college tutorials together. To begin with, it was a case of Alan catching up, for David Champernowne had been much better taught, and Alan’s work was still poorly expressed and muddled. Indeed, his friend ‘Champ’ had the distinction of publishing a paper11 while still an undergraduate, which was more than Alan did. The two supervisors of mathematics at King’s were A.E. Ingham, serious but with a wry humour, the embodiment of mathematical rigour, and Philip Hall, only recently elected a Fellow, under whose shyness lay a particular friendly disposition. Philip Hall liked taking Alan, and found him full of ideas, talking excitedly in his own strange way, in which his voice went up and down in pitch rather than in stress. By January 1932 Alan was able to write in an impressively off-hand way:
I pleased one of my lecturers rather the other day by producing a theorem, which he found had previously only been proved by one Sierpinski, using a rather difficult method. My proof is quite simple so Sierpinski* is scored off.
But it was not all work, because Alan joined the college Boat Club. This was unusual for a scholar, for the university was stuck with the polarising effect of the public schools, and students were supposed to be either ‘athletes’, or ‘aesthetes’. Alan fitted into neither category. There was also the other problem of mental and physical balance, for he fell in love again, this time with Kenneth Harrison, who was another King’s scholar of his year, studying the Natural Sciences Tripos. Alan talked to him a good deal about Christopher, and it became clear that Kenneth, who also had fair hair and blue eyes, and who also was a scientist, had become a sort of reincarnation of his first great flame. One difference, however, was that Alan did speak up for his own feelings, as he would never have dared with Christopher. They did not meet with reciprocation, but Kenneth admired the straightforwardness of his approach, and did not let it stop them from talking about science.
At the end of January 1932, Mrs Morcom sent back to Alan all the letters between him and Christopher which he had surrendered to her in 1931. She had copied them out – quite literally – in facsimile. It was the second anniversary of his death. Mrs Morcom sent a card asking him to dinner on 19 February at Cambridge, and he in turn made the arrangements for her stay. It was not the most convenient weekend, he being engaged with the Lent boat races and obliged to be abstemious at dinner. But Alan found time to show her round: Mrs Morcom noted that his rooms were Very untidy’, and they went on to see where Alan and Christopher had stayed in Trinity for the scholarship examination, and where Mrs Morcom imagined Christopher would have sat in Trinity chapel.
In the first week of April, Alan went to stay at the Clock House again, this time with his father. Alan slept in Christopher’s sleeping bag. They all went together to see the window of St Christopher, now installed in Catshill parish church, and Alan said that he could not have imagined anything more beautiful of its kind. Christopher’s face had been incorporated into the window – not as the sturdy St Christopher fording the stream, but as the secret Christ. On Sunday he went to communion there, and at the house they held an evening gramophone concert. Mr Turing read and played billiards with Colonel Morcom, while Alan played parlour games with Mrs Morcom. Alan went out one day for a long walk with his father, and they had another day at Stratford-upon-Avon. On the last evening, Alan asked Mrs Morcom to come and say goodnight to him, as he lay in Christopher’s place in bed.
The Clock House still held the spirit of Christopher Morcom. But how could this be? Could the atoms of Alan’s brain be excited by a non-material ‘spirit’, like a wireless set resonating to a signal from the unseen world? It was probably on this visit12 that Alan wrote out for Mrs Morcom the following explanation:
It used to be supposed in Science that if everything was known about the Universe at any particular moment then we can predict what it will be through all the future. This idea was really due to the great success of astronomical prediction. More modern science however has come to the conclusion that when we are dealing with atoms and electrons we are quite unable to know the exact state of them; our instruments being made of atoms and electrons themselves. The conception then of being able to know the exact state of the universe then really must break down on the small scale. This means then that the theory which held that as eclipses etc. are predestined so were all our actions breaks down too. We have a will which is able to determine the action of the atoms probably in a small portion of the brain, or possibly all over it. The rest of the body acts so as to amplify this. There is now the question which must be answered as to how the action of the other atoms of the universe are regulated. Probably by the same law and simply by the remote effects of spirit but since they have no amplifying apparatus they seem to be regulated by pure chance. The apparent non-predestination of physics is almost a combination of chances.
As McTaggart shews matter is meaningless in the absence of spirit (throughout I do not mean by matter that which can be a solid a liquid or a gas so much as that which is dealt with by physics e.g. light and gravitation as well, i.e. that which forms the universe). Personally I think that spirit is really eternally connected with matter but certainly not always by the same kind of body. I did believe it possible for a spirit at death to go to a universe entirely separate from our own, but I now consider that matter and spirit are so connected that this would be a contradiction in terms. It is possible however but unlikely that such universes may exist.
Then as regards the actual connection between spirit and body I consider that the body by reason of being a living body can ‘attract’ and hold on to a ‘spirit’, whilst the body is alive and awake the two are firmly connected. When the body is asleep I cannot guess what happens but when the body dies the ‘mechanism’ of the body, holding the spirit is gone and the spirit finds a new body sooner or later perhaps immediately.
As regards the question of why we have bodies at all; why we do not or cannot live free as spirits and communicate as such, we probably could do so but there would be nothing whatever to do. The body provides something for the spirit to look after and use.
Alan could have found many of these ideas in his reading of Eddington while still at school. He had told Mrs Morcom that she would like The Nature of the Physical World, and this would have been because of the olive branch that Eddington held out from the throne of science towards the claims of religion. He had found a resolution of the classical problem of determinism and free will, of mind and matter, in the new quantum mechanics.
The idea that Alan said ‘used to be supposed in Science’ was familiar to anyone who studied applied mathematics. In any school or university problem, there would always be just sufficient information supplied about some physical system to determine its entire future. In practice, predictions could not be performed except in the most simple of cases, but in principle there was no dividing line between these and systems of any complexity. It was also true that some sciences, thermodynamics and chemistry for instance, considered only averaged-out quantities, and in those theories information could appear and disappear. When the sugar has dissolved in the tea, there remains no evidence, on the level of averages, that it was ever in the form of a cube. But in principle, at a sufficiently detailed level of description, the evidence would remain in the motion of the atoms. That was the view as summed up by Laplace13 in 1795:
Given for one instant an intelligence which could comprehend all the forces by which nature is animated and the respective situations of the beings who compose it – an intelligence sufficiently vast to submit these data to analysis – it would embrace in the same formula the movements of the greatest bodies and those of the lightest atom; for it, nothing would be uncertain and the future, as the past, would be present to its eyes.
From this point of view, whatever might be said about the world on other levels of description (whether of chemistry, or biology, or psychology, or anything else), nevertheless, there was one level of description, that of microscopic physical detail, in which every event was completely determined by the past. In the Laplacian view, there was no possibility of any undetermined events. They might appear undetermined, but that would only be because one could not in practice perform the necessary measurements and predictions.
The difficulty was that there was one kind of description of the world to which people were strongly attached, namely that of ordinary language, with deciding and choosing, justice and responsibility. The problem lay in the lack of any connection between the two kinds of description. The physical ‘must’ had no connection with the psychological ‘must’, for no one would feel like a puppet pulled by strings because of physical law. As Eddington declared:
I have an intuition much more immediate than any relating to the objects of the physical world; this tells me that nowhere in the world as yet is there any trace of a deciding factor as to whether I am going to lift my right hand or my left. It depends on the unfettered act of volition not yet made or foreshadowed. My intuition is that the future is able to bring forth deciding factors which are not secretly hidden from the past.
But he was not content to keep ‘science and religion in watertight compartments’, as he put it. For there was no obvious way in which the body was excused obedience to the laws of matter. There had to be some connection between the descriptions – some unity, some integrity of vision. Eddington was not a dogmatic Christian, but a Quaker who wished to preserve some idea of free consciousness, and an ability to perceive a ‘spiritual’ or ‘mystical’ truth directly. He had to reconcile this with the scientific view of physical law. And how, he asked, could ‘this collection of ordinary atoms be a thinking machine?’ Alan’s problem was the same, only with the intensity of youth. For he believed that Christopher was still helping him – perhaps by ‘an intuition much more immediate than any relating to the objects of the physical world.’ But if there was no immaterial mind, independent of the physics of the brain, then there was nothing to survive, nor any way in which a surviving spirit might act upon his brain.
The new quantum physics offered such a reconciliation, because it seemed that certain phenomena were absolutely undetermined. If a beam of electrons were directed at a plate in which there were two holes, then the electrons would divide between the two, but there seemed no way of predicting the path that any particular electron would follow, not even in principle. Einstein, who in 1905 had made a very important contribution to the early quantum theory with a description of the related photo-electric effect, was never convinced that this was really so. But Eddington was more readily persuaded, and was not shy of turning his expressive pen to explain to a general audience that determinism was no more. The Schrödinger theory, with its waves of probability, and the Heisenberg Uncertainty Principle (which, formulated independently, turned out to be equivalent to Schrödinger’s ideas) gave him the idea that mind could act upon matter without in any way breaking physical laws. Perhaps it could select the outcome of otherwise undetermined events.
It was not as simple as that. Having painted the picture of mind controlling the matter of the brain in this way, Eddington admitted that he found it impossible to believe that manipulating the wave-function of just one atom could possibly give rise to a mental act of decision. ‘It seems that we must attribute to the mind power not only to decide the behaviour of atoms individually but to affect systematically large groups – in fact to tamper with the odds on atomic behaviour.’ But there was nothing in quantum mechanics to explain how that was to be done. At this point his argument became suggestive in character, rather than precise – and Eddington did tend to revel in the obscurity of the new theories. As he went on, the concepts of physics became more and more nebulous, until he compared the quantum-mechanical description of the electron with the ‘Jabberwocky’ in Through the Looking Glass:
Something unknown is doing we don’t know what – that is what our theory amounts to. It does not sound a particularly illuminating theory. I have read something like it elsewhere:-
The slithy toves
Did gyre and gimble in the wabe.
Eddington was careful to say that in some sense the theory actually worked, for it produced numbers which agreed with the outcome of experiments. Alan had grasped this point back in 1929: ‘Of course he does not believe that there are really about 1070 dimensions, but that this theory will explain the behaviour of an electron. He thinks of 6 dimensions, or 9, or whatever it may be without forming any mental picture.’ But it seemed no longer possible to ask what waves or particles really were, for their hard nineteenth century billiard-ball concreteness had evaporated. Physics had become a symbolic representation of the world, and nothing more, Eddington argued, edging towards a philosophical idealism (in the technical sense) in which everything was in the mind.
This was the background of Alan’s assertion that ‘We have a will which is able to determine the action of the atoms probably in a small portion of the brain, or possibly all over it.’ Eddington’s ideas had bridged the gap between the ‘mechanism’ of the body, which Alan had learnt from Natural Wonders, and the ‘spirit’ in which he wanted to believe. He had found another source of support in the Idealist philosopher McTaggert, and added ideas about reincarnation. But he had in no way advanced upon or even clarified Eddington’s view, having ignored the difficulties which Eddington had pointed out in discussing the action of the ‘will’. Instead, he had taken a slightly different direction, one fascinated with the idea of the body amplifying the action of the will, and more generally concerned with the nature of the connection between mind and body in life and death.
These ideas did, in fact, show the shape of things to come, though in 1932 there was little outward evidence of future development. In June he had found himself placed in the second class in the Part I of the Tripos. ‘I can hardly look anyone in the face after it. I won’t try to offer an explanation, I shall just have to get a 1st in Mays* to shew I’m not really so bad as that,’ he wrote to Mrs Morcom. But more significant, in reality, was the fact that he had ordered as his last prize from Sherborne a book that promised a serious account of the interpretation of quantum mechanics. It was an ambitious choice of study, a book only published in 1932. It was the Mathematische Grundlagen der Quantenmechanik, the Mathematical Foundations of Quantum Mechanics, by the young Hungarian mathematician John von Neumann.
On 23 June it was his twentieth birthday, and then on 13 July what would have been Christopher’s twenty-first. Mrs Morcom sent Alan a ‘Research’ fountain pen, such as Christopher had shown off, as a present. Alan wrote from Cambridge, where he spent the ‘Long Vacation Term’:
14/7/32
My dear Mrs Morcom,
… I remembered Chris’ birthday and would have written to you but for the fact that I found myself quite unable to express what I wanted to say. Yesterday should I suppose have been one of the happiest days of your life.
How very kind of you it was to think of sending me a ‘Research’ pen. I don’t think anything else (of that kind) could remind me better of Chris; his scientific appreciation and dexterous manipulation of it. I can so well remember him using it.
But if he was twenty, and preparing to confront the work of European mathematicians, he was still a boy away from home, away from Sherborne. The summer holidays were spent much as those of the previous year:
Daddy and I have just been to Germany, for just over a fortnight. We spent most of the time walking in the Schwarzwald, though Daddy of course was not up to much more than 10 miles a day. My knowledge of the language wasn’t altogether of the kind that [was] most wanted. I have learnt nearly all my German by reading half a German mathematical book.† I got home somehow or other…
Yours affectionately, Alan M. Turing
Alan had another holiday camping with John in Ireland, where he amazed his family by turning up at Cork in a pig-boat. Then for the first two weeks of September he joined O’Hanlon for a second and last time on Sark. Alan was ‘a lively companion even to the extent of mixed bathing at midnight,’ wrote14 O’Hanlon, who had struck a modern note by allowing two girls on the party. Alan had taken some fruit-flies with him, as he was studying genetics in a rather haphazard way. Back at Guildford the Drosophilae escaped and infested the Turing home for weeks, not at all to Mrs Turing’s pleasure. O’Hanlon was sufficiently detached from the ‘nation in miniature’ to write15 of Alan as ‘human and lovable’, saying:
† Not the von Neumann book, however, which he only received in October 1932.
I look back on holidays in Cornwall and Sark among the great enjoyments of my life: in all his companionship and whimsical humour, and the diffident shake of the head and rather high pitched voice as he propounded some question or objection or revealed that he had proved Euclid’s postulates or was studying decadent flies – you never knew what was coming.
The all-encompassing system still allowed some moments of freedom. And Sherborne had also left Alan with one friendship that lasted – with Victor. Alan’s younger friend had been obliged to leave school at the same time, his father suffering from financial loss at what was the worst of the Depression. He had failed his School Certificate (telling Alan that it was because of too much time spent on chess and codes) but quickly caught up by passing it at a London crammers, and began what Alan called ‘his grim life as a chartered accountant’. At Christmas 1932 Alan stayed with the Beuttells for two weeks and worked in Alfred Beuttell’s office near Victoria. The visit was overshadowed by the fact that Victor’s mother had died on 5 November. The deep shadow was a link, for both boys were having to deal with the fact of early death. The link was close enough to break Alan’s usual reserve as to his beliefs – just as Mrs Morcom had broken it – and rather grudgingly to discuss his ideas about religion and survival. Victor believed very strongly, not only in the essential Christian ideas, but in extra-sensory perception and in reincarnation. To him, Alan appeared as one who wanted so much to believe, but whose scientific mind made him an unwilling agnostic, and who was under great tension as a result. Victor saw himself as a ‘crusader’, trying to keep Alan on the straight and narrow, and they had fierce arguments, the more so as Alan did not like being challenged by a boy of seventeen. They talked about who had rolled the stone away, and how the five thousand had really been fed. What was myth and what was fact? They argued about the after-life, and the pre-life too. Victor would say to Alan, ‘Look, no one has ever been able to teach you any mathematics – perhaps you have remembered it from a previous life.’ But, as Victor saw it, Alan could not believe in such a thing ‘without a mathematical formula’.
Victor’s father, meanwhile, had thrown himself into research and work to overcome his bereavement. Alan’s work in his office was concerned with calculations required for his commission as lighting consultant to the Freemasons’ new headquarters in Great Queen Street. Alfred Beuttell was a pioneer in the scientific measurement of illumination, and the development of a lighting code16 based on ‘first principles’ as part of the ‘reduction of the physiology of vision to a scientific and mathematical basis’. His work for the Masons involved elaborate calculations to estimate the illumination at the floor level, in terms of the candle power of lights installed and the reflecting properties of the walls. Alan, who was not allowed into the Masonic building, had to work from imagination to check Mr Beuttell’s figures.
Alan became friendly with Mr Beuttell, who told him about his success in Monte Carlo as a young man, when he had managed to live for a month on his winnings. He showed Alan his gambling system, which Alan took back to Cambridge and studied. On 2 February 1933 he wrote back with the result of his analysis, which was that the system yielded an expected gain of exactly zero, and that accordingly Mr Beuttell’s winnings had been entirely due to luck and not to skill. He also sent a formula he had worked out for the illumination of the floor of a hemispheric room lit from its centre – not, admittedly, an immediately useful result, but a very neat one.
Standing up to Mr Beuttell’s ideas about his gambling system took some courage, as he was a forceful man, whose heart of gold was buried deep, with strong opinions on many subjects. An eclectic Christian tending to Theosophy, he was a great believer in the unseen world, and told Alan that his invention of the Linolite electric lamp had been sent to him from beyond. This Alan found too much to swallow. But he also had ideas about the brain, which he had formed since the early 1900s, according to which it worked on electric principles, with differences of potential determining moods. An electric brain! – there lay a more scientific idea. They had long discussions on these lines.
Alan and Victor also went down to Sherborne together for the house supper, and after Christmas Alan wrote to Blamey, saying:
I still haven’t quite decided what I am going to do when I grow up. My ambition is to become a don at King’s. I am afraid it may be more ambition than profession though. I mean it is not very likely I shall ever become one.
Glad you had a good beano for your coming of age. Personally when my time comes I shall retire into a corner of England far from home and sulk. In other words I don’t want to come of age (Happiest days of my life at school etc.)
Sherborne was part of him; and, essentially loyal to his past, he did not make the mistake of trying to cast it out. Although, indeed, the official speeches about training, leadership and the future of the Empire had left him almost untouched, there were aspects of the distinctive English public school culture in which he genuinely shared. Its dowdy, Spartan amateurism, in which possessions and consumption played a small role, were his. So was its combination of conventionality and weird eccentricity; so too, to some degree, was its anti-intellectualism. For Alan Turing did not think of himself as placed in a superior category by virtue of his brains, and only insisted upon playing what happened to be his own special part. And if the public school was founded upon deprivation and suppression, this was of a kind which gave its products the privilege of knowing that their thoughts and actions were considered significant. In setting out to do something in life, Alan exhibited in a pure form the sense of moral mission that headmasterly sermons sought so laboriously to inculcate.
But he could not stay with one foot in the nineteenth century; Cambridge had introduced him to the twentieth. There had been a moment in 1932 when after a college Feast, Alan wandered quite drunk into David Champernowne’s rooms, only to be told to ‘get a grip on himself’. ‘I must get a grip on myself, I must get a grip on myself,’ Alan repeated in a very droll fashion, so that Champ always liked to think that this had marked a turning point. Be this as it may, it was indeed the year 1933 which brought Alan closer to the problems of the modern world, and in which he began to interact with it.
On 12 February 1933, Alan marked the third anniversary of Christopher’s death:
Dear Mrs Morcom,
I expect you will be thinking of Chris when this reaches you. I shall too, and this letter is just to tell you that I shall [be] thinking of Chris and of you tomorrow. I am sure that he is as happy now as he was when he was here.
Your affectionate Alan.
Others were to remember that week for another reason: on 9 February the Oxford Union resolved that under no circumstances would it fight for King and Country. There were parallel sentiments at Cambridge, not necessarily of complete pacifism, but of a kind which rejected any war fought for that slogan. Patriotism was not enough, after the First World War; there might legitimately be a defence of ‘collective security’ but not a ‘national war’. Newspapers and politicians reacted as though the Enlightenment had never happened, but enlightened scepticism was particularly alive at King’s, and Alan began to find that it was more than a rather grand and frightening house in a giant public school.
King’s enjoyed special privileges within the university system, and was distinguished by its opulence, thanks to a fortune amassed by John Maynard Keynes. But it also prized a moral autonomy that had been at its most pure and intense in the early 1900s, as Keynes described:17
… We entirely repudiated a personal liability on us to obey general rules. We claimed the right to judge every individual case on its merits, and the wisdom, experience, and self-control to do so successfully. This was a very important part of our faith, violently and aggressively held, and for the outer world it was our most obvious and dangerous characteristic. We repudiated entirely customary morals, conventional wisdom. We were, that is to say, in the strict sense of the term, immoralists. The consequences of being found out had, of course, to be considered for what they were worth. But we recognised no moral obligation on us, no inner sanction, to conform or to obey.…
E.M. Forster had more gently, but more widely, portrayed an insistence on the priority of individual relationships over every kind of institution. In 1927 Lowes Dickinson, the King s historian and first advocate of a ‘League of Nations’, wrote18 in his autobiography:
I have seen nothing lovelier than Cambridge at this time of year. But Cambridge is a lovely backwater. The main stream is Jix* and Churchill and Communists and Fascists and hideous hot alleys in towns, and politics, and that terrible thing called the ‘Empire’, for which everyone seems to be willing to sacrifice all life, all beauty, all that is worthwhile, and has it any worth at all? It’s a mere power engine.
They spoke of mere power, that was the point. Even Keynes, involved in state affairs and devoted to economics, did so in the belief that with such tawdry problems solved, people could start to think about something important. It was an attitude very different from the cult of duty, which made a virtue out of playing the expected part in the power structure. King’s College was very different from Sherborne School.
It was also part of the King’s attitude to life that it regarded games, parties and gossip to be natural pleasures, and assumed that clever people would still enjoy ordinary things. Although King’s had only gradually moved away from its original role as a sister foundation to Eton, there were among its dons those who made a positive effort to encourage candidates who did not come from public schools and tried to make them feel at home. There was great emphasis on the mixing between dons and undergraduates in what was a small college, with less than sixty students in each year. No other college was like this, and so Alan Turing gradually woke up to the fact that by chance he had arrived in a unique environment, which was as much his element as any institution could be. It corroborated what he always knew, which was that his duty was to think for himself. The match was not perfect, for a number of reasons, but it was still a great stroke of fortune. At Trinity he would have been a lonelier figure; Trinity also inherited the moral autonomy, but without the personal intimacy that King’s encouraged.
The year 1933 only brought to the surface ideas which in King’s had a long history. Alan shared in the climate of dissent:
26/5/33
Dear Mother,
Thank you for socks etc.… Am thinking of going to Russia some time in vac but have not yet quite made up my mind.
I have joined an organisation called the ‘Anti-War Council’. Politically rather communist. Its programme is principally to organize strikes amongst munitions and chemical workers when government intends to go to war. It gets up a guarantee fund to support the workers who strike.
… There has been a very good play on here by Bernard Shaw called ‘Back to Methuselah’.
Yours, Alan
For a short time, Anti-War Councils sprung up across Britain and united pacifists, communists and internationalists against a ‘national’ war. Selective strikes had, in fact, prevented the British government from intervening on the Polish side against the Soviet Union in 1920. But for Alan the real point lay not in political commitments, but in the resolve to question authority. Since 1917 Britain had been deluged by propaganda to the effect that Bolshevik Russia was the kingdom of the devil, but in 1933 anyone could see that something had gone completely wrong with the western trading and business system. With two million people unemployed, there was no precedent for what was above all a baffling situation, in which no one knew what should be done. Soviet Russia, after its second revolution of 1929, offered the solution of state planning and control, and there was great interest among intellectual circles in how it was working. It was the testing-ground of the Modern. Alan probably enjoyed riling his mother with a nonchalant ‘rather communist’: the point lay not in this or that label, but in the fact that his generation were going to think for themselves, take a wider view of the world than their parents had done, and not be frightened by bogey words.
Alan did not in fact go to see Russia for himself. But even if he had, he would have found himself ill-disposed to become an enthusiast for the Soviet system. Nor did he become a ‘political’ person in the Cambridge of the 1930s. He was not sufficiently interested in ‘mere power’. Buried in the Communist Manifesto was the declaration that the ultimate aim was to make society ‘an association, in which the free development of each is the condition for the free development of all.’ But in the 1930s, to be a communist meant identifying with the Soviet regime, which was a very different matter. Those at Cambridge who perceived themselves as members of a responsible British prefect class might well identify with the Russian rulers as with a sort of better British India, collectivising and rationalising the peasants for their own good. For products of the English public school, apt to despise trade, it was but a small step to reject capitalism, and place faith in greater state control. In many ways the Red was a mirror image of the White. Alan Turing, however, was not interested in organising anyone, and did not wish to be organised by anyone else. He had escaped from one totalitarian system, and had no yearning for another.
Marxism claimed to be scientific, and it spoke to the modern need for a rationale of historical change that could be justified by science. As the Red Queen told Alice, ‘You may call it “nonsense” if you like, but I’ve heard nonsense, compared with which that would be as sensible as a dictionary.’ But Alan was not interested in the problems of history, while the marxist attempts to explain the exact sciences in terms of ‘prevailing modes of production’ were very remote from his ideas and experience. The Soviet Union judged relativity and quantum mechanics by political criteria, while the English theorist Lancelot Hogben sustained an economic explanation of the development of mathematics only by restricting attention to its most elementary applications. Beauty and truth, which motivated Alan Turing as they had always inspired mathematicians and scientists, were lacking. The Cambridge communists took upon themselves something of the character of a fundamentalist sect, with the air of being saved, and the element of ‘conversion’ met in Alan Turing the same scepticism as he had already turned upon Christian beliefs. With his fellow sceptic Kenneth Harrison he would mock the communist line.
On economic questions, indeed, Alan came to think highly of Arthur Pigou, the King’s economist who had played a slightly earlier part than Keynes in patching up nineteenth century liberal capitalism. Pigou held that more equal distribution of income was likely to increase economic welfare, and was an early advocate of the welfare state. Broadly similar in their outlook, both Pigou and Keynes were calling for increased state spending during the 1930s. Alan also began to read the New Statesman, and could broadly be identified with the middle-class progressive opinion to which it was addressed, concerned both for individual liberty and for a more rationally organised social system. There was much talk about the benefits of scientific planning (so that Aldous Huxley’s 1932 satire Brave New World could treat it as the intellectuals’ already dated orthodoxy), and Alan went to talks on progressive ventures such as the Leeds Housing Scheme*. But he would not have seen himself as one of the scientific organisers and planners.
In fact his idea of society was that of an aggregate of individuals, much closer to the views of democratic individualism held by J.S. Mill than that of socialists. And to keep his individual self intact, self-contained, self-sufficient, uncontaminated by compromise or hypocrisy,† was his ideal. It was an ideal far more concerned with the moral than with the economic or political; and closer to the traditional values of King’s than to the developing currents of the 1930s.
Like many people (E.M. Forster among them) he found a special pleasure in discovering Samuel Butler’s Erewhon. Here was a Victorian writer who had doubted the moral axioms, playing with them in Looking-Glass fashion by attaching the taboos on sex to the eating of meat, describing Anglican religion in terms of transactions in ornamental money, and exchanging the associations of ‘sin’ with those of ‘sickness’. Alan also much admired Butler’s successor Bernard Shaw, enjoying his light play with serious ideas. For the well-read sophisticate of the 1930s, Butler and Shaw were already out-worn classics, but for one from Sherborne School they still held a liberating magic. Shaw had taken up what Ibsen* called ‘the revolution of the Spirit’, and wanted to show true individuals on the stage, those who lived not by ‘customary morals’ but by inner conviction. But Shaw also asked hard questions about what kind of society could contain such true individuals: questions highly pertinent to a young Alan Turing. Back to Methuselah, which Alan thought ‘a very good play’ in May 1933, was an attempt at what Shaw called ‘politics sub specie aeternitatis’. With its science-fiction view of Fabian ideas, treating with contempt the sordid realities of Asquith and Lloyd George, it suited Alan’s idealist frame of mind.
One subject, however, did not feature in Bernard Shaw’s plays, and only very rarely in the New Statesman.19 In 1933 its drama critic reviewed The Green Bay Tree, which was about ‘a boy … adopted for immoral purposes by a wealthy degenerate,’ and said it was ‘well worth seeing for anyone who finds a pervert a less boring subject for the drama than a man with a diseased liver.’ In this respect, King’s College was unique. Here it was possible to doubt an axiom which Shaw left unquestioned and Butler skated over nervously.
It was only possible because no one breached the line that separated the official from the unofficial worlds. The consequences of being found out were the same in King’s as anywhere else, and the same double life was imposed by the outside world. It was a ghetto of sexual dissent, with the advantages and disadvantages of ghetto life. The internal freedom to express heretical thoughts and feelings was certainly of benefit to Alan. He was, for instance, helped by the fact that Kenneth Harrison derived from his father, himself a graduate of King’s, a liberal understanding of other people’s homosexual feelings. But the world of Keynes and Forster, the parties and comings and goings of Bloomsbury people, lay far above Alan’s head. There was a glossiness about King’s, whose greatest strength lay in the arts, and drama in particular, in which he had no share. He would have been too easily deterred and frightened by the more theatrical elements in expressing his homosexuality. If at Sherborne his sexuality was described in terms of ‘filth’ and ‘scandal’, he now also had to come to terms with that other kind of labelling that the world found so important: that of the pansy, an affront and traitor to masculine supremacy. He did not find a place in this compartment; nor did the King’s aesthete set, flourishing in its protected corner, reach out to a shy mathematician. As in so many ways, Alan was the prisoner of his own self-sufficiency. King’s could only protect him while he worked out the problems for himself.
It was the same with regard to religious belief, for while agnosticism was all but de rigueur in King’s, he was not the person to follow a trend, only to be stimulated and liberated by the freedom to ask hitherto forbidden questions. In developing his intellectual life, he did not form the social connections that a less shy person could have made. Unlike most of his close acquaintances, he was a member neither of the ‘Ten Club’ nor of the Massinger Society – two King’s undergraduate societies of which the first read plays and the other discussed far into the night, over mugs of cocoa, papers on culture and moral philosophy. He was too awkward, even uncouth, to fit into these comfortable gatherings. Nor was he elected to the exclusive university society, the Apostles, which drew much of its membership from King’s and Trinity. In many ways, he was too ordinary for King’s.
In this respect he had something in common with one of his new friends, James Atkins, who was the third mathematical scholar of Alan’s year. James and Alan got on well together, in an amiable manner that lacked any deep conversations about Christopher or science, and it was James whom Alan asked to come with him for a few days walking in the Lake District.
They were away from 21 to 30 June, so that Alan did achieve his objective of being away from home on 23 June, his ‘coming of age’. In fact they were walking that day from the youth hostel at Mardale over High Street to Patterdale. The weather was unusually hot and sunny, leading Alan at one point to sunbathe naked, and perhaps encouraging him in the gentle sexual approach that he made a few days later, as they rested on the hillside. This almost accidental but electric moment was perhaps less important to Alan than to James, who had been particularly repressed at his public school and was catching up years of self-knowledge, mentally and physically. There was no repetition during the holiday, while he thought it over. In the following two weeks, he found himself roused to feelings of affection and desire for Alan, and expected to see him when he returned to Cambridge on 12 July for the long vacation term. This was not so much to study mathematics as to take part in concerts during the International Congress of Musical Research, for James found in music the absoluteness that Alan found in pure mathematics.
James did not know that the same day Alan had gone to the Clock House to remember Christopher. At Easter, he had stayed there again, taken communion at his shrine, and had written:
20/4/33
My dear Mrs Morcom,
I was so pleased to be at the Clockhouse for Easter. I always like to think of it specially in connection with Chris. It reminds us that Chris is in some way alive now. One is perhaps too inclined to think only of him alive at some future time when we shall meet him again; but it is really so much more helpful to think of him as just separated from us for the present.
His July visit coincided with the dedication of the memorial window on 13 July, which would have been Christopher’s twenty-second birthday. The local children had the day off school, and laid flowers beneath the stained-glass window. A family friend preached on ‘Kindness’ in Christopher’s memory. They all sang Christopher’s favourite hymn:
Gracious Spirit, Holy Ghost
Taught by Thee we covet most
Of thy gifts at Pentecost
Holy heavenly Love
In a marquee at the Clock House, a conjuror amused the children over their buns and lemonade; Rupert demonstrated Christopher’s experiment with the iodates and sulphites, and his uncle explained it to them. They blew bubbles and sent up balloons.
Alan returned to Cambridge two or three weeks after this bittersweet ceremony, and so it was not long before James indicated that he would like to continue the sexual contact that Alan had sparked off. But there was always a sense that Alan never again showed the initiative which the summer sun had elicited, and there was a complexity which James could never penetrate. The associations of Christopher, which Alan did not share with James, might have been part of the reason. The visit would have refreshed the memory of pure, intense romantic love, of a kind which did not exist within his relationship with James. Instead, they were satisfied with an easy-going sexual friendship in which there was no pretence of being in love. But at least Alan knew that he was not alone.
Sometimes he seemed ruffled. At the Founder’s Feast in December 1933, there was an incident when an undergraduate from James’s old school said to Alan in an obnoxious manner, ‘Don’t look at me like that, I’m not a homosexual.’ Alan, upset by this attack, said to James, ‘If you want to go to bed, it’ll be one-sided.’ But this was the exceptional moment in a relationship which continued – to a lessening degree – for several years.
No one else knew of this, although in more general terms, as the Feast incident illustrated, Alan was not particularly secretive about his sexuality. There was another undergraduate for whom Alan (as he told James) had longings, and their names were linked by scurrilous clues like ‘See under 2 down’ for a crossword puzzle in an abortive King’s rag magazine. In the autumn of 1933 Alan also made another friend, with whom the main link was discussion of sex. This was Fred Clayton, who was a very different character. While both Alan and James were reserved, but got on with it without making a fuss, with Fred it was the reverse. His father was headmaster of a small village school near Liverpool, and he had not been through the public school training. A rather small, rather young classics scholar, he had been cox of the boat in which Alan rowed, but their acquaintanceship developed as Fred became aware of Alan as someone whose sexuality seemed to be made no secret, either by himself or by others.
Fred was very interested in an exchange of views and emotional experiences, feeling himself very puzzled by sex, and confronted by ex-public schoolboys much more conscious of homosexual attraction. He had taken advantage of the King’s freedom of discussion, and had been told by a Fellow that he ‘seemed a pretty normal bisexual male’. But it was not as simple as that, and nothing was ever simple for Fred Clayton.
Alan told his friend about how much he resented having been circumcised, and also of his earliest memories of playing with the gardener’s boy (presumably at the Wards’ house), which he thought had perhaps decided his sexual pattern. Rightly or wrongly, he gave Fred, and others too, the impression that public schools could be relied upon for sexual experiences – although more important perhaps was that schooldays continued to loom large in his consciousness of sexuality. Fred read Havelock Ellis and Freud, and also made discoveries in the classics which he would convey to his mathematical friend, not noted otherwise for an interest in Latin and Greek.
Puzzlement was an entirely reasonable reaction, in the conditions of 1933, when even in King’s there was so little to go on for those outside the most chromium-plated circles. These conversations were whispers in a crushing, deafening silence. It was not the effect of the law, whose prohibition of all male homosexual activity played but a tiny part in the Britain of the 1930s, in direct terms. It was more as J.S. Mill had written20 of heresy:
… the chief mischief of the legal penalties is that they strengthen the social stigma. It is that stigma which is really effective, and so effective is it, that the profession of opinions which are under the ban of society is much less common in England than is, in many other countries, the avowal of those which incur risk of judicial punishment.
Modern psychology had made a twentieth-century difference; the 1920s had given to the avant-garde the name of Freud to conjure with. But his ideas were used in practice to discuss what had ‘gone wrong’ with homosexual people, and such intellectual openings were outweighed by the continual efforts of the official world to render homosexuality invisible – a process in which the academic world played its part along with prosecutions and censorship. As for respectable middle class opinion, it was represented by the Sunday Express in 1928, greeting The Well of Loneliness with the words, ‘I had rather give a healthy boy or a healthy girl a phial of prussic acid than this novel.’ The general rule remained that of unmentionability above all else, leaving even the well-educated homosexual person with nothing more encouraging than the faint signals from the ancient world, the debris of the Wilde trials, and the rare exceptions to the rules supplied by the writings of Havelock Ellis and Edward Carpenter.
In a peculiar environment such as Cambridge, it might be a positive advantage to enjoy homosexual experience, simply in terms of the opportunity for physical release. The deprivation was not one of laws but of the spirit – a denial of identity. Heterosexual love, desire and marriage were hardly free from problems and anguish, but had all the novels and songs ever written to express them. The homosexual equivalents were relegated – if mentioned at all – to the comic, the criminal, the pathological, or the disgusting. To protect the self from these descriptions was hard enough, when they were embedded in the very words, the only words, that language offered. To keep the self a complete and consistent whole, rather than split into a facade of conformity, and a secret inner truth, was a miracle. To be able to develop the self, to increase its inner connections and to communicate with others – that was next to impossible.
Alan was at the one place that could support that development. Here, after all, was the circle round which Forster passed the manuscript of his novel Maurice which conveyed so much about being ‘an unmentionable of the Oscar Wilde sort’. How to complete the work, that was one problem. It had to have its own integrity of feeling, yet be credible as a story of the real world. There was a fundamental contradiction, which was not resolved by having his hero escape into the ‘greenwood’ of a happy ending.
There was another contradiction, in that this attempt at communication remained secret for fifty years.21 But here at least was the place where these contradictions were understood, and although Alan’s self-contained nature placed him on the edge of King’s society, he was protected from the harshness of the outside world.
If Alan enjoyed Back to Methuselah, it would also have been because Shaw dramatised his theory of the Life Force, which raised the same questions as the ‘spirit’. One of Shaw’s characters said ‘Unless this withered thing religion, and this dry thing science, come alive in our hands, alive and intensely interesting, we may just as well go out and dig the garden until it is time to dig our graves.’ This was Alan’s problem in 1933, although he could not accept Shaw’s easy solution. Bernard Shaw had no compunction about rewriting science if it did not agree with his ideas; determinism had to go, if it conflicted with a Life Force. Shaw fixed on Darwin’s theory of evolution, which he discussed as if it were an account of every kind of change, social and psychological change included, and rejected it as a ‘creed’: he wrote22 that
What damns Darwinian Natural Selection as a creed is that it takes hope out of evolution, and substitutes a paralysing fatalism which is utterly discouraging. As Butler put it, it ‘banishes Mind from the universe.’ The generation that felt nothing but exultant relief when it was delivered from the tyranny of an Almighty Busybody by a soulless Determinism has nearly passed away, leaving a vacuum which Nature abhors.
Science, for Shaw, had to be a Life Force, of which the super-intelligent Oracle of A.D. 3000 could say ‘Our physicists deal with it. Our mathematicians express its measurements in algebraic equations.’
But for Alan, science had to be true, rather than comforting. Nor did that mathematician and physicist John von Neumann have anything to say that lent credence to a Life Force. His Mathematische Grundlagen der Quantenmechanik had arrived in October 1932, but perhaps Alan had put off tackling it until the summer, when he also obtained books on quantum mechanics by Schrödinger and Heisenberg. On 16 October 1933 he wrote:
My prize book from Sherborne is turning out very interesting, and not at all difficult reading, although the applied mathematicians seem to find it rather strong.
Von Neumann’s account was very different from Eddington’s. In his formulation, the state of a physical system evolved perfectly deterministically; it was the observation of it that introduced an element of absolute randomness. But if this process of observation were itself observed from outside, it could be regarded as deterministic. There was no way of saying where the indeterminacy was; it was not localised in any particular place. Von Neumann was able to show that this strange logic of observations — quite unlike anything encountered with everyday objects – was consistent in itself, and agreed with known experiments. It left Alan sceptical about the interpretation of quantum mechanics, but certainly gave no support to the idea of the mind manipulating wave-functions in the brain.
Alan would not only have found von Neumann’s book ‘very interesting’ because it was tackling a subject of such philosophical importance to himself. It would also have been because of the way in which von Neumann approached his scientific subject as much as possible by logical thought. For science, to Alan Turing, was thinking for himself, and seeing for himself, and not a collection of facts. Science was doubting the axioms. He had the pure mathematician’s approach to the subject, allowing a free rein to thought, and seeing afterwards whether or not it had application to the physical world. He would often argue on these lines with Kenneth Harrison, who took the more traditional scientific view of experiments and theories and verification.
The ‘applied mathematicians’ would have found von Neumann’s study of quantum mechanics to be ‘rather strong’ because it required a considerable knowledge of recent pure-mathematical developments. He had taken the apparently different quantum theories of Schrödinger and Heisenberg, and by expressing their essential ideas in a much more abstract mathematical form, shown their equivalence. It was the logical consistency of the theory, not the experimental results, that von Neumann’s work treated. This suited Alan, who sought that kind of toughness, and it made a beautiful example of how the expansion of pure mathematics for its own sake had borne unexpected fruit in physics.
Before the war, Hilbert had developed a certain generalisation of Euclidean geometry, which involved considering a space with infinitely many dimensions. This ‘space’ had nothing to do with physical space. It was more like an imaginary graph on which could be plotted all musical sounds, by thinking of a flute, or violin, or piano tone as made up of so much of the fundamental, so much of the first harmonic, so much of the second harmonic, and so on – each kind of sound requiring (in principle) the specification of infinitely many ingredients.* A ‘point’ in such a ‘space’, a ‘Hilbert space’, would correspond to such a sound; then two points could be added (like adding sounds), and a point could be multiplied by a factor (like amplifying a sound).
Von Neumann had noticed that ‘Hilbert space’ was exactly what was needed to make precise the idea of the ‘state’ of a quantum-mechanical system, such as that of an electron in a hydrogen atom. One characteristic of such ‘states’ was that they could be added like sounds, and another was that there would generally be infinitely many possible states, rather like the infinite series of harmonics above a ground. Hilbert space could be used to define a rigorous theory of quantum mechanics, proceeding logically from clear-cut axioms.
The unforeseen application of ‘Hilbert space’ was just the kind of thing that Alan would produce to support his claim for pure mathematics. He had seen another vindication in 1932, when the positron was discovered. For Dirac had predicted it on the basis of an abstract mathematical theory, which depended upon combining the axioms of quantum mechanics with those of special relativity. But in arguing about the relationship between mathematics and science, Alan Turing found himself tackling a perplexing, subtle, and to him personally important aspect of modern thought.
The distinction between science and mathematics had only been clarified in the late nineteenth century. Until then it might be supposed that mathematics necessarily represented the relations of numbers and quantities appearing in the physical world, although this point of view had really been doomed as soon as such concepts as the ‘negative numbers’ were developed. The nineteenth century, however, had seen developments in many branches of mathematics towards an abstract point of view. Mathematical symbols became less and less obliged to correspond directly with physical entities.
In school algebra – eighteenth century algebra, in effect – letters would be used as symbols for numerical quantities. The rules for adding and multiplying them would follow from the assumption that they were ‘really’ interpreted in terms of numbers, but it would not be necessary nor indeed always appropriate to do so.
The point of such abstraction was that it liberated algebra, and indeed all mathematics, from the traditional sphere of counting and measurement. In modern mathematics, symbols might be used according to any rules whatever, and might be interpreted in ways far more general than in terms of numerical quantities, if indeed they bore any interpretation at all. Quantum mechanics presented a fine example of where the expansion and liberation of mathematics for its own sake had paid off in physics. It had proved necessary to create a theory not of numbers and quantities, but of ‘states’ – and ‘Hilbert space’ offered exactly the right symbolism for these. Another related development in pure mathematics, which quantum physicists was now busy exploiting, was that of the ‘abstract group’. It had come about through mathematicians putting the idea of ‘operation’ into a symbolic form, and treating the result as an abstract exercise.* The effect of abstraction had been to generalise, to unify, and to draw new analogies. It had been a creative and constructive movement, for by changing the rules of these abstract systems, new kinds of algebra with unforeseen applications had been invented.
On the other hand, the movement towards abstraction had created something of a crisis within pure mathematics. If it was to be thought of as a game, following arbitrary rules to govern the play of symbols, what had happened to the sense of absolute truth? In March 1933 Alan acquired Bertrand Russell’s Introduction to Mathematical Philosophy, which addressed itself to this central question.
The crisis23 had first appeared in the study of geometry. In the eighteenth century, it was possible to believe that geometry was a branch of science, being a system of truths about the world, which Euclid’s axioms boiled down into an essential kernel. But the nineteenth century saw the development of geometrical systems different from Euclid’s. It was also doubted whether the real universe was actually Euclidean. In the modern separation of mathematics from science, it became necessary to ask whether Euclidean geometry was, regarded as an abstract exercise, a complete and consistent whole.
It was not clear that Euclid’s axioms really did define a complete theory of geometry. It might be that some extra assumption was being smuggled into proofs, because of intuitive, implicit ideas about points and lines. From the modern point of view it was necessary to abstract the logical relationships of points and lines, to formulate them in terms of purely symbolic rules, to forget about their ‘meaning’ in terms of physical space, and to show that the resulting abstract game made sense in itself. Hilbert, who was always down-to-earth, liked to say: ‘One must always be able to say “tables, chairs, beer-mugs”, instead of “points, lines, planes”.’
In 1899, Hilbert succeeded in finding a system of axioms which he could prove would lead to all the theorems of Euclidean geometry, without any appeal to the nature of the physical world. However, his proof required the assumption that the theory of ‘real numbers’* was satisfactory. ‘Real numbers’ were what to the Greek mathematicians were the measurements of lengths, infinitely subdivisible, and for most purposes it could be assumed that the use of ‘real numbers’ was solidly grounded in the nature of physical space. But from Hilbert’s point of view this was not good enough.
Fortunately it was possible to describe ‘real numbers’ in an essentially different way. By the nineteenth century it was well understood that ‘real numbers’ could be represented as infinite decimals, writing the number π for instance as 3.14159265358979.… A precise meaning had been given to the idea that a ‘real number’ could be represented as accurately as desired by such a decimal – an infinite sequence of integers. But it was only in 1872 that the German mathematician Dedekind had shown exactly how to define ‘real numbers’ in terms of the integers, in such a way that no appeal was made to the concept of measurement. This step both unified the concepts of number and length, and had the effect of pushing Hilbert’s questions about geometry into the domain of the integers, or ‘arithmetic’, in its technical mathematical sense. As Hilbert said, all he had done was ‘to reduce everything to the question of consistency for the arithmetical axioms, which is left unanswered.’
At this point, different mathematicians adopted different attitudes. There was a point of view that it was absurd to speak of the axioms of arithmetic. Nothing could be more primitive than the integers. On the other hand, it could certainly be asked whether there existed a kernel of fundamental properties of the integers, from which all the others could be derived. Dedekind also tackled this question, and showed in 1888 that all arithmetic could be derived from three ideas: that there is a number 1, that every number has a successor, and that a principle of induction allows the formulation of statements about all numbers. These could be written out as abstract axioms in the spirit of the ‘tables, chairs and beer-mugs’ if one so chose, and the whole theory of numbers could be constructed from them without asking what the symbols such as ‘1’ and ‘+’ were supposed to mean. A year later, in 1889, the Italian mathematician G. Peano gave the axioms in what became the standard form.
In 1900 Hilbert greeted the new century by posing seventeen unsolved problems to the mathematical world. Of these, the second was that of proving the consistency of the ‘Peano axioms’ on which, as he had shown, the rigour of mathematics depended. ‘Consistency’ was the crucial word. There were, for instance, theorems in arithmetic which took thousands of steps to prove – such as Gauss’s theorem that every integer could be expressed as the sum of four squares. How could anyone know for sure that there was not some equally long sequence of deductions which led to a contradictory result? What was the basis for credence in such propositions about all numbers, which could never be tested out? What was it about those abstract rules of Peano’s game, which treated ‘+’ and ‘1’ as meaningless symbols, that guaranteed this freedom from contradictions? Einstein doubted the laws of motion. Hilbert doubted even that two and two made four – or at least said that there had to be a reason.
One attack on this question had already been made in the work of G. Frege, starting with his 1884 Grundlage der Arithmetik. This was the logistic view of mathematics, in which arithmetic was derived from the logical relationships of the entities in the world, and its consistency guaranteed by a basis in reality. For Frege, the number ‘1’ clearly meant something, namely the property held in common by ‘one table’, ‘one chair’, ‘one beer-mug’. The statement ‘2 + 2 = 4’ had to correspond to the fact that if any two things were put together with any other two things, there would be four things. Frege’s task was to abstract the ideas of ‘any’, ‘thing’, ‘other’, and so forth, and to construct a theory that would derive arithmetic from the simplest possible ideas about existence.
Frege’s work was, however, overtaken by Bertrand Russell, whose theory was on the same lines. Russell had made Frege’s ideas more concrete by introducing the idea of the ‘set’. His proposal was that a set which contained just one thing could be characterised by the feature that if an object were picked out of that set, it would always be the same object. This idea enabled one-ness to be defined in terms of same-ness, or equality. But then equality could be defined in terms of satisfying the same range of predicates. In this way the concept of number and the axioms of arithmetic could, it appeared, be rigorously derived from the most primitive notions of entities, predicates and propositions.
Unfortunately it was not so simple. Russell wanted to define a set-with-one-element, without appealing to a concept of counting, by the idea of equality. Then he would define the number ‘one’ to be ‘the set of all sets-with-one-element’. But in 1901 Russell noticed that logical contradictions arose as soon as one tried to use ‘sets of all sets’.
The difficulty arose through the possibility of self-referring, self-contradictory assertions, such as ‘this statement is a lie.’ One problem of this kind had emerged in the theory of the infinite developed by the German mathematician G. Cantor. Russell noticed that Cantor’s paradox had an analogy in the theory of sets. He divided the sets into two kinds, those that contained themselves, and those that did not. ‘Normally’, wrote Russell, ‘a class is not a member of itself. Mankind, for example, is not a man.’ But the set of abstract concepts, or the set of all sets, would contain itself. Russell then explained the resulting paradox in this way:
Form now the assemblage of classes which are not members of themselves. This is a class: is it a member of itself or not? If it is, it is one of those classes that are not members of themselves, i.e. it is not a member of itself. If it is not, it is not one of those classes that are not members of themselves, i.e. it is a member of itself. Thus of the two hypotheses – that it is, and that it is not, a member of itself – each implies its contradictory. This is a contradiction.
This paradox could not be resolved by asking what, if anything, it really meant. Philosophers could argue about that as long as they liked, but it was irrelevant to what Frege and Russell were trying to do. The whole point of this theory was to derive arithmetic from the most primitive logical ideas in an automatic, watertight, depersonalised way, without any arguments en route. Regardless of what Russell’s paradox meant, it was a string of symbols which, according to the rules of the game, would lead inexorably to its own contradiction. And that spelt disaster. In any purely logical system there was no room for a single inconsistency. If one could ever arrive at ‘2 + 2 = 5’ then it would follow that ‘4 = 5’, and ‘0 = 1’, so that any number was equal to 0, and so that every proposition whatever was equivalent to ‘0 = 0’ and therefore true. Mathematics, regarded in this game-like way, had to be totally consistent or it was nothing.
For ten years Russell and A.N. Whitehead laboured to remedy the defect. The essential difficulty was that it had proved self-contradictory to assume that any kind of lumping together of objects could be called ‘a set’. Some more refined definition was required. The Russell paradox was by no means the only problem with the theory of sets, but it alone consumed a large part of Principia Mathematical, the weighty volumes which in 1910 set out their derivation of mathematics from primitive logic. The solution that Russell and Whitehead found was to set up a hierarchy of different kinds of sets, called ‘types’. There were to be primitive objects, then sets of objects, then sets of sets, then sets of sets of sets, and so on. By segregating the different ‘types’ of set, it was made impossible for a set to contain itself. But this made the theory very complicated, much more difficult than the number system it was supposed to justify. It was not clear that this was the only possible way in which to think about sets and numbers, and by 1930 various alternative schemes had been developed, one of them by von Neumann.
The innocuous-sounding demand that there should be some demonstration that mathematics formed a complete and consistent whole had opened a Pandora’s box of problems. In one sense, mathematical propositions still seemed as true as anything could possibly be true; in another, they appeared as no more than marks on paper, which led to mind-stretching paradoxes when one tried to elucidate what they meant.
As in the Looking-Glass garden, an approach towards the heart of mathematics was liable to lead away into a forest of tangled technicalities. This lack of any simple connection between mathematical symbols and the world of actual objects fascinated Alan. Russell had ended his book saying, ‘As the above hasty survey must have made evident, there are innumerable unsolved problems in the subject, and much work needs to be done. If any student is led into a serious study of mathematical logic by this little book, it will have served the chief purpose for which it has been written.’ So the Introduction to Mathematical Philosophy did serve its purpose, for Alan thought seriously about the problem of ‘types’ – and more generally, faced Pilate’s question: What is truth?
Kenneth Harrison was also acquainted with some of Russell’s ideas, and he and Alan would spend hours discussing them. Rather to Alan’s annoyance, however, he would ask ‘but what use is it?’ Alan would say quite happily that of course it was completely useless. But he must also have talked to more enthusiastic listeners, for in the autumn of 1933 he was invited to read a paper to the Moral Science Club. This was a rare honour for any undergraduate, especially one from outside the faculty of Moral Sciences, as philosophy and its allied disciplines were called at Cambridge. It would have been a quite unnerving experience, speaking in front of professional philosophers, but he wrote with customary sangfroid to his mother:
26/11/33
… I am reading a paper to the Moral Science Club on Friday. Something by way of being Mathematical Philosophy. I hope they don’t know it all allready.
The minutes24 of the Moral Science Club recorded that on Friday 1 December 1933:
The sixth meeting of the Michaelmas term was held in Mr Turing’s rooms in King’s College. A.M. Turing read a paper on ‘Mathematics and logic’. He suggested that a purely logistic view of mathematics was inadequate; and that mathematical propositions possessed a variety of interpretations, of which the logistic was merely one. A discussion followed.
R.B. Braithwaite (signed).
Richard Braithwaite, the philosopher of science, was a young Fellow of King’s; and it might well have been through him that the invitation was made. Certainly, by the end of 1933, Alan Turing had his teeth into two parallel problems of great depth. Both in quantum physics and in pure mathematics, the task was to relate the abstract and the physical, the symbolic and the real.
German mathematicians had been at the centre of this enquiry, as in all mathematics and science. But as 1933 closed, that centre was a gaping, jagged hole, with Hilbert’s Göttingen ruined. John von Neumann had left for America, never to return, and others had arrived in Cambridge. ‘There are several distinguished German Jews coming to Cambridge this year,’ wrote Alan on 16 October. ‘Two at least to the mathematical faculty, viz. Born and Courant.’ He might well have attended the lectures on quantum mechanics that Born gave that term, or those of Courant* on differential equations the next term. Born went on to Edinburgh, and Schrödinger to Oxford, but most exiled scientists found America more accommodating than Britain. The Institute for Advanced Study, at Princeton University, grew particularly quickly. When Einstein took up residence there in 1933, the physicist Langevin commented, ‘It is as important an event as would be the transfer of the Vatican from Rome to the New World. The Pope of physics has moved and the United States will become the centre of the natural sciences.’
It was not Jewish ancestry alone that attracted the interference of Nazi officialdom, but scientific ideas themselves, even in the philosophy of mathematics:25
A number of mathematicians met recently at Berlin University to consider the place of their science in the Third Reich. It was stated that German mathematics would remain those of the ‘Faustian man’, that logic alone was no sufficient basis for them, and that the Germanic intuition which had produced the concepts of infinity was superior to the logical equipment which the French and Italians had brought to bear on the subject. Mathematics was a heroic science which reduced chaos to order. National Socialism had the same task and demanded the same qualities. So the ‘spiritual connexion’ between them and the New Order was established – by a mixture of logic and intuition
To English minds, the wonder was that any state or party could interest itself in abstract ideas.
Meanwhile to the New Statesman, Hitler’s rancour at the Treaty of Versailles only vindicated what Keynes and Lowes Dickinson had always said. The difficulty was that being fair to Germany now meant making concessions to a barbarous regime. Conservative opinion, however, perceived the new Germany in terms of a balance of nation states, in which it was a renewed potential threat to Britain, but also a strong ‘bulwark’ against the Soviet Union. It was in this context that the Cambridge Anti-War movement revived in November 1933. Alan wrote:
12/11/33
There has been a lot happening this week. The Tivoli Cinema had arranged to shew a film called ‘Our Fighting Navy’ which was blatant militarist propaganda. The Anti-War movement organized a protest. The organization wasn’t very good and we only got 400 signatures of wh[ich] 60 or more were from King’s. The film was eventually withdrawn, but this was on account of the shindy that the militarists made outside the cinema when they had heard of our protest and had got it into their heads that we were going to break up the Cinema.-
A further comment, that ‘There was a very successful A[nti]-W[ar] demonstration yesterday’, referred to the Armistice Day wreath-laying ceremony, which this year had more the flavour of a political statement. This was not wholly pacifist in spirit. Alan’s friend James Atkins had decided that he was a pacifist, and Alan himself that he was not. But very influential was the suggestion that the First World War had been whipped up by the self-interest of the armament manufacturers. There was great feeling, in which probably Alan shared, that glorification of weapons should not be allowed to make a second great war more likely.
It was Eddington, who as a Quaker was a pacifist and internationalist, who stimulated the next outward and visible step in Alan’s career. This time it was not in connection with the ‘Jabberwocky’ of quantum mechanics, but through his course of lectures on the methodology of science26 which Alan attended in the autumn of 1933. Eddington touched upon the tendency of scientific measurements to be distributed, when plotted on a graph, on what was technically called a ‘normal’ curve. Whether it was the wingspans of Drosophilae, or Alfred Beuttell’s winnings at Monte Carlo, the readings would tend to bunch around a central value, and die away on either side, in a specific way. To explain why this should be so was a problem of fundamental importance in the theory of probability and statistics. Eddington offered an outline of why it was to be expected, but this did not satisfy Alan who, sceptical as ever, wanted to prove an exact result by rigorous pure-mathematical standards.
By the end of February 1934 he had succeeded. It did not require a conceptual advance, but still this was the first substantial result of his own. Typically, for him, it was one that connected pure mathematics with the physical world. But when he showed his work to someone else, he was told that the Central Limit Theorem, as the result was called, had already been proved in 1922 by a certain Lindeberg.27 Working in his self-contained way, he had not thought to find out first whether his objective had already been attained. But he was also advised that provided due explanation was given, it might still be acceptable as original work for a King’s fellowship dissertation.
From 16 March to 3 April 1934, Alan joined a Cambridge party to go skiing in the Austrian Alps. It had a vaguely Quaker, internationalist link with Frankfurt University, whose ski-hut near Lech on the Austro-German border they used. The flavour of cooperation was soured by the fact that the German ski coach was an ardent Nazi. On his return, Alan wrote:
29/4/34
… We had a very amusing letter from Micha, the German leader of the skiing party … He said ‘… but in thoughts I am in your middle’…
I am sending some research I did last year to Czüber* in Vienna, not having found anyone in Cambridge who is interested in it. I am afraid however that he may be dead, as he was writing books in 1891.
But first the final Tripos examination had to be got out of the way; Part II from 28 to 30 May and then the Schedule B papers28 from 4 to 6 June. In between the examinations he had to rush down to Guildford to see his father. Mr Turing, who was now sixty, underwent a prostate operation after which he was never again in the good health he had so far enjoyed.
He passed with distinction, making him what was called a ‘B-star Wrangler’ along with eight others. It was only an examination, and Alan deprecated the fuss that his mother made over sending telegrams, and tried to persuade her not to come to the Degree Day formalities on 19 June. But it did mean the award by King’s of a research studentship at £200 per annum, and this enabled him to stay on to try for a fellowship – a serious ambition of which he could now feel more confident than he had in 1932. Several others of his year stayed, including Fred Clayton and Kenneth Harrison. David Champernowne had switched to economics and had not yet taken his degree. James had found himself disoriented by the abstract nature of Part II, and gained a Second. He was not sure how to begin his career, and for the next few months, during which he came to visit Alan several times, did some private tuition work.
By the end of Alan’s undergraduate period, his depression was lifting and new industry was arising, just as in the world outside. He had begun to put down firm Cambridge roots, and to cut a figure as one less subdued and more ready with wit and good humour. It was still true that he belonged neither to an ‘aesthete’ nor to an ‘athlete’ compartment. He had continued to row in the boat club, and got on amiably with the other members, once downing a pint of beer in one go. He played bridge with others of his year, though with the usual defect of serious mathematicians he could not be trusted to add up the scores. The visitor to his room would find a disarray of books and notes and unanswered letters about socks and underpants from Mrs Turing. Round the walls were stuck various mementoes – Christopher’s picture, for one – but also, for those with eyes to see, magazine pictures with male sex-appeal. He also liked to root around in sales and street markets, and picked up a violin in London, on Farringdon Road, for which he took some lessons. This did not produce very aesthetic results, but there was a little of the ‘aesthete’ side in him, inasmuch as it debunked the pompous and stiff-upper-lip models of behaviour. It was all somewhat mystifying to Mrs Turing, when at Christmas 1934 Alan asked for a teddy-bear, saying he had never had one as a little boy. The Turings usually dutifully exchanged more useful and improving presents. But he had his way, and Porgy the bear was installed.
Graduation meant little change in his general way of life, except that he gave up rowing and resumed running. After the degree day he took a cycling trip to Germany, asking an acquaintance, Denis Williams, to come with him. A first-year student of the Moral Sciences Tripos, Denis knew Alan from the Moral Science Club, the King’s boat club and the skiing trip. They took their bicycles on the train as far as Cologne, and then did thirty miles or so a day. One purpose of the trip was to visit Göttingen, where Alan consulted some authority, presumably in connection with the Central Limit Theorem.
A peculiar gangster regime there might be in Berlin, but Germany was still best for student travel, with cheap fares and youth hostels. They could hardly avoid seeing the swastika flags draped everywhere, but to English eyes they seemed less sinister than ridiculous. Once they stopped in a mining village, where they heard the miners singing on their way to work – a welcome contrast to the contrived Nazi displays. In the youth hostel Denis chatted with a German traveller, bidding goodbye amiably with a ‘Heil Hitler’, as foreign students generally did simply as a matter of polite conformity to local custom. (There had also been cases of them being assaulted when they failed to do so.) Alan came in and happened to see this. He said to Denis, ‘You shouldn’t have said that, he was a Socialist.’ He must have spoken with the German earlier, and Denis was struck by the fact that someone had identified himself to Alan as an opponent of the regime. But it was not that Alan reacted as a signed-up anti-fascist, it was that he could not go through with a ritual with which he did not agree. To Denis it was more like another incident on their trip, when two working-class boys from England happened to catch up with them and Denis said that it would be polite to invite them over to have a drink. ‘Noblesse oblige’, said Alan, which made Denis feel very small and insincere.
They happened to be in Hanover a day or two after 30 June 1934, when the SA was overthrown. Alan’s knowledge of German, although it was culled from mathematical textbooks, was better than Denis’s, and he translated from the newspaper an account of how Roehm first had been given the chance to commit suicide and had then been shot. They were rather surprised by the attention given to his demise by the English press. But then, this was a symbolic event with resonances going beyond the plain fact that Hitler thereby gained supreme power. It removed a major contradiction within the Nazi party, trumpeting its intention to turn Germany into a giant stud farm. To grateful conservatives it was the end of ‘decadent’ Germany. Later, when Hitler was thoroughly unpopular, the opposite connection could be drawn, and Nazidom painted as itself ‘decadent’ and ‘perverse’. Behind it lay the powerful leitmotiv that Hitler so skilfully orchestrated: that of the homosexual traitor.
For some Cambridge students a sight of the new Germany, and a brush with its crudities, might engender a powerful anti-fascist commitment. That step was not for Alan Turing. He was always friendly to the anti-fascist cause, but nothing would make him a ‘political’ person. His was the other road to freedom, that of dedication to his craft. Let others do what they could; he would achieve something right, something true. He would continue the civilisation that the anti-fascists defended.
In the summer and autumn of 1934, he continued to work on his dissertation.29 The deadline for its submission was 6 December, but Alan handed it in a month early, and was ready for a next step. Eddington, who had played so important a part in his early development, had suggested his dissertation problem to him. The next suggestion came from Hilbert, although not so directly. In the spring of 1935, while his dissertation went the rounds of the King’s Fellows, Alan went to a Part III course on Foundations of Mathematics. It was given by M.H.A. Newman.
Newman, then nearly forty, was with J.H.C. Whitehead the foremost British exponent of topology. This branch of mathematics could be described as the result of abstracting from geometry such concepts as ‘connected’, ‘edge’ and ‘neighbouring’ which did not depend upon measurement.* In the 1930s it was unifying and generalising much of pure mathematics. Newman was a progressive figure in a Cambridge where classical geometry was more strongly represented.
The basis of topology was the theory of sets, and so Newman had been drawn into the foundations of set theory. He had also attended the 1928 international congress at which Hilbert represented the Germany excluded in 1924. Hilbert had revived his call for an investigation into the foundations of mathematics. And it was in Hilbert’s spirit, rather than as a continuation of Russell’s ‘logistic’ programme, that Newman lectured. Indeed, the Russell tradition had petered out, for Russell himself had left Cambridge in 1916 when first convicted and deprived of his Trinity College lectureship; and of his contemporaries, Wittgenstein had turned in a different direction, Harry Norton had gone mad, and Frank Ramsey had died in 1930. This left Newman as the only person in Cambridge with a deep knowledge of modern mathematical logic, although there were others, Braithwaite and Hardy amongst them, who were interested in the various approaches and programmes.
The Hilbert programme was essentially an extension of the work on which he had started in the 1890s. It did not attempt to answer the question which Frege and Russell had tackled, that of what mathematics really was. In that respect it was less philosophical, less ambitious. On the other hand, it was more far-reaching in that it asked profound and difficult questions about the systems such as Russell produced. In fact Hilbert posed the question as to what were, in principle, the limitations of a scheme such as that of Principia Mathematica. Was there a way of finding out what could, and what could not, be proved within such a theory? Hilbert’s approach was called the formalist approach, because it treated mathematics as if a game, a matter of form. The allowable steps of proof were to be considered like the allowable moves in a game of chess, with the axioms as the starting position of the game. In this analogy, ‘playing chess’ corresponded to ‘doing mathematics’, but statements about chess (such as ‘two knights cannot force checkmate’) would correspond to statements about the scope of mathematics. And it was with such statements that the Hilbert programme was concerned.
At that 1928 congress, Hilbert made his questions quite precise. First, was mathematics complete, in the technical sense that every statement (such as ‘every integer is the sum of four squares’) could either be proved, or disproved. Second, was mathematics consistent, in the sense that the statement ‘2 + 2 = 5’ could never be arrived at by a sequence of valid steps of proof. And thirdly, was mathematics decidable? By this he meant, did there exist a definite method which could, in principle, be applied to any assertion, and which was guaranteed to produce a correct decision as to whether that assertion was true.
In 1928, none of these questions was answered. But it was Hilbert’s opinion that the answer would be ‘yes’ in each case. In 1900 Hilbert had declared ‘that every definite mathematical problem must necessarily be susceptible of an exact settlement … in mathematics there is no ignorabimus’; and when he retired in 1930 he went further:30
In an effort to give an example of an unsolvable problem, the philosopher Comte once said that science would never succeed in ascertaining the secret of the chemical composition of the bodies of the universe. A few years later this problem was solved.… The true reason, according to my thinking, why Comte could not find an unsolvable problem lies in the fact that there is no such thing as an unsolvable problem.
It was a view more positive than the Positivists. But at the very same meeting, a young Czech mathematician, Kurt Gödel, announced results which dealt it a serious blow.
Gödel was able to show31 that arithmetic must be incomplete: that there existed assertions which could neither be proved nor disproved. He started with Peano’s axioms for the integers, but enlarged through a simple theory of types, so that the system was able to represent sets of integers, sets of sets of integers, and so on. However, his argument would apply to any formal mathematical system rich enough to include the theory of numbers, and the details of the axioms were not crucial.
He then showed that all the operations of ‘proof’, these ‘chess-like’ rules of logical deduction, were themselves arithmetical in nature. That is, they would only employ such operations as counting and comparing, in order to test whether one expression had been correctly substituted for another – just as to see whether a chess move was legal or not would only be a matter of counting and comparing. In fact, Gödel showed that the formulae of his system could be encoded as integers, so that he had integers representing statements about integers. This was the key idea.
Gödel continued to show how to encode proofs as integers, so that he had a whole theory of arithmetic, encoded within arithmetic. It was an exploitation of the fact that if mathematics were regarded purely as a game with symbols, then it might as well employ numerical symbols as any other. He was able to show that the property of ‘being a proof or of ‘being provable’ was no more and no less arithmetical than the property of ‘being square’ or ‘being prime’.
The effect of this encoding process was that it became possible to write down arithmetical statements which referred to themselves, like the person saying ‘I am lying.’ Indeed Gödel constructed one particular assertion which had just such a property, for in effect it said ‘This statement is unprovable.’ It followed that this assertion could not be proved true, for that would lead to a contradiction. Nor could it be proved false, for the same reason. It was an assertion which could not be proved or disproved by logical deduction from the axioms, and so Gödel had proved that arithmetic was incomplete, in Hilbert’s technical sense.
There was more to it than this, for one remarkable thing about Gödel’s special assertion was that since it was not provable, it was, in a sense, true. But to say it was ‘true’ required an observer who could, as it were, look at the system from outside. It could not be shown by working within the axiomatic system.
Another point was that the argument assumed that arithmetic was consistent. If, in fact, arithmetic were inconsistent, then every assertion would be provable. So more precisely, Gödel had shown that formalised arithmetic must either be inconsistent, or incomplete. He was also able to show that arithmetic could not be proved consistent within its own axiomatic system. To do so, all that would be required would be a proof that there was a single proposition (say, 2 + 2 = 5) which could not be proved true. But Gödel was able to show that such a statement of existence had the same character as the sentence that asserted its own unprovability. And in this way, he had polished off the first two of Hilbert’s questions. Arithmetic could not be proved consistent, and it was certainly not consistent and complete. This was an amazing new turn in the enquiry, for Hilbert had thought of his programme as one of tidying up loose ends. It was upsetting for those who wanted to find in mathematics something that was absolutely perfect and unassailable; and it meant that new questions came into view.
Newman’s lectures finished with the proof of Gödel’s theorem, and thus brought Alan up to the frontiers of knowledge. The third of Hilbert’s questions still remained open, although it now had to be posed in terms of ‘provability’ rather than ‘truth’. Gödel’s results did not rule out the possibility that there was some way of distinguishing the provable from the non-provable statements. Perhaps the rather peculiar Gödelian assertions could somehow be separated off. Was there a definite method, or as Newman put it, a mechanical process which could be applied to a mathematical statement, and which would come up with the answer as to whether it was provable?
From one point of view this was a very tall order, going to the heart of everything known about creative mathematics. Hardy, for instance, had said32 rather indignantly in 1928 that
There is of course no such theorem, and this is very fortunate, since if there were we should have a mechanical set of rules for the solution of all mathematical problems, and our activities as mathematicians would come to an end.
There were plenty of statements about numbers which the efforts of centuries had failed either to prove or disprove. There was Fermat’s so-called Last Theorem, which conjectured that there was no cube which could be expressed as the sum of two cubes, no fourth power as sum of two fourth powers, and so on. Another was Goldbach’s conjecture, that every even number was the sum of two primes. It was hard to believe that assertions which had resisted attack so long could in fact be decided automatically by some set of rules. Furthermore, the difficult problems which had been solved, such as Gauss’s Four Square Theorem, had rarely been proved by anything like a ‘mechanical set of rules’, but by the exercise of creative imagination, constructing new abstract algebraic concepts. As Hardy said, ‘It is only the very unsophisticated outsider who imagines that mathematicians make discoveries by turning the handle of some miraculous machine.’
On the other hand, the progress of mathematics had certainly brought more and more problems within the range of a ‘mechanical’ approach. Hardy might say that ‘of course’ this advance could never encompass the whole of mathematics, but after Gödel’s theorem, nothing was ‘of course’ any more. The question deserved a more penetrating analysis.
Newman’s pregnant phrase ‘by a mechanical process’ revolved in Alan’s mind. Meanwhile, the spring of 1935 saw two other steps forward. The fellowship election was held on 16 March. Philip Hall had just become an elector, and argued for Alan, saying that his full strength had not been shown in his rediscovery of the Central Limit Theorem. But his advocacy was not needed. Keynes, Pigou and the Provost, John Sheppard, all had an assessment of him for themselves. He was elected, the first of his year, as one of the forty-six Fellows. The boys of Sherborne School enjoyed a half-holiday, and there was a clerihew that circulated:
Turing
Must have been alluring
To get made a don
so early on.
He was still only twenty-two. The fellowship carried with it £300 a year for three years, which would normally be extended to six, and no explicit duties. He was entitled to room and board when he chose to reside at Cambridge, and to dine at High Table. On his first evening in the senior common room, he played Rummy and won a few shillings from the Provost. But he tended to prefer the company at dinner of his friends David Champernowne, Fred Clayton and Kenneth Harrison. It did not change his style of life, but did make him free for three years to pursue thought in any way he chose – as free as anyone could be without a private income. He supplemented his fellowship by supervising undergraduates in next-door Trinity Hall. If they came to his rooms hoping for a glimpse of King’s eccentricity, they were sometimes rewarded, as when Alan sat Porgy the teddy bear by the fire, in front of a book supported by a ruler, and greeted them with ‘Porgy is very studious this morning.’
The election coincided with what Alan called a ‘small-scale discovery’ which consituted a first publishable paper. It was a neat result in group theory, which he announced to Philip Hall (whose own research lay in that field) on 4 April, saying he was ‘thinking of doing this sort of thing seriously.’ It was submitted and published33 by the London Mathematical Society later in the month.
The result was a small improvement to a paper by von Neumann,34 which developed the theory of ‘almost periodic functions’* by defining them with reference to ‘groups’. As it happened, von Neumann arrived at Cambridge later that month. He was spending a summer away from Princeton, and gave a lecture course at Cambridge on the subject of ‘almost periodic functions’. Alan certainly met him this term, and most likely through attending this course.
They were very different men. When Alan Turing was born, von Neumann Janos was the eight-year-old son of a rich Hungarian banker.35 There was for him no public school training, and by 1922, before Alan was floating his paper boats at Hazelhurst, the eighteen-year-old von Neumann had published his first paper. Budapest Janos became Göttingen Johann, one of Hilbert’s disciples, and then in 1933 became Princeton Johnny, adopting English as his fourth language. The paper on ‘almost periodic functions’ was his fifty-second, part of an immense output which had moved from the axioms of set theory and quantum mechanics, to the topological groups which were the pure-mathematical underpinning of quantum theory, but taking in numerous other topics on the side.
John von Neumann was one of the most important figures in twentieth-century mathematics, but he was a man who added worldly to intellectual success. He enjoyed a commanding manner, a sophisticated, racy humour, a training in engineering, a wide knowledge of history – and a salary of $10,000 over and above his substantial private income. He cut a figure very different from that of the twenty-two-year old in the shabby sports jacket, sharp but shy with a hesitant voice that had trouble with one language, let alone four. But mathematics did not see these things, and it might well have been the result of a meeting of minds when on 24 May Alan wrote home: ‘… I have applied for a visiting Fellowship at Princeton for next year.’†
An additional reason would be, however, that Alan’s friend Maurice Pryce, whom he had met at the scholarship examinations in 1929, and with whom he had kept in touch, was ready to go to Princeton in September, having secured a fellowship there. In any case, it was becoming more and more clear that Princeton was the new Göttingen; there was a flow of first-rate mathematicians and physicists to and fro across the Atlantic. It was an aspect of the continuing transfer of power from Europe, and from Germany in particular, to America. No one who wanted to do something, as Alan did, could any longer ignore the United States.
Alan continued work in group theory during 1935.36 He also thought of working in quantum mechanics, and approached R.H. Fowler, Professor of Mathematical Physics, for a suitable problem to work on. Fowler suggested trying to explain the dielectric constant of water, one of his favourite research topics. But Alan made no progress. And this problem, as indeed the whole field of mathematical physics, which offered so much to attract the ambitious young mathematicians of the 1930s, was put aside. For he had seen something new, something at the centre of mathematics, something at his centre. It owed almost nothing to the Tripos; it used only the commonest in Nature. It was profoundly ordinary, and yet led to a spectacular idea.
† It is not clear from the context whether ‘next year’ means 1935-6, or 1936-7.
It had become his habit to run long distances in the afternoons, along the river and elsewhere, even as far as Ely. It was at Grantchester, so he said later, lying in the meadow, that he saw how to answer Hilbert’s third question. It must have been in the early summer of 1935. ‘By a mechanical process’, Newman had said. So Alan Turing dreamed of machines.
‘For, of course, the body is a machine. It is a vastly complex machine, many, many times more complicated than any machine ever made by hands; but still after all a machine.’ Such was Brewster’s paradoxical assertion. At one level, the body was living, not a machine. But at another, more detailed level of description, that of the ‘living bricks’, it was all determined. It was not the power of the machine that was the point of the remark; it was its lack of will.
It was not the determinism of physics, or chemistry, or of biological cells, that was involved in Hilbert’s question about decidability. It was something more abstract. It was the quality of being fixed in advance, in such a way that nothing new could arise. And the operations were to be operations on symbols, rather than on things of any particular mass or chemical composition.
Alan had to abstract this quality of being determined, and apply it to the manipulation of symbols. People had spoken, as Hardy did, of ‘mechanical rules’ for mathematics, of ‘turning the handle’ of a miraculous machine, but no one had actually sat down to design one. This was what he set out to do. For although he was not really ‘the very unsophisticated outsider’ of whom Hardy spoke, he attacked the problem in a peculiarly naive way, undaunted by the immensity and complexity of mathematics. He started from nothing, and tried to envisage a machine that could tackle Hilbert’s problem, that of deciding the provability of any mathematical assertion presented to it.
There were, of coure, machines in existence which manipulated symbols. The typewriter was one such. Alan had dreamt of inventing typewriters as a boy; Mrs Turing had a typewriter; and he could well have begun by asking himself what was meant by calling a typewriter ‘mechanical’. It would mean that its response, to any particular action of the operator, was perfectly certain. One could describe in advance exactly how the machine would behave in any contingency. But there was more to be said even about a humble typewriter than that. The response would depend upon the current condition, or what Alan called the current configuration, of the machine. In particular, a typewriter would have an ‘upper case’ configuration and a ‘lower case’ configuration. This was an idea which Alan put in a more general and abstract form. He would consider machines which at any time would be in one of a finite number of possible ‘configurations’. Then if, as with the typewriter keyboard, there were only a finite number of things that could be done to the machine, a complete account of the behaviour of the machine could be given, once for all, in finite form.
However, the typewriter had a further feature which was essential to its function. Its typing point could move, relative to the page. Its typing action would be independent of the position of this point on the page. Alan incorporated this idea too into his picture of the more general machine. It was to have internal ‘configurations’, and a variable position on a printing line. The action of the machine would not depend upon its position.
Neglecting details as to margins, line control, and so forth, these ideas would suffice to give a complete description of the nature of a typewriter. An exact account of the configurations and positions allowed, and of how the character keys determined the symbols printed, the shift key the change of configuration from ‘lower’ to ‘upper’, and the space bar and backspace the printing position, would bring out the features most relevant to its function. If an engineer took this account, and created a physical machine which met its specifications, the result would be a typewriter, regardless of its colour, weight, or other attributes.
But a typewriter was too limited to serve as a model. It dealt with symbols, but it could only write them, and it required a human operator to choose the symbols and changes of configuration and position, one at a time. What, Alan Turing asked, would be the most general kind of machine that dealt with symbols? To be a ‘machine’ it would have to retain the typewriter’s quality of having a finite number of configurations, and an exactly determined behaviour in each. But it would have to be capable of much more. And so he imagined machines which were, in effect, super-typewriters.
To simplify the description he imagined his machines working with just one line of writing. This was only a technicality, which allowed margins and line control to be forgotten. But it was important that the supply of paper was to be assumed unlimited. In his picture, the typing point of his super-typewriter could progress indefinitely to left or right. For the sake of definiteness, he imagined the paper as being in the form of a tape, marked off into unit squares, such that just one symbol could be written on any one square. Thus his machines were to be finitely defined, but they would be allowed an unlimited amount of space on which to work.
Next, the machine would be able to read, or using his word, to ‘scan’ the square of tape on which it rested. It would still of course be able to write symbols, but now also to erase them. But it would only be able to move one place to the left or the right at a time. What role remained to the human operator of the typewriter? He did mention the possibility of what he called ‘choice machines’, in which an external operator would have the job of making decisions at certain points. But the thrust of his argument was directed at what he called automatic machines, in which human intervention would play no part. For the goal of his development was the discussion of what Hardy had called ‘a miraculous machine’ – a mechanical process which could work on Hilbert’s decision problem, reading a mathematical assertion presented to it, and eventually writing a verdict as to whether it was provable or not. The whole point was that it should do so without the interference of human judgment, imagination or intelligence.
Any ‘automatic machine’ would work away by itself, reading and writing, moving to and fro, all in accordance with the way in which it was constructed. At every step its behaviour would be completely determined by the configuration it was in and the symbol it had read. To be precise, the construction of the machine would determine, for each combination of configuration and symbol scanned:
whether to write a new (specified) symbol in a blank square, to leave the existing one unchanged, or to erase it and leave a blank square
whether to remain in the same configuration, or to change to some other (specified) configuration
whether to move to the square on the left, or to the right, or to stay in the same position.
If all this information, defining an automatic machine, were written out, it would form a ‘table of behaviour’ of a finite size. It would completely define the machine in the sense that whether physically constructed or not, the table would hold all the relevant information about it. From this abstract point of view, the table was the machine.
Every different possible table would define a machine with a different kind of behaviour. There would be infinitely many possible tables, corresponding to infinitely many possible machines. Alan had rendered the vague idea of a ‘definite method’ or a ‘mechanical process’ into something very precise: a ‘table of behaviour’. And so now he had a very precise question to answer: was there or was there not one of these machines, one of these tables, that could produce the decision that Hilbert asked for?
An example machine: The following ‘table of behaviour’ completely defines a machine with the character of an adding machine. Started with the ‘scanner’ somewhere to the left of two groups of 1’s, separated by a single blank space, it will add the two groups, and stop. Thus, it will transform

into

The task of the machine is to fill in the blank space, and to erase the last ‘1’. It will therefore suffice to provide the machine with four configurations. In the first it moves along the blank tape looking for the first group of Ts. When it moves into the first group, it goes into the second configuration. The blank separator sends it into the third configuration, in which it moves along the second group until it encounters another blank, which acts as the signal to turn back, and to enter the fourth and final configuration in which it erases the last ‘1’ and marks time for ever.
The complete table is:
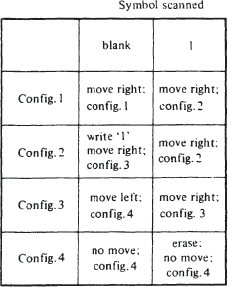
Even a very simple machine of this kind, as shown in the example, would be doing more than sums. The machine would effect acts of recognition, such as ‘finding the first symbol to the right’. A rather more complicated machine could perform multiplication, by repeated acts of copying out one group of 1’s, while erasing one at a time of another group of 1’s, and recognising when it had finished..Such a machine could also effect acts of decision, as for instance in deciding whether one number was divisible by another, or whether a given number was prime or composite. Clearly there was scope for exploiting this principle to mechanise a vast range of ‘definite methods’. But could there be such a machine that could decide Hilbert’s question about provability?
This was much too hard a problem to approach by trying to write a ‘table’ to solve it. But there was an approach which led to the answer by a back door route. Alan hit on the idea of the ‘computable numbers’. The crucial notion was that any ‘real number’ which was defined by some definite rule could be calculated by one of his machines. For instance, there would be a machine to calculate the decimal expansion of π, rather as he had done at school. For it would require no more than a set of rules for adding, multiplying, copying, and so forth. being an infinite decimal, the work of the machine would never end, and it would need an unlimited amount of working space on its ‘tape’. But it would arrive at every decimal place in some finite time, having used only a finite quantity of tape. And everything about the process could be defined by a finite table, left alone to work on a blank tape.
This meant that he had a way of representing a number like π, an infinite decimal, by a finite table. The same would be true of the square root of three, or the logarithm of seven – or any other number defined by some rule. Such numbers he called the ‘computable numbers’.
More precisely, the machine itself would know nothing about decimals or decimal places. It would simply produce a sequence of digits. A sequence that could be produced by one of his machines, starting on a blank tape, he called a ‘computable sequence’. Then an infinite computable sequence, prefaced by a decimal point, would define a ‘computable number’ between 0 and 1. It was in this more strict sense that any computable number between 0 and 1 could be defined by a finite table. It was important to his argument that the computable numbers would always be expressed as infinite sequences of digits, even if these were all 0 after a certain point.
But these finite tables could now be put into something like alphabetical order, beginning at the most simple, and working through larger and larger ones. They could be put in a list, or counted; and this meant that all the computable numbers could be put in a list. It was not a practical proposition actually to do it, but in principle the idea was perfectly definite, and would result in the square root of three being say 678th in order, or the logarithm of π being 9369th. It was a staggering thought, since this list would include every number that could be arrived at through arithmetical operations, finding roots of equations, and using mathematical functions like sines and logarithms – every number that could possibly arise in computational mathematics. And once he had seen this, he knew the answer to Hilbert’s question. Probably it was this that he suddenly saw on the Grantchester meadow. He would have seen the answer because there was a beautiful mathematical device, ready to be taken off the shelf.
Fifty years earlier, Cantor had realised that he could put all the fractions – all the ratios or rational numbers – into a list. Naively it might be thought that there were many more fractions than integers. But Cantor showed that, in a precise sense, this was not so, for they could be counted off, and put into a sort of alphabetical order. Omitting fractions with cancelling factors, this list of all the rational numbers between 0 and 1 would begin:
1/2 1/3 1/4 2/3 1/5 1/6 2/5 3/4 1/7 3/5 1/8 2/7 4/5 1/9 3/7 1/10…
Cantor went on to invent a certain trick, called the Cantor diagonal argument, which could be used as a proof that there existed irrational numbers. For this, the rational numbers would be expressed as infinite decimals, and the list of all such numbers between 0 and 1 would then begin:
The trick was to consider the diagonal number, beginning
.5306060020040180.…
and then to change each digit, as for instance by increasing each by 1 except by changing a 9 to a 0. This would give an infinite decimal beginning
.6417171131151291.…
a number which could not possibly be rational, since it would differ from the first listed rational number in the first decimal place, from the 694th rational number in the 694th decimal place, and so forth. Therefore it could not be in the list; but the list held all the rational numbers, so the diagonal number could not be rational.
It was already well-known – it was known to Pythagoras – that there were irrational numbers. The point of Cantor’s construction was actually rather different from this. It was to show that no list could possibly contain all the ‘real numbers’, that is, all infinite decimals. For any proposed list would serve to define another infinite decimal which had been left out. Cantor’s argument showed that in a quite precise sense there were more real numbers than integers. It opened up a precise theory of what was meant by ‘infinite’.
However, the point relevant to Alan Turing’s problem was that it showed how the rational could give rise to the irrational. In exactly the same way, therefore, the computable could give rise to the uncomputable, by means of a diagonal argument. As soon as he had made that observation, Alan could see that the answer to Hilbert’s question was ‘no’. There could exist no ‘definite method’ for solving all mathematical questions. For an uncomputable number would be an example of an unsolvable problem.
There was still much work to do before his result was clear. For one thing, there was something paradoxical about the argument. The Cantor trick itself would seem to be a ‘definite method’. The diagonal number was defined clearly enough, it appeared – so why could it not be computed? How could something that was constructed in this mechanical way be uncomputable? What would go wrong, if it were attempted?
Suppose one tried to design a ‘Cantor machine’ to produce this diagonal uncomputable number. Roughly speaking, it would start with a blank tape, and write the number 1. It would then have to produce the first table, and then execute it, stopping at the first digit that it wrote, and adding on one. Then it would start again, with the number 2, produce the second table, executing it as far as the second digit, and writing this down, adding on one. It would have to continue doing this for ever, so that when its counter read ‘1000’, it would produce the thousandth table, execute it as far as the thousandth digit, add on one to this and write it down.
One part of this process could certainly be done by one of his machines. For the process of ‘looking up the entries’ in a given table, and working out what the corresponding machine would do, was itself a ‘mechanical process.’ A machine could do it. There was a difficulty in that the tables were naturally thought of in two-dimensional form, but then it was only a technical matter to encode them in a form in which they could be put on a ‘tape’. In fact, they could be encoded as integers, rather as Gödel had represented formulae and proofs as integers. Alan called them ‘description numbers’, so that there was a description number corresponding to each table. In one way this was just a technicality, a means of putting tables on to the tape, and arranging them in an ‘alphabetical order’. But underneath there lay the same powerful idea that Gödel had used, that there was no essential distinction between ‘numbers’ and operations on numbers. From a modern mathematical point of view, they were all alike symbols.
With this done, it followed that one particular machine could simulate the work done by any machine. He called it the universal machine. It would be designed to read description numbers, decode them into tables, and execute them. It could do what any other machine would have done, if it were provided with the description number of that machine on its tape. It would be a machine to do everything, which was enough to give anyone pause for thought. It was, furthermore, a machine of perfectly definite form. Alan worked out an exact table for the universal machine.
This was not the trouble with mechanising the Cantor process. The difficulty lay in the other requirement, that of producing the tables, in their ‘alphabetical order’, for the computable numbers. Suppose that the tables were encoded as description numbers. In practice, they would not use up all the integers; in fact, the system Alan devised would encode even the simplest tables into enormous numbers. But that would not matter. It would be essentially a ‘mechanical’ matter to work through the integers in turn, and to pass over those which did not correspond to proper tables. That was a technicality, almost a matter of notation. The real problem was more subtle. The question was this: given (say) the 4589th properly defined table, how could one tell that it would produce a 4589th digit? Or indeed, that it would produce any digits at all? It might trundle back and forth in a repeated cycle of operations for ever, without producing more figures. It this were the case, the Cantor machine would be stuck, and could never finish its job.
The answer was that one could not tell. There was no way of checking in advance that a table would produce an infinite sequence. There might be a method for some particular table. But there was no mechanical process – no machine – that could work on all instruction tables. There was nothing better than the prescription: ‘take the table and try it out’. But this procedure would take an infinite time to find out whether infinitely many digits emerged. There was no rule that could be applied to any table, and be guaranteed to produce the answer in a finite time, as was required for the printing of the diagonal number. The Cantor process, therefore, could not be mechanised, and the uncomputable diagonal number could not be computed. There was no paradox after all.
Alan called the description numbers which gave rise to infinite decimals the ‘satisfactory numbers’. So he had shown that there was no definite method of identifying an ‘unsatisfactory number’. He had pinned down a clearly specified example of something Hilbert said did not exist – an unsolvable problem.
There were other ways of demonstrating that no ‘mechanical process’ could eliminate the unsatisfactory numbers. The one he himself favoured was one which brought out the connection with self-reference in the question. For supposing that such a ‘checking’ machine did exist, able to locate the unsatisfactory numbers, it could be applied to itself. But this, he showed, led to a flat contradiction. So no such checking machine could exist.
Either way, he had found an unsolvable problem, and it required only a technical step to show that this settled Hilbert’s question about mathematics, in the exact form in which it had been posed. Alan Turing had dealt the death-blow to the Hilbert programme. He had shown that mathematics could never be exhausted by any finite set of procedures. He had gone to the heart of the problem, and settled it with one simple, elegant observation.
But there was more to what he had done than a mathematical trick, or logical ingenuity. He had created something new – the idea of his machines. And correspondingly, there remained a question as to whether his definition of the machine really did include everything that could possibly be counted as a ‘definite method’. Was this repertoire of reading, writing, erasing, moving and stopping enough? It was crucial that it was so, for otherwise the suspicion would always lurk that some extension of the machine’s faculties would allow it to solve a greater range of problems. One approach to this question led him to demonstrate that his machines could certainly compute any number normally encountered in mathematics. He also showed that a machine could be set up to churn out every provable assertion within Hilbert’s formulation of mathematics. But he also gave some pages of discussion37 that were among the most unusual ever offered in a mathematical paper, in which he justified the definition by considering what people could possibly be doing when they ‘computed’ a number by thinking and writing down notes on paper:
Computing is normally done by writing certain symbols on paper. We may suppose this paper is divided into squares like a child’s arithmetic book. In elementary arithmetic the two-dimensional character of the paper is sometimes used. But such a use is always avoidable, and I think that it will be agreed that the two-dimensional character of paper is no essential of computation. I assume then that the computation is carried out on one-dimensional paper, i.e. on a tape divided into squares. I shall also suppose that the number of symbols which may be printed is finite. If we were to allow an infinity of symbols, then there would be symbols differing to an arbitrarily small extent.
An ‘infinity of symbols’, he wished to argue, did not correspond to anything in reality. It might be argued that there was an infinity of symbols, in that
an Arabic numeral such as 17 or 999999999999999 is normally treated as a single symbol. Similarly in any European language words are treated as single symbols (Chinese, however, attempts to have an enumerable infinity of symbols).
But he disposed of this objection with the observation that
The differences from our point of view between the single and compound symbols is that the compound symbols, if they are too lengthy, cannot be observed at one glance. This is in accordance with experience. We cannot tell at a glance whether 9999999999999999 and 999999999999999 are the same.
Accordingly, he felt justified in restricting a machine to a finite repertoire of symbols. Next came a most important idea:
The behaviour of the computer at any moment is determined by the symbols which he is observing, and his ‘state of mind’ at that moment. We may suppose that there is a bound B to the number of symbols or squares which the computer can observe at one moment. If he wishes to observe more, he must use successive observations. We will also suppose that the number of states of mind which need to be taken into account is finite. The reasons for this are the same character as those which restrict the number of symbols. If we admitted an infinity of states of mind, some of them will be ‘arbitrarily close’ and will be confused. Again, the restriction is not one which seriously affects computation, since the use of more complicated states of mind can be avoided by writing more symbols on the tape.
The word ‘computer’ here meant only what that word meant in 1936: a person doing calculations. Elsewhere in the paper he appealed to the idea that ‘the human memory is necessarily limited,’ but this was as far as he went in a discussion of the nature of the human mind. It was a bold act of imagination, a brave suggestion that ‘states of mind’ could be counted, on which to base his argument. It was especially noteworthy because in quantum mechanics, physical states could be ‘arbitrarily close’. He continued with his discussion of the human computer:
Let us imagine the operations performed by the computer to be split up into ‘simple operations’ which are so elementary that it is not easy to imagine them further divided. Every such operation consists of some change in the physical system consisting of the computer and his tape. We know the state of the system if we know the sequence of symbols on the tape, which of these are observed by the computer (possibly with a special order), and the state of mind of the computer. We may suppose that in a simple operation not more than one symbol is altered. Any other changes can be split up into simple changes of this kind. The situation in regard to the squares whose symbols may be altered in this way is the same as in regard to the observed squares. We may, therefore, without loss of generality, assume that the squares whose symbols are changed are always ‘observed’ squares.
Besides these changes of symbols, the simple operations must include changes of distribution of observed squares. The new observed squares must be immediately recognisable by the computer. I think it is reasonable to suppose that they can only be squares whose distance from the closest of the immediately previously observed squares does not exceed a certain fixed amount. Let us say that each of the new observed squares is within L squares of an immediately previously observed square.
In connection with ‘immediate recognisability’, it may be thought that there are other kinds of square which are immediately recognisable. In particular, squares marked by special symbols might be taken as immediately recognisable. Now if these squares are marked only by single symbols there can be only a finite number of them, and we should not upset our theory by adjoining these marked squares to the observed squares. If, on the other hand, they are marked by a sequence of symbols, we cannot regard the process of recognition as a simple process. This is a fundamental point and should be illustrated. In most mathematical papers the equations and theorems are numbered. Normally the numbers do not go beyond (say) 1000. It is, therefore, possible to recognise a theorem at a glance by its number. But if the paper was very long, we might reach Theorem 157767733443477; then, further on in the paper, we might find ‘… hence (applying Theorem 157767734443477) we have…’. In order to make sure which was the relevant theorem we should have to compare the two numbers figure by figure, possibly ticking the figures off in pencil to make sure of their not being counted twice. If in spite of this it is still thought that there are other ‘immediately recognisable’ squares, it does not upset my contention so long as these squares can be found by some process of which my type of machine is capable.…
The simple operations must therefore include:
(a) Changes of the symbol on one of the observed squares
(b) Changes of one of the squares observed to another square within L squares of one the previously observed squares.
It may be that some of these changes necessarily involve a change of state of mind. The most general single operation must therefore be taken to be one of the following:
(A) A possible change (a) of symbol together with a possible change of state of mind;
(B) A possible change (b) of observed squares, together with a possible change of state of mind.
The operation actually performed is determined, as has been suggested [above] by the state of mind of the computer and the observed symbols. In particular, they determine the state of mind of the computer after the operation is carried out.
‘We may now construct a machine,’ Alan wrote, ‘to do the work of this computer.’ The drift of his argument, indeed, was obvious, with each ‘state of mind’ of the human computer being represented by a configuration of the corresponding machine.
These ‘states of mind’ being a weak point of the argument, he added an alternative justification of the idea that his machines could perform any ‘definite method’ which did not need them:
We suppose [still] that the computation is carried out on a tape; but we avoid introducing the ‘state of mind’ by considering a more physical and definite counterpart of it. It is always possible for the computer to break off from his work, to go away and forget all about it, and later to come back and go on with it. If he does this he must leave a note of instructions (written in some standard form) explaining how the work is to be continued. This note is the counterpart of the ‘state of mind’. We will suppose that the computer works in such a desultory manner that he never does more than one step at a sitting. The note of instructions must enable him to carry out one step and write the next note. Thus the state of progress of the computation at any stage is completely determined by the note of instructions and the symbols on the tape…
But these arguments were quite different. Indeed, they were complementary. The first put the spotlight upon the range of thought within the individual – the number of ‘states of mind’. The second conceived of the individual as a mindless executor of given directives. Both approached the contradiction of free will and determinism, but one from the side of internal will, the other from that of external constraints. These approaches were not explored in the paper, but left as seeds for future growth.*
Alan had been stimulated by Hilbert’s decision problem, or the Entscheidungs problem as it was in German. He had not only answered it, but had done much more. Indeed, he would entitle his paper ‘On Computable Numbers, with an application to the Entscheidungs problem.’ It was as though Newman’s lectures had tapped some stream of enquiry which had been flowing all the time and which found in this question an opportunity to emerge. He had done something, for he had resolved a central question about mathematics, and had done so by crashing in as an unknown and unsophisticated outsider. But it was not only a matter of abstract mathematics, not only a play of symbols, for it involved thinking about what people did in the physical world. It was not exactly science, in the sense of making observations and predictions. All he had done was to set up a new model, a new framework. It was a play of imagination like that of Einstein or von Neumann, doubting the axioms rather than measuring effects. Even his model was not really new, for there were plenty of ideas, even in Natural Wonders, about the brain as a machine, a telephone exchange or an office system. What he had done was to combine such a naive mechanistic picture of the mind with the precise logic of pure mathematics. His machines – soon to be called Turing machines – offered a bridge, a connection between abstract symbols, and the physical world. Indeed, his imagery was, for Cambridge, almost shockingly industrial.
Obviously there was a connection between the Turing machine and his earlier concern with the problem of Laplacian determinism. The relationship was indirect. For one thing, it might be argued that the ‘spirit’ he had thought about was not the ‘mind’ that performed intellectual tasks. For another, the description of the Turing machines had nothing to do with physics. Nevertheless, he had gone out of his way to set down a thesis of ‘finitely many mental states’, a thesis implying a material basis to the mind, rather than stick to the safer ‘instruction note’ argument. And it would appear that by 1936 he had indeed ceased to believe in the ideas that he had described to Mrs Morcom as ‘helpful’ as late as 1933 – ideas of spiritual survival and spiritual communication. He would soon emerge as a forceful exponent of the materialist view and identify himself as an atheist. Christopher Morcom had died a second death, and Computable Numbers marked his passing.
Beneath the change there lay a deeper consistency and constancy. He had worried about how to reconcile ideas of will and spirit with the scientific description of matter, precisely because he felt so keenly the power of the materialist view, and yet also the miracle of individual mind. The puzzle remained the same, but now he was approaching it from the other side. Instead of trying to defeat determinism, he would try to account for the appearances of freedom. There had to be a reason for it. Christopher had diverted him from the outlook of Natural Wonders, but now he had returned.
There was another point of constancy, in that he was still looking for some definite, down-to-earth resolution of the paradox of determinism and free will, not a wordy philosophical one. Earlier, in this search, he had favoured Eddington’s idea about the atoms in the brain. He would remain very interested in quantum mechanics and its interpretation, a problem that von Neumann had by no means resolved, but the Jabberwocky would not be his problem. For now he had found his own métier, by formulating a new way of thinking about the world. In principle, quantum physics might include everything, but in practice to say anything about the world would require many different levels of description. The Darwinian ‘determinism’ of natural selection depended upon the ‘random’ mutation of individual genes; the determinism of chemistry was expressed in a framework where the motion of individual molecules was ‘random’. The Central Limit Theorem was an example of how order could arise out of the most general kind of disorder. A cipher system would be an example of how disorder could arise by means of a determinate system. Science, as Eddington took care to observe, recognised many different determinisms, many different freedoms. The point was that in the Turing machine, Alan had created his own determinism of the automatic machine, operating within the logical framework he held to be appropriate to the discussion of the mind.
He had worked entirely on his own, not once discussing the construction of his ‘machines’ with Newman. He had a few words with Richard Braithwaite at the High Table one day on the subject of Gödel’s theorem. Another time he put a question about the Cantor method to Alister Watson, a young King’s Fellow (a communist, as it happened) who had turned from mathematics to philosophy. He described his ideas to David Champernowne, who got the gist of the universal machine, and said rather mockingly that it would require the Albert Hall to house its construction. This was fair comment on Alan’s design in Computable Numbers, for if he had any thoughts of making it a practical proposition they did not show in the paper.38 Just south of the Albert Hall, in the Science Museum, were lurking the remains of Babbage’s ‘Analytical Engine’, a projected universal machine of a hundred years before. Quite probably Alan had seen them, and yet if so, they had no detectable influence upon his ideas or language. His ‘machine’ had no obvious model in anything that existed in 1936, except in general terms of the new electrical industries, with their teleprinters, television ‘scanning’, and automatic telephone exchange connections. It was his own invention.
A long paper, full of ideas, with a great deal of technical work and evidence of more left unpublished, Computable Numbers must have dominated Alan’s life from spring 1935 through the following year. In the middle of April 1936, returning from Easter at Guildford, he called on Newman and gave him the draft typescript.
There were many questions to be asked about the discoveries that Gödel and he had made, and what they meant for the description of mind. There was a profound ambiguity to this final settlement of Hilbert’s programme, though it certainly ended the hope of a too naive rationalism, that of solving every problem by a given calculus. To some, including Gödel himself, the failure to prove consistency and completeness would indicate a new demonstration of the superiority of mind to mechanism. But on the other hand, the Turing machine opened the door to a new branch of deterministic science. It was a model in which the most complex procedures could be built out of the elementary bricks of states and positions, reading and writing. It suggested a wonderful mathematical game, that of expressing any ‘definite method’ whatever in a standard form.
Alan had proved that there was no ‘miraculous machine’ that could solve all mathematical problems, but in the process he had discovered something almost equally miraculous, the idea of a universal machine that could take over the work of any machine. And he had argued that anything performed by a human computer could be done by a machine. So there could be a single machine which, by reading the descriptions of other machines placed upon its ‘tape’, could perform the equivalent of human mental activity. A single machine, to replace the human computer! An electric brain!
The death of George V, meanwhile, marked a transition from protest at the old order to fear of what the new might hold in store. Germany had already defeated the new Enlightenment; had already injected iron into the idealist soul. March 1936 saw the re-occupation of the Rhineland: it meant that the future lay with militarism. Who then could have seen the connection with the fate of an obscure Cambridge mathematician? Yet connection there was. For one day Hitler was to lose the Rhineland, and it would be then, and only then, that the universal machine could emerge into the world of practical action. The idea had come out of Alan Turing’s private loss. But between the idea and its embodiment had to come the sacrifice of millions. Nor would the sacrifices end with Hitler; there was no solution to the world’s Entscheidungs problem.
* John Bennett was a boy in the house, who himself died later in 1930 on a lone winter trek across the Rockies.
* For comparison: a skilled worker earned about £160 per annum; unemployment benefit ran at £40 per annum for a single man.
* W. Sierpinski, a prominent twentieth century Polish pure mathematician.
* ‘Mays’ were the semi-official second year examinations.
*Joynson Hicks, the reactionary Home Secretary.
* This gave him a tenuous link with his mother, who had shares in a Bethnal Green housing association. Alan’s reaction was approval that they planned the flats for the families who needed them rather than vice versa.
†‘Regarding Aunt J’s funeral’, Alan wrote in January 1934 to his mother, ‘I am not v. keen on going, and I think it would be consummate hypocrisy if I did. But if you think anyone will be the better for my attending I will see whether it can be managed.’
* Alan also considered Ibsen’s plays ‘remarkably good’.
* The analogy is not intended to be exact; Hilbert space and quantum mechanical ‘states’ differ in an essential way from anything in ordinary experience.
* The word ‘group’, as used in mathematics, has a technical meaning quite distinct from its use in ordinary language. It refers to the idea of a set of operations, but only when that set of operations meets certain precise conditions. These may be illustrated by considering the rotations of a sphere. If A, B and C are three different rotations, then one can see that:
(i) there exists a rotation which exactly reverses the effect of A.
(ii) there exists a rotation which has exactly the same effect as performing A, and then B.
Let this rotation be called ‘AB’. Then
(iii) AB, followed by C, has the same effect as A, followed by BC.
These are essentially the conditions required for the rotations to form a ‘group’. Abstract group theory then arose by taking these conditions, representing them appropriately with symbols, and then abandoning the original concrete embodiment. The resulting theory might profitably be applied to rotations, as indeed it was, in quantum mechanics. It could also apply to the apparently unrelated field of ciphering. (Ciphers enjoy the ‘group’ properties: a cipher must have a well-defined decipherment operation which reverses it, and if two ciphering operations are performed in succession, the result is another cipher.) But by the 1930s it was accepted that ‘groups’ could be explored in the abstract, without any concrete representation or application in mind.
* There is nothing ‘real’ about ‘real numbers’. The term is a historical accident, arising from the equally misleading terms ‘complex numbers’ and ‘imaginary numbers’. The reader not familiar with these expressions could think of ‘real numbers’ as ‘lengths defined with a hypothetical infinite precision.’
* Alan acquired a copy, soon heavily annotated, of Hilbert and Courant’s Methoden der Mathematischen Physik in July 1933.
* The author of one of the books which described the Central Limit Theorem.
* A simple example of a topological problem is that of the ‘four colour theorem’. This states that a map such as one of the English counties can always be coloured with just four colours, in such a way that no two adjoining counties share the same colour. Alan himself took some interest in this problem, but it was to remain an unproved assertion until 1976.
* A recent development in pure mathematics, extending and generalising the idea of ‘periodicity’.
* The arguments also implied two rather different interpretations of the machine ‘configuration’. From the first point of view, it was natural to think of the configuration as the machine’s internal state – something to be inferred from its different responses to different stimuli, rather as in behaviourist psychology. From the second point of view, however, it was natural to think of the configuration as a written instruction, and the table as a list of instructions, telling the machine what to do. The machine could be thought of as obeying one instruction, and then moving to another instruction. The universal machine could then be pictured as reading and decoding the instructions placed upon the tape. Alan Turing himself did not stick to his original abstract term ‘configuration’, but later described machines quite freely in terms of ‘states’ and ‘instructions’, according to the interpretation he had in mind. This free usage will accordingly be employed in what follows.