3

New Men

I hear it was charged against me that I sought to destroy institutions,

But really I am neither for nor against institutions,

(What indeed have I in common with them? or what with the

destruction of them?)

Only I will establish in the Mannahatta and in every city of these

States inland and seaboard,

And in the fields and woods, and above every keel little or large that

dents the water,

Without edifices or rules or trustees or any argument,

The institution of the dear love of comrades.

Almost on the same day that Alan announced his discovery to Newman, someone else completed a demonstration that the Hilbert Entscheidungs-problem was unsolvable. It was at Princeton, where the American logician Alonzo Church had finished his argument for publication¹ on 15 April 1936. Church’s essential idea, showing the existence of an ‘unsolvable problem’, had been announced a year earlier, but only at this point did he put it exactly in the form of answering Hilbert’s question.

A new idea had found its way into two human minds simultaneously and independently. At first, this was not known at Cambridge, and Alan wrote to his mother on 4 May:

 

I saw Mr Newman four or five days after I came up. He is very busy with other things just at present and says he will not be able to give his whole attention to my theory for some week or so yet. However he examined my note for C.R.* and approved it after some alterations. I also got it vetted by a French expert, and sent it off. I have had no acknowledgement of it, which is rather annoying. I don’t think the full text will be ready for a fortnight or more yet. It will probably be about fifty pages. It is rather difficult to decide what to put into the paper now and what to leave over till a later occasion.

When Newman did read it in mid-May, he could hardly believe that so simple and direct an idea as the Turing machine would answer the Hilbert problem over which many had been labouring for the five years since Gödel had disposed of the other Hilbert questions. His first impression was that it must be wrong, for some more sophisticated machine would be able to solve the ‘unsolvable problem’, and that one would then continue on and on. But finally he satisfied himself that no finitely defined machine could possibly do more than was allowed by the Turing construction.

Then Church’s paper arrived from across the Atlantic. It pre-empted the result, and threw into jeopardy the publication of Alan’s work, scientific papers not being allowed to repeat or copy one another. But what Church had done was something rather different, and in a certain sense weaker. He had developed a formalism called the ‘lambda-calculus’* and, with the logician Stephen Kleene, had discovered that this formalism could be used to translate all the formulae of arithmetic into a standard form. In this form, proving theorems was a matter of converting one string of symbols of the lambda-calculus into another string, according to certain rather simple rules. Church had then been able to show that the problem of deciding whether one string could be converted into another string was unsolvable, in the sense that there existed no formula of the lambda-calculus which could do it. Having found one such unsolvable problem, it had become possible to show that the exact question that Hilbert had posed must also be unsolvable. But it was not obvious that ‘a formula of the lambda-calculus’ corresponded to the notion of a ‘definite method’. Church gave verbal arguments for the assertion that any ‘effective’ method of calculation could be represented by a formula of the lambda-calculus. But the Turing construction was more direct, and provided an argument from first principles, closing the gap in Church’s demonstration.

So Alan was able to submit his paper on 28 May 1936 to the London Mathematical Society for publication in its Proceedings, and Newman wrote to Church:

31 May 1936

Dear Professor Church,

An offprint which you kindly sent me recently of your paper in which you define ‘calculable numbers’, and shew that the Entscheidungs problem for Hilbert logic is insoluble, had a rather painful interest for a young man, A.M. Turing, here, who was just about to send in for publication a paper in which he had used a definition of ‘Computable numbers’ for the same purpose. His treatment – which consists in describing a machine which will grind out any computable sequence – is rather different from yours, but seems to be of great merit, and I think it of great importance that he should come and work with you next year if that is at all possible. He is sending you the typescript of his paper for your criticisms.

If you find that it is right, and of merit, I should be greatly obliged if you could help Turing to get to Princeton next year, by writing to the Vice-Chancellor, Clare College, Cambridge, in support of Turing’s application for the Procter Fellowship. If he fails to win this he can still just manage to come, I think, since he is a Fellow of King’s College, but it would be a very tight fit. Is there any possibility of a small supplementary grant at the Princeton end? … I should mention that Turing’s work is entirely independent: he has been working without any supervision or criticism from anyone. This makes it all the more important that he should come into contact as soon as possible with the leading workers on this line, so that he should not develop into a confirmed solitary.

There was no one in England who could referee the paper for publication in the London Mathematical Society Proceedings, and in fact Church himself was the only person who could reasonably do so. Newman wrote to the Secretary of the London Mathematical Society, F.P. White, explaining the position:

31 May 1936

Dear White,

I think you know the history of Turing’s paper on Computable numbers. Just as it was reaching its final state an offprint arrived, from Alonzo Church of Princeton, of a paper anticipating Turing’s results to a large extent.

I hope it will nevertheless be possible to publish the paper. The methods are to a large extent different, and the result is so important that different treatments of it should be of interest. The main result of both Turing and Church is that the Entscheidungs problem on which Hilbert’s disciples have been working for a good many years – i.e. the problem of finding a mechanical way of deciding whether a given row of symbols is the enunciation of a theorem provable from the Hilbert axioms – is insoluble in its general form. …

Alan reported to his mother on 29 May:

 

I have just got my main paper ready and sent in. I imagine it will appear in October or November. The situation with regard to the note for Comptes Rendus was not so good. It appears that the man I wrote to, and whom I asked to communicate the paper for me had gone to China, and moreover the letter seems to have been lost in the post, for a second letter reached his daughter.

Meanwhile a paper has appeared in America, written by Alonzo Church, doing the same things in a different way. Mr Newman and I have decided however that the method is sufficiently different to warrant the publication of my paper too. Alonzo Church lives at Princeton so I have decided quite definitely about going there.

He had applied for a Procter Fellowship. Princeton offered three of these, one in the gift of Cambridge, one of Oxford, one of the Collège de France. He was not to be successful, for the Cambridge one went that year to R.A. Lyttleton, the mathematician and astronomer. But he must have found that his King’s fellowship would provide just enough funds.

Meanwhile, it was now necessary for the publication of the paper that he should include a demonstration that its definition of ‘computable’ – that is, as anything that could be computed by a Turing machine – was exactly equivalent to what Church had called ‘effectively calculable’, meaning that it could be described by a formula in the lambda-calculus. So he studied Church’s work from the papers which he and S.C. Kleene had produced in 1933 and 1935, and sketched out the required demonstration in an appendix to the paper which was finished on 28 August. The correspondence of ideas was quite straightforward, since Church had used a definition (that of a formula being ‘in normal form’) which corresponded to the Turing definition of ‘satisfactory’ machines, and had then used a Cantor diagonal argument to produce an unsolvable problem.

If he had been a more conventional worker, he would not have attacked the Hilbert problem without having read up all of the available literature, including Church’s work. He then might not have been pre-empted – but then, he might never have created the new idea of the logical machine, with its simulation of ‘states of mind’, which not only closed the Hilbert problem but opened up quite new questions. It was the advantage and the disadvantage of working as what Newman called ‘a confirmed solitary’. Both with the Central Limit Theorem and with the Entscheidungs problem, he had been the Captain Scott of mathematics, coming in a splendid second place. And while he was not the person to think of mathematics and science as a sort of competitive game, it was obviously a disappointment. It meant months of delay, and obscured the originality of his own attack. It confused his moment of coming out into the world.

As for the Central Limit Theorem, his fellowship dissertation was entered for the Cambridge mathematical essay competition, the Smith’s Prize, that summer. This caused a flurry down at Guildford, where Mrs Turing and John spent a frantic half-hour on hands and knees doing up the parcel, which Alan had left until the last minute before sending off. John had married in August 1934 and Alan had by now become an uncle. Neither his brother, nor his parents, had the faintest inkling of the philosophical problems which underlay his work, or which underlay his life. News of Alan’s successes came as glowing reports from a higher and higher Sixth Form. Mrs Turing, with her interest in the spiritual world, would have been the most sensitive to Alan’s concern with free will, but even she never saw this fundamental connection. For Alan never expatiated on his inner problems, and only occasionally did rather cryptic hints of them emerge.

The university, like King’s, took a charitable view of Alan’s rediscovery of the theorem, and it won him the prize and hence £31. By now he had taken up sailing as a holiday pastime, and thought of putting the money towards buying a boat. But he decided against it, perhaps needing it for his year in America.

Victor Beuttell came to stay with Alan at Cambridge in the early summer. Alan was returning the hospitality that the Beuttells had offered him but another reason for Victor’s visit was that he had now joined the family firm and had been set to work on developing the K-ray system. The geometry that he had discussed with Alan at school had helped him, but he was hoping to have Alan’s advice on the new problem which was to make a double-sided system so that both sides of a poster could be illuminated evenly by a single light source. (It was required by a brewery chain). Alan, however, said he was too preoccupied with his own work, and instead they went off to watch the May Bumps boat races.

Once they were talking about art and sculpture and it was in this connection that Alan suddenly amazed Victor by saying that he found the male form beautiful, and the female unattractive. Victor now found himself a double crusader, and tried to convince Alan that Jesus had indicated the right course by befriending Mary Magdalene. Alan had no answer to this, but then this was not a problem of reason. All he could do was to express the sensation of being in a Looking-Glass world, in which from his point of view the conventional ideas were the wrong way about. This was probably the first time that he opened the subject outside the King’s ambience.

It was difficult for Victor, who was a not particularly mature twenty-one, to know how to react. An element of trust now came into his staying in Alan’s room, though Alan remained ‘a perfect gentleman’. But Victor did not reject Alan’s friendship. Instead, they continued to agree to disagree on this subject as they did on religion. They talked of what hereditary or environmental influences might determine it one way or the other. But whatever these were, it was clear that here was part of Alan that was so; that part of his reality was shaped that way. For him, without a God, there was nothing to appeal to but some inner consistency. As in mathematics, that consistency could not be proved by a rule-book, and there was no deus ex machina to hand down decisions as to right and wrong. The axioms of his life were becoming clear by now, although how to live them out was quite another question. He had wanted the commonest in nature; he liked ordinary things. But he found himself to be an ordinary English homosexual atheist mathematician. It would not be easy.

Alan also paid a visit to the Clock House before going out west, the first for three years. Mrs Morcom was now semi-invalid, but still mentally as vigorous as ever. She noted in her diary:

 

September 9 (Wednesday) … Alan Turing came … He has come for a farewell visit before going out to America for 9 months (Princetown) to study under 2 great authorities on his subject: Godel (Warsaw) Alonso Church and Kleene. We had talk before dinner and again later to bring us up to date with our news. … He and Edwin played billiards.

 

September 10: … Alan and Veronica to farms and Dingleside. … V and Alan tea up here with me. Had long talk with Alan about his work and whether in his subject (some abstruse branch of logic) one would come to ‘dead end’ etc.

 

September 11: Alan went down to church alone to see Chris’ window and the little garden which he hadn’t seen before since it was finished – only the day he came to the dedication of the window… Alan taught me game called ‘Go’ – rather like Peggity.

 

September 12: … Rupert and Alan had tea in my room and then I took them all by surprise by coming down to dinner. There were 10 of us – a jolly party. Gramophone concert… Men billiards.

 

September 13 … Alan did problems with R[eginald] … Alan Rup[ert] and 2 girls bathed at Cadbury’s pool … Rup[ert] and Alan tea with me … Alan tried to explain what he is working at … they went off to catch 7.45 New Street.

Alan lost Rupert when it came to the satisfactory and the unsatisfactory description numbers. It would have been hard for Mrs Morcom to feel that this ‘abstruse branch of logic’ had anything to do with the scientific imagination of her lost son, so that Alan had done something that Christopher had been called away from.

Mrs Turing saw Alan off at Southampton on 23 September, when he embarked on the Cunard liner, the Berengaria. He had picked up a sextant in the Farringdon Road market to amuse himself on the voyage. He also went equipped with all the standard upper-middle-class British prejudices about America and Americans, and the five days on the Atlantic did little to disabuse him. From ‘41°20′N, 62°W’, he complained:2

 

It strikes me that Americans can be the most insufferable and insensitive creatures you could wish. One of them has just been talking to me and telling me of all the worst aspects of America with evident pride. However they may not all be like that.

The towers of the Manhattan skyline swam into view next morning, on 29 September, and Alan entered the New World:

 

We were practically in New York at 11.00 a.m. on Tuesday but what with going through quarantine and passing the immigration officers we were not off the boat until 5.30 p.m. Passing the immigration officers involved waiting in a queue for over two hours with screaming children round me. Then, after getting through the customs I had to go through the ceremony of initiation to the U.S.A., consisting of being swindled by a taxi-driver. I considered his charge perfectly preposterous, but as I had already been charged more than double English prices for sending my luggage, I thought it was possibly right.

Alan inherited his father’s belief that to take a taxi was the height of extravagance. But America, with its infinite variety, was not all ‘like that’, and Princeton, where he arrived late that evening on the train had little in common with the ‘mass of canaille’ of the cheapest Tourist Class. For if Cambridge embodied class, then Princeton spoke wealth. Perhaps of all the élite American universities, Princeton was the most self-contained, insulated from the squalor of the depression. One could look out and never know that America had a problem. In fact, it hardly looked like America at all, for with its mock Gothic architecture, its restriction to male students, its rowing on the artificial Carnegie Lake, Princeton tried to outdo the detachment of Oxford and Cambridge. It was the Emerald City in the land of Oz. And as if the isolation from ordinary America were not enough, the Graduate College was separated off from the undergraduate life, to stand upon its gentle prominence, overlooking a clean sweep of fields and woods. The tower of the Graduate College was an exact replica of that of Magdalen College Oxford, and it was popularly called the Ivory Tower, because of that benefactor of Princeton, the Procter who manufactured Ivory Soap.

Mathematics at Princeton had been greatly augmented by the endowment of five million dollars for the foundation, in 1932, of the Institute for Advanced Study. Until 1940 the Institute had no separate building of its own. Those whom it funded, almost all mathematicians and theoretical physicists, shared the space of Fine Hall, home of the regular Princeton mathematical faculty. Although for technical purposes the distinction had to be drawn, in practice no one knew nor cared who was Princeton University and who was IAS. The doubled department had attracted some of the greatest names in world mathematics, and especially the exiles from Germany. It was in some ways an all-American foundation, in others like some immigrant ship still traversing the Atlantic. The richly funded Princeton fellowships also attracted research students of a world class, although more from England than from any other country. There were none from King’s, but Alan’s friend Maurice Pryce from Trinity was in residence for a second year. Here, amidst the huddled élite of the exiled European intelligentsia, lay the opportunity for Alan Turing to follow up his major result. His first report home, on 6 October, betrayed no lack of self-confidence.

 

The mathematics department here comes fully up to expectations. There is a great number of the most distinguished mathematicians here. J.v. Neumann, Weyl, Courant, Hardy, Einstein, Lefschetz, as well as hosts of smaller fry. Unfortunately there are not nearly so many logic people here as last year. Church is here of course, but Gödel, Kleene, Rosser and Bernays who were here last year have left. I don’t think I mind very much missing any of these except Gödel. Kleene and Rosser are, I imagine, just disciples of Church and have not much to offer that I could not get from Church. Bernays is I think getting rather ‘vieux jeu’ that is the impression I get from his writing, but if I were to meet him I might get a different impression.

Of these, Hardy was only visiting from Cambridge for a term.

 

At first he was very standoffish or possibly shy. I met him in Maurice Pryce’s rooms the day I arrived, and he didn’t say a word to me. But he is getting much more friendly now.

Hardy was something of a Turing of an earlier generation; he was another ordinary English homosexual atheist, who just happened to be one of the best mathematicians in the world. He was more fortunate than Alan in that his chief interest, the theory of numbers, fell cleanly within the classical framework of pure mathematics. He did not have Alan’s problem, of having to create his own subject. And his work was much more regular, more professional, than ever Alan’s was. But both were refugees from the system, for whom Keynesian Cambridge was the only possible home, although neither belonged to the more glamorous circles. Both were passive resisters, though Hardy was slightly less passive; he had been president of the Association of Scientific Workers out of principle, and had Lenin’s picture in his rooms. As the older man, his views were that much more firmly cast. Bertrand Russell once wittily distinguished catholic from protestant sceptics, according to the tradition they had rejected, and on this model Alan was, at this stage, more of a Church of England atheist. Hardy, however, played upon the English refusal to take ideas seriously, by becoming an atheist evangelical. At the same time, he found the pleasures of ritual in his devotion to the game of cricket. There was no one who knew more about it, although when in America he transferred his allegiance to baseball. He would organise cricket matches at Trinity, with Disbelief playing against Belief and the Almighty challenged to rain out the unbelievers. Hardy delighted in making a game out of anything, especially atheism.

Alan would have attended his advanced lectures and classes at Cambridge, and therefore felt aggrieved at being ignored. Although ‘friendly’, the relationship was not one that overcame a generation and multiple layers of reserve. And if this was true of his acquaintanceship with Hardy, who saw the world through such very similar eyes, it was all the more so of Alan’s other professional contacts with elders. Although he was emerging as a figure of the serious academic world, he found it hard to shed the outlook and manners of an undergraduate.

The list of names in Alan’s letter in itself meant little except that he might attend their lectures and seminars. Einstein would be seen occasionally in the corridors, but was almost incommunicado. S. Lefschetz was a pioneer in topology, which was at the centre of Princeton mathematics, and indeed a principal growth point of modern mathematics, but Alan’s personal contact with him was probably characterised by an occasion when Lefschetz questioned whether he would understand L.P. Eisenhart’s lecture course on Riemannian geometry, a question Alan considered insulting. Courant and Weyl, with von Neumann, covered the whole mainstream of pure and applied mathematics, bringing something of Hilbert’s Göttingen to life again on the western shore. But of them it was probably only von Neumann who had contact with Alan, through shared interests in group theory.

As for the logicians, Gödel had returned to Czechoslovakia. Kleene and Rosser had made more substantial contributions to logic than Alan’s letter suggested, but had taken up positions elsewhere, and he would never meet either of them. The Swiss logician P. Bernays, a close associate of Hilbert, and another exile from Göttingen, had returned to Zürich. Thus the impression that Alan had given to Mrs Morcom, of working with two or three major authorities, was incorrect. It was a matter of working with Church alone, except inasmuch as there were graduates studying logic on a lower level. And Church was a retiring man himself, not given to a great deal of discussion. In short, Princeton did not cure Alan of being a ‘confirmed solitary’. He wrote:

 

I have seen Church two or three times and I get on with him very well. He seems quite pleased with my paper and thinks it will help him to carry out a programme of work he has in mind. I don’t know how much I shall have to do with this programme of his, as I am developping [sic] the thing in a slightly different direction, and shall probably start writing a paper on it in a month or two. After that I may write a book.

Whatever these plans were, they did not come to fruition; there was no paper which fell into this description, nor a book.

He conscientiously attended Church’s lectures, which were rather on the ponderous and laborious side. In particular, he took notes of Church’s theory of types, reflecting his continued interest in that aspect of mathematical logic. There were something like ten students present, including a younger American, Venable Martin, whom Alan befriended and helped with understanding the course. Alan remarked:

 

The graduate students include a very large number who are working in mathematics and none of them mind talking shop. It is very different from Cambridge in that way.

At Cambridge it was thought in very bad taste at High Table, or anywhere, for a person to speak only of his speciality. But this was not a feature of the English university that Princeton had imported along with the architecture. The English students, all from Oxford or Cambridge, would be amused at such American greetings as ‘Hi, pleased to meet you, what courses are you taking?’ English work was hidden under a decent show of well-bred amateurishness. This pretended negligence astonished the earnest devotees of the work ethic. But for Alan, who was excluded from the smarter circles of Cambridge society for his lack of sophistication, the more straightforward approach was an attraction. In that way America suited him – but not in other respects. To his mother, he wrote on 14 October:

 

Church had me out to dinner the other night. Considering that the guests were all university people I found the conversation rather disappointing. They seem, from what I can remember of it, to have discussed nothing but the different states they came from. Description of travel and places bores me intensely.

He enjoyed the play of ideas, and in the same letter he let slip a hint of ideas in which Bernard Shaw himself might have found a plot:

 

You have often asked me about possible applications of various branches of mathematics. I have just discovered a possible application of the kind of thing I am working on at present. It answers the question ‘What is the most general kind of code or cipher possible’, and at the same time (rather naturally) enables me to construct a lot of particular and interesting codes. One of them is pretty well impossible to decode without the key, and very quick to encode. I expect I could sell them to H.M. Government for quite a substantial sum, but am rather doubtful about the morality of such things. What do you think?

Ciphering would be a very good example of a ‘definite method’ applied to symbols, something that could be done by a Turing machine. It would be essential to the nature of a cipher that the encipherer behave like a machine, in accordance with whatever rules had been fixed in advance with the receiver of the message.

As for a ‘most general code or cipher possible’, in a sense any Turing machine could be regarded as encoding what it read on its tape, into what it wrote on the tape. However, to be useful there would have to be an inverse machine, which could reconstruct the original tape. His result, whatever it was, must have started on these lines. But as for the ‘particular and interesting codes’ he offered no further clue.

Nor did he touch again on the conflict indicated by the word ‘morality’: what was he to do? Mrs Turing, of course, was a Stoney; she assumed that science existed for the sake of useful applications, and she was not the person to doubt the moral authority of His Majesty’s Government. But the intellectual tradition to which Alan belonged was quite different. It was not only for the detachment of Cambridge, but for a very significant section of modern mathematical opinion that G.H. Hardy spoke when he wrote:3

 

The ‘real’ mathematics of the ‘real’ mathematicians, the mathematics of Fermat and Euler and Gauss and Abel and Riemann, is almost wholely ‘useless’ (and this is true of ‘applied’ as of ‘pure’ mathematics). It is not possible to justify the life of any genuine professional mathematician on the ground of the ‘utility’ of his work. … The great modern achievements of applied mathematics have been in relativity and quantum mechanics, and these subjects are, at present at any rate, almost as ‘useless’ as the theory of numbers. It is the dull and elementary parts of applied mathematics, as it is the dull and elementary parts of pure mathematics, that work for good or ill.

In making explicit his response to the growing separation of mathematics from applied science, Hardy attacked the shallowness of the current ‘left-wing’ Lancelot Hogben interpretation of mathematics in terms of social and economic utility, an interpretation based on the ‘dull and elementary’ aspects of the subject. Hardy spoke more for himself, however, in holding that ‘useful’ mathematics had in any case worked more for ill than for good, being preponderantly military in application. He held the total uselessness of his own work in the theory of numbers to be a positive virtue, rather than a matter for apology:

 

No-one has yet discovered any warlike purpose to be served by the theory of numbers or relativity, and it seems very unlikely that anyone will do so for many years.

Hardy’s own near-pacifist convictions stemmed from before the Great War, but no one touched by the Anti-War movements of the 1930s could fail to be unaware of a view that military applications were to be shunned. If Alan had now discovered something like a ‘warlike purpose’ in the play of symbols, he was faced, at least in embryo, with a mathematician’s dilemma. Behind the off-hand, teasing words to his mother, there lay a serious question.

Meanwhile the English students were brightening the Graduate College life with amusements of their own:

 

One of the Commonwealth Fellows, Francis Price (not to be confused with Maurice Pryce …) arranged a hockey match the other day between the Graduate College and Vassar, a women’s college (amer.)/university (engl.) some 130 miles away. He got up a team of which only half had ever played before. We had a couple of practice games and went to Vassar in cars on Sunday. It was raining slightly when we arrived, and what was our horror when we were told the ground was not fit for play. However, we persuaded them to let us play a pseudo-hockey match in their gymn. at wh[ich] we defeated them 11–3. Francis is trying to arrange a return match, which will certainly take place on a field.

The amateurism was deceptive, since Shaun Wylie, the topologist, and Francis Price, the physicist, both from New College, Oxford, were players of a national standard. Alan was hardly in the same class (even if he was not now ‘watching the daisies grow’), but enjoyed the games. Soon they were playing three times a week amongst themselves, and sometimes against local girls’ schools.

The effete English playing a women’s game might well have amazed the native Princeton students, but within the establishment there was a somewhat embarrassing anglophilia, in that all the most stuffy and mannered aspects of the English system were admired. In the summer of 1936, the Princeton chapel had been packed for a memorial service for George V. There was a professor in the Graduate College who harped upon his admiration for the royalty in a way that to educated English ears seemed only vulgar. As for George V’s successor, the revelations of Edward VIII’s Mediterranean cruise and Mrs Simpson created a particular sensation at Princeton. Alan wrote to his mother on 22 November:

 

I am sending you some cuttings about Mrs Simpson as representative sample of what we get over here on this subject. I don’t suppose you have even heard of her, but some days it has been ‘front page stuff’ here.

Indeed, the British newspapers maintained their silence until 1 December, when the bishop of Bradford remarked that the King stood in need of God’s grace, and Baldwin showed his hand. On 3 December, Alan wrote:

 

I am horrified at the way people are trying to interfere with the King’s marriage. It may be that the King should not marry Mrs Simpson, but it is his private concern. I should tolerate no interference by bishops myself, and I don’t see that the King need either.

But the King’s marriage was not a private matter, but one that reflected upon the British state. It was a prophetic episode for Alan, ‘horrified’ at government interference with an individual life. For his class, the horror was rather that the King himself had betrayed King and Country, a logical paradox more upsetting than any that Russell or Gödel had found.

On 11 December the Windsors went into their butterfly life of exile, and the reign of George VI began. Alan wrote that day:

 

I suppose this business of the King’s abdication has come as rather a shock to you. I gather practically nothing was known of Mrs Simpson in England till about ten days ago. I am rather divided in my opinion of the whole matter. At first I was wholly in favour of the King retaining the throne and marrying Mrs Simpson, and if this were the only issue it would still be my opinion. However I have heard tales recently which seem to alter it rather. It appears that the King was extremely lax about state documents, leaving them about and letting Mrs Simpson and friends see them. There had been distressing leakages. Also one or two other things of same character, but this is the one I mind about most. However, I respect David Windsor for his attitude.

Alan’s respect extended to the acquisition of a gramophone record of the abdication speech. He further wrote on 1 January:

 

I am sorry that Edward VIII has been bounced into abdicating. I believe the Government wanted to get rid of him and found Mrs Simpson a good opportunity. Whether they were wise to try to get rid of him is another matter. I respect Edward for his courage. As for the Archbishop of Canterbury I consider his behaviour disgraceful. He waited until Edward was safely out of the way arid then unloaded a whole lot of quite uncalled-for abuse. He didn’t dare do it whilst Edward was King. Further he had no objections to the King having Mrs Simpson as a mistress, but marry her, that wouldn’t do at all. I don’t see how you can say that Edward was guilty of wasting his ministers’ time and wits at a critical moment. It was Baldwin who opened the subject.

The archbishop’s broadcast, of 13 December, had denounced the King for abandoning his duties for a mere ‘craving for private happiness’; the pursuit of happiness had never been accorded a high priority by the British rulers. Alan’s views on marriage and morals were those of a modernist; in a discussion at King’s with his theological contemporary Christopher Stead he had said that people should let their natural feelings take their course – and as for bishops, a class of person particularly dear to Mrs Turing, they epitomised for him the ancien régime. He talked to Venable Martin, his American friend from Church’s logic class, about the ‘very shabby way’ in which the King had been treated.

As for work, on 22 November he wrote to Philip Hall:

 

I have not made any very startling discoveries over here, but I shall probably be publishing two or three small papers: just bits and pieces. One of them will be a proof of Hilbert’s inequality if it really turns out to be new, and another on groups which I did about a year ago and Baer thinks is worth publishing. I shall write these things up and then have another go at the Math[ematical] logic.

I find that ‘Go’ is only played very little here now, but I have had two or three games.

Princeton is suiting me very well. Beyond the way they speak there is only one – no two! – feature[s] of American life which I find really tiresome, the impossibility of getting a bath in the ordinary sense, and their ideas on room temperature.

By ‘the way they speak’, Alan meant such complaints as:4

 

These Americans have various peculiarities in conversation which catch the ear somehow. Whenever you thank them for anything, they say ‘You’re welcome’. I rather liked it at first, thinking I was welcome, but now I find it comes back like a ball thrown against a wall, and become positively apprehensive. Another habit they have is to make the sound described by authors as ‘Aha’. They use it when they have no suitable reply to a remark, but think that silence could be rude.

The proofs of Computable Numbers had been sent to him at Princeton just after he had arrived, so that publication of the paper was imminent. Meanwhile, Alonzo Church had suggested that Alan might be able to give one of the regular seminars, to launch his discovery into the mainstream of Princeton mathematics. On 3 November he had written home:

 

Church has just suggested to me that I should give a lecture to the Mathematical Club here on my Computable Numbers. I hope I shall be able to get an opportunity to do this, as it will bring the thing to people’s attention a bit. I don’t expect the lecture will come off for some time yet.

In fact he only had to wait a month, but then there was a disappointment:

 

There was rather bad attendance at the Maths Club for my lecture on Dec. 2. One should have a reputation if one hopes to be listened to. The week following my lecture G.D. Birkhoff came down. He has a very good reputation and the room was packed. But his lecture wasn’t up to the standard at all. In fact everyone was just laughing about it afterwards.

It was also disappointing that when in January 1937 Computable Numbers at last appeared in print, there was so little reaction. Church reviewed it for the Journal of Symbolic Logic, and thereby put the words ‘Turing machine’ into published form. But only two people asked for offprints: Richard Braithwaite back at King’s and Heinrich Scholz,⁵ the almost lone representative of logic left in Germany, who wrote back saying that he had given a seminar on it at Münster, and begged almost plaintively for two copies of any future papers, explaining how difficult it was for him to keep abreast of developments otherwise. The world was rather less of a single country for mathematics now. Alan wrote home on 22 February:

 

I have had two letters asking for reprints. … They seemed very much interested in the paper. I think possibly it is making a certain amount of impression. I was disappointed by its reception here. I expected Weyl who had done some work connected quite closely with it some years ago, at least to have made a few remarks about it.

He might also have expected John von Neumann to have made a few remarks about it. Here was a truly powerful Wizard playing against Alan’s version of the innocent Dorothy. Like Weyl, he had been very interested in the Hilbert programme and had once hoped to fulfil it, although his active interest in mathematical logic had ended with Gödel’s theorem. He once claimed6 that after 1931 he never read another paper in logic, but this was at most a half-truth, for he was a prodigious reader, working long before anyone else got up in the morning, and covering the whole gamut of mathematical literature. Yet there was not a word about him at this point in Alan’s letters to his mother or Philip Hall.

As for the general readership of the LMS Proceedings, there were a number of reasons why Alan’s paper was unlikely to make an impression upon them. Mathematical logic seemed to be a marginal area of research, which many mathematicians would consider either as tidying up what was obvious anyway, or as creating difficulties where none really existed. The paper started attractively, but soon plunged (in typical Turing manner) into a thicket of obscure German Gothic type in order to develop his instruction tables for the universal machine. The last people to give it a glance would be the applied mathematicians who had to resort to practical computation in some field such as astrophysics or fluid dynamics, where the equations did not allow an explicit solution. There was little encouragement offered to them to do so. Computable Numbers made no concession to practical design, not even for the limited range of logical problems to which the machines were applied in the paper itself. For instance, he had made a convention that the machines should print out the ‘computable numbers’ on alternate squares of the ‘tape’, and use the intervening squares as working space. But it would have been much easier if he had made a more generous allowance of working space. So there was little about his work to attract anyone from outside the narrow circle of mathematical logic – with the possible exception of pure mathematicians who would be interested in the distinction between the computable numbers and the real numbers. It had nothing obvious to do with what Lancelot Hogben called ‘the world’s work’.

There was one person, one of those few who were professionally interested in mathematical logic, who read the paper with a very considerable personal interest. This was Emil Post, a Polish-American mathematician teaching at the City College of New York, who since the early 1920s had anticipated some of Gödel and Turing ideas in unpublished form.7 In October 1936 he had submitted to Church’s Journal of Symbolic Logic a paper⁸ which proposed a way of making precise what was meant by ‘solving a general problem’. It referred specifically to Church’s paper, the one which solved the Hilbert decision problem but required an assertion that any definite method could be expressed as a formula in his lambda-calculus. Post proposed that a definite method would be one which could be written in the form of instructions to a mindless ‘worker’ operating on an infinite line of ‘boxes’, who would be capable only of reading the instructions and

(a) Marking the box he is in (assumed empty),

(b) Erasing the mark in the box he is in (assumed marked),

(c) Moving to the box on his right,

(d) Moving to the box on his left,

(e) Determining whether the box he is in, is or is not marked.

It was a very remarkable fact that Post’s ‘worker’ was to perform exactly the same range of tasks as those of the Turing ‘machine’. And the language coincided with the ‘instruction note’ interpretation that Alan had given. The imagery was perhaps that much more obviously based upon the assembly line. Post’s paper was much less ambitious than Computable Numbers; he did not develop a ‘universal worker’ nor himself deal with the Hilbert decision problem. Nor was there any argument about ‘states of mind’. But he guessed correctly that his formulation would close the conceptual gap that Church had left. In this it was only by a few months that he had been pre-empted by the Turing machine, and Church had to certify that the work had been completely independent. So even if Alan Turing had never been, his idea would soon have come to light in one form or another. It had to. It was the necessary bridge between the world of logic and the world in which people did things.

In another sense, it was that very bridge between the world of logic, and the world of human action, that Alan Turing found so difficult. It was one thing to have ideas, but quite another to impress them upon the world. The processes involved were entirely different. Whether Alan liked it or not, his brain was embodied in a specific academic system, which like any human organization, responded best to those who pulled the strings and made connections. But as his contemporaries observed him, he was in this respect the least ‘political’ person. He rather expected truth to prevail by magic, and found the business of advancing himself, by putting his goods in the shop window, too sordid and trivial to bother with. One of his favourite words was ‘phoney’, which he applied to anyone who had gained some position or rank on what Alan considered an inadequate basis of intellectual authority. It was a word that he applied to the referee of one of the group-theory papers he submitted in the spring, who had made a mistaken criticism of it.

He knew that he ought to make more effort on his own behalf, and he could not help noticing that his friend Maurice Pryce was someone who both had the intellectual ability, and made sure that it was used to its best advantage.

Both of them had come a long way since that week in Trinity in December 1929. Alan had been the first to be elected a Fellow (thanks to King’s looking generously at his dissertation subject). But Maurice had just now been elected a Fellow of Trinity, which was that bit more impressive. And everyone could see that it was he who was the rising star. Their interests had developed in a complementary way, for Maurice had taken up quantum electrodynamics, while keeping up an interest in pure mathematics. But both alike were interested in fundamental problems. They had quite often met at Cambridge lectures, sometimes exchanging notes over tea; it had transpired that the Pryces also lived at Guildford, and Maurice had once been invited to tea at 8 Ennismore Avenue, where Mrs Turing had welcomed him as one of the deserving poor from the grammar school. Alan had visited and admired the laboratory that Maurice had fixed up in the Pryce garage.

At Princeton, Maurice had been supervised in his first year by Pauli, the Austrian quantum physicist, but this year was loosely under the wing of von Neumann. And Maurice knew everyone; everyone knew him. He would be seen at the von Neumanns’ luxuriant parties, spectacles ‘like eighteenth-century operas’, although there were less of these this year, because the von Neumann marriage was in difficulties. And if any of the English graduate students came to know John von Neumann, to find him sociable, exuberant, and a pretended playboy with an encyclopaedic knowledge, then it was Maurice Pryce – and certainly not Alan Turing. But at the other end of the scale, it was also Maurice who knew how to engage the reclusive Hardy in conversation. He could get on with everyone, and indeed it was he who made Alan himself feel welcome in the New World.

King’s had sheltered Alan from the more pushy aspects of academic life, which in America were more noticeable. He fitted no better into the American Dream, of winning through the competition, than into the conservative British idea of life, of playing a programmed part in the system.

But King’s also sheltered him from hard realities in another way. At Cambridge he could joke about it. When Victor visited in May 1936 there had been a small scandal, a certain old Shirburnian being caught with ‘a lady’ in his room and sent down. Alan commented wryly that it was not a sin of which he was guilty. Alan was not a moaner, and tried always to show a sense of humour, but there was nothing particularly funny about the problem that he faced in coming out into the world.

In Back to Methuselah, Bernard Shaw imagined super-intelligent beings of 31,920 A.D. growing out of the concerns of art, science and sex (‘these childish games – this dancing and singing and mating’) and turning away to think about mathematics. (‘They are fascinating, just fascinating. I want to get away from our eternal dancing and music, and just sit down by myself and think about numbers.’) This was all very well for Shaw, for whom mathematics could symbolise intellectual enquiry beyond his reach. But Alan had to think about mathematics at twenty-four, when he had by no means tired of the ‘childish games’. He did not divide his mind into rigidly separate compartments, once saying that he derived a sexual pleasure from mathematics. Then with his new friend Venable Martin, he went to H.P. Robertson’s lectures on relativity in the new year of 1937, and also went canoeing, perhaps in the stream that fed Carnegie Lake. At one point he9 ‘indirectly indicated’ an ‘interest in having a homosexual relation’, but his friend made it clear that he was not interested. Alan never broached the matter again and it did not affect their relationship in other ways.

The New Jersey poet would have understood. But Alan did not see the America of Walt Whitman, only the land of sexual prohibition. The country of Daddy and Mama had adopted homosexuality as a deeply Un-American activity, especially since the twentieth century clean-up had got under way. At Princeton there was no one talking about a ‘pretty normal bisexual male’. Alan was lucky to be rebuffed by so tolerant a person as Venable Martin.

He faced the difficulty that confronted any homosexual person who had successfully resolved the internal psychological conflicts attendant on waking up in a Looking-Glass world. The individual mind was not the whole story; there was also a social reality which was not at all the mirror image of heterosexual institutions. The late 1930s offered him no help in coping with it. Except for those with eyes to see through the stylised heterosexuality of Fred Astaire and Busby Berkeley, the times favoured ever more rigid models of ‘masculine’ and ‘feminine’. There was, all the time, quite another America of cruising blocks and steam baths and late-night bars, but to an Alan Turing this might as well have been on another planet. He was not ready to make the social adaptation that his sexuality, at least outside Cambridge, demanded.

He could reasonably have felt that there was no acceptable adaptation; that this particular mind-body problem had no solution. For the time being his shyness kept him from confronting the harshness of this social reality, and he continued to try to cope at an individual level, making gentle approaches to some of those he met through his work. It was not a great success.

Alan did spend some time in New York at Thanksgiving, but this was because duty called him to accept the invitation of a right-wing cleric who was a friend of Father Underhill,* Mrs Turing’s favourite priest. (‘He is a kind of American Anglo-Catholic. I liked him but found him a bit diehard. He didn’t seem to have much use for President Roosevelt.’) Alan spent his time ‘pottering about Manhattan getting used to their traffic and subways (underground)’ and went to the Planetarium. More relevant, perhaps, to Alan’s emotional state, perhaps, was the holiday at Christmas when Maurice Pryce took him on a skiing trip in New Hampshire for two weeks:

 

He suggested going on the 16th and on the 18th we left. A man called Wannier attached himself to the party at the last moment. Probably just as well; I always quarrel if I go on holiday with one companion. It was charming of Maurice to ask me to join him. He has been very kind to me whilst I have been here. We spent the first few days at a cottage where we were the only guests. Afterwards we moved to a place where there were several Commonwealth Fellows and others of various nationalities. Why we moved I don’t know, but I imagine Maurice wanted more company.

Perhaps Alan wanted Maurice more to himself, for his friend was something of a grown-up Christopher Morcom. They drove back through Boston, where the car broke down, and on their return,

 

Maurice and Francis Price arranged a party with a Treasure Hunt last Sunday. There were 13 clues of various kinds, cryptograms, anagrams, and others completely obscure to me. It was all very ingenious, but I am not much use at them.

One clue was ‘Role of wily Franciscan’, which wittily attracted the party into the bathroom that Francis Price and Shaun Wylie shared, to locate the next clue in the toilet paper. Shaun Wylie himself was amazingly good at anagrams. The treasure hunt bemused the more earnest Americans with its ‘undergraduate humour’, and ‘typical English whimsy’, There were charades and play-readings, in which Alan joined. At lunchtimes they would play chess and Go and another game called Psychology. Tennis began as the snow melted, and the hockey was energetically continued. ‘Virago Delenda Est’, wrote Francis Price on the notice board as they set off for an away match, and some bolder spirit crossed out the first ‘a’. On the playing-fields of Princeton, from which in May 1937 they watched the flames of the Hindenburg illuminate the horizon, the new men rehearsed an Anglo-American alliance.

Alan enjoyed all this, but his social life was a charade. Like any homosexual man, he was living an imitation game, not in the sense of conscious play-acting, but by being accepted as a person that he was not. The others thought they knew him well, as in conventional terms they did; but they did not perceive the difficulty that faced him as an individualist jarring with the reality of the world. He had to find himself as a homosexual in a society doing its best to crush homosexuality out of existence; and less acute, though equally persistent as a problem in his life, he had to fit into an academic system that did not suit his particular line of thought. In both cases, his autonomous self-hood had to be compromised and infringed. These were not problems that could be solved by reason alone, for they arose by virtue of his physical embodiment in the social world. Indeed, there were no solutions, only muddles and accidents.

At the beginning of February 1937 the offprints of Computable Numbers arrived and some he sent out to personal friends. One went to Eperson (who had now left Sherborne for the more suitable Church of England), and one to James Atkins, who had now taken up a career as a schoolmaster, and was teaching mathematics at Walsall Grammar School. James also had a letter10 from Alan which described, in a rather detached way, that he had been feeling depressed and mentioned that he had even thought of a scheme for ending his life. It involved an apple and electrical wiring.

Perhaps this was a case of depression after the triumph; the writing of Computable Numbers would have been like a love affair, now over but for mopping-up operations. Now he had the problem of continuing. Had he killed off the spirit? Was his work a ‘dead end’? He had done something, but what was it for? It was all very well for Bernard Shaw’s Ancients to live on truth alone, but it was asking a great deal of him. Indeed, it was not his ideal. ‘As regards the question of why we have bodies at all, why we do not or cannot live free as spirits and communicate as such, we probably could do so but there would be nothing whatever to do. The body provides something for the spirit to look after and use.’ But what was his body to do, without the loss of innocence, or the compromise of truth?

The months from January to April 1937 were absorbed in writing up a paper on the lambda-calculus, and two on group theory.¹¹ Of these, the logic paper represented a small development of Kleene’s ideas. The first group theory paper was work related to that of Reinhold Baer, the German algebraist now attached to the IAS, which had mostly been done in 1935. But the second was a new departure, which arose through contact with von Neumann. It was a problem suggested by the emigré Polish mathematician S. Ulam, that of asking whether continuous groups could be approximated by finite groups, rather like approximating a sphere by polyhedra. Von Neumann had passed the problem on to Alan, who successfully dealt with it by April, when it was submitted. This was fast work, although as he had shown that continuous groups could not in general be approximated in this way, it was a rather negative result. Nor, he wrote, was he ‘taking these things so seriously as the logic.’

Meanwhile the possibility had arisen of staying at Princeton for a second year. Alan wrote home on 22 February:

 

I went to the Eisenharts regular Sunday tea yesterday and they took me in relays to try and persuade me to stay another year. Mrs. Eisenhart mostly put forward social or semi-moral semi-sociological reasons why it would be a good thing to have a second year. The Dean weighed in with hints that the Procter Fellowship was mine for the asking (this is worth $2000 p.a.) I said I thought King’s would probably prefer that I return, but gave some vague promise that I would sound them on the matter. The people I know here will all be leaving, and I don’t much care about the idea of spending a long summer in this country. I should like to know if you have any opinions on the subject. I think it is most likely I shall come back to England.

Dean Eisenhart was an old-fashioned figure, who in his lectures would apologise for using the modern abstract group, but very kind. He and his wife made noble efforts to entertain the students at their tea-parties. Whatever his parents thought, Philip Hall had sent Alan the notice of vacancies for Cambridge lectureships, and this Alan would much have preferred if he could gain one. A lectureship would in effect mean a permanent home at Cambridge, which was the only possible resolution of his problems in life, as well as being due recognition of his achievements. Alan wrote back to him on 4 April:

 

I am putting in for it, but offering fairly heavy odds against getting it.

He also wrote to his mother, who was just setting off on a pilgrimage to Palestine:

 

Maurice and I are both putting in for it, though I don’t suppose either of us will get it: I think it is a good thing to start putting in for these things early, so as to get one’s existence recognised. It’s a thing I am rather liable to neglect. Maurice is much more conscious of what are the right things to do to help his career. He makes great social efforts with the mathematical big-wigs.

As he forecast, he failed to gain a Cambridge appointment. Ingham wrote from King’s, encouraging him to stay for another year, and this made up his mind. He wrote on 19 May:

 

I have just made up my mind to spend another year here, but I shall be going back to England for most of the summer in accordance with previous programme. Thank you very much for your offer of help with this: I shall not need it, for if I have this Procter as the Dean suggests I shall be a rich man, and otherwise I shall go back to Cambridge. Another year here on the same terms would be rather an extravagance. …

My boat sails June 23. I might possibly do a little travelling here before the boat goes, as there will be very little doing here during the next month and it’s not a fearfully good time of year for work. More likely I shall not as I don’t usually travel for the sake of travelling.

I am sorry Maurice won’t be here next year. He has been very good company.

I am glad the Royal Family are resisting the Cabinet in their attempt to keep Edward VIII’s marriage quiet.

Since he was staying another year, he decided he should take a PhD degree, as Maurice had done. For his thesis, Church had suggested a topic that had come up in his lecture course, relating to the implications of Gödel’s theorem. Alan had written in March that he was ‘working out some new ideas in logic. Not so good as the computable numbers, but quite hopeful.’ These ideas would see him through.

As for the Procter Fellowship, it did indeed fall into his lap. It was for the Vice-Chancellor of Cambridge University to nominate the Fellow, so there were letters of recommendation sent to him. One of these was from the Wizard himself, who wrote:12

June 1, 1937

Sir,

Mr A.M. Turing has informed me that he is applying for a Proctor [sic] Visiting Fellowship to Princeton University from Cambridge for the academic year 1937–1938. I should like to support his application and to inform you that I know Mr Turing very well from previous years: during the last term of 1935, when I was a visiting professor in Cambridge, and during 1936–1937, which year Mr Turing has spent in Princeton, I had opportunity to observe his scientific work. He has done good work in branches of mathematics in which I am interested, namely: theory of almost periodic functions, and theory of continuous groups.

I think that he is a most deserving candidate for the Proctor Fellowship, and I should be very glad if you should find it possible to award one to him.

 

I am, Respectfully, John von Neumann

Von Neumann would have been asked to write the letter, because his name carried such weight. But why did he make no mention of Computable Numbers, a far more substantial piece of work than the papers to which he referred? Had Alan failed to make him aware of it, even after the paper had been printed, and reprints sent round? If Alan had an entrée with von Neumann, the first thing he should have done was to exploit it to help bring Computable Numbers to attention. It would be typical of what was perceived as his lack of worldly sense, if he had been too shy to push his work upon the ‘mathematical bigwig’.

Against Alan’s prediction, and perhaps to his mild chagrin, the redoubtable Maurice Pryce had been appointed to a Cambridge lectureship, as had Ray Lyttleton, the current Procter Fellow. And Alan did after all spend some time in travel, for Maurice Pryce sold him his car, a 1931 V8 Ford, which had taken him all over the continent on the tour that as a Commonwealth Fellow he had been obliged to make in summer 1936. Maurice taught him to drive, which was not an easy task, for Alan was ham-handed and not good with machines. Once he nearly reversed into the Carnegie Lake and drowned them both. Then on about 10 June they took off together for a Turing family visit, which no doubt Mrs Turing had long been urging upon Alan. It was to a cousin on her mocher’s side who had emigrated from Ireland. Jack Crawford now nearly seventy, was the retired Rector of Wakefield, Rhode Island.

The visit was not quite the expected grim chore of conventional politeness, for Alan approved of Jack Crawford, who in his youth had studied at the then Royal College of Science in Dublin:

 

I enjoyed the time I spent at Cousin Jack’s. He is an energetic old bird. He has a little observatory with a telescope that he made for himself. He told me all about the grinding of mirrors.… I think he comes into competition with Aunt Sybil for the Relations Merit Diploma. Cousin Mary is a little bit of a thing you could pick up and put in your pocket. She is very hospitable and rather timid: she worships Cousin Jack.

They were ordinary people, who made Alan feel more at home than did the grand Princeton figures. In their old-fashioned country way, they put Alan and Maurice in the same double bed.

The compartments of life were fractured. Maurice was amazed – he had not had the slightest suspicion. Alan apologised and withdrew at once. Then he blazed out, not with a trace of shame, but with anger, with a story of how his parents had been away in India so long, and of his years in boarding schools. It had all been said before, in The Loom of Youth:

 

Then Jeffries’ wild anger, the anger that had made him so brilliant an athlete, burst out: ‘Unfair? Yes, that’s the right word; it is unfair. Who made me what I am but Fernhurst? … And now Fernhurst, that has made me what I am, turns round and says, “You are not fit to be a member of this great school!” and I have to go. …’

The deeply embarrassing moment brought to light a vein of self-pity that he otherwise never showed, as well as an analysis which he must have known to be facile. It would not do. It was time to look forward, not backward – but to what? How was he to continue? Maurice accepted the explanation, and they never spoke of it again. Alan boarded the Queen Mary on his twenty-fifth birthday, and on 28 June disembarked at Southampton. He missed the Fourth of July softball match at the Graduate College, between the British Empire and the Revolting Colonies.

Back for three months in the mild Cambridge summer of 1937, there were three major projects on hand. First there was some tidying up of Computable Numbers. Bernays, in Zurich, had perhaps rather annoyingly found some errors13 in his proof that the Hilbert decision problem, in its precise form, was unsolvable, and these had to be put right by a correction note in the LMS Proceedings. He also completed a formal demonstration¹⁴ that his own ‘computability’ coincided exactly with Church’s ‘effective calculability’. By now there existed yet a third definition of the same sort of idea. This was the ‘recursive function’, which was a way of making absolutely precise the notion of defining a mathematical function in terms of other more elementary functions; Gödel had suggested it, and it had been taken up by Kleene. It was implicit in Gödel’s proof of the incompleteness of arithmetic. For when Gödel showed that the concept of proof by chess-like rules was an ‘arithmetical’ concept, one as ‘arithmetical’ as finding a highest common factor or something of the kind, he was really saying it could be done by a ‘definite method’. This idea, when formalised and extended somewhat, led to the definition of the ‘recursive function’. And now it had turned out that the general recursive function was exactly equivalent to the computable function. So Church’s lambda-calculus, and Gödel’s way of defining arithmetical functions, both turned out to be equivalent to the Turing machine. Gödel himself later acknowledged¹⁵ the Turing machine construction as the most satisfactory definition of a ‘mechanical procedure’. At the time, it was a very striking and surprising fact, that three independent approaches to the idea of doing something in a definite way, had converged upon equivalent concepts.

The second project concerned the ‘new ideas in logic’ for a doctoral thesis. The basic idea was to see if there was any way in which to escape the force of Gödel’s result that there would always be true but unprovable assertions within arithmetic. This was not a new question, for Rosser, now at Cornell, had produced a paper¹⁶ in March 1937 which took it up. But Alan planned a rather more general attack on the question.

His third project was a very ambitious one, for he had decided to try his strength on the central problem of the theory of numbers. It was not a new interest, for he had possessed Ingham’s book on the subject since 1933. But in 1937 Ingham sent him some recent papers,¹⁷ on learning that he wished to make an attack himself. It was ambitious because the question he chose was one that had long absorbed and defeated the greatest pure mathematicians.

Although the prime numbers were such ordinary things, it was easy to pose quite baffling questions about them in a few words. One question had been solved very early on. Euclid had been able to show that there were infinitely many prime numbers, so that although in 1937 the number 2¹²⁷ – 1 = 170141183460469231731687303715884105727 was the largest known prime, it was also known that they continued for ever. But another property that was easy to guess, but very hard to prove, was that the primes would always thin out, at first almost every other number being prime, but near 100 only one in four, near 1000 only one in seven, and near 10,000,000,000 only one in 23. There had to be a reason for it.18

In about 1793, the fifteen-year-old Gauss noticed that there was a regular pattern to the thinning-out. The spacing of the primes near a number n was proportional to the number of digits in the number n; more precisely, it increased as the natural logarithm of n. Throughout his life Gauss, who apparently liked doing this sort of thing, gave idle leisure hours to identifying all the primes less than three million, verifying his observation as far as he could go.

Little advance was made until 1859, when Riemann developed a new theoretical framework in which to consider the question. It was his discovery that the calculus of the complex numbers^* could be used as a bridge between the fixed, discrete, determinate prime numbers on the one hand, and smooth functions like the logarithm – continuous, averaged-out quantities – on the other. He thereby arrived at a certain formula for the density of the primes, a refinement of the logarithm law that Gauss had noticed. Even so, his formula was not exact, and nor was it proved.

Riemann’s formula ignored certain terms which he was unable to estimate. These error terms were only in 1896 proved to be small enough not to interfere with the main result, which now became the Prime Number Theorem, and which stated in a precise way that the primes thinned out like the logarithm – not just as a matter of observation, but proved to be so for ever and ever. But the story did not end here. As far as the tables went it could be seen that the primes followed this logarithmic law quite amazingly closely. The error terms were not only small compared with the general logarithmic pattern; they were very small. But was this also true for the whole infinite range of numbers, beyond the reach of computation? – and if so what was the reason for it?

Riemann’s work had put this question into a quite different form. He had defined a certain function of the complex numbers, the ‘zeta-function’. It could be shown that the assertion that the error terms remained so very small, was essentially equivalent to the assertion that this Riemann zeta-function took the value zero only at points which all lay on a certain line in the plane. This assertion had become known as the Riemann Hypothesis. Riemann had thought it Very likely’ to be true, and so had many others, but no proof had been discovered. In 1900 Hilbert had made it his Fourth Problem for twentieth century mathematics, and at other times called it ‘the most important in mathematics, absolutely the most important’. Hardy had bitten on it unsuccessfully for thirty years.

This was the central problem of the theory of numbers, but there was a constellation of related questions, one of which Alan picked for his own investigation. The simple assumption that the primes thinned out like the logarithm, without Riemann’s refinements to the formula, seemed always to overestimate the actual number of primes by a certain amount. Common sense, or ‘scientific induction’, based on millions of examples, would suggest that this would always be so, for larger and larger numbers. But in 1914 Hardy’s collaborator J.E. Littlewood had shown that this was not so, for there existed some point where the simple assumption would underestimate the cumulative total of primes. Then in 1933 a Cambridge mathematician, S. Skewes, had shown19 that if the Riemann Hypothesis were true, a crossover point would occur before

which, Hardy commented, was probably the largest number ever to serve any definite purpose in mathematics.^* It could be asked whether this enormous bound might be reduced, or whether one could be found that did not depend upon the truth of the Riemann Hypothesis, and these were the problems that Alan now undertook.

One new departure at Cambridge was his acquaintance with Ludwig Wittgenstein, the philosopher. He would have seen Wittgenstein before at the Moral Science Club, and Wittgenstein (like Bertrand Russell) had received a copy of Computable Numbers. But it was in this summer of 1937 that Alister Watson, the King’s Fellow, introduced them and they met sometimes in the botanical gardens. Watson had written a paper20 on the foundations of mathematics for the Moral Science Club, in which he made use of the Turing machine. Wittgenstein, whose first work had been as an engineer, always liked practical, down-to-earth constructions and would have approved of the way that Alan had made a vague idea so definite. Curiously, the failure of the Hilbert programme had also meant the end of the point of view advanced by Wittgenstein in his first phase, in the Tractatus Logico-Philosophicus, that every well-posed problem could be solved.

Alan probably had a boating holiday – either on the Norfolk Broads, or at Bosham on Chichester Harbour. He also stayed for a while with the Beuttells in London. Although Mr Beuttell in principle espoused liberal causes of feminism and profit-sharing, his own firm was run on strictly autocratic lines, and so was his family. Victor’s younger brother Gerard was studying physics at Imperial College, but his father was extremely annoyed that he spent his time flying model aeroplanes to investigate wind currents, and put a stop to his studies. Alan was furious to hear this, saying that Gerard had a contribution to make to science,²¹ and was doubly upset because he respected his father. He also roared with approval when he heard that Gerard had told his father, in connection with his infringing some petty rule of the family firm, that he would only obey ‘sensible rules’.

It was also in London that Alan met James again for a weekend. They stayed at a rather sordid bed-and-breakfast place near Russell Square. They went to see a film or two and Elmer Rice’s play Judgment Day about the Reichstag fire trial. Alan must have found it a relief to be with someone who did not reject his sexual advances, although it was always clear that James aroused in him neither deep feelings, nor a special physical attraction. The relationship was not able to develop beyond this point. After this weekend, James had almost no further experience for about twelve years. Although Alan was more exploratory, this would be his story too. His life would not change until much water had flowed under the bridge.

On 22 September, Alan met up at Southampton with an American friend from Graduate College, Will Jones. They had arranged to travel back together, and boarded the German liner, the Europa. Will Jones had spent the summer at Oxford, and it was he who chose the German ship, simply because it was faster. A more dutiful anti-fascist than Alan would not have used it, but on the other hand a more conventional person would not have spent the voyage in learning Russian, enjoying the shocked German expressions as he wielded a textbook emblazoned with hammer and sickle.

On the boat, wrote Alan on arrival, he

 

Was very glad to have Will Jones as travelling companion. There didn’t seem to be anyone very interesting on board so Will and I whiled away the time with philosophical discussions, and spent half of one afternoon in trying to find the speed of the boat.

Back at Princeton, Alan and Will Jones spent much time talking together. Will Jones came from the old white South of deepest Mississippi, and had studied philosophy at Oxford. So this was not the stereotyped meeting of Yankee brashness and old world elegance, far from it. Will Jones came from quite another America, just as Alan represented a plain-speaking, pragmatic, liberal England. As a philosopher with a serious interest in science, Will Jones also rose above the usual boundaries of arts and sciences. He was currently writing a dissertation on the claim of Kant that moral categories could be justified even if human actions were as determined as the motions of the planets. He canvassed Alan’s opinion as to whether quantum mechanics had affected the argument – so much the problem to which Alan had addressed himself five or so years before! But now he gave the impression that he had long been happy with the Russellian view, that at some level the world must evolve in a mechanistic way. He was not now very interested in philosophical, as opposed to scientific, discussions of the problem of free will. Perhaps the trace of his former conflict lay in his very vehemence in the materialist direction. ‘I think of people as pink-coloured collections of sense-data,’ he once joked. If only it were so easy! Symbolically, the Research fountain pen that Mrs Morcom had given him in 1932 was lost on the voyage.

Will Jones also had Alan explain to him some of the theory of numbers, and enjoyed the way that Alan did it, showing how from the most simple axioms, all the properties could be precisely derived – an approach quite different from the rote-learning of school mathematics. Alan never talked to Will about his emotional problems, but it might well be that he derived moral support in a much more general way, for Will appreciated in him the embodiment of the moral philosophy of G.E. Moore and Keynes.

Alan and Will had become aquainted through being members of the same circle of friends the previous year, and another of the circle had also returned to Princeton. This was Malcolm MacPhail, a Canadian physicist, who became involved in a sideline that Alan took up.22

 

It was probably in the fall of 1937 that Turing first became alarmed about a possible war with Germany. He was at that time supposedly working hard on his famous thesis but nevertheless found time to take up the subject of cryptanalysis with characteristic vigour. … on this topic we had many discussions. He assumed that words would be replaced by numbers taken from an official code book and messages would be transmitted as numbers in the binary scale. But, to prevent the enemy from deciphering captured messages even if they had the code book, he would multiply the number corresponding to a specific message by a horrendously long but secret number and transmit the product. The length of the secret number was to be determined by the requirement that it should take 100 Germans working eight hours a day on desk calculators 100 years to discover the secret factor by routine search!

Turing actually designed an electric multiplier and built the first three or four stages to see if it could be made to work. For the purpose he needed relay-operated switches which, not being commercially available at that time, he built himself. The Physics Department at Princeton had a small but well equipped machine shop for its graduate students to use, and my small contribution to the project was to lend Turing my key to the shop, which was probably against all the regulations, and show him how to use the lathe, drill, press etc. without chopping off his fingers. And so, he machined and wound the relays; and to our surprise and delight the calculator worked.

Mathematically, this project was not advanced, for it used only multiplication. But although it used no advanced theory, it involved applications of ‘dull and elementary’ mathematics which were by no means well known in 1937.

For one thing, the binary representation of numbers would have seemed a novelty to anyone then engaged in practical computations. Alan had used binary numbers in Computable Numbers. There they brought in no point of principle, but made it possible to represent all the computable numbers as infinite sequences of 0s and 1s alone. In a practical multiplier, however, the advantage of binary numbers was more concrete: it was that the multiplication table then reduced to:

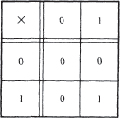
The binary multiplication table being so trivial, the work of a multiplier would be reduced to carrying and adding operations.

A second aspect of his project was its connection with elementary logic. The arithmetical operations with 0s and 1s could be thought of in terms of the logic of propositions. Thus the trivial multiplication table, for instance, could be considered as equivalent to the function of the word AND in logic. For if p and q were propositions, then the following ‘truth-table’ would show in what circumstances ‘p AND q’ was true:

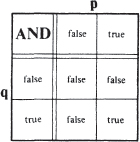
It was the same game, with a different interpretation. All of this would have been entirely familiar to Alan, the calculus of propositions appearing on the first page of any text on logic. It was sometimes called ‘Boolean Algebra’ after George Boole, who had formalised what he optimistically called ‘the laws of thought’ in 1854. Binary arithmetic could all be expressed in terms of Boolean algebra, using AND, OR, and NOT. His problem in designing the multiplier would be to use Boolean algebra to minimise the number of these elementary operations required.

This, as a paper exercise, would be very similar to that of designing a ‘Turing machine’ for the same problem. But in order to embody it in working machinery, it required some means of arranging for different physical ‘configurations’. This was achieved by the switches, for the whole point of a switch would be that it could be in one of two states, ‘on’ or ‘off’, ‘0’ or ‘1’, ‘true’ or ‘false’. The switches that he used were operated by relays, and in this way electricity played its first direct part in his urge to connect logical ideas with something that physically worked. There was nothing new about the electromagnetic relay, which had been invented by the American physicist Henry a hundred years earlier. Its physical principle was the same as that of the electric motor, an electric current, passing through a coil, causing a magnetic head to move. However, the point of a relay was that the magnetic head would either open or close another electrical circuit. It would act as a switch. The name ‘relay’ derived from its use in early telegraph systems, to allow an enfeebled electric signal to set off a fresh, clean click. It was this all-or-nothing logical function of relays that made them necessary by the million in the automatic telephone exchanges proliferating in the United States and Britain alike.

It was not well-known in 1937 that the logical properties of combinations of switches could be represented by Boolean algebra, or by binary arithmetic, but this was not hard for a logician to see. Alan’s task was to embody the logical design of a Turing machine in a network of relay-operated switches. The idea would be that when a number was presented to the machine, presumably by setting up currents at a series of input terminals, the relays would click open and closed, currents would pass through, and emerge at output terminals, thus in effect ‘writing’ the enciphered number. It would not actually use ‘tapes’ but from a logical point of view it came to the same thing. Turing machines were coming to life, for the first stages of his relay multiplier actually worked. Alan’s rather surreptitious access to the physics workshop was, however, symbolic of the problem that he faced in creating that life, by overcoming the line drawn between mathematics and engineering, the logical and the physical.

As a cipher the idea was surprisingly feeble, the more so when set against his claim of a year earlier. Did he not credit the Germans with being able to find the highest common factor of two or more numbers in order to find the ‘secret number’ used as key? Even if some added sophistication removed this loophole, it would still suffer from the crippling practical disadvantage that a single incorrectly transmitted digit would render the entire message indecipherable.

It might be that it was never intended very seriously, and that he had gone off at a tangent in meeting the challenge of designing a binary multiplier. But as a reader of the New Statesman,* sent to him from England, he had no particular reason to be frivolous in speaking of Germany. Every week there were frightening articles about German policy inside and outside the new Reich. Even if the prospect of war work was more the excuse to take up a ‘dull and elementary’ (but fascinating) sideline than anything like the call of duty, he would not have been alone if he found that Nazi Germany had resolved his qualms about ‘morality’.

There was also another machine he had in mind, but this had nothing to do with Germany, except in the very different sense that it came out of the work of Riemann. Its purpose was to calculate the Riemann zeta-function. Apparently he had decided that the Riemann hypothesis was probably false, if only because such great efforts had failed to prove it. Its falsity would mean that the zeta-function did take the value zero at some point which was off the special line, in which case this point could be located by brute force, just by calculating enough values of the zeta-function.

This programme had already been started; indeed Riemann himself had located the first few zeroes and checked that they all lay on the special line. In 1935-6, the Oxford mathematician E.C. Titchmarsh had used the punched-card equipment which was then used for the calculation of astronomical predictions to show that (in a certain precise sense) the first 104 zeroes of the zeta-function did all lie on the line. Alan’s idea was essentially to examine the next few thousand or so in the hope of finding one off the line.

There were two aspects to the problem. Riemann’s zeta-function was defined as the sum of an infinite number of terms, and although this sum could be re-expressed in many different ways, any attempt to evaluate it would in some way involve making an approximation. It was for the mathematician to find a good approximation, and to prove that it was good: that the error involved was sufficiently small. Such work did not involve computation with numbers, but required highly technical work with the calculus of complex numbers. Titchmarsh had employed a certain approximation which – rather romantically – had been exhumed from Riemann’s own papers at Göttingen where it had lain for seventy years. But for extending the calculation to thousands of new zeroes a fresh approximation was required; and this Alan set out to find and to justify.

The second problem, quite different, was the ‘dull and elementary’ one of actually doing the computation, with numbers substituted into the approximate formula, and worked out for thousands of different entries. It so happened that the formula was rather like those which occurred in plotting the positions of the planets, because it was of the form of a sum of circular functions with different frequencies. It was for this reason that Titchmarsh had contrived to have the dull repetitive work of addition, multiplication, and of looking up of entries in cosine tables done by the same punched-card methods that were used in planetary astronomy. But it occurred to Alan that the problem was very similar to another kind of computation which was also done on a large practical scale – that of tide prediction. Tides could also be regarded as the sum of a number of waves of different periods: daily, monthly, yearly oscillations of rise and fall. At Liverpool there was a machine23 which performed the summation automatically, by generating circular motions of the right frequencies and adding them up. It was a simple analogue machine; that is, it created a physical analogue of the mathematical function that had to be calculated. This was a quite different idea from that of the Turing machine, which would work away on a finite, discrete, set of symbols. This tide predicting machine, like a slide rule, depended not on symbols, but on the measurement of lengths. Such a machine, Alan had realised, could be used on the zeta-function calculation, to save the dreary work of adding, multiplying, and looking up of cosines.

Alan must have described this idea to Titchmarsh, for a letter²⁴ from him dated 1 December 1937 approved of this programme of extending the calculation, and mentioned: ‘I have seen the tide-predicting machine at Liverpool, but it did not occur to me to use it in this way.’

There were some diversions. The hockey playing continued, although without Francis Price and Shaun Wylie the team had lost its sparkle. Alan found himself involved in making the arrangements. He also played a good deal of squash. At Thanksgiving he drove north to visit Jack and Mary Crawford for a second time. (‘I am getting more competent with the car.’) Before Christmas, Alan took up an invitation from his friend Venable Martin to go and stay with him. He came from a small town in South Carolina.

 

We drove down from here in two days and then I stayed there for two or three days before I came back to Virginia to stay with Mrs Welbourne. It was quite as far south as I had ever been – about 34°. The people seem to be all very poor down there still, even though it is so long since the civil war.

Mrs Welbourne was ‘a mysterious woman in Virginia’ who had a habit of inviting English students from the Graduate College for Christmas. ‘I didn’t make much conversational progress with any of them,’ Alan had to confess of her family. Alan and Will Jones organised another treasure hunt, although it lacked the élan of the previous year; one of the clues was in his collected Shaw. And in April he and Will made a trip to visit St John’s College, Annapolis, and Washington. ‘We also went and listened to the Senate for a time. They seemed very informal. There were only six or eight of them present and few of them seemed to be attending.’ They looked down from the gallery and saw Jim Farley, Roosevelt’s party boss. It was another world.

The main business of the year was the completion of his PhD thesis,25 investigating whether there was any way of escaping the force of Gödel’s theorem. The fundamental idea was to add further axioms to the system, in such a way that the ‘true but unprovable’ statements could be proved. But arithmetic, looked at in this way, had a distinctly hydra-headed nature. It was easy enough to add an axiom so that one of Gödel’s peculiar statements could be proved. But then Gödel’s theorem could be applied to the enlarged set of axioms, producing yet another ‘true but unprovable’ assertion. It could not be enough to add a finite number of axioms; it was necessary to discuss adding infinitely many.

This was just the beginning, for as mathematicians well knew, there were many possible ways of doing ‘infinitely many’ things in order. Cantor had seen this when investigating the notion of ordering the integers. Suppose, for example, that the integers were ordered in the following way: first all the even numbers, in ascending order, and then all the odd numbers. In a precise sense, this listing of the integers would be ‘twice as long’ as the usual one. It could be made three times as long, or indeed infinitely many times as long, by taking first the even numbers, then remaining multiples of 3, then remaining multiples of 5, then remaining multiples of 7, and so on. Indeed, there was no limit to the ‘length’ of such lists. In the same way, extending the axioms of arithmetic could be done by one infinite list of axioms, or by two, or by infinitely many infinite lists – there was again no limit. The question was whether any of this would overcome the Gödel effect.

Cantor had described his different orderings of the integers by ‘ordinal numbers’, and Alan described his different extensions of the axioms of arithmetic as ‘ordinal logics’. In one sense it was clear that no ‘ordinal logic’ could be ‘complete’, in Hilbert’s technical sense. For if there were infinitely many axioms, they could not all be written out. There would have to be some finite rule for generating them. But in that case, the whole system would still be based on a finite number of rules, so Gödel’s theorem would still apply to show that there were still unprovable assertions.

However, there was a more subtle question. In his ‘ordinal logics’, the rule for generating the axioms was given in terms of substituting an ‘ordinal formula’ into a certain expression. This was itself a ‘mechanical process’. But it was not a ‘mechanical process’ to decide whether a given formula was an ordinal formula. What he asked was whether all the incompleteness of arithmetic could be concentrated in one place, namely into the unsolvable problem of deciding which formulae were ‘ordinal formulae’. If this could be done, then there would be a sense in which arithmetic was complete; everything could be proved from the axioms, although there would be no mechanical way of saying what the axioms were.

He likened the job of deciding whether a formula was an ordinal formula to ‘intuition’. In a ‘complete ordinal logic’, any theorem in arithmetic could be proved by a mixture of mechanical reasoning, and steps of ‘intuition’. In this way, he hoped to bring the Gödel incompleteness under some kind of control. But he regarded his results as disappointingly negative. ‘Complete logics’ did exist, but they suffered from the defect that one could not count the number of ‘intuitive’ steps that were necessary to prove any particular theorem. There was no way of measuring how ‘deep’ a theorem was, in his sense; no way of pinning down exactly what was going on.

One nice touch on the side was his idea of an ‘oracle’ Turing machine, one which would have the property of being able to answer one particular unsolvable problem (like recognising an ordinal formula). This introduced the idea of relative computability, or relative unsolvability, which opened up a new field of enquiry in mathematical logic. Alan might have been thinking of the ‘oracle’ in Back to Methuselah, through whose mouth Bernard Shaw answered the unsolvable problems of the politicians with ‘Go home, poor fool’!

Less clear from his remarks in the paper was to what extent he regarded such ‘intuition’, the ability to recognise a true but unprovable statement, as corresponding to anything in the human mind. He wrote that

 

Mathematical reasoning may be regarded rather schematically as the exercise of a combination of two faculties, which we may call intuition and ingenuity. (We are leaving out of account that most important faculty which distinguishes topics of interest from others; in fact, we are regarding the function of the mathematician as simply to determine the truth or falsity of propositions.) The activity of the intuition consists in making spontaneous judgments which are not the result of conscious trains of reasoning. …

and he claimed that his ideas on ‘ordinal logics’ represented one way of formalising this distinction. But it was not established that ‘intuition’ had anything to do with the incompleteness of finitely defined formal systems. After all, no one knew of this incompleteness until 1931, while intuition was a good deal older. It was the same ambiguity as in Computable Numbers, which mechanised mind, yet pointed out something beyond mechanisation. Did this have a significance for human minds? His views were not clear at this stage.

As for the future, his intention was to return to King’s, provided that, as expected, they renewed his Fellowship which was, in March 1938, at the end of its first three years. On the other hand, his father wrote advising him (not very patriotically, perhaps) to find an appointment in the United States. For some reason King’s College was slow in notifying him that the extension of his fellowship had been made. Alan wrote to Philip Hall on 30 March:

 

I am writing a thesis for a Ph.D, which is proving rather intractable, and I am always rewriting parts of it. …

I am rather worried about the fact that I have heard nothing about re-election to my Fellowship. The most plausible explanation is simply that there has been no re-election, but [I] prefer to think there is some other reason. If you would make some cautious enquiries and send me a postcard I should be very grateful.

I hope Hitler will not have invaded England before I come back.

After the union with Austria on 13 March everyone was beginning to take Germany seriously. Meanwhile, Alan did dutifully go to Eisenhart and ask him ‘about possible jobs over here; mostly for Daddy’s information, as I think it is unlikely I shall take one unless you are actually at war before July. He didn’t know of one at present, but said he would bear it all in mind.’ But then a job materialised. Von Neumann himself offered a research assistant-ship at the IAS.

This might have meant a certain priority being given to von Neumann’s research areas – at that time in the mathematics associated with quantum mechanics and other areas of theoretical physics, and not including logic or the theory of numbers. On the other hand, a position with von Neumann would be the ideal start to the American academic career, which, presumably, Alan’s father thought wise. Competition was intense, and the market, already in depression, was flooded by European exiles. The stamp of approval from von Neumann would carry great weight.

In professional terms, this was a big decision. But all Alan wrote of the opportunity to Philip Hall on 26 April was: ‘Eventually a possibility of a job here turned up’, and to Mrs Turing on 17 May ‘I had an offer of a job here as von Neumann’s assistant at $1500 a year but decided not to take it.’ For he had cabled King’s to check that the fellowship had been renewed, and since it had, the decision was clear.

Despite himself, he had made his name in the Emerald City. It was not entirely necessary to have a reputation in order to be listened to. By this time, von Neumann was aware of Computable Numbers, even if he had not been a year earlier. For when he travelled with Ulam to Europe in this summer of 1938, he proposed26 a game of ‘writing down on a piece of paper as big a number as we could, defining it by a method which indeed has something to do with some schemata of Turing’s.’^* But whatever the attractions, remunerations and compliments, the real issue was much simpler. He wanted to go home to King’s.

The thesis, which in October he had hoped to finish by Christmas, was delayed. ‘Church made a number of suggestions which resulted in the thesis being expanded to an appalling length.’ A clumsy typist himself, he engaged a professional, who in turn made a mess of it. It was eventually submitted on 17 May. There was an oral examination on 31 May, conducted by Church, Lefschetz and H.F. Bohnenblust. ‘The candidate passed an excellent examination, not only in the special field of mathematical logic, but also in other fields.’ There was a quick test in scientific French and German as well. It was vaguely absurd, to be examined in this way while at the same time he was refereeing the PhD thesis of a Cambridge candidate. This, as it happened, he had to reject. (To Philip Hall on 26 April: ‘I hope my remarks don’t encourage the man to go and rewrite the thing. The difficulty with these people is to find out a really good way of being blunt. However I think I’ve given him something to keep him quiet a long time if he really is going to rewrite it.’) The PhD was granted on 21 June. He made little use of the title, which had no application at Cambridge, and which elsewhere was liable to prompt people to retail their ailments.

His departure from the land of Oz was rather different from that in the fable. The Wizard was not a phoney, and had asked him to stay. While Dorothy had disposed of the Wicked Witch of the West, in his case it was the other way round. Though Princeton was fairly secluded from the orthodox, Teutonic side of America, it shared in a kind of conformity that made him ill at ease. And his problems remained unresolved. He was inwardly confident – but as in the Murder in the Cathedral which he saw performed in March (Very much impressed’) he was living and partly living.

In one way, however, he resembled Dorothy. For all the time, there was something that he could do, and which was just waiting for the opportunity to emerge. On 18 July Alan disembarked at Southampton from the Normandie, with the electric multiplier mounted on its breadboard and wrapped up securely with brown paper. ‘Will be seeing you in the middle of July’, he had written to Philip Hall, ‘I also expect to find the back lawn crisscrossed with 8 ft. trenches.’ It had not come to that, but there were more discreet preparations, in which he could take part himself.

Alan was right in thinking that H M Government was concerned with codes and ciphers.* It maintained a department to do the technical work. In 1938 its structure was still a legacy of the Great War, a continuation of the organisation discreetly known as Room 40 that the Admiralty had set up.

After the initial break of a captured German code book, passed to the Admiralty by Russia in 1914, a great variety of wireless and cable signals had been deciphered by a mostly civilian staff, recruited from universities and schools. The arrangement had the peculiar feature that the director, Admiral Hall, enjoyed control over diplomatic messages (for instance the famous Zimmermann telegram). Hall was no stranger to the exercise of power.²⁷ It was he who showed Casement’s diary to the press, and there were more important instances of his²⁸ ‘acting on intelligence independently of other departments in matters of policy that lay beyond the concerns of the Admiralty.’ The organisation survived the armistice, but in 1922 the Foreign Office succeeded in detaching it from the Admiralty. By then it had been renamed as the ‘Government Code and Cypher School’, and was supposed to study²⁹ ‘the methods of cypher communication used by foreign powers’ and to ‘advise on the security of British codes and cyphers.’ It now came technically under the control of the head of the secret service,^† himself nominally responsible to the Foreign Secretary.

The director of GC and CS, Commander Alastair Denniston, was allowed by the Treasury to employ thirty civilian Assistants,³⁰ as the high-level staff were called, and about fifty clerks and typists. For technical civil service reasons, there were fifteen Senior and fifteen Junior Assistants. The Senior Assistants had all served in Room 40, except perhaps Feterlain, an exile from Russia who became head of the Russian section. There was Oliver Strachey, who was brother of Lytton Strachey and husband of Ray Strachey, the well-known feminist, and there was Dillwyn Knox, the classical scholar and Fellow of Kings until the Great War. Strachey and Knox had both been members of the Keynesian circle at its Edwardian peak. The Junior Assistants had been recruited as the department expanded a little in the 1920s; the most recently appointed of them, A.M. Kendrick, had joined in 1932.

The work of GC and CS had played an important part in the politics of the 1920s. Russian intercepts leaked to the press helped to bring down the Labour government in 1924. But in protecting the British Empire from a revived Germany, the Code and Cypher School was less vigorous. There was a good deal of sucess in reading the communications of Italy and Japan, but the official history31 was to describe it as ‘unfortunate’ that ‘despite the growing effort applied at GC and CS to military work after 1936, so little attention was devoted to the German problem.’

One underlying reason for this was economic. Denniston had to plead for an increase in staff to match the military activity in the Mediterranean. In the autumn of 1935, the Treasury allowed an increase of thirteen clerks, although only on a temporary basis of six months at a time. It was a typical communication³² from Denniston to the Treasury in January 1937 that read:

 

The situation in Spain … remains so uncertain that there is an actual increase in traffic to be handled since the height of the Ethiopian crisis, the figures for cables handled during the last three months of 1934, 1935 and 1936 being

1934	10,638
1935	12,696
1936	13,990

 

During the past month the existing staff has only been able to cope with the increase in traffic by working overtime.

During 1937, the Treasury agreed to an increase in the permanent staff. But this measure did not meet a situation in which:³³

 

The volume of German wireless transmissions … was increasing; it was steadily becoming less difficult to intercept them at British stations; yet even in 1939, for lack of sets and operators, by no means all German Service communications were being intercepted. Nor was all intercepted traffic being studied. Until 1937-38 no addition was made to the civilian staff as opposed to the service personnel at GC and CS; and because of the continuing shortage of German intercepts, the eight graduates then recruited were largely absorbed by the same growing burden of Japanese and Italian work that had led to expansion of the Service sections.

It was not simply a question of numbers and budgets, however. This elderly department was failing to rise to the mechanical challenge of the late 1930s. The years after the First World War had been ‘the golden age of modern diplomatic codebreaking’.34 But now the German communications presented GC and CS with a problem beyond their powers – the Enigma machine:³⁵

 

By 1937 it was established that, unlike their Japanese and Italian counterparts, the German Army, the German Navy and probably the Air Force, together with other state organisations like the railways and the SS used, for all except their tactical communications, different versions of the same cypher system – the Enigma machine which had been put on the market in the 1920s but which the Germans had rendered more secure by progressive modifications. In 1937 GC and CS broke into the less modified and less secure model of this machine that was being used by the Germans, the Italians and the Spanish nationalist forces. But apart from this the Enigma still resisted attack, and it seemed likely that it would continue to do so.

The Enigma machine was the central problem that confronted British Intelligence in 1938. But they believed it was unsolvable. Within the existing system, perhaps it was. In particular, this department of classicists, a sort of secret shadow of King’s down in Broadway Buildings, did not include a mathematician.

No addition was made to permanent staff in 1938 to meet this striking deficiency. But³⁶ ‘plans were made to take on some 60 more cryptanalysts in the event of war.’ And this was where Alan Turing came into the story, for he was one of the recruits. He might possibly have been in touch with the government since 1936. Or he might have stepped off the Normandie with the intention of demonstrating his multiplier. But more likely he was suggested to Denniston through one of the elder dons who had worked in Room 40 in the First World War. One of these was Professor Adcock, a Fellow of King’s since 1911. Had Alan ever spoken of codes and ciphers on the King’s High Table, his enthusiasm could quickly have been communicated to GC and CS. One way or another, he was a natural recruit. On his return in the summer of 1938, he was taken on to a course at the GC and CS headquarters.

Alan and his friends could see that war was likely, despite all the hopes of 1933, and found it important to see that they were used in some sensible way, rather than in leading cannon-fodder over the top. It was hard to separate this feeling from that of wanting to avoid injury, and the government’s policy for reserving intellectual talent came as some relief, releasing them from guilt. In this way, Alan Turing made his fateful decision, and chose to begin his long association with the British government. For all his suspicion of ‘HM Government’, it must have been exciting to be allowed to see the back of the shop. But it meant that he had for the first time surrendered a part of his mind, with a promise to keep the government’s secrets.

Though stern and demanding, the government that he joined, like the White Queen who took Alice on her journey, was in a muddled state, struggling with safety pins and string. The failure to make a serious effort at the Enigma was but one aspect of an incoherent strategy, which all the world could see in September 1938. Until that month, British people could still convince themselves that there were logical ‘solutions’ to German ‘grievances’ within the existing framework. After that month, moral debates about fairness and self-determination finally ceased to cloak the essential reality of power. The Cambridge population re-assembled for what was to be ‘the year under the terror’ in the words of Frank Lucas, a King’s don. The White Queen had squealed before the prick of the needle actually came. London children had been evacuated to Newnham College, and the male undergraduates had felt themselves on the brink of enlistment. Nothing was clear, but that something dreadful was in the offing. Radical agitation emphasised the devastating power expected of the modern air raid, while the government seemed to have nothing in mind but the building of bombers to execute a counter-attack.

The old world might be nearing its end, but there was a little escape into fantasy on offer from the new. Snow White and the Seven Dwarfs arrived at Cambridge in October, and Alan played exactly the part expected by Cambridge of King’s dons by going to see it with David Champernowne. He was very taken with the scene where the Wicked Witch dangled an apple on a string into a boiling brew of poison, muttering

 

Dip the apple in the brew
Let the Sleeping Death seep through

He liked to chant the prophetic couplet over and over again.

Alan also invited Shaun Wylie over from Oxford as guest at the college feast. Shaun Wylie and David Champernowne had been fellow scholars at Winchester. Alan had mentioned the multiplying cipher idea to Champ, but he told Shaun about the summer course, saying that he had put his name forward to the authorities as a possible recruit. The Princeton treasure hunts therefore had a serious consequence. He also said that he had been studying probability theory, and would like to experiment with tossing coins, but would feel silly if someone came in, although in King’s he need hardly have worried about appearing eccentric. They also played war games. David Champernowne had ‘Denis Wheatley’s exciting new war game – Invasion’, for which they invented new rules to make it a better game. Maurice Pryce, then in his second year as a university lecturer, had a conversation with Alan about the new idea of uranium fission, and Maurice found an equation for the conditions required for a chain reaction to start.*

Presumably Alan had again applied for a lectureship, but if so he had again been disappointed. However, he had offered to the faculty a course for the spring term on Foundations of Mathematics. (Newman was not giving one this year.) This they accepted,37 awarding the rather nominal £10 fee, as was the custom for mathematically respectable, but not officially commissioned Part III lectures. He was also asked to assess the claims of Friedrich Waismann, the philosopher from the Vienna Circle, exiled in Britain and expelled for misbehaviour from Wittgenstein’s retinue, who wanted to lecture on Foundations of Arithmetic. So Alan had carved out a small niche for himself.

On 13 November 1938, Neville Chamberlain attended the Armistice Day service in the University Church, and a bishop gratifyingly referred to the ‘courage, insight and perseverance of the Prime Minister in his interviews with Herr Hitler that saved the peace of Europe six weeks ago.’ But some Cambridge opinion was more in touch with reality. In King’s, Professor Clapham chaired a committee for the reception of Jewish refugees allowed in by the government after the November wave of violence in Germany. These were events with a particular meaning for Alan’s friend Fred Clayton, who between 1935 and 1937 had spent time studying first in Vienna and then in Dresden, with experiences very different from the jolly hockey-sticks of Princeton.

They meant two very difficult and hurtful things. On the one hand, he was highly conscious of the implications of the Nazi regime. On the other, there were two boys, one the younger son of a Jewish widow living in the same house in Vienna, one at the school where he had taught in Dresden. The November 1938 events had put the Vienna family in great peril, and he received appeals for help from Frau S—. He tried to help her get her sons to England, and this was achieved just before Christmas by the Quakers’ Relief Action. They found themselves in a refugee camp on the coast at Harwich, and wrote to Fred, who soon made a visit. In the dank, freezing, slave-market atmosphere some other young refugees rendered some German and English songs, and the passage from Schiller’s Don Karlos about Elizabeth receiving those fleeing from the Netherlands. Fred was already very fond of Karl, an affection which fatherless Karl returned, and went away to help find someone to foster him.

On hearing this story, Alan’s reaction was wholehearted. One wet Sunday in February 1939 he cycled with Fred to the camp at Harwich. He had conceived the idea of sponsoring a boy who wanted to go to school and university. Most of the boys were only too glad to be free of school for good. Of the very few exceptions, one was Robert Augenfeld – ‘Bob’ from the moment of his arrival in England – who had decided when he was ten that he wanted to be a chemist. He came from a Viennese family of considerable distinction and his father, who had been an aide-de-camp in the First World War, had instructed him to insist he should continue with his education. He had no means of support in England, and Alan agreed to sponsor him. It was impractical, for Alan’s fellowship stipend would run to nothing of the kind, although he had probably saved some of Procter’s money. His father wrote asking ‘Is it wise, people will misunderstand?’ which annoyed Alan, although David Champernowne thought his father had a good point.

But the immediate practical problems were soon solved. Rossall, a public school on the Lancashire coast, had offered to take in a number of refugee boys without fee. Fred’s protégé Karl was going to take a place there, and this was arranged for Bob as well. Bob had to travel up north to be interviewed, where Rossall accepted him with the proviso that he should first improve his English at a preparatory school. On the way he had been looked after by the Friends in Manchester, and they in turn approached a rich, Methodist, mill-owning family to take him in. (Karl was fostered in just the same way.) This settled his future, and although Alan was ultimately responsible for him, and Bob always felt a great debt, he did not have to pay for more than some presents and school kit to help the boy get started. His recklessness had been justified, although it certainly helped that Bob was mentally as tough as Alan, having survived the loss of everything he knew, and being determined to fight for his own future education.

Meanwhile Alan was becoming more closely involved with the problems of GC and CS. At Christmas there was another training session at the headquarters in Broadway. Alan went down and stayed at an hotel in St James’s Square with Patrick Wilkinson, the slightly senior classics don at King’s, who had also been drawn in. Thereafter, every two or three weeks, he would make visits to help with the work. He found himself attached to Dillwyn Knox, the Senior Assistant, and to young Peter Twinn, a physics postgraduate from Oxford, who had joined as a new permanent Junior when a vacancy was advertised in February. Alan would be allowed to take back to King’s some of the work they were doing on the Enigma. He said he ‘sported his oak’ when he studied it, as well he might. It was wise of Denniston not to wait until hostilities opened before letting his reserve force see the problems. But they were getting nowhere. A general knowledge of the Enigma machine was not enough upon which to base an attack.

It would have amazed Mrs Turing, if she had known that her younger son was being entrusted with state secrets. Alan had by this time developed a skilful technique for dealing with his family, and his mother in particular. They all thought of him as devoid of common sense, and he in turn would rise to the role of absent-minded professor. ‘Brilliant but unsound’, that was Alan to his mother, who undertook to keep him in touch with all those important matters of appearance and manners, such as buying a new suit every year (which he never wore), Christmas presents, aunts’ birthdays, and getting his hair cut. She was particularly quick to note and comment on anything that smacked of lower-middle-class manners. Alan tolerated this at home, using his persona as the boy genius to advantage. He avoided confrontation – in the case of religious observance by singing Christmas hymns while he worked over Easter and vice versa, or by referring in conversation to ‘Our Lord’ with a perfectly straight face. He was not exactly telling lies, but successfully avoiding hurt by deception. This was not something he would do for anyone else, but for him, as for most people, the family was the last bastion of deceit.

There was, however, another side to the relationship: Mrs Turing did sense that he had done something incomprehensibly important, and was most impressed by the interest aroused in his work abroad. Once a letter came from Japan! For some reason she was particularly struck by the fact that Scholz was going to mention Alan’s work in the 1939 revision of the German Encyklopädie der mathematischen Wissenschaften.38 It needed such official-sounding reverberations for her to feel that anything had happened. Alan in turn was not above using his mother as a secretary; she sent out some of the reprints of Computable Numbers while he was in America. He also made an effort to explain mathematical logic and complex numbers to her – but with a complete lack of success.

It was in the spring of 1939 that he gave his first Cambridge lecture course. He started with fourteen Part III students, but ‘no doubt the attendance will drop off as the term advances,’ he wrote home. He must have kept at least one, for he had to set questions on his course for the examination in June. One of these asked for a proof of the result of Computable Numbers. It must have been very pleasing to be able to set as an examination problem in 1939, the question that Newman had posed as unanswered only four years before.

But at the same time, Alan joined Wittgenstein’s class on Foundations of Mathematics. Although this had the same title as Alan’s course, it was altogether different. The Turing course was one on the chess game of mathematical logic; extracting the neatest and tightest set of axioms from which to begin, making them flower according to the exact system of rules into the structures of mathematics, and discovering the technical limitations of that procedure. But Wittgenstein’s course was on the philosophy of mathematics; what mathematics really was.

Wittgenstein’s classes were unlike any others; for one thing, the members had to pledge themselves to attend every session. Alan broke the rules and received a verbal rap on the knuckles as a result: he missed the seventh class, very possibly because of his journey to the Clock House where, on 13 February, an entire side chapel of the parish church was dedicated to Christopher, on the ninth anniversary of his death. This particular course extended over thirty-one hours, twice a week for two terms. There were about fifteen in the class, Alister Watson among them, and each had to go first for a private interview with Wittgenstein in his austere Trinity room. These interviews were renowned for their long and impressive silences, for Wittgenstein despised the making of polite conversation to a far more thorough-going degree than did Alan. At Princeton, Alan had told Venable Martin of how Wittgenstein was ‘a very peculiar man’, for after they had talked about some logic, Wittgenstein had said that he would have to go into a nearby room to think over what had been said.

Sharing a brusque, outdoor, spartan, tie-less appearance (though Alan remained faithful to his sports jacket, in contrast to the leather jacket worn by the philosopher), they were rather alike in this intensity and seriousness. Neither one could be defined by official positions (Wittgenstein, then fifty, had just been appointed Professor of Philosophy in succession to G.E. Moore), for they were unique individuals, creating their own mental worlds. They were both interested only in fundamental questions, although they went in different directions. But Wittgenstein was much the more dramatic figure. Born into the Austrian equivalent of the Carnegies, he had given away a family fortune, spent years in village school-teaching, and lived alone for a year in a Norwegian hut. And even if Alan was a son of Empire, the Turing household had precious little in common with the Palais Wittgenstein.

Wittgenstein39 wanted to ask about the relationship of mathematics to ‘words of ordinary everyday language’. What, for instance, did the chess-like ‘proofs’ of pure mathematics, have to do with ‘proof’ as in ‘The proof of Lewy’s guilt is that he was at the scene of his crime with a pistol in his hand’? As Wittgenstein kept saying, the connection was never clear. Principia Mathematica only pushed the problem to another place: it still required people to agree on what it meant to have ‘a proof; it required people to agree what counting and recognising and symbols meant. When Hardy said that 317 was a prime because it was so, what did this mean? Did it only mean that people would always agree if they did their sums right? How did they know what were the ‘right’ rules? Wittgenstein’s technique was to ask questions which brought words like proof, infinite, number, rule, into sentences about real life, and to show that they might make nonsense. As the only working mathematician in the class, Alan tended to be treated as responsible for everything that mathematicians ever said or did, and he rather nobly did his best to defend the abstract constructions of pure mathematics against Wittgenstein’s attack.

In particular, there was an extended argument between them about the whole structure of mathematical logic. Wittgenstein wanted to argue that the business of creating a watertight, automatic logical system had nothing to do with what was ordinarily meant by truth. He fastened upon the feature of any completely logical system, that a single contradiction, and a self-contradiction in particular, would allow the proof of any proposition:

WITTGENSTEIN: … Think of the case of the Liar. It is very queer in a way that this should have puzzled anyone – much more extraordinary than you might think. … Because the thing works like this: if a man says ‘I am lying’ we say that it follows that he is not lying, from which it follows that he is lying and so on. Well, so what? You can go on like that until you are black in the face. Why not? It doesn’t matter. … it is just a useless language-game, and why should anybody be excited?

TURING: What puzzles one is that one usually uses a contradiction as a criterion for having done something wrong. But in this case one cannot find anything done wrong.

WITTGENSTEIN: Yes – and more: nothing has been done wrong. … where will the harm come?

TURING: The real harm will not come in unless there is an application, in which a bridge may fall down or something of that sort.

WITTGENSTEIN: … The question is: Why are people afraid of contradictions? It is easy to understand why they should be afraid of contradictions in orders, descriptions, etc., outside mathematics. The question is: Why should they be afraid of contradictions inside mathematics? Turing says, ‘Because something may go wrong with the application.’ But nothing need go wrong. And if something does go wrong – if the bridge breaks down – then your mistake was of the kind of using a wrong natural law. …

TURING: You cannot be confident about applying your calculus until you know that there is no hidden contradiction in it.

WITTGENSTEIN: There seems to me to be an enormous mistake there. … Suppose I convince Rhees of the paradox of the Liar, and he says, ‘I lie, therefore I do not lie, therefore I lie and I do not lie, therefore we have a contradiction, therefore 2 × 2 = 369.’ Well, we should not call this ‘multiplication’, that is all. …

TURING: Although you do not know that the bridge will fall if there are no contradictions, yet it is almost certain that if there are contradictions it will go wrong somewhere.

WITTGENSTEIN: But nothing has ever gone wrong that way yet. …

But Alan would not be convinced. For any pure mathematician, it would remain the beauty of the subject, that argue as one might about its meaning, the system stood serene, self-consistent, self-contained. Dear love of mathematics! Safe, secure world in which nothing could gó wrong, no trouble arise, no bridges collapse! So different from the world of 1939.

He did not complete his research into the Skewes problem, which was left as an error-strewn manuscript40 and never taken up by him again. But he continued to pursue the more central problem, that of examining the zeroes of the Riemann zeta-function. The theoretical part, that of finding and justifying a new method of calculating the zeta-function, was finished at the beginning of March, and was submitted for publication.⁴¹ This left the computational part to be done. In this respect there had been a development. Malcolm MacPhail had written⁴² in connection with the electric multiplier:

 

How is your University fixed with storage batteries and lathes and so on which you can use for your machine? It’s such a pity that you will have to alter it. Hope you do not find it too much bunched together to be hard to work with. By the way if you are going to have time to work on it this fall and want some help don’t hesitate to ask my brother. I told him about the machine and how it worked. He’s very enthusiastic about your method of drawing wiring diagrams which rather surprised me. You know how conservative and old-fashioned engineers tend to be.

 

It so happened that his brother, Donald MacPhail, was a research student attached to King’s, studying mechanical engineering. The multiplier made no progress, but Donald MacPhail did now join in the zeta-function machine project.

Alan was not the only person to be thinking about mechanical computation in 1939. There were a number of ideas and initiatives, reflecting the growth of new electrical industries. Several projects were on hand in the United States. One of these was the ‘differential analyser’ that the American engineer Vannevar Bush had designed at the Massachusetts Institute of Technology in 1930. This could set up physical analogues of certain differential equations – the class of problem of most interest in physics and engineering. A similar machine had then been built by the British physicist D.R. Hartree out of Meccano components at Manchester University. This in turn had been followed by the commissioning of another differential analyser at Cambridge, where in 1937 the mathematical faculty had sanctioned a new Mathematical Laboratory to house it. One of Alan’s fellow ‘B-stars’ of 1934, the applied mathematician M.V. Wilkes, had been appointed as its junior member of staff.

Such a machine would have been useless for the zeta-function problem. Differential analysers could simulate only one special kind of mathematical system, and that only to a limited and very approximate extent. Similarly the Turing zeta-function machine would be entirely specific to the even more special problem on hand. It had no connection whatever with the Universal Turing Machine. It could hardly have been less universal. On 24 March he applied43 to the Royal Society for a grant to cover the cost of constructing it, and on their questionnaire wrote,

 

Apparatus would be of little permanent value. It could be added to for the purpose of carrying out similar calculations for a wider range of t^* and might be used for some other investigations connected with the zeta-function. I cannot think of any applications that would not be connected with the zeta-function.

Hardy and Titchmarsh were quoted as referees for the application, which won the requested £40. The idea was that although the machine could not perform the required calculation exactly, it could locate the places where the zeta-function took a value near zero, which could then be tackled by a more exact hand computation. Alan reckoned it would reduce the amount of work by a factor of fifty. Perhaps as important, it would be a good deal more fun.

The Liverpool tide-predicting machine made use of a system of strings and pulleys to create an analogue of the mathematical problem of adding a series of waves. The length of the string, as it wrapped itself round the pulleys, would be measured to obtain the total sum required. They started with the same idea for the zeta-function summation, but then changed to a different design. In this, a system of meshing gear wheels would rotate to simulate the circular functions required. The addition was to be done not by measuring length, but weight. There would in fact be thirty wave-like terms to be added, each simulated by the rotation of one gear wheel. Thirty weights were to be attached to the corresponding wheels, at a distance from their centres, and then the moment of the weights would vary in a wave-like way as the wheels rotated. The summation would be performed by balancing the combined effect of the weights by a single counterweight.

The frequencies of the thirty waves required ran through the logarithms of the integers up to 30. To represent these irrational quantities by gear wheels they had to be approximated by fractions. Thus for instance the frequency determined by the logarithm of 3 was represented in the machine by gears giving a ratio of 34 × 31/57 × 35. This required four gear wheels, with 34, 31, 57 and 35 teeth respectively, to move each other so that one of them could act as the generator of the ‘wave’. Some of the wheels could be used two or three times over, so that about 80, rather than 120 gear wheels were required in all. These wheels were ingeniously arranged in meshing groups, and mounted on a central axis in such a way that the turning of a large handle would set them in simultaneous motion. The construction of the machine demanded a great deal of highly accurate gear-cutting to make this possible.

Donald MacPhail drew up a blueprint of the design,44 dated 17 July 1939. But Alan did not leave the engineering work to him. In fact his room, in the summer of 1939, was liable to be found with a sort of jigsaw puzzle of gear wheels across the floor. Kenneth Harrison, now a Fellow, was invited in for a drink and found it in this state. Alan tried and lamentably failed to explain what it was all for. It was certainly far from obvious that the motion of these wheels would say anything about the regularity with which the prime numbers thinned out, in their billions of billions out to infinity. Alan made a start on doing the actual gear-cutting, humping the blanks along to the engineering department in a rucksack, and spurning an offer of help from a research student. Champ lent a hand in grinding some of the wheels, which were kept in a suitcase in Alan’s room, much impressing Bob when he came down from his school at Hale in August.

Kenneth Harrison had been much amazed, for he well knew from conversations with Alan that a pure mathematician worked in a symbolic world and not with things. The machine seemed to be a contradiction. It was particularly remarkable in England, where there existed no tradition of high status academic engineering, as there was in France and Germany and (as with Vannevar Bush) in the United States. Such a foray into the practical world was liable to be met with patronising jokes within the academic world. For Alan Turing personally, the machine was a symptom of something that could not be answered by mathematics alone. He was working within the central problems of classical number theory, and making a contribution to it, but this was not enough. The Turing machine, and the ordinal logics, formalising the workings of the mind; Wittgenstein’s enquiries; the electric multiplier and now this concatenation of gear wheels – they all spoke of making some connection between the abstract and the physical. It was not science, not ‘applied mathematics’, but a sort of applied logic, something that had no name.

By now he had edged a little further up the Cambridge structure, for in July the faculty asked that he should give his lectures on Foundations of Mathematics again in spring 1940, this time for the full fee of £50. In the normal course of events he could have expected fairly soon to be appointed to a university lectureship, and most likely to stay at Cambridge forever, as one of its creative workers in logic, number theory and other branches of pure mathematics. But this was not the direction in which his spirit moved.

Nor was it the direction of history. For there was to be no normal course of events. In March, the remains of Czecho-Slovakia slid into German control. On 31 March, the British government gave its guarantee to Poland, and committed itself to defending east European frontiers, while alienating the Soviet Union, already the world’s second industrial power. It was a device to deter Germany, not to aid Poland, there being no way in which Britain could render assistance to its new ally.

It might have seemed that there was, equally, no way in which Poland could help the United Kingdom. Yet there was. In 1938, the Polish secret service had dropped a hint that they held information on the Enigma. Dillwyn Knox had gone to negotiate for it, but returned empty-handed, complaining that the Poles were stupid and knew nothing. The alliance with Britain and France had changed the position. On 24 July, British and French representatives attended a conference in Warsaw and this time came away with what they wanted.

A month later everything changed again, the Anglo-Polish alliance becoming even more impractical than before. As far as Intelligence was concerned, the year had gained little for Britain. There was now a new wireless interception station at St Albans, replacing the old arrangement whereby the Metropolitan Police did the work at Grove Park. But there was still45 ‘a desperate shortage of receivers for wireless interception’, despite the pleas of GC and CS since 1932. The great exception was the fluke, handed over on a silver platter by the Poles.

The news-stands were announcing the Ribbentrop-Molotov pact as Alan set off from Cambridge for a week’s sailing holiday, together with Fred Clayton and the refugee boys. They went to Bosham, his usual holiday haunt, where he had hired a boat. Several anxieties lay beneath the quiet surface. The boys, who had not been sailing before, thought the two men incompetent, and altered their watches so that they would turn back in good time. ‘The lame leading the blind,’ was what Bob thought of it. Fred, however, was more worried about the emotional undertones of the holiday. Alan teased him a good deal, mocking the idea that after a couple of terms at Rossall a boy would be innocent of sexual experience.*

One day they sailed across to Hayling Island, and went ashore to look at the RAF planes lined up on the airfield. The boys were not very impressed with what they saw. The sun went down and the tide went out, and the boat was stuck in the mud. They had to leave it and wade across to the island to get back by bus, their legs encrusted with thick black mud. Karl said they looked like soldiers in long black boots.

It was at Bosham that King Cnut had shown his advisers that his powers did not extend to stemming the tide. The thin line of aircraft, charged with turning back the bombers, did not that August evening inspire much greater confidence. And who could have guessed that this shambling, graceless yachtsman, squelching bare-legged in the mud and grinning awkwardly at embarrassed Austrian boys, was to help Britannia rule the waves?

For now he would give no 1940 lectures. Nor indeed would he ever return to the safe world of pure mathematics. Donald MacPhail’s design would never be realised, and the brass gear wheels would lie packed away in their case. For other, more powerful wheels were turning: not only Enigma wheels, but tank wheels. The bluff was called, so the deterrent had failed to work. Yet Hitler had miscalculated, for this time British duty would be done. Parliament kept the government to its word, and there would be war with honour.

It was much as Back to Methuselah had prophesied in 1920:

 

And now we are waiting, with monster cannons trained on every city and seaport, and huge aeroplanes ready to spring into the air and drop bombs every one of which will obliterate a whole street, until one of you gentlemen rises in his helplessness to tell us, who are as helpless as himself, that we are at war again.

Yet they were not quite as helpless as they seemed. At eleven o’clock on 3 September, Alan was back at Cambridge, sitting in his room with Bob, when Chamberlain’s voice came over the wireless. His friend Maurice Pryce would soon be giving serious thought to the practical physics of chain reactions. But Alan had committed himself to the other, logical, secret. It would do nothing for Poland. But it would connect him with the world, to a degree surpassing the wildest dream.

* An abstract in French for the scientific journal Comptes Rendus. Mrs Turing helped with the French and the typing.

^* The lambda-calculus represented an elegant and powerful symbolism for mathematical processes of abstraction and generalisation.

^* He became bishop of Bath and Wells in 1937.

^* The ‘complex’ number calculus exemplified the progress of mathematical abstraction. Originally, complex numbers had been introduced to combine ‘real’ numbers with the ‘imaginary’ square root of minus one, and mathematicians had agonised over the question of whether such things really ‘existed’. From the modern point of view, however, complex numbers were simply defined abstractly as pairs of numbers, and pictured as points in a plane. A simple rule for the definition of the ‘multiplication’ of two such pairs was then sufficient to generate an enormous theory. Riemann’s work in the nineteenth century had played a large part in its ‘pure’ development; but it was also found to be of great usefulness in the development of physical theory. Fourier analysis, treating the theory of vibrations, was an example of this. The quantum theory developed since the 1920s went even further in according complex numbers a place in fundamental physical concepts. None of these mathematical ideas are essential to what follows, although such connections between ‘pure’ and ‘applied’ were certainly relevant to a number of aspects of Alan Turing’s later work.

^* 10³⁴ is 10,000,000,000,000,000,000,000,000,000,000,000 – a number comparable with the number of elementary particles in a large building. But 10¹⁰³⁴ is far bigger: as 1 followed by 10³⁴ zeroes it would require books with the mass of Jupiter to print it in decimal notation. It could be thought of as the number of possible man-made objects. Skewes’ number was much bigger again, as 1 followed by 10¹⁰³⁴ zeroes! In actual fact mathematicians had certainly thought about numbers far larger than these, here we have only gone through three stages of growth, but it is not difficult to make up a new notation to express the idea of going through ten such stages, or 10¹⁰, or 10¹⁰; or of regarding even these as just the first step in a process of super-growth, and rhen defining super-super-growth, and then.... Such definitions, indeed,had already played a role in the theory of ‘recursive functions’, one of the other approaches to the idea of ‘definite method’ which had been found equivalent to thet of the Turing machine. But Skewes’ number was certainly remarkably large for a problem which could be expressed in such elementary terms.

^* Certainly one attraction to Alan of the New Statesman would have been its exceptionally demanding puzzle column. In January 1937 he was delighted when his friend David Champernowne defeated such runners-up as M.H.A. Newman and J.D. Bermal in giving a witty solution, phrased in Carrollian language, to a problem set by Eddington called ‘Looking Glass Zoo’. (It depended upon a knowledge of the matrices used by Dirac in his theory of the electron.) But Alan’s comments on the Abdication, naive in idealism perhaps but certainly not ill-informed, indicate very clearly that his interest in the journal would not have been confined to this feature.

^* Ulam writes further that ‘von Neumann had great admiration for him and mentioned his name and “brilliant ideas” to me already, I belive, in early 1939,. ... At any rate von Neumann mantioned to me Turings’s name several times in 1939 in conversations, concerning mechanical ways to develop formal mathematical systems.’

^* In what follows, code refers to any conventional system of communicating text, whether secret or not. Cipher is used for communications designed to be incomprehensible to third parties. Cryptography is the art of writing in cipher; cryptanalysis that of deciphering what has been concealed in cipher. Cryptology covers both the devising and breaking of ciphers. At the time, these distinctions were not made, and Alan Turing himself referred to cryptanalysis as ‘cryptography’.

^†The British spying organisation, variously entitled SIS, M16. Apart from this top-level administrative overlap it was and remained essentially distinct from the cryptanalytic department.

^* David Champernowne also discussed the principle of the chain reaction with Alan after reading an article about it by J.B.S. Haldane in the Daily Worker.

^* that is, for looking at even more zeroes of the zeta-function.

^* Alan was wrong.