5

Running Up

One’s-self I sing, a simple separate person,
Yet utter the word Democratic, the word En-Masse.

Of physiology from top to toe I sing,
Not physiognomy alone nor brain alone is worthy for the Muse,
I say the Form complete is worthier far,
The Female equally with the Male I sing.

Of Life immense in passion, pulse and power,
Cheerful, for freest action form’d under the laws divine,
The Modern Man I sing.

The surrender at Stalingrad had marked the beginning of the end for Germany. The war had turned. Yet in the south and west there was little evidence of progress for the Allies. The African war dragged on, the Luftwaffe still mounted raids on Britain. And the ports were sheltering the survivors of what had been the most damaging convoy battle of the war, fought in mid-Atlantic while Alan had waited in New York.

When Churchill and Roosevelt had conferred at Casablanca, they had good reason to suppose that, with Atlantic U-boat Enigma restored, the sinkings could be kept down to the level of late 1941. In January they were. But in February they had doubled, nearly back to 1942 levels. And then in March they were the worst of the war: ninety-five ships, amounting to three-quarters of a million tons. Massed U-boats had been able to sink twenty-two out of the 125 ships that had set out in convoy on the eastbound Atlantic passage that month. There was a reason for the deteriorating Allied control of events, one scarcely credible. It was not just that the convoys had sailed during the nine days’ blackout caused by the change to the U-boat weather report system. It was that all the time, and to an ever-increasing degree, the convoy routeing cipher, among others, was being broken by the B. Dienst.

Convoy SC. 122 had started out on 5 March, HX.229 on 8 March, and the smaller and more fortunate HX.229A the next day. On 12 March, SC. 122 was re-routed to the north to avoid what was thought to be the position of a U-boat line, the Raubgraf. This signal was intercepted and deciphered. On 13 March the Raubgraf attacked a westward-bound convoy, thus openly betraying its position; SC.122 and HX.229 were both diverted again. Both diversion signals were intercepted and deciphered within four hours. The Raubgraf group could not catch up with SC.122 but 300 miles to the east, the forty-strong Stürmer and Dränger lines were sent to intercept them. There was ill luck on the German side – they were confused as to which convoy was which – but good luck too, for one of the Raubgraf happened to sight HX.229 by chance, and beckoned the others on. In London they could see the two convoys moving into the midst of the U-boat lines – but it was too late to do anything but to have them fight it out. On 17 March, they were surrounded by U-boats, and over the three days that followed twenty-two vessels were sunk, for the loss of one U-boat. Chance had played its part in this particular action, but underlying these and other current engagements lay the systematic failure of Allied communications.

In London and Washington, the first suspicion that this was so had been aroused in February 1943, when it was noticed that three U-boat line diversions were ordered within thirty minutes to operate successfully against a convoy on the 18th. Clear proof came only in mid-May when three doubly-enciphered Enigma messages showed evidence of the decipherment of particular Allied transmissions. Identifiable Enigma information had gone since 1941 into one-time-pad messages, and so had not been directly compromised. But it was implicit in the daily U-boat Situation Report, which by February 1943 was being decrypted. Yet again, the German authorities imputed Allied knowledge to a combination of airborne radar and the treachery of their officers. In a futile gesture, they reduced the number of people allowed to know about U-boat traffic. Again and again, only an a priori faith in the machine prevented them from seeing the truth. The Allies had very nearly given their own game away.

It was a dismal story, not perhaps one of individuals, but of the system. Neither in London nor in Washington was there a section in a position to do the very difficult detailed work of sorting out what the German command must have known, from what it could have known. The cryptanalysts were not given access to Allied dispatches – of which, in any case, there was no complete record. At the OIC they were still understaffed, underequipped, and under great strain with the convoy battles.

The cryptographic and operational authorities were working to standards which to Hut 8 eyes would seem criminally negligent. For one thing, the convoy routeing cipher, introduced as a joint Anglo-American system, was in fact an old British book cipher which the B. Dienst were able to recognise. Although in December 1942 a ‘recipherment of indicators’ had caused a setback for the B. Dienst, every kind of mistake was still being made. According to the American post-mortem:1

 

USN-British Naval Communications were so complex, and often repetitious, that no-one seemed to know how many times a thing might not be sent and by whom – and in what systems. It is possible that the question of cipher compromise might have been settled earlier than May had the Combined Communications system been less obscure and had there been closer cooperation between the British and the US in such matters.

while according to Travis’s German counterpart,²

 

The Admiral at Halifax, Nova Scotia, was a big help to us. He sent out a Daily Situation Report which reached us every evening and it always began ‘Addressees, Situation, Date’, and this repetition of opening style helped us to select very quickly the correct code in use at that time. …

All the time, while minds and technology were being pushed to the limit at Bletchley in the attack on German signals, the most elementary blunders were being made in the defence of their own. The result was that since late 1941, the German successes had been owed not only to the growing numerical strength of the U-boat fleet, but to their knowledge of Allied convoy routes; and during 1942 the effect of the Enigma blackout was only half the story.

Unlike the German authorities, the British were capable of recognising a mistake. The error was not that of the Admiralty alone, for GC and CS had exercised that part of its remit which called it to advise upon cipher security. But it was a part of GC and CS which had been left untouched by the revolutions elsewhere, and whose timescale still ran in terms of years. In 1941 it had devised a new system, which in 1942 the Admiralty had agreed to introduce in June 1943. Even allowing for the fact that it took six months simply to equip the Navy with new tables, this was a story of delays normal in peacetime, but bearing no connection with the new standards applied to anything considered essential for the war. If it were the decipherment of exciting messages, or airborne radar to make German cities visible for night raids, or the atomic bomb, then new industries could be conjured up in months. The less glamorous work of convoy protection called forth no such effort. Although the principle of integration had been applied so powerfully at Bletchley, it had not been extended to match up the two sides of its work.

They had learnt, but it was a painful way to learn, and those who had suffered most were unable to benefit from the lesson. They were at the bottom of the sea. Fifty thousand Allied seamen died in the course of the war, trying to mind their own business in the most gruelling conditions of the western war; 360 in the March 1943 convoy battle alone. Nor were their trials then over; the Merchant Navy cipher system continued to be breakable for the rest of 1943, long after the Navy was protected by the introduction of its new system on 10 June. Peculiarly vulnerable, and given the lowest priority, the merchant shipping ran a danger of which few knew, and whose enormity even fewer could appreciate.

In retrospect the failure of Allied naval communications vindicated the policy urged before the war by Mountbatten, and rejected by the Admiralty, that cipher machines should be employed. After 1943 the Navy joined the other services in an increasing use both of the Typex and of the equivalent American machine. Against these the B. Dienst made no headway. And yet the modernists such as Mountbatten might have been right for the wrong reason. Machine ciphers were not inherently secure, as the Enigma proved. The Foreign Office continued to use a hand system based on books; it remained unbroken. Bletchley deciphered the Italians’ naval machine system; but was increasingly powerless against their book ciphers. What was enciphered on a machine might all the easier be deciphered on a machine. It was not the machine, but the whole human system in which it was embodied, that mattered. Behind the mis-match of Allied cryptanalytic and cryptographic standards there lay another question: were the Typex transmissions really more secure than those of the Enigma? Perhaps the most salient fact was the negative one: that the B. Dienst made no serious effort against them, just as in 1938 no serious effort had been made against the Enigma. If an attack upon the Typex had been made with the resources mobilised at Bletchley, the story might have been very different.3 But perhaps they had no Alan Turing – nor a system in which an Alan Turing could be used.

Such was the background against which Alan returned to base himself in Hut 8. The game had gone sour. The cryptanalysts tended to assume that their productions were being fed into a system that knew what it was doing, and it was a shock when they were told of the convoy cipher fiasco. Hut 8 itself had been taken over by Hugh Alexander during Alan’s absence. There was a story that a form had come round, asking for the name of the head of the section. Alexander had said, ‘Well, I suppose I am,’ and thereafter he remained in smooth control of the naval Enigma. There were no further crises, despite the later proliferation of German naval key-systems. The introduction of an alternative fourth wheel in July 1943 for the U-boat system caused them no problem; they were able to deduce its wiring without a capture. None of this needed Alan any more; indeed several of the high-level analysts were moved to more innovative work on Fish. Nor, indeed, did the U-boat Enigma need the British effort now. Although the British* produced the first working high-speed four-wheel Bombe in June 1943, the Americans produced more and better Bombes after August. By the end of 1943 they had taken over the U-boat work entirely, and had spare capacity for other Enigma problems.

If they did not need Alan Turing on what had become a routine task, his help might well have been of use in the cryptographic context, where 1943 saw a slightly greater degree of cooperation and coordination prevail. He had already been introduced to the job of inspecting speech cipher systems, and to the delicate work of Anglo-American liaison. The Allies now had the problem of recovering from the delays and narrow vision of 1942, at a time when communications were expanding enormously and growing towards their great climax. The times had been out of joint, something they could not afford to allow in the intricate plans for 1944. For Alan Turing this would be dull and dispiriting work compared with the excitement of the relay race; but it was the job crying out for expert attention.4

After June 1943 the Atlantic war turned dramatically in favour of the Allies, with ship sinkings reduced to tolerable levels. In retrospect, March 1943 had seen ‘the crisis’ of the battle of the Atlantic, and thereafter it could be claimed that ‘the U-boat was defeated’. But more truly, 1943 saw a continuing state of crisis, one in which it was not the boat but the system that was beaten from day to day by a superior system. At last they introduced long-range air patrols to cover the mid-Atlantic gap. And the logical advantage held by the U-boats in 1940 had been reversed. They were now visible from afar through the Enigma (by the end of 1943 the British had a clearer idea of where they were than did their own command), and at close range through the airborne radar work of TRE. Meanwhile the convoy communications became secure. The combination was a winning one, and the Atlantic poker game appeared as a quiet front, only noticed when occasionally the cheating failed to work. But from the German point of view it was not a quiet front at all. For them, 1943 saw a tremendous stepping up of the attack. At the end of the year they would have over 400 U-boats to deploy, equipped with elaborate measures to counter the radar detection they believed responsible for all their failure to find convoys. The fleet was still alive and aggressive, even if individual U-boats were increasingly short-lived. It was a game of perfect information – or Sigint, as it became in the new language of 1943 – for one player. But the other did not admit defeat. The Second World War was not a game.

The introduction of the fourth rotor in February 1942 thus had effects unknown in Germany. That it was employed half-heartedly and foolishly, allowing it to be mastered after December 1942, meant the loss of the battle of the Atlantic. But that it had been employed at all meant that it had introduced electronic engineers to Bletchley and hence to the Fish problem. And while 1943 saw a general resolution of Anglo-American friction over Intelligence, by means of an agreement to divide the world between them – Britain taking Europe and America taking Asia – the US Navy retained its more aggressive stance. Their rapid development of Bombes reflected the fact that the Atlantic was now an American sea. Alan Turing’s work had denied the ocean lanes to Germany, and secured them for the United States.

Alan had written to Joan while away in America, asking her what she would like as a present, but in her reply she had not been able to answer this question because of the censorship. In the event he brought back a good quality fountain pen for her – and others too had presents. There were Hershey bars among the sweets he left for general consumption in Hut 8, and he also brought an electric shaver for Bob, making a transformer to convert it from the American to the British voltage. He told Joan how seeing Mary Crawford in January, just after Jack had died, had affected him with a sense of how much they had meant to each other. He hinted that they should ‘try again’, but Joan did not take up the hint; she knew that it was over.

He showed her a book on Go, and lay on the floor in his room at the Crown Inn demonstrating some of the situations in the game. And he also lent her a remarkable new novel. It was by his friend Fred Clayton, though under a pseudonym,5 and had been published in January 1943. The Cloven Pine, as it was called, in a cryptic reference to Ariel’s imprisonment by Sycorax in The Tempest, vented groans about politics and sex which were closer to Fred’s experiences and problems than to Alan’s, Fred having set his plot in the Germany of 1937 and 1938, and drawing upon his complex and conflicting reactions to the Vienna and Dresden of a little earlier.

He had tried to understand the collapse of the ideals of 1933. On one level, he showed German individuals, no less and no more lovable than English individuals. On another, he showed the system, the Nazi system. And while he portrayed himself as the Englishman, asking how Germans could believe such things, he tried to see himself and English attitudes through German eyes. In an internationalist gesture, The Cloven Pine was dedicated jointly to George, his younger brother, and to Wolf, one of the boys in Dresden that he had known. ‘Freedom and consistency of mind’, he had the German boy of his story think to himself, analysing English liberalism, ‘They were illusions! What freedom or consistency was there in this Self, a thing of moods that did not understand one another. …’ It was the conclusion of a King’s liberal, trying hard to comprehend the absolute denial of Self.

There was a second thread to his story, that of the English schoolmaster’s friendship with the German boy which remained ‘suspended in an atmosphere of semi-Platonic sentimentality’. This for Joan represented a quality of self-restraint that deserved admiration, but Alan, who had often teased Fred in terms rather like these, would probably have taken a different view. The book was saved from the obvious danger, one that Evelyn Waugh had mocked in Put Out More Flags, by the stringency and sophistication with which it examined the contradictions. The personal realities were ever questioning, and questioned by, a political background which included the late-1930s Nazi propaganda about boy-corrupting Jews and Catholic clergy. On this level it served Alan as a way of saying that of his ‘tendencies’ could not be separated from his place in society, nor regarded as peripheral to his own freedom and consistency of mind.

Although he had dropped away from the direct cryptanalytic work, Alan remained within the Bletchley fold, and was to be seen in the cafeteria off duty. Conversation at these times often revolved round mathematical and logical puzzles, and Alan was particularly good at taking some quite elementary problem and showing how some point of principle lay behind it – or conversely, illustrating some mathematical argument with an everyday application. It was part of his special concern for connecting the abstract and the concrete, as well as a pleasure in demystifying the higher mathematician’s preserve. It might be wallpaper patterns for an argument about symmetries. His ‘paper tape’ in Computable Numbers had the same flavour, bringing an ‘abstruse branch of logic’ down to earth with a bump.

One person who appreciated this approach was Donald Michie, to whom as a classicist it all came as fresh and new. He became very friendly with Alan, and in 1943 they began to meet every Friday evening in a pub at Stony Stratford, just north of Bletchley itself, to play chess and talk – or more often, for Donald to listen. The Prof’s chess had always been something of a joke at Bletchley, being all the more exposed to invidious comparison when the chess masters arrived. Harry Golombek had been able to give him queen odds, and still win; or when Alan resigned he was able to turn the board round and win from the position given up as hopeless. He complained that Alan had no idea how to make the pieces work together, and it might well be that as in his social behaviour, he was too conscious of what he was trying to do, to play with fluency. As Jack Good saw it, he was too intelligent to accept as obvious the moves that others might make without thinking. He always had to work it out from the beginning. There had been an amusing moment when Alan had come off a night shift (this would have been in late 1941) and then played a game with Harry Golombek in the early morning. Travis had looked in and was embarrassed to find, as he thought, his senior cryptanalyst playing while on duty. ‘Er … er … want to see you about something, Turing,’ he said awkwardly, like the housemaster catching a sixth-former with a cigarette in the toilet. ‘Hope you can beat him,’ he added to Golombek as they left the room, assuming quite wrongly that the master cryptanalyst was the champion player. But young Donald Michie was a player of Alan’s standard.

These meetings were an opportunity for Alan to develop the ideas for chess-playing machines that had begun in his 1941 discussion with Jack Good. They often talked about the mechanisation of thought processes, bringing in the theory of probability and weight of evidence, with which Donald Michie was by now familiar. The development of machines for cryptanalytic work had in any case stimulated discussion as to mathematical problems that could be solved with the mechanical aid – that of finding large prime numbers, for instance, was a topic that came up in lunchtime conversations, rather to the amazement of Flowers, the electronic engineer, who could see no point in it. But Alan’s talk went in rather a different direction. He was not so much concerned with the building of machines designed to carry out this or that complicated task. He was now fascinated with the idea of a machine that could learn. It was a development of his suggestion in Computable Numbers that the states of a machine could be regarded as analogous to ‘states of mind’. If this were so, if a machine could simulate a brain in the way he had discussed with Claude Shannon, then it would have to enjoy the faculty of brains, that of learning new tricks. He was concerned to counter the objection that a machine, however intricate its task, would only be doing what a person had explicitly designed it to do. In these off-duty discussions they spent a good deal of time on what would be said to count as ‘learning’.

Implicit in these discussions was the materialist view that there was no autonomous ‘mind’ or ‘soul’ which used the mechanism of the brain. (He had perhaps hardened his stance as an atheist, and his conversation was more free with anti-God and anti-church jokes than it would have been before the war.) To avoid philosophical discussions about what ‘mind’ or ‘thought’ or ‘free will’ were supposed to be, he favoured the idea of judging a machine’s mental capacity simply by comparing its performance with that of a human being. It was an operational definition of ‘thinking’, rather as Einstein had insisted on operational definitions of time and space in order to liberate his theory from a priori assumptions. This was nothing new – it was an entirely standard line of rationalist thought. Indeed in 1933 he had seen it on the stage, for in Back to Methuselah Shaw had a future scientist produce an artificial ‘automaton’ which could show, or at least imitate, the thought and emotions of twentieth century people. Shaw had the ‘man of science’ assert that he had no way of drawing a line between ‘an automaton and a living organism’. Far from it being a novelty, Shaw was trying to make this argument appear a dated piece of Victoriana. Again, his Natural Wonders book had accepted the rationalist view, with a chapter called ‘Where some of the Animals do their Thinking’ which treated thought, intelligence and learning as differing only in degree as between monocellular animals and human beings. It was no new idea, therefore, when Alan talked in terms of an imitation principle: that if a machine appeared to be doing as well as a human being, then it was doing as well as a human being. But it gave a sharp, constructive edge to their discussions.

Meanwhile Donald Michie had been plucked from the Testery, and Jack Good from Hut 8, to work as Newman’s first staff on a very exciting development of the Fish analysis. Donald Michie had continued to work on refinements of the Turingismus method, reporting informally to Alan on their progress – advances reflected in the fact that at the beginning of 1943 a proportion of the Fish signals were being read regularly and with little delay. The Turing theory of statistics, with its formalisation of ‘likeliness’ and ‘weight of evidence’, and with its ‘sequential analysis’ idea, were also playing a general part in the Fish work, in which it found greater application than in the Enigma methods. But by the spring of 1943, Newman’s ideas for mechanisation had begun to bear fruit. Here the new developments with electronic technology, in which the crucial steps had been taken while Alan was in America, were in themselves very significant.

The Post Office engineers had been able to install a first electronic counting machine in Hut F, where Newman and his two assistants worked, in about April 1943. This and its successors were called the ‘Robinsons’.* Although they had overcome some of the engineering problems associated with passing paper tape very rapidly through an electronic counter, these ‘Robinsons’ still suffered from many defects. They were prone to catch fire; the paper tapes were always breaking; and the counts were unreliable. This was because the slower parts of the counting process were performed by the old relays, and these produced an electrical interference effect upon the electronic components. But the fundamental technological problem was that of synchronising the ingestion of the two separate paper tapes demanded by the method. For all these reasons, the Robinsons proved too unreliable and too slow for effective cryptanalytic use. They were employed only for research purposes. There was also another fundamental difficulty, not so much physical as logical, which made the machine method too slow. In using it for the cryptanalytic process, the operator would constantly have to produce fresh tapes, resorting for this purpose to an⁶ ‘auxiliary machine that was used to produce the tapes which formed one of the two inputs to the Heath Robinson.’

But even before the first Robinson was finished, Flowers had made a revolutionary proposal which both solved the problem of tape synchronisation, and did away with the laborious production of fresh tapes. The idea was to store the Fish key-patterns internally, and in electronic form. If this were done, only one tape would be required. The difficulty lay in the fact that such internal storage would require the more extensive use of electronic valves. It was a suggestion regarded with deep suspicion by the established experts, Keen and Wynn-Williams. But Newman understood and supported Flowers’ initiative.

By any normal standards, this project was a stab in the technological dark. But they were not in normal times, but in the conditions of 1943. What happened next was a development unthinkable even two years before. Flowers simply told Radley, director of the Post Office laboratories, that it was necessary for Bletchley work. Under instructions from Churchill to give Bletchley’s work absolute priority, without questions or delay, Radley had no decision to make, although the development consumed half the resources of his laboratories. Construction began in February 1943 and the machine that Flowers had envisaged was completed after eleven months of night-and-day working. No one but Flowers, Broadhurst and Chandler who together had designed the machine had been permitted to see all the parts, let alone to know what the machine was for. There were no drawings for many of the parts, only the designers’ originals; there were no manuals, no accounts, nor questions asked about materials and labour consumed. In the laboratory the machine was assembled, wired and made to work in separate sections which did not come together until the whole machine was installed and working at Bletchley in December 1943.

In three years, they had caught up with half a century of technological progress. Dillwyn Knox died in February 1943, passing just before the Italian empire he had done a good deal to undermine, and with him the pre-industrial mind. They had been forced into one scientific revolution by the Enigma, and already they were in the throes of a second. The all-electronic machine proved to be much more reliable than the Robinsons, as well as faster. They called it the Colossus, and it demonstrated that the colossal number of 1500 electronic valves, if correctly used, could work together for long periods without error. This was an astonishing fact for those trained in the conventional wisdom. But in 1943 it was possible both to think and do the impossible before breakfast.

Alan knew about all these developments, but declined the invitation to play a direct part.7 Newman built up an increasingly large and powerful group, drawing in the best talent from the other huts and from the mathematical world outside. Alan moved in the opposite direction; he was not a Newman, skilled in overall direction, and still less was he a Blackett, moving in political circles. He had not fought to retain control of naval Enigma, but had retreated before Hugh Alexander’s organising power. If he had been a quite different person, he could now have made his position one of great influence, it being the time for sitting on coordinating committees, Anglo-American committees, future policy committees. But he had no concern for finding a place in anything but scientific research itself. Other scientists were finding the war to be awarding them a power and influence denied in the 1930s, and thrived upon it. For Alan Turing, the war had certainly brought new experiences and ideas, and the chance to do something. But it had given him no taste for organising other people, and it had left his axioms unchanged. A confirmed solitary, he wanted something of his own again.

It would also take more than the Second World War to change his mother’s ideas, which in December 1943 focussed as always upon the duty of choosing Christmas presents. Alan wrote to her⁸ on 23 December:

My dear Mother,

Thank you for your enquiry as to what I should like for Christmas, but really I think we had better have a moratorium this year. I can think of a lot of things I should like which I know to be unobtainable, e.g. a nice chess set to replace the one that was stolen from here while I was away, and which you gave me in 1922 or so: but I know it is useless to try at present. There is an old set here that I can use till the war is over.

I had a week’s leave fairly recently.* Went up to the lakes with Champernowne and stayed in Prof. Pigou’s cottage on Buttermere. I had no idea it was worth while to go amongst the mountains at this time of year, but we had the most marvellous weather, with no rain at all and snow only for a few minutes when we were up on Great Gable. Unfortunately Champernowne caught a chill and retired to bed half-way through. This was in the middle of November, so I don’t think I’ll be taking Christmas leave until February.…

Yours, Alan

But by Christmas 1943, as the Scharnhorst was sunk with Enigma help, Alan had set out on a new project, this time something of his own. He handed over his files on American machinery to Gordon Welchman, who left Hut 6 at this point to take on an overall coordinating role. Welchman had lost interest in mathematics, but found a new life in the study of efficient organisation, and was particularly attracted to American liaison. But Alan, since returning from America, had spent a good deal of time on the devising of a new speech encipherment process. And while other mathematicians might be content to use electronic equipment, or to know about it in general terms, he was determined to build upon his Bell Labs experience and actually create something that worked with his own hands. In late 1943 he became free to devote time to some experiments.

Speech encipherment was not now regarded as an urgent problem. On 23 July 1943, the X-system had been inaugurated for conversations at top level between London and Washington (the extension to the War Room was not completed for another month). The Chiefs of Staff memorandum⁹ of that date stated that ‘The British experts, who were appointed to examine the secrecy [sic] of the equipment, have expressed themselves as completely satisfied’; it also listed the twenty-four British top brass, from Churchill downwards, who were allowed to use it, and the forty Americans, from Roosevelt downwards, whom they might call. This solved the problem of high-level Atlantic communications, although it meant that the British had to go cap in hand to use it, and found themselves outdone by the links to the Philippines and Australia that the Americans were busily installing. Nor did they necessarily want to have all their transmissions recorded by the Americans, the alliance never being so close that the British government confided all to the United States. There was every incentive, from the point of view of future policy, to develop an independent British high-grade speech system. It was Britain, not the United States, that was supposed to be the centre of a world political and commercial system.

But this was not undertaken, and nor did Alan’s new idea have the potential for such a development. The principle he had in mind would be impossible to apply with the variable time-delays and fading experienced with short-wave transatlantic radio transmissions. It would never be the rival of the X-system, which overcame these problems, and this was made clear at the start. It bore the mark of something that he wanted to achieve for himself, rather than of something he had been asked to provide. The war was no longer calling for his original attack on problems, and he found himself almost redundant after 1943. Neither was his idea backed with more than a token share of resources. It was like going back to early, grudging days. To pursue it he had to move to a rather different establishment. While the Bletchley industry continued, with ten thousand people now at work on rolling secrets off the production line, not only deciphering and translating but doing a great deal of the interpretation and appreciation over the heads of the services, Alan Turing gradually transferred himself to nearby Hanslope Park.

While the Government Code and Cypher School had expanded to dimensions quite unimaginable in 1939, the secret service had also mushroomed in a variety of directions. Just before the war, it had recruited Brigadier Richard Gambier-Parry to improve its radio communications. Gambier-Parry, a veteran of the Royal Flying Corps and a genial paternalist to whom junior officers would refer as ‘Pop’, had thereafter spread his wings much further. His first chance had come in May 1941 when the secret service managed to detach from MI5 the Radio Security Service, then responsible for tracking down enemy agents in Britain. It was he who had taken it over. With all such enemy agents soon under control, the role of the RSS had been diverted into that of intercepting enemy agents’ radio transmissions from all over the world. Now known as ‘Special Communications Unit No. 3’, this organisation used a number of large receiving stations centred on the one at Hanslope Park, a large eighteenth century mansion in a remote corner of north Buckinghamshire.

Gambier-Parry had also acquired the responsibility for other aspects of secret service work. These included providing the transmitters for the black broadcasting organisation, which began its ‘Soldatensender Calais’ broadcasts on 24 October 1943. (The studios where journalists and German exiles concocted their ingenious falsities were at Simpson, another Buckinghamshire village.) SCU3 had further taken under its wing the manufacture of the cryptographic system Rockex, which was to be used for top-grade British telegraph signals. Such traffic now amounted to a million words a day to America alone – pre-eminently, of course, carrying Bletchley’s productions. The Rockex represented a technical improvement to the Vernam one-time teleprinter cipher system.

One problem with the Vernam principle was that the cipher-text, regarded as a teleprinter input in the Baudot code, was bound to include many occurrences of the operational or ‘stunt’ symbols, those which produced not letters but ‘line feed’, ‘carriage return’ and so forth. For this reason, the cipher-text could not be handed over to a commercial telegraph company for transmission in Morse, as was often desirable. It was Professor Bayly, the Canadian engineer at Stephenson’s organisation in New York,* who had devised a method of suppressing the unwanted characters and replacing them in such a way that the resulting cipher-text could be printed neatly on a page. This required the development of electronics which could automatically ‘recognise’ the unwanted telegraph symbols. The problem involved logical circuits such as appeared in the Colossus, albeit on a much more modest scale, using electronic switching for Boolean operations applied to the holes of telegraph tape.

Alan’s father, Julius Turing, in about 1907.

On the beach: Alan and his brother John at St Leonard’s in 1917.

On the cliffs: Alan and his mother at St Lunaire, Brittany, in 1921 (see page 10).

Colonel Morcorm, Mr Morcom and Christopher on holiday, summer 1929.

George Maclure, Peter Hogg and Alan setting out on their hike from Godalming, surrey Easter 1931 (see page 58).

Alan Turing in a Guildford street, a chance snapshot taken in 1934.

A brushed-up Alan with his father and mother and a family friend (right) outside 8 Ennismore Avenue in 1938.

Boy and buoys at Bosham, August 1939 (see page 158). From the front: Alan, Bob, Karl and Fred Clayton.

The naval Enigma machine with its lid raised to show the four rotors.

The Colossus in operation at Bletchley Park, 1944–5, showing the rapid punched tape input mechanism.

In Contrast the complete Delilah terminal fitted easily on to a table top (note the scale).

The key unit, with lid removed to show both rotors and multivibrators.

Robin Gandy in Summer 1953, on holiday in France.

A sporting second in a three-mile race: possibly the event of 26 December 1946 (see page 353).

The pilot ACE computer, on show at the NPL in November 1950. Jim Wilkinson is the righthand figure.

The prototype Manchester computer. The six racks shown are essentially those of the ‘baby machine’ which ran its first program in June 1948; by June 1949 when this photograph was taken the machine had roughly doubled in size.

Alan Turing with two Ferranti engineers at the console of the ‘Mark I’ computer at Manchester, 1951.

Alan Mathison Turing on election of Fellowship of the Royal Society, 1951.

By late 1943, the research had been completed. An inventive telegraph engineer, R.J. Griffith, had been borrowed from Cable and Wireless Ltd to do the detailed design. The manufacture was now going ahead at Hanslope Park, where Griffith was also at work on the problem of generating the key-tapes automatically, by using electronic random noise.

Hanslope Park, with its web of connections with secret enterprise and electronic cryptographic work, was therefore a natural place for the Turing speech encipherment project to be based. The Post Office Research Station might have housed it, but it was a great deal further from Bletchley than was Hanslope, which was only ten miles to the north. It was a rather strange place, strange for its very appearance of being an ordinary military station, with all the accoutrements of military ranks and language. Quite different from Bletchley Park, where the military had been obliged to adjust to the young Cambridge intelligentsia, here a service mentality was unaffected by the advent of modern technology. Here there was not a civilian cafeteria but an officers’ mess, where framed in passepartout lay the clue, a quotation from Henry V:

 

The King hath note of all that they intend,

By interception which they dream not of

But in fact Gambier-Parry’s staff were working in a dream war themselves, one in which they knew neither the significance of what they were doing, nor what anyone else did. The newcomer would spend many months before being able to work out that the organisation came under the direction of the secret service.

Alan’s first contact with Hanslope Park came in about September 1943, when he cycled the ten miles from Bletchley to inspect the possibilities. A senior ex-Post Office man, W.H. ‘Jumbo’ Lee, was deputed to look after his requirements. Hanslope was not exactly a model of spit-and-polish smartness; some of its uniformed personnel were ‘real soldiers’ but many were of an unmilitary disposition, transferred straight from the Post Office, Cable and Wireless, and similar organisations. There was, however, a sufficiently military air at Hanslope for a misunderstanding to arise when ‘Jumbo’ Lee introduced Alan to his superior, Major Keen. ‘Dick’ Keen was the top British expert on radio direction-finding, who had written the only textbook on the subject during the First World War, and spent much of the Second on writing a new edition. Alan and ‘Jumbo’ Lee stood together at his door and Keen waved them away, assuming from his appearance that Alan was a cleaner or delivery boy.

Hanslope Park had a precedent for the arrival of a cryptographic project, but whereas Griffith had demanded, and received, a new workshop and adequate staff, Alan simply took what he was given, which was not very much. In fact his project was granted bench-space in a large hut where a number of other research projects were being conducted, and he was offered some mathematical assistance in the form of Mary Wilson, who did direction-finding analysis with Keen. She was a graduate from a Scottish university, and working with Keen had considerably raised the standard from the early days when people said ‘Two fixes are better than three – there is no triangle of error.’ Instead, they were offering to the analysts ellipses on the map which represented the area in which the point of transmission could be asserted to be with such-and-such a probability. But she did not have enough mathematics to understand what Alan wanted when he explained his idea. (He helped her later with the direction-finding work, though expressing a somewhat dim view of her training.) So over the next six months he had to work alone on the project, coming in a couple of days a week, not every week. Two army signalmen were assigned to assemble pieces of electronic equipment under his direction, but that was all.

In mid-March 1944 that there was a distinct change in the Hanslope staffing, with an influx of mathematical and engineering expertise. Such a change was needed. There was, for instance, an occasion when ‘Jumbo’ Lee showed Alan a problem on which they were stuck. It was no more than a trigonometrical series (in connection with aerial design) easily within the grasp of a Cambridge scholarship candidate, but he was most impressed when Alan immediately produced the answer, the more so as Post Office engineers had been laboriously summing it term by term. The authorities had chosen five new young officers, selected from those taking courses at the Army Radio School near Richmond in Surrey. Two of them would take special places in Alan Turing’s life. Indeed, this was a fresh start for him. In 1943, he had met Victor Beuttell over lunch in London, with some of their personal troubles coming out. (Victor had finally rebelled against his father, and joined the RAF.) They would never see each other again; but the personal rapport that thereby lapsed was to be found within new friendships.

The first was Robin Gandy, the undergraduate who in 1940 had stoutly maintained ‘Hands off Finland’ at Patrick Wilkinson’s party in the face of Alan’s quizzical scepticism. His arrival brought to Hanslope a breath of the King’s spirit. He had been conscripted into the ranks in December 1940, with six months on a coastal defence battery, until his mathematical mind had enjoyed more recognition, as he became a radar operator, and then an instructor. After being commissioned into REME, a series of courses, sandwiched with practical experience, had taught him about all the radio and radar equipment used by the British forces.

The second was yet another Donald. This was Donald Bayley, who came from a quite different background, that of Walsall Grammar School (where Alan’s friend James Atkins had taught him mathematics) and Birmingham University, where he had graduated in electrical engineering in 1942. He also had been commissioned into REME and had likewise shot ahead in all the courses.

Both were introduced to the large ‘laboratory’ hut where the research projects were in progress, and found Alan at work there. If civilians from Cambridge were apt to find him unusually careless in appearance, his divergences from respectability were very much more noticeable at military Hanslope. With holes in his sports jacket, shiny grey flannel trousers held up with an ancient tie, and hair sticking out at the back, he became the cartoonist’s ‘boffin’ – an impression accentuated by his manner of practical work, in which he would grunt and swear as solder failed to stick, scratch his head and make a strange squelching noise as he thought to himself, and yelp when shocked by the current that he forgot to turn off before soldering the joints in his ‘bird’s nest’ – so they called it – of electronic valves.

But Robin Gandy was struck in another way on about the first day that he set to work investigating the effectiveness of high-permeability cores in the transformers of the radio receivers. There were two engineers in his section, who started the tedious task of testing the things, when Alan pottered in, and decided that it should all be solved from theoretical principles – in this case, it being an electromagnetic problem, from Maxwell’s equations. These he wrote down at the top of his paper, just as though it were some contrived Tripos question instead of one from real life, and eventually performed a tour de force of partial differential equations to get an answer.

Donald Bayley was impressed in a similar way by the speech encipherment project, which at Hanslope became known as the Delilah. Alan had offered a prize for the best name, and awarded it to Robin for his suggestion of Delilah, the biblical ‘deceiver of men’. It made full use of his experience in cryptanalysis, and as Alan would explain, was designed to meet the basic condition that even if the equipment were compromised, it would still provide complete security. Yet the system he had conceived on board the Empress of Scotland a year earlier was essentially very simple.10 It was a mathematician’s design, and one which had depended upon Alan asking ‘But why not?’

What he had done was to consider the roomful of equipment which made up the X-system, and to ask what were the crucial features which made it into a secure speech cipher. The Vocoder was not essential, although it had been the starting point of the project. Nor was the business of quantising the output amplitudes into a number of discrete levels. By jettisoning these he reduced the number of ideas involved to two: the fact that it sampled the speech at a succession of moments in time, and the fact that it used modular addition, like a one-time pad.

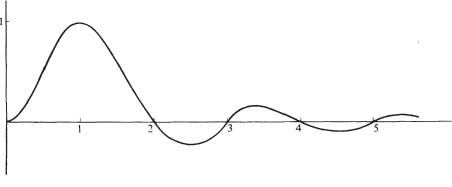
The Delilah was based on these two ideas from the beginning, while in the X-system they had arrived by a back-door route. The point about sampling was that it removed the redundancy of the continuous sound wave. Any sound signal could be represented by a curve such as:

The point was that it would be unnecessary to transmit the whole curve. It would be sufficient to communicate the knowledge of certain points on the curve, provided that the recipient could thereupon perform the exercise of ‘joining the dots’ to reconsitute the curve. This could be done, at least in principle, provided that it was known how sharply the curve was allowed to wiggle in between the points. Since sharp wiggles would correspond to high frequencies, it followed that provided there was a limit on the frequencies contained in the signal, then a sequence of discrete points, or samples, of the curve, taken at regular intervals, would contain all the information of the signal. Since telephone channels did in any case cut off high frequencies, the restriction on allowed ‘wiggling’ of the curve was no real restriction at all, and in fact a rather small number of samples could be shown to suffice to convey the signal.

The idea was well-known to communication engineers. In the X-system, it was the practice to sample each of the twelve 25 Hz channels fifty times a second. These figures were illustration of a general result, that it was necessary to sample at a rate of twice the maximum variation in frequency of the sound, or bandwidth. There was an exact mathematical result to this effect, proved as early as 1915 but which Shannon had re-stated11 and discussed with Alan at Bell Labs. If, for instance, the sound signal were restricted to frequencies less than 2000 Hz, then a sample taken 4000 times a second would be exactly enough to reconstitute the signal. There would be precisely one curve of the stated frequency restriction that passed through all the sampled points. Alan described and proved this result to Don Bayley as the ‘Bandwidth theorem’. His ‘Why not?’ had come in asking why this elegant fact could not be made the pivot on which to turn the whole encipherment process.

The figure of 2000 Hz was in fact the one he intended to use, and his encipherment process would start with the speech signal being sampled 4000 times a second. The Delilah would then have to effect the addition of these sampled speech amplitudes to another stream of key amplitudes. The addition would be done in modular fashion, meaning that while speech sample amplitude of 0.256 units and key amplitude 0.567 units would be added to give 0.823 units, the addition of 0.768 and 0.845 would give 0.613, not 1.613. The result of all this would be a train of sharp ‘spikes’, of heights varying between zero and one unit*:

The next problem was that of how to transmit the information of these ‘spike’ heights to the receiver. In contrast to the X-system, Alan planned no quantisation of amplitudes here. He wanted to transmit them as directly as possible. In principle the ‘spikes’ themselves could be transmitted, but being of such short duration, a few microseconds in fact, they would require a channel which could carry very high frequencies. No telephone circuit could do this. To use a telephone channel the information of the ‘spikes’ would have to be encoded into an audio-frequency signal. Alan’s proposal was to feed each ‘spike’ into a specially devised electronic circuit with an ‘orthogonal’ property. This meant that its response to a spike of unit amplitude would be a wave with unit height after one time interval, and with zero height at every other unit time interval:

Assuming the circuit to be ‘linear’, meaning that the input of a ‘spike’ of say half a unit would produce exactly half of this response, the effect of feeding into it the train of ‘spikes’ would be to ‘join the dots’ in a very precise way. The information of each ‘spike’ would go exactly into the amplitude of the response of this circuit one unit of time later, and nowhere else.

The transmission would then be straightforward, and could be achieved by perfectly standard means; the decipherment process did not require any further new ideas.* Apart from the question of supplying a key-system, this was all that was required for the Delilah to effect an ‘adding-on’ encipherment of speech, the analogy of what agents like Muggeridge, or the machines which produced the Fish signals, or the Rockex, were all alike doing for telegraph or teleprinter. If the key were truly ‘random’, or without any discernible pattern, such a speech cipher system would be as secure as the Vernam one-time cipher for telegraph tape, and on exactly the same argument. From the enemy’s point of view, if all keys were equally probable, then all messages would be equally likely. There would be nothing to go on.^†

The disadvantage of the simple Delilah system, as compared with the X-system, was that its output signal would be one of bandwidth 2000 Hz, rather than a stream of digits, and that it would have to be communicated perfectly, or all would be lost. In particular, any variation in time delay, or distortion in amplitudes, would ruin the decipherment process. Sender and receiver would have to keep in time to the microsecond for the same reason. This was why it could never be used for long-range short-wave transmissions. But it could be used for local short-wave, for VHF and for telephone communication. For tactical or domestic purposes, therefore, it held considerable potential.

Don Bayley was very eager to work on the Delilah, but it was not at first allowed. He was assigned to other tasks, and it only gradually became possible for him to spend time on Alan’s project. It was several months before formal permission was granted for his participation, and even then it was only on the understanding that he would have to do other jobs from time to time.

Alan’s waiting for help coincided with the time when everyone was waiting for the rather more important question of the Second Front. And it was, after all, the enterprise for which all his efforts, fascinating and depressing alike, had helped to secure the conditions. But back at Bletchley Park there was quite a different reason for excitement in Newman’s section. They had shown that even in the time of intricate planning and coordination, there was room for initiative. In fact there had been a scramble at the last minute in the latest development of the treasure hunt. Again it was the fresh generation that had done it, disproving an assumption that something could not be done. It was something they could be proud to tell Alan Turing about.

Using the new electronic Colossus, installed since December, Jack Good and Donald Michie had made the marvellous discovery that by making manual changes while it was in operation, they could do work that hitherto it had been assumed would have to be done by hand methods in the Testery. The discovery meant that in March 1944 an order had been placed with Dollis Hill for six more Colossi by 1 June. This demand could not possibly be met, but with desperate efforts one Mark II Colossus was finished on the night of 31 May, and others followed. The Mark II included technical improvements, was five times faster, and also incorporated 2400 valves. But the essential point was that it incorporated the means for performing automatically the manual changes that Jack Good and Donald Michie had made. The original Colossus, by recognising and counting, was able to produce the best match of a given piece of pattern with the text. The new Colossus, by automating the process of varying the piece of pattern, was able to work out which was the best one to try out. This meant that it performed simple acts of decision which went much further than the ‘yes or no’ of a Bombe. The result of one counting process would determine what the Colossus was to do next. The Bombe was merely supplied with a ‘menu’; the Colossus was provided with a set of instructions.

This greatly extended the role of the machine in bringing Fish to a state of ‘cornucopian abundance’. As with the Bombe, it was not that the Colossus did everything. It was at the centre of an extremely sophisticated and complex theory, in which far from being ‘dull and elementary’, the mathematics involved was by now at the frontiers of research. There were in fact many ways in which the Colossus could be used, exploiting the flexibility offered by its variable instruction table. It took the analysts’ work into a quite new realm of enchantment. In one of the main uses, the human and the machine would work together:12

 

…The analyst would sit at the typewriter output and call out instructions for a Wren to make changes in the programs. Some of the other uses were eventually reduced to decision trees and were handed over to the machine operators.

These ‘decision trees’ were like the ‘trees’ of the mechanical chess-playing schemes. It meant that some of the work of the intelligent analyst had been replaced by the electronic hardware of the Colossi; some went into the devising of instructions for them; some into the ‘decision trees’ that could be left to uncomprehending ‘slaves’; and some retained for the human mind. When off duty, they had talked about the machines playing chess, taking intelligent decisions automatically. In their work, in this new extraordinary phase, the arbitrary dispensations of the German cryptographic system had brought something like this into being – and even more uncanny for those who did it, a sense of dialogue with the machine. The line between the ‘mechanical’ and the ‘intelligent’ was very, very slightly blurred. Whatever its application to the great surprise that awaited the Germans, they were having a wonderful time in seeing the history of the future.

No one at Hanslope, seeing the strange civilian boffin cycling across with a handkerchief around his nose (it was his hay fever period) could have connected him with the success of the assault on Normandy. And by now his part in the necessary conditions for making it was something that lay in the past; the success he wanted was of something truly and more wholly his own. As ten years before, it was his privilege to continue in his own way, with the least waste of energy, the civilisation which demanded harsher sacrifice from others. And it was another kind of invasion that he had in mind, one not yet ready for announcement.

The successful passage of 6 June 1944 roughly coincided with the point at which it became possible for Alan and Don Bayley to get down to work on constructing the Delilah equipment, clearing up the rather messy efforts that the Prof had made on his own. The main task was that of building the circuit to produce the highly accurate ‘orthogonal’ response. It was the design of this circuit that had absorbed most of Alan’s earlier thought and experiment. He had realised that it could be synthesised out of standard components. This was an entirely new idea to Don Bayley, as was the mathematics of Fourier theory* that had been used to attack it. It was a tough problem, which Alan said had involved spending a whole month in working out the roots of a seventh degree equation. Although he was an amateur and self-taught electronic engineer, he was able to tell his new assistant a good deal about the mathematics of circuit design, and for that matter was by now able to show most of them in the laboratory hut a thing or two about electronics. But it needed Don to bring his practical experience to bear on the problem, and to tame the straggly bird’s nest. He also kept beautifully neat notes of their experiments, and generally kept Alan in order.

Alan came in most mornings on his bicycle – sometimes in pouring rain, of which he appeared oblivious. He had been offered the use of an official car to take him to and fro, but declined it, preferring the use of his own motive power. Once, very unusually, he was late in, and even more dishevelled than usual. As explanation he produced a grubby wad of £200 in notes, explaining that he had dug them up out of their hiding-place in a wood and that there were two silver bars still to be recovered.

But late in the summer, as the bridgehead was finally established and the Allied armies swept their way across France, he gave up his lodgings with Mrs Ramshaw at the Crown Inn, and moved to the Officers’ Mess at Hanslope Park. At first he occupied a room on the top floor of the mansion (he had one to himself, enjoying a rather more privileged status than the junior officers), and then later moved into a cottage in the walled kitchen garden, which he shared with Robin Gandy and a large tabby cat. The cat was called Timothy, and had been brought to Hanslope by Robin on his return from staying with friends in London. Alan was well-disposed towards Timothy, even though (or perhaps because) it had a way of launching playful swats at the typewriter keys when he was at work.

As a place to hibernate while they waited for the war to end, Hanslope enjoyed one special advantage. The mess officer was Bernard Walsh, the proprietor of Wheeler’s, the smart oyster restaurant in Soho. As if by magic, fresh eggs and partridges found their way on to the Hanslope dining table, while the rest of Britain chomped its way through Woolton pie and reconstituted egg. These might be supplemented by a rabbit from the copse, or a duck egg from the pond which lay at the bottom of the meadow surrounding the house, and Alan was also able to have the apple that as a rule he would always eat before going to bed. He would go out for walks or runs round the fields, and might be seen thoughtfully chewing on leaves of grass as he loped along, or perhaps burrowing around for mushrooms. During the year, a timely Penguin guide13 to edible and inedible fungi had appeared, of which he made use to bring back amazing specimens for Mrs Lee (who organised the day-to-day catering) to cook for him. He particularly relished the name of the most poisonous of all, the Death Cap or Amanita phalloides. He would roll the name off his tongue with glee, and they would all search for it, but they never found a specimen.

Once of an evening he went out for a run and managed to break his ankle by slipping on a slime-covered brick which formed part of the garden path, just as he was getting into his stride. He had to be sent off in an ambulance to have it set in hospital. But at other times the Prof delighted everyone by winning the sports day race, and by defeating the young Alan Wesley (another of the March intake) who rashly challenged him to a circuit of the large field. He was accepted (with due respect to his differences) as one of a crowd of junior officers. At lunchtimes, they would gather in the mess, and look at the newspapers: the Daily Mirror first, for the comic strip Jane. Don Bayley, who was very keen on military matters, might tell them about the developing strategy of the eastward moving armies, while Alan might hold forth on some topic of a scientific or technical flavour, such as why water was opaque to electromagnetic radiation of the radar wavelength, or how a rocket could accelerate its own fuel quickly enough. They would sometimes go for lunchtime walks together, Timothy the cat accompanying them. Robin Gandy was learning Russian – not because of his earlier membership of the Communist party (which had lapsed in 1940), but because of his admiration for the Russian classics. Robin still considered himself a fellow-traveller, and in this respect 1941 had not changed Alan’s view that he was quite misguided. But there was little discussion of politics at Hanslope, where the prevailing attitude was that of doing the job without asking questions.

Every month or so there was a Mess Night at which dress uniform, or in Alan’s case a dinner jacket, would be required, and at which pheasant might be on the menu. This he would enjoy, for although generally so austere he liked to live it up occasionally, dancing vigorously with the ladies of the ATS afterwards. There was plenty of social gossip and intrigue, which Alan rather liked hearing about, and discussing with Mrs Lee and Mary Wilson. Sometimes his own rather glamorous position as the mysterious Prof, coupled with his unthreatening friendly way with the women members of staff, aroused a mild jealousy. In this respect, he kept his own secret.

It was the first time in his life that he had mixed with ordinary people for any length of time, people picked out neither by social class nor by a special kind of intellect. It was a typical Turing irony that this should happen at an establishment working for the secret service. He liked its unpretentiousness, and perhaps the escape from the intellectual pressure at Bletchley. He certainly had the pleasure of being a large fish in a small pond. This liking was reciprocated. There was an occasion when he was invited to a drinking-party organised by the Other Ranks. For some reason it did not come off, but he was still very pleased: partly at breaching social class barriers, but surely also because of the allure, felt almost inescapably by a homosexual of his background, of that vast unknown England of working-class men.

In the evenings most of the officers would play billiards or drink in the bar, and sometimes Alan did too. But Donald Bayley, Robin Gandy and Alan Wesley had the idea of doing something more mind-improving, and asked Alan to give a course of lectures on mathematical methods. They found a place upstairs in the mansion, which in the winter of 1944 was a singularly cold classroom, and retired thither, somewhat to the amazement of the less zealous. Alan wrote out notes, which the others would copy, mainly on Fourier analysis and related material using the calculus of complex numbers. He illustrated his discussion of the idea of ‘convolution’ – the blurring or spreading out of one function in a way defined by some other function – with the example of a mushroom fairy ring.

It was not only the mushroom which currently reflected his interest in biological form; on his return from runs he would often show examples of the Fibonacci numbers to Don Bayley, producing fir cones as he had in 1941. He was still sure there had to be a reason for it. And he found time for mathematical study of his own, taking up von Neumann’s Mathematical Foundations of Quantum Mechanics again. In the evening there might also be chess, or card games, which he enjoyed, although these also brought out his most childish side in which – just as when a little boy – if he thought that someone else had cheated or changed the rules, he would storm out and slam the door. Such behaviour also typified his dealings with authority, which he still naively expected to maintain literal truth-telling and constancy of policy.

It was like the last two terms at school, staying on after having won a scholarship, without any clear function but accorded a gratifying respect. In August 1944, at about the same time as he came to live at the Hanslope mess, a small extension was built on to the large laboratory hut, and one of the four ten-foot by eight-foot rooms in it was allocated for work on Delilah. This gave him a more self-contained world in which to experiment, read, and think for the future. It was an odd position for ‘the top cryptanalyst in England’, waiting for his opponent to concede the game now dragging on and on. The Delilah project made more sense now that he had a qualified engineer to sort it out, but even this had been something of an accident. Don Bayley had not been assigned to it, but had been obliged to enveigle his way into participation, and there were always pressures on him to forsake it for other duties. Alan was irritated when this happened and would sometimes help in getting them out of the way.

Once, for instance, his advice was sought on the question of whether the ‘wide-band’ amplifiers, used in the process of distributing signals from a single large aerial to several different receivers, were introducing an element of noise into the system. He devised some experiments for testing them and did a little theoretical analysis. For this there was an outing to Cambridge, to search for appropriate literature on thermal noise. They had the privilege of an official car, and Don Bayley was rather pleased at being able to make a first visit to Cambridge. Before they went, Alan told the others not to call him ‘Prof’ while they were there.

Alan certainly enjoyed working together with his assistant in this way, but it meant being involved in what was very small stuff compared with his role in naval Enigma, or in Anglo-American liaison. Don knew that he had worked in cryptanalysis, and had been to America, but virtually nothing else. Alan did not supply any more to go on, and it was particularly striking at Hanslope, where with most people a few leading questions and a suggestion of already knowing more than was really the case would usually prise out further details. This method did not work with the Prof.* It was not simply the government’s secrets that he protected with a uniquely rigid silence, but all personal confidences too. He treated all promises with a perhaps rather annoying literalness, as sacrosanct pieces of his own mind. (He often complained of politicians that they never kept their promises.) It left his colleague very puzzled as to his status. Alan showed himself slightly put out when after a short while he was taken to be one of the SCU3 staff, and made it clear he considered himself something rather better. But he had no discernible superior to whom to report, and no one ever came to see the progress of the Delilah.

There were a few social visits by his Bletchley colleagues, and evidence of one piece of Bletchley work on which he was consulted. This was to do with the design of a new Enigma-type machine which Gordon Welchman was currently organising. It was to encipher Baudot-code messages, and so had rotors with thirty-two rather than twenty-six contacts. This he also described to Shaun Wylie, explaining how he had been shown the proposed machine and complained that it had a period of only 32 × 32 × 32. Meeting resistance, he had embarked on cranking through the settings by hand, only to discover that it was even worse – the period was only 32 × 32. His algebraic work on this problem stimulated some pure-mathematical offshoots which he kept for himself.14

There was some cryptographic consultation at Hanslope too, perhaps more typical of the work he had been doing since returning from America. He was asked to check that the Rockex key-tapes that were being generated by electronic noise were, in fact, sufficiently random. Unprotected by the buffer of a Hut 4 or a Hugh Alexander in such dealings with the military, there were often failures of communication. Speaking too technically about ‘the imaginary part of the error’, he found the top brass had stopped listening. What he perceived as incompetence and stupidity would often send him into a black mood. In that case he would often take off for a run round the large field at the south of the Hanslope Park mansion to work off his feelings.

There was another issue which created argument and frustration, this time in the Delilah hut itself. Alan suddenly dropped into the conversation, with apparent casualness, the fact that he was a homosexual. His young Midlands assistant was both amazed and profoundly upset. He had heard mention of homosexuality only through jokes at school (which he was not the sort of person to find amusing) and through the vague allusions to ‘grave charges’ employed by the popular Sunday newspapers reporting court cases. It was not only what Alan told him that he found repellent, but the unapologetic attitude.

But it was the attitude of a Cambridge background that was as different from Don Bayley’s as mathematics from engineering. Alan’s assistant had equally firm, clear views, and said rather sharply that he had never before met anyone who not only admitted to what he considered at best distasteful A few lines from Alan Turing’s attack on the problem of designing rotor wirings, showing his use of group theory. The extract might be thought to show also the influence of Timothy the cat on his work, but in fact this was typical of his typewriting standard. and at worst disgusting propensities, but who seemed to think it perfectly natural and almost to be proud of it. Alan in turn was upset and disappointed by this reaction, which he described as only too typical of society at large. But this was, perhaps, one of the very few times that he had ever directly sampled the opinions of society at large. The reality, whether he liked it or not, was that most ordinary people would think of his feelings as alien and nauseating. His own attitudes having hardened since before the war – perhaps since breaking the engagement, but surely also because of increased confidence in himself after the work he had done – he did not drop the subject in embarrassment, but continued to argue in such a way that the exchange became quite heated. The progress of the Delilah was jeopardised.

Alan had ridden roughshod over fundamental differences. But he managed to overcome the difficulties in a way that did not mean either of them backing down. Don Bayley was able to cope by regarding it as another Turing eccentricity, and by weighing it against the advantage of working on such high-level ideas with a person whom in other ways he had come to like, and thought he knew quite well. So the Delilah survived the revelation. By the end of 1944, the equipment which did the sampling of the speech signal, and which processed the enciphered samples, was finished. They had proved it to work satisfactorily by setting up both a transmitting and a receiving end within the laboratory, and feeding both with an identical ‘key’, in the form of random noise from a radio receiver working with its aerial removed. It remained to design and build a system for feeding identical key to terminals that would in practice be far apart.

In principle the Delilah could have used a one-time key recorded on gramophone records as the X-system did, analogous to the ‘one-time pad’ for telegraph transmissions. But Alan had chosen to devise a system which, though as good as ‘one-time’, would not require the shipping of thousands of tapes or records, but would instead allow sender and receiver to generate the identical key simultaneously at the time of transmission.

It was in this aspect of the Delilah that his cryptanalytic experience came into play. The work they had done so far constituted the mechanism for ‘adding on’ to speech. The crucial question of what to add was the one on which he had spent much of his time since 1938. In this he could act as the mathematical Cambridge and Bletchley figure, rather than someone who had joined in, somewhat awkwardly and embarrassingly, with the expanding world of electronic engineering.

Although he could not say, nor even hint, the task amounted to creating something like the Fish key generator. It had to be deterministic, for otherwise it could not be produced identically at two independent ends. But it had to be sufficiently devoid of pattern or repetition, to be as secure as something truly ‘random’, such as electronic noise. Any kind of mechanism would, inevitably, have some pattern to it; the job was to make sure that it was one that the enemy cryptanalyst could not possibly detect. So in doing this for the Delilah, he was finally scoring off the half-hearted efforts of German cryptography. In fact, he was doing very much better, for the Delilah key would have to be supplied in sequences of hundreds of thousands of numbers. It was like enciphering not telegraph messages, but War and Peace.

The idea of generating a key for speech encipherment in this way was not entirely new. The X-system was not always used with one-time gramophone records for the key. There was an alternative, called ‘the threshing machine’. But this only had to produce a stream of digits at a rate of 300 a second, and was only used for testing or for low-status signals. The Delilah was much more demanding.

The generator had to be electronic, and the basic unit he used was the ‘multivibrator’ – a pair of valves possessing the property of locking into an oscillation between ‘on’ and ‘off, with a length which would be some integral multiple of a basic period. His key generator made use of the outputs of eight such multivibrators, each locked into a different mode of oscillation. But that was just the beginning. These outputs were fed into several circuits with non-linear elements, which combined them in a complicated way. He had worked out a circuit design which ensured that the energy of the output would be spread as evenly as possible over the whole frequency range, and he explained to Donald Bayley with the aid of Fourier theory that this would endow the amplitude of the resulting output with the necessary degree of ‘randomness’ for cryptographic security.

There had to be some variability in the circuits, or else the generator would produce the same noise over and over again. This was allowed for by making the interconnections required for the combination of the eight multivibrator outputs to pass through the wirings rather like those of an Enigma, with rotors and a plugboard. So a setting of this ‘Enigma’ would serve to define a particular sequence of key, in a way that both sender and receiver could agree upon in advance. With the rotors fixed in position, the key would not repeat itself for about seven minutes. In practical operation, speech in one direction of transmission could be limited to this time and a new key sequence started off on reversing the direction of transmission. This could be done simply by stepping on the rotors. There were enough rotor and plugboard positions for the resulting system to be as safe – according to his theory – as a genuinely random one-time key.

Getting the Delilah system to work as a whole was a job which pushed their resources to the limit. The system was useless unless sender and receiver could keep their multivibrators in time to the microsecond. They spent most of the first half of 1945 in achieving the necessary precision. They also had to test the output of the Delilah key generator, when they had built it, for the evenness over the frequency range which the calculations predicted for it. It was typical of the conditions in which they worked that they had no frequency analyser. Alan would have seen one at Bell Labs, and there was one known to exist at Dollis Hill, but at Hanslope they had to make one for themselves. It provided a challenge of the desert island sort, which Alan as usual enjoyed. After a lot of work they had a device, but when they first tried it out, Alan had to confess ‘It’s a bit of an abortion, isn’t it!’ – so they called it the ABORT Mark I.

To requisition anything at all required an act of skilful and aggressive diplomacy in handling the administrators. All they could obtain was a double-beam oscilloscope and an audio-frequency Hewlett-Packard oscillator. They even had to fight for this, first being fobbed off with an inferior one, and having to demand something better from SCU3’s Controller, Colonel Maltby. For Alan, the process was as baffling as it ever was for Alice in the Looking Glass shop, trying to locate what she needed on the White Queen’s shelves. Dealing with Maltby on the telephone drove Alan to extremes of nervousness, and people remarked upon how his speech, halting at the best of times, was on these occasions an almost indecipherable scrambling operation itself. He hated the showmanship that was required in negotiating for equipment. It was forever his bitter complaint that more adept players – ‘Charlatans’, ‘Politicians’, ‘Salesmen’ – would get their way not through expertise but through clever talk. He still tended to expect reason to prevail as if by magic.

It was a small-scale, homely example of the conflict that permeated the British war effort. But the Delilah project, manifestly too late for the German war, could not possibly expect a high priority, as he must have known. It was not like the work at Bletchley. And so even if angry over what he saw as incomprehensible waste and stupidity, he could also afford to stand aside and see the establishment in a more detached way. In this respect he and Robin Gandy would see things in very much the same light, and they both enjoyed reading Nigel Balchin’s novel The Small Back Room, which had appeared in 1943. This presented with unconcealed bitterness, yet also with a mordant wit, the frustrations felt by young scientists trying to get the war won and over with, and hamstrung by games of one-upmanship and empire-defending. At Hanslope a number of amusing stories were told, fairly or unfairly, about the plots and coups of the upper echelons, but Alan certainly did not suffer from all the tribulations Balchin described, and in particular he was spared the problem of dealing with dead-wood ‘eminent scientists’ who stifled initiative in the name of efficiency. In fact no one took any interest, scientific or otherwise, in the Delilah project. This remained true even when the addition of the key generator showed that he had a means of giving complete speech security with two small boxes of equipment.

The army officers emerged in Balchin’s book as ‘red-tabbed stooges’ who had entered a ‘profession for fools’, but to Alan the army system was less pernicious than ludicrous. He was very fond of Trollope’s novels and kept a stock of them in the Hanslope cottage. He would hold forth on the similarities between the organisation of the Church of England and that of the army; with the help of Robin Gandy and Don Bayley he would seek out parallels between the Barchester machinations and those of the Hanslope hierarchy. They worked out a correspondence between the respective ranks, so that a lieutenant-colonel became a dean, and a major-general a bishop, while a brigadier was pegged at the status of suffragan bishop (the cheapest kind of bishop, Alan explained).

Occasionally there would be episcopal visitations, when Gambier-Parry and Maltby would look in to pay their respects and listen to the Delilah output, but this would be for reasons of form rather than out of real interest, as they had no direct responsibility for the work and only the haziest of notions of what Alan and Don Bayley were up to. Nor was it much use asking, since Alan was quite incomprehensible to them, a fact which was somewhat uncongenial since they claimed some scientific knowledge. The visitors were liable to be treated to a rendering of Winston Churchill’s voice, since they used a gramophone recording of one of his speeches to test the Delilah· It was the broadcast made on 26 March 1944 in which after dwelling rather uncharacteristically on the subject of post-war housing policy, the Prime Minister had turned to more immediate prospects:15

 

…The hour of our greatest effort is approaching. We march with valiant Allies who count on us as we count on them. The flashing eyes of all our soldiers, sailors and airmen must be fixed upon the enemy on their front. The only homeward road for all of us lies through the arch of victory. The magnificent Armies of the United States are here or are pouring in. Our own troops, the best trained and the best equipped we have ever had, stand at their side in equal numbers and in true comradeship. Leaders are appointed in whom we all have faith. We shall require from our own people here, from Parliament, from the Press, from all classes, the same cool, strong nerves, the same toughness of fibre, which stood us in good stead in those days when we were all alone under the blitz.

With the help of the ABORT Mark I they could check that the Delilah had enciphered Churchill’s phrases into a White Noise – a perfectly even and uninformative hiss. And then, by passing the output into the decipherment process, they could recover:

 

And here I must warn you that in order to deceive and baffle the enemy as well as to exercise the forces, there will be many false alarms, many feints, and many dress rehearsals. We may also ourselves be the object of new forms of attack from the enemy. Britain can take it. She has never flinched or failed. And when the signal is given, the whole circle of avenging nations will hurl themselves upon the foe and batter out the life of the cruellest tyranny which has ever sought to bar the progress of mankind.

It was not very good policy to test the Delilah with the same recording over and over again, because even when in the spring of 1945 they got it to work, it still helped to know the words when listening to the output. The deciphered speech had to compete with a noisy background,* and a 4000 Hz whistle. The latter arose from a 4000 Hz signal used to synchronise sender and receiver, and which was only imperfectly filtered out of the final speech output. But the Delilah actually worked - that was the joy of it, for all its deficiencies. Alan had created a sophisticated piece of electronic technology out of nothing, and it worked. They did go as far as making a proper sixteen-inch disc recording of the effect, which entailed a trip to the black broadcasting studios at Simpson, since Hanslope lacked the requisite equipment. While they were there, Alan’s braces burst. Harold Robin, the chief engineer of the organisation, produced some bright red cord from an American packing case. Alan used it every day thereafter as his normal way of keeping his trousers up.

As the chief goose would surely have guessed, Churchill’s prophecies had owed something to the continued supply of golden eggs, and so did the fact that by the time the Delilah was enciphering them, the words had come true. The pre-invasion ‘feint’ had succeeded in outwitting the German command, as they had been able to tell by listening in. At the critical points of the Normandy campaign, they had enjoyed the advantage of hearing the story from the other side. But he might well have wondered why it was taking so appallingly long to finish the war.

As month after over-confident month passed, the technological developments at Bletchley became less and less relevant to fighting the war. If Sigint continued to help with the general knowledge, it failed resoundingly at critical points. For all the wonders of the electronic revolution, the Allies had been taken completely by surprise in December 1944 when the front, already held far longer than anyone expected, threatened to settle into another and more gruesome 1917. There had been a radio silence. It was perhaps more the fault of the military that no serious assessment had been made of the German forces at Arnhem. But there was a limit to what Sigint could do. Knowledge of the ‘new forms of attack’ from the pilotless VI and rocket-propelled V2 had not sufficed to stop them. And most remarkably, even the U-boat war, pre-eminently the war of information, was no walkover for the Allies. One factor was a political one: the RAF insisted on its role as an independent war-winning organisation, and devoted itself to the devastation of German cities rather than to the careful elimination of U-boats. But an increasing use of radio silence made cryptanalysis almost irrelevant at the end. The extraordinary fact was that when Dönitz took over from Hitler in April 1945, he still commanded a powerful, if suicidal, force. More U-boats were patrolling the American coasts than at any time since the mid-war winter, and new types of true submarines – rather than submersible boats – were in service. They were too late, like the new Enigmas that were ready but never came into service, but not very much too late.

The tapes whizzed round, the rotors spun, the Wrens followed their decision trees, but in the last months the mathematicians, finally given everything they wanted, had whizzed on into a world of their own. (Though what was real, and what absurd, would now be hard to tell.) Brute force, rather than wit and ingenuity, characterised the final Allied effort. This was not Alan Turing’s war. The achievement of his work was more the defensive one, rather appropriate for him, who only wanted to be left in peace. There had been no repetition of the Atlantic of 1917, and the almost impossible had been made possible in time, just before German science and industry was being used seriously. As for the Europe of 1945, the Dresden of his friend, the Warsaw where it had begun, was this the victory of anyone’s intelligence? Had the poker game of 1941 done anything for this? It did not bear thinking about.

Indeed, hardly anyone was permitted to think about it. The ‘cracking from within’ of 1918 had often filled British strategists of the Second World War with comforting delusions of easy victory, but it had also created a betrayal myth on which the Nazi party had capitalised. The great crack in logical control achieved by Bletchley Park no doubt had its influence upon the strategists of its aftermath, but this time there was no popular impact. It was completely hushed up. The victorious western governments had a common interest, for obvious reasons, in concealing the fact that the world’s most sophisticated communication system had been mastered.

No one questioned that this had to be so. Those who knew a part of their story transferred it to a sealed compartment of the mind, so that the whole war became a blank out of which only stories about bicycles could emerge. The Bletchley vision had taken a few people on a time travel trip, into a world of Our Ford where science had an answer for everything. Now they had to come back to the mid-1940s. Some, of course, had been grappling with the grimy reality of the 1940s all the time, and knew how almost impossible it had been to bridge the gap. Alan Turing, however, had been able more than most to protect himself from the abrasion. It would not be easy for him to adjust. And as one acquainted with a wider span of knowledge than any other of the ‘men of the Professor type’, it meant a particularly acute mind-splitting operation. On VE day, 8 May 1945, he joined Robin Gandy, Don Bayley and Alan Wesley for a walk in the nearby woods at Paulerspury. ‘Well, the war is over, now you can tell all,’ said Don, not very seriously. ‘Don’t be bloody silly,’ said Alan – and that was the last word.

The Delilah was finished at about the same time as the German surrender. There was no particular drive to improve standards for the Japanese war, nor for future purposes, and its fundamental advance met with little enthusiasm. Radley and another engineer, R.J. Halsey, came to Hanslope to inspect it in somewhat perplexed fashion. The Post Office did have some system of their own under development – possibly based on the Vocoder, on which they had requested and received information in 1941. Their main concern was that the crackly output of the Delilah was too poor to be commercially acceptable, as indeed it was. They showed no sign of interest in the potential of the principle. Alan then spent some time himself at Dollis Hill in the summer of 1945, where he explained his system to a somewhat sceptical Flowers.

It was all over except the details – and Alan was never good at bothering with the last details. He was happy to leave it for Don Bayley to work on. For he had other ideas in mind. He had several times discussed with Don the question of his plans for peacetime, and had said that he was expecting to return to his King’s fellowship and a cut back to £300 per annum. There were eighteen months of his 1938 fellowship still to run, but beyond this he now had a longer period assured, since on 27 May 1944, making a rather special gesture of confidence, King’s had prolonged the tenure of his fellowship by a further three years. He could go back as if the war had never happened, and continue from where he had left off in 1939. A university lectureship might soon come his way.16 And yet the war had happened, and everything had changed. It had not simply been an interruption to the course of his intellectual career, as for some of the ‘professor type’ it might have been. It had mobilised his inner life. His ideas had been enmeshed with its critical developments, and they had been able to grow with the scale of the war itself. The world had learned to think big, and so had he. For though expecting to return to Cambridge, Alan had also told Don Bayley from the start of their collaboration that he wanted ‘to build a brain’.

His use of the word ‘brain’ was entirely consistent with his bold appeal to ‘states of mind’ ten years before. If the states of a Turing machine could be compared with ‘states of mind’, then its physical embodiment could be compared with a brain. One important aspect of this comparison, important to anyone who was concerned with the mystery of mind, the apparent paradox of free will and determinism, was that the Turing machine model was one independent of physics. The argument from Laplacian physical determinism could be shrugged aside with the observation that no such prediction could ever be performed in practice. This rebuttal could not be applied to a Turing machine, in which everything that happened could be described in terms of a finite set of symbols, and worked out with complete precision in terms of discrete states. Later he would articulate this himself:¹⁷

 

The prediction which we are considering is however rather nearer to practicability than that considered by Laplace. The system of the ‘universe as a whole’ is such that quite small errors in the initial conditions can have an overwhelming effect at a later time. The displacement of a single electron by a billionth of a centimetre at one moment might make the difference between a man being killed by an avalanche a year later, or escaping. It is an essential property of the mechanical systems which we have called ‘discrete state machines’ that this phenomenon does not occur.

To understand the Turing model of ‘the brain’, it was crucial to see that it regarded physics and chemistry, including all the arguments about quantum mechanics to which Eddington had appealed, as essentially irrelevant. In his view, the physics and chemistry were relevant only in as much as they sustained the medium for the embodiment of discrete ‘states’, ‘reading’ and ‘writing’. Only the logical pattern of these ‘states’ could really matter. The claim was that whatever a brain did, it did by virtue of its structure as a logical system, and not because it was inside a person’s head, or because it was a spongy tissue made up of a particular kind of biological cell formation. And if this were so, then its logical structure could just as well be represented in some other medium, embodied by some other physical machinery. It was a materialist view of mind, but one that did not confuse logical patterns and relations with physical substances and thing, as so often people did.

In particular it was a different claim from that of behaviourist psychology, which spoke of reducing psychology to physics. The Turing model did not seek to explain one kind of phenomenon, that of mind, in terms of another. It did not expect to ‘reduce’ psychology to anything. The thesis was that ‘mind’ or psychology could properly be described in terms of Turing machines because they both lay on the same level of description of the world, that of discrete logical systems. It was not a reduction, but an attempt at transference, when he imagined embodying such systems in an artificial ‘brain’.

Alan probably did not know much in 1945 about the actual physiology of human brains: quite possibly no more than from jolly pictures of the brain as a humming telephone exchange in the Children’s Encyclopaedia, or from the passage in Natural Wonders describing the ‘small thinking place in the brain’:

 

Directly over the ear, a place that you can almost cover with your thumb, lies the most important part of all, the place where we remember and handle words. At the bottom of this word spot, we remember how words sound. An inch farther up and toward the back, we remember how words look in print. A little farther up and forward lies the ‘speech center’ from which, when we want to talk, we direct the tongue and lips what to say. Thus we get our word-hearing, our word-seeing, and our word-speaking centers close together, so that when we speak we have close by and handy our memory of what we have heard in words, and of what we have read.

But that would have been quite sufficient. He would have seen pictures of nerve cells (there were a few in Natural Wonders), but at the level at which he was approaching the description of mind, the details were not important. In speaking of ‘building a brain’ he did not mean that the components of his machine should resemble the components of a brain, or that their connections should imitate the manner in which the regions of the brain were connected. That the brain stored words, pictures, skills in some definite way, connected with input signals from the senses and output signals to the muscles, was almost all he needed. But ten years before, he had also had to fight his own way through to the crucial idea that Brewster glossed over; he had rejected the idea of a ‘we’ behind the brain that somehow ‘did’ this signalling and organising of the memory. The signalling and the organisation had to be all that there was.

But in describing the Turing machines ten years before, he had also justified his formalisation of the idea of ‘mechanical’ with a complementary argument, that of the ‘instruction note’. This put the emphasis not on the internal workings of the brain, but upon the explicit instructions that a human worker could follow blindly. In 1936 such ‘instruction notes’ had entered his experience through the rules of Sherborne School, other social conventions, and of course in the mathematical formulae that one could apply ‘without thinking’. But in 1945 a great deal of water had flowed under the bridge, and the ‘instruction notes’ that had been somewhat fanciful in 1936, just as were the theoretical logical machines, had become exceedingly concrete and practical. The cornucopian abundance was one of messages ‘based on a machine and broken on a machine’, and these machines were Turing machines, in which the logical transformation of symbols was what mattered, not physical power. And in designing such machines, and in working out processes that could be given to people acting like machines – the ‘slaves’ – they had effectively been writing elaborate ‘instruction notes’.

This was a different, but not incompatible, approach to the idea of ‘brain’. It was the interplay between the two approaches that perhaps fascinated Alan most – just as at Bletchley there had been a constant play between human intelligence, and the use of machines or ‘slave’ methods. His ‘weight of evidence’ theory had shown how to transfer certain kinds of human recognition, judgment and decision into an ‘instruction note’ form. His chess-playing methods did the same thing – as did the games on the Colossi – and posed the question as to where a line could be drawn between the ‘intelligent’ and the ‘mechanical’. His view, expressed in terms of the imitation principle, was that there was no such line, and neither did he ever draw a sharp distinction between the ‘states of mind’ approach and the ‘instruction note’ approach to the problem of reconciling the appearances of freedom and of determinism.

All these questions remained to be explored, for the exigencies of the German cipher machines had barely scratched the surface of what could be done. It was yet to be seen how much could be achieved by writing ‘instruction notes’, and yet to be seen whether a machine could behave like a brain in developing ‘thinking spots’ for itself. As he had stressed in his discussions with Donald Michie, it had to be shown that a machine could learn. To explore these questions it would be necessary to have machines on which to experiment. But the almost incredible fact was that it would require only one machine, for the performance of any and all such experiments. For a universal Turing machine could imitate the behaviour of any Turing machine whatever.

In 1936 the Universal Turing Machine had played a purely theoretical part in his attack upon the Hilbert Entscheidungs problem. But in 1945 it had a very much more practical potential. For the Bombes and Colossi and all the other machines and mechanical processes were parasitic beasts, dependent upon the whims and blindness of the German cryptographers. A change of mind on the other side of the Channel would mean that all the engineering that had been required to construct them would suddenly become useless. It had happened right from the start, with the Polish ‘fingerprint’ file, their perforated sheets and their simple Bombe, and it had nearly led to catastrophe in the blackout of 1942. The construction of special machines had led the cryptanalysts into one problem after another with the acquisition and application of new technology. But a universal machine, if only it could be realised in practice, would require no fresh engineering, only fresh tables, encoded as ‘description numbers’ and placed upon its ‘tape’. Such a machine could replace not only Bombes, Colossi, decision trees and all the other mechanical Bletchley tasks, but the whole laborious work of computation into which mathematicians had been conscripted by the war. The zeta function machine, the calculation of roots of seventh order equations, the large sets of equations arising in electrical circuit theory – they could all alike be performed by a single machine. It was a vision beyond the comprehension of most people in 1945, but not beyond Alan Turing. As he would write later in 1945:18

 

There will positively be no internal alterations to be made even if we wish suddenly to switch from calculating the energy levels of the neon atom to the enumeration of groups of order 720.

or as he would put it in 1948,¹⁹

 

We do not need to have an infinity of different machines doing different jobs. A single one will suffice. The engineering problem of producing various machines for various jobs is replaced by the office work of ‘programming’ the universal machine to do these jobs.

From this point of view, a ‘brain’ would not be just some bigger or better machine, some superior kind of Colossus. It did not develop out of an experience of things, but out of a consciousness of underlying ideas. A universal machine would not just be a machine; it would be all machines. It would replace not only the physical Bletchley machinery, but all that was routine – almost all that those ten thousand people had been doing. And not even the ‘intelligent’ work of the high-level analysts would be sacrosanct. For a universal machine could also play out the workings of human brains. Whatever a brain did, any brain, could in principle be placed as a ‘description number’ on the tape of a Universal Machine. This was his vision.

But there was nothing in the paper design of the Universal Turing Machine that suggested it could be made a practical proposition. In particular, there was nothing about its speed of operation. The tables of Computable Numbers could be realised by people sending postcards to each other, without affecting the theoretical argument. But if a universal machine were to be of any practical use, it would have to be able to run through millions of steps in a reasonable tune. This demand for speed could only be met by electronic components. And this was where the revolution of 1943 had made all the difference in the world.

More precisely, the point was that electronic components could be regarded as operating upon discrete, on-or-off, quantities, and so could realise a Turing machine. This he had learnt in 1942, and thereafter he had known all about the Robinsons, the X-system, and the Rockex; he had also picked up a fund of radar knowledge from his new friends at Hanslope. But above all there were the two developments that had begun in 1943. Whatever its usefulness to the war effort, the technical success of the Colossi told him that thousands of electronic valves could be used in conjunction – something that few could have believed in until it had been done. And then he had worked with his own bare hands on the Delilah. There had been a method in his madness all along. By working in these second-rate conditions, on a device that officialdom had not called for, he had proved that he could carry off an electronic project of his own. Coordinated with his theoretical ideas and his experience of mechanical methods, this direct knowledge of electronic technology formed the last link in his plans. He had learned how to build a brain – not an electric brain, as he might possibly have imagined before the war – but an electronic brain. It was thus that ‘round about 1944’, Alan’s mother heard him talking20 about ‘his plans for the construction of a universal [machine] and of the service such a machine might render to psychology in the study of the human brain.’

There was a further fundamental consideration besides that of discreteness, reliability and speed: that of sheer size. There would have to be room on the ‘tape’ of a universal machine both for the ‘description numbers’ of the machines it had to imitate, and its workings. The abstract universal machine of 1936 was equipped with a ‘tape’ of infinite length, meaning that although at any stage the amount of tape used would be finite, it was assumed that as more space was required it could always be made available.

In a practical machine, space would always be limited in extent – and for that reason no physical machine could actually realise a truly universal machine. Still, Alan had suggested in Computable Numbers that human memory was finite in extent. If this were so then the human brain itself could hold only a limited number of ‘tables of behaviour’, and a sufficiently large tape could contain them all. The finiteness of any practical machine would not, on this argument, debar it from having a brain-like quality. The question was, however, how much ‘tape’ would be required for a machine that could actually be built: enough to make it interesting, but not more than would be technically feasible. And how could such storage be arranged without inconceivable expense in terms of electronic valves?

This practical question was one more up Don Bayley’s street. As the European war ground to its end, and the problems of the Delilah were essentially solved, it became clear that Alan’s interest had turned to ‘the brain’. He described to his assistant the universal machine of Computable Numbers, and its ‘tape’ on which instructions would be stored. They began thinking together about ways in which to realise a ‘tape’ that could store such information. And thus it was that in this remote station of the new Sigint empire, working with one assistant in a small hut, and thinking in his spare time, an English homosexual atheist mathematician had conceived of the computer *

That was not how the world was to see it, and the world was not being entirely unfair. Alan Turing’s invention had to take its place in an historical context, in which he was neither the first to think about constructing universal machines, nor the only one to arrive in 1945 at an electronic version of the universal machine of Computable Numbers.

There were, of course, all manner of thought-saving machines in existence, going back to the invention of the abacus. Broadly these could be classed into two categories, ‘analogue’ and ‘digital’. The two machines on which Alan worked just before the war were examples of each kind. The zeta-function machine depended on measuring the moment of a collection of rotating wheels. This physical quantity was to be the ‘analogue’ of the mathematical quantity being calculated. On the other hand, the binary multiplier had depended upon nothing but observations of ‘on’ and ‘off’. It was a machine not for measuring quantities, but for organising symbols. In practice, there might be both analogue and digital aspects to a machine. There was not a hard-and-fast distinction. The Bombe, for instance, certainly operated on symbols, and so was essentially ‘digital’, but its mode of operation depended upon the accurate physical motion of the rotors, and their analogy with the enciphering Enigma. Even counting on one’s fingers, by definition ‘digital’, would have an aspect of physical analogy with the objects being counted. However, there was a practical consideration which provided the effective distinction between an analogue and a digital approach. It was the question of what happened when increased accuracy was sought.

His projected zeta-function machine would have well illustrated the point. It was designed to calculate the zeta-function to within a certain accuracy of measurement. If he had then found that this accuracy was insufficient for his purpose of investigating the Riemann Hypothesis, and needed another decimal place, then it would have meant a complete reengineering of the physical equipment – with much larger gear-wheels, or a much more delicate balance. Every successive increase in accuracy would demand new equipment. In contrast, if the values of the zeta-function were found by ‘digital’ methods – by pencil and paper and desk calculators – then an increase in accuracy might well entail a hundred times more work, but would not need any more physical apparatus. This limitation in physical accuracy was the problem with the pre-war ‘differential analysers’, which existed to set up analogies (in terms of electrical amplitudes) for certain systems of differential equations. It was this question which set up the great divide between ‘analogue’ and ‘digital’.

Alan was naturally drawn towards the ‘digital’ machine, because the Turing machines of Computable Numbers were precisely the abstract versions of such machines. His predisposition would have been reinforced by long experience with ‘digital’ problems in cryptanalysis – problems of which those working on numerical questions would be entirely ignorant, by virtue of the secrecy surrounding them. He was certainly not ignorant of analogue approaches to problem-solving. Apart from the zeta-function machine, the Delilah had an important ‘analogue’ aspect. It depended crucially on accurate measurement and transmission of the amplitudes, in contrast to the X-system, which made them ‘digital’. He might well have admitted that for certain problems, the analogue solution could not remotely be rivalled by a digital method. Putting a model aircraft in a wind tunnel would immediately produce a picture of stresses and vortices that centuries of calculation would never obtain. In 1945 there was plenty of scope for debating the relative practical usefulness of analogue and digital devices, and the priorities for construction. But so far as Alan Turing was concerned, this was a debate for other people. He was committed to the digital approach, flowing out of the Turing machine concept, and with its potential universality at the centre. No analogue machine could lay claim to universality, such devices being constructed to be physical analogies of particular problems. It followed that his ideas had to find their place among, and compete with, the prevailing developments of digital calculators.

There had been machines to add and multiply numbers, the digital equivalents of the slide rule, since the seventeenth century. Alan had a desk calculator at Hanslope, and used it for the calculation of circuit properties. It was a very long step indeed from such devices to the idea of a practical universal machine. But as Alan knew by this time, that step had been made a hundred years before, by the British mathematician Charles Babbage (1791-1871). He used to speak to Don Bayley of Babbage, and knew something of what Babbage had planned.

After working on a ‘Difference Engine’, to mechanise the particular numerical method used in the construction of mathematical tables, Babbage had conceived (by 1837) of an Analytical Engine, whose essential property was that of mechanising any mathematical operation. It embodied the crucial idea of replacing the engineering of different machines for different tasks, by the office work of producing new instructions for the same machine. Babbage did not have a theory like that of Computable Numbers, to argue for universality, and his attention was focussed upon operations using numbers in decimal notation. Yet he did perceive that its mechanism could serve to effect operations upon symbols of any kind whatever,* and in this and other ways the Analytical Engine came close in its conception to the Universal Turing Machine. Babbage wanted a ‘scanner’, in effect, working on a stream of instructions, and putting them into operation. He hit on the idea of coding the instructions on punched cards, such as then were used for the weaving of complicated patterns in brocade. His plans also called for storing numbers in the form of positions of gear wheels. Each instruction card would cause an arithmetical operation such as ‘subtract the number in location 5 from that in location 8, and put the result in location 16.’ This required machinery he called the ‘mill’ to do the arithmetical operations, but the crucial innovation of Babbage’s plans did not lie in the efficient mechanisation of adding and multiplying. It lay in his perception that it was the mechanisation of the organising or logical control of the arithmetic that mattered.

In particular, Babbage had the vital idea that it must be possible to move forwards or backwards among the stream of instruction cards, skipping or repeating, according to criteria which were to be tested by the machine itself in the course of its calculation. This idea, that of ‘conditional branching’, was his most advanced. It was equivalent to the freedom allowed to Turing machines, that of changing ‘configuration’ according to what was read on the tape, and it was this that made Babbage’s planned machine a universal one, as he himself was well aware.

Without ‘conditional branching’, the ability to mechanise the word IF, the grandest calculator would be no more than a glorified adding machine. It might be thought of as an assembly line, everything being laid down from start to finish, and there being no possibility of interference in the process once started. The facility of ‘conditional branching’, in this model, would be analogous to specifying not only the routine tasks of the workers, but the testing, deciding and controlling operations of the management. Babbage was well-placed to perceive this idea, his book On the Economy of Machinery and Manufactures being the foundation of modern management.

These ideas were a hundred years ahead of their time, and were never to be embodied in working machinery during Babbage’s lifetime. Government funding did not solve the problems created by his grossly over-ambitious specifications; the project was not advanced by Babbage’s contempt for committees, administrators, and other scientists; nor did his own efforts to bring mechanical engineering to an entirely new standard, and his absorption in every theoretical and practical aspect of the work, overcome these difficulties.

Indeed, it was exactly a hundred years from the conception of the Analytical Engine, until there were substantially new developments either in the theory or in the construction of such a universal machine. On the side of theory, 1937 saw the publication of Computable Numbers, which made all these ideas precise, explicit, and conscious. On the practical side, there had been the inevitable Looking Glass war as the revived and expanding electrical industry of the 1930s provided rival powers with new opportunities.

The first development had, in fact, occurred in 1937 Germany, at the Berlin home of K. Zuse, an engineer who had rediscovered many of Babbage’s ideas, though not that of conditional branching. Like the Babbage machine his first design, which was actually built in 1938, was mechanical and not electrical. But he had avoided the thousands of meshing ten-spoke gear wheels that Babbage had demanded, by the simple expedient of having his machine work in binary arithmetic. This was not a deep theoretical advance, but from any practical point of view it was an immense simplification. It was also a liberation from the usual engineer’s assumption that numbers had to be represented in the decimal way. Alan had used the same idea at the same time in his 1937 electric multiplier. Zuse had quickly moved on to construct further versions of his machine which made use of electromagnetic relays rather than mechanical elements, and with collaborators experimented with electronics before the end of the war. Zuse calculators were used in aircraft engineering but not in code-breaking; it was argued that the war would be over too soon. Short-term Nazism left Zuse in 1945 desperately trying to save his work from destruction.

These events were unknown on the Allied side, where roughly parallel but larger developments had been taking place. In Britain there was no such digital calculator, controlled by a sequence of instructions, except the Colossi. This was in marked contrast with the situation in the United States. The British success, frantic but triumphant, had been achieved at the last moment by individuals giving their all to wartime public service. The Americans, so much richer in capitalist enterprise, were years ahead in pursuing two different, perhaps slightly unimaginative, approaches to the Babbage idea-and in doing so even in peacetime, just as they were ahead in the analogue differential analyser of the earlier 1930s. For again it was 1937 when at Harvard the physicist H. Aiken began to realise it in terms of electromagnetic relays. The resulting machine was built by IBM and turned over to the US Navy for secret work in 1944. It was lavish and impressive in scale, but like Zuse’s machines, did not embody conditional branching, even though Aiken knew of Babbage’s plans. The instructions had to be followed rigidly from beginning to end. Aiken’s machine was also more conservative than Zuse’s in that it based the arithmetical machinery on the decimal notation.

The second American project was under way at Bell Laboratories. Here the engineer G. Stibitz had first only thought of designing relay machines to perform decimal arithmetic with complex numbers, but after the outbreak of war had incorporated the facility to carry out a fixed sequence of arithmetical operations. His ‘Model III’ was under way in the New York building at the time of Alan’s stay there, but it had not drawn his attention.

There was another person, however, who did make a thorough examination of these two advanced projects, and who like Alan had the mind with which to form a more abstract view of what was happening. This was that other mathematician of the wizard war, John von Neumann. He had been connected with US Army ballistic research as a consultant since 1937. From 1941 most of his time had been spent upon the applied mathematics of explosions and aerodynamics. In the first six months of 1943 he was in Britain, conferring on those subjects with G.I. Taylor, the British applied mathematician. It was then that he had first become involved in programming a large calculation, in the sense of organising how it could best be done by people working on desk calculators. Back in the United States, his entry in September 1943 into the atomic bomb project had taken him into similar problems with shock waves, whose prediction by numerical computation required months of slogging work. In 1944 he toured the available machines in search of help. W. Weaver, at the National Development and Research Commission, had put him in touch with Stibitz, and on 27 March 1944 von Neumann wrote22 to Weaver:

 

Will write to Stibitz: my curiosity to learn more about the relay computation method, as well as my expectations concerning possibilities in this direction, are much aroused.

On 10 April he wrote again to say that Stibitz had shown him ‘the principle and working of his relay counting mechanisms’. On 14 April he wrote to R. Peierls at Los Alamos about the ‘shock decay problem’, saying that it could probably be mechanised, and adding that he was now also in touch with Aiken. In July 1944 there were negotiations to use the Harvard-IBM machine. But then everything changed. For the pressure of wartime demands had brought about the same technological revolution as had happened at Bletchley, and at exactly the same time. In quite another place, namely the engineering department of the University of Pennsylvania (the Moore School), work had begun on yet another large calculator in April 1943. This was the ENIAC – the Electronic Numerical Integrator and Calculator.

The new machine was designed by the electronic engineers J.P. Eckert and J. Mauchly, although von Neumann’s first knowledge of it, apparently something of an accident, came through talking on a railroad station with H.H. Goldstine, a mathematician associated with the project. Von Neumann seized upon the possibilities opened up by a machine that when built would perform arithmetical operations a thousand times faster than Aiken’s. From August 1944 he was regularly attending ENIAC team meetings, writing on 1 November 1944 to Weaver:

 

There are some other things, mostly connected with mechanised computation, which I should like a chance to talk to you about. I am exceedingly obliged to you for having put me in contact with several workers in this field, especially with Aiken and Stibitz. In the meantime I have had a very extensive exchange of views with Aiken, and still more with the group at the Moore School…who are now in the process of planning a second electronic machine. I have been asked to act as their adviser, mainly on the matters connected with logical control, memory, etc.

The ENIAC project was immensely impressive, quite enough to give people allowed to see it the sensation of seeing the future. It employed no fewer than 19,000 electronic valves. As such it surpassed the Colossi, with which in many ways it was comparable, though one difference was that in the summer of 1945 the ENIAC was still incomplete, and would come too late to have any use whatever in the war.

It required a greater total number of valves than the Colossi because it stored long decimal numbers – the more so because of the primitive system the designers had employed whereby ten valves were allocated to each decimal digit required, a ‘9’ being represented by the ninth of those valves being ‘on’. In contrast the Colossi operated on single pulses which represented the logical ‘yes’ or ‘no’ of holes in telegraph tape.

But this was a fairly superficial point of difference. Both alike demonstrated that thousands of valves, hitherto regarded as too unreliable for operation en masse, could be kept in simultaneous use.* And the ENIAC project was embodying the idea that Zuse, Aiken and Stibitz had missed. Like the Mark II Colossi, with their ability to automate acts of decision, the results of one counting operation automatically deciding what step was taken next, the ENIAC would have a form of conditional branching. It was designed so that it could be made to hop to and fro within the stock of instructions supplied to it, repeating sections as many times as the progress of the calculation showed was necessary, without the interference of human management. None of this went beyond what Babbage had envisaged – except that electronic components were so much faster, and that the ENIAC was (or was nearly) a reality.

Like the Colossus, the ENIAC had been designed for a specific task, that of calculating artillery range tables. Essentially it was to simulate the trajectories of shells through varying conditions of air resistance and wind velocity, which involved the summation of thousands of little pieces of trajectory. It had external switches which would be set to store the constant parameters for a trajectory calculation, and further external devices for setting up the instructions on how to calculate the segments of motion. Then there would be valves to hold the intermediate working figures. In these arrangements it resembled the Colossi. But in both cases, people had quickly discovered the possibility for using the machines for a wider range of tasks than those for which they had been designed. The role of the original Colossus had been much extended by Donald Michie and Jack Good, and then the Mark II had once been set up to punch out a deciphered message, although this was done out of interest, not for the sake of efficiency. Even though a parasite on the German cipher machine, the flexibility offered by its instruction table facility was such that it could even be ‘almost’ set up to perform numerical multiplication. The ENIAC was flexible in a more serious way, and von Neumann had already discovered that it could be used, when ready, for Los Alamos problems.*

But the ENIAC had not been conceived as a universal machine, and in one important respect the designers had departed from Babbage’s line of development. Babbage had been proud of the fact that the planned Analytical Engine would be able to ingest an unlimited number of instruction cards. The Aiken relay machine enjoyed the same feature, although cards had been replaced by a sort of pianola roll. But on the ENIAC the state of affairs was different. Its operations, being electronic, would be so fast as to make it impossible to supply cards or tape quickly enough. The engineers had had to find a way to make the instructions available to the machine in electronic times of a few millionths of a second.

On the ENIAC they were arranging for this by a system of external devices which would set up the instructions for each job. It took the form of making connections with plugs as on a manual telephone exchange. (The Colossi had something very similar.) The advantage of this solution was that the instructions would in effect be available instantaneously, once the plugging work was done. The disadvantage was that the sequence of instructions was limited in length, and that it would take a day or so to do the plugging. It would be like building a new machine for each different task. Both ENIAC and Colossus were like kits out of which many slightly different machines could be made. Neither sought to embody the true universality of Babbage’s conception, in which the machinery would be entirely unchanged, and only the instruction cards rewritten.

But even when von Neumann joined the ENIAC team as ‘adviser’ in late 1944, Eckert and Mauchly had perceived a quite different solution to their problem. This was to leave the hardware alone, and to make the instructions available at electronic speeds by storing them internally, in electronic form. The ENIAC was designed to store its arithmetical working internally, and the point of the original Colossus had been that it would hold Fish key-patterns internally. It was a quite different matter to consider holding the instructions to the machine internally. Instructions were naturally thought of as coming from the outside, to act upon an inside. But the ‘second electronic machine’ mentioned in von Neumann’s letter to Weaver was intended to incorporate this new idea.

Every tradition of common sense and clear thinking would tend to suggest that ‘numbers’ were entirely different in kind from ‘instructions’. The obvious thing was to keep them apart: the data in one place, and the stock of instructions to operate on the data, in another place. It was obvious – but wrong. In March and April 1945, the ENIAC team had prepared a proposal, the Draft Report on the EDVAC. The EDVAC – the Electronic Discrete Variable Calculator – was the planned ‘second electronic machine’.

The report was dated 30 June 1945, and signed by von Neumann. It was not his design, but the description of it bore the mark of his more mathematical mind rising above the technicalities.

In particular, it articulated the very cautious, circumspect, but quite new idea, at which the ENIAC team had arrived in planning a better machine. It discussed the different kinds of storage that existing machines required: intermediate results, instructions, fixed constant parameters, statistical data, and then stated that

 

The device requires a considerable memory. While it appeared, that various parts of this memory have to perform functions which differ somewhat in their nature and considerably in their purpose, it is nevertheless tempting to treat the entire memory as one organ.

But such a proposal, that of the ‘one organ’, was equivalent to adopting the ‘one tape’ of the Universal Turing Machine, on which everything – instructions, data, and working – was to be stored. This was the new idea, different from anything in Babbage’s design, and one which marked a turning point in proposals for digital machines. For it threw all the emphasis on to a new place – the construction of a large, fast, effective, all-purpose electronic ‘memory’. And in its way it made everything much more simple, less cluttered in conception. Von Neumann might well have seen it as ‘tempting’, because it was almost too good an idea to be true. But it had been in Computable Numbers all the time.

So the spring of 1945 saw the ENIAC team on the one hand, and Alan Turing on the other, arrive naturally at the idea of constructing a universal machine with a single ‘tape’. But they did so in rather different ways. The ENIAC, now already shown to be out-of-date in principle even before it was finished, had been something of a sledgehammer in cracking open the problem. And von Neumann had been obliged to hack his way through the jungle of every known approach to computation, assimilating all the current needs of military research and the capabilities of American industry. The result was something close to the Lancelot Hogben view of science: the political and economic needs of the day determining new ideas.

But when Alan Turing spoke of ‘building a brain’, he was working and thinking alone in his spare time, pottering around in a British back garden shed with a few pieces of equipment grudgingly conceded by the secret service. He was not being asked to provide the solution to numerical problems such as those von Neumann was engaged upon; he had been thinking for himself. He had simply put together things that no one had put together before: his one-tape universal machine, the knowledge that large-scale electronic pulse technology could work, and the experience of turning cryptanalytic thought into ‘definite methods’ and ‘mechanical processes’. Since 1939 he had been concerned with little but symbols, states, and instruction tables – and with the problem of embodying these as effectively as possible in concrete forms. Now he could consummate it all.

And now the war was over, his motives were much nearer to those of G.H. Hardy than to the practicalities of the world’s work. They had more to do with the paradox of determinism and free will, than with the effecting of long calculations. Of course, no one was likely to pay for a ‘brain’ that had no useful application. And in this respect Hardy would have found justification of his views regarding the applications of mathematics. On 30 January 1945 von Neumann had written24 that the EDVAC was being designed for three-dimensional ‘aerodynamic and shock-wave problems …shell, bomb and rocket work …progress in the field of propellants and high explosives’. Such, in Churchill’s phrase, would be the ‘progress of mankind’. Alan Turing too would have to come a long way from the logic of Hilbert and Gödel if he was really to build a brain.

The Draft Report on the EDVAC did carry a more theoretical burden (one reflecting von Neumann’s interests) in that it drew attention to the analogy between a computer, and the human nervous system. The use of the word ‘memory’ was an aspect of this. In its way, it was ‘building a brain’. However, its emphasis was placed not on an abstract thesis concerning ‘states of mind’, but on the similarities between input and output mechanisms, and afferent and efferent nerves respectively. It also drew upon the 1943 paper written by the Chicago neurologists W.S. McCulloch and W. Pitts, which analysed the activity of neurons in logical terms, and used their symbolism for describing the logical connections of electronic components.

McCulloch and Pitts had been inspired by Computable Numbers, and so in a very indirect way, the EDVAC proposal owed something to the concept of the Turing machine. One of its curiosities, however, was that it made no mention of Computable Numbers, nor made precise the universal machine concept. Yet von Neumann had been familiar with it before the war, and must surely have recognised the connection when he liberated himself from the assumption that data and instructions had to be stored in different ways. According to S. Frankel,²⁵ who worked at Los Alamos on the atomic bomb and was one of the first to use the ENIAC,

 

in about 1943 or ‘44 von Neumann was well aware of the fundamental importance of Turing’s paper of 1936 ‘On computable numbers …’ …Von Neumann introduced me to that paper and at his urging I studied it with care.…he firmly emphasised to me, and to others I am sure, that the fundamental conception is owing to Turing – insofar as not anticipated by Babbage, Lovelace and others.

So the Wizard might well have learnt something from Dorothy. However, the essential point about these two initiatives, American and British, was not the rather tenuous connection between them. It was their very marked independence.²⁶

Whatever ideas had flowed westwards, the Draft Report on the EDVAC was the first to put them together in writing. So once again, British originality had been pipped at the post by an American publication – and at a time when everyone was looking to the west. The Americans had won, and Alan was a sporting second. This time, however, American priority was nothing but an advantage to the Turing plans, for it provided the political and economic impetus that his own ideas alone could never have enjoyed.

Indeed, it was probably only the existence of the ENIAC and the EDVAC idea that made possible the next stage of Alan Turing’s life. For in June he had a telephone call at Hanslope. It was from J. R. Womersley, Superintendent of the Mathematics Division at the National Physical Laboratory.

Womersley was a new man in a new post in a new organisation. The National Physical Laboratory was not new; it had been set up in shabby, suburban Teddington in 1900, the British response to state-sponsored German scientific research. Its site was carved out of Bushy Park, itself largely given over to Supreme Headquarters, Allied Expeditionary Forces. It was the most extensive government laboratory in the United Kingdom, enjoying a high reputation within its traditional sphere, that of setting and maintaining physical standards for the benefit of British industry. Its current Director, installed in 1938, was Sir Charles Galton Darwin, grandson of the theorist of evolution and himself an eminent Cambridge applied mathematician. His major contribution had been in the field of X-ray crystallography, and like Humpty Dumpty, who was able to explain the Jabbervocky, he was regarded as the27 ‘interpreter of the new quantum theory to experimental physicists.’ Large, awesome, and remote, during the war he had spent a year as director of what became the British Central Scientific Mission in Washington, and had been the first scientific adviser to the British Army.

The Mathematics Division, however, was new. Indeed, it was a computational equivalent of the planned welfare state, the product of a calculators’ Beveridge Report. In about March 1944 a proposal²⁸ had been mooted for an independent Mathematical Station, and this suggestion, a fine example of wartime planning for peace, went to a large interdepartmental committee, itself a manifestation of cooperation and coordination unthinkable in peacetime days. The government accepted the principle of continuing the funding found necessary in war, and a centralised, rationalised institution was planned to take over the various ad hoc offices which had done the mostly dreary work of numerical computation for military purposes. Sir Charles Darwin had persuaded the committee to establish it as a division of the NPL.

 

But the telephone call to Hanslope was not made at Darwin’s behest. It was made on the initiative of his subordinate, Womersley, who had been selected as head of the new Division on 27 September 1944. Womersley, a bulky Yorkshireman then attached to the Ministry of Supply and a member of the interdepartmental committee, was probably the nominee of D.R. Hartree, who in mathematical matters was a power behind the Darwin throne. Womersley had appeared as joint author with Hartree of a 1937 paper on the application of the differential analyser to partial differential equations.

The official research programme for the new Division in October 1944 included ‘Investigation of the possible adaptation of automatic telephone equipment to scientific computing’ and ‘Development of electronic counting device suitable for rapid computing’. Behind these words there were more definite intentions to imitate the American developments. Hartree, with his differential analyser at Manchester University, already had an interest in computing machinery, and had a finger in many wartime scientific projects. In the high levels where he moved, some details of the secret Aiken and ENIAC machines filtered through. Such knowledge was reflected in Womersley’s report in December 1944, which, though it placed emphasis upon building a large differential analyser, remarked on the speed of electronics, and suggested that ‘a machine can be made to perform certain cycles of operations mechanically …the instructions to the machine [could] depend on the result of previous operations …the problem is already being tackled in the USA.’ The press release29 in April 1945, when the new Division was officially inaugurated, only made mention of ‘analytical engines, including the differential analyser and other machines both existing and awaiting invention …it is certain that this field is capable of great developments, but it is more difficult to predict in what directions they will lie.’ But it seemed that the direction in which to look was westwards, and in February 1945, Womersley had been packed off on a two-month tour of the computing installations of the United States, where on 12 March he was the first non-American to be allowed access to the ENIAC, and to be informed of the EDVAC report.

By 15 May, Womersley was back at the NPL ‘revising his plans’. The American revelations were enough to give anyone pause for thought. But they held a particular meaning for Womersley, who held one very unusual card up his sleeve. Before the war, while employed at Woolwich Arsenal on practical computation, he had learnt of Turing machines. Even more remarkably, for a mathematician-in-the-street, he had not been daunted by the abstruse language of mathematical logic. According to his claim:³⁰

 

1937-38 Paper Computable Numbers seen by JRW and read. JRW met C.I. Norfolk, a telephone engineer who had specialised in totalisator design and discussed with him the planning of a ‘Turing Machine’ using automatic telephone equipment, Rough schematics prepared, and possibility of submitting a proposal to NPL discussed. It was decided that machine would be too slow to be effective.

 

June 1938 JRW purchased a uniselector and some relays on Petty Cash at RD Woolwich for spare-time experiments. Experiments abandoned owing to pressure of work on ballistics.

On seeing Aiken’s machine at Harvard, Womersley had written home to his wife that he saw it as ‘Turing in hardware’. And thus it was that in June 1945, according to his account:

 

JRW meets Professor M.H.A. Newman.* Tells Newman he wishes to meet Turing. Meets Turing same day and invites him home. JRW shows Turing the first report on the EDVAC and persuades him to join NPL staff, arranges interview and convinces Director and Secretary.

Alan would be appointed a Temporary Senior Scientific Officer at £800 per annum. Don Bayley, when told of this, did not think much of the rank, but Alan told him that it was the highest to which they could recruit, and that he had been assured of a promotion within a few weeks. It was not quite ‘Fivepence farthing for one – twopence for two’, as of the eggs that the Sheep offered Alice in the Looking Glass shop, but at £600 for naval Enigma, and £800 for the digital computer, the British government had certainly acquired a bargain in Alan Turing. Alan claimed that Womersley had asked him whether he knew ‘the integral of cos x’ which as Don Bayley immediately said, was a ludicrously trivial question to ask any prospective SSO, let alone a B-star Wrangler. ‘Ah’, said Alan, in a joke against his own capacity for carelessness, ‘but what if I had got it wrong?

On his side, Womersley expressed himself to colleagues as delighted with the capture of Alain Turing for his new department. And for Alan, who was careless about rank and terms of appointment, it was still the exciting prospect of having the British government itself support the realisation of a Universal Turing Machine. He had done his bit for them; now they could return the compliment. The NPL had been founded ‘to break down the barrier between theory and practice’, and this was exactly what Alan proposed to do. Whatever his doubts about the Civil Service, it offered him a chance. When he bid farewell to Joan Clarke and the others tidying up Hut 8, he talked excitedly of the future of automatic computers, and reassured them that mathematicians would not be put out of work.

In the general election of July 1945 he voted for the Labour party. ‘Time for a change’, he said vaguely later. It was hardly remarkable for one who belonged to a generation that had been champing at the bit while the ‘broad-bottomed’, as G.H. Hardy used to call them, ruled the roost. The conflicts of ‘the small back room’ were reflected in the hustings. The war had obliged the planning and state control that had been urged upon deaf ears in the 1930s, and the Labour party offered to preserve what Churchill proposed to dismantle – as Lloyd George had done in 1919. But Alan Turing was no Labour party stalwart, no more than he had been a ‘political’ person in the 1930s. The Abdication had roused him more than the Beveridge Report. As an admirer of Bernard Shaw, a reader of the New Statesman, and a wartime scientist up against the blinkered inertia of the old regime, he would approve of reform. But organisation and reorganisation did not really interest him.

His attitudes still had more in common with the democratic individualism of J.S. Mill than with the planners of 1945. But he did not share Mill’s interest in commercial competition. Indeed, he did not know anything about it. His life had been in interlocking schools, universities and government service. In his undergraduate days business had been a holiday, and the small Beuttell and Morcom firms were themselves exceptions to the twentieth century trend, representing a spirit which had largely died with Gladstone. And during the war, the contractors for equipment had been working on carte blanche government contracts in which ordinary considerations of profit had no application.

Money, commerce, and competition had played no obvious part in the central developments in which Alan Turing was enmeshed, developments which had allowed him in many ways to remain the idealistic undergraduate. His retention of a primitive liberalism, his ‘championing of the underdog’ as it was seen at Hanslope, like his obsession with the absolutely basic, had the flavour of more Utopian thinkers than Mill. Tolstoy was a figure that he brought to one person’s mind,31 and Claude Shannon had perceived him as like Nietzsche, ‘beyond Good and Evil’. But perhaps closer in spirit than either of these, and certainly closer to home, was another late nineteenth-century figure who had lurked more in the back room of political consciousness. That awkward figure Edward Carpenter, while sharing much in common with each of these European thinkers, had criticised Tolstoy for a restrictive attitude to sex and Nietzsche for overbearing arrogance. And in Carpenter, at a time when socialism was supposed to be about better organisation, lay the example of an English socialist not interested in organisation but in science, sex and simplicity – and with bringing these into mutual harmony. Born in 1844, he had written words³² during the First World War that already fitted a small boy at St Leonards-on-Sea, and which Alan Turing had continued to act out quite regardless of the opinions of more respectable persons:

 

I used to go and sit on the beach at Brighton and dream, and now I sit on the shore of human life and dream practically the same dreams. I remember about the time that I mention – or it may have been a trifle later – coming to the distinct conclusion that there were only two things really worth living for – the glory and beauty of Nature, and the glory and beauty of human love and friendship. And to-day I still feel the same. What else indeed is there? All the nonsense about riches, fame, distinction, ease, luxury and so forth – how little does it amount to! It really is not worth wasting time over. These things are so obviously secondhand affairs, useful only and in so far as they may lead to the first two, and short of their doing that liable to become odious and harmful. To become united and in line with the beauty and vitality of Nature (but, Lord help us! we are far enough off from that at present), and to become united with those we love – what other ultimate object in life is there? Surely all these other things, these games and examinations, these churches and chapels, these district councils and money markets, these top-hats and telephones and even the general necessity of earning one’s living – if they are not ultimately for that, what are they for?

Behind all the foibles and funny stories, and behind all the fuss made about his appearance and manners, lay the fact that as a boy he had never been able to understand how anyone could see life in any other way than this, and that at thirty-three only the war against Nazi Germany had dented that clinging to first principles.

There was a closer parallel than this, for Carpenter had been a Cambridge mathematician, and one fascinated by the same theme of mind in a deterministic world. He had the same upper-middle-class background, a parallel interest in biological growth. And he had abandoned Christian belief, while identifying himself as a homosexual. His book Homogenic Love, appearing in 1895, had been the first English work to place homosexual desire within a contemporary psychological and social context (rather than in that of ancient Greece), and to do so as part of a wholesale attack on ‘fixed moral codes’ – very close to the ‘general rules’ that Keynes, much more privately, rejected. And although not entirely relinquishing the idea that homosexuals had some special part to play, an idea not found in Alan Turing’s book, the burden of his argument was that ‘homogenic love’ should be part of the general give and take, the creative anarchy of life – neither good nor evil in itself, but as sociable, as selfish, as messy as anything else.

 

By 1945 this could be taken as Alan Turing’s view, for if sometimes he had seen his sexuality as a cross to bear, it was more and more a fact of life, one as much at the heart of what he was as that equally unasked-for, equally amoral, love of natural science. But in defending this view in 1945 he was taking a line that in fifty years hardly anyone had dared say in public more clearly than Carpenter. Not all the modernity of the war had changed this fact, and since his consciousness of sex had become clearer in 1933, there had been little but ‘semi-platonic sentimentality’ allowed.* Others, of course, were more content than he to remain the deceivers of men. And they were wise in worldly terms, for it remained a taboo more dangerous than the Soviet heresy. Untouched by electronic revolutions, unmentioned in the debates of 1945, it was not a subject for political people. But Alan Turing was not one of those.

The early Labour Party had been open to Carpenter’s ideals of a more simple life, and even of a New Morality. His naively lucid questioning of what life was for, and of what socialism was going to make it, had played a part in its more innocent days. Even when in power, in 1924, the first Labour cabinet had sent him a letter of thanks on his eightieth birthday. But the thirties had put paid to that. In 1937 George Orwell had ridiculed what remained of such impractical, distracting naiveté in The Road to Wigan Pier:

 

One sometimes gets the impression that the mere words ‘Socialism’ and ‘Communism’ draw towards them with magnetic force every fruit-juice drinker, nudist, sandal-wearer, sex-maniac, Quaker, ‘Nature Cure’ quack, pacifist and feminist in England.

In 1944 it was E.M. Forster, a liberal rather than a socialist, who remembered Carpenter’s centenary, and his cautious eulogy33 was that of a man forgotten. Both he and Lowes Dickinson had been influenced by Carpenter’s ideas – the happy pastoral ending in the ‘greenwood’ of the still unpublished Maurice was drawn from Carpenter’s rather scandalous life near Sheffield with a younger working-class man – and the more democratic side of King’s College, its lack of ‘stuffiness’ as well as its comparative openness to sexual dissent, owed something to his legacy.

The Labour party still had Carpenter’s song England Arise! as well as The Red Flag, but the shift of support to it in 1945 reflected the success of new men and modern methods rather than the sentiments of either anthem. There was now a political consciousness of the importance of science (though hardly in the way Carpenter would have wanted), but not of sex or simplicity. In 1937 – just as the first large calculators began the arithmetical relay race – George Orwell had been as repelled by the creed of ‘mechanization, rationalization, modernization’, as by the vegetarians and simple-lifers. But the war had brought it to power, and for good reason: Britain would have succumbed without it.

Orwell escaped from the dichotomy by appealing to an England of ‘ordinary, decent’ people. Alan Turing might have liked to do the same, but he was now hopelessly saddled with a mind full of extraordinary, indecent contradictions. It contained the greatest development of ‘mechanization, rationalization, modernization’ of the war, and another which was the greatest ever conceived, while still longing for ‘the commonest in nature’, and while still being precisely what Orwell meant by a ‘sex maniac’. He could not avoid these things, and having surrendered half of his mind to the government, was not free to try. He had done something, in a way that Orwell had not, and had passed the point of no return.

The paradox was not his alone, although his life took it to a peculiar intensity. The war had dealt a sharp blow to ‘fixed moral codes’, with social changes accelerated, old authorities questioned and new talents employed. Everyone had been made conscious of the defects of the old system, and more insidiously, of the fact that systems could be changed when survival made it necessary. To the dismay of conservative forces, British society had undergone a second and more thorough shaking up, this time with knowledge and ideas communicated to those excluded from participation in peace – ordinary men, the young, and even women. Bletchley Park had seen this happen as much as anywhere else. It had not been all a story of ‘men of the Professor type’; there had been boys of eighteen, ‘female mathematicians’, and Post Office engineers who had risen from the bottom of the ladder, all playing crucial parts.

In other ways, too, the consciousness of being a community, sharing a very limited common wealth, had brought people closer to the ‘least waste of energy’ of Alan Turing, spartan but not joyless. Even at a place such as Hanslope, enmeshed in the technical machinations of the secret service, the pleasures of Mess Nights, mountain-walking holidays, mushroom-cooking, games and self-education had taken on that enhanced value that Carpenter had rather laboriously tried to explain as ‘the Simplification of Life’.

There was a new spirit, and yet it was a spirit within a machine. A much enlarged state apparatus, and the more centralised economy, were the legacy of the great battle for intelligence and coordination. This time it would not be undone. And it was the machine, rather than glimpses of workers’ control, that inspired Ernest Bevin:34 ‘Calculation of profits and all the other things that have cluttered up progress in the past has to go and the great genius of our managers and technicians is being given full play. …’ It was true. Unhindered by wasteful competition and by the false economies of public parsimony, the Government Code and Cypher School and the Post Office had proved capable of managing fantastic feats. Now the development of the electronic computer was being taken over by the National Physical Laboratory for the public good. It deserved two cheers, as Forster would say, two cheers for managerial socialism. But management and techniques had not been the whole story, important as they might be. There had been something else, something now fading away while they waited for the other war to finish.

With Hitler out of the way, the games of Red and White could resume. Attlee replaced Churchill at the Potsdam conference when the results of the British election were known. Alan Turing went to Germany at the same time, in a party made up of five British and six American experts to report on German progress in communications. Flowers was one of the other British members. They left on 15 July, and arrived in Paris on a fine hot day. Here they were to meet the Americans, but the military headquarters had no idea who they were, so they took the day off. Late in the afternoon the telegrams from London came through, and they were assigned to the military transit camp, a hotel near the Madeleine. The same thing happened next day at Frankfurt when they reported to the American army headquarters in the I.G. Farben building. It was Patton’s area, and they were warned not to continue into Bavaria without permission from his staff, or they would be arrested by the military police. After another day they set off in a jeep along the pot-holed roads, going ‘hell for leather’ over 200 miles to make their destination before nightfall. They were stopped thirty-seven times by the MP’s because, being civilians, they had no tin hats.

So Alan Turing re-entered the ruined land of Gauss and Hilbert under watchful American eyes and in a military jeep. The party stayed at a communications laboratory at Ebermannstadt, near Bayreuth, which they had to reach by trudging up a thousand feet of mountain. It had been a hospital, and still bore a red cross on its roof, so they simply slept in the hospital beds. Women from the village came and did their washing, in return for a fragment of soap. Only he and Flowers had any cryptological interest, and the other members of the party did not (as far as they knew) know that they had. One of the captured German scientists proudly produced a machine of the Fish type, and explained how many billions of steps it would go through without repeating the key. Alan and Flowers just blinked and said, ‘Really!’ when he went on to tell them that none the less their mathematicians had reckoned it impregnable only for two years, and that then there would be a chance of it being broken.

While they were there, the mushroom cloud fulfilled the wilder prophecies of 1939. The quantum mechanics that Hardy had so recently pronounced gloriously useless, had come of age. It was the outward sign of the new men’s work. Maurice Pryce had played an early part in the British research, and the final touch had been added by von Neumann, calculating the height at which it should explode to effect the maximum destruction. The clouds rolled over the second enemy, that would-be latecomer to old-fashioned empire, and warned a potential new one. The Americans had solved the final problem of the war. Yet without the sequence of events that had kept the Enigma on the Allied side in 1943, the war of 1945 might have been very different, with the first atomic weapons reserved for the concrete pens of raiding U-boats.

The great secret was out – or rather, it was known that there was a secret, which made it so very different from the other one. American soldiers came up to the Ebermannstadt station with the news, which did not surprise Alan. He had known of the possibility before the war, and was good at picking up straws in the wind. After his return from America, he had posed both to Jack Good and to Shaun Wylie a question about a chain reaction, expressed in terms of barrels of gunpowder. He had also spoken of a possible ‘U-bomb’ at Hanslope lunchtimes. He gave a talk on the basic physical principle to the others at Ebermannstadt.

He remained in Germany until about the middle of August, and then returned to write his report on the visit. After six years, the war was officially finished. He had given his help in breaking the slave states, and in giving victory to the Yankees. Perhaps, less directly, his work had played a part in deciding the new boundaries of Animal Farm. But in 1945 few were dwelling upon the state of the eastern menagerie, although at Bletchley Park the new men had left the means with which to resume the politics of the 1920s.

No longer responsible for the world, they could get things right at home. In this respect Alan Turing was as fortunate as anyone. Even if his work had often been wasted, he had made the most of the war for himself, and emerged ready to contribute to the peace. The British had avoided defeat, and owed America for that. The ending of Lend-Lease was only the beginning of new problems. The power of British capital had shrunk, and its empire was to melt away. Yet arising in the mind were seeds of other kinds of growth.

 

* Wynn-Williams did make some progress, but this machine was probably the work of Keen and BTM.

^* There was more than one kind of Robinson: a ‘Peter Robinson’ and a ‘Robinson and Cleaver’ after London department stores, and a ‘Heath Robinson’ after the famous cartoonist specialising in elaborate machines to perform absurdly simple tasks.

^* It was from 16 to 22 November 1943.

^* Hence the name Rockex, coined by Travis and inspired by that better-known feature of the Rockefeller Center, the Rockettes.

^* Technically, of course, there was more to it than this. The speech would first be filtered to remove frequencies above 2000 Hz, and to restrict it to a specific range in amplitude so that it could be described at any point by a number between 0 and 1. Then in fact the encipherment was done by adding a continuous key signal first, and then taking the sample by making the resulting speech-plus-key signal modulate a pulse train. The ‘remaindering’ process would then be performed, chopping down a ‘spike’ by one unit if it exceeded one unit in amplitude.

^* The output of the ‘orthogonal’ circuit would have the characteristics of random noise in the frequency range up to 2000 Hz. It would be deciphered by performing the sampling process (in strict synchrony, of course, with the sender), and a modular subtraction of the identical key. This would yield the samples of the original speech signal, and it was then a standard procedure, requiring only a low-frequency filter, to recover the speech itself.

^† As Alan would stress in explaining the system, this depended crucially upon the use of modular addition. If ordinary unremaindered addition were used, then there would be a correlation between the speech amplitudes and the speech-plus-key amplitudes, and this the cryptanalyst could exploit. Indeed, this is precisely what the ear does in sorting out speech from background noise.

^* Fourier theory very naturally involved the use of the ‘complex numbers’, and so did other aspects of the analysis of electronic circuits. the mathematics that he needed was at the undergraduate level – nothing as advances as the work on the Riemann zeta-function before the war. as with statistical theory he developed at bletchley, this was a very good eample of how quite elemetary nineteenth-century mathematics had applications to the techology of the 1940s that no one had seen, or had tried to seee.

^* He once expressed himself as shocked by the indiscreet talk at a college dinner of a certain eminent wartime scientist.

^* The signal-to-noise ratio was only l0dB, meaning that the speech had only ten times the power of the noise.

^* That is, he had arrived at the automatic electronic digital computer with internal program storage. In what follows, the word ‘computer’ will be reserved for machines satisfying all these conditions. But in 1945 the word ‘computer’ meant what it had meant in 1935: either a person who did computations, or any type of machine (in anti-aircraft artillery, for instance) which mechanised that computation. It was not for about ten years that ‘computer’, or even ‘digital computer’, took on the new meaning. Meanwhile a variety of more cumbersome terms were used, and correspondingly the concept was less clear at the time than it later became, particularly regarding the internally stored program. Alan Turing had not invented a thing, but had brought together a powerful collection of ideas; since the ideas condensed into exactly what became ‘the computer’ it does not do too grave an injury to history to employ the word anachronistically. In fact the anachronism reflects quite well the difficulty that he faced in communicating to the 1940s a picture that belonged to the 1960s.

^* Certainly Ada, Countess of Lovelace, writing her interpretation²¹ of Babbage’s ideas in 1842, expressed this idea in a passage of prophetic insight:

The bounds of arithmetic were, however, outstepped the moment the idea of applying the cards had occurred; and the Analytical Engine does not occupy common ground with mere ‘calculating machines’. It holds a position wholly its own; and the considerations it suggests are most interesting in their nature. In enabling mechanism to combine together general symbols, in successions of unlimited variety and extent, a uniting link is established between the operations of matter and the abstract mental processes of the most abstract branch of mathematical science. A new, a vast and a powerful language is developed for the future use of analysis, in which to wield its truths so that these may become of more speedy and accurate practical application for the purposes of mankind than the means hitherto in our possession have rendered possible. Thus not only the mental and the material, but the theoretical and the practical in the mathematical world, are brought into more intimate and effective connexion with each other. We are not aware of its being on record that anything partaking of the nature of what is so well designated the Analytical Engine has been hitherto proposed, or even thought of, as a practical possibility, any more than the idea of a thinking or of a reasoning machine.

^* But neither was the first in this respect. At Iowa State University, J.V. Atanasoff had been using electronics for mechanising arithmetical operations since 1939.

^* Indeed its first serious use, in late 1945, would be on a trial calculation for the hydrogen bomb.

^* Here one must assume that the secrecy surrounding Bletchley operations had been breached sufficiently for Womersley (through Darwin and Hartree, perhaps also through Blackett), to learn of the existence of the electronic Colossus and also of Alan’s general whereabouts.

^*Indeed the second Waugh, in 1945, had largely revisited the semi-platonic sentimentality of the first.