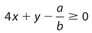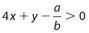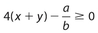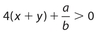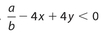CHAPTER 8:
Working with Two or More Unknowns

“Understanding more complex problems will be gratifying to you.”
SOLVING SIMULTANEOUS EQUATIONS
We can solve two equations in two unknowns, also known as simultaneous equations, in five basic ways. Only two are practical for this exam: substitution and elimination. Sometimes we use a combination of these two.
Substitution
In substitution, we find an unknown with a coefficient of 1, solve for that variable, and substitute it in the other equation.
Example 1: Solve for x and y:

(1)

(2)
Solution:
In equation (2) x = 5y + 14. Substituting this into equation (1), we get 3(5y + 14) + 4y = 4. Solving, we get y = − 2; x = 5y + 14 = 5(-2) + 14 = 4. The answer is x = 4 and y = − 2.
Example 2: Solve for x and y:
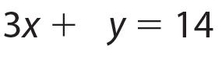
1
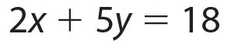
2
Solution:
In equation (1), we solve for y: y = 14 − 3x, and substitute it into equation (2). Equation (2) then becomes 2x + 5(14 − 3x) = 18. Solving this equation, we get 2x + 70 − 15x = 18, or −13x = − 52. So x = 4. Since y = 14 − 3x, y = 14 − 3(4) = 2. The answer is x = 4 and y = 2.
We can check by substituting these values into the original equations to see that they are solutions to both equations.
Elimination
If none of the original coefficients of any of the terms is 1, it is usually better to use the elimination method. There are several ways to eliminate one of the variables, as seen in the following examples. Once we have eliminated one of the variables, we can solve for the other variable by using substitution.
Example 3:
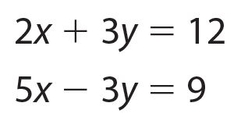
Solution:
If we add the equations, term by term, we can eliminate the y term. We get 7x = 21, so x = 3; substituting x = 3 into either equation, we get y = 2. So the answer is x = 3, y = 2.
Example 4:
Solve for x and y:
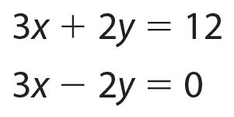
Solution:
Again, just add the equations. The y term cancels out, and we get 6x = 12; x = 2. We substitute this value for x into either equation to find a value for y: 3x + 2y = 12; 3(2) + 2y = 12; 2y = 6; so y = 3. The answer is x = 2 and y = 3.
Example 5:
Solve for x and y:
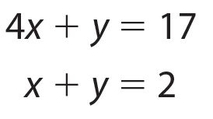
Solution:
If adding doesn’t work to eliminate one variable, try subtracting. We get 3x = 15, so x = 5, and y = −3, by substitution into the second equation, the easier one. Mathematicians always try to do things the easiest way possible!
Example 6:
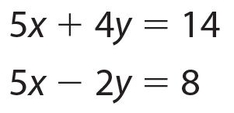
Solution:
Subtracting, we get 6y = 6; so y = 1; substituting, we get x = 2.
If adding or subtracting doesn’t work, we must find two numbers that when we multiply the first equation by one of them and the second equation by the other, and then add (or subtract) the resulting equations, one letter is eliminated, as shown in the following examples.
Example 7:

(1)
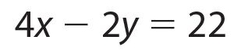
(2)
Solution:
To eliminate x, multiply the first equation by 4 and the second by −5; then add.
4(5x + 3y) = 4(11) or 20x + 12y = 44
− 5(4x − 2y) = −5(22) or − 20x + 10y = − 110
Adding, we get 22y = − 66; so y = −3. We could substitute now, but we could also eliminate y by multiplying the original equation (1) by 2 and equation (2) by 3. Let’s do that.
2(5x + 3y) = 2(11) or 10x + 6y = 22
3(4x − 2y) = 3(22) or 12 x − 6y = 66
Adding, we get 22x = 88; so x = 4. The answer is x = 4, y = −3.
Example 8:
Solve for x and y:
5x + 4y = 11 2x − 3y = 9
Solution:
Let’s look at 5x and 2x. If we multiply 5x by 2 and 2x by − 5 and then add, the x terms will disappear.
2(5x + 4y) = 2(11) or 10x + 8y = 22
− 5(2x − 3y) = (−5)(9) or −10x + 15y = −45
Adding these two new equations, we get 23y = − 23; so y = −1. We can then get x by substitution into either original equation. Using the second equation (again, the easier one), we get 2x − 3(−1) = 9, or 2x = 6, so x = 3.The answer is x = 3 and y = −1.
Practice in Solving Simultaneous Equations
For those of you who are curious, the other three basic ways of solving simultaneous equations are by using graphs, matrices, or determinants.
 Let’s do some exercises.
Let’s do some exercises.
Exercise 1:
If x + y = 12 and x − y = 18, y − 3 =
- −6
- −3
- 0
- 12
- 15
Exercise 2:
3x + 2y = 61 and 4x + 5y = 16; x + y =
- 3
- 5
- 7
- 11
- Cannot be determined
Exercise 3:
6x − 7y = 42 and 3x − 10y = 27; x + y =
- 3
- 5
- 7
- 11
- Cannot be determined

Sometimes “cannot be determined” can occur as an answer; however, I’ve never found it could be the answer for two questions in a row.
| Quantity A | Quantity B | |
|---|---|---|
| Exercise 4: 6x + 6y = 48 | The mean of x and y | 4 |
| Exercise 5: If x = y + 3 and y = z + 7, x (in terms of z) = | ||
- z −10
- z − 4
- z
- z + 4
- z + 10
Exercise 6:
Two apples and 3 pears cost 65 cents, and 5 apples and 4 pears cost $1.10. Find the cost of one pear:
- 10
- 15
- 20
- 25
- 30
Exercise 7:
As in Exercise 6, 2 apples and 3 pears cost 65 cents, and 5 apples and 4 pears cost $1.10. Find the cost in cents of one pear and one apple together:
- 10
- 15
- 20
- 25
- 30
Exercise 8:
Find x + y:
7x + 4y = 27 x − 2y = −3
- 1
- 3
- 5
- 7
- 9
Exercise 9:
For lunch, Ed buys 3 hamburgers and one soda for $12.50, and Mei buys one hamburger and one soda for $5.60. How much does Ed pay for his hamburgers?
- $2.15
- $3.45
- $6.90
- $10.35
- $18.10
 Let’s look at the answers.
Let’s look at the answers.
Answer 1 :
The answer is (A). Adding, we get 2x = 30. So x = 15. By substitution, we get y = −3; so − 3 − 3 = −6.
Answer 2:
The answer is (D). This is a trick. We could solve for x and y, but it takes a long time. The problem asks for x + y. Eighty percent of the time, just add the equations. Here we get 7x + 7y = 77; so x + y = 11.
Answer 3:
The answer is (B). Another trick. We subtract the equations and get 3x + 3y = 15; so x + y = 5.
Answer 4:
The answer is (C). x + y = 8; the mean is defined as 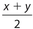 , so the mean is 4.
, so the mean is 4.
Answer 5:
The answer is (E). x = y + 3 = (z + 7) + 3 = z + 10.
Answer 6:
The answer is (B). The equations are
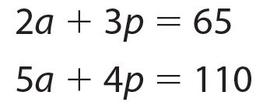
In solving for p, eliminate a by multiplying the top equation by 5 and the bottom by −2.
5(2a + 3p) = 5(65) or 10a + 15 p = 325
−2(5a + 4p) = −2(110) or −10a − 8p = −220
Adding, we get 7p = 105; p = 15.
Answer 7:
The answer is (D). Much more often, we get a problem like this. The equations are the same as in Exercise 6, but rather than asking for the cost of one apple or the cost of one pear, this exercise asks for the cost of one apple plus one pear. The trick is simply to add the original equations to get 7a + 7p = 175. Dividing both sides by 7, we get a + p = 25.
Answer 8:
The answer is (C). Less frequently, when adding doesn’t work, try subtracting. If we subtract here, the difference becomes 6x + 6y = 30. So x + y = 5.
Answer 9:
The answer is (D). The equations are
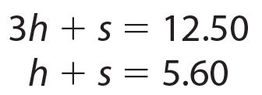
Subtracting, we get 2h = 6.90, so h = 3.45. Thus, Ed’s three hamburgers cost $10.35.
NEW WORD PROBLEMS
Let’s try some “new” word problems. The only true difference from what we saw in Chapter 7 involves tens and units digit problems.
Digit Problems
If we have a two-digit number, it is represented by t for the tens digit and u for the units digit. For example, for 68, t = 6 and u = 8. The value of the number is represented by 10t + u. The number 68 would thus be 10(6) + 8. The number with the digits reversed is 10u + t, or 86 = 8(10) + 6. The sum of the digits is t + u, or 6 + 8 = 14, in this case.
Example 9:
In a two-digit number, the sum of the digits is 8. If the digits are reversed, the new number is 36 more than the original number. What is the number?
Solution:
There are two methods to answer this question:
Method A: t + u = 8 is the first equation. The new number, 10u + t is (=) 36 more than the original number, or 10t + u + 36. So the equation is 10u + t = 10t + u + 36, or 9u − 9t = 36. In this type of problem only, we can divide the equation by 9 and get u − t = 4. Since t + u = 8, adding these two equations gives 2u = 12, or u = 6, so t = 2, and the number is 26.
Method B: Since t + u = 8, the only possible answers could be 17, 26, or 35, since the number with the digits reversed is bigger. 71 − 17 ≠ 38, but 62 − 26 = 36; so the number is 26.
Mixture Problems
Mixture problems with two unknowns are treated similarly to how we did mixture problems with one unknown in the last chapter. It often helps to construct a chart.
Example 10:
How many pounds of peanuts at $3.00 a pound must be mixed with $7.00-per-pound cashews to give 20 pounds of a $6.00-per-pound mixture?
Solution:
Construct a chart with the given information.
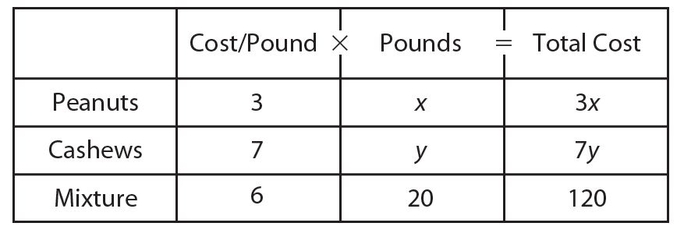
Let x = pounds of peanuts and y = pounds of cashews. According to the chart,
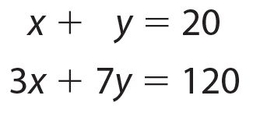
Since we want x, multiply the top equation by −7, and add the result to the second equation.
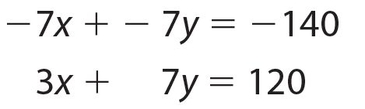
Adding, we get −4x = −20, so x = 5 pounds of peanuts.
Age Problems
Age problems with two unknowns are treated similarly to how we did age problems with one unknown in the last chapter. It often helps to construct a chart.
Example 11:
Joan is 4 times the age of Ben. In 4 years, Joan will be 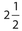 times the age of Ben. Ben will be how many years old then?
times the age of Ben. Ben will be how many years old then?
Solution:
Construct a chart with the given information.
| Age now | Age in 4 years | |
|---|---|---|
| Joan | x | x + 4 |
| Ben | y | y + 4 |
Let x = Joan’s age and y = Ben’s age. The first equation is x = 4y.
In 4 years, the equation is  , or 2(x + 4) = 5(y + 4).
, or 2(x + 4) = 5(y + 4).
By the Distributive Law (Chapter 5), 2x + 8 = 5y + 20, or 2x − 5y = 12.
But we know x = 4y. So, by substitution, 2(4y) − 5y = 12, or 3y = 12, so y = 4 (Ben’s present age). In 4 years, Ben will be y + 4 = 8 years old.
Fraction Problems
Sometimes, trial and error finds the answer for you. Simply substitute the answer choices into the problem to see what works. But you should also be able to set up simultaneous equations. You might ask, “What is the best method? ”The answer is, “Whatever gives you the answer the fastest.” Everyone is different.
Example 12:
A fraction when reduced is 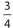 . If 1 is subtracted from the numerator 4 and 2 is added to the denominator, the ratio becomes
. If 1 is subtracted from the numerator 4 and 2 is added to the denominator, the ratio becomes 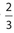 . What is the 3 original fraction?
. What is the 3 original fraction?
Solution:
We have 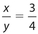 , or 3y = 4x, which gives us −4x + 3y = 0. We also have
, or 3y = 4x, which gives us −4x + 3y = 0. We also have 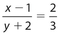 , or, by cross-multiplication, 3(x − 1) = 2(y + 2). This gives us 3x − 2y = 7. Our simultaneous equations are
, or, by cross-multiplication, 3(x − 1) = 2(y + 2). This gives us 3x − 2y = 7. Our simultaneous equations are
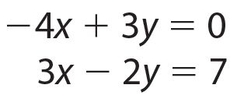
If we eliminate x by multiplying the top equation by 3 and the bottom equation by 4 and adding the resulting equations, we get y = 28, and by substitution, x = 21. So the original fraction is 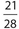 .
.
 Let’s do a few exercises.
Let’s do a few exercises.
Exercise 10:
In a two-digit number, the tens digit is the square of the units digit. The difference between the number and the number reversed is 54. The original number is
- . 24
- . 39
- . 42
- 71
- 93
Exercise 11:
How many ounces of 40% alcohol must be mixed with 10 ounces of 70% alcohol to give a solution that is 45% alcohol?
- . 20
- 30
- . 40
- . 50
- . 60
Exercise 12:
May’s age is twice Fay’s age. In 15 years, Fay will be 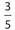 as old as May. The sum of their original ages is 5
as old as May. The sum of their original ages is 5
- . 66
- 75
- 90
- . 96
- . 105
Exercise 13:
If 4 less than x is the same as 7 more than the product of 4 and y, which answer choice is true?
- . x + 4y − 11 = 0
- . x + y + 15 = 0
- . x + y + 7 = 0
- . x + 4y − 11 = 0
- 4y − x + 11 = 0
Exercise 14:
The product of 4 and the sum of x and y is at least as large as the quotient of a divided by b. This can be written as
Exercise 15:
The sum of the digits of a two-digit number is 10. The number reversed is 18 more than the original number. The original number is
- 19
- 28
- 37
- 46
- 55
Exercise 16:
The equation of line 1 is x − y = 6 and the equation of line 2 is ax − by = 20, where a, b are integers. In exactly how many points may these lines intersect? Indicate all correct answers.
- 0
- 1
- 2
- 3
- 5
- Infinite number
Exercise 17:
One hamburger costs $2.00 and a bottle of soda costs $1.25. John must buy twice as many hamburgers as bottles of soda. If he will spend less than $20, how many hamburgers can he buy? Indicate all correct answers.
- 2
- 3
- 4
- . 6
- . 8
- 10
Exercise 18:
If y = x2 and y = x + 6 are graphed on the same coordinate axes, which of the following points lie on both curves? Indicate all correct answers.
- (−2, 9)
- (−2, 4)
- (1, 1)
- (2, 4)
- (3, 9)
- (4, 16)
Exercise 19:
A principal sells $600 worth of tickets to a school play. Children’s tickets cost $5 each and adult tickets cost $8 each. Which of the following could be the number of children’s tickets sold? Indicate all correct answers.
- 20
- 24
- 40
- 60
- 80
- 104
Exercise 20:
What is the y-coordinate of the intersection point of the lines represented by 3x + 5y = 5 and 2x − 5y = 55? Be sure your answer is in fraction form.

Exercise 21:
Four pears and five apples cost $7. Two pears and one apple cost $5. What is the combined cost of one pear and one apple?

Exercise 22:
The sum of the digits of a two-digit number is 9. If the digits are reversed, the new number is 27 greater than the original number. What is the product of the digits?
 Let’s look at the answers.
Let’s look at the answers.
Answer 10:
The answer is (E). Trial and error is best for this problem. Of the answer choices, the only possible ones are 42 since 22 = 4, and 93 since 32 = 9. However, only for 93 is the second criterion true: 93 − 39 = 54.
Answer 11:
The answer is (D). This is a mixture problem. The principle is this: If we have 10 ounces of 70% alcohol, the amount of alcohol is 10(.70) = 7 ounces of alcohol. Now construct a chart for this problem; eliminate the decimal point since all items in this will have a decimal.
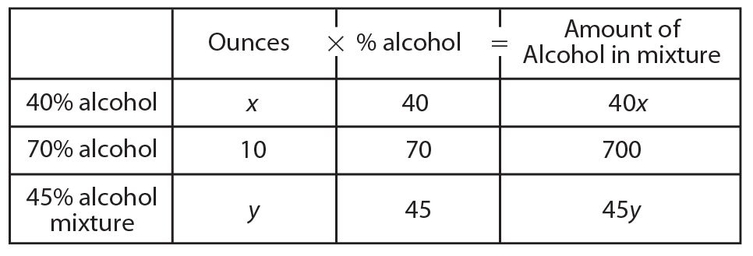
We let x = the amount of 40% alcohol, and y = the total ounces in the mixture. We get x + 10 = y and 40(x) + 10(70) = 45(y), since we can eliminate all decimal points in this equation. Substitute the first equation fory because we want x: 40x + 700 = 45(x + 10), or 45x + 450 = 40x + 700. Thus, 5x = 250, and x = 50.
Answer 12:
The answer is (C). Consruct a chart in which May’s age is y and Fay’s age is x.
| Age now | Age in 15 years | |
|---|---|---|
| May | y | y + 15 |
| Fay | x | x + 15 |
From the chart y = 2x and 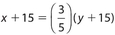 , or 5(x + 15) =
, or 5(x + 15) =
3(y + 15). Then 5x + 30 = 3y. Substituting y = 2x, we get 5x + 30 = 3(2x), so x = 30 and y = 60.The sum of their ages is x + y = 90.
Answer 13:
The answer is (E). x − 4 = 4y + 7. When we rearrange the terms, we see that only (E) is correct.
Answer 14:
The answer is (C). 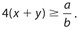 When we rearrange the terms, we see that only (C) is correct.
When we rearrange the terms, we see that only (C) is correct.
Answer 15:
The answer is (D). t + u = 10 and 10u + t = 10f + u + 18, or 9u − 9t = 18. Dividing both sides of this equation by 9, we get u − t = 2. We thus have t + u = 10 and u − t = 2. Adding these equations, we get 2u = 12, so u = 6 and t = 4. Thus, the number is 46. We could have used trial and error for this problem.
Answer 16:
The correct answers are (A) and (B). In general, two lines may intersect in zero, one, or an infinite number of points. Choice (A) is correct if line 2 is parallel to line 1, which can occur if the slopes of their lines are equal. The slope of line 1 is 1, and the slope of line 2 is also 1 if a = b. If a ≠ b, then choice (B) is correct because lines 1 and 2 will intersect in exactly one point. Choice (F) is wrong because two lines can share an infinite number of points only if they are the same line. This would require that one equation is a multiple of the other equation, but a and b are integers, and 20 is not a multiple of 6.
Answer 17:
The correct answers are (A), (C), and (D). Let x represent the number of bottles of soda and 2x represent the number of hamburgers. Then $1.25x + ($2.00)(2x) < $20.00. Dropping the dollar signs and simplifying the left side of the inequality, we get 5.25x < 20.00. Then x < 3.8. Since x must be an integer, the only positive allowable values are 1, 2, and 3. Thus, the number of hamburgers John can buy, represented by 2x, are 2, 4, and 6. (Note that choice (B) is impossible, because John would have to buy 1.5 bottles of soda.)
Answer 18:
The correct answers are (B) and (E). The points of intersection can be found by the equation x2 = x + 6, which can be written as x2 − x − 6 = 0. Then (x + 2)(x − 3) = 0, so x = −2 or x = 3. We can use the equation y = x + 6 to determine the corresponding y values. If x = −2, then y = 4. If x = 3, then y = 9. Thus, the two intersection points are (−2, 4) and (3, 9). (Note that we could have used the equation y = x2 to arrive at the same two points of intersection.)
Answer 19:
The correct answers are (B), (C), (E), and (F). Each of the number of adult and student tickets must be a nonnegative integer. If x represents the number of student tickets and y represents the number of adult tickets, then 5x + 8y = 600. For answer choice (B), when x = 24, (5)(24) + 8y = 600. This equation simplifies to 8y = 600 − (5)(24) = 480, which means that y = 60. By substituting each of the given x values (number of student tickets) into 5x + 8y = 600, the corresponding y value must be a nonnegative integer. For choices (C), (E), and (F), the y values are 50, 25, and 10, respectively. Choice A is wrong because (5)(20) + 8y = 600 leads to 8y = 500, so y is not an integer (it is 62.5). Choice D is wrong because (5)(60) + 8y = 600 leads to 8y = 300, so y isn’t an integer (it is 37.5). You don’t actually have to find y—you just have to realize it will have to be a positive integer.
Answer 20:
The answer is 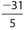 . Adding the equations, we get 5x = 60. Then x = 12. Substitute this value of x into either equation. Using the equation 3x + 5y = 5, we get (3)(12) + 5y = 5. Then 5y = 5 − 36 = −31. Therefore,
. Adding the equations, we get 5x = 60. Then x = 12. Substitute this value of x into either equation. Using the equation 3x + 5y = 5, we get (3)(12) + 5y = 5. Then 5y = 5 − 36 = −31. Therefore, 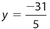 .
.
Answer 21:
The correct answer is 2. Let x represent the cost of one pear and let y represent the cost of one apple. Then 4x + 5y = 7 and 2x + y = 5. Adding these equations leads to 6x + 6y = 12, which simplifies to x + y = 2. Thus, the combined cost of one pear and one apple is $2. (Do not put the dollar sign inside the box.)
Answer 22:
The correct answer is 18. Let t represent the tens digit and u represent the units digit of the original number. Then the original number is represented by 10t + u, so the new number is represented by 10u + t. Then t + u = 9 and 10u + t = 10t + u + 27. The second of these two equations simplifies to −9t + 9u = 27, which can be further simplified to −t + u = 3. Add the equations t + u = 9 and −t + u = 3 to get 2u = 12. Thus u = 6. Since the sum of the digits is 9, t = 3. Therefore, the product of the digits is (6)(3) = 18.
Let’s take a break from algebra and word problems now, and look at some familiar lines and shapes.