CHAPTER 10:
About Angles and Triangles

“Understanding the area and its perimeter will enhance your chances for success.”
Before I wrote this chapter, I formulated in my head how the chapter would go. Too many of the questions on angles had to do with triangles. So I decided to write the chapters together. Let’s start with some definitions.
TYPES OF ANGLES
There are several ways to classify angles, such as by angle measure, as shown here:
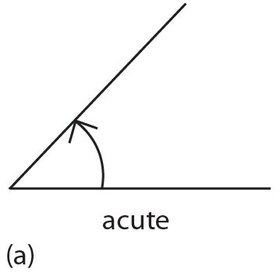
Acute angle: An angle of less than 90°.
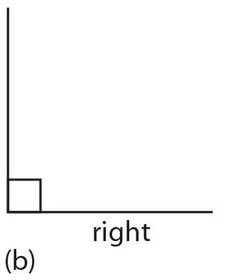
Right angle: A 90° angle. As we will see, some other words that indicate a right angle or angles are perpendicular (⊥), altitude, and height.
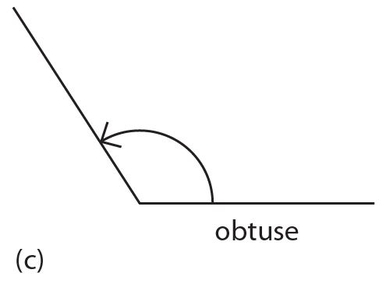
Obtuse angle: An angle of more than 90° but less than 180°.
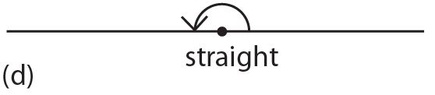
Straight angle: An angle of 180°.
Reflex angle: An angle of more than 180° but less than 360°.
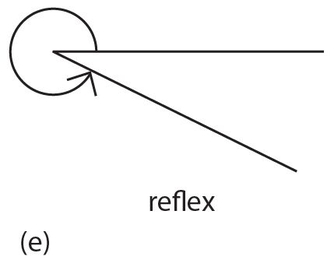
Angles are also named for their relation to other angles, such as:
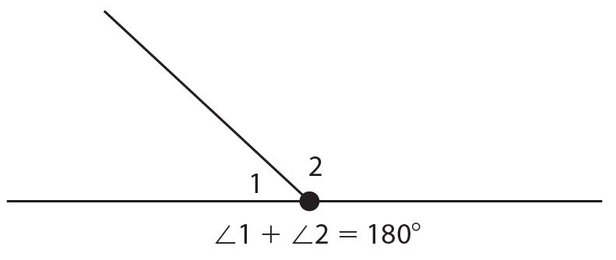
Supplementary angles: Two angles that total 180°.
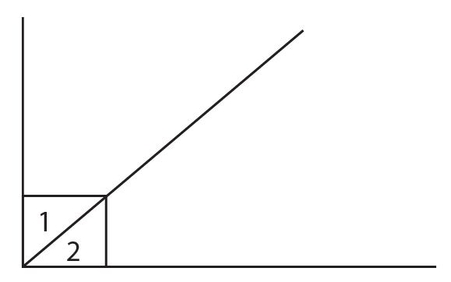
Complementary angles: Two angles that total 90°.
A note of interest: Once around a circle is 360°. The reason that it is 360° is that the ancient Babylonians, about 7,000 years ago, thought there were 360 days in a year. Three hundred sixty degrees is unique to the planet Earth.
You probably learned that angles are congruent and measures of angles are equal. I am using what I learned; it is simpler and makes understanding easier. So “angle 1 equals angle 2” (or ∠1 = ∠2 ) means the angles are both congruent and equal in degrees.
ANGLES FORMED BY PARALLEL LINES
Let’s look at angles formed when a line crosses two parallel lines. In the figure below, L1 || L2′, and t is a transversal, a line that cuts two or more lines. It is not important that you know the names of these angles, although many of you will. It is important only to know that angles formed by a line crossing parallel lines that look equal are equal. The angles that are not equal add to 180°. In this figure, ∠1 = ∠4 = ∠5 = ∠8 and ∠2 = ∠3 = ∠6 = ∠7. Any angle from the first group added to any angle from the second group totals 180°.
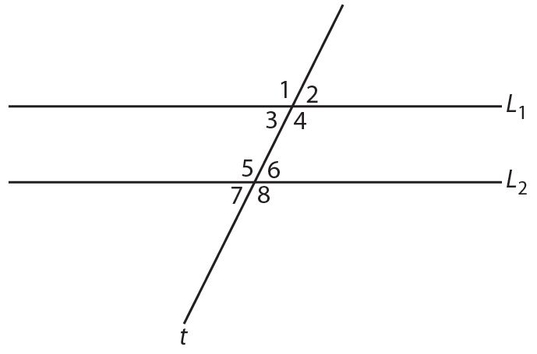
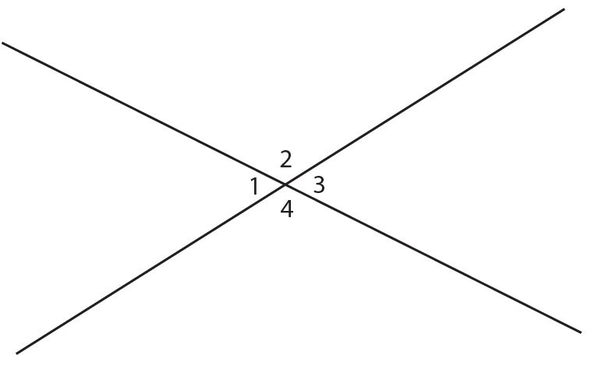
Vertical angles, which are the opposite angles formed when two lines cross, are equal. In the figure below, ∠1 = ∠3 and ∠2 = ∠4 . Also, ∠1 + ∠2 = ∠2 + ∠3 = ∠3 + ∠4 = ∠4 + ∠1 =180°.
 Let’s do some exercises.
Let’s do some exercises.
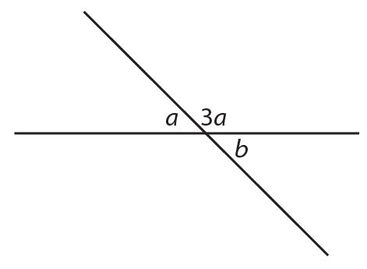
Exercise 1:
∠b =
- 45°
- 60°
- 90°
- 105°
- 135°
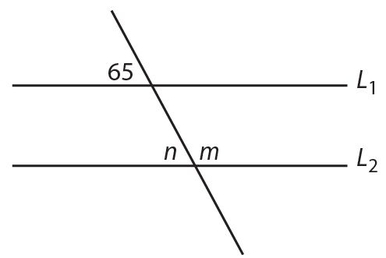
Exercise 2:
L1 ∥ L2. m − n =
- 30°
- 50°
- 65°
- 90°
- 180°
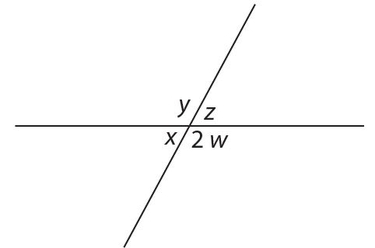
Exercise 3:
y + z =
- . 180° − x
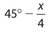
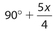
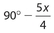
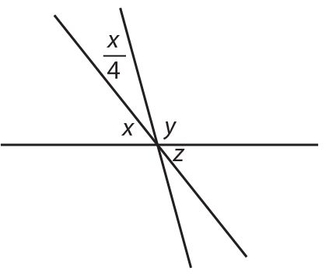
Exercise 4:
180° − w =
- x + w
- x + y
- y + z
- y − z
- z − w
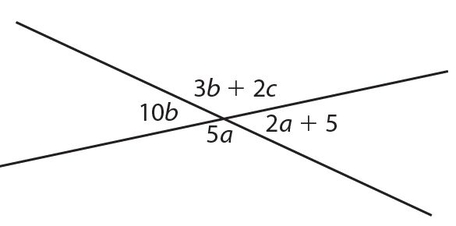
Exercise 5:
b =
- 5.5°
- 7°
- 10°
- 12.5°
- Cannot be determined
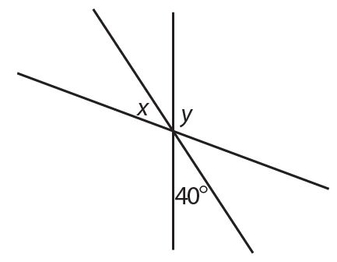
Exercise 6:
y (in terms of x) =
- x
- x + 40°
- 140° − x
- 140° + x
- 320° − x
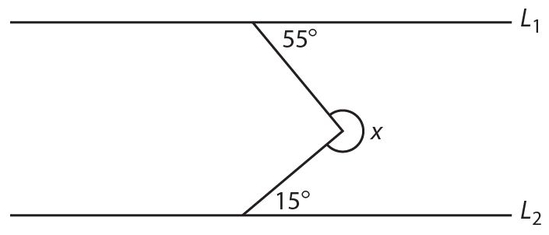
Exercise 7:
∠x =
- 70°
- 110°
- 210°
- 290°
- 345°
 Now let’s look at the answers.
Now let’s look at the answers.
Answer 1:
The answer is (A). 3a + a = 180°; a = 45° and b = a = 45°.
Answer 2:
The answer is (B). n = 65° and n + m = 180°; so m = 115°, and m − n = 50°.
Answer 3:
The answer is (B). 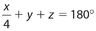 , so
, so 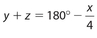 .
.
Answer 4:
The answer is (A). Below the line, x + 2w = x + w + w = 180°, so x + w = 180° − w.
Answer 5:
The answer is (A). This is a toughie. Don’t look at vertical angles, look at the supplementary angles. On the bottom, we have 5a + 2a + 5° = 180°, so 7a = 175°, and a = 25°. Then, on the left, 10b + 5a = 180°. Substituting a = 25°, we get 10b = 180° − 125° = 55°, or b = 5.5°.
We could also have looked at the vertical angles, once we determined that a = 25°. Then 10b = 2a + 5° = 2(25°) + 5° = 55°, so b = 5.5°.
Answer 6:
The answer is (C). x + y + 40° = 180°; so y = 140° − x.
Answer 7:
The answer is (D). Draw L3 ∥ L1 and L2.
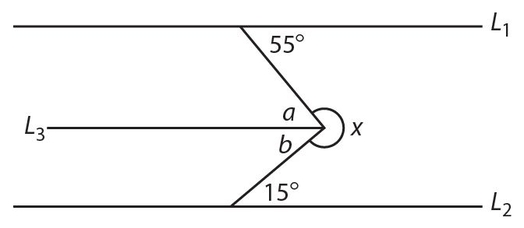
∠x = 360° − 70° = 290°.
So many angle questions on the GRE involve triangles that we ought to look at triangles next.
TRIANGLES
Basics about Triangles
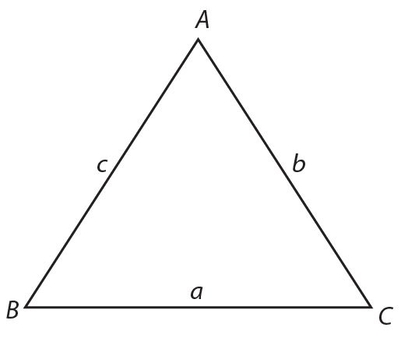
A triangle is a polygon with three sides. Angles are usually indicated with capital letters. The side opposite the angle is indicated with the same letter, only lowercase.
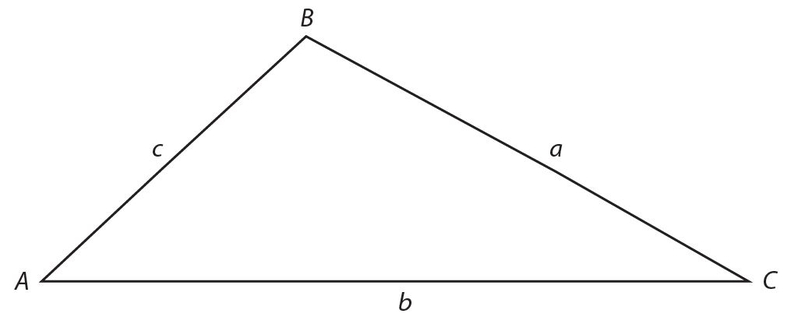
You should know the following general facts about triangles.
The sum of the angles of a triangle is 180°.
The altitude, or height (h), of ΔABC shown below is the line segment drawn from a vertex perpendicular to the base, extended if necessary. The base of the triangle is AC = b.
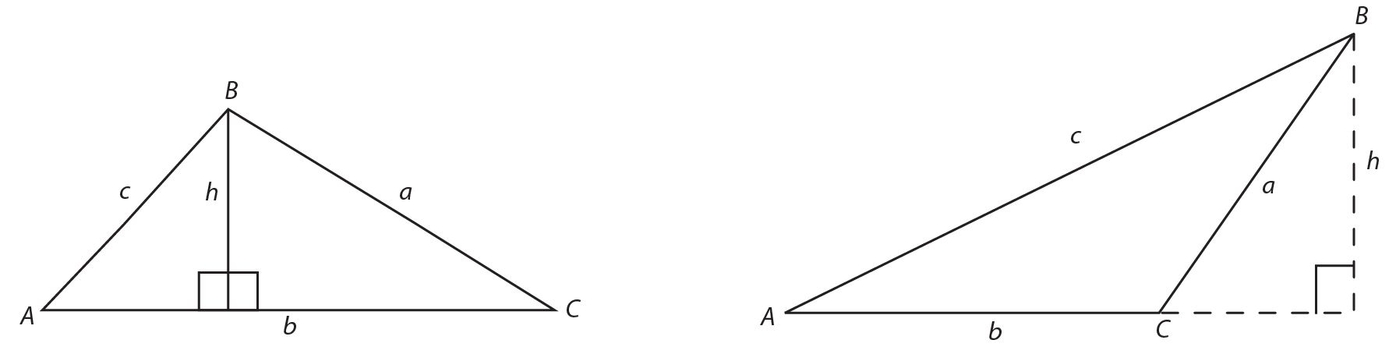
The perimeter of a triangle is the sum of the three sides: p = a + b + c.
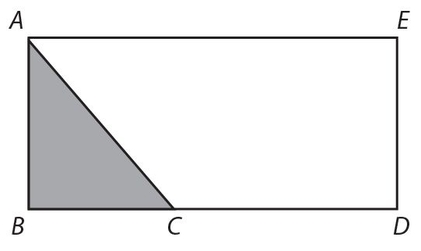
The area of a triangle is 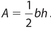 . The reason is that a triangle is half a rectangle. Since the area of a rectangle is base times height; a triangle is half a rectangle, as shown in the figure below.
. The reason is that a triangle is half a rectangle. Since the area of a rectangle is base times height; a triangle is half a rectangle, as shown in the figure below.
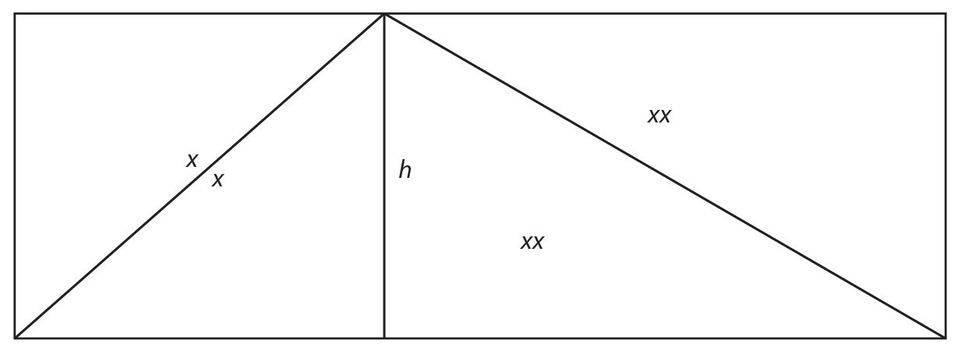
An angle bisector is a line that bisects an angle in a triangle. In the figure below, BD bisects ∠ABC if ∠1 = ∠2.
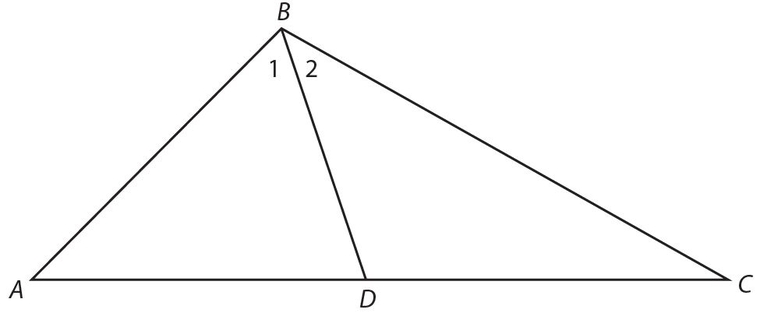
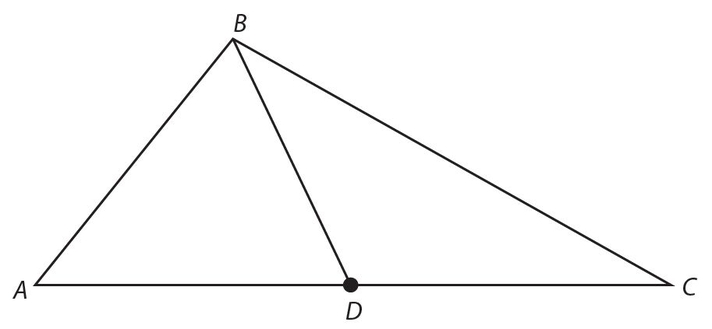
A median is a line drawn from any angle of a triangle to the midpoint of the opposite side. In the figure below, BD is a median to side AC if D is the midpoint of AC.
There are many kinds of triangles. One way to describe them is by their sides.
A scalene triangle has three unequal sides and three unequal angles.
An isosceles triangle has at least two equal sides. In the figure below, side BC (or a) is called the base; it may be equal to, greater than, or less than any other side. The legs, AB = AC (or b = c) are equal. Angle A is the vertex angle; it may equal the others, or be greater than or less than the others. The base angles are equal: ∠B = ∠C.
An equilateral triangle is a triangle with all equal sides. All angles equal 60°, so this triangle is sometimes called an equiangular triangle. For an equilateral triangle of side s, the perimeter p = 3s, and the area 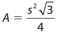 . This formula seems to be very popular lately, and you may see it on the GRE.
. This formula seems to be very popular lately, and you may see it on the GRE.
Triangles can also be described by their angles.
An acute triangle has three angles that are less than 90°.
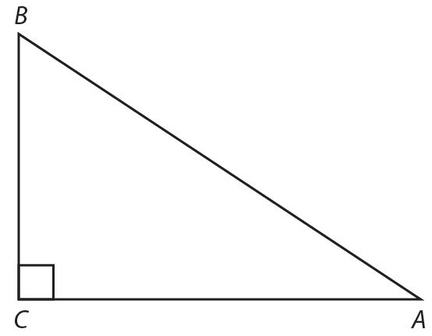
A right triangle has one right angle, as shown in the figure below. The right angle is usually denoted by the capital letter C. The hypotenuse AB is the side opposite the right angle. The legs, AC and BC, are not necessarily equal. ∠A and ∠B are always acute angles.
An obtuse triangle has one angle between 90° and 180°.
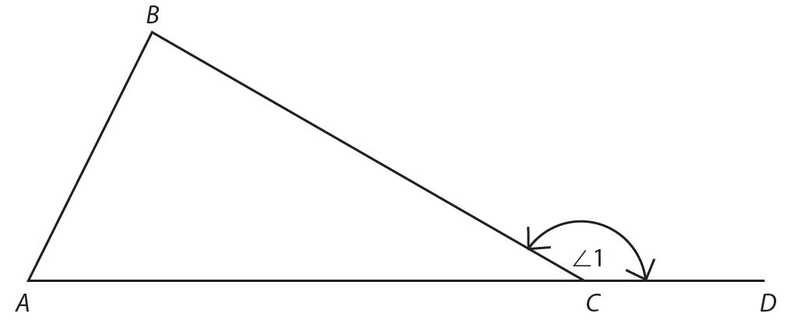
An exterior angle of a triangle is formed by extending one side. In the figure below, ∠1 is an exterior angle. An exterior angle equals the sum of its two remote interior angles: ∠1 = ∠A + ∠B.
There are two other facts about triangles you should know:
- The sum of any two sides of a triangle must be greater than the third side.
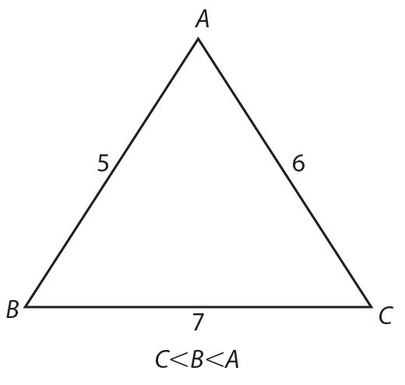
- The largest side lies opposite the largest angle; and the largest angle lies opposite the largest side, as shown in the figure below.
Example 1:
Give one set of angles for a triangle that satisfies the following descriptions:
| Description | Solution |
|---|---|
| a. Scalene, acute | 50°, 60°, 70° |
| b. Scalene, right | 30°, 60°, 90°: We will deal with this one soon. |
| c. Scalene, obtuse | 30°, 50°, 100° |
| d. Isosceles, acute | 20°, 80°, 80° |
| e. Isosceles, right | Only one: 45°, 45°, 90°: We will deal with this one soon also. |
| f. Isosceles, obtuse | 20°, 20°, 140° |
| g. Equilateral | Only one: three 60° angles |
Let’s first do some exercises with angles. Then we’ll turn to area and perimeter exercises. We’ll then visit our old friend Pythagoras and his famous theorem.
 Let’s do some more exercises.
Let’s do some more exercises.
Exercise 8:
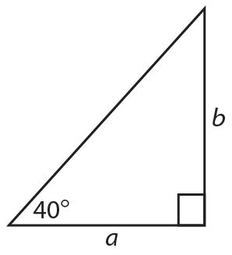
| Quantity A | Quantity B |
|---|---|
| a | b |
Exercise 9:
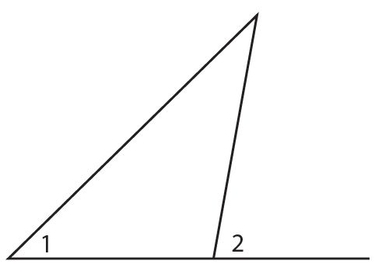
| ∠1 | ∠2 |
Exercise 10: L1 || L2
| x+y | 180° |
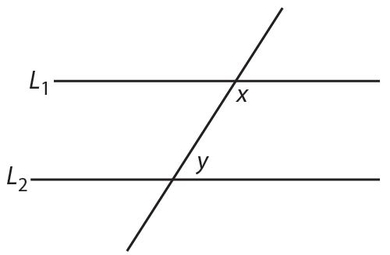
Exercise 11:
If two sides of a triangle are 4 and 7, and if only integer measures are allowed for the sides, the third side must be taken from which set?
- {5,6,7,8,9,10,11}
- {4,5,6,7,8,9,10}
- {3,4,5,6,7,8,9,10}
- {3,4,5,6,7,8,9,10,11}
- {1,2,3,4,5,6,7,8,9,10,11}
Exercise 12:
Arrange the sides in order, largest to smallest, for the figure shown below.
- a>b>c
- a>c>b
- b>a>c
- . b > c > a
- . c > a > b
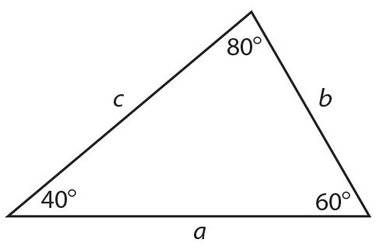
Exercise 13:
x = 2y; z =
- . 30°
- 40°
- 50°
- 60°
- 90°
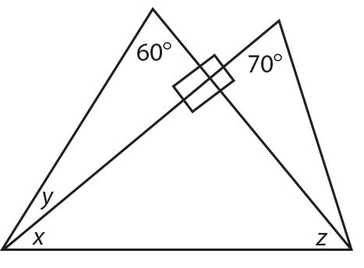
Exercise 14:
WX bisects ∠ZXY; ∠Z =
- . 20°
- 40°
- . 50°
- . 60°
- 70°
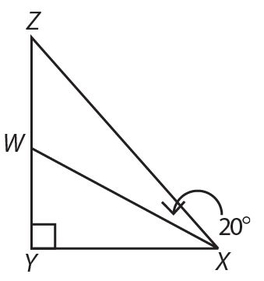
Exercise 15:
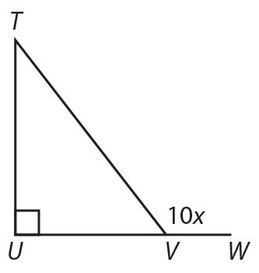
∠TVW = 10x; x could be
- . 3°
- . 6°
- 9°
- 16°
- 20°
Exercise 16:
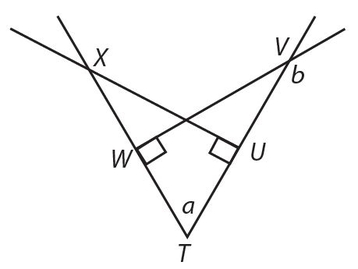
Write b in terms of a:
- a + 90°
- 2a
- 2a + 90°
- . 180° − a
- 180° − 2a
Exercise 17:
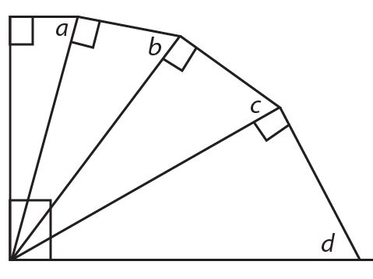
a + b + c + d =
- 90°
- 180°
- 270°
- 360°
- 450°
Exercise 18:
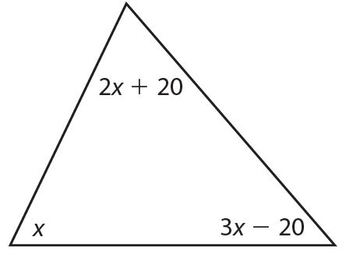
The largest angle is
- 30°
- 50°
- 70°
- 80°
- 90°
Exercise 19:
L1 || AB; y =
- 40°
- 60°
- . 70°
- 80°
- Cannot be determined
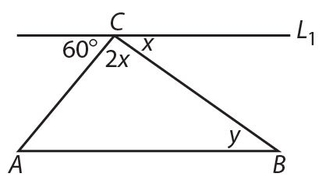
Exercise 20:
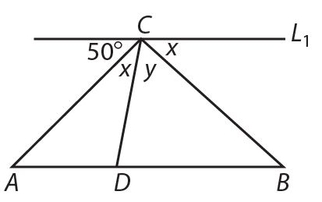
L1 || AB; y =
- . 40°
- 60°
- 70°
- 80°
- Cannot be determined
Use ∆ABC for Exercises 21 and 22.
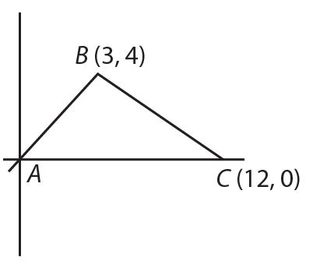
Exercise 21:
The area of ∆ABC is
- 18
- 24
- 36
- 48
- 60
Exercise 22:
The perimeter of ∆ABC is
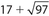
- . 27
- . 32
- .
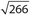
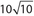
For Exercises 23 and 24, use this figure of a square with an equilateral triangle on top of it, AE = 20.
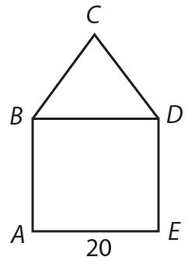
Exercise 23:
The perimeter of ABCDE is
- 50
- 100
- 120
- 160
- . 200
Exercise 24:
The area of ABCDE is
- 600
- . 100(4 + √2)
- 100(4 + √3)
- 800
- 1,000
For Exercises 25 and 26, use ∆ABC with midpoints X, Y, and Z.
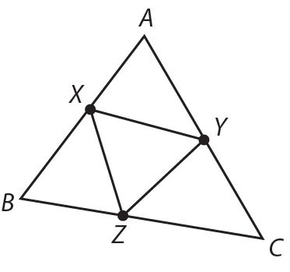
Exercise 25:
If the perimeter of ∆ABC is 1, the perimeter of ∆XYZ is
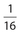
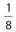
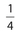
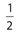
- 1
Exercise 26:
If the area of ∆ABC is 1, the area of ∆XYZ is
- .
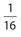
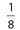 8
8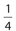
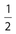
- 1
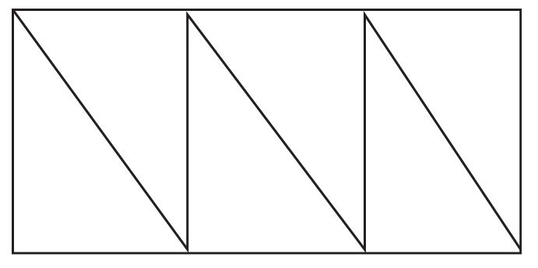
Exercise 27:
In the figure shown, 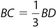 . If the area 3 of ∆ABC = 10, the area of rectangle ABDE is
. If the area 3 of ∆ABC = 10, the area of rectangle ABDE is
- 30
- 40
- 60
- 120
- Cannot be determined
 Let’s look at the answers.
Let’s look at the answers.
Answer 8:
The answer is (A). Since a is opposite the 50° angle, it is larger than b, which is opposite the 40° angle. Beware! The figure is not drawn to scale.
Answer 9:
The answer is (B). Since ∠2 is an exterior angle, it is equal to the sum of the two remote interior angles, so it is bigger than either of them.
Answer 10:
The answer is (C). Any two unequal angles formed in this figure total 180°.
Answer 11:
The answer is (B). The third side s must be greater than the difference and less than the sum of the other two sides, or > 7 − 4 and < 7 + 4. Thus the third side must be between 3 and 11.
Answer 12:
The answer is (B). Judge the relative lengths of the sides by the sizes of the angles opposite them. Then a > c > b.
Watch out for the words “Not drawn to scale.” If it is a simple figure,“not drawn to scale” usually means it is not drawn to scale, and you cannot assume relative sizes without being given actual measurements. However, if it is a semi-complicated or complicated figure, the figure probably is drawn to scale.
Answer 13:
The answer is (A). y = 30°; x = 60°; and z = 30°.
Answer 14:
The answer is (C). ∠ZXY = 40°, so ∠Z must be 50°.
Answer 15:
Only answer (D) is correct. ∠TVW must be between 90° and 180°, so 9° < x < 18°.
Answer 16:
The answer is (A). This is really tricky. UX is drawn to confuse you. In ∆TVW, b is the exterior angle, so b = a + 90°.
Answer 17:
The answer is (C). The sum of 4 triangles is 4 × 180° = 720°. The sum of 5 right angles (don’t forget the one in the lower left of the figure, which is the sum of four acute angles of the triangles) is 450°; so a + b + c + d = 720° − 450° = 270°.
Answer 18:
The answer is (D). x + 2x+ 20 + 3x − 20 = 180, or 6x = 180, so x = 30. 2x + 20 = 80 and 3x − 20 = 70. The largest angle is 80°.
Answer 19:
The answer is (A). 2x + x + 60 = 180; x = 40°. But y = x = 40° (because L1 || AB).
Answer 20:
The answer is (E). y cannot be determined.
The GRE occasionally asks a question for which there is no answer. However, I’ve never seen two in a row and I’ve seen thousands of similar questions.
Answer 21:
The answer is (B). 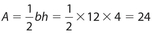
Answer 22:
The answer is (A). Use the distance formula to find sides AB and BC.
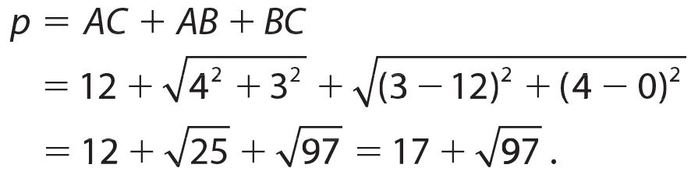
Answer 23:
The answer is (B). Do not include BD; p = 5 × 20 = 100.
Answer 24:
The answer is (C).
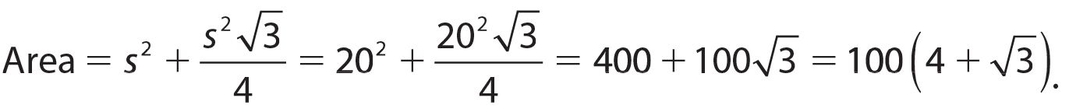
Answer 25:
The answer is (D). If the perimeter of ∆ABC is 1, and all the sides of ∆XYZ are half of those of ∆ABC, so is the perimeter.
Answer 26:
The answer is (C). If the sides of ∆XYZ are half of those of ∆ABC, the area of ∆XYZ is 
Answer 27:
The answer is (C). If we draw lines parallel to DE to divide the original rectangle into three congruent rectangles, and then divide each rectangle into two triangles, we see that each triangle is one-sixth of the rectangle. So the area of the rectangle is 6(10) = 60.
We’ll have more of these type of exercises as part of Chapter 12, Circles.
Let’s go on to good old Pythagoras.
PYTHAGOREAN THEOREM
This is perhaps the most famous math theorem of all. Most theorems have one proof. A small fraction of these have two. This theorem, however, has more than a hundred, including three by past presidents of the United States. We’ve had some smart presidents who actually knew some math.
The Pythagorean theorem simply states:
In a right triangle, the hypotenuse squared is equal to the sum of the squares of the legs.
In symbols, c2 = a2 + b2.
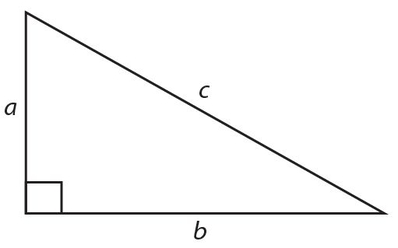
As a teacher, I must show you one proof.
Proof:
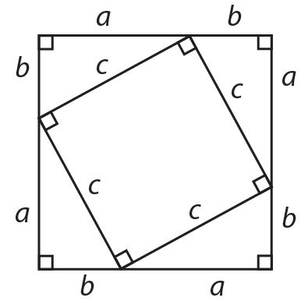
In this figure, the larger square equals the smaller square plus the four congruent triangles. ln symbols, 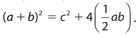
Multiplying this equation out, we get a2 + 2ab + b2 = c2 + 2ab.Then, canceling 2ab from both sides, we get c2 = a2 + b2. The proof is complete.
There are two basic problems for the Pythagorean theorem that you need to know how to do: finding the hypotenuse and finding one of the legs of the right triangle.
Example 2:
Solve for x:
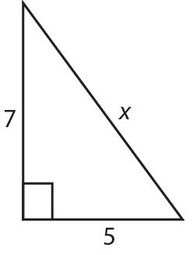
Solution:
x2 = 72+ 52; 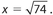 .
.
Example 3:
Solve for x:
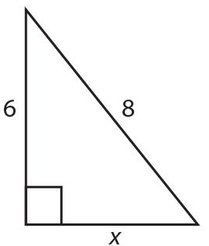
Solution:
82 = 62 + x2, or x2 = 64 − 36 = 28. So 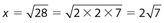
Notice that the hypotenuse squared is always by itself, whether it is a number or a letter.
Pythagorean Triples
lt is a good idea to memorize some Pythagorean triples. These are the measures of sides of triangles that are always right triangles. The hypotenuse is always listed third in the group.
The 3-4-5 group:
3-4-5, 6-8-10, 9-12-15, 12-16-20, 15-20-25
The 5-12-13 group:
5-12-13, 10-24-26
The rest:
8-15-17, 7-24-25, 20-21-29, 9-40-41, 11-60-61
Special Right Triangles
You ought to know two other special right triangles, the isosceles right triangle (with angles 45°-45°-90°) and the 30°-60°-90° right triangle. The facts about these triangles can all be found by using the Pythagorean theorem.
- The 45°-45°-90° isosceles right triangle:
- The legs are equal.
- To find a leg given the hypotenuse, divide by √2 (or multiply by
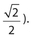
- To find the hypotenuse given a leg, multiply by √2 .
Example 4:
Find x and y for this isosceles right triangle.
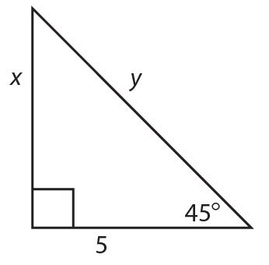
Solution:
x = 5 (the legs are equal); y = 5√2.
Example 5:
Find x and y for this isosceles right triangle.
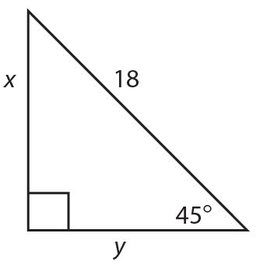
Solution:
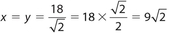 .
. - The 30°-60°-90° right triangle.
- If the shorter leg (opposite the 30° angle) is not given, get it first. It is always half the hypotenuse.
- To find the short leg given the hypotenuse: divide by 2.
- To find the hypotenuse given the short leg: multiply by 2.
- To find the short leg given the long leg: divide by √3 (or multiply by
 ).
). - To find the long leg given the short leg: multiply by √3 .
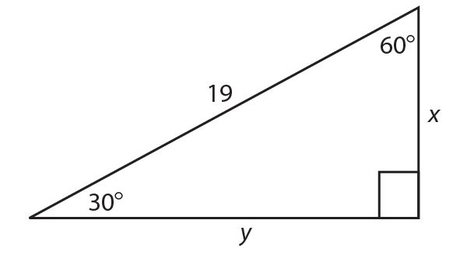
Example 6:
Find x and y for this right triangle.
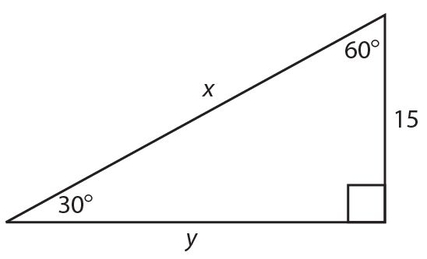
Solution:
The short leg is given (15); x = 2(15) = 30;
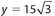 .
.Example 7:
Find x and y for this right triangle.
Solution:
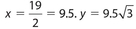 .
.Example 8:
Find x and y for this right triangle.

Solution:
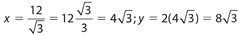
 Let’s do a few exercises.
Let’s do a few exercises.
Exercise 28:
Two sides of a right triangle are 3 and √5 .
- I. The third side is 2.
- II. The third side is 4.
- III. The third side is
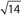 .
.
Which of the following choices is correct?
- Statement II is true
- Statement III is true
- Statements I and II are true
- Statements I and III are true
- Statements I, II, and III are true
Exercise 29:
The area of square ABCD =
- 50
- 100
- 225
- 576
- 625
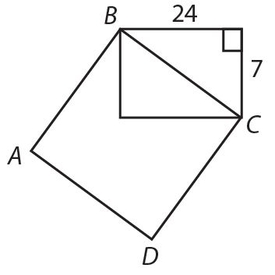
Exercise 30:
x =
- 16
- 18
- 20
- 22
- 24
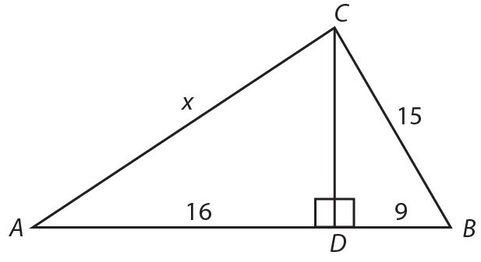
Exercise 31:
c2 − b2 =
- 72
- 144
- 216
- 252
- 288
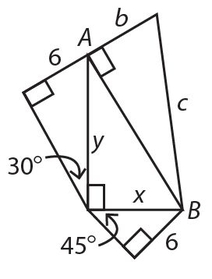
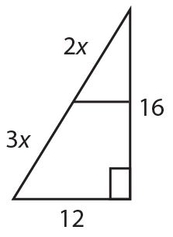
Exercise 32:
x =
- 1
- 2
- 3
- 4
- 4.5
Exercise 33:
A 25-foot ladder is leaning on the floor. Its base is 15 feet from the wall. If the ladder is pushed until it is only 7 feet from the wall, how much farther up the wall is the ladder pushed?
- 4 feet
- 8 feet
- 12 feet
- 20 feet
- 24 feet
Exercise 34:
A triangle has a base of 4 units and a height of 2 units. Which of the following could be its perimeter, in units? Indicate all correct choices.
- 12
- 16
- 24
- 48
- 400,000
- 6.023 × 1023
Exercise 35:
Which of the following represents the lengths of the sides of a right triangle? Indicate all correct choices.
- 8, 9, 10
- 5, 12, 13
- 8, 15, 17
- 7, 24, 25
- 10, 40, 41
- 11, 22, 33
Exercise 36:
For which of the following figures and dimensions will the area be 32? Indicate all correct choices.
- Rectangle with a base of 8 and a height of 4
- Triangle with a base of 8 and a height of 4
- . Parallelogram with a base of 4 and a height of 8 to that base
- Rhombus with a base of 4 and a height of 8
- Trapezoid with a median of 8 and a height of 4
Exercise 37:
Which of the following could represent the measures of two of the angles of an isosceles triangle? indicate all correct choices.
- 40° and 60°
- 50° and 80°
- 59° and 62°
- 45° and 90°
- 20° and 120°
Exercise 38:
The lengths of two sides of a triangle are 7 and 11. Which of the following could be the length of the third side? Indicate all correct choices.
- 3
- 5
- 11
- 16
- 18
- 20
Exercise 39:
If two parallel lines are cut by a transversal, which of the following always illustrate congruent angles? Indicate all correct choices.
- Corresponding angles
- Alternate exterior angles
- Alternate interior angles
- Interior angles on the same side of the transversal
- Exterior angles on the same side of the transversal
Exercise 40:
Two sides of a right triangle are 3 and 4. Which of the following could be the length of the third side? Indicate all correct choices.
- 2
- √5
- √7
- 4
- 5
- 7
Exercise 41:
The median to the base of an isosceles triangle is 10. If the base is 6, what is the area?

Exercise 42:
The area of an equilateral triangle with side of 100 is expressed in simplest form as a√b . What is the value of a?

Exercise 43:
Two of the angles of a triangle measure 30° and 40°. In degrees, what is the sum of the exterior angles?

 Let’s look at the answers.
Let’s look at the answers.
Answer 28:
The answer is (D). Try the Pythagorean theorem with various combinations of 3, √5, and x (the third side). The only ones that work are Statement I: 22 + (√5)2 = 32, and Statement III: 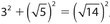 .
.
Answer 29:
The answer is (E). We recognize the right triangle as a 7-24-25 triple, so side BC = 25. The area of the square is (25)2 = 625.
Answer 30:
The answer is (C). This is a 15-20-25 triple, so x = 20.
Answer 31:
The answer is (C). We see that AB is the side of two triangles. By the Pythagorean theorem, we get c2− b2 = x2 + y2 = (6√2)2 + 122 = 72 + 144 = 216.
Answer 32:
The answer is (D). This triangle is a 12-16-20 triple, so 3x + 2x = 5x = 20, and x = 4.
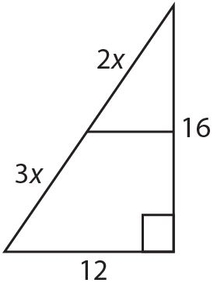
Answer 33:
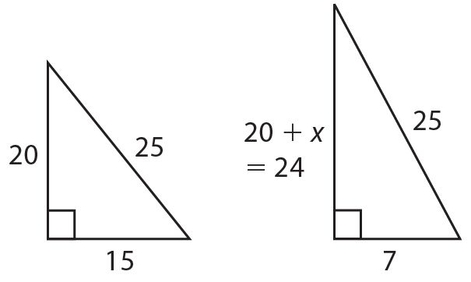
The answer is (A). The first figure shows a 15-20-25 right triangle with the ladder 20 feet up the wall. The second figure is a 7-24-25 triple with the ladder 24 feet up the wall. The ladder is pushed another 24 − 20 = 4 feet up the wall.
Answer 34:
The correct answers are (A), (B), (C), (D), (E), and (F). Remarkably, there is no maximum perimeter! As one of the base angles approaches 180°, the lengths of the other two sides increase without bound. (There is a minimum perimeter of 4 + 4√2 if the triangle is isosceles.)
Answer 35:
The correct answers are (B), (C), and (D). The sum of the squares of the two shortest sides must equal the square of the longest side. For choice (B), 52 + 122 = 25 + 144 = 169 = 132. For choice (C), 82 + 152= 64 + 225 = 289 = 172. For choice (D), 72 + 242 = 49 + 576 = 625 = 252. However, choice (A), 82 + 92 = 145 ≠ 102, and choice (E), 102 + 402 = 1,700 ≠ 412, are wrong. Choice (F) is wrong not only because 112 + 222 ≠ 332, but also because the sum of 11 and 22 is not greater than 33. In any triangle, the sum of the lengths of any two sides must exceed the length of the third side.
Answer 36:
The correct answers are (A), (C), (D), and (E). In each of choices (A), (C), and (D), the area is the product of the base and height. For choice E, the area of a trapezoid is 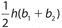 , where h is the height and each of b1 and b2 is a base. Note that
, where h is the height and each of b1 and b2 is a base. Note that 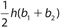 can also be written as
can also be written as 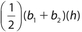 , and the expression
, and the expression 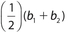 is the value of the median. Choice (B) is wrong because the area of a triangle is one-half the product of a base and its associated height.
is the value of the median. Choice (B) is wrong because the area of a triangle is one-half the product of a base and its associated height.
Answer 37:
The correct answers are (B), (C), and (D). For an isosceles triangle, at least two angles must have the same measure. In choice (B), the measure of the third angle is 180° − 50° − 80° = 50°. In choice (C), the measure of the third angle is 180° − 59° − 62° = 59°. In choice (D), the measure of the third angle is 180° − 45° − 90° = 45°. For choices (A) and (E), the measure of the third angle would be 80° and 40°, respectively.
Answer 38:
The correct answers are (B), (C), and (D). The sum of the lengths of any two sides of a triangle must exceed the length of the third side. The simplest way to check any triple of numbers is to add the two smallest lengths. For choice (B), 7 + 5 > 11. For choice (C), 7 + 11 > 11. For choice (D), 7 + 11 > 16. Choice (A) is wrong because 3+ 7 < 11. Choice (E) is wrong because 7 + 11 = 18. Choice (F) is wrong because 7 + 11 < 20.
Answer 39:
The correct answers are (A), (B), and (C). Interior (or exterior) angles on the same side of the transversal are supplementary, so they are equal only when the transversal is perpendicular to the two parallel lines. Therefore, choices (D) and (E) are not correct choices.
Answer 40:
The correct answers are (C) and (E). In a right triangle, the sum of the squares of the two shortest sides must equal the square of the hypotenuse. If the two shortest sides are 3 and 4, then the hypotenuse must be 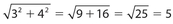 . However, if the hypotenuse is 4, then the third side must be
. However, if the hypotenuse is 4, then the third side must be 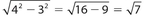 .
.
Answer 41:
The correct answer is 30. The median to the base of an isosceles triangle is identical to the altitude to the base. Thus, the area is 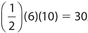 .
.
Answer 42:
The correct answer is 2,500.The area of an equilateral triangle is
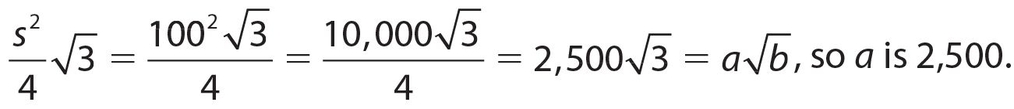
Answer 43:
The answer is 360. The sum of the exterior angles of any polygon, regardless of any individual measures of interior angles, is always 360°.
Congruent Triangles
The GRE will contain questions concerning the congruence and similarity (see next section) of triangles, but (thankfully) there will be no proofs.
Two triangles are congruent if each of the three sides and angles of one triangle are equal to each of the three sides and angles of a second triangle. The symbol for congruence is ≅. The order in which the letters of each triangle are listed is important. By stating that ∆ABC ≅ ∆DEF, we are declaring that the following six congruencies are true: 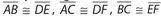 , ∠A ≅ ∠D, ∠B ≅ ∠E, and ∠C ≅ ∠F.
, ∠A ≅ ∠D, ∠B ≅ ∠E, and ∠C ≅ ∠F.
Two triangles can be proved to be congruent with just a minimum of three sets of congruencies. Let’s discuss each of these situations. In each example, we can state that ∆ABC ≅ ∆DEF.
Side-Side-Side (SSS): Three sides of one triangle are congruent, respectively, to the three sides of a second triangle. A diagram is shown below.
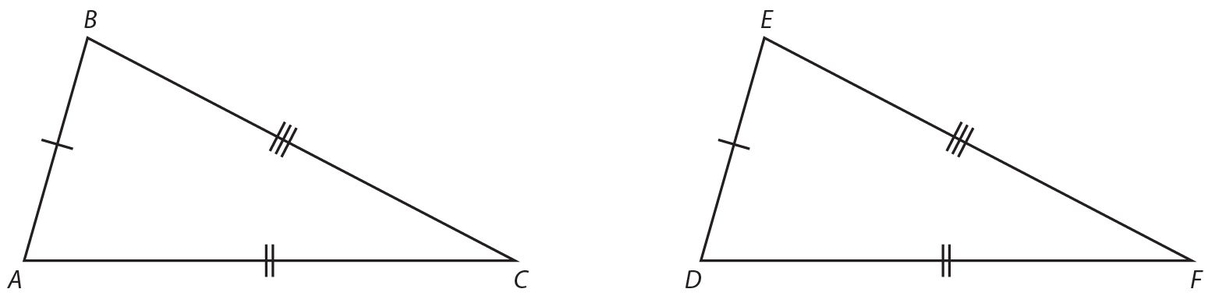
The indicated markings show that 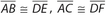 , and
, and  .
.
Side-Angle-Side (SAS): Two sides and the included angle of one triangle are congruent, respectively, to two sides and the included angle of a second triangle. A diagram is shown below.
The indicated markings show that 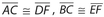 , and ∠C ≅ ∠F.
, and ∠C ≅ ∠F.
Angle-Side-Angle (ASA): Two angles and the included side of one triangle are congruent, respectively, to two angles and the included side of a second triangle. A diagram is shown below. Note that vertices C and F are the same point.
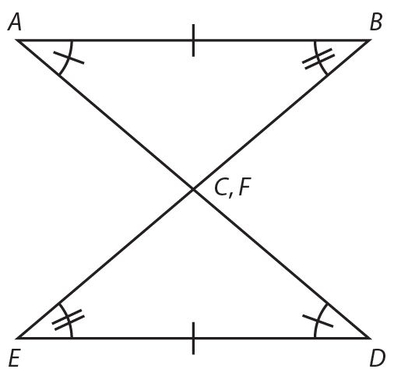
The indicated markings show that  , ∠A ≅ ∠D, and ∠B ≅ ∠E.
, ∠A ≅ ∠D, and ∠B ≅ ∠E.
Side-Angle-Angle (SAA): Two angles and a non-included side of one triangle are congruent, respectively, to two angles and the corresponding non-included side of a second triangle. A diagram is shown below.
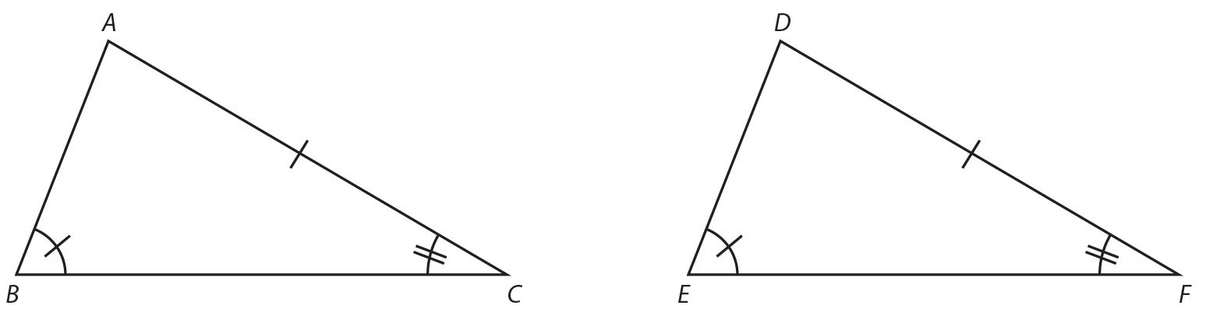
The indicated markings show that 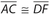 , ∠B ≅ ∠E, and ∠C ≅ ∠F .
, ∠B ≅ ∠E, and ∠C ≅ ∠F .
Hypotenuse-Leg (HL): This situation is unique to right triangles. The hypotenuse and leg of one right triangle are congruent to the hypotenuse and leg of a second right triangle. A diagram is shown below.
The indicated markings show that there is a right angle at vertices B and E. Also,  and
and  .
.
It is important to recognize when certain combinations of congruencies between some of the parts of two triangles do not imply that the triangles are congruent. These are known as fallacies. Here are the two most popular fallacies.
Side-Side-Angle (SSA): Two sides of one triangle are congruent to two sides of a second triangle. In addition, a pair of non-included angles are congruent. The following diagram shows that the two triangles need not be congruent.
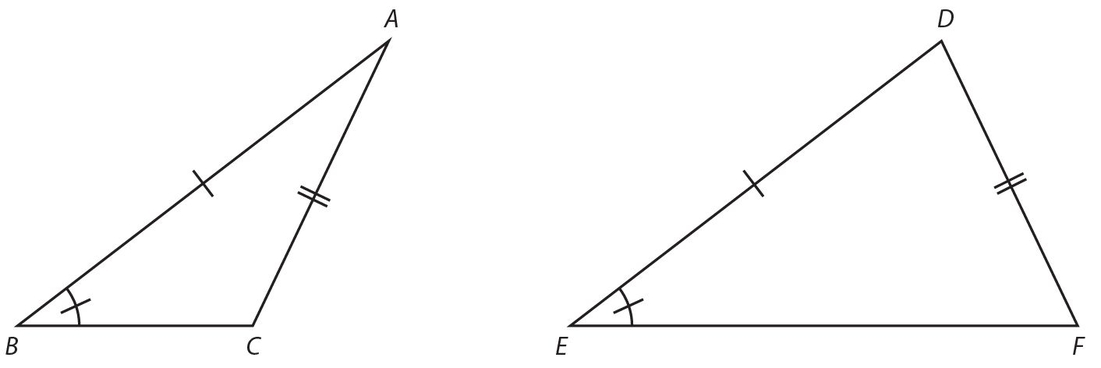
The indicated markings show that 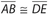 ,
, 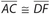 , and ∠B ≅ ∠E. Note that BC is not congruent to
, and ∠B ≅ ∠E. Note that BC is not congruent to 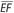 , and that ∠A, ∠C, ∠D, and ∠F are different in their measures.
, and that ∠A, ∠C, ∠D, and ∠F are different in their measures.
Angle-Angle-Angle (AAA): Each of three angles of one triangle is congruent to three corresponding angles in a second triangle. The following diagram shows that the two triangles need not be congruent.
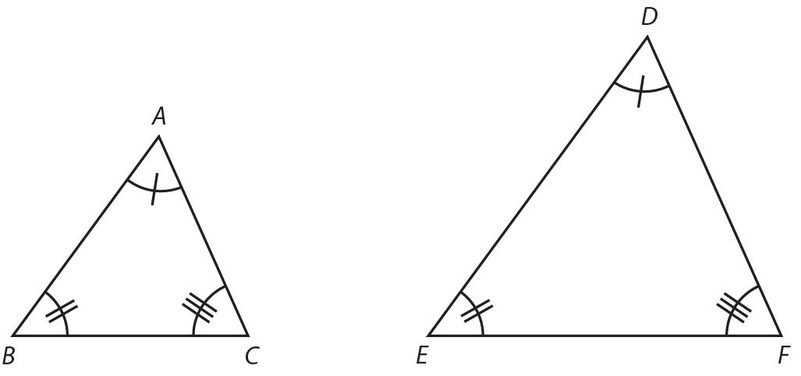
The indicated markings show that ∠A ≅ ∠D, ∠B ≅ ∠E, and ∠C ≅ ∠F. Note that the second triangle is larger than the first triangle. Although these triangles are not congruent, there does exist a relationship between them. This relationship, similarity, is discussed in the next section.
Note that in any ∆ABC, ∠A is opposite 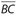 , ∠B is opposite
, ∠B is opposite 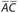 , and ∠C is opposite
, and ∠C is opposite 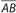 . This assignment of letters is consistent for any triangle; so, if we are given ∆XYZ, ∠X must lie opposite
. This assignment of letters is consistent for any triangle; so, if we are given ∆XYZ, ∠X must lie opposite 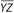 .
.
Be aware that a GRE test question may mention that two sides are either “equal” or “congruent.” In taking the GRE, you need not make any distinction between these two words, although in most geometry books, congruence refers to the actual sides, whereas equality refers to distances.
 Let’s try this exercise on congruent triangles.
Let’s try this exercise on congruent triangles.
Exercise 44:
Which of the following would be sufficient to conclude that ΔABC ≅ ΔXYZ? Indicate all correct answers.
- AB = XY, AC = YZ, and BC XZ.
- AB = XY, AC = XZ, and ∠A ≅ ∠X.
- ∠A ≅ ∠X, ∠C ≅ ∠Z, and BC = YZ
- ∠C ≅ ∠Z, ∠B ≅ ∠Y, and ∠A ≅ ∠X.
- Each of ∠B ≅ ∠Y are right angles and AC = XZ.
- ∠B ≅ ∠Y, BC = YZ, and ∠C ≅ ∠Z.
Answer 44:
The correct answers are (B), (C), and (F). Choice (B) is correct by Side-Angle-Side (SAS). Choice (C) is correct by Side-Angle-Angle (SAA). Choice (F) is correct by Angle-Side-Angle (ASA). Answer choice (A) is wrong because the letters of the vertices are not matched correctly. Answer choice (D) is wrong because there is no pair of congruent sides. Answer choice (E) is wrong because there are only two given matched congruencies.
Similar Triangles
Two triangles are similar if the corresponding pairs of angles are congruent. Technically, we only need two pairs of congruent angles. Since the sum of the angles of any triangle must be 180°, two pairs of congruent angles imply that the third pair must also be congruent. The symbol for similarity is ~. In the diagram below, ∆ABC ~ ∆DEF, with  and
and  representing the corresponding altitudes of these triangles.
representing the corresponding altitudes of these triangles.
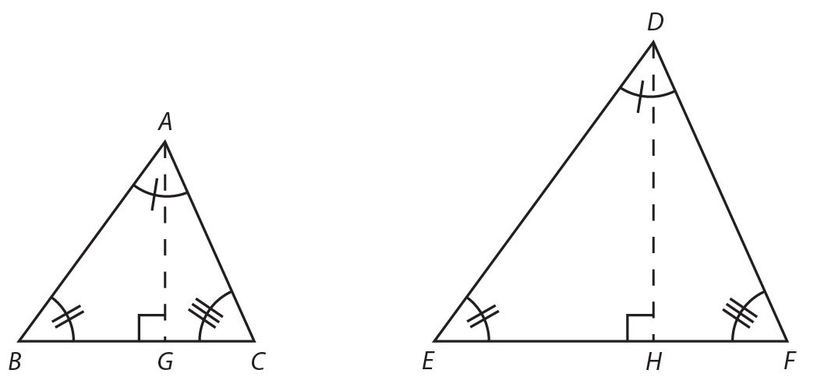
Although the corresponding sides are not congruent, the ratio of any two corresponding sides must be constant. This means that 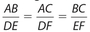 .There are three additional key ratios.
.There are three additional key ratios.
- The ratio of the perimeters of these two triangles must equal the ratio of any two corresponding sides. For example,
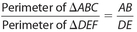 .
. - The ratio of any two corresponding linear measures, such as altitudes, is in the same ratio as a pair of corresponding sides. In the diagram above,
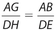 .
. - The ratio of the areas of these two triangles must equal the square of the ratio of any two corresponding sides. For example,
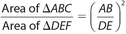 .
.
Note that this also means if we are given the areas of two similar triangles, we may conclude that the ratio of any two corresponding sides is the square root of the corresponding ratio of the areas. For example, we could express this relationship mathematically as  .
.
Just as we had established congruency between triangles with a minimum set of equalities, we can also prove that two triangles are similar with a minimum amount of information. In each of the following examples, we can state that ∆ABC ~ ∆DEF.
Side-Side-Side (SSS): The ratios of the three pairs of corresponding sides are in proportion. This means that 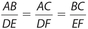 . A diagram, with numerical values, is shown below.
. A diagram, with numerical values, is shown below.
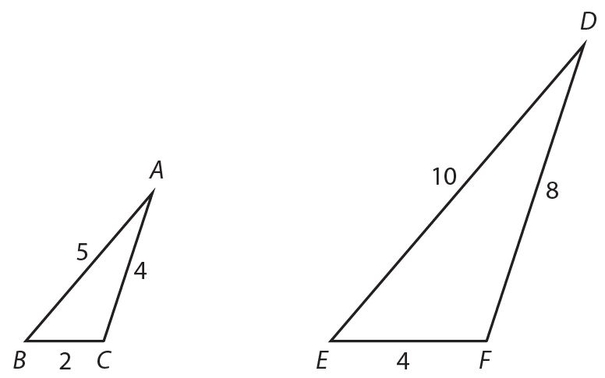
Notice that each side of the second triangle is double the size of the corresponding side of the first triangle. The inverse of these ratios would also be equal; that is 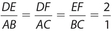 .
.
Side-Angle-Side (SAS): The ratio of two pairs of corresponding sides forms a proportion and the corresponding included angles are congruent. A diagram, with numerical values, is shown below.
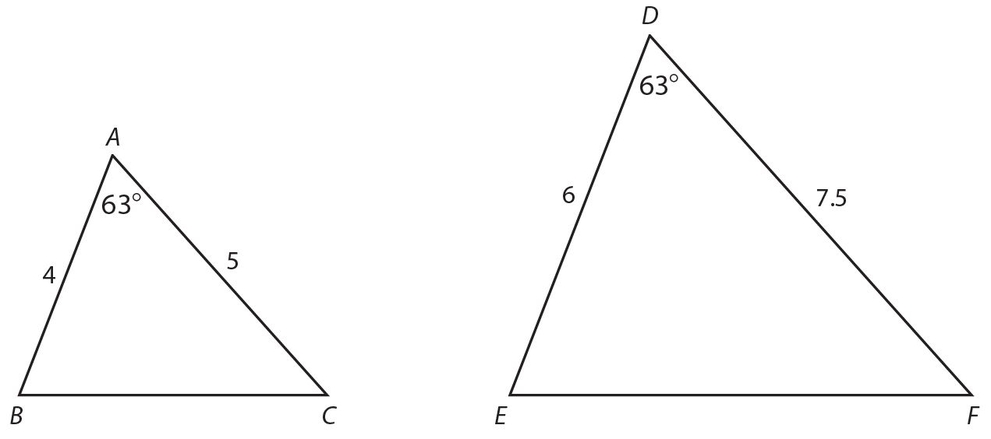
Note that 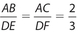 and that ∠A ≅ ∠D .
and that ∠A ≅ ∠D .
Angle-Angle (AA): Each of two angles of one triangle is congruent to each of two corresponding angles of a second triangle. A diagram, with numerical values, is shown below.
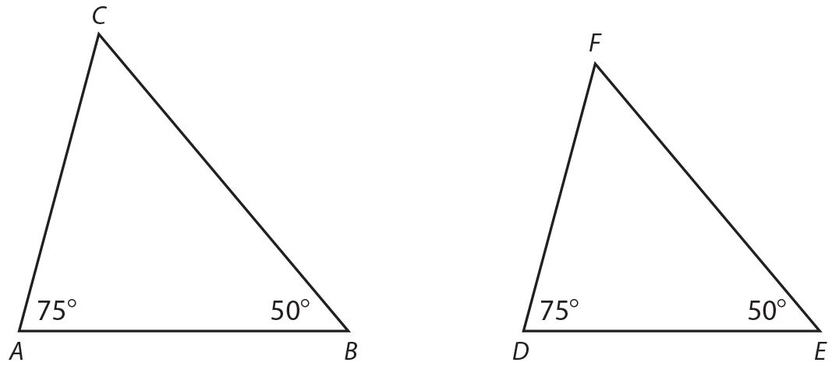
Note that the measure of each of ∠C and ∠F must be 180° − 50° − 75° = 55° because the sum of the measures of the angles of any triangle is 180°. This property is sometimes referred to as Angle-Angle-Angle (AAA).
Example 9:
The ratio of the corresponding sides of two similar triangles is 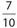 .
.
If the perimeter of the smaller triangle is 21, what is the perimeter of the larger triangle?
Solution:
The ratio of the perimeters is the same as the ratio of the corresponding sides. Let x represent the perimeter of the larger triangle. Then 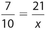 . Cross-multiply to get 7x = 210.Therefore, x = 30.
. Cross-multiply to get 7x = 210.Therefore, x = 30.
Example 10:
The ratio of the areas of two similar triangles is 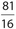 .One side of the smaller triangle is 10. What is the length of the corresponding side of the larger triangle?
.One side of the smaller triangle is 10. What is the length of the corresponding side of the larger triangle?
Solution:
The ratio of any two corresponding sides equals the square root of the ratio of the areas, which becomes 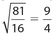 .Let x represent the length of the side of the larger triangle. Then
.Let x represent the length of the side of the larger triangle. Then 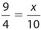 . Cross-multiply to get 4x = 90. Thus, x = 22.5.
. Cross-multiply to get 4x = 90. Thus, x = 22.5.
 Let’s try a few exercises on similar triangles.
Let’s try a few exercises on similar triangles.
Exercise 45:
Which of the following would be sufficient to conclude that ∆CDE~ ∆RST? Indicate all correct answers.
- Each of ∠D and ∠S is a right angle,
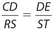 .
. 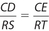 and ∠D ≅ ∠S.
and ∠D ≅ ∠S.- ∠E ≅ ∠T and
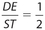 .
. - ∠C ≅ ∠R and ∠E ≅ ∠T.
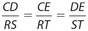 .
.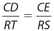 and each of ∠C and ∠R is a right angle.
and each of ∠C and ∠R is a right angle.
Exercise 46:
The ratio of the corresponding sides of two similar triangles is 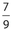 . If one side of the smaller triangle is 35, how much larger is the corresponding side of the larger triangle?
. If one side of the smaller triangle is 35, how much larger is the corresponding side of the larger triangle?

Exercise 47:
∠GHJ is similar to ∠KLM . If the measure of ∠G is 60° and ∠J is twice as large as ∠H, what is the measure (in degrees) of ∠M?

Exercise 48:
The ratio of the areas of two similar triangles is  . What is the ratio of 36 their perimeters? Write your answer as a ratio of integers.
. What is the ratio of 36 their perimeters? Write your answer as a ratio of integers.
Exercise 49:
The ratio of a pair of corresponding sides of two similar triangles is  . 8 The area of the smaller triangle is 36. What is the area of the larger triangle?
. 8 The area of the smaller triangle is 36. What is the area of the larger triangle?
 Let’s look at the answers.
Let’s look at the answers.
Answer 45:
The correct answers are (A), (D), and (E). Choice (A) is correct by Side-Angle-Side (SAS). Choice (D) is correct by Angle-Angle (AA). Choice (E) is correct by Side-Side-Side (SSS). Answer choice (B) is wrong because it illustrates two pairs of corresponding sides and a corresponding pair of nonincluded angles. Answer choice (C) is wrong because it illustrates only one pair of corresponding sides and one pair of corresponding angles. Answer choice (F) is wrong because the letters that represent the vertices are not matched in the correct order.
Answer 46:
The correct answer is 10. Let x represent the corresponding side of the larger triangle. Then 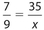 . Cross-multiply to get 7x = 315, from 9 x which x = 45. Therefore, the larger side is 45 − 35 = 10 more than the smaller side.
. Cross-multiply to get 7x = 315, from 9 x which x = 45. Therefore, the larger side is 45 − 35 = 10 more than the smaller side.
Answer 47:
The correct answer is 80. Let x represent the measure (in degrees) of ∠H and let 2x represent the measure (in degrees) of ∠J . Then 60 + x + 2x = 180. This equation simplifies to 3x = 180 − 60 = 120. This means that x = 40, so the measure of ∠J, in degrees, must be 80. Since the triangles are similar, the number of degrees in the corresponding ∠M is also 80.
Answer 48:
The correct answer is 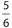 . The ratio of the perimeters equals the square root of the ratio of the areas, which is
. The ratio of the perimeters equals the square root of the ratio of the areas, which is 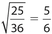 .
.
Answer 49:
The correct answer is 256. The ratio of the areas equals the square of the ratio of any pair of corresponding sides, which is 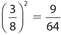 . Let x represent the area of the larger triangle. Then
. Let x represent the area of the larger triangle. Then 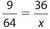 . Cross-multiply to get 9x = 2,304. Therefore x = 256.
. Cross-multiply to get 9x = 2,304. Therefore x = 256.
That’s all for angles and triangles for now. We will see more when circles are discussed in Chapter 12. For now, though, let’s look at rectangles and other polygons.