CHAPTER 12:

Circles

e9780738668499_i1322.jpg

“Although sometimes it seems you are going in circles, you are really heading toward your goal. ”

Circles are a favorite topic of the GRE. Circles allow many short questions that can be combined with the other geometric chapters. Let’s get started.

PARTS OF A CIRCLE

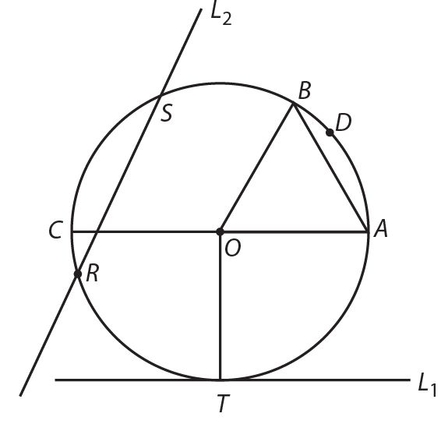
e9780738668499_i1323.jpg

We all know what a circle looks like, but maybe we’re not familiar with its “parts.”

O is the center of the circle. A circle is often named by its center, so this is circle O.

OA, OT, OC, and OB are radii (singular: radius); a radius is a line segment from the center to the circumference, or edge, of the circle.

 

e9780738668499_i1324.jpg

All radii (r) of a circle are equal. This is a postulate or axiom, a law taken to be true without proof. It is probably a good idea to tell you there are no proofs on the GRE, as there were when you took geometry.

AC is the diameter, d, the distance from one side of the circle through the center to the other d side; e9780738668499_i1325.jpg.

 

L1 is a tangent, a line that touches a circle in one and only one point.

T is a point of tangency, the point where a tangent touches the circle. The radius to the point of tangency (OT) is always perpendicular to the tangent, so OT ⊥ L1.

L2 is a secant, a line that passes through a circle in two places.

RS is a chord, a line segment that has each end on the circumference of the circle. The diameter is the longest chord in a circle.

OADBO is a sector (a pie-shaped part of a circle). There are a number of sectors in this figure; others include BOCSB and OATRCSBO. We will see these again soon.

An arc is any distance along the circumference of a circle.

Arc ADB is a minor arc because it is less than half a circle.

Arc BDATRC is a major arc because it is more than half a circle.

Arc ATRC is a semicircle because it is exactly half a circle

Whew! Enough! However, we do need some more facts about circles.

 

The following are mostly theorems, proven laws. Again, there are no proofs on the GRE, but you need to be aware of these facts.

AREA AND CIRCUMFERENCE

Area of a circle:

A = πr2

Circumference (perimeter of a circle):

C = 2πr or πd.

SECTORS

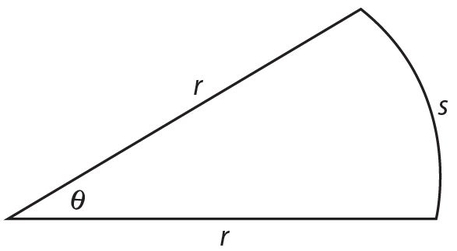
e9780738668499_i1326.jpg

Area of a sector:

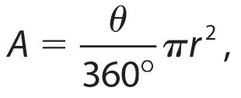
e9780738668499_i1327.jpg

where θ (theta) is the angle of the sector in degrees.

Arc length of a sector:

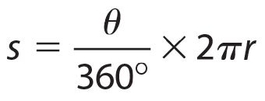
e9780738668499_i1328.jpg

Perimeter of a sector:

p = s + 2r,

 

where s is the arc length

Example 1:

Find the area and perimeter of a 60° sector of a circle of diameter 12.

Solution:

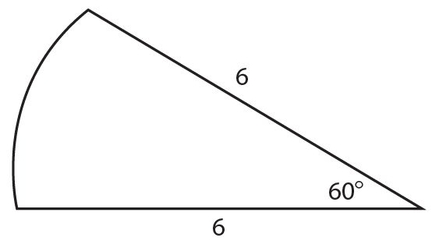
e9780738668499_i1329.jpg

If the diameter is 12, the radius is 6. The sector is pictured here. Its area is 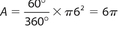e9780738668499_i1330.jpg square units. Although you should know that pi (π) is about 3.14, I’ve never seen a problem for which you had to multiply 6 times 3.14. The answer is left in terms of π. The perimeter of the sector is 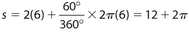e9780738668499_i1331.jpg units.

e9780738668499_i1332.jpg Let’s do some exercises.

For Exercises 1 through 5, refer to the following circle. O is the center of the circle.

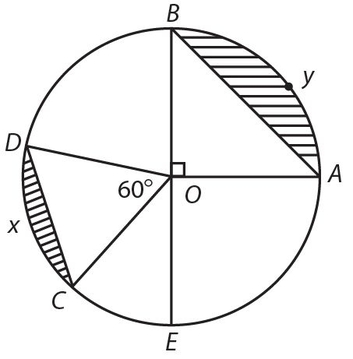
e9780738668499_i1333.jpg

Exercise 1:

If the area of ∆AOB is 25, the area of circle O is

  1. 12.5π
  2. 25π
  3. 50π
  4. 100π
  5. 200π

Exercise 2:

If OA = 8, the area of the shaded region BAYB is

  1. 16(π − 2)
  2. 16(π − 1)
  3. 8(2π − 1)
  4. 64(π − 1)
  5. 32(π − 2)

Exercise 3:

If CD = 10, the perimeter of sector DOCXD is

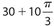
  1. e9780738668499_i1334.jpg
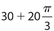
  2. e9780738668499_i1335.jpg
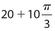
  3. e9780738668499_i1336.jpg
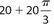
  4. e9780738668499_i1337.jpg
  5. 30 + 30π

Exercise 4:

If OC = 2, the area of the shaded portion DCXD is

  1. π − √3
  2. 2π −√3
  3. 4π −√3
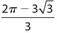
  4. e9780738668499_i1338.jpg
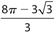
  5. e9780738668499_i1339.jpg

Exercise 5:

If the area of ACOD is 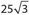e9780738668499_i1340.jpg, the perimeter of semicircle EOBDXCE is

  1. 10π
  2. 10(π + 1)
  3. 10(π + 2)
  4. 10(2π + 1)
  5. 20(π + 1)

I bet you get the idea.

e9780738668499_i1341.jpg Let’s look at the answers.

Answer 1:

The answer is (C). 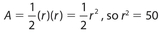e9780738668499_i1342.jpg. The area of the circle is thus πr2 = 50π. Notice that once you have a value for r2, you don’t have to find r to do this problem.

Answer 2:

The answer is (A). The area of region BAYB is the area of one-fourth of a circle minus the area of ΔAOB. So the area is 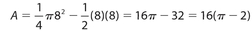e9780738668499_i1343.jpg.

Answer 3:

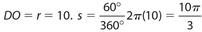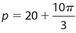The answer is (C). The perimeter of sector DOCXD = 2r + s, where s is the length of arc CXD. ΔCOD is equilateral, so CD = CO = e9780738668499_i1344.jpg. So the perimeter of sector DOCXD is e9780738668499_i1345.jpg.

Answer 4:

The answer is (D). The area of region DCXD is the area of sector ODXCO minus the area of ΔDOC, when OC = 2. So the area is 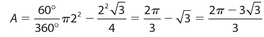e9780738668499_i1346.jpg.

Answer 5:

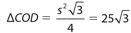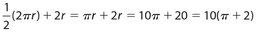The answer is (C). We must first find the radius. The area of equilateral e9780738668499_i1347.jpg. So s2 = 100, and s = r = 10. The perimeter of the semicircle is e9780738668499_i1348.jpg.

There are a few more things we need to know. When we talked about two intersecting lines earlier, we saw that CE might equal ED; however, if the description of the figure doesn’t say so, you cannot assume it. Also, ED might be perpendicular to CE, but if it doesn’t say so, you cannot assume it, either. In fact, we can say CD bisects AB at E only if we know that AE = EB or E is the midpoint of AB.

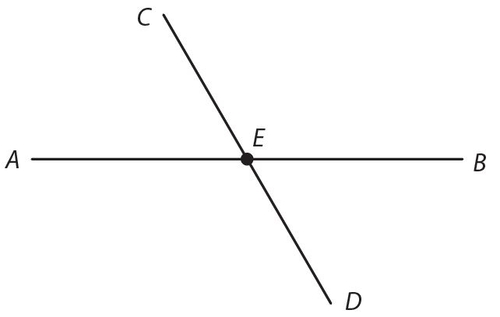
e9780738668499_i1349.jpg

Now we consider two intersecting lines in a circle, such as chord AB and radius CO in circle O.

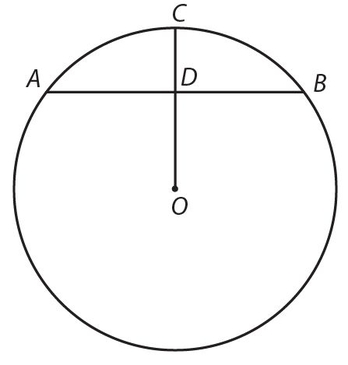
e9780738668499_i1350.jpg

If one of the following facts is true, all are true:

  1. OD ⊥ AB
  2. CO bisects AB
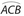  3. CO bisects e9780738668499_i1351.jpg (read “arc ACB”)

e9780738668499_i1352.jpg Let’s do some more exercises.

For Exercises 6 and 7, use this figure, which is a triangle-semicircle shape.

e9780738668499_i1353.jpg

Exercise 6:

The perimeter of this figure is

  1. 14 + 5π
  2. 14 + 10π
  3. 24 + 5π
  4. 24 + 10π
  5. 12 + 10π

Exercise 7:

The area of the figure is

  1. . e9780738668499_i1354.jpg
  2. . 24 + 25π
  3. . 24 + 50π
  4. 48 + 25π
  5. 48 + 50π

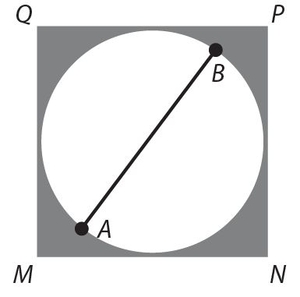
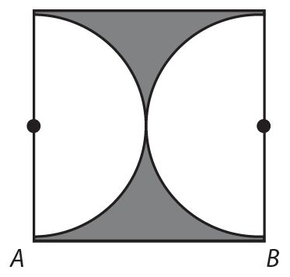
Exercise 8:

A circle is inscribed in (inside and touching) figure MNPQ, which has all right angles. Diameter AB = 10. The area of the shaded portion is

  1. . 100 − 12.5π
  2. 100 − 25π
  3. . 40 − 10π
  4. 40 − 5π
  5. 100 − 100π
    e9780738668499_i1355.jpg

Exercise 9:

If AB = 10, the area of the shaded portion in the figure is

  1. 100 − 12.5π
  2. 100 − 25π
  3. 40 − 10π
  4. 40 − 5π
  5. 100 − 100π
    e9780738668499_i1356.jpg

For Exercises 10 and 11, use this figure. The perimeter of the 16 semicircles is 32π.

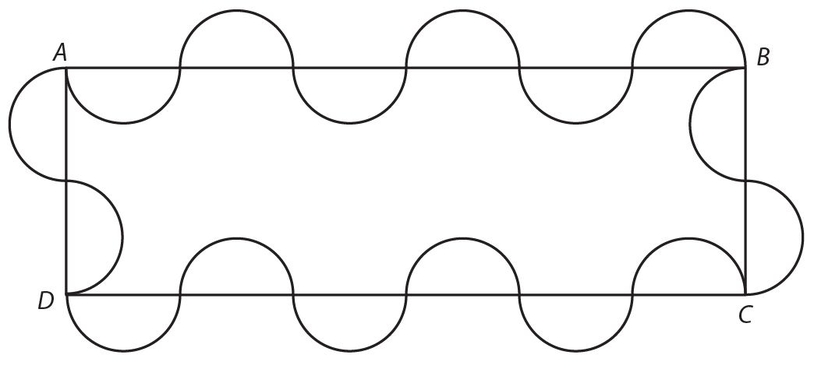
e9780738668499_i1357.jpg

Exercise 10:

The area of rectangle ABCD is

  1. . 64
  2. . 128
  3. . 192
  4. . 16π
  5. . Cannot be determined

Exercise 11:

The area inside the region formed by the semicircular curves from A to B to C to D and back to A is

  1. . 64
  2. . 128
  3. . 192
  4. . 16π
  5. . Are you for real??!!

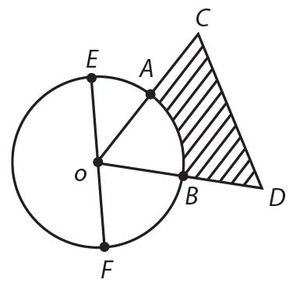
Exercise 12:

In the figure, EF = CD = 12, B is the midpoint of OD, and A is the midpoint of CO. The area of the shaded portion is

  1. . 36(4√3 − π)
  2. . 6(6√3 − π)
  3. . 144(π − 3)
  4. . 72(3√3 − π)
  5. . 36(6√3 − π)
    e9780738668499_i1358.jpg

For Exercises 13 and 14, use this figure.

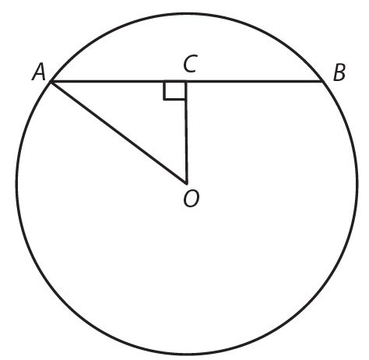
e9780738668499_i1359.jpg

Exercise 13:

If the diameter = 20, OC ⊥ AB, and ∠ A = 30° , AB =

  1. . 10
  2. . 5
  3. . 5√3
  4. . 10√3
  5. .5√2

Exercise 14:

If OC bisects AB, AB = 16, and OC = 6, the area of circle O is

  1. . 10π
  2. . 20π
  3. . 40π
  4. . 100π
  5. . 400π

Exercise 15:

In a circle with center O, diameter 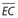e9780738668499_i1360.jpg is perpendicular to chord 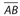e9780738668499_i1361.jpg at point D. Which of the following statements are true? Indicate all correct choices.

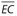  1. e9780738668499_i1362.jpg bisects minor arc AB.
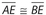  2. e9780738668499_i1363.jpg.
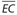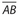  3. e9780738668499_i1364.jpg bisects e9780738668499_i1365.jpg.
  4. OA = OB.
  5. OD is the distance between 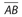e9780738668499_i1366.jpg and point O.

Exercise 16:

Which of the following lengths is sufficient information to find the area of a circle? Indicate all correct choices.

  1. Radius
  2. Diameter
  3. Circumference
  4. Any chord
  5. Each of two intersecting chords
  6. A chord that is perpendicular to a tangent of the circle

Exercise 17:

A circle with a diameter of 12 has the same area as a square. To the nearest tenth, what is the side of the square?

e9780738668499_i1367.jpg

Exercise 18:

A sector of a circle has a central angle of 90°. If the radius of the circle is 10, the perimeter of this sector can be represented as a + bπ. What is the sum of a and b?

e9780738668499_i1368.jpg

Exercise 19:

The radius of a circle is 4. To the nearest tenth, what is the area of a sector whose central angle is 60°?

e9780738668499_i1369.jpg

e9780738668499_i1370.jpg Let’s look at the answers.

Answer 6:

The answer is (A). The figure is a 6-8-10 Pythagorean triple, but 10 is not part of the perimeter. 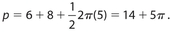e9780738668499_i1371.jpg.

Answer 7:

The answer is (A). 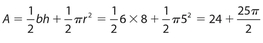e9780738668499_i1372.jpg.

Answer 8:

The answer is (B). The area is the area of the square minus the area of the circle. A = s2 − πr2 = 102 − π52 = 100 − 25π.

Answer 9:

The answer is (B). Exercise 8 and Exercise 9 are exactly the same problems. In Exercise 8, we could also say the square circumscribes the circle.

Answer 10:

The answer is (C). Each semicircle has arc length 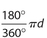e9780738668499_i1373.jpg, and there are 16 semicircles, so 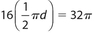e9780738668499_i1374.jpg, or 8πd = 32π, so d = 4. The rectangle’s dimensions are thus 8 and 24. The area is A = b × h = 8(24) = 192.

Answer 11:

The answer is (C). Believe it or not, Exercise 11 is exactly the same as Exercise 10! You can think of the areas of the “outer” semicircles as canceling out the areas of the “inner” semicircles, and you are left with only the area of rectangle ABCD.

Answer 12:

The answer is (B). The information is enough to tell us the triangle is equilateral and L AOB = 60°. The shaded area is the area of ΔCOD minus the area of sector OABO. Thus,

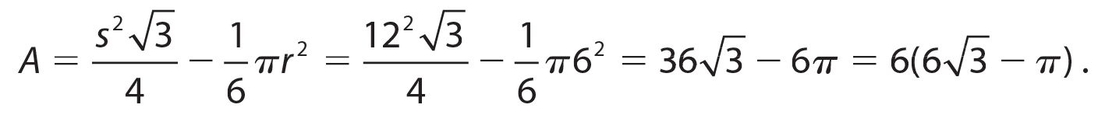
e9780738668499_i1375.jpg

Answer 13:

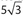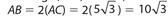The answer is (D). AO, the radius, is 10; CO, the side opposite the 30° angle, is 5; and AC, the side opposite the 60° angle, is e9780738668499_i1376.jpg. e9780738668499_i1377.jpg.

Answer 14:

The answer is (D). To find the area of the circle, we need to find the radius OA. We know AC is 8 and OC is 6. We have a 6-8-10 right triangle, so AO = r = 10. The area is π(10)2 = 100π.

Answer 15:

The correct answers are (A), (B), (C), (D), and (E). Choices (A), (B), and (C) can be proven formally. Choice (D) is true because any two radii of the same circle must be congruent. Choice (E) is true because of the definition of the distance between a line segment and a point.

Answer 16:

The correct answers are (A), (B), (C), and (F). Choice (A) is correct because the area of a circle is πr2, where r is the radius. Choice (B) is correct because, given the diameter, we can determine the radius by dividing by 2, and then apply the area formula. Choice (C) is correct because, given the circumference, the radius can be found by dividing by 2π, and then applying the area formula. For choice (F), this chord must be the diameter, and thus the radius and area can be determined.

Answer 17:

The correct answer is 10.6. The radius of the circle is 6, so its area is (π)(62) = 36π. Thus, the side of the square must be 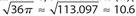e9780738668499_i1378.jpg.

Answer 18:

The correct answer is 25. The circumference of the circle is (2)(π)(10) = 20π. The arc of this sector represents 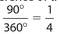e9780738668499_i1379.jpg of the circumference, which is 5π. The perimeter of the sector consists of two radii and the corresponding arc length. Then the perimeter of the sector is 20 + 5π = a + bπ. Therefore, the sum of a and b is 25.

Answer 19:

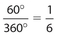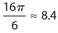The correct answer is 8.4. The area of the circle is (π)(42) = 16π. Then the area of the sector must be e9780738668499_i1380.jpg of the area of the circle. Thus, the area of the sector is e9780738668499_i1381.jpg.

EQUATION OF A CIRCLE

Another property of circles that is required for the GRE test is its equation in the xy-coordinate plane. The definition of a circle is the set of all points at a fixed distance from a given point. The fixed distance is called the radius and the given point is called the center. Let the center be represented by the coordinates (h, k) and let r represent the radius. Then the equation of this circle is (x − h)2 + (y − k)2 = r2. If a point (a, b) lies inside the circle, then (a − h)2 + (b − k)2 < r2. Likewise, if a point (c, d) lies outside the circle, then (c − h)2 + (d − k)2 > r2.

The following diagram shows the graph of (x − 1)2 + (y + 2)2 = 9.

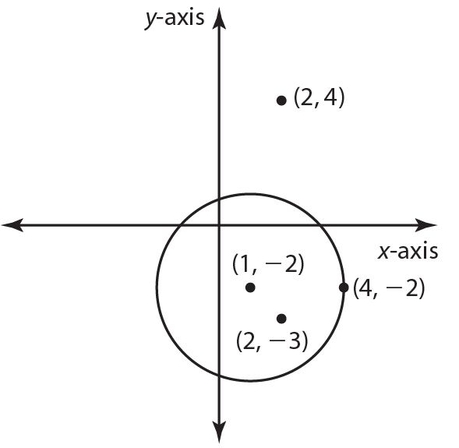
e9780738668499_i1382.jpg

The equation can be written in the form (x − 1)2 + (y − (− 2))2 = 9. This means that h = 1 and k = −2, so the center is located at (1, −2). The point (4, −2) is on the circle because (4 − 1)2 + (−2 + 2)2 = 32 + 02 = 9. The point (2, −3) is inside the circle because (2 − 1)2 + (−3 + 2)2 = 12 + (−1)2 = 2 < 9. Also, note that the point (2,4) is outside the circle because (2 − 1)2 + (4 + 2)2 = 12 + (6)2 = 1 + 36 = 37 > 9.

 

e9780738668499_i1383.jpg

Never write the equation of a circle as (x − h) + (y − k) = r.

e9780738668499_i1384.jpg Let’s do some more exercises.

Exercise 20:

What is the sum of the coordinates of the center of a circle whose equation is (x − 4)2 + (y + 7)2 = 100?

e9780738668499_i1385.jpg

Exercise 21:

To the nearest hundredth, what is the radius of a circle whose equation is (x + 5)2 + (y − 3)2 = 20?

e9780738668499_i1386.jpg

Exercise 22:

Which of the following points lie outside the circle whose equation is (x + 2)2 + (y + 4)2 = 25? Indicate all correct answers.

  1. (1, −2)
  2. . (3, −4)
  3. . (−3, −1)
  4. . (2, −2)
  5. . (4, −5)
  6. . (0, 1)

Exercise 23:

The point (6, 2) lies inside the circles associated with which of the following equations? Indicate all correct answers.

  1. (x − 3)2 + (y − 2)2 = 16
  2. (x − 1)2 + (y + 4)2 = 65
  3. (x + 1)2 + (y + 6)2 = 113
  4. (x + 2)2 + (y + 1)2 = 70
  5. (x + 7)2 + (y + 3)2 = 200
  6. (x − 4)2 + (y + 5)2 = 60

Exercise 24:

Which one of the following equations represents a circle with its center at (−1, −6) and with a radius of 16?

  1. (x + 1)2 + (y + 6)2 = 256
  2. (x − 1)2 + (y − 6)2 = 256
  3. (x − 6)2 + (y − 1)2 = 256
  4. (x + 6)2 + (y + 1)2 = 16
  5. (x + 1)2 + (y + 6)2 = 16

e9780738668499_i1387.jpg Let’s look at the answers.

Answer 20:

The correct answer is −3. Rewrite the equation as (x − 4)2 + (y − (−7))2 = 100 to identify h = 4 and k = −7. Therefore, the center is located at (4, −7), and the sum of its coordinates is −3. Note that the fact that r2 = 100 isn’t needed to find the center.

Answer 21:

The correct answer is 4.47. Since r2 = 20, the radius is 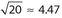e9780738668499_i1388.jpg

Answer 22:

The correct answers are (E) and (F). By substitution, choice (E) becomes (4 + 2)2 + (−5 + 4)2 = 62 + (−1)2 = 37 > 25, and choice (F) becomes (0 + 2)2 + (1 + 4)2 = 22 + 52 = 29 > 25. Each of choices (A), (B), (C), and (D) are wrong because substitution of their values into the left side of the equation (x + 2)2 + (y + 4)2 = 25 does not produce a number greater than 25. The left sides of the equation for choices (A), (B), (C), and (D) become 5, 25, 10, and 20, respectively.

Answer 23:

The correct answers are (A), (B), (E), and (F). The easiest way to determine the correct responses is to substitute 6 for x and 2 for y in each equation and compare the two sides of the equation. If the two sides are equal, (6, 2) lies on the circle; if the left side is smaller, (6, 2) lies inside the circle; if the left side is larger, (6, 2) lies outside the circle. The results for each answer choice are

  1. (6 − 3)2 + (2 − 2)2 = 32 + 02 = 9 < 16, which means inside the circle.
  2. (6 − 1)2 + (2 + 4)2 = 52 + 62 = 25 + 36 = 61 < 65, which means inside the circle.
  3. (6 + 1)2 + (2 + 6)2 = 72 + 82 = 49 + 64 = 113, which means on the circle.
  4. (6 + 2)2 + (2 + 1)2 = 82 + 32 = 64 + 9 = 73 > 70, which means outside the circle.
  5. (6 + 7)2 + (2 + 3)2 = 132 + 52 = 169 + 25 = 194 < 200, which means inside the circle.
  6. (6 − 4)2 + (2 + 5)2 = 22 + 72 = 4 + 49 = 53 < 60, which means inside the circle.

Answer 24:

The correct answer is (A). The equation (x + 1)2 + (y + 6)2 = 256 can be rewritten as (x − (−1))2 + (y − (−6))2 = 162. In this form, h = −1, k = −6, and r = 16. Note that choice (E) is wrong because we need r2, not r.

Okay. Now let’s go from two dimensions to three dimensions.