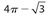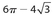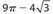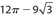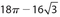Practice Test 1
Section 2
Directions: Each of Questions 1-9 consists of two quantities. Compare the quantities in Quantities A and B and choose
 if Quantity A is greater.
if Quantity A is greater. if Quantity B is greater.
if Quantity B is greater. if the two quantities are equal.
if the two quantities are equal. if the relationship cannot be determined from the information given.
if the relationship cannot be determined from the information given.

Questions 7-9 use the following inequality: − 15 < x < − 11
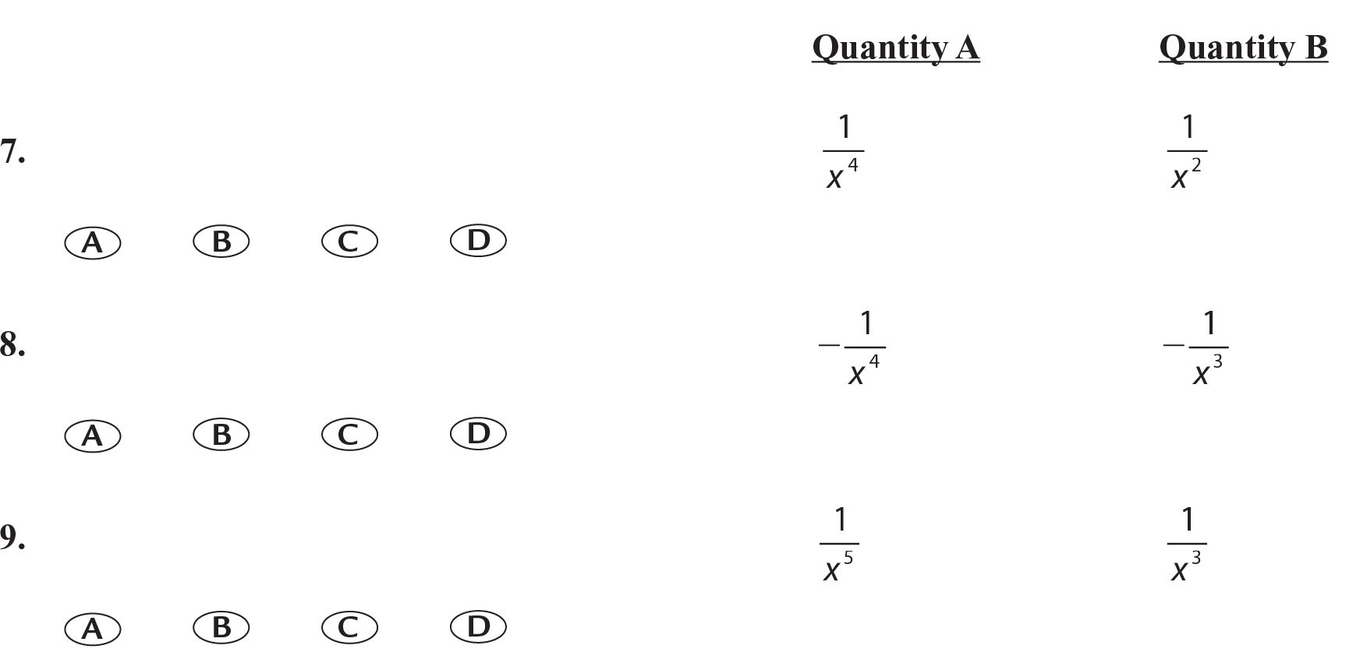
Directions: Questions 10-25 have several different formats. Unless otherwise indicated, select a single answer choice. For numeric entry questions, follow the instructions below.
Numeric Entry Questions
Enter your answer in the answer box(es) below the question.
- Your answer may be an integer, a decimal, or a fraction, and it may be negative.
- If a question asks for a fraction, there will be two boxes—one for the numerator and one for the denominator.
- Equivalent forms of the correct answer, such as 2.5 or 2.50, are all correct. Fractions do not need to be reduced to lowest terms.
- Enter the exact answer unless the question asks you to round your answer.
- 10. In a large lecture hall, the ratio of men to women is 2:3. If there are 365 people in the lecture hall, how many women are there?
 73
73 105
105 126
126 219
219 257
257
- 11. The area of a circle is 1. What is the length of its diameter?

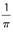

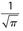

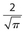
 π
π
- 12. Look at the following diagram of a rectangular solid:
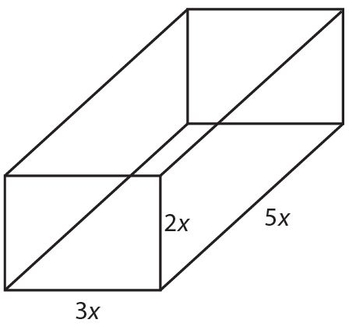
What is the surface area?
 30x3
30x3 31x2
31x2 50x2
50x2 60x3
60x3 62x2
62x2
- 13. Which of the following are sufficient to determine that the slope of a line is positive? Indicate all correct answers.
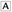 The x-intercept is five times the y-intercept.
The x-intercept is five times the y-intercept.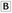 The line contains the point (3, 2) and the x-intercept is positive.
The line contains the point (3, 2) and the x-intercept is positive. The x-intercept is the negative reciprocal of the y-intercept.
The x-intercept is the negative reciprocal of the y-intercept. The line is perpendicular to one of the axes.
The line is perpendicular to one of the axes.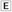 The sign of the slope and the y-intercept are identical.
The sign of the slope and the y-intercept are identical. The line contains the origin.
The line contains the origin.
- 14. Which of the following are equivalent to (x + 10)2? Indicate all correct answers.
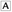 x2 + 100
x2 + 100 (x − 10)2 + 40x
(x − 10)2 + 40x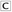 (x)(x + 5) + (5)(x + 5)
(x)(x + 5) + (5)(x + 5)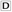 (x − 5)(x + 5) + (5)(4x + 25)
(x − 5)(x + 5) + (5)(4x + 25) (x + 5)(x + 5) + (10)(x + 8)
(x + 5)(x + 5) + (10)(x + 8)
- 15. The expression 2n + 2n is equivalent to which one of the following?
 2n+1
2n+1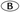 2n+2
2n+2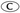 2n+3
2n+3 4n
4n
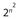
For Questions 16, 17, and 18, use the following chart.
Specialty Store Larger Shoe Sizes
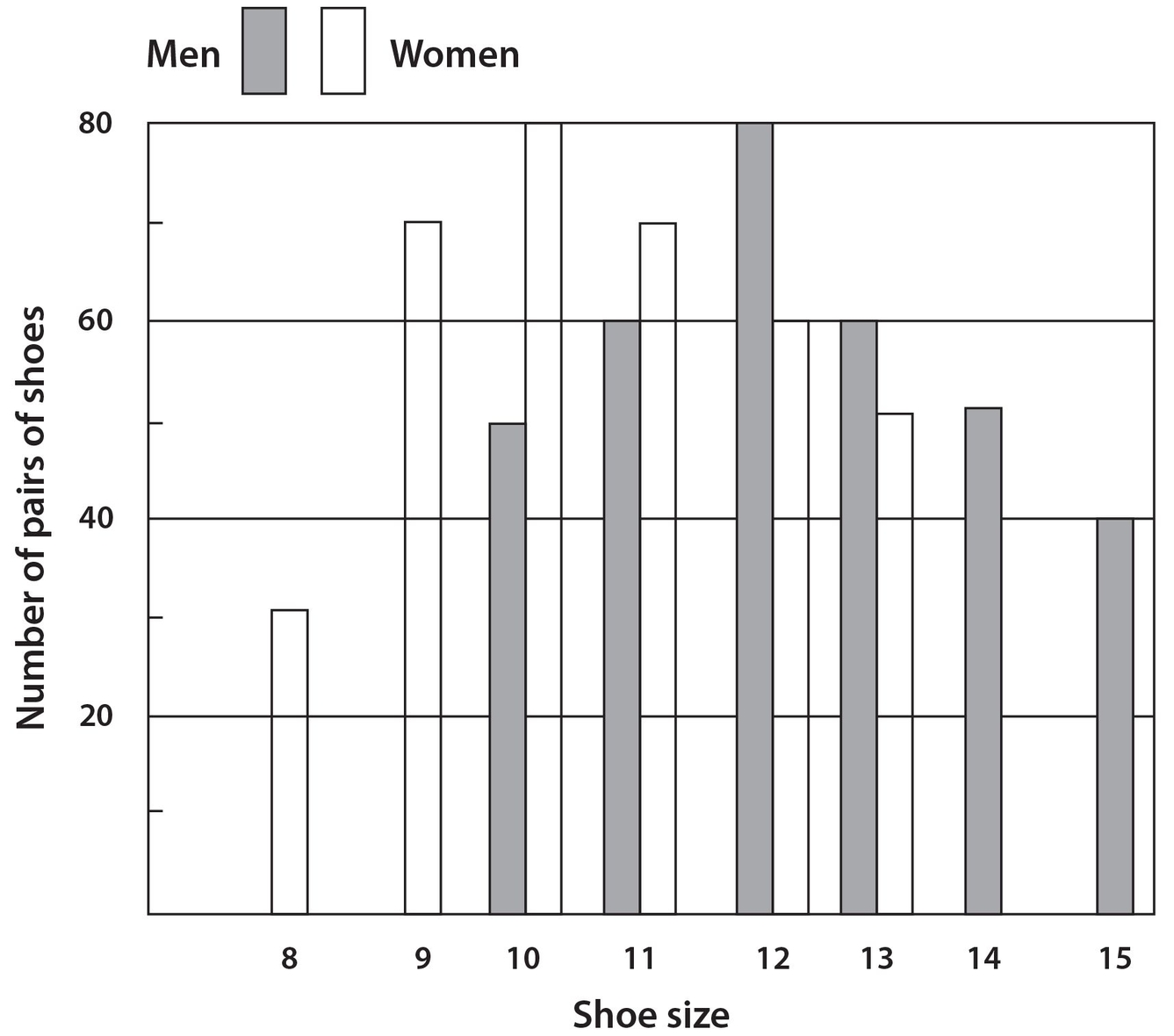
- 16. If 40% of the women’s size 12 shoes are black, and 25% of these black shoes have high heels, how many women’s size 12 black shoes do not have high heels?
 52
52 32
32 28
28 24
24 18
18
- 17. The number of pairs of men’s shoes that are larger than size 13 is what percent of the total number of pairs of shoes in the store? Write your answer to the nearest whole number.

- 18. For women’s shoes, the average price for any given size is 10% higher than the average price for the next smallest size. Suppose that the average price for a pair of women’s shoes of size 8 is $200. Then the selling price for all women’s shoes of size 10 would be how much greater than the selling price for all women’s shoes of size 8?

- 19. There are seven men and nine women in a room. A committee of five people is to be chosen. If the committee has three men and two women, how many different committees are possible?
 1,260
1,260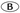 1,250
1,250 1,245
1,245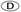 1,240
1,240 1,225
1,225
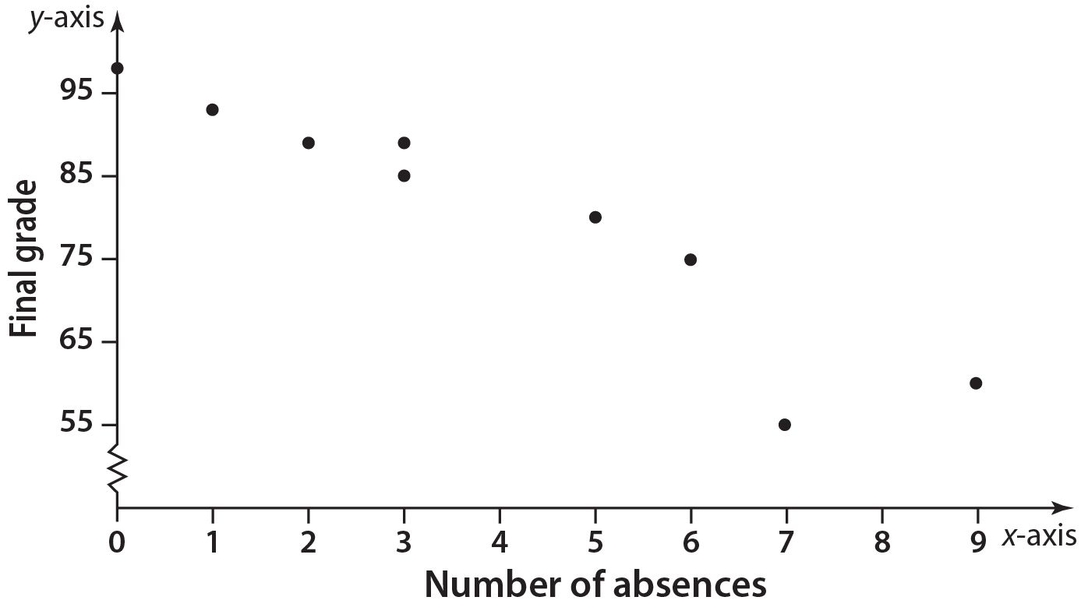
- 20. Look at the following diagram.
This is called a ______
 histogram.
histogram.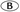 line graph.
line graph.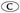 pictogram.
pictogram. bar graph.
bar graph. scatter plot.
scatter plot.
- 21. If
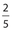 of n equals
of n equals 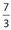 , what is the value of
, what is the value of 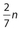 ?
?

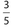
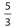
 6
6 35
35 210
210
- 22. If
 , which of the following is true?
, which of the following is true?
 x = 0 and y ≠ 0
x = 0 and y ≠ 0 x = 6 and y = 4
x = 6 and y = 4 x ≠ 6 and y ≠ 4
x ≠ 6 and y ≠ 4 x = 6 and y ≠ 4
x = 6 and y ≠ 4 x ≠ 6 and y = 4
x ≠ 6 and y = 4
For Questions 23 and 24, use the following diagram of a Norman window, which consists of a rectangle surmounted by a semicircle.
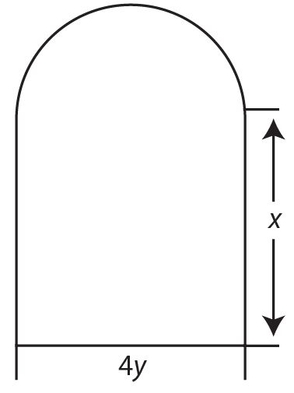
- 23. What is the perimeter of this figure?
 2x + 8y + 4πy
2x + 8y + 4πy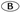 2x + 4y + 4πy
2x + 4y + 4πy 2x + 4y + 2πy
2x + 4y + 2πy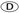 2x + 4y + πy
2x + 4y + πy
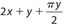
- 24. What is the area of this figure?

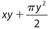
 4xy + 4πy2
4xy + 4πy2 4xy + 2πy2
4xy + 2πy2 4xy + πy2
4xy + πy2
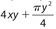
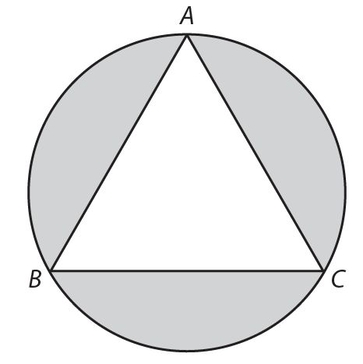
- 25. The figure below shows equilateral triangle ABC inscribed in a circle. If AB = 6, what is the combined area of the shaded regions?
ANSWERS AND EXPLANATIONS
- (C)
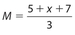 , which means that 3M = 5 + x + 7. Then
, which means that 3M = 5 + x + 7. Then 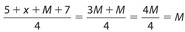 .
. - (D) Either of m and
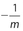 can be positive and the other will be negative.
can be positive and the other will be negative. - (B) N2 = (y − x)2 = y2 − 2xy + x2. Since x, y > 2, both x, y are positive. Thus, y2 − 2xy + x2 must be less than x2 + y2.
- . (D) The value of q is unknown. If
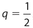 , then
, then 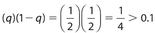 . If q = 0.1, then (q)(1 − q) = (0.1)(0.9) = 0.09 < 0.1.
. If q = 0.1, then (q)(1 − q) = (0.1)(0.9) = 0.09 < 0.1. - (A) Since 2’ = 2, m − n = 1. Thus, m = n + 1, which means that m > n.
- (C) By definition, 2 ◯ y = y2 − 2y. Then y2 − 2y = −1, which can be written as y2 − 2y + 1 = 0. Factor the left side to get (y − 1 )(y − 1) = 0. Thus, y = 1.
- (B) For −15 < x < −11, x2 < x4. If the reciprocal of each quantity is used, the inequality sign is reversed. Thus,
 .
. - (B) For a negative value of x,
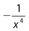 has a negative value and
has a negative value and 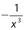 has a positive value.
has a positive value. - (A) For −15 < x < − 11, x5 < x3. By taking the reciprocal of each quantity, the inequality sign is reversed. Thus,
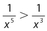 .
. - (D) Let 2x represent the number of men and 3x represent the number of women. Then 2x + 3x = 365, which becomes 5x = 365. This means that x = 73. Thus, the number of women is (3)(73) = 219.
- (D) 1 = πr2, so
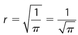 . Then the diameter must be (2)
. Then the diameter must be (2) 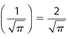 .
. - (E) The surface area is (2)(2)(3x) + (2)(2x)(5x) + (2)(3x)(5x) = 12x2 + 20x2 + 30x2 = 62x2.
- (C) If the x-intercept is the negative reciprocal of the y-intercept, then one of x and y is negative and the other is positive. A line containing these two intercepts must be positive. None of the other answer choices gives sufficient information for determining a positive slope.
- (B, D) (x + 10)2 = x2 + 20x + 100. For choice (B), (x − 10)2 + 40x = x2 − 20x + 100 + 40x = x2 + 20x + 100. For choice (D), (x − 5)(x + 5) + (5)(4x + 25) = x2 − 25 + 20x + 125 = x2 + 20x + 100. Choice (A) is obviously incorrect. The simplified expressions for choices (C) and (E) are x2 + 10x + 25 and x2 + 20x + 105.
- (A) 2n + 2n = (2)(2n) = (21)(2n) = 2n+1.
- (E) There are 60 pairs of women’s shoes in size 12. Then (0.40)(60) = 24 pairs of size 12 are black. Of these, 100% − 25% = 75% do not have high heels. Thus, the required number is (0.75)(24) = 18.
- 13 There are 340 pairs of men’s shoes and 360 pairs of women’s shoes. The number of pairs of men’s shoes that are larger than size 13 is 90. Thus, the required percent is
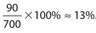 .
. - 13,360 There are 30 pairs of size 8 shoes, for which the total selling price is (30($200) = $6,000. The average price of each pair of size 9 shoes is ($200)(1.10) = $220, and the average price of each size 10 shoes is ($220)(1.10) = $242. Since there are 80 pairs of size 10 shoes, the total selling price is (80)($242) = $19,360. Thus, the difference in total price is $19,360 − $6,000 = $13,360.
- (A) The number of ways to choose three men is
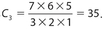 . The number of ways to choose two women is
. The number of ways to choose two women is 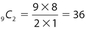 . Therefore, the number of different committees is (35)(36) = 1,260.
. Therefore, the number of different committees is (35)(36) = 1,260. - (E) A scatter plot is a graph of points that represent ordered pairs of variables.
- (B) We are given that
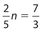 , so
, so 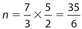 . Thus,
. Thus, 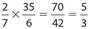 .
. - (D) Whenever a fraction has a value of zero, the numerator must equal zero and the denominator must not equal zero. Then x − 6 = 0 and y − 4 ≠ 0, which means that x = 6 and y ≠ 4.
- (C) The base of the rectangle is 4y and there are two heights whose combined lengths are 2x. The semicircle at the top contains a diameter of length 4y, so its length is
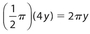 . Thus, the perimeter is 2x + 4y + 2πy.
. Thus, the perimeter is 2x + 4y + 2πy. - (C) The area of the rectangular portion is the product of the base and height, which is 4xy. For the semicircle, its radius is
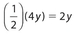 . Then the area of the semicircle is
. Then the area of the semicircle is 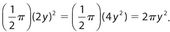 . Thus, the area of the figure is 4xy + 2πy2.
. Thus, the area of the figure is 4xy + 2πy2. - (D) Redraw the figure and connect the center of the circle (point O) with points B and C. Also, draw
 perpendicular to
perpendicular to 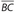 at point E.
at point E.
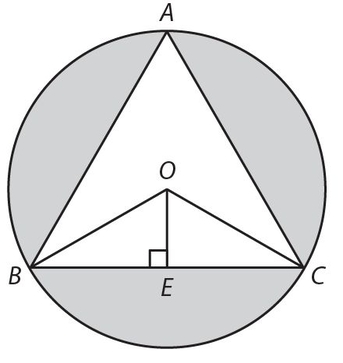
We know that m∠ABC = 60° and it can be proven that
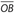 bisects ∠ABC. This means that ΔBOE is a 30°-60°-90° right triangle, with m∠OBE = 30°.
bisects ∠ABC. This means that ΔBOE is a 30°-60°-90° right triangle, with m∠OBE = 30°.It can be shown that E is the midpoint of
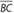 , so BE = 3.
, so BE = 3.  is a radius and also the hypotenuse of ΔBOE We determine that m∠BOE = 60° and since BE = 3,
is a radius and also the hypotenuse of ΔBOE We determine that m∠BOE = 60° and since BE = 3, 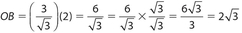 Then the area of the circle is (π)(2√3)2 = 12π. The area of ΔABC is
Then the area of the circle is (π)(2√3)2 = 12π. The area of ΔABC is 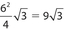 .The area of the combined shaded regions is the difference between the areas of the circle and the triangle, which is 12π − 9√3.
.The area of the combined shaded regions is the difference between the areas of the circle and the triangle, which is 12π − 9√3.