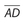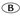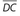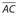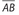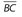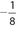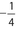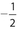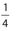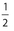Practice Test 2
Section 2
Directions: Each of Questions 1-9 consists of two quantities. Compare the quantities in Quantities A and B and choose
 if Quantity A is greater.
if Quantity A is greater. if Quantity B is greater.
if Quantity B is greater. if the two quantities are equal.
if the two quantities are equal. if the relationship cannot be determined from the information given.
if the relationship cannot be determined from the information given.
3.Circle A has an area of 4π and circle B has a circumference of 4π.

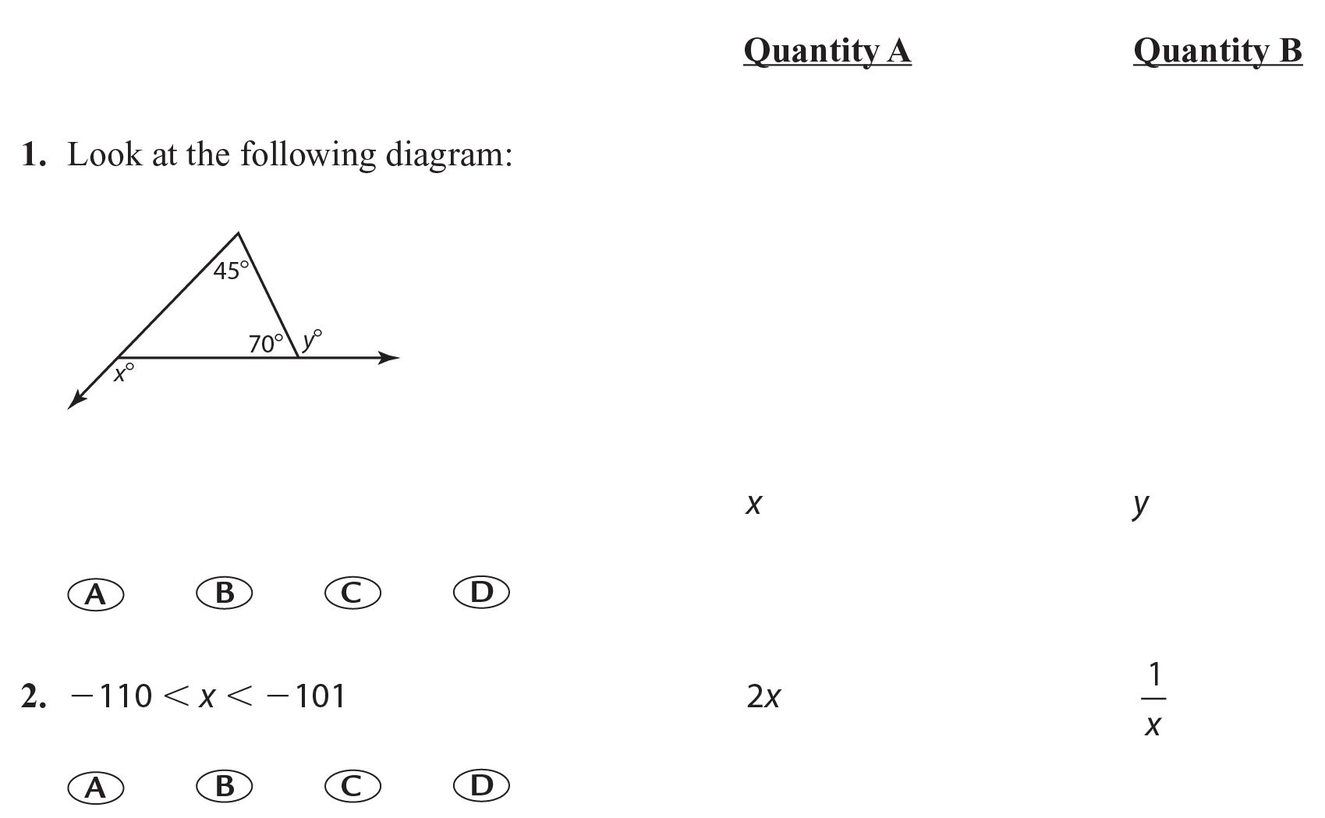
5.Look at the following diagram, in which line L1 is parallel to line L2


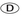
| Quantity A | Quantity B |
|---|---|
| 50 | 2x − 200 |
6.Car A is traveling at 60 miles per hour for one mile. Car B is traveling at 50 miles per hour for one and one-half miles.

9.WXYZ is a square, as shown below:
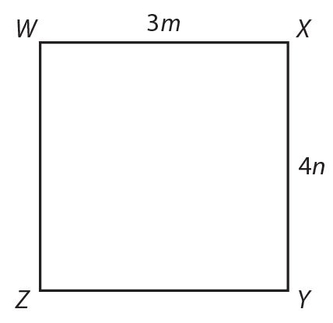
| 9m2 | 16n2 |
Directions: Questions 10–25 have several different formats. Unless otherwise indicated, select a single answer choice. For numeric entry questions, follow the instructions below.
Numeric Entry Questions
Enter your answer in the answer box(es) below the question.
- Your answer may be an integer, a decimal, or a fraction, and it may be negative.
- If a question asks for a fraction, there will be two boxes—one for the numerator and one for the denominator.
- Equivalent forms of the correct answer, such as 2.5 or 2.50, are all correct. Fractions do not need to be reduced to lowest terms.
- Enter the exact answer unless the question asks you to round your answer.
- 10. Look at the following figure. Note: The figure is not drawn to scale.
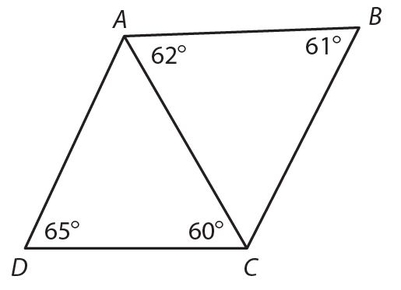
Which is the largest side?
- 11. If 3 (2x − 1) + 4 = 2x, what is the value of x?
- 12. In a small group of children, one girl who is looking at all the other children sees an equal number of boys and girls. One boy who is looking at all the other children sees twice as many girls as boys. Which of the following is the correct composition of this group?
 3 boys and 4 girls
3 boys and 4 girls 3 boys and 3 girls
3 boys and 3 girls 4 boys and 3 girls
4 boys and 3 girls boys and 5 girls
boys and 5 girls 5 boys and 4 girls
5 boys and 4 girls
- 13. Currently, John is 16 years old and his father is 50 years old. In how many years will John be half as old as his father?
 10
10 12
12 16
16 18
18 20
20
- 14. If 3 bligs equals 5 bloogs and 7 bloogs equals 8 blugs, what is the ratio of bligs to blugs? Write your answer as a fraction.
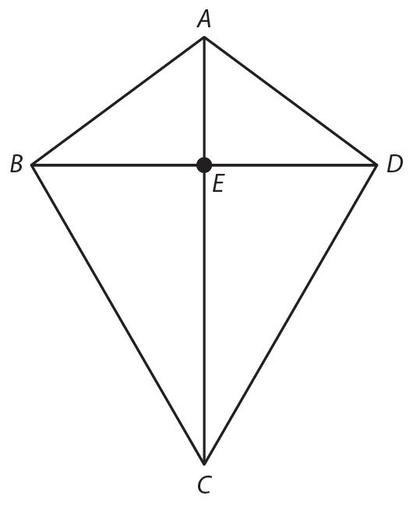
- 15. The figure shown below is a kite, for which AC > BD.
If AB = 10, AE = 6, and BC = 17, what is the product of BD and AC?

For Questions 16−20, use the following circle graphs. There are a total of 2,000 employees.

- 16. The number of divorced employees is three times the number of widowed employees. How many divorced employees are there?
 200
200 300
300 400
400 500
500 600
600
- 17. How many employees are married and have five children?
 75
75 60
60 54
54 45
45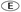 30
30
- 18. What is the combined total of the number of employees who are either single or married with at least 3 children?

- 19. Of the employees who are married with just one child, there are four times as many of them who work full-time as work part-time. Assuming that all employees of this hospital work either full-time or part-time, the number of full-time employees who are married with just one child represent what percent of the entire number of employees?

- 20. Next year, the Growing Strong Hospital plans to increase its staff by 10%. If all the new employees happen to be single, then the number of single employees will increase by what percent?

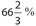
 40%
40%
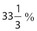
 20%
20% 10%
10%
- 21. Which of the following is equivalent to
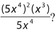
 x3
x3
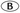 5x3
5x3  x7
x7  5x7
5x7  5x15
5x15 - 22. Given the data, 2, 2, 5, 7, 9, and 17, what is the sum of the mean, median, and mode?
 13
13 14
14 15
15 16
16 17
17
- 23. In a group of 35 students, all of them take at least one of the subjects French and Spanish. If 25 students take Spanish and 10 students take both languages, how many students take French but not Spanish?

- 24. A radio that usually sells for $60 is discounted 25% on Monday. On Wednesday, the price is further discounted another 10% from Monday’ s price. If there is a state sales tax of 4%, what would be the final price of this radio? Round off your answer to the nearest dollar.

- 25. If x6 = m and
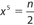 , which of the following expressions is equivalent to x?
, which of the following expressions is equivalent to x?
 2mn
2mn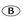
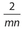
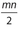
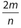

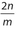
ANSWERS AND EXPLANATIONS
- (A) The missing angle in the triangle is 180° − 45° − 70° = 65°. Then x = 180 − 65 = 115 and y = 180 − 70 = 110.
- (B) The value of 2x is less than −200, whereas the value of
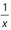 is between −1 and 0.
is between −1 and 0. - (C) Let r represent the radius of circle A. Since the area is 4π, πr2 = 4π. Then r2 = 4, so r = 2. Let R represent the radius of circle B. Since the circumference of circle Β is 4π, 2πR = 4π. Then 2R = 4, so R = 2.
- (C) Using the distributive property, each expression is equivalent to 8x + 8y.
- (B) Since the lines are parallel, interior angles on the same side of the transversal are supplementary. Then x = 180 − 50 = 130. Thus, 2x − 200 = (2)(130) − 200 = 60.
- (B) Car A is traveling at 60 miles per hour, so the time needed to travel one mile is
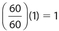 minute. Car B is traveling at 50 miles per hour, so the time needed to travel one and one-half miles is
minute. Car B is traveling at 50 miles per hour, so the time needed to travel one and one-half miles is 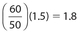 minutes.
minutes. - (D) If x4 = y4, then x = y or x = −y. Therefore, we cannot determine which of x and y is larger.
- (B) By squaring both sides,
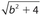 becomes b2 + 4 and b + 2 becomes (b + 2)2 = b2 + 4b + 4. Since b > 0, b2 + 4b + 4 is larger than b2 + 4.
becomes b2 + 4 and b + 2 becomes (b + 2)2 = b2 + 4b + 4. Since b > 0, b2 + 4b + 4 is larger than b2 + 4. - (C) Since the figure is a square, 3m = 4n. Thus, the area of the square can be expressed as either (3m)2 = 9m2 or (4n)2 = 16n2.
- (E) In any triangle, the largest side is opposite the largest angle. In ΔADC, m∠DAC = 180° − 65° − 60° = 55°. This means that
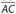 is the largest side of ΔADC. In ΔBAC, m∠BCA = 180° − 62° − 61° = 57°. This means that
is the largest side of ΔADC. In ΔBAC, m∠BCA = 180° − 62° − 61° = 57°. This means that 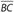 is the largest side of ΔBAC. Since
is the largest side of ΔBAC. Since 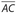 is part of ΔBAC, we can claim that BC > AC. Thus,
is part of ΔBAC, we can claim that BC > AC. Thus, 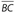 must be the largest of the segments for both triangles.
must be the largest of the segments for both triangles. - (B) Using the distributive property, the equation becomes 6x − 3 + 4 = 2x. Then 6x + 1 = 2x, which simplifies to 1 = −4x. Thus,
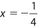 .
. - (A) Let x represent the number of boys and y represent the number of girls. Then one girl is looking at x boys and y − 1 girls. Since she sees an equal number of girls and boys, x = y − 1, which can be written as y = x + 1. At this point, the only two possible answer choices for which y = x + 1 are A and D. We also know that one boy is looking at x − 1 boys and y girls. Since he sees twice as many girls as boys, y = 2(x − 1). By substitution, we can write x + 1 = 2(x − 1). This equation simplifies to x + 1 = 2x − 2. Then 1 = x − 2, so x = 3. Consequently, y = 4, which means there are 3 boys and 4 girls.
- (D) Let x represent the required number of years. Then
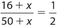 . Cross-multiply to get (2)(16 + x) = (1)(50 + x), which simplifies to 32 + 2x = 50 + x. Then 32 + x = 50, so x = 18.
. Cross-multiply to get (2)(16 + x) = (1)(50 + x), which simplifies to 32 + 2x = 50 + x. Then 32 + x = 50, so x = 18. 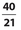 Since 3 bligs equals 5 bloogs, 1 blig is equivalent to
Since 3 bligs equals 5 bloogs, 1 blig is equivalent to 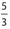 bloogs. Likewise, since 8 blugs equals 7 bloogs, 1 blug is equivalent to
bloogs. Likewise, since 8 blugs equals 7 bloogs, 1 blug is equivalent to 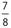 bloog. Thus, the ratio of 1 blig to 1 blug can be expressed as
bloog. Thus, the ratio of 1 blig to 1 blug can be expressed as 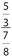 , which becomes
, which becomes 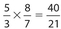 . 3 7 21
. 3 7 21- 336 For a kite, the diagonals are perpendicular to each other and the longer diagonal bisects the shorter diagonal. Using the Pythagorean theorem for ΔABE, (BE)2 + 62 = 102. So,
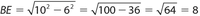 . = Since E is the midpoint of
. = Since E is the midpoint of 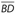 , BD = 16. Using the Pythagorean theorem for ΔΒEC, (EC)2 + 82 = 172. So,
, BD = 16. Using the Pythagorean theorem for ΔΒEC, (EC)2 + 82 = 172. So, 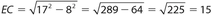 . Then AC = 6 + 15 = 21. Finally, the product of BD and AC is (16)(21) = 336.
. Then AC = 6 + 15 = 21. Finally, the product of BD and AC is (16)(21) = 336. - (E) The combined percent of the number of widowed and divorced employees is 100% − 20% − 25% − 15% = 40%. Let x represent the percent of widowed employees and let 3x represent the percent of divorced employees. Then x + 3x = 40, which becomes 4x = 40. So x = 10 and 3x = 30. Thus, the number of divorced employees is (0.30)(2,000) = 600.
- (E) The number of employees who are married with at least one child is (0.25)(2,000) = 500. Of these 500 employees, 100% − 25% − 22% − 35% − 12% = 6% of them have five children. Therefore, the required number is (0.06)(500) = 30.
- 565 The number of single employees is (0.15)(2,000) = 300. We have already determined that the number of married employees with at least one child is 500. Of these 500 employees, 35% + 12% + 6% = 53% have at least 3 children. This means that (0.53)(500) = 265 employees are married with at least 3 children. Therefore, the required number is 300 + 265 = 565.
- 5 Of the 500 employees who are married with children, (0.25)(500) = 125 of them have just one child. For this group of employees, let x represent the number of part-time workers and let 4x represent the number of full-time workers. Then x + 4x = 125, which becomes 5x = 125. We find that x = 25, so the number of full-time workers in this group is (4)(25) = 100. Thus, the required percent is
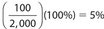 .
. - (A) The number of employees who will be hired next year is (2,000)(0.10) = 200. Currently, there are (0.15)(2,000) = 300 single employees. If all the new employees are single, this will raise the number of single employees to 500. The percent increase is
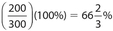 .
. - (D)
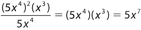 .
. - (C) The mean is
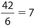 , the median is
, the median is 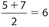 , and the mode is 2. Thus, the required sum is 15.
, and the mode is 2. Thus, the required sum is 15. - 10 Let n(F) represent the number of students who take French and let n(S) represent the number of students who take Spanish. Then n (F or S) = n(F) + n(S) − n(F and S). So, 35 = n(F) + 25 − 10, which simplifies to 35 = n(F) + 15. Then n(F) = 20. Thus, the number of students who take French but not Spanish is 20 − 10 = 10.
Alternative solution (using simple math): Since the number who take Spanish is 25 and the number who take both French and Spanish is 10, then 25 − 10 = 15 is the number who take only Spanish. Of the remaining students, we then know that 35 − 15 = 20 take French, and since 10 take both languages, 10 take French only.
- 42 After Monday’ s discount, the price of the radio becomes, ($60)(0.75) = $45. Following Wednesday’s discount, the price becomes ($45)(0.90) = $40.50. Finally, we include the sales tax so that the final price is ($40.50)(1.04) = $42.12 ≈ $42.
- (D)
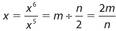 .
.