INTRODUCTION
Hi! My name is Bob Miller, and this is the introduction to a book that will help you do great on the quantitative section of the New GRE. This book will help you achieve your goal—getting admitted to the graduate school of your choice. It is important to know that a perfect score is not necessary. You only need a score that is high enough to get you into the school of your choice. ETS has changed the score scale from 130 to 170, in units of one. Therefore, a score of 169 is possible.
This book gives you everything you need to master math on the GRE revised General Test. All the topics in this book are covered in a way most readers have found easy to understand and sometimes even enjoyable. The kinds of questions on the GRE quantitative section are approximately 10% arithmetic, 40% algebra, 15% geometry, and 35% data analysis. (No advanced math such as trig or calculus or geometric proofs will be found on this test.) However, I’ve found great variation from test to test in the past. Some of the topics overlap each other. So even these percentages are very approximate. This book teaches you the topics you need, has many questions that are worked out in detail for you, and provides many other review questions and answers.
According to ETS, the test consists of either two or three math sections (one is an ungraded field test). There are 20 questions in each section on the computer-based test and 25 questions on each section on the paper-and-pencil test, with a time limit of 35 minutes. A calculator is provided for both the computer-based and paper-and-pencil versions—a major change. It is a simple calculator with only addition, subtraction, multiplication, division, and square root keys. There are memory keys and a special key on the computer—a button that will allow you to directly transfer your answer to the answer sheet.
On either version of the test, you may return to any question in a section. On the computerized version, you can add a check to problems and come back to them, changing answers if you choose. Once a section is finished, however, you cannot go back. Some advice: Never change an answer unless you are 100% sure the new answer is correct. On the last test I took, I went against my own advice and went from a correct answer to a wrong one!
There will be four types of questions. The first is the standard (single-answer) multiple-choice question, about 45% of the test (again, percentages are very approximate). The second is a multiple-answer multiple choice, which accounts for about 10% of the questions. The third is numeric entry, again about 10% of the test. The last is quantitative comparisons, about 35% of the test. Let’s talk about each type.
The first multiple-choice type is the one with which you are most familiar. There are five possible answers. You are to pick the correct answer and fill in the oval.
Question: If 2a = 3b = 4c = 20, what is the value of 9abc?
1,000
2,000
3,000
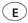8,000
9,000
Answer: (2a) (3b) (4c) = 24abc = (20)3 the = 8,000. Then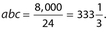 
Thus,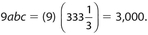 
The next type is the new multiple-answer multiple-choice question, with three to six answer choices. One or more of the answers will be correct, and you must fill in all the correct boxes. No credit will be given unless all the correct boxes are filled in. There must be at least one correct answer, but it is possible that all the answers might be correct. If a question requires two correct answers, you will get credit only if you fill in both correct answers.
Question: If 3 < x < 7, and x is an integer, then x might be
−5
1
3
4
6
2π
Answer: (D) and (E) are the correct answers. Choices (A) and (B) are obviously wrong; for choice (C), 3 is not greater than 3; for choice (F), 2π ≈ 6.28 but it is not an integer!
The third kind of question is the numeric entry. In plain English, this means to fill in the blank(s). The paper version and computer version are very different. On the computerized version, a rectangular blank must be filled in. If there is a fraction, there will be a rectangle, a fractional bar, and another rectangle under the bar. Fractions on either version of the test do not have to be reduced to be correct. The paper version has a grid to fill in. Any place on the grid with the correct answer will be correct. Beware that on this part of the test, you must give the answer exactly as the question asks. For example, suppose the answer was calculated to be 45.2%. If the rectangular box has a % sign after it, you must put only 45.2 in the box. On the gridded test 45.2 must be filled in.
Question: A jar has 7 red balls and 3 orange balls. Two balls are drawn, one at a time, without replacement. What is the probability of selecting two red balls? Write your answer as a fraction.
Answer: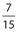 
The probability for selecting the first red ball is 
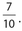For the second selection, there are nine balls left, of which six are red. So the probability of selecting a second red ball is 
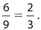Therefore, the required probability is 
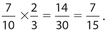(Examples of other acceptable answers are 
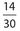and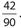 
)
An answer of 0.452, the same answer as a decimal, will be marked wrong. If the problem asks you to round off the answer to the nearest integer, you must put 45. All other answers are incorrect. You must give exactly the answer asked for!
The last question type is quantitative comparison. Your answer is actually the answer to “how do these two quantities compare?” Your answer choices are:
if Quantity A is greater.
if Quantity B is greater.
if the two Quantities are equal.
if the relationship cannot be determined from the information given.
Here’s an example. (Fill in the correct oval.)
| Quantity A | Quantity B |
|---|---|
| (45678−87654) | (87654−45678) |
The answer is B. You do not have to do the problem. You only need to know that B is larger because B is positive and A is negative. I always found these problems the easiest because you don’t have to work many of them out. Hints about this section: If A and B have only numbers, the answer is never D. The answer can always be determined. If there are only letters, the answer can only be C or D. If given more specific information about where the unknown numbers are (as an example, say, x > 4 and y > 6) or there is a mix of numbers and letters, any answer is possible.
With the New GRE, ETS is giving more real-life situations. This doesn’t change the nature of the problem. It only changes the location of the problem from a zoo to a factory. The math remains the same.
I tried to write this book as I wished my books had been written when I was a student. Good luck on the New GRE.
