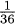APPENDIX A
ANSWERS TO SELECTED EXERCISES

SOLUTIONS FOR CHAPTER 1

1.5.b 10,862

1.5.d 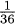= .02777…

1.6.c 2,1,5

1.6.e 1;20

1.7.b 1;19

1.9.b 1;26

1.11 The squares have sides 1/2 and 1/3.

1.16.a 319,700 ft³

1.19 7.5

1.21.a 20

1.21.b 31

1.21.c 213

1.21.d 101

1.23 24 meters

1.34 k = π/4

1.41 45°

1.47 6 feet

1.50 A = 16π ft², V = 32π/3 ft³

1.54.a a ≈ 5.196, b = 3

1.59 sin 15° = sin(60° – 45°) = sin 60° cos 45° – cos 60° sin 45° ≈ .259

1.62 90°, 90°, and 90°

1.65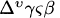

SOLUTIONS FOR CHAPTER 2

2.2 x = 1, y = 2, z = – 2

2.6.a True

2.6.b False

2.6.c True

2.6.d True

2.13 The sum of all the entries in the square is

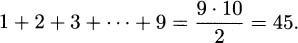
Since there are three rows, each row sum must be 45/3 = 15.

2.18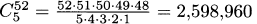

2.21 Using Brahmagupta’s method on (12,17) and (12,17), we get (408,577).

2.23 We have s = 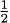(8 + 12 + 6 + 16) = 21, and hence

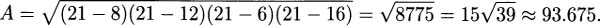
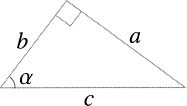
2.27 Using the labeling in the image below, sin α = α/c and cos α = b/c. By the Pythagorean Theorem, we have a² + b² = c². Putting these together,

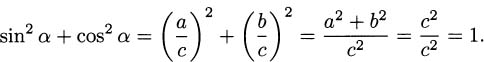
2.28.a π/3

2.28.b π/4

2.28.c π/12

2.28.d 4π

2.30 arctan 0 = 0

2.34 Since 1 – z² = 2z, or z² + 2z – 1 = 0, the quadratic formula gives z = – 1 ± 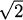. Abu Kamil would probably have thrown out the negative solution, so z = – 1 + 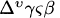= 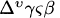– 1. Since y² = z, we have 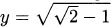(again ignoring negative solutions). Since y = (10 – x)/x, we have (10 – x)/x = 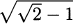. Solving this yields

(Note that setting 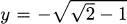gives another root. Even though y is negative, x is not. What is the approximate value of x?)

2.41

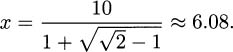
2.42

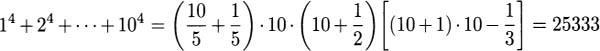
2.45 121/17 and 167/17 denarii

2.47.a 6

2.47.b 9

2.47.c 700

2.47.d 2900

2.53.a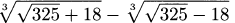

2.53.b 3

2.54

SOLUTIONS FOR CHAPTER 3

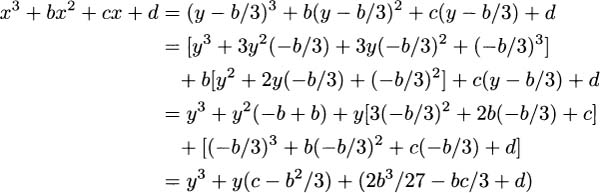
3.2 –0.17609

3.5 302

3.8 2/3

3.10 (x – 3)² + (y – 2)² = 25

3.14 x⁵ + 5x⁴y + 10x³y² + 10x²y³ + 5xy⁴ + y⁵

3.17.a y – 2 = (x – 4)

3.22 0, 1, i, –i

3.24 x⁵ – x

3.25 i

3.30 π²/12

3.33 eⁱ ≈ 0.54 + 0.84i

3.40 There are 24 (= 4 · 3 · 2 · 1) permutations.

3.52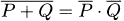

3.61 No. The left side is divisible by 4 and the right side is not.

3.62 Number the coaches 1, 2, 3, …, and number the people in each coach by their seat number, 1, 2, 3, Then give a card to each person, with the sum of the two numbers on the card. Assign people rooms in order of their card numbers. There will be multiple people with the same card number (except for the smallest card number). Serve people with the same card number in order of their coach number. This defines an ordering on all the arriving people, so they can all be given rooms.

3.64.d Note that we cannot divide by 0.

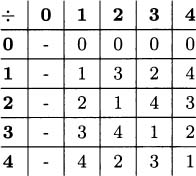
3.73 The entropy of an information source with two symbols is

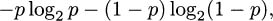
where the symbols occur with probabilities p and 1 – p. Let this function be f(p). We want to show that the maximum of f occurs where p = 1/2. We do this by taking the derivative of f and finding where it is equal to 0. To take a derivative, we may as well assume that the logarithms are natural logs, since the conversion to logs base 2 only involves a multiplicative constant (it won’t affect where f’ is 0). Using the product rule, we obtain

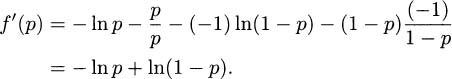
Setting this equal to 0, we find that p = 1/2. Do we really have a maximum? Find the second derivative and show that it is negative.

SOLUTIONS FOR CHAPTER 4

4.1 We are told in the section that the height function for a falling pencil is y = 4 – 16t². We can verify that when t = 0.25, the height is y = 4 – 16(0.25)² = 3 ft.

Let h be a small positive number. The average velocity of the pencil over the time interval [0.25,0.25 + h] is

If we let h go to zero, we see that the instantaneous velocity is –8 ft/s.

4.2.a To find the time t when the pencil strikes the ground, set

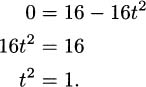
This has solutions of t = – 1 s and t = 1s. Since the pencil strikes the ground after we drop it, we use t = 1s.

Let h be a small positive number. Then the average velocity of the pencil over the time interval [1 – h, 1] is

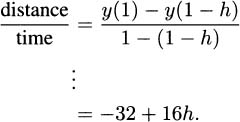
Letting h go to zero, we get a velocity of –32 ft/s.

4.5.a Hint: find y when t = 0.

4.5.c The instantaneous velocity is approximately 0. The arrow reaches a height of slightly more than 627 ft.

4.6 Let x = 3 + h be a value near the point of tangency (3,9). Since y = x², the second point on our secant is (x, y) = (3 + h, (3 + h)²). That makes the slope of the secant line

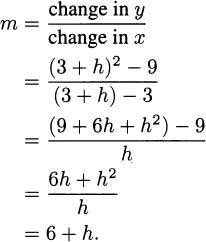
By letting h approach 0, we find that the slope of the tangent line is m = 6. The equation for the tangent can then be obtained from the point-slope formula for a line, using the base point (3,9):

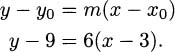
4.7 Hint: you should get a slope of m = –8 for the tangent line.

4.9

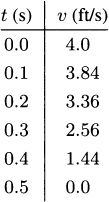
4.12.d Pencils strike the floor faster on Earth and slower on the Moon.

4.13 By definition,

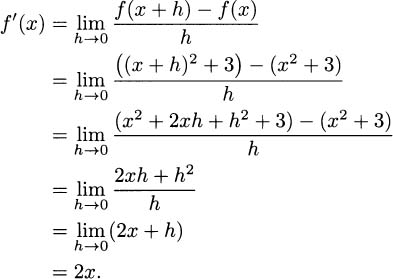
So f′(x) = 2x.

4.16 f′(x) = 3.

4.20.b f′(x) = 2x + 1

4.21.c x′(t) = 7.5t² +14t + 6.3

4.22 Hint: find the derivative, set it equal to 0, and solve for x.

4.27.b Using the product rule,

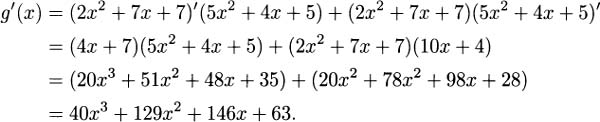
If we expand g first, we get

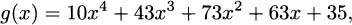
which has the same derivative.

4.30 The fastest solution uses f(x) = x(x + 1)(x + 2) and g(x) = x + 3, since you computed f′(x) in the previous exercise.

Another reasonable choice is f(x) = x(x + 1) and g(x) = (x + 2)(x + 3).

For fun, you could try f(x) = x(x + 2) and g(x) = (x + 1)(x + 3). For this choice,

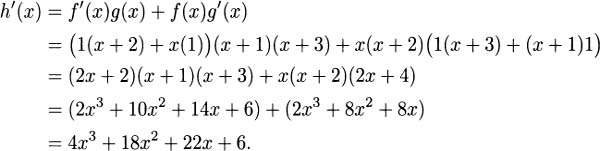
4.34.b Hint: although you can take the derivative of the bottom using the product rule, it will go a bit faster if you expand the denominator before you apply the quotient rule.

4.34.d The derivative is

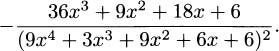
4.35.b From 4.34.d, the point of tangency is (1,1/33) and the slope is m = – 23/363. Using the point-slope form of a line gives a tangent line of

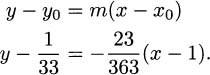
4.38.b Hint: rewrite the function as f(x) = (x² + 7)^1/3 and apply the chain rule.

4.40.c The derivative is

Critical points occur where x = 0 or x = 2. Checking values around 0,

indicates that (0,0) is a minimum. Near 2, the table

shows that the function has a critical point at (2,4) that is not an extremum.

4.40.e Hint: the derivative is never zero, but don’t forget to check where it is undefined.

4.41.c The derivative is y′(t) = 2t – 5, so the only critical point occurs when t = 5/2. If we realize that y is the formula for a parabola that opens upward, we conclude that (5/2, –9/4) is a minimum. We can also check values directly:

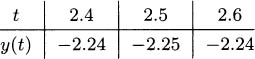
4.42.c In the last exercise, we found that the only critical point happens when x = 5/2. We check that value and the ends of the interval:

The maximum occurs at (0,4), and the minimum occurs at (2.5, –2.25).

4.46.b y = 6/x

4.46.c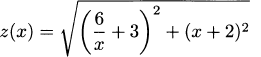

4.46.e approximately 7.02 m

4.47.a Hint: use the Pythagorean Theorem.

4.47.c Hint: the area is hard to optimize since it has a square root in it. Use this trick instead. The area will be smallest at the same time that area² is smallest. Use algebra to show that area² = 90x³ – 10125x² + 364500x – 4100625. Then use a derivative to solve for the values of x that make this smallest or largest.

4.48.a 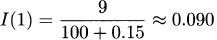amps or 90 milliamps

4.48.b Use the quotient rule, and simplify selectively.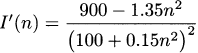

4.48.c Hint: a fraction is 0 if the numerator is 0. Notice, by the way, that this fraction is never undefined. How do we know that?

4.48.d The maximum current is approximately 1.16 amps.

4.48.e Don’t think too hard.

4.50 ΔS ≈ ±90 cm²

4.55.c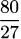

4.56.b

4.59.a 16,000

4.59.b $3,199,000

4.61 $1,680

4.64.a 11.896 years compared to 72/6 = 12 years

4.65.c f(t) = 1000e^{(ln 1.05)t} ≈ 1000e^0.04879t

4.67.a Hint: use the product rule.

4.67.b There is more than one possible approach. Write A(t) = 100/e^t using rules of exponents, and apply the quotient rule to get

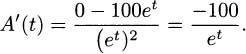
Another approach is to use the chain rule. The outside function is g(t) = 100e^t and the inside function is f(t) = –t. Hence

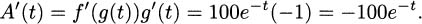
4.67.g There is more than one possible approach. We can write f(x) = ln 3 + ln x using the logarithm identities. Now, ln 3 is a constant, so

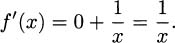
Another approach is to use the chain rule, and this also gives us

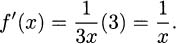
4.68 The point of tangency is (1, e¹) ≈ (1,2.71828). The slope is m = y′(1) = e¹ ≈ 2.71828, since the exponential function is its own derivative. Using the point-slope form of a line, the tangent is

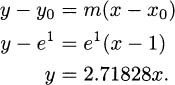
4.70.a We have A(138) ≈ 5.5 mg, which is half of the original 11 mg. The half-life of Polonium-210 is approximately 138 days.

4.70.b We have A′(0) ≈ –0.05522 mg/day. The negative sign indicates that the amount of Polonium-210 is decreasing.

4.71.a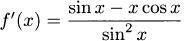

4.71.d Write g(t) = (sin(t/7))^1/2 and apply the chain rule.

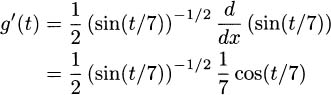
4.73 Using the quotient rule,

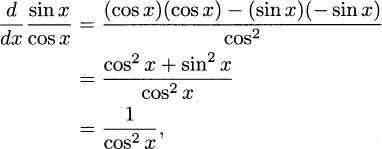
and most books use the identity 1/cosx = sec x to rewrite this as

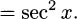
4.77.c They must be equal.

4.81 By the Fundamental Theorem of Calculus,

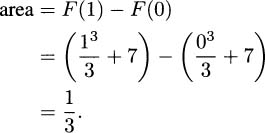
Notice the way the 7 cancels out.

4.83.a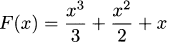

4.83.e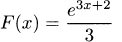

4.84.b 7 sin x – ln x + C

4.84.e Hint: we don’t have a specific rule for this type of function. You’ll have to guess the answer and take a derivative to check that you are correct.

4.85.c Use F(x) = (x + 1)⁴. The area is F(1) – F(0) = 15.

4.87.a Hint: is v(0) positive or negative?

4.87.b When t ≈ 0.92 s, because the professor has quit rising and is now falling.

4.87.c Approximately 1.94 m high.

4.87.f When t ≈ 1.84 s

4.90.b 4.5 m/s²

4.91.c By the chain rule,

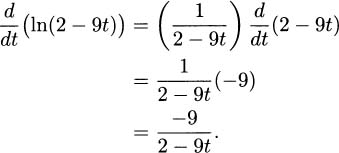
4.92.c Use the product and the chain rule to get ln(2 – 9t).

4.95 20/9

4.97.b The bartender would have run out of beer. Or maybe not. If the bar could hold an infinite number of mathematicians, …

SOLUTIONS FOR CHAPTER 5

5.1 False

5.3.b The last two digits must be 00, 25, 50, or 75.

5.4.a q = 11, r = 5

5.4.b q = 1501, r = 3

5.4.c q = –4, r = 3

5.6.b True

5.6.e False

5.7 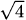and 117/3459753

5.14.a 11

5.14.c 1

5.20 The last row is 360, upper left, and 11.

5.21 Just 5

5.26 There is only one such triplet.

5.27 Since 2|1000! and 2 | 2, we have 2 dividing 1000! + 2, so 1000! + 2 is composite. The same argument works in general. For 2 ≤ n ≤ 1000, since n | 1000! and n | n, we have n dividing 1000! + n, so 1000! + n is composite.

5.29 u = 1, v = – 2

5.31 ±1, ±3

5.34 The set consists of the multiples of 3.

5.41 2²⁵ + 1 = 641 × 6,700,417

5.44.a 16 = 2⁴

5.44.b 59 is prime

5.44.c 72 = 2³ · 3²

5.44.d 105 = 3 · 5 · 7

5.44.e 3 · 1633 = 70² – 1 = (70 – 1)(70 + 1) = 69 × 71, so 1633 = 23 × 71

5.48 2 × 3³ × 17 = 918

5.53 x = 0, y = 11; x = 2, y = 10; x = 4, y = 9;…; x = 22, y = 0

5.55 10 pens and 1 notebook, or 3 pens and 4 notebooks

5.57.a (3 + 4t, – 1 – 3t)

5.57.d (– 32 + 13t, 48 – 19t)

5.60 51 – 140 – 149

5.61 m = 2, n = 1

5.64 If you turn an even number of coins, the parity of the number of heads is unchanged. If you turn an odd number of coins, the parity of the number of heads is changed.

5.67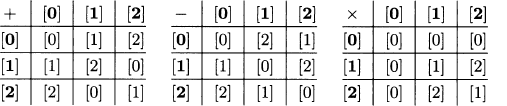

5.69.a Yes, k = 3

5.69.b No

5.69.c Yes, k = – 6

5.69.d No

5.72.a [0]₈

5.72.b [1]₃

5.72.c [0]₇

5.74 [5]8

5.78 3

5.80 Note that 12 divides 4! = 24, and, since n! is a multiple of 4! for every n > 4, we know that 12 divides all of them as well. So

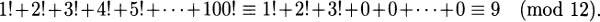
5.82.a x = 4 (mod 16)

5.82.b No solutions

5.82.c x is congruent to 2, 5, or 8 modulo 9

5.82.d x ≡ 5 (mod 7)

5.83.a [x] = [2]₃

5.83.b No solutions

5.83.c [x] = [5]₁₁

5.83.d [x] = [3]₇

5.87 y = 8

5.89 Suppose that xⁿ + yⁿ = zⁿ, and let p be a prime divisor of n. Then n = pk for some k, and we have a solution (x^k)^p + (y^k)^p = (z^k)^p.

5.95 This appendix is too small to contain it.