Capítulo V. Modelos espaciales de la regla de la mayoría

 

 

 

Nuestra historia hasta este momento ha destacado el dilema en la toma de decisiones grupales por la contrapartida que existe generalmente entre la coherencia de estas decisiones, por un lado, y la equidad del método de toma de decisiones, por el otro. Vimos que si consideramos un conjunto limitado de circunstancias que puede estar enfrentando el grupo, entonces podríamos evitar el dolor que causa esta disyuntiva. Dicho de otra forma, si resulta que las preferencias de los individuos se arreglan de una manera en particular —que refleje un consenso de algún tipo específico— entonces las decisiones grupales (sin duda alguna, las adoptadas mediante la regla de la mayoría) resultan muy bien. En el capítulo anterior describí las preferencias de pico único como un tipo de consenso que facilita la coherencia en la toma de decisiones mediante la regla de la mayoría; en éste quiero presentar una caracterización geométrica intuitiva de esa condición.

No obstante, para ser sinceros, este material se puede volver aburrido rápidamente. El autor de este libro, y quizás algunos lectores, disfrutamos las cantaletas técnicas y los discursos filosóficos, pero, en su mayoría, los lectores sin duda se mostrarán impacientes y ansiosos por ver algún beneficio concreto. Creo que la lectura de este capítulo constituye una inversión importante. Una vez que haya dado a la cualidad del pico único una representación geométrica, estaré en condiciones de aplicarla a algunas situaciones políticas interesantes, a saber, la contienda electoral entre dos partidos y la adopción de decisiones de las comisiones legislativas.

 

V.1. Formulación espacial

V.1.1. La geometría sencilla de la regla de la mayoría

 

Suponga que en esencia el problema de un grupo es escoger un punto de una línea, es decir, el grupo debe seleccionar algún parámetro numérico único. Por ejemplo, la junta de directores de un banco debe adoptar una decisión sobre la tasa de interés semanal para las hipotecas a treinta años. Las tasas de interés pertinentes son, en efecto, puntos de una línea: un extremo es 0 por ciento, mientras que el otro extremo es un número positivo, digamos 10 por ciento. Representamos ese intervalo como [0, 10]. En esta y en otras circunstancias, quiero que el lector imagine a un grupo de personas cada una de las cuales tiene un punto de la línea, que es el que más desea, y preferencias que disminuyen a medida que se toman en consideración los puntos que se alejan en cualquier dirección.

gráfica V.1

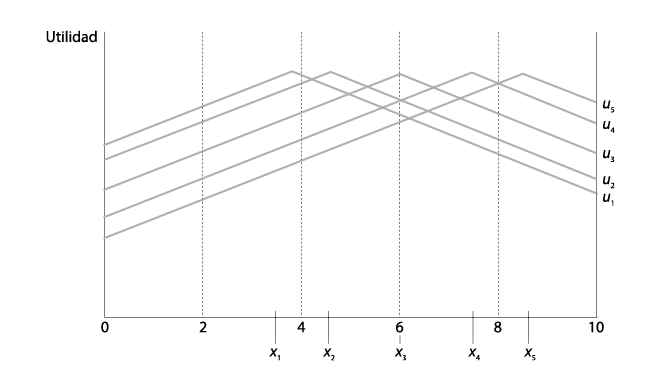
En la gráfica V.1 mostramos las preferencias de las de cinco personas de la junta directiva del banco, G = {1, 2, 3, 4, 5}. La junta se reúne para decidir la tasa de interés que se aplicará a las hipotecas residenciales la semana siguiente. Cada individuo i ∈ G tiene un punto favorito, al que llamamos punto de dicha o punto ideal, representado por x_i y situado en el intervalo [0, 10] (trazado como eje horizontal), que representa la tasa de interés que prefiere en primer lugar.1 Así, el director 1 tiene una tasa de interés preferida en primer lugar, x₁, de un poco menos que 4 por ciento, la del director 2, x₂, es de un poco más que 4 por ciento, y así sucesivamente. En el eje vertical escribí la leyenda “utilidad” para medir las preferencias; y por cada individuo he representado gráficamente una función de utilidad que representa las preferencias de ese director para varios niveles de tasas de interés en el intervalo [0, 10]. Naturalmente, la función de utilidad, representada como u_i para el director o la directora i, es más alta en el caso de la alternativa preferida en primer lugar por i, es decir x_i, y disminuye a medida que se toman en consideración puntos más distantes. Así, la directora 5 prefiere en primer lugar una tasa de interés de 8.25 por ciento y su preferencia disminuye con tasas más altas o más bajas. Por razones obvias (examínese la gráfica), decimos que las preferencias de esos individuos son de “pico único”, el cual definimos como sigue:

Condición del pico único. Se dice que las preferencias de los miembros de un grupo son de pico único si las alternativas en consideración pueden ser representadas como puntos de una línea y cada una de las funciones de utilidad que representan las preferencias por dichas alternativas tiene un máximo en algún punto de la línea y desciende a ambos lados de ese máximo.

¿Existe alguna relación entre esta definición de la cualidad del pico único y la definición de Black presentada en el capítulo anterior? Es decir, ¿tienen algo que ver las funciones de utilidad de pico único, como las que se muestran en la gráfica V.1, con el hecho de que todos los votantes estén de acuerdo en que alguna alternativa “no es la peor”? ¡Por supuesto que sí! Tómense de manera indistinta tres tasas de interés de las mostradas en la gráfica V.1, digamos 3 por ciento, 5 por ciento y 9 por ciento: es muy fácil ver que 5 por ciento no es la peor entre esas tres tasas de interés para ninguno de los cinco miembros del grupo. En realidad, afirmamos que, dados tres valores de tasas de interés que usted elija, cualquiera no es el peor para ninguno de los cinco banqueros. ¡Eso es lo que significa la condición de pico único!

gráfica V.2

Con el propósito de desarrollar algunas herramientas que utilizaremos en los análisis subsecuentes, examinemos a uno de los banqueros aislado (con lo que en realidad queremos decir: analicemos una función de utilidad aislada). En la gráfica V.2 mostramos al más mezquino de los miembros de la junta de directores del banco, la directora 5, cuya tasa de interés favorita es bastante alta: x₅ = 8.25 por ciento. Ahora considérese una tasa de interés específica, y = 7 por ciento. El conjunto de puntos que la directora 5 prefiere a y es el conjunto representado gráficamente como P₅(y) en la gráfica V.2; dicho conjunto va de 7 a 9.5 por ciento. A éste se le llama el conjunto preferido a y de la directora 5. Dadas sus preferencias, si y fuera una propuesta, entonces P₅(y) describiría todos los puntos que ella preferiría a y. Como lo muestra la gráfica, P₅(y) se calcula determinando el grado de utilidad para y e identificando todas las tasas de interés del eje horizontal con los niveles de utilidad más altos que la utilidad para y.2

gráfica V.3

En la gráfica V.3 muestro los “conjuntos preferidos a y” de los cinco directores (nótese que, en esta figura, y está un poco abajo de 6 por ciento). Obsérvese que esos conjuntos se superponen en cierto grado; por ejemplo, existen dos puntos en común entre P₄(y) y P₅(y), lo cual significa que existen puntos específicos que tanto el director 4 como la directora 5 prefieren a y.3 Son de gran interés los puntos que una mayoría prefiere a y, a los cuales se denomina el conjunto que vence a y. Ese conjunto de puntos se escribe como V(y) y se define como sigue: supongamos que M es el conjunto de mayorías de nuestro grupo de banqueros, G, es decir, es el conjunto de coaliciones de tres personas (hay diez de esas coaliciones), de coaliciones de cuatro personas (hay cinco de ellas) y de la coalición del total. Como vemos, hay dieciséis diferentes coaliciones de mayorías en M, las cuales se encuentran listadas en el cuadro V.1. Por cada coalición de mayoría considérese la intersección común de los conjuntos (si existe alguno) de puntos preferidos a y; se trata de todos los puntos que esa mayoría en particular prefiere a y. Así, en la gráfica V.3, los miembros de la mayoría {3, 4, 5} comparten puntos que cada uno prefiere a y. Tómese la unión de esos dieciséis conjuntos y eso es V(y).4

cuadro V.1

Las coaliciones de mayorías de G = {1, 2, 3, 4, 5}

Tamaño de la coalición	Coaliciones
3	(1, 2, 3), (1, 2, 4), (1, 2, 5), (1, 3, 4), (1, 3, 5), (1, 4, 5), (2, 3, 4), (2, 3, 5), (2, 4, 5), (3, 4, 5)
4	(1, 2, 3, 4), (1, 2, 3, 5), (1, 2, 4, 5), (1, 3, 4, 5), (2, 3, 4, 5)
5	(1, 2, 3, 4, 5)

Ahora ya es bastante sencillo describir las decisiones coherentes de los grupos. Suponga que el conjunto que vence a alguna alternativa no tiene ningún elemento. Cuando esto sucede para la alternativa x decimos que “x tiene un conjunto que la vence vacío” y los escribimos como V(x) = ∅, donde ∅ significa “vacío” en la notación de conjuntos. Entonces dicha alternativa es una clara candidata para la decisión del grupo. ¿Por qué? Simplemente porque V(x) = ∅ significa que no existe ninguna otra alternativa que alguna de las dieciséis coaliciones de mayoría prefiera a x. Es difícil negarse a elegir x si en su lugar no existe nada en lo que alguna mayoría esté de acuerdo. Por otra parte, si el conjunto que vence a x no está vacío, es decir que V(x) ≠ ∅, entonces es difícil justificar la elección de x. ¿Cómo se puede elegir x cuando es claro que alguna mayoría del grupo desea alguna otra alternativa específica? Y si el conjunto que las vence es no-vacío para cada una de las alternativas (es decir que ninguna alternativa tiene un conjunto que la vence vacío) entonces tenemos un problema: las preferencias del grupo son incoherentes, puesto que alguna mayoría prefiere otra cosa a cada una de las opciones disponibles.

Por el momento, la interrogante es si existe una x que posea un conjunto que la vence vacío. Si permitimos que los individuos de G posean cualquier preferencia completa y transitiva —condición de dominio universal de Arrow— entonces, como ya lo vimos, la respuesta es “no necesariamente”. ¿Por qué? Porque conforme a la condición U de Arrow, es posible que las preferencias mayoritarias sean cíclicas, en cuyo caso no tenemos V(x) ≠ ∅ para ninguna alternativa. Ahora bien, si las preferencias tienen restricciones, entonces es posible obtener una respuesta diferente.

Teorema del votante mediano de Black. Si los miembros de un grupo G tienen preferencias de pico único, entonces el punto ideal del votante mediano tiene un conjunto que lo vence vacío.

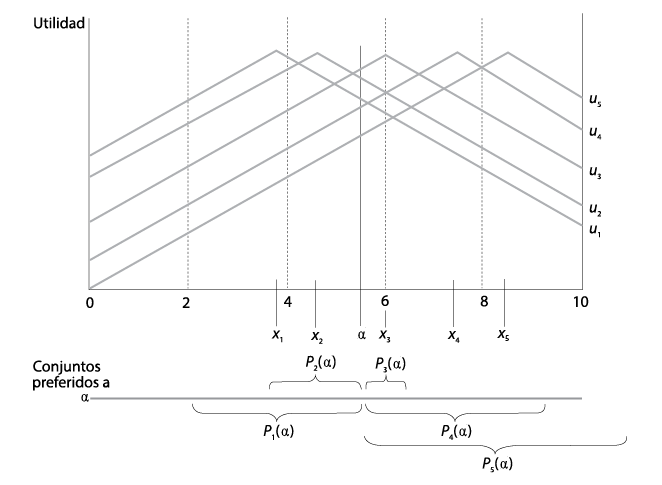
En la gráfica V.4 mostramos un grupo de individuos con preferencias de pico único. El punto ideal del votante mediano de ese grupo es el del señor 3.5 La afirmación del teorema de Black —el mismo Duncan Black que vimos en el capítulo anterior— es que V(x3) = ∅ y que x3 es la decisión de la mayoría.

Podemos demostrar este teorema valiéndonos del ejemplo de los cinco miembros de la junta del banco. Considérese cualquier punto arbitrario del conjunto posible de tasas de interés, [0, 10], a la izquierda de x3, digamos el punto denominado α en la gráfica V.4. Obsérvese que los miembros 1 y 2 prefieren α a x3, pero que los miembros 3, 4 y 5 prefieren x3 a α. En consecuencia, la mayoría prefiere x₃ a α. Pero α es cualquier punto arbitrario a la izquierda de x3, así que lo mismo se puede deducir de cualquiera de esos puntos: sabemos que al menos los miembros 3, 4 y 5 preferirán x3 a α (y es posible que algunos de los miembros restantes compartan también esa preferencia). Enseguida, considérese cualquier punto arbitrario a la derecha de x3 (no aparece en la figura). Los miembros 4 y 5 pueden preferirlo a x3, pero los miembros 1, 2 y 3 sostienen la preferencia opuesta, por lo que la mayoría prefiere x3. El argumento es exactamente el mismo que en el caso anterior de α, puesto que seleccionamos una alternativa arbitraria a la derecha de x3. En resumen, sabemos ahora que una mayoría prefiere el punto ideal del votante mediano a cualquier punto arbitrario a la derecha o a la izquierda de él; en otras palabras, x3 vence a todos los puntos restantes. Por ende, el punto ideal del votante mediano tiene un conjunto que lo vence vacío por lo que ésta es la decisión de la mayoría.

gráfica V.4

Antes de complicar este resultado clave, debo mencionar que en este ejemplo teórico existen cuando menos tres supuestos ocultos que ameritan cierto debate. En primer lugar, en nuestro ejemplo el grupo G tiene un número impar de miembros. Así, en la gráfica V.4 pudimos mostrar los cinco miembros del grupo, con el miembro número 3 como el único en la mediana. ¿Qué pasaría si el grupo tuviera un número par de miembros? Suponga, por ejemplo, que ignoramos a la directora 5 en la figura, y en lugar de ella nos concentramos en el grupo truncado G’ = {1, 2, 3, 4}. Ahora, los dos miembros 2 y 3 son medianas. Dado que se necesitan tres votos para constituir una mayoría, tenemos que V(x2) = ∅ y también V(x3) = ∅. Asimismo, el conjunto que vence a cualquier punto del intervalo entre esos dos puntos, [x2, x3], es vacío. Técnicamente, entonces, el teorema del votante mediano de Black es válido, ya sea que el tamaño del grupo sea par o impar. Pero, cuando un grupo es par en número, el hecho de que pueda haber votaciones empatadas significa que puede haber más de una alternativa que posea la propiedad de que no pueda ser vencida. La inexistencia de un vencedor único resulta una monserga: es un poco como tener más de un pretendiente al trono, o como tener más de una persona que afirme ser el rey de las canicas. Por esa razón, los grupos establecen cierto procedimiento para romper los empates mucho antes de llevar a cabo cualquier deliberación de importancia o, mejor aún, se aseguran de que el grupo sea impar en número.6

En segundo lugar, hemos supuesto una participación total. Supusimos que todos los que tienen el derecho a sufragar lo ejercen. Desde luego, eso no tiene que pasar en todo ejemplo particular de una decisión en grupo. Si los miembros 4 y 5 de la junta del banco se quedan dormidos alguna semana, entonces la directora 2 se convierte en el votante mediano de la junta, reducida ahora a tres personas; si los miembros 1 y 3 están fuera de la ciudad la semana siguiente, entonces el director 4 se convierte en el votante mediano. En cada uno de esos casos, al igual que en el de toda la junta, es válido el resultado del votante mediano. Sin embargo, la identidad del votante mediano (es decir, quién es el votante mediano de entre todos los votantes) dependerá de cuáles miembros del grupo son los que participan. Podemos pronosticar la decisión del grupo si hacemos supuestos sobre la participación (suponer que todos votan, por ejemplo) o podemos hacer pronósticos condicionales en la participación (si 4 y 5 se quedan dormidos esa mañana, por ejemplo, entonces anticipamos que x2 será la decisión del grupo, pero, si todos votan, entonces x3 será la decisión predicha).

En tercer lugar, hemos supuesto que quienes ejercen el derecho al sufragio lo hacen sinceramente. Pero, como ya lo hemos visto en capítulos anteriores, a veces los miembros de un grupo tienen la oportunidad y los incentivos para tergiversar sus preferencias y no revelarlas honestamente. Éste es un tema de gran interés que abordaremos en su propio capítulo, el número VI.

 

V.1.2. La geometría (ligeramente) más complicada de la regla de la mayoría

 

Los modelos unidimensionales de decisión con la condición del pico único permiten reflexionar de manera bastante sofisticada sobre la política real: generan expectativas muy nítidas sobre la manera como se lleva a cabo la política en esos contextos. Sin embargo, existen muchísimas situaciones sociales que no se pueden reducir a asuntos unidimensionales.

Recuérdese el juego de “la división del dinero”. Si participase en él un grupo de tres individuos, entonces sería necesario tener dos dimensiones en las cuales representar los resultados. La primera dimensión corresponde a la cantidad que recibe el jugador 1, mientras que la segunda corresponde a la cantidad que recibe el jugador 2 (réstese la suma de esos dos números de la cantidad total de dinero que se debe dividir y se obtendrá la cantidad que recibe el jugador 3).7 Espero haber convencido antes al lector de que los juegos distributivos, como el de la división del dinero, son comunes en la vida política. En consecuencia, debe concederse que, por nítidos y complejos que sean los modelos unidimensionales, éstos constituyen casos especiales de un arreglo multidimensional más general. Por lo tanto, necesitamos ver cómo es ese arreglo más general.

Podemos explicar casi todo lo que es necesario centrando nuestra atención en una circunstancia bidimensional, como la de la gráfica V.5 (la cual tiene en realidad tres dimensiones; en breve aclararemos por qué). Consideramos un problema de presupuesto en el que un grupo de legisladores, quizá una comisión de gastos, debe decidir cómo dividir el presupuesto entre “armas” y “mantequilla” (que simbolizan la competencia entre los programas de defensa y los programas domésticos). Así, los resultados se describen mediante dos números: dinero gastado en mantequilla y dinero gastado en armas. El conjunto de resultados, el cual se llama espacio de políticas públicas, es bidimensional y es el dominio en el que se expresan las preferencias.8 La tercera dimensión de la gráfica V.5, denominada “utilidad”, nos permite trazar las gráficas tridimensionales de las preferencias de los legisladores. Como antes, suponemos que un legislador tiene un punto ideal en el espacio de políticas públicas. Su función de preferencia, o de utilidad, se encuentra en su máximo sobre ese punto. En la mayoría de las aplicaciones, además se supone que las preferencias descienden con la “distancia” a partir del punto ideal del legislador. En la gráfica V.5 se muestra un legislador típico, con un punto ideal y una función de preferencia típicos. La función de preferencia del legislador es un “montículo” que alcanza su grado de utilidad más alto justo sobre su punto ideal, en el que m1 unidades monetarias se gastan en mantequilla y a1 unidades en armas. Ese punto ideal (m1, a1) se sitúa en el plano del espacio de políticas públicas mantequilla-armas.

gráfica V.5

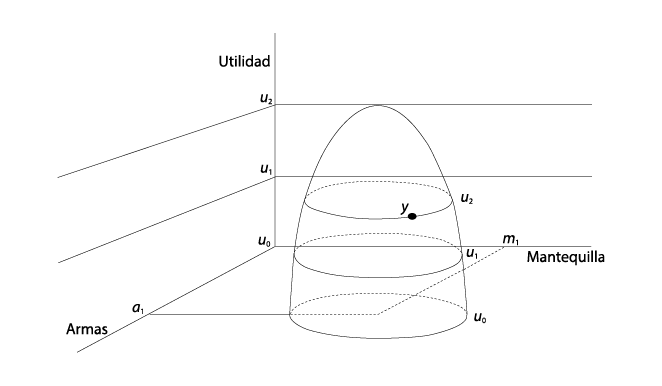
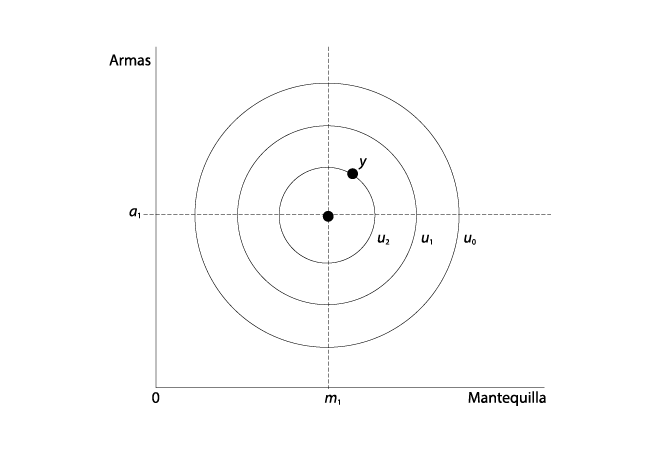
Esta misma información se puede representar de manera más conveniente en la gráfica V.6. Ahí, el lector mira desde arriba el plano mantequilla-armas. Es como si usted estuviera volando en helicóptero sobre el pico del montículo de las preferencias de la gráfica V.5. La posición del punto ideal de nuestro legislador típico es exactamente la misma que en la gráfica V.5. Pero, en lugar de añadir una tercera dimensión (que saldría de la página hacia el lector), para poder representar de manera gráfica su función de preferencia, sobreponemos “capas” de su función de utilidad al espacio de políticas públicas, lo cual genera un conjunto de círculos circunscritos llamados curvas de indiferencia. Cada círculo es una capa del montículo de la política de la gráfica V.5; es un lugar geométrico de políticas públicas que dejan indiferente al legislador (puesto que todos los puntos del círculo se encuentran en la misma rebanada y, por ende, a la misma altura en la función de utilidad de la gráfica V.5). Ahora bien, como la distancia a partir de un punto ideal es una medida de las preferencias, los puntos dentro de un círculo con ese punto ideal como centro son igualmente preferidos por ese legislador, puesto que son equidistantes del punto ideal. La lógica es la misma cuando se compara un círculo con otro. Un legislador prefiere un punto dentro de un círculo con un radio menor a uno dentro de un círculo con un radio mayor, porque ello significa que el primer punto está más cerca de su punto ideal que el segundo.9

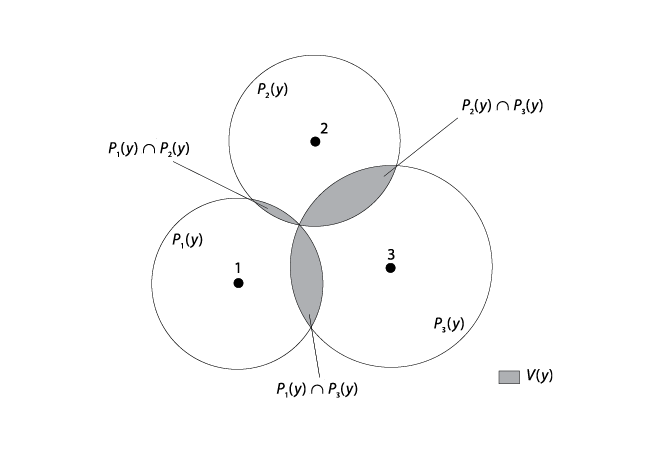
Obsérvese el punto representado por y en la gráfica V.6. El círculo que pasa por y con centro en el punto ideal de nuestro legislador contiene todos los puntos que le son indiferentes a y. Lo anterior significa que, en virtud de que todos los puntos al interior del círculo se encuentran más cerca de su punto ideal, el legislador los prefiere a y. Es decir, podemos denominar a los puntos dentro del círculo como el conjunto preferido a y de nuestro legislador, lo cual es una generalización natural de ese mismo concepto en el ejemplo unidimensional presentado antes en este capítulo. La gráfica V.7 muestra los puntos ideales de tres legisladores y la curva de indiferencia que pasa por la alternativa y de cada legislador. La curva más todos los puntos dentro de ella comprenden el conjunto preferido a y de cada legislador, representado por P_i(y). La intersección sombreada, P1(y) ∩ P2(y), nos indica los puntos preferidos a y tanto por el legislador 1 como por el legislador 2; P1(y) ∩ P3(y) son los puntos preferidos a y por los legisladores 1 y 3; y finalmente P2(y) ∩ P3(y) nos indica los puntos preferidos a y por los legisladores 2 y 3. Puesto que dos de tres legisladores forman una mayoría, la unión de esos tres “pétalos” es el conjunto que vence a y, V(y). Cada pétalo contiene los puntos que una coalición mayoritaria específica prefiere a y.

gráfica V.6

gráfica V.7

Si desplazamos los puntos ideales de los tres legisladores de la gráfica V.7 de tal suerte que formen una hilera, tenemos una situación como la representada en la gráfica V.8. ¿Puede el lector determinar el conjunto que vence al punto ideal del legislador mediano, V(x2)? Los pasos están planteados en esa figura. El conjunto preferido a x2 por el legislador 2 está vacío (¿cómo podría preferir algo al punto que prefiere en primer lugar?). Las curvas de indiferencia de las legisladoras 1 y 3 que pasan por x2 y tienen como centro sus puntos ideales respectivos son tangentes una a la otra. No se sobreponen en absoluto. Por lo tanto, V(x2) = ∅ puesto que ninguna mayoría {1, 2}, {1, 3}, {2, 3} o {1, 2, 3} prefiere otros puntos a x2. Esto es, ninguno de los miembros de ninguna coalición de mayoría tiene conjuntos preferidos a x2 que se intersecan. Consecuentemente x2 es la decisión de la mayoría.

gráfica V.8

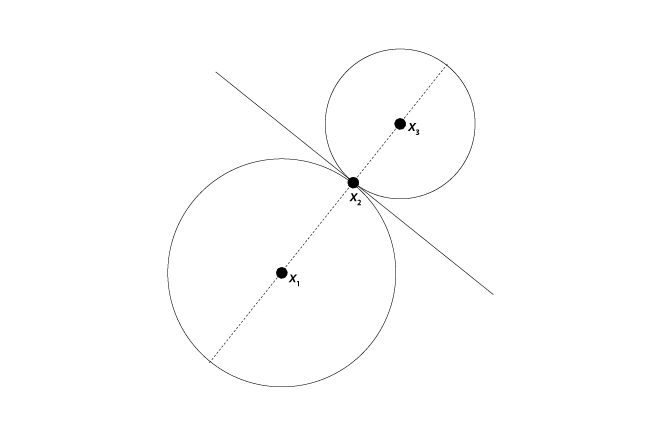
Si volvemos a examinar la gráfica V.8, podemos ver por qué ocurrió eso. Considere la línea gruesa que pasa por x₂ perpendicular a la línea punteada. Escoja cualquier punto del lado de x1 de esa línea gruesa que no se encuentre sobre la línea punteada; tendremos que x₂ está más cerca de x3 que el punto seleccionado. Por lo tanto, una mayoría {2, 3} prefiere x₂ antes que cualquiera de esos puntos. A partir de un argumento exactamente igual, una mayoría {1, 2} prefiere x2 a cualquier punto del lado x3 de la línea más oscura que no se encuentre sobre la línea punteada. Así, los únicos puntos que quedan son aquellos sobre la línea punteada. Es decir, aun cuando el problema de la decisión en grupo es realmente bidimensional, las preferencias individuales se alinean de tal manera que hacen que el problema sea, en efecto, unidimensional. En esa línea, cada uno de los legisladores tiene preferencias de pico único (el lector deberá convencerse de esto), de las que x2 es el punto ideal mediano. En consecuencia, aquí sí tiene validez el teorema del votante mediano de Black, que es precisamente lo que demuestra la gráfica V.8.

Tener alineados los puntos ideales de los legisladores es muy conveniente, ¿cierto? Y también muy improbable: ciertamente es más probable que la configuración de puntos ideales sea completamente arbitraria como en la gráfica V.7 que tenerlos perfectamente alineaditos como en la gráfica V.8. Por lo tanto, aunque nos sería más fácil analizar contextos unidimensionales por las excelentes herramientas que tenemos, tales como el teorema del votante mediano, en realidad hay muchas circunstancias políticas interesantes que son multidimensionales. Cabe preguntarnos: ¿podemos hacer predicciones acerca de una votación por mayoría cuando hay múltiples dimensiones? La respuesta es sí, pero las noticias no son muy buenas.

La muy improbable distribución de las preferencias individuales de la gráfica V.8 nos proporciona las bases para la generalización. Lo que permite que el punto ideal del legislador 2 surja como la decisión de la mayoría es el hecho de que los puntos ideales de los otros legisladores estén distribuidos de forma simétrica en torno a ese punto ideal. Obviamente, el legislador 2 se opone a cualquier movimiento para alejarse de su punto ideal, pero también se opone a dicho movimiento al menos uno de los otros legisladores. Esto se puede observar gracias a la línea gruesa por x2 que es perpendicular a la línea punteada que contiene los tres puntos ideales. Los legisladores 1 y 2 prefieren x2 a cualquier punto que se encuentre del lado de la legisladora 3; y los legisladores 2 y 3 prefieren x2 a cualquier punto que se encuentre del lado de la legisladora 1.

Ahora añadamos a la historia dos votantes más que sean simétricos de la misma manera que hemos mencionado (véase la gráfica V.9): los votantes 2, 4 y 5 se encuentran en una línea, al igual que 1, 2 y 3. Seguimos encontrando que V(x2) = ∅, porque cualquier alejamiento de x2 cuenta con la oposición de cuando menos tres de los cinco votantes. El lector puede probar esta proposición trazando una línea recta a través de x2 en cualquier ángulo. Siempre habrá dos votantes que querrán desplazarse a algún punto a un lado de la línea recta, dos que querrán desplazarse a puntos al otro lado de la línea recta y uno (el legislador 2) absolutamente contento de permanecer en x2. Puesto que ninguna mayoría favorecería ir en ninguna dirección (siempre habría tres votos en contra), el conjunto que vence a x2 estará vacío. Algo en la distribución simétrica de los votantes en torno a un punto común parece producir una decisión mayoritaria coherente.

gráfica V.9

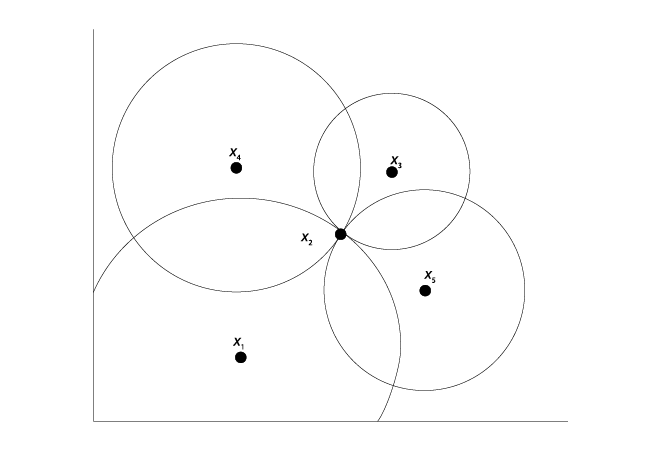
De hecho, podemos ser mucho más específicos. Pensemos en un conjunto de n votantes (donde n es cualquier número, al que consideraremos impar para simplificar la representación), cuyos puntos ideales son x1, x2,…, x_n. Esos puntos ideales n se encuentran en el espacio multidimensional de política pública, como el representado en la gráfica V.9 (aunque los resultados que presentamos más adelante también aplican para espacios de política pública de más de dos dimensiones). Decimos que los puntos ideales se distribuyen en simetría radial si se cumplen las siguientes condiciones:

 

1)  Existe un punto ideal sobresaliente, al que denominamos x*

2)  Los n–1 puntos ideales restantes pueden dividirse en pares. (Ello es posible dado que n es impar y por lo tanto n –1 es par)

3)  Los dos puntos ideales de cualquier par, digamos x_i y x_j más x* están todos situados en línea, con x* entre x_i y x_j.

 

En la gráfica V.9, x2 es el punto sobresaliente, x1–x3 y x4–x5 son los pares de puntos ideales restantes y x2 se encuentra en una línea entre los puntos ideales de cada par. Obsérvese que la simetría radial no requiere que los dos puntos ideales de un par sean equidistantes del punto sobresaliente (x3 está más cerca de x2 que x1); simplemente, deben estar alineados con él.

El economista Charles Plott observó que, cuando se tienen múltiples dimensiones, la simetría radial de los puntos ideales capta una propiedad que las preferencias de pico único poseen en los espacios unidimensionales. En un famoso artículo publicado en 1967, estableció el siguiente resultado:

Teorema de Plott. Si los votantes poseen preferencias espaciales basadas en la distancia, y si sus puntos ideales están distribuidos en simetría radial, siendo x* el punto ideal sobresaliente, y el número de votantes es impar, entonces V(x*) = ∅.

 

El teorema de Plott generaliza el teorema del votante mediano de Black a más de una dimensión10 y proporciona las condiciones para la tendencia centrípeta que observamos en el marco unidimensional estudiado por Black. Así, en la gráfica V.9, que muestra a los cinco legisladores cuyos puntos ideales satisfacen la simetría radial, x2 es la decisión de la mayoría; es decir, es preferido por una mayoría a cualquier otro punto en el espacio de políticas públicas.

Ésa es la buena nueva. La mala nueva es que el teorema de Plott no proporciona condiciones muy generales. Volvamos a la gráfica V.9 y en nuestra imaginación desplacemos x4 una pequeña distancia hacia el ángulo superior derecho (digamos un centímetro). Tracemos ahora una línea recta que pase por x2, pero apenas por debajo de x5. Como ahora x3, x4 y x5 se sitúan todos por arriba de esa línea, ello significa que hay una mayoría —{3, 4, 5}— que prefiere alejarse de x2. Específicamente, hay puntos del lado superior derecho de la línea imaginaria que pasa a través de x2 que los votantes 3, 4 y 5 prefieren a x2, por lo que V(x2) ≠ ∅. Es decir, la condición de Plott de la simetría radial es en extremo sensible a las pequeñas perturbaciones de las posiciones de los puntos ideales de los votantes. Lo anterior puede expresarse de una manera particularmente drástica. Imagínese los puntos ideales de un millón de votantes distribuidos en simetría radial en torno al punto ideal del votante número 1 000 001. Así, de acuerdo con el teorema de Plott, V(x1 000 001 ) = ∅. Ahora, suponga que dos nuevos votantes se mudan a la comunidad y que sus puntos ideales no son simétricamente radiales respecto a x1 000 001. Esta pequeña perturbación del problema de la votación —después de todo, ¿cuán grande puede ser el efecto de la introducción de dos nuevos votantes en una población de más de un millón de ellos? —destruye por completo el equilibrio anterior.11

Si los alejamientos de la simetría radial fueran sucesos relativamente inusuales, entonces la sensibilidad a las distribuciones de los puntos ideales del teorema de Plott no serían en realidad malas noticias. Pero, como el lector puede comprender de manera intuitiva, el requisito de la simetría radial es muy restrictivo; uno no esperaría que los grupos tuvieran sus preferencias distribuidas “naturalmente” de una manera tan balanceada como ésa. Por lo tanto, los alejamientos de esta condición adquieren una importancia mayor. En lo que constituye una de las declaraciones teóricas más extraordinarias en la disciplina, Richard McKelvey (1976) demostró cuán importantes son exactamente esas desviaciones de la simetría radial.

Teorema del caos de McKelvey. En los marcos espaciales multidimensionales, con excepción del caso de una distribución rara de puntos ideales (como la simetría radial) que difícilmente ocurre de manera natural, no habrá un punto con un conjunto que lo vence vacío bajo la regla de la mayoría. En lugar de ello, se generará el caos: no habrá ningún vencedor de Condorcet, podrá ocurrir cualquier cosa y quienquiera que controle el orden de la votación podrá determinar el resultado final.

Comencé buscando la manera de restringir la condición del dominio universal de Arrow con el propósito de ver si existían dominios más reducidos en los que la regla de la mayoría funcionase aceptablemente bien. En las situaciones de decisión unidimensionales, vimos que la cualidad del pico único es suficiente, y que en las situaciones multidimensionales, lo es una distribución radial simétrica de los puntos ideales. Sin embargo, las pequeñas desviaciones a partir de los puntos ideales generan el caos. Ningún punto es el preferido por una mayoría de todos los contendientes, por lo que es difícil justificar cualquier decisión en particular del grupo (puesto que, una vez que se haya propuesto alguna, habrá alguna alternativa que una mayoría prefiere a aquélla). Esto, a su vez, significa que siempre habrá ciclos de mayorías.

De hecho, McKelvey establece que todos los puntos se encuentran en un gran ciclo, es decir, que la situación se presta para que la manipule quienquiera que controle el orden del día. Lo que McKelvey demuestra es lo siguiente: elija dos puntos cualesquiera en el espacio de políticas públicas y denomínelos s (punto inicial) y t (punto final). Resulta que se puede encontrar una secuencia de puntos z1, z2, …, zk (con un número finito k) tales que z1 PG s, z2 PG z1, z3 PG z2, …, zk PG zk-1, y t PG zk. En otras palabras, a partir de cualquier punto inicial, hay una secuencia de votaciones mediante las cuales una mayoría desplazará el resultado a cualquiera de los puntos finales (entre ellos, digamos, el punto ideal del formulador de la agenda).

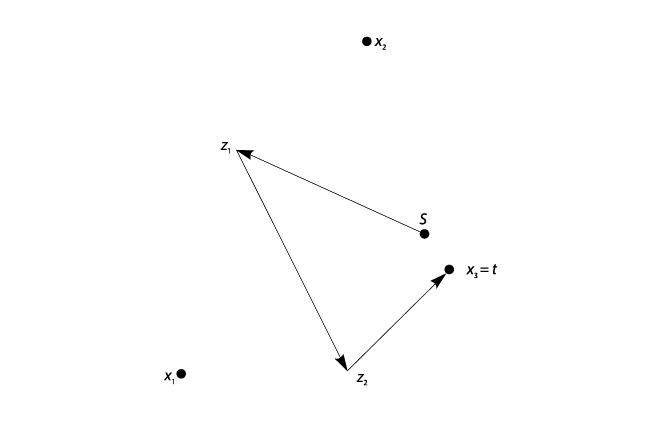
Lo anterior queda ilustrado en la gráfica V.10 en el caso de la legislatura de tres miembros. Los puntos ideales de los tres legisladores son x1, x2 y x3. El punto s es el statu quo anterior. Si el legislador 3 fuera el formulador de la agenda, facultado para hacer mociones y ordenarlas en una secuencia de votaciones, entonces, con un reducido número de pasos —de hecho, con sólo tres pasos— él podría producir el resultado x3, su propio punto ideal. Primero propone z1, que tanto el legislador 1 como el legislador 2 prefieren a s. Por lo tanto, z1 PG s. Después propone z2, que tanto él como el legislador 1 prefieren a z1. Por lo tanto, z2 PG z1. Entonces, en el paso final, propone su punto ideal, x3, que tanto él como el legislador 2 prefieren a z2. ¡Listo! Eligiendo astutamente las alternativas sobre las cuales votar, ha llevado el proceso legislativo a un resultado final situado en su política ideal: t = x3.12

gráfica V.10

 

V.2. Aplicaciones

 

Las aplicaciones del modelo espacial son tan abundantes y ricas que es difícil saber por dónde empezar. Como no tenemos tiempo que desperdiciar y más adelante utilizaremos el modelo espacial en una diversidad de contextos, veremos por ahora un conjunto limitado de aplicaciones. Así pues, comencemos por el principio: con el modelo de competencia electoral de Downs. Anthony Downs fue uno de los primeros especialistas en utilizar el modelo espacial para comprender la política. Su aplicación también demuestra tanto las fortalezas como las debilidades del supuesto simplificador que considera el mundo político como un modelo unidimensional. Después volveremos la vista hacia el análisis de las instituciones, en el que haremos un examen unidimensional y multidimensional de la política legislativa.

 

V.2.1. Elecciones espaciales

 

Los verdaderos orígenes del modelo espacial se encuentran en un famoso trabajo escrito en 1929 por Harold Hotelling. Economista interesado en las decisiones que tomaban las empresas para ubicar sus establecimientos, Hotelling estaba especialmente fascinado por la observación —cierta entonces como en la actualidad— de que las compañías en competencia casi siempre colocaban sus tiendas de menudeo unas al lado de otras o en la acera de enfrente. Los expendios de gasolina se encuentran en las contraesquinas de un cruce de calles; un par de grandes tiendas de departamentos sirven de “ancla” a un centro comercial de los suburbios; Starbucks y Peet’s Coffee & Tea son prácticamente vecinos; y en los pueblos de Estados Unidos, en los viejos tiempos, los almacenes rivales —como Woolworth y Kresge— se situaban uno justo enfrente del otro. ¿Por qué los “competidores”, que tienen un enorme mercado geográfico para dividirse entre sí, se establecen tan cerca unos de otros?13

Voy a dejar a un lado la cuestión de la ubicación desde el punto de vista económico, no sin destacar que Hotelling reflexionaba que los partidos políticos parecían comportarse de una manera muy semejante a los competidores económicos. Las reflexiones de Hotelling se convirtieron en el tema principal del clásico estudio de Anthony Downs (1957), An Economic Theory of Democracy (Una teoría económica de la democracia), en el que desarrolló profundamente el “modelo espacial de competencia electoral” e hizo una amplia exposición de él.

La parte “espacial” del modelo de Downs consiste en un continuo ideológico unidimensional, [0, 100]. La escala del continuo es proporcional a la actividad económica en manos del sector privado, por lo que el extremo de la izquierda refleja una economía completamente socializada, mientras que el de la derecha se identifica con una economía absolutamente de empresa privada. Aunque en la vida real la competencia política consiste en adoptar posiciones y expresar puntos de vista sobre múltiples asuntos políticos, Downs supone que, al fin y al cabo, el debate político se reduce a la ideología: ¿queremos que algún bien, servicio o propósito sea proporcionado por el gobierno o por el sector privado? La competencia política, entonces, es un concurso entre políticos resueltos a obtener el control del gobierno, apelando a los votantes con ofrecimientos de planes, plataformas o programas —puntos de vista, de hecho— alternativos. Y sus propuestas se identifican con diferentes posiciones en la línea del continuo ideológico izquierda-derecha.

Como primer acercamiento al alboroto de las campañas electorales, promesas de campaña y votaciones, esto no es malo. Se concibe a los políticos como resueltos buscadores de la victoria. Son “alumnos”, por así decirlo, de la escuela política Vince Lombardi cuyo lema es: “Ganar no lo es todo; es lo único”.14 Downs suponía que los políticos buscan la mayor cantidad de votos, aunque, en algunas variaciones de su modelo, los políticos buscan maximizar su probabilidad de ganar, o bien buscan maximizar la pluralidad de sus votos (por pluralidad se entiende la diferencia entre sus votos y los de su competidor más cercano). En todo caso, al inicio, la mayoría de los modelos espaciales de competencia electoral consideraban que los votos eran la moneda de cambio en ese ámbito, que los políticos estaban centrados exclusivamente en ganar las elecciones, y que éstos lograban ganar prometiendo políticas públicas, plataformas y programas que atrajeran a los votantes. En ese contexto espacial, se representa a un candidato mediante alguna posición en el continuo ideológico, un punto del intervalo [0, 100].

Downs suponía que los votantes sólo estaban interesados en los aspectos políticos: los bienes y servicios producidos por el gobierno (o dejados al sector privado); la forma y contenido de la regulación gubernamental del sector privado; la distribución del impuesto, el desempleo y las cargas de la inflación; las políticas gubernamentales sobre cuestiones sociales, como el aborto y el divorcio; y los asuntos de la guerra y la paz. Los votantes se interesan mucho en esos asuntos y hacen su evaluación de los candidatos en consecuencia. Sin embargo, sus gustos son heterogéneos, por lo que, así como hay políticos de izquierda y de derecha, también hay votantes de izquierda y de derecha. Cada votante se identifica específicamente con algún punto del [0,100] —el punto ideal del votante— en el espacio ideológico y se supone que sus preferencias disminuyen respecto a los puntos más distantes de su ideal. Es decir, el conjunto de votantes puede representarse mediante las preferencias de pico único. En la gráfica V.11 se muestra a un electorado de 625 votantes (en realidad, cinco “tipos” diferentes de votantes con 125 votantes cada tipo). Un votante del tipo i (i = 1, 2, 3, 4, 5) tiene un punto ideal x_i y sus preferencias disminuyen con la distancia a partir de ese punto x_i.

gráfica V.11

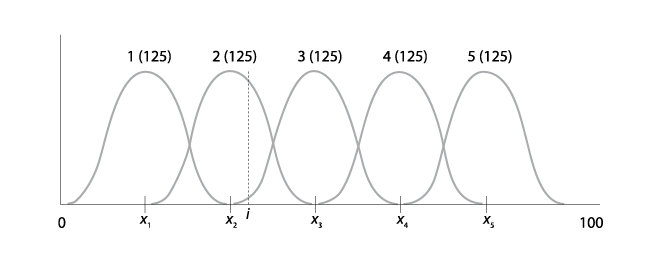
La versión más famosa del modelo de Downs entraña una competencia entre dos candidatos. La pregunta que se hace Downs respecto a una distribución de votantes como la de la gráfica V.11 es ¿dónde se situarán dos ambiciosos buscadores de la victoria? Podemos darnos cierta idea de la respuesta si fijamos la posición de uno de los candidatos. Fijemos la posición de I, la candidata de izquierda, en i, como se muestra en la figura. ¿Qué posición, d, deberá adoptar D, el candidato de derecha, para maximizar sus votos? Para responder a esta pregunta necesitamos una regla para calcular votos. La regla de Downs es que cada votante vota por el candidato cuya posición esté más cercana a su punto ideal.15

Ahora ya podemos responder a las preguntas planteadas en el párrafo anterior. El candidato D debe acercarse infinitesimalmente a I por su lado derecho. De esa manera, D obtendrá todos los votos a la derecha de i y, como i está a la izquierda del punto mediano de la distribución de votantes, ello significa que D obtendrá más de la mitad de todos los votos.16 Esto es, D obtiene los 375 votos de los votantes de los tipos 3, 4 y 5, mientras que I sólo obtiene los 250 votos de los tipos 1 y 2. Dicho de una manera más general, la posición de I divide al electorado en dos grupos: los votantes con puntos ideales menores a i y los que tienen puntos ideales mayores que i. La respuesta óptima de D es una posición d exactamente junto a I del lado del grupo más grande. Así, hemos calculado cómo respondería D a cualquier movimiento hecho por I. Por lo tanto, I sabe que tendrá el grupo más pequeño y, ya que ella también quiere maximizar sus votos, tratará de hacer que ese grupo pequeño sea lo más grande posible. La manera de hacerlo, como habrá adivinado el lector, es estableciendo i como igual al punto ideal del votante mediano, puesto que entonces los grupos a la izquierda y a la derecha serán de igual tamaño. Si i y d estuvieran a horcajadas del punto ideal del votante mediano, x3, entonces cada posición sería óptima respecto a la otra y la elección terminaría en un empate virtual.

Llegamos a la misma conclusión si fijamos la posición de D primero y dejamos que I responda de manera óptima. Dada cualquier posición d elegida por D, I establecerá i justo junto a d del lado del grupo más grande. En las mismas circunstancias, lo mejor que D puede hacer es “desplazarse a la mediana”.

Finalmente, suponga que I y D deben anunciar sus plataformas políticas de manera simultánea. Si una vez anunciadas un candidato se queda “atorado” en su posición durante toda la etapa de la campaña, es probable que le preocupe que su posición pueda ser vulnerable. Una posición es vulnerable si la del oponente se encuentra más cerca de la mediana de la distribución de los votantes, puesto que, conforme a la regla de cálculo de Downs, el oponente obtendrá entonces más de la mitad de los votos.17 La única posición que no puede ser vulnerada es la que se encuentre exactamente en el punto ideal mediano. Si, por otra parte, los candidatos no están “atorados” en sus posiciones anunciadas, sino que pueden revisar su plataforma política durante el transcurso de la campaña, entonces observaremos uno de dos patrones. Si ambos anuncios iniciales se encuentran del mismo lado del punto ideal mediano, entonces habrá un patrón “saltante” que converge, puesto que la posición vulnerable (como acabamos de definirla) saltará sobre la posición de su oponente, con el propósito de estar más cerca de la mediana. A su vez, la ahora posición vulnerable del oponente saltará sobre la otra, y así sucesivamente. Seguirán saltando uno sobre otro cual ranas, hasta que ya no se pueda saltar más, a saber, hasta que ambas posiciones hayan convergido a la mediana. Si, por otra parte, los anuncios iniciales se encuentran en lados opuestos al punto ideal mediano, entonces habrá una serie de acercamientos a la mediana desde cada lado a medida que el más distante se desplace hacia ella.18

Todas estas circunstancias hacen supuestos ligeramente diferentes sobre la secuencia de los diversos sucesos que tienen lugar en el transcurso de la campaña; y sin embargo, en cada una de ellas hay convergencia común al punto ideal del votante mediano. Y esa tendencia centrípeta es precisamente lo que pronostica el teorema del votante mediano de Black. En suma, el modelo de Downs provee una razón fundamental sobre por qué los sistemas de votación mayoritaria son centrípetas.19

La lógica del teorema de Black, tal como la elaboró Downs en el contexto electoral, me hace pensar en aquellas ocasiones en las que alguien dice algo muy atinado o bastante evidente, ¡una vez que ha sido dicho! Es en esas ocasiones cuando piensas ¿cómo no se me ocurrió a mí antes? A Downs, un ciudadano estadounidense, lo motivó la misma observación que han hecho muchos observadores extranjeros prácticamente desde nuestro origen como nación: lo semejantes que son los partidos políticos en Estados Unidos. Según muchos comentaristas foráneos, los Partidos Demócrata y Republicano son Patachunta y Patachún, Tararí y Tarará, botellas vacías que sólo difieren en sus etiquetas.20 De manera más reciente, los observadores de la política británica han comenzado a notar que el partido perdedor siempre se transforma para parecerse un poco a su más exitoso oponente. Durante el periodo posterior a la Segunda Guerra Mundial, los tories británicos aceptaron en gran medida el Estado benefactor defendido por el Partido Laborista, mientras que, en tiempos modernos, este último ha arriado ligeramente sus velas más socialistas con el propósito de parecerse un poco más, ante los ojos de los votantes, al Partido Conservador de Margaret Thatcher y John Major. En el siglo xxi ambos partidos se han acercado al centro, ambos dejando atrás las características extremistas que antes los definían.

gráfica V.12

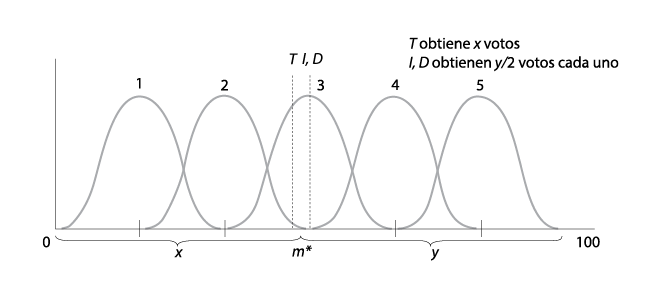
Sin duda alguna, las fuerzas centrípetas que identificó Downs son plausibles; sin embargo, es obvio que los partidos no siempre convergen. ¿Por qué sucede eso? El modelo espacial de Downs es muy fácil de utilizar como “herramienta para descubrir”, por lo que podemos variar algunos de sus supuestos y ver qué pasa. Piénsese, por ejemplo, que no predeterminamos que haya dos candidatos. ¿Qué pasaría si la izquierdista (I ) y la derechista (D ) no fueran los únicos dos contendientes? Supongamos que hay otra candidata, a la que llamaremos tercia (T ), que puede participar en la competencia si cree que tiene oportunidad de ganar. Suponga que I y D se sitúan en la mediana (llamémosla m*), es decir que i = d = m*. Note que cuando hay más de dos candidatos, el que tiene más votos, no necesariamente una mayoría absoluta, gana la elección. Entonces T sin duda alguna tiene oportunidad de ganar. Puede situarse cerca de un lado o el otro de la mediana, ganar casi todos los votos de ese lado y, así, vencer a I y D, que terminarían dividiéndose los votos restantes (véase la gráfica V.12). Por otra parte, si las posiciones de I y D están dispersas con suficiente amplitud, entonces T puede situarse entre ellos en alguna posición t. Obtendrá los votos de los votantes cuyos puntos ideales se encuentren en el intervalo [(i + t) / 2, (t + d) / 2]. El límite izquierdo de ese intervalo es el punto medio entre las posiciones de I y T, mientras que el límite derecho es el punto medio entre la posición de T y D. Conforme a la misma regla de cálculo de Downs, I obtiene todos los votantes en el intervalo [0, (i + t) / 2] y D obtiene todos los votantes en [(t + d) / 2, 100]. Si hay más votantes en el primer intervalo que en el segundo o en el tercero, entonces gana T. Así, cuando existe la posibilidad de participación de un tercero, I y D no pueden situarse ni demasiado cerca ni demasiado lejos uno del otro.

Lo que sí podrían hacer I y D es encontrar dos posiciones de disuasión bajo las cuales ambos obtendrían aproximadamente el mismo número de votos y la tercera candidata no tendría la capacidad de situarse en ningún lugar que le diera la victoria (hecho que la disuadiría de participar en absoluto). Lo que se quiere decir con esto es: cuando se amplía el modelo inicial de Downs para tomar en consideración algún factor que él hubiera omitido —por ejemplo, la posibilidad de participación de un tercer candidato— descubrimos que puede haber ocasiones y circunstancias en las que no es aconsejable que los partidos establecidos (I y D) hagan movimientos de convergencia hacia la mediana.

gráfica V.13

De hecho, se han llevado a cabo investigaciones precisamente sobre esta cuestión: la posible participación de un tercer candidato en el modelo de dos candidatos de Downs.21 Ésta es una posible extensión de los supuestos originales de Downs que produce posiciones divergentes de los candidatos; pero existen otras extensiones. Los candidatos, por ejemplo, pueden tener sus propias preferencias sobre políticas públicas, y estas preferencias de los candidatos son a menudo conocidas por los votantes. Así, suponga que I y D tienen sus propios puntos ideales de política pública en i* y d*, respectivamente (estos puntos se muestran en la gráfica V.13). Ambos pueden declarar programas políticos en otras posiciones, digamos i ≠ i* y d ≠ d*. Pero, ¿por qué habrían de creer los votantes en esas declaraciones políticas? No se necesita ser un cínico para pensar que, una vez que alguno de ellos gane, se verá tentado a poner en práctica su política preferida (i* o d*), en vez de la que declaró (i o d). No se puede confiar en que los políticos harán lo que dicen cuando tienen preferencias propias. Así que una vez más los candidatos no convergerán, en esta ocasión porque no tiene caso hacerlo: los votantes no les creerán aun cuando hagan esa promesa. Usando la jerga de la disciplina, decimos que “no existe la tecnología del cumplimiento de promesas”, es decir, aunque los candidatos quisieran, simplemente no se pueden comprometer de manera creíble a nada.

¿Qué pasaría si los candidatos pudieran comprometerse a cumplir lo que prometen? ¿Qué pasaría si los candidatos tuviesen preferencias políticas, como en el párrafo anterior, pero también tuviesen a la mano la tecnología del cumplimiento de promesas? Por ejemplo, podríamos estar en un mundo en el cual los políticos saben que una reputación de engaño y falsedad sería un serio obstáculo para su victoria en futuras campañas electorales. En ese caso lo único que necesitarían sería decir “lo juro” y los votantes les creerían. Así, por la razón que sea, suponga, por un lado, que las promesas de un candidato son creíbles, pero que, por el otro, los candidatos todavía tienen preferencias específicas sobre las políticas públicas que se ponen en práctica. ¿Qué harían los candidatos en esas circunstancias? En un estupendo trabajo, Randall Calvert (1985) demuestra que, al igual que en el caso en el que a los candidatos no les importan un comino las políticas públicas, ambos convergerán en el punto ideal del votante mediano.

Volviendo a la gráfica V.13, I quiere un resultado cercano a i* y D quiere que la política final sea cercana a d*. Si resulta que esos dos puntos son equidistantes de m* y si cada candidato o candidata anunció (de manera creíble) su política ideal, entonces la elección terminará en un empate (y, presumiblemente, se determinará al vencedor mediante una moneda lanzada al aire). Pero, desplazándose sólo un poco hacia el centro, I podría ganar la elección a un costo muy pequeño para ella en lo que respecta a la política pública. Eso sería terrible para D: no que hubiera perdido la elección, sino que una política pública cercana a i* sería espantosa. Pero podría evitarlo si se desplazara hacia el centro un poco más de lo que lo hubiera hecho I, lo que, a su vez, alentaría a I a moverse un poco más y así sucesivamente. Al final, aun cuando ambos candidatos tuviesen preferencias sobre políticas públicas y en realidad no les importara en absoluto quién ganara la elección, sino únicamente qué política sería llevada a la práctica, de todas maneras convergerían en el punto ideal del votante mediano.

Está de más decir que se podría jugar con el modelo de Downs en una interesante variedad de sentidos, y muchos especialistas lo han hecho.22 Lo que hemos demostrado en esta sección es que el sencillo modelo espacial de Downs, con una competencia sobre una dimensión ideológica entre dos candidatos que buscan la victoria, lleva a una convergencia en la política. La política que surge de las fuerzas competitivas captadas por el modelo es el punto ideal del votante mediano. Para el observador casual este resultado describe lo que ocurre a menudo en las elecciones reales, cuando los candidatos tratan de suavizar sus posturas más extremistas con el propósito de halagar a los votantes y ganarse su favor en el centro de las cosas. Así, una vez que Bill Clinton venció a sus oponentes del Partido Demócrata en 1992 (Jesse Jackson y Mario Cuomo), se enfiló hacia el centro ideológico y contendió en la elección presidencial como un “demócrata nuevo” más conservador. Por su parte, el presidente en funciones, George H.W. Bush, también se movió hacia el centro; para tratar de deshacerse de algunos de sus atributos conservadores de línea dura, aceptó hacer una concesión moderada con su lema “ningún nuevo impuesto”. En 2000, el republicano George W. Bush (hijo de George H.W.) compitió contra el demócrata Al Gore como un “conservador compasivo”. En 2008, el demócrata Barack Obama se mostró más moderado en las elecciones generales, tras haber conseguido la nominación durante una competencia muy reñida contra Hillary Clinton; los republicanos nominaron a su candidato más moderado, John McCain. En muchas otras elecciones vemos una dinámica similar: candidatos partidarios de la izquierda y la derecha tratando de salirse por la tangente, matizando y haciendo concesiones con el propósito de parecer más centristas.

Con todo, la convergencia no siempre es completa. En ocasiones, un candidato, mujer u hombre, frena la convergencia por temor a perder el apoyo de sus bases o incluso a provocar la participación de un tercero. Así, los activistas de los derechos civiles, los sindicatos y los trabajadores gubernamentales —elementos de las bases del Partido Demócrata— prácticamente imposibilitaron que el candidato Walter Mondale convergiera en el centro en la elección presidencial de 1984. Los elementos del movimiento conservador obligaron a Ronald Reagan a cumplir con sus promesas ideológicas en la misma elección. En las elecciones presidenciales de 1968, 1980 y 1992, participaron candidatos de terceros partidos (George Wallace, John Anderson y Ross Perot, respectivamente), entre otras razones porque consideraron que los candidatos habían convergido demasiado,23 en otras, porque se pensó que habían permanecido demasiado cerca de sus partidarios más extremistas.24 Así, el que haya tanto demasiada como muy poca convergencia puede proporcionar el impulso para el desafío de un tercero.

Obviamente, sólo he arañado la superficie del modelo espacial de Downs de competencia entre partidos, y sólo cubrí algunos de los muchos mecanismos y razones fundamentales conforme a los cuales los competidores tratan de converger en la política ideal del votante mediano, por una parte, o mantienen perfiles de política distintos, por la otra. Esto, por sí mismo, sugiere la riqueza del enfoque de Downs.

Con todo, los fenómenos electorales no son el único centro de atención del modelo espacial. En una misión paralela que podría entenderse como una especie de “elecciones a pequeña escala”, también se ha empleado el modelo espacial para estudiar la selección de políticas públicas en el marco legislativo. Pasamos ahora a esto, examinando ambas versiones del modelo espacial; la unidimensional y la multidimensional.

 

V.2.2. Modelos espaciales de legislaturas

 

Haremos un examen mucho más exhaustivo de las legislaturas en la cuarta parte, pues lo que aquí me interesa, de manera primordial, es ver lo que puede hacerse con los modelos espaciales. Veremos que son una herramienta analítica muy poderosa para representar la manera como interactúan el comportamiento (racional) basado en las preferencias y las características estructurales de las instituciones para producir los resultados finales. El modelo sugiere que los resultados legislativos dependen, en esencia, no sólo de lo que los legisladores quieran sino también de cómo llevan a cabo los asuntos en la legislatura.

Para mantener las cosas lo más simples posible, consideramos que la legislatura es un conjunto n de individuos, en el que n es un número impar y cada individuo emite un voto. El conjunto adopta sus decisiones mediante la regla de la mayoría. La situación más elemental, la que examinaremos primero, es el caso unidimensional en el que la legislatura debe elegir un punto de una línea. Cada legislador, i, tiene un punto ideal x_i, y preferencias de pico único. El votante mediano es el legislador m con el punto ideal x_m. En esas circunstancias, sabemos que x_m puede vencer a cualquier otro punto de la dimensión en una competición por la mayoría (teorema de Black). Quizá lo más sorprendente sea el hecho de que las preferencias medianas prevalecen en una comparación entre cualesquier dos alternativas, por lo que si m prefiere x a y, entonces también lo prefiere la mayoría.25

Además de las preferencias del legislador mediano, x_m, identificamos otras dos características distintivas de la situación. Siempre que una legislatura tiene frente a sí una alternativa, existe un statu quo establecido, representado por x0. Se trata de la política vigente en el momento en que la legislatura toma la decisión. Suponemos que se mantiene en vigor si la legislatura decide no cambiarla.26 La segunda característica de interés común a la mayoría de las legislaturas es un acuerdo de división del trabajo conocido como sistema de comisiones. En ese sistema, una comisión es un subconjunto del conjunto de n legisladores (dentro de un momento describiremos algunas de sus facultades específicas). El punto ideal mediano de los miembros de la comisión lo representamos mediante x_c. Así como las preferencias mayoritarias de toda la legislatura son iguales a las preferencias del votante mediano de la misma, las preferencias mayoritarias en el seno de una comisión son una copia de las preferencias del miembro mediano de la comisión. Debido a esas igualdades, sólo necesitamos considerar x0, x_m y x_c para nuestro análisis. Ahora pondremos el modelo espacial a trabajar, analizando las decisiones sobre políticas públicas que toma una legislatura de n miembros poseedora de un sistema de comisiones.

Consideramos tres regímenes o arreglos institucionales de toma de decisiones. El primero es la regla de la mayoría pura. Existe un statu quo y cualquier legislador puede presentar una moción para modificarlo. Una vez propuesta, la moción se enfrenta a él. Si gana, se convierte en el nuevo statu quo; si pierde, va a dar al lugar adonde van todas las propuestas perdedoras: una especie de cementerio de elefantes. Una vez más, la asamblea queda abierta a alguna nueva moción (contra el antiguo statu quo, si sobrevivió, o contra el nuevo statu quo, si prevaleció la propuesta anterior). Este procedimiento de presentación de mociones y votaciones sobre las mismas continúa hasta que ningún otro miembro de la legislatura desee hacer una nueva moción.27

El segundo régimen es el sistema de comisiones con regla de cierre. Bajo este régimen, en primera instancia, una comisión nombrada previamente decide si la legislatura considerará hacer modificaciones a las políticas públicas en vigor. Usando la jerga de los politólogos, la comisión tiene el poder para “cerrar las puertas” a cualquier propuesta de modificación a las políticas públicas. En ese caso decimos que tiene facultad de custodio de la agenda, puesto que, en sentido metafórico, la comisión logra secuestrar el orden del día.28 En segunda instancia, si se abren las puertas bajo este régimen, sólo la comisión puede hacer una propuesta (a lo cual llamamos poder monopólico para proponer). En tercera instancia, el pleno de la legislatura puede votar la propuesta de la comisión, pero sólo para aprobarla o rechazarla ya que la propuesta está cerrada a modificaciones. Por lo tanto, se dice que la propuesta se rige por una regla de cierre y que la comisión presenta a la legislatura una propuesta de “tómenlo o déjenlo”.

El tercer régimen que examinamos es el sistema de comisiones con regla de apertura. Éste es igual al descrito en el párrafo anterior salvo por la tercera característica. Conforme a la regla de apertura, una vez que la comisión ha hecho una propuesta, el pleno de la legislatura puede abrir la sesión para hacer modificaciones. Una vez que la comisión ha abierto las puertas y hecho una propuesta, cede su acceso monopólico al orden del día.

Examinaremos cada uno de los tres sistemas tanto en el marco unidimensional como en el multidimensional. Queremos saber si existe algo regular o rutinario que podamos esperar de esos regímenes alternos de la regla de la mayoría. En conclusión, deseamos ofrecer algunas breves observaciones comparativas sobre esos regímenes; una consideración exhaustiva puede encontrarse en los capítulos xi y xii, donde abordamos las instituciones de manera más sistemática.

 

Regla de la mayoría pura. Comienzo con una decisión tomada por la legislatura en un marco espacial unidimensional. En el régimen con la regla de la mayoría pura no hay comisiones, por lo que sólo necesitamos conocer las posiciones de x_m y x0. Una situación típica se ejemplifica en la parte superior de la gráfica V.14. A partir del punto ideal mediano y el statu quo, determinamos el conjunto que el legislador mediano prefiere a x0, P_m(x0).29 Puesto que hemos establecido que las preferencias del legislador mediano son las mismas que las preferencias de una mayoría de legisladores, este intervalo es el conjunto de mociones que prevalecerían sobre x0 en una competencia por mayoría. Si se le otorga la palabra a alguien y éste hace una moción fuera de ese conjunto, la moción será demolida, mientras que cualquier moción dentro de ese conjunto saldrá victoriosa y se convertirá en el nuevo statu quo. Es evidente que el proceso político definido de esta manera producirá resultados que dejan sin modificación el statu quo o lo acercan a x_m (ya que cada uno de los puntos de P_m(x0) está más cerca de x_m que x0). Conforme prosiga el proceso de votar y hacer nuevas mociones, la alternativa ganadora convergerá a x_m. Además, no se alejará una vez que haya alcanzado x_m (puesto que, como lo demostramos antes, el statu quo no puede desplazarse más allá de x_m con ninguna votación). Vemos así que en el régimen legislativo de regla de la mayoría pura existe una tendencia centrípeta al igual que en el modelo de Downs para las elecciones. Por esta razón es por lo que consideramos que las decisiones legislativas adoptadas mediante la regla de la mayoría pura son como una “elección a pequeña escala”.

La gran utilidad de los modelos espaciales de decisión legislativa es que permiten llevar a cabo lo que los economistas llaman estática comparativa, que consiste en hacer preguntas del tipo ¿qué pasaría si...? Al tener un resultado de equilibrio de nuestro montaje básico, como lo hicimos en el párrafo anterior, podemos preguntarnos ahora cuáles son las modificaciones que sufre cuando los parámetros pertinentes cambian. Ya vimos que en realidad sólo hay dos parámetros pertinentes: x0 y x_m. Manteniendo fijo este último, primero nos preguntamos qué ocurriría si el primero cambiase, esto es, ¿qué pasaría con el resultado final si el statu quo estuviese más cerca o más lejos del punto ideal del legislador mediano? La respuesta es ¡nada! Aunque las diferentes posiciones de x0 afectarían a P_m(x0) y, por ende, a las mociones que podrían resultar vencedoras en algún momento, sabemos que, a la larga, el resultado convergerá en x_m, sin importar cuál sea la posición de x0. Por lo tanto, una conclusión interesante que extraemos del modelo de la regla de la mayoría pura es que no posee una desviación conservadora que haga pesar excesivamente las decisiones anteriores. El pasado (reflejado en el statu quo) influirá en la “senda” (restringiendo qué mociones pueden ser las vencedoras en diferentes etapas del proceso), pero no afectará el resultado final.

gráfica V.14

Al invertir el énfasis y mantener fijo x0, nos preguntamos ahora qué pasaría si x_m fuera diferente. La respuesta está representada gráficamente en la parte inferior de la gráfica V.14 cuando x_m se encuentra en una línea entre 0 y 1. La posición de x_m en el intervalo [0, 1] se da en el eje horizontal y el resultado de equilibrio de ese intervalo se da en el eje vertical. La gráfica es una línea de 45° que muestra que (dado cualquier x0) el resultado de equilibrio sigue a la perfección el rastro de la identidad del punto ideal mediano: se trata de los resultados exactamente centrípetas. No sólo la decisión legislativa llevada a cabo mediante la regla de la mayoría pura converge en el punto ideal mediano, sino, además, si el punto ideal mediano cambiase, también lo haría el resultado de equilibrio. Así, una segunda conclusión interesante que podemos extraer de la regla de la mayoría pura es que es perfectamente sensible a las tendencias hacia el centro: el punto ideal del legislador mediano es, por definición, el punto central de la distribución de las preferencias. La regla de la mayoría pura produce un resultado en ese punto y, si dicho punto cambiase, el resultado legislativo “seguiría su rastro”.

 

Sistema de comisiones con regla de cierre. En su mayoría, las legislaturas no son instituciones con regla de la mayoría pura. Incluso las asambleas comunales y otras instituciones semejantes a la regla de la mayoría pura, a veces vistas con romanticismo por los observadores, requieren algún mecanismo para determinar el contenido de la agenda y el orden mismo en el que serán abordados sus puntos. Algunas legislaturas establecen una sola comisión del orden del día para decidir esos asuntos. No obstante, la mayoría de las legislaturas (la de Estados Unidos, sin duda alguna) utiliza un sistema de comisiones basado en la división del trabajo que distribuye las facultades del orden del día por tema político. Los subconjuntos de legisladores gozan de una influencia desproporcionada sobre el orden del día en ciertas jurisdicciones de políticas específicas. En su jurisdicción, la comisión le sirve al pleno de la legislatura como un formulador de la agenda.

En la cuarta parte me extenderé mucho más sobre estos temas. Pero por ahora necesito centrar mi atención únicamente en lo que distingue a la regla de cierre de la regla de la mayoría pura: ahora, además de x0 y x_m, hay un tercer parámetro de interés, a saber, el punto ideal mediano de una comisión que controla el orden del día, x_c.30 Muchas de las conclusiones que extraigamos respecto a éste dependerán de las posiciones relativas de x0, x_c y x_m.

Como antes lo sugerimos, el procedimiento para adoptar las decisiones consiste en que la comisión no haga ninguna propuesta en absoluto, en cuyo caso x0 permanecerá en su lugar, o bien que haga una moción para modificar el statu quo, misma que el pleno de la legislatura deberá aceptar o rechazar sin condiciones. ¿Qué haría una comisión de ese tipo? Para responder a esta pregunta determinamos una vez más P_m(x0) como en la parte superior de la gráfica V.14. Se trata de un conjunto cuyos puntos límite son el propio x0 y x* y que contiene los únicos puntos que una mayoría legislativa prefiere a x0. La comisión, personificada por su votante mediano, c, trata esos puntos como su “conjunto de oportunidades” y elige su favorito como la moción que va a hacer (si acaso hace alguna moción). Examinemos los tres ordenamientos de los parámetros pertinentes (hay seis ordenamientos en total, pero los que omitimos son simplemente reflejos de los que consideramos):

Caso 1. (x0 ≤ xm ≤ xc)

En este caso, el legislador mediano se encuentra entre el statu quo y el miembro mediano de la comisión, mientras que x* es el límite derecho de P_m(x0), como se muestra en la gráfica V.14. Si x_c ≤ x*, entonces la comisión propondrá su punto ideal mediano, el cual será aprobado después por una mayoría legislativa (puesto que se encuentra dentro de P_m(x0)). Si, por otra parte, x* < x_c, entonces lo mejor que puede hacer la comisión es proponer x*, que será aprobado por una mayoría legislativa.* En cualquiera de los dos casos, tanto la comisión como el pleno de la legislatura desean alejarse del statu quo en la misma dirección. El resultado final desplazará x0 en esa dirección, más allá de lo que el votante mediano querría, pero no siempre tan lejos como querría el miembro mediano de la comisión.

 

Caso 2. (x0 ≤ xc≤ xm)

En este caso, el miembro mediano de la comisión se encuentra entre el statu quo y la mediana de toda la legislatura. Asimismo, de manera automática tenemos que x_c ∈ P_m(x0). En consecuencia, la comisión puede obtener la aprobación de la mayoría legislativa para x_c.

 

Caso 3. (xm ≤ x0 ≤ xc)

En el último caso, el statu quo se encuentra entre los dos puntos medianos. Éste es un caso muy interesante porque la comisión y la mayoría legislativa están en desacuerdo. La comisión desea moverse hacia la derecha, mientras que una mayoría del pleno de la legislatura quiere desplazarse hacia la izquierda. La facultad de la comisión como guardiana de la agenda le rinde muchos dividendos en este caso, porque, simplemente, elegirá mantener cerrado el orden del día.**

 

En consecuencia, lo primero que aprendemos respecto al régimen con la regla de cierre es que sólo puede ocurrir un número muy limitado de cosas; tres en particular. Si x_c se encuentra en el interior del conjunto preferido a x0 de la mediana legislativa, entonces el resultado es x_c. Si no se encuentra en el interior, entonces es posible cualquiera de los dos puntos finales de P_m(x0): x0 si la comisión y la mediana legislativa están en desacuerdo; x* en caso contrario. En el régimen con la regla de la mayoría pura, en cambio, sólo una cosa puede ocurrir: x_m, algo que nunca ocurre con el régimen con la regla de cierre (a menos que, por coincidencia, x_m = x_c o bien, x_m = x0). Lo anterior sugiere que otorgar a un grupo privilegiado el control sobre el orden del día que viene con la facultad de custodio de la agenda no carece de consecuencias: la facultad de cerrar las puertas desalienta los resultados centrípetos, debido a que arrastra el proceso en la dirección del grupo que controla la agenda.

Hay una gran variedad de ejercicios de estática comparativa que podríamos hacer. Centraremos nuestra atención en uno: dadas una mediana legislativa y una mediana de la comisión fijas, ¿qué ocurre si x0 cambia? (Cuando hacemos esta pregunta no queremos decir literalmente que el statu quo cambie de repente. Más bien, estamos preguntando qué ocurriría si el statu quo fuera más extremo o menos.) En el caso número 1, por ejemplo, si x0 estuviese más a la izquierda, entonces P_m(x0) sería mayor (x* se desplazaría hacia la derecha). En cierto momento abarcaría x_c (si todavía no lo contiene). Es decir, a medida que x0 se aleje de la mediana de la cámara, habrá una discontinuidad cuando x_c pase, de encontrarse fuera del conjunto de m preferido a x0, al interior de ese conjunto. Dicho con rudeza, cuanto peor sea el statu quo, desde la perspectiva de m, tanto más probable será que c se salga con la suya.31 El mismo patrón prevalece a medida que x0 se desplaza hacia la derecha. Al principio se desplaza hacia x_m, por lo que el conjunto de m preferido a x0 se contrae; sin embargo, una vez que “rebasa” a x_m, el conjunto preferido comienza a expandirse nuevamente.32

 

Caso V.1

Disposiciones de vigencia limitada y presupuesto base cero

 

En la década de los setenta, los analistas de la política pública desarrollaron dos conceptos en un intento por contrarrestar las crecientes presiones sobre el presupuesto. El primero recibió el nombre de disposición de vigencia limitada. El problema que se había identificado era la persistencia del gasto que podría haber sobrevivido a su utilidad. Parece ser que, una vez que un proyecto se encontraba registrado en los libros de contabilidad, nunca salía de ellos. Con una disposición de vigencia limitada como parte de la legislación de autorización, el proyecto tendría que ser renovado después de un periodo específico con el propósito de alargar su vida. En otras palabras, la vigencia de un proyecto prescribiría automáticamente, a menos que la legislatura emprendiera alguna otra acción.*

Al segundo concepto se le denominó presupuesto base cero. Éste, relacionado también con el problema del gasto que se incrementaba sin ningún control, exigía que las agencias burocráticas justificaran el presupuesto de un proyecto “a partir de cero”, en vez de sólo justificar el incremento del gasto propuesto sobre el presupuesto del año anterior. Se argumentó que ese procedimiento reduciría la ineficiencia acumulativa y persistente de los presupuestos de las agencias.

Para los propósitos de nuestro análisis, las disposiciones de vigencia limitada y los presupuestos de base cero son similares, porque generan situaciones en las que el statu quo alternativo a una propuesta es cero. Considérese el caso de un presupuesto base cero para una agencia. La mediana legislativa se encuentra en x_m y el presupuesto del año anterior de la agencia se encuentra en B. Ahora, supongamos que la agencia hace una propuesta para el presupuesto del año próximo, misma que la legislatura puede aceptar o rechazar mediante la regla de la mayoría. Suponemos que conforme a los procedimientos ordinarios, el rechazo de la legislatura a la propuesta de la agencia da como resultado que el presupuesto del año anterior, B, se mantenga en su lugar el año siguiente. Conforme al presupuesto base cero, por otra parte, suponemos que el rechazo legislativo provoca que se parta completamente de cero para el nuevo presupuesto de la agencia.

A primera vista, parecería que el procedimiento de presupuestar a partir de cero es algo muy severo para la agencia. Y ésa es la idea, puesto que ese método fue diseñado para limitar su poder en las negociaciones del presupuesto. Sin embargo, la elaboración del presupuesto a partir de cero en realidad incrementa las facultades discrecionales de la agencia, lo cual se aprecia en la siguiente gráfica. Si, conforme a los procedimientos ordinarios, B es el resultado de restablecimiento (el resultado si la legislatura rechaza la propuesta de la agencia), entonces la legislatura lo aprobará, siempre y cuando la agencia proponga un presupuesto en la región gris (cualquier propuesta de ese tipo se encontrará en P_m(B)). Es decir, conforme a los procedimientos ordinarios, la agencia podría obtener la aprobación de un presupuesto tan grande como B*. Si, por otra parte, estuviese en vigor el procedimiento de elaboración del presupuesto a partir de cero, entonces la agencia podría obtener un presupuesto tan grande como N, puesto que N se encuentra en P_m(0). En su forma pura, tanto las disposiciones de vigencia limitada como el presupuesto base cero proporcionan incentivos perversos. Su lógica era la de disciplinar a agencias y presupuestos que estuvieran “fuera de control”, no empoderarlos. (El lector podría explorar las consecuencias de un régimen de presupuesto base cero en el que las propuestas de las agencias pueden ser enmendadas por la legislatura.)

 

 

 

Para concluir este breve tratamiento del régimen con regla de cierre, permítasenos poner énfasis nuevamente en el hecho de que los parámetros clave son x0, x_c y x_m. Una catástrofe electoral que no logre modificar las relaciones entre esos parámetros no modificará los resultados políticos (hecho que puede desconcertar a quienes no manejen la teoría que exponemos aquí). Si, por ejemplo, unas elecciones legislativas provocaran una renovación generalizada de los legisladores en ejercicio, pero lo hicieran de manera simétrica, de tal suerte que x_m no sufriese cambios, entonces “cuanto más cambiaran las cosas tanto más permanecerían iguales”. De manera similar, si, antes de unas elecciones, los legisladores c y m estuviesen en desacuerdo total, como se definió en el ejemplo anterior número 3, entonces, por generalizado que fuera, el cambio electoral no modificaría el desacuerdo entre c y m (posiblemente renovado), simplemente mantendría el statu quo anterior. Los impedimentos institucionales implícitos en el régimen con la regla de cierre presentan un marcado contraste con la hipersensibilidad de la regla de la mayoría pura.

 

Sistema de comisiones con regla de apertura. Hemos visto hasta ahora que, si bien existe todo un continuo de posibles resultados finales, sólo una cosa, es decir x_m, puede suceder conforme al régimen con la regla de la mayoría pura y sólo una de tres cosas, es decir x_c, x0 o x*, conforme al régimen con la regla de cierre. En nuestro análisis del régimen con la regla de apertura descubriremos que sólo existen dos posibilidades: o las puertas se abren a cambios en el statu quo, en cuyo caso x_m será el resultado final, o bien las puertas se mantienen carradas, en cuyo caso x0 prevalecerá. Son los únicos dos resultados posibles. Consideraré ambos casos, como lo hicimos con el régimen anterior.

En el régimen con la regla de apertura, la comisión también tiene la iniciativa. Si no hace ninguna moción, entonces se mantiene x0. Si hace una moción, entonces esta última está abierta a la modificación (de ahí el término “regla de apertura”). En este caso suponemos que las modificaciones alternativas siguen siendo propuestas hasta que ningún legislador desee hacer otra. Así, la propuesta de la comisión se enfrenta inicialmente contra la primera modificación, el vencedor contra la siguiente, y así de manera sucesiva, hasta que todas hayan sido tomadas en cuenta. La sobreviviente de esa secuencia se enfrenta entonces al statu quo (esta última votación recibe a menudo el nombre de “votación sobre el dictamen final”).33

Este procedimiento se parece mucho al régimen con la regla de la mayoría pura, con la excepción de que la comisión tiene la facultad de hacer la primera jugada. Una vez que abre las puertas, nos encontramos en el mundo de la regla de la mayoría pura, lo cual significa que, una vez que una propuesta ha sido hecha, será modificada una y otra vez y las sucesivas modificaciones vencedoras harán que el proceso converja en x_m. En realidad, ni siquiera importa cuál es la propuesta inicial de la comisión. La realidad es:

 

Abrir las puertas → x_m

Mantener cerradas las puertas → x0

 

La decisión de la comisión es realmente muy simple. Si el votante mediano de la comisión, la legisladora c, prefiere x_m a x0, entonces hace una moción (cualquiera); si prefiere x0 a x_m, entonces la comisión mantiene cerrado el orden del día. Así, todo lo que necesitamos hacer es analizar el conjunto que la legisladora c prefiere a x0, es decir P_c(x0), para ver si x_m forma parte de él o no.

Retomando los tres casos posibles de la sección anterior, dado el ordenamiento de parámetros del caso número 1 (x0 ≤ x_m ≤ x_c), la comisión claramente prefiere x_m a x0 así que abrirá las puertas. Dado el ordenamiento del caso número 3 (x_m ≤ x0 ≤ x_c), es evidente que la comisión tiene la preferencia opuesta así que dejará las puertas cerradas. El ordenamiento del caso número 2 (x0 ≤ x_c ≤ x_m) es más interesante. Si la política ideal de la comisión c se encuentra a menos de la mitad del camino entre x0 y x_m, entonces ésta mantendrá cerrado el orden del día; si está a más de medio camino, entonces hará una moción.

gráfica V.15

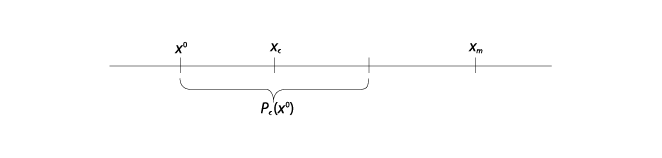
La primera de las dos situaciones del caso número 2 se muestra en la gráfica V.15. Lo que la hace particularmente interesante es que representa una situación muy frustrante. Debido a que la comisión prefiere el statu quo al punto ideal del legislador mediano, mantendrá cerrado el orden del día. Pero tanto una mayoría de la comisión como una mayoría de la cámara preferiría cualquier punto de P_c(x0) a x0. Es decir, el ambiente de la regla de apertura, que a primera vista parece otorgar mayor autoridad a la mayoría legislativa, en realidad penaliza tanto a la mayoría de la comisión como a la mayoría legislativa. Otorga demasiada autoridad a la cámara: el derecho a modificar siempre que así lo desee. Su fuerza es su debilidad, porque no puede prometer que no hará uso de su autoridad; no obstante, se encontraría en una mejor posición si pudiera prometer, de manera creíble, que no modificaría la propuesta en P_c(x0) hecha por la comisión (porque, si pudiera comprometerse por anticipado en eso, entonces la comisión estaría preparada para abrir las puertas a cambios en la agenda).

Caso V.2

Pensamiento estratégico y la importancia de las concesiones

 

Nuestro análisis de los regímenes con regla de cierre y regla de apertura aborda la cuestión general de la manera en que los políticos y otros interesados piensan sobre las posibilidades legislativas. En las situaciones unidimensionales, como hemos visto, los políticos sitúan una propuesta en la dimensión de la política relativa a sus propias preferencias y al statu quo que de otro modo prevalecería si el cambio propuesto es rechazado. Cuando se enfrenta a una decisión entre la propuesta y el statu quo, el político o política vota por la alternativa más cercana a su alternativa ideal. Hemos demostrado que, en el régimen con la regla de apertura, una vez que ha sido hecha una propuesta, la dinámica del procedimiento de modificaciones lleva inevitablemente a un resultado único: el punto ideal del legislador mediano. En el régimen con la regla de cierre, una propuesta resulta vencedora sólo si se encuentra más cerca del statu quo que de la alternativa ideal del votante mediano.

Esa dinámica es una lección necesaria para los miembros de grupos de presión dedicados a gestionar el apoyo de los legisladores a cierta causa, llamados cabilderos.* Si algún cabildero con principios particularmente dogmáticos, es decir, necio, insiste en promover su ideología sin entender la dinámica que explicaré aquí, puede llevarse una gran decepción. Los defensores de una legislación propuesta deben considerar las preferencias de los responsables de tomar las decisiones, las reglas de procedimiento en vigor y la posición relativa del statu quo. La falta de disposición para hacer concesiones a la luz de esas realidades puede mantener en su lugar el statu quo, aun cuando exista la posibilidad de vencerlo con resultados que serían satisfactorios para el cabildero miembro de un grupo de presión. Lo anterior se ilustra en la siguiente figura donde la mediana legislativa es x_m, el statu quo es x0 y la política ideal del cabildero de un grupo de presión poderoso es I.

 

Sin entrar en los detalles específicos concernientes a la manera como los cabilderos de los grupos de presión influyentes ejercen su poder, suponga que el cabildero I se encuentra en posición de debilitar cualquier propuesta de modificación del statu quo —“sobornando”, quizás, a legisladores influyentes, es decir, contribuyendo a sus comités de campaña— si le parece que el cambio no es de su agrado. En el régimen con la regla de cierre, lo mejor que I puede esperar es el punto de acuerdo mutuo C: una política tan sólo un poco más cercana a x_m que x0. Si el cabildero se rehúsa de forma testaruda a aceptar C por buscar algo más extremo, pierde. En el régimen con la regla de apertura, debe estar preparado para aceptar x_m, pues a ese punto es adonde el proceso de modificación llevará el resultado final. En cualquiera de esos dos casos, el cabildero debe ser capaz de prever el mejor trato que pueda lograr y conformarse con él. En especial, debe mostrarse particularmente sensible al hecho de que “el mejor trato que pueda lograr” dependerá de las reglas de procedimiento para las modificaciones. Aun cuando cuente con el poder suficiente como para debilitar las modificaciones propuestas a x0, no puede imponer su propia voluntad. Necesita un poco de ayuda de sus amigos (legisladores).

Algunos observadores han citado la falta de ese pensamiento estratégico como la razón del fracaso de la Enmienda sobre Derechos Iguales** y de la Propuesta 174 en California, que hubiera puesto en vigor la selección de escuelas bajo un sistema de vales o vouchers.*** Al no estar dispuestos a ceder, los cabilderos mantuvieron una postura más extremista de lo que les convenía. Sin darse cuenta, perjudicaron su propia causa al mantener una propuesta más allá del punto de acuerdo que respondía a la realidad estratégica. Los políticos o los electores votaron en contra de sus propuestas, cuando es posible que se hubieran aprobado versiones más moderadas si hubieran estado dispuestos a hacer concesiones. La importancia del pensamiento estratégico de este tipo será abordada con mayor detalle en el capítulo siguiente.

 

V.2.3. Extensiones multidimensionales

 

Una vez que se pasa a las dimensiones múltiples, las cosas se vuelven un poco más inciertas. En un régimen con la regla de la mayoría pura, los resultados del teorema del caos, de McKelvey, ocupan un lugar preponderante. Dejando a un lado la circunstancia altamente inverosímil de que las preferencias de los legisladores estén distribuidas en simetría radial, sabemos que, dada cualquier x en el espacio de políticas públicas, V(x) ≠ ∅. Cualquier propuesta puede perder. En particular, dado cualquier statu quo, x0 tiene un conjunto ganador V(x0) no vacío. Siempre que se haga una moción de ese conjunto, se reemplazará el statu quo. Pero x1 ∈ V(x0) a su vez, tendrá su propio conjunto ganador V(x1) no vacío. Una moción x2 ∈ V(x1) reemplazará a x1. Conforme a los supuestos que hemos hecho acerca de la votación legislativa,34 el statu quo existente se reemplaza de manera continua.

Suponga que alteramos el arreglo muy ligeramente. Mantenemos la condición del régimen con la regla de la mayoría pura de que todos son libres de hacer una moción para modificar el statu quo, pero suponemos que la adopción de decisiones tiene lugar en una dimensión a la vez, en un orden preestablecido. La primera persona con facultades para hacer una moción en la dimensión designada inicialmente propone su modificación a x0; esto sólo puede modificar x0 en la dimensión que esté en consideración en ese momento. El grupo continúa centrado en modificar el statu quo en esa dimensión hasta que ya nadie propone más modificaciones. Una vez que completa su tarea, el grupo vuelve su atención a la siguiente dimensión. Continúa de esa manera hasta que ya no quede ninguna dimensión en la que algún otro legislador desee alterar el nivel del statu quo.

Como se muestra en la gráfica V.16, es fácil ver que esta versión multidimensional de la regla de la mayoría pura copia el resultado del marco unidimensional. Hay tres legisladores con puntos ideales: xa = (x_a1, x_a2), xb = (x_b1, xb2) y x_c = (x_c1, x_c2). Dado cualquier statu quo (no representado en la gráfica), x0 = (x01, x02), las mociones se toman en consideración, primero, en la dimensión número 1 y, luego, en la dimensión número 2. Al final del día, cuando ya han sido hechas todas las mociones y se han llevado a cabo todas las votaciones, el resultado final es la mediana multidimensional, x_m = (x_c1, x_c2), puesto que el legislador c es el legislador mediano en la primera dimensión y el legislador a lo es en la segunda dimensión. Lo anterior no significa que V(x_m) = ∅; en realidad hay puntos que tanto a como c, por ejemplo, prefieren a x_m. Más bien significa que en cualquier dimensión —digamos la primera— mientras se mantenga la política fija en la otra dimensión —es decir la segunda— ningún movimiento que se aleje de x_c1 sería apoyado por una mayoría. Dado cualquier punto en la línea horizontal que pasa por x_m —los puntos en los que la política cambia en la primera dimensión, pero permanece fija en la segunda— dos de los tres legisladores preferirán siempre x_m a dicho punto. Lo mismo aplica en el caso de los puntos en la línea vertical que pasa por x_m. Los únicos puntos preferidos a x_m por una mayoría exigen cambios inmediatos en ambas dimensiones.

gráfica V.16

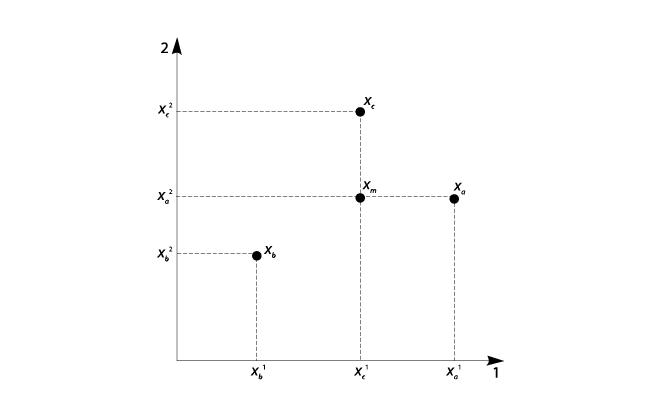
gráfica V.17

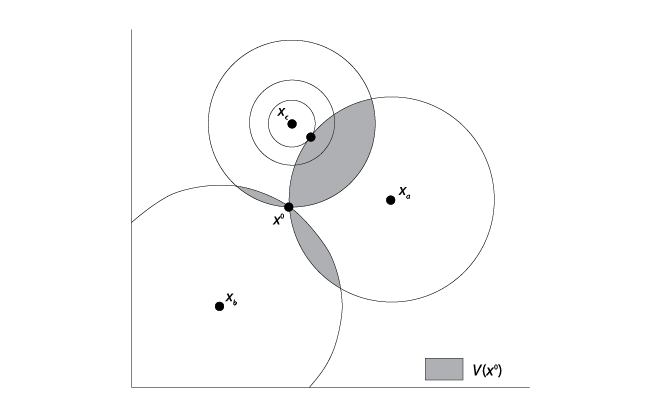
Así, la versión multidimensional de la regla de la mayoría pura produce una o dos conclusiones posibles dependiendo de si hay una estructura institucional adicional o no. En el caso puro, el statu quo es continuamente vulnerable al cambio. Las decisiones que adopta el grupo nunca son muy durables, debido a que siempre hay alguien interesado en que se introduzca una moción para modificarlas y siempre hay alguna mayoría interesada en acceder a ello. En el caso de la estructura institucional que tiene la forma de adopción de decisiones por dimensión, el resultado es tanto predecible como centrípeto. El punto ideal mediano de cada dimensión prevalece conforme al procedimiento antes descrito (aunque, por supuesto, no tiene que ser el mismo votante mediano en cada ocasión).

En el capítulo XII sobre legislaturas abordaré las versiones multidimensionales de los regímenes con regla de apertura y regla de cierre, por lo que ahora seremos particularmente breves al respecto. Considere la gráfica V.17 que es una reproducción de las posiciones espaciales de la gráfica V.14. Imagínese que la legisladora c está encargada de formular la agenda y que el statu quo es x0. Si el pleno de la legislatura somete a modificaciones las propuestas de la legisladora, entonces habremos vuelto al anárquico y desordenado sistema de la mayoría con la regla de apertura. Pero bajo un régimen con la regla de cierre, la legisladora puede hacer una propuesta de tómenlo o déjenlo, es decir, que no esté sujeta a modificaciones, sino a un voto de aceptación o rechazo. Las regiones sombreadas en forma de pétalos comprenden el conjunto de oportunidades de c, es decir, V(x0). Los círculos centrados en x_c son varias de las curvas de indiferencia de c. Su objetivo es desplazar el resultado final de la política a la curva de indiferencia de radio más pequeño —y, por ende, lo más cerca posible de su punto ideal— que todavía se encuentre dentro de V(x0). En esta gráfica, el punto (¡un gran punto negro!), en la tangente entre uno de los pétalos de V(x0) y la curva de indiferencia más pequeña de la legisladora c, es la propuesta que hará y que después apoyará una mayoría (a y c). Por lo tanto, en el régimen con la regla de cierre, la persona que controle el orden del día tiene un poder considerable, a pesar de estar restringido por las preferencias de la mayoría.

 

V.3. Conclusión

 

El modelo espacial será utilizado una y otra vez en los análisis del resto del libro. En este capítulo he presentado los ingredientes básicos y explorado brevemente la regla de la mayoría en marcos electorales y de grupos pequeños; pero he supuesto una gran ingenuidad de parte de nuestros votantes y legisladores (como si sólo los candidatos y los formuladores de la agenda fueran astutos). En el capítulo VI buscaré matizar esa característica tan fuera de la realidad. En el capítulo VII avanzo más allá de la regla de la mayoría para examinar la multitud de maneras como se ha manifestado la creatividad humana en la concepción de los métodos, en ocasiones extraños e intrincados, para que los grupos tomen alguna decisión.

Lo emocionante del modelo espacial para un especialista en ciencia política es la oportunidad que ofrece de captar muchos de los detalles interesantes de la competencia política —ya sea entre candidatos en unas elecciones o entre mociones alternativas en una asamblea legislativa— y, al mismo tiempo, hacerlo de una manera clara y simple. Sé que el lector no tiene que estar de acuerdo con esto último, puesto que este capítulo ha exigido toda su atención y una lectura cuidadosa. No obstante, durante los últimos treinta años, más o menos, los especialistas en ciencia política han encontrado que este modelo sirve como el elemento fundamental para el análisis de las rivalidades políticas de todo tipo.

Desde luego, un solo capítulo de un libro únicamente puede describir el modelo espacial en su forma más simple, pero aun la formulación más somera tiene consecuencias implícitas. En el contexto de la regla de la mayoría pura unidimensional con preferencias de pico único, por ejemplo, ya sea en la contienda electoral entre dos partidos o en la decisión legislativa sobre una política, la atracción magnética del punto ideal del participante mediano es poderosa. La política mayoritaria está sujeta a fuerzas centrípetas, lo que produce resultados que los observadores describen con términos como “concesión”, “moderado” o “centrista”. Así, en última instancia, el modelo espacial simple proporciona las razones o explicaciones del desplazamiento inexorable de la competencia bajo la regla de la mayoría hacia el centro de las preferencias de los participantes. Su valor sorpresa reside en el hecho de que su dinámica centrípeta no se debe a que “ahí es donde están los votos”. Como antes lo demostramos, el desplazamiento hacia el punto ideal del votante mediano es una tendencia de equilibrio en un arreglo de regla de la mayoría pura, aun cuando haya muy pocos votantes en el centro de las cosas.

En la esfera legislativa, donde las reglas de procedimiento y las comisiones encargadas del orden del día restringen el funcionamiento de la regla de la mayoría pura, hubo otras sorpresas. Al menos en el mundo de la política unidimensional, sólo es posible un número limitado de resultados. Un sistema de comisiones que funcione conforme a la regla de apertura puede producir sólo uno de dos resultados posibles. Al fungir como un cancerbero que “cierra las puertas” a cualquier moción de cambio, una comisión puede mantener la política pública en el statu quo. Por el contario, si la comisión hace una moción cualquiera, la secuencia de modificaciones permitidas conforme a la regla de apertura llevará el resultado al punto ideal del legislador mediano. Ésas son las únicas posibilidades. En un régimen con la regla de cierre, existen tres posibilidades: si se mantiene cerrado el orden del día (posiblemente porque la comisión y la legislatura están en desacuerdo y el statu quo se encuentra entre sus puntos ideales medianos respectivos), éste permanece intacto. Si el punto ideal mediano de la comisión se encuentra entre el statu quo y el punto ideal del legislador mediano, entonces se propondrá y aprobará el punto ideal de la comisión. Finalmente, si el punto ideal del legislador mediano se encuentra entre el statu quo y el punto ideal mediano de la comisión, entonces el resultado será el punto más cercano al punto ideal mediano de la comisión que deje indiferente al legislador mediano de toda la legislatura justo entre ese punto y el statu quo. Los detalles se encuentran en este capítulo. La sorpresa, no obstante, se encuentra en las conclusiones: primero, de que sólo un reducido número de cosas son posibles bajo diversos regímenes de procedimientos legislativos y, segundo, que ese reducido número de cosas difiere de un régimen a otro. Dicho de otra manera, los arreglos institucionales —los métodos políticos para las negociaciones— son profundamente importantes para los resultados que surgen del proceso político.

El modelo espacial también nos permite comenzar a reunir explicaciones acerca de las razones por las cuales la convergencia en el centro no siempre es completa. La tendencia centrípeta siempre está presente, eso es seguro, pero también puede haber tendencias compensatorias. En el contexto del modelo de elecciones de Downs, por ejemplo, señalamos que un político puede temer perder su apoyo de los extremos, a favor de la abstención o de un tercero que participe, si converge demasiado con su oponente. En el ámbito legislativo, los formuladores de la agenda más poderosos pueden impedir, a través del control de las mociones y modificaciones, que el proceso converja en la política ideal del legislador mediano, ya sea porque el encargado de la agenda puede proponer y hacer aprobar algo que le agrada más, ya sea porque decide mantener cerrado el orden del día.

Así, las grandes ventajas del modelo espacial son su simplicidad (relativa), su poder analítico y las “sorpresas” que produce. No sólo comenzamos a entender cosas que durante mucho tiempo hemos apreciado de una manera intuitiva (como la tendencia a la moderación en los sistemas de regla de la mayoría), sino, también, hemos desarrollado una comprensión compleja de cosas nuevas. Aunque, sin duda alguna, no es una herramienta explicativa perfecta, es un buen comienzo.

Uno de los asuntos que abordé de manera breve y aleatoria fue el pensamiento estratégico. En muchas de las aplicaciones de los modelos espaciales, en particular en los primeros tiempos de la elaboración de esos modelos, se supone que los votantes y legisladores son “honestos” en su comportamiento al votar: cuando se ven frente a dos alternativas, simplemente votan por su preferida, sin considerar las consecuencias. Sin embargo, existen muchas circunstancias en las que una persona racional pensará las cosas de principio a fin de una manera más compleja y en ocasiones llegará a la conclusión de que, en una oportunidad de voto en particular, no deberá votar por su alternativa preferida. A esa actitud la denomino comportamiento “sofisticado” o “estratégico” y es el tema del capítulo siguiente.

 

 

Rincón experimental

Decisiones grupales bajo la regla de la mayoría

 

Imagine a un grupo que debe tomar una decisión. Suponga, por ejemplo, que un grupo de cinco individuos debe elegir un punto en un plano bidimensional similar al de la gráfica V.8, donde cada individuo valora los puntos dentro del plano de manera diferente. La señora 1 prefiere los puntos que se encuentran en la región sudoeste del plano; el señor 3 prefiere los que están hacia el noreste; los demás prefieren puntos en otras partes del plano. En pocas palabras, existe un conflicto entre las preferencias de los distintos miembros de este grupo. Existen varias teorías acerca de las decisiones grupales que pretenden analizar y explicar situaciones como ésta. En un artículo clásico, Morris Fiorina y Charles Plott (1978) buscan evaluar dichas teorías mediante experimentos con grupos de personas reales. (Fiorina y Plott usaron sobre todo estudiantes universitarios, pero otros investigadores han experimentado con empleados de universidad, hombres y mujeres de negocios, habitantes de pueblos pequeños, etc.) En este “rincón experimental”, me concentraré en uno de sus experimentos. En realidad, ésta es una ligera variante que llevo a cabo con mis propios estudiantes.

Comencemos con un grupo con un número impar de miembros. Cada uno de ellos recibe de los experimentadores preferencias experimentales definidas. Para un grupo de cinco miembros, como el de la Gráfica V.8, el miembro 1 tiene su punto ideal o favorito en x₁, el miembro 2 lo tiene en x2, y así sucesivamente. Sus preferencias son euclidianas, lo cual significa que cada miembro prefiere que el resultado final esté en el punto más cercano a su punto ideal y no en uno que se encuentre más alejado. Por tanto, 3, por ejemplo, se mostrará indiferente entre todos los puntos que formen un círculo centrado sobre su punto ideal (porque todos están a la misma distancia de x₃) y preferirá cualquier punto que se encuentre en un círculo de menor radio a cualquiera en uno de mayor radio (porque el primero es más cercano a x₃ que el segundo). En el experimento, las dimensiones horizontales y verticales tienen un rango que va de cero a cien. Se fija un statu quo, x0, en las coordenadas (100, 100) en el extremo noreste del plano bidimensional. Los participantes reciben dinero dependiendo del resultado final —más dinero cuanto más se acerca el resultado a su punto ideal y menos dinero cuanto más se aleja—. Cada participante conoce sus propias preferencias y pagos, pero no los de los demás.

El procedimiento para tomar las decisiones es el siguiente. Un individuo es seleccionado de forma aleatoria por el experimentador para hacer una propuesta. Por ejemplo, si se elige a 1, ella podría decir “Propongo cambiar el statu quo de (100,100) a (25,50)”. Esta moción se somete a votación mayoritaria. Si la mayoría la aprueba, entonces (25,50) se convierte en el nuevo statu quo; si se rechaza la propuesta (los empates cuentan como rechazo), entonces (100, 100) permanece como statu quo. Se selecciona entonces a un nuevo individuo para que proponga una moción. Este proceso se repite de manera que toda persona elegida aleatoriamente proponga un cambio. En cualquier momento puede haber una moción para cerrar el debate: cualquier sujeto puede proponer que se termine la sesión. Esta moción se somete a votación de manera inmediata y, si es aprobada, el debate termina y se paga a todos el valor que corresponda a cada uno acorde al statu quo vigente. Si se rechaza la moción, se siguen aceptando propuestas hasta que nadie quiera someter una nueva moción. (Incluso si alguien aún quiere hacer alguna propuesta, la sesión debe terminar una vez que se alcanza un límite de tiempo.)

¿Qué es lo que sucede? Mi experiencia llevando a cabo este experimento por casi dos décadas en el salón de clases sugiere que la teoría espacial de la regla de la mayoría funciona bastante bien. Para ilustrar, regresemos a la gráfica V.8, donde preferencias semejantes a las que se muestran ahí satisfacen el teorema de Plott (preferencias basadas en distancia, un número impar de sujetos, puntos ideales distribuidos de manera radialmente simétrica). La teoría de la regla de la mayoría implica que el resultado final debería ser el punto ideal del individuo 2, porque x2 puede vencer a cualquier otro punto en una comparación sometida a la mayoría. Mientras exista alguien que proponga dicho punto, éste se convertirá en el nuevo statu quo y no podrá ser desbancado por cualquier propuesta subsecuente. En experimentos reales, las personas tantean en un inicio, en parte porque apenas se están familiarizando con el contexto y en parte porque aún no conocen las preferencias de los demás. Una vez que se familiarizan con la dinámica, las cosas se llevan a cabo con rapidez. Las personas buscan ser elegidas para hacer mociones; se hacen y aprueban propuestas que mueven el statu quo del punto en el extremo noreste hacia el “centro”. Cada propuesta, como predice la teoría, mueve el statu quo más cerca de x2, punto identificado por el teorema de Plott como el resultado final (el equilibrio del proceso de la regla de la mayoría). Lógicamente, siempre existe una mayoría que prefiere un punto más cercano a x2 sobre uno más lejano, por lo que las propuestas que muevan el statu quo más cerca de x2 deberían prevalecer mientras aquellas que lo mueven más lejos deberían ser rechazadas. Esto es lo que sucede típicamente en los experimentos que he llevado a cabo, aunque en ocasiones se comete algún error. Incluso si esto sucede, rápidamente se proponen mociones correctivas. Existen esfuerzos intermitentes de concluir la votación (sobre todo cuando el statu quo está cerca del punto ideal de algún individuo), pero por lo general una mayoría rechaza este tipo de mociones hasta que se alcanza x2. Una vez que se llega a x2, las mociones subsecuentes son rechazadas y, al final, los participantes se cansan de proponer más mociones y aprueban una moción para concluir la votación. Una sesión experimental típica termina rápidamente; rara vez se alcanza el límite de tiempo.

No obstante, si la distribución de puntos ideales no es semejante a la de la gráfica V.8 y viola la simetría radial, la regla de la mayoría no conduce a un equilibrio como x2. El teorema de McKelvey entra en vigor. ¿Qué pasa en estas condiciones experimentales? Mi experiencia al llevar a cabo el experimento en este contexto indica que el teorema de McKelvey captura la situación adecuadamente. Las mayorías aprueban propuestas que alteran el statu quo pero nunca se llega a un punto específico. Con más frecuencia que en la situación anterior, el límite de tiempo determina cuándo se termina la sesión. El resultado final se encuentra en algún lugar intermedio en la distribución de preferencias, pero no se centra en un punto específico como cuando se cumplían las condiciones de Plott. No se trata exactamente de un “caos”, pero los resultados no muestran la misma regularidad que cuando las preferencias están distribuidas de manera radialmente simétrica.

Como ejercicio final, he añadido una pequeña innovación al diseño experimental de Fiorina y Plott. En algunas sesiones hago del conocimiento de cada participante no sólo su propio punto ideal, sino también el de los demás. ¿Se observa alguna diferencia? La teoría sugiere que no debería ser el caso —existe ya sea un punto de equilibrio de Plott o las variaciones que implica el teorema de McKelvey—. La información adicional no altera estos hechos. Experimentalmente, los resultados son más o menos los mismos que en el contexto de información limitada. Aunque el bullicio entre los estudiantes durante los experimentos deja entrever cierta envidia y competitividad cuando el statu quo aprobado parece beneficiar al compañero de la banca de a lado.

Al menos en esta situación controlada de manera muy cuidadosa, la regla de la mayoría, con sólo las características institucionales más elementales, funciona básicamente en la manera en que los teoremas de Plott y McKelvey sugieren. Ciertamente, contra un gran número de competidores teóricos, Plott y Fiorina concluyen que esta teoría de la regla de la mayoría es superior.

 

 

Problemas y preguntas de discusión

 

1. Considere una sociedad que consta de tres individuos, 1, 2 y 3, que deben elegir entre tres proyectos de presupuesto, x, y y z. Sus preferencias en relación con estos tres proyectos son las siguientes: xP1 y P1z, y P2zP2x y zP3 x P3y.

 

a)  Escriba la relación de preferencias mayoritarias para estas preferencias (por ejemplo, indique cuál alternativa vencería a cuál cuando dos de ellas compiten).

b)  ¿Permite el teorema del votante mediano de Black predecir qué alternativa será elegida si el grupo utiliza la regla de la mayoría? ¿Por qué sí o por qué no?

c)  Suponga que el grupo votará de acuerdo con la agenda v = (y, x, z) para elegir el proyecto de presupuesto, lo que quiere decir que el grupo elegirá primero entre y y x; después entre la alternativa que resulte ganadora y z; la alternativa que gane en la segunda votación será el proyecto elegido. Si cada individuo vota de manera sincera en cada etapa de la agenda, ¿cuál será el resultado? ¿Cuál sería el resultado si v’ = (z, x, y) o v’’ = (z, y, x)?

 

2. En la comisión financiera del Senado estadounidense, al debatir un proyecto de reforma en materia de salud, existen algunos miembros que exigen un esquema de seguridad social financiado enteramente por el gobierno (“la opción pública”), otros que se oponen de manera radical a dicha estrategia y un tercer grupo que favorece un punto intermedio con una “cooperativa de servicios de salud”, una especie de organización sin fines de lucro afiliada al gobierno. Tanto los que están a favor de la opción completamente pública como los que se oponen a ella están de acuerdo en que la cooperativa es el segundo mejor resultado. ¿Qué puede usted decir acerca de las preferencias de este grupo? ¿Podría predecir el resultado de una votación si supiera cuántos miembros tiene cada uno de los tres perfiles de preferencias?

Algunos de los miembros más liberales de la comisión empiezan a sufrir una fuerte presión política por parte de grupos de interés que favorecen la opción pública, y éstos los convencen de que sería mejor votar en contra de la cooperativa, y esperar hasta un momento más propicio, si no se pudiera lograr elegir la opción enteramente financiada por el gobierno. ¿Qué puede usted decir acerca de este nuevo conjunto de preferencias? ¿Podría siempre predecir el resultado de una votación si supiera cuántos miembros tiene cada perfil de preferencias?

 

3. Un ejemplo famoso de preferencias que violan la condición de pico único se presentó en el artículo “La opinión pública y la guerra en Vietnam”, de Verba et al. (1967). El estudio encontró que la mayoría de las personas identificaba una política específica como su punto ideal en un espacio unidimensional que iba desde la reducción o el cese de la intervención estadounidense en un extremo; a la continuación de la intervención estadounidense en el centro; a la expansión de la intervención estadounidense en el otro extremo. Además, la mayor parte de las personas consideró que las políticas públicas eran menos deseables conforme más se alejaban de su punto ideal. No obstante, una pequeña parte de la población favorecía ya fuera una retirada de Estados Unidos o una expansión de la intervención en lugar de la política oficial vigente. ¿Qué propiedad de un perfil de preferencias sociales no se respeta en este ejemplo? ¿Qué tan generalizada debe ser la ausencia de preferencias de pico único para que se viole la transitividad grupal? Ilustre esta cuestión gráficamente y, después, explique si las preferencias acerca de la política estadounidense en la guerra de Vietnam se representarían mejor utilizando dos o más dimensiones de política pública. ¿Qué podría incluirse en dichas dimensiones?

 

4. En una corporación, se encarga a un comité de gobernanza de siete miembros la asignación de fondos para los bonos de fin de año, y se designa a un subcomité especial para que investigue y después proponga al comité completo un valor total para cada bono. Las reglas de la corporación establecen que el subcomité puede traer propuestas ante el comité completo bajo un procedimiento de enmienda preestablecido (ya sea una regla de apertura o de cierre). Todas las decisiones en el comité y en el subcomité se llevan a cabo utilizando la regla de la mayoría; el mínimo que el comité puede asignar a un bono es $0 y el máximo es $12 000. Las preferencias de cada miembro del comité en relación con los diferentes montos que pueden asignarse son de pico único y simétricas en torno al punto ideal de cada miembro. El orden es el siguiente: Bobby y Emma: 0; Amy: 1 500; Cathy: 6 000; Frank: 7 500; Geri: 10 000; David: 12 000.

Responda las siguientes preguntas utilizando ilustraciones gráficas cuando sea útil.

 

a)  El subcomité está compuesto por Frank, Geri y David. ¿Cuál es el monto favorito del subcomité?

b)  El año pasado, el comité asignó $3 000 para los bonos y, bajo las reglas del comité, éste es el nivel de financiamiento del statu quo (se decidirá este año, también, si el comité completo no hace cambios). Asumiendo que el subcomité tiene una propuesta para el comité bajo la regla de cierre, ¿cuál es la propuesta del subcomité y cuál será el resultado? ¿Por qué?

c)  Asuma ahora que el subcomité hace su propuesta al comité bajo la regla de apertura. ¿Va el subcomité a “abrir la reja” llevando su propuesta al pleno? En caso afirmativo, ¿cuál será dicha propuesta? ¿Cuál será el resultado? Explique por qué.

d)  Suponga que el comité de gobernanza sigue el “presupuesto base cero”, en el que las asignaciones de cada año se fijan inicialmente en cero y el comité procede a votar las nuevas propuestas que haga el subcomité. En este caso, ¿cuál será el resultado si se vota bajo una regla de cierre? ¿Y si se hace bajo una regla de apertura? Comente las implicaciones del “presupuesto base cero”.

 

5. Una legislatura va a votar en torno a una política que puede representarse en un espacio de una sola dimensión, en una escala del cero al uno. Una comisión, cuyo punto ideal para este ejercicio puede ser cualquier punto en el eje x, presentará la propuesta de política inicial ante una legislatura con un punto ideal mediano M. El statu quo está actualmente en el punto SQ. Dibuje una línea que muestre el equilibrio para cualquier punto ideal de la comisión en caso de que la propuesta de la comisión se considere bajo una regla de cierre. En ejes diferentes, lleve a cabo el mismo ejercicio para el caso en que la propuesta se considere bajo una regla de apertura. Posteriormente, resuelva el mismo ejercicio para ambos tipos de regla (utilizando una línea punteada en los dos ejes ya creados). Asuma que la legislatura opera sobre el principio de “presupuesto base cero”, de manera que si no se aprueba una ley en esta sesión, la política se revertirá a BC = 0.

¿Cuál es el impacto del “presupuesto base cero” bajo una regla de cierre? En promedio, ¿están los equilibrios más lejos o más cerca de la mediana de la legislatura? ¿Qué sucede con la regla de apertura?

gráfica V.18

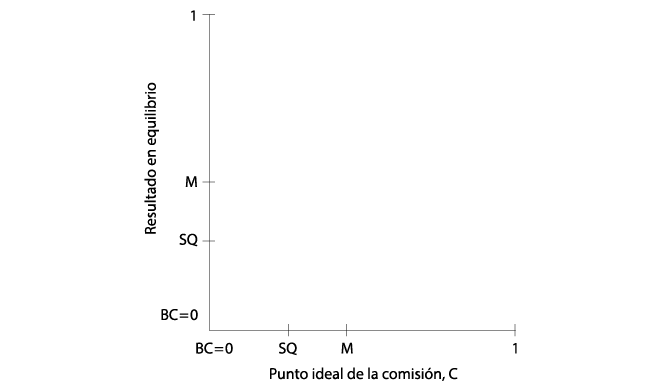
6. Una legislatura con tres grupos, similar a la que se muestra en la gráfica V.7, está intentando llegar a un acuerdo en un asunto que tiene dos dimensiones políticas. La legislatura utiliza la regla de la mayoría, y los bordes de indiferencia son circulares. Suponga que los grupos 2 y 3 llegan a un acuerdo donde 3 obtiene su política ideal en la dimensión horizontal y el resultado en la dimensión vertical está a un tercio de la distancia moviéndose del punto ideal de 2 hacia el de 3. Dibuje los conjuntos “preferidos a” para 2 y 3, y muestre que existen otros posibles acuerdos entre 2 y 3 que serían más favorables para ambos. Considere el conjunto de acuerdos que 2 y 3 podrían lograr y no pueden cambiarse sin perjudicar a uno u otro grupo. ¿Cómo se ve este conjunto? Dicho conjunto es conocido como la “curva de acuerdos” para los grupos 2 y 3. Dibuje la curva de acuerdos para todas las otras coaliciones mayoritarias posibles. ¿Es alguno de los puntos en estas curvas de acuerdos un punto con un conjunto ganador vacío bajo la regla de la mayoría?

Ahora suponga que la legislatura opera bajo la regla de unanimidad. Si el statu quo se encuentra en el punto de acuerdo entre 2 y 3 descrito anteriormente, ¿sería posible para los tres grupos encontrar una propuesta más benéfica para todos? ¿Qué sucede si el statu quo se encuentra, más bien, en el punto ideal de 2 en la dimensión horizontal y a la mitad de la distancia entre los puntos ideales de 2 y 3 en la dimensión vertical? ¿Qué propuestas tienen conjuntos ganadores vacíos cuando se utiliza la regla de unanimidad? ¿Contradice la existencia de dichos conjuntos el teorema del caos de McKelvey?

 

7. Asuma que un cuerpo de votantes tiene cinco miembros: A, B, C, D y E. Cada uno tiene puntos ideales en un espacio de dos dimensiones dados por A: (1,4), B: (4,4), C: (2,2), D: (1,1) y E: (2,1), donde la primera coordenada indica la política ideal de cada individuo en la dimensión X y la segunda indica la política ideal de cada individuo en la dimensión Y. Asuma, además, que cada miembro prefiere un resultado cercano a su punto ideal por sobre uno que se encuentra más alejado. Siempre se vota por pares de plataformas X-Y, de manera que todas las propuestas se hacen en forma de pares ordenados (x, y). ¿Existe un equilibrio si el cuerpo utiliza la regla de la mayoría?

Suponga ahora que se designa al jugador B como el único formulador de la agenda. Si el statu quo se encuentra en el punto ideal de C, ¿es posible para B construir una agenda que conduzca eventualmente a su propio punto ideal bajo la aprobación del cuerpo legislativo entero? En caso de que sí, construya dicha agenda (puede asumir que todos votan de manera sincera y que el formulador de la agenda puede siempre persuadir a los legisladores que muestran indiferencia entre dos pares ordenados para que voten por el que él prefiere). ¿Qué teorema ilustra esta situación?

 

8. Es posible que el aforismo político más famoso pertenezca a Otto von Bismarck: “La política es el arte de lo posible”. Haga un comentario al respecto, haciendo referencia al teorema del votante mediano de Black, el teorema del caos de McKelvey y la discusión de reglas legislativas (especialmente el caso V.2).

 

9. Esta pregunta requiere que considere la relación entre el teorema de Arrow y el teorema del caos de McKelvey. ¿Acaso las intransitividades grupales que motivaron las ideas de Arrow ocurren en los contextos multidimensionales y con la regla de la mayoría que asume McKelvey? ¿Está vinculado el mensaje de McKelvey de que “cualquier cosa puede suceder” con cualquiera de las lecciones del teorema de Arrow? ¿Tener control sobre el orden del día otorga la habilidad de determinar el resultado en el mundo de Arrow? ¿Sucede esto en todos los casos? Desarrolle algunos breves ejemplos con tres personas y tres resultados para mostrar que los resultados perversos del modelo espacial multidimensional pueden ocurrir, aunque no siempre, en el mundo discreto de Arrow.

 

10. Anthony Downs utilizó la lógica de toma de decisiones en una dimensión articulada por primera vez por Duncan Black para entender la política en la “comisión” más grande que se puede imaginar: el electorado. Señaló que si sólo existieran dos partidos, y si los políticos con puntos de vista extremistas tuvieran pocos incentivos para formar partidos propios, entonces las promesas y plataformas electorales de los dos partidos serían muy similares.

 

a)  ¿Por qué sucede esto? ¿Cómo se sigue dicha conclusión del teorema del votante mediano de Black?

a)  Downs asume que los políticos sólo están interesados en ganar puestos electorales. Si los políticos tienen preferencias de política pública propias, ¿existe un resultado diferente (i. e. algo que no sea convergencia)? ¿Bajo qué circunstancias sucede esto?

a)  ¿Qué otros supuestos de Downs acerca del número de candidatos, el comportamiento electoral o las dimensiones del espacio podrían explicar las aparentes diferencias entre las plataformas partidarias en Estados Unidos y otros lugares?

 

1 Recuérdese que “i ∈ G” significa “el elemento i del conjunto G”, donde i representa a cualquiera de los cinco directores del banco.

 

2 Incluiremos el punto final de este conjunto en el conjunto de tasas preferidas a y, aun cuando, técnicamente hablando, el punto final es una alternativa que el miembro del grupo clasifica en el mismo nivel de utilidad que y.

 

3 En la notación matemática de conjuntos, podemos representar esos puntos comunes como la intersección de los dos conjuntos preferidos a y: P4(y) ∩ P5(y). (El símbolo ∩ es el de la “intersección”, por lo que A ∩ B significa “los puntos que pertenecen tanto al conjunto A como al conjunto B”).

 

4 En la gráfica V.3, resulta que los miembros de sólo una de las dieciséis mayorías, {3, 4, 5}, tienen conjuntos P_i(y) coincidentes. Los miembros de las restantes quince mayorías (listadas en el cuadro V.1) no estan de acuerdo en ningún punto que prefieran conjuntamente a y. En consecuencia, V(y) = P3(y) ∩ P4(y) ∩ P5(y).

 

5 La mediana de un conjunto ordenado de izquierda a derecha es un punto tal que al menos la mitad de los puntos está a su derecha y al menos la mitad de los puntos está a su izquierda.

 

6 Por ejemplo, la Constitución de Estados Unidos exige que el Senado tenga un número par de miembros, pero establece un procedimiento para romper empates. El vicepresidente de Estados Unidos, quien actúa como presidente del Senado, puede votar sólo en caso de empate. De manera similar, las reglas permanentes de la Cámara de Representantes prevén una regla para romper los empates que estipula que una moción se rechaza si no logra obtener más votos a favor que en contra, es decir, pierde en caso de empate.

 

7 Por lo general, cuando se divide una cantidad fija entre n categorías (o personas), sólo se necesitan n – 1 dimensiones para desplegar los resultados.

 

8 Si el monto del presupuesto se fijara por adelantado, entonces, dados el argumento del párrafo anterior y la nota, sólo necesitaríamos una dimensión, digamos, dinero para la defensa. Una vez establecido esto, el dinero para los otros programas nacionales queda estrictamente determinado: es lo que resta. Cuando el presupuesto no ha sido determinado por adelantado, entonces necesitamos ambas dimensiones para desplegar todos los resultados.

 

9 Éste es el más simple de los marcos multidimensionales, en el que el espacio de políticas públicas es bidimensional y las preferencias se miden mediante la distancia. Ahí las curvas de indiferencia serán círculos centrados en el punto ideal del legislador. En un marco con más de dos dimensiones, las “curvas” de la indiferencia serán esferas; o con cuatro o más dimensiones serán hiperesferas. Una segunda clase de complejidad, que aplica tanto en la situación bidimensional (la más simple) como en las situaciones de más dimensiones, consiste en permitir que las preferencias se relacionen con la distancia, pero de una manera más compleja. Una dimensión de la política puede ser “más importante” para un legislador que otra. Así, el movimiento que lo aleje de su punto ideal a lo largo de una dimensión tendrá un efecto más marcado en sus preferencias que un movimiento idéntico a lo largo de la otra dimensión. Dicho de otra manera, en este ejemplo, las preferencias descienden con la distancia ponderada a partir del punto ideal (donde las ponderaciones reflejan el peso de cada dimensión para el legislador). En ese ejemplo, las curvas de la indiferencia ya no serían círculos, sino elipses. Dichas complejidades son interesantes, pero aquí me apegaré a la formulación más básica.

 

10 Cuando decimos que un resultado “generaliza” otro, queremos decir que este último es un caso especial del primero. Así, el resultado de Black del votante mediano es la versión unidimensional del teorema de Plott, en la que el punto ideal del votante mediano es el punto sobresaliente y los pares de puntos ideales de los votantes, uno a cada lado de la mediana, están distribuidos en torno a él en simetría radial.

 

11 La sensibilidad es un poco menos severa cuando el número de votantes es par. En ese caso, el punto sobresaliente no es el punto ideal de un votante. Es posible tener algunos desplazamientos de los puntos ideales de los votantes sin que ello perturbe el hecho de que el conjunto que vence al punto sobresaliente sea vacío.

 

12 Debemos señalar que los miembros de cada coalición de mayoría de este ejemplo votan a ciegas por sus preferencias, como corderos que siguen el cencerro al matadero. Los legisladores parecen suave arcilla en manos del astuto formulador de la agenda, el legislador 3. En el siguiente capítulo dotaremos a los “seguidores” de cierta complejidad mediante la cual podrán controlar a su “líder”.

 

13 En muchas ciudades es aún más sorprendente el que se establezcan decenas de distribuidoras de automóviles a lo largo de un corto trecho de una vía pública importante (en Boston, por ejemplo, hay más de treinta competidores en la llamada Automile).

 

14 Para quienes son demasiado jóvenes para recordarlo, Vincent Lombardi fue el legendario entrenador de fútbol americano de los Empacadores de Green Bay y, al final de su carrera, de los Pieles Rojas de Washington. Para Lombardi, nada era más importante que ganar. Aunque no es precisamente un imperativo que eleve el espíritu, la máxima de Lombardi es una muy buena definición inicial de lo que se requiere para lograr el éxito en la política nacional de la mayoría de los países, el mundo de los negocios y la Liga Nacional de Fútbol Americano.

 

15 Dadas dos posiciones de los candidatos, digamos α y β en [1, 100], donde α está a la izquierda de β, el punto medio es (α + β)/2. El candidato situado en α recibe los votos de todos los votantes con puntos ideales a la izquierda de ese punto medio, mientras que el candidato situado en β obtiene los votos de todos los votantes con puntos ideales a la derecha del punto medio. Los votantes cuyo punto ideal coincide con el punto medio son indiferentes entre los dos candidatos, puesto que las posiciones de éstos se encuentran a la misma distancia de su punto ideal. Estos últimos lanzan una moneda al aire para decidir por quién votar.

 

16 Si ocurriera que I estuviese a la derecha del punto mediano de la distribución de votantes, entonces D mejoraría sus votos apretándose contra I por su lado izquierdo, con lo que obtendría la mayoría de los votos.

 

17 En realidad, una posición es vulnerable si la posición del oponente está más cerca de la mediana. La posición más cercana a la mediana gana más de la mitad de los votos.

 

18 Desde luego, si los políticos están muy bien informados respecto a las preferencias de los votantes, no necesitan proceder de manera tentativa hacia la mediana saltando o con acercamientos. En lugar de ello, pueden desplazarse directamente hasta ella.

 

19 Obsérvese que la razón fundamental no es que la mediana esté “donde están los votantes”. Sin duda alguna, ello puede ser cierto: en muchas circunstancias, la mediana del espectro está donde se encuentran las preferencias de la mayoría de las personas y los números se hacen cada vez más pequeños a medida que uno se desplaza hacia los puntos más extremos de la distribución. Pero volvamos a la gráfica V.11 y supongamos que los extremos son los más abundantes, esto es, supongamos que los tipos 1 y 5 tienen 250 votantes cada uno, los tipos 2 y 4 tienen 62 votantes cada uno y el tipo 3 está constituido por un solo votante. ¿Sería diferente en este caso la lógica de Downs que hemos descrito antes? Creemos que no. La fuerza centrípeta es la misma, aun cuando el “centro” sea ¡el menos poblado de votantes!

 

20 Tal vez podría interesar al lector saber que el libro de Downs tuvo su origen como tesis de doctorado en economía en la Universidad de Stanford, donde uno de los miembros del jurado dictaminador fue Kenneth Arrow. Noten que la teoría de Downs tenía, por un lado, ciclos e inestabilidad al estilo del teorema de Arrow y, por el otro, su opuesto: configuraciones partidistas estables. Su investigación buscó dar sentido a esas cuestiones aparentemente incompatibles y lo logró gracias a la cualidad del pico único.

 

21 El lector interesado en el tema puede consultar un resumen de la mayoría de esas investigaciones en Shepsle (1991).

 

22 El lector interesado puede encontrar un resumen de la extensa bibliografía al respecto en los dos volúmenes siguientes: Enelow y Hinich (1984); Enelow y Hinich (1990). Una reseña más reciente es “Economic Models of Elections”, escrita por Dewan y Shepsle (2011).

 

23 En 1968, Wallace participó del lado derecho porque, dijo, “no existe absolutamente ninguna diferencia” entre el demócrata Hubert Humphrey y el republicano Richard Nixon.

 

24 Tanto Anderson como Perot buscaron captar el centro, el cual creían había sido abandonado por Carter y Reagan en 1980 y por Clinton y Bush en 1992, respectivamente.

 

25 Esto puede demostrarse de la siguiente manera: suponga que x_m, x e y son todos puntos de la dimensión y que x_m ≤ x ≤ y. El legislador m claramente prefiere x a y. Pero entonces también lo hace cada uno de los legisladores a la izquierda de m. Juntos, esos legisladores constituyen una mayoría, por lo que una mayoría prefiere x a y. De forma similar, por las mismas razones, si y ≤ x ≤ x_m, entonces tanto m como una mayoría (todos los legisladores a la derecha de m) prefieren x a y. En consecuencia, hemos demostrado que, siempre que x e y estén del mismo lado de la mediana, una mayoría estará de acuerdo con las preferencias del votante mediano. Supóngase, entonces, que x ≤ x_m ≤ y y que m prefiere x a y. Piénsese en la legisladora justo a la izquierda de m; su punto ideal se encuentra más cerca de x y más lejos de y que lo que estaba el punto ideal de m. Por lo tanto, si m prefiere x a y, con toda seguridad ella también lo hará. Pero entonces, también lo harán todos los otros votantes a la izquierda del punto ideal de m y, una vez más, todos juntos constituyen una mayoría. Esto establece que una mayoría siempre está de acuerdo con las preferencias del votante mediano.

 

26 En algunas circunstancias, la política correspondiente del statu quo no se mantiene en su lugar, a menos que la legislatura emprenda una acción positiva para mantenerla. Si la legislatura no logra hacer nada, entonces el statu quo regresa a alguna política específica (conocida, de manera bastante natural, como el punto de restablecimiento). Lo anterior es cierto, por ejemplo, en los reglamentos que poseen disposiciones de vigencia limitada, ejemplo que exploramos más adelante, en el caso V.1.

 

27 Una variación de esta “regla de terminación” es permitir que en cualquier momento pueda hacerse una moción para cerrar el pleno a nuevas mociones (en otras palabras, una moción para hacer una votación final y después levantar la asamblea, al menos en lo que respecta al asunto que se esté tratando). 

 

28 Por “facultad de custodio de la agenda” traduzco lo que en inglés se denomina gatekeeping agenda power [Nota del traductor].

 

29 Como supusimos que las preferencias de los legisladores se basan en la distancia, sabemos que el legislador m prefiere a x0 todos los puntos que se encuentren más cerca de x_m que x0, lo cual determina el conjunto P_m(x0) mostrado en la gráfica V.14.

 

30 Como en este caso trabajamos con el modelo unidimensional, únicamente nos interesa el ideal mediano de una sola comisión. En los contextos multidimensionales, donde hay muchas jurisdicciones en las que se arreglan las dimensiones del espacio de la agenda política, necesitaríamos conocer las preferencias políticas de las diferentes comisiones, cada una responsable de su paquete de cuestiones políticas. En la cuarta parte desarrollaremos más este tema.

 

31 La definición clásica de este resultado, además de la explicación de algunas de sus consecuencias políticas, se encuentra en Romer y Rosenthal (1978).

 

32 El lector puede tratar de ver qué ocurre a medida que x0 se modifica en los casos 2 y 3.

 

33 Un procedimiento alternativo consistiría en permitir una enmienda a una moción, después de que la comisión la ha presentado, y votarla directamente. La moción vencedora permanecería abierta al pleno de la asamblea y estaría sujeta a otra enmienda. El proceso continuaría hasta que ya no hubiera más enmiendas posibles, después de lo cual se llevaría a cabo una votación final entre la alternativa que hubiera resultado victoriosa y el statu quo.

 

34 En particular, estamos suponiendo que todos votan por sus preferencias sinceramente, en vez de votar estratégicamente (un supuesto que explicaré y relajaré en el capítulo siguiente).

 

* En realidad, una mayoría legislativa es indiferente entre x0 y x*. Supongo que un votante indiferente vota por la moción propuesta al pleno de la asamblea (alternativamente, la comisión podría proponer un punto justo a la izquierda de x*, lo que garantizaría una mayoría absoluta).

 

** La comisión podría desplazar una propuesta hacia algún punto a la derecha de x0, pero sería derrotada, por lo que bien podría mejor no molestarse y mantener cerrado el orden del día, en particular si la molestia tuviese algún costo. Por otra parte, si algún grupo de presión externo se sintiere alentado por el hecho de que la comisión diese al menos una buena pelea y recompensara en consecuencia a la comisión, entonces esta última podría desear “molestarse” (aunque el resultado permanecería sin cambios: x0 se mantendría en su lugar).

 

* En el mundo anglosajón se conoce a estas disposiciones como sunset provisions, literalmente, “disposiciones crepusculares”. Dicha metáfora sugiere que “se pondrá el sol” sobre la disposición si los legisladores no la renuevan [Nota del traductor].

 

* En inglés al “cabildero” se le conoce como lobbyist [Nota del traductor].

 

** Véase Mansbridge (1986).

 

*** Véase Anderson y Einstein (1993).