
Can cryptography be the basis for a new financial system? This is what cryptocurrencies have been trying to answer since at least 2008, when Bitcoin was proposed by Satoshi Nakamoto (who to this day has yet to reveal his or their identity). Before that, the term crypto was always used in reference to the field of cryptography. But since the creation of Bitcoin, I have seen its meaning quickly change, now being used to refer to cryptocurrencies as well. Cryptocurrency enthusiasts, in turn, have become more and more interested in learning about cryptography. This makes sense as cryptography is at the core of cryptocurrencies.
What’s a cryptocurrency? It is two things:
It’s a digital currency. Simply put, it allows people to transact currency electronically. Sometimes a currency backed by a government is used (like the US dollar), and sometimes a made-up currency is used (like the bitcoin). You likely already use digital currencies—whenever you send money to someone on the internet or use a checking account, you are using a digital currency! Indeed, you don’t need to send cash by mail anymore, and most money transactions today are just updates of rows in databases.
It’s a currency that relies heavily on cryptography to avoid using a trusted third party and to provide transparency. In a cryptocurrency, there is no central authority that one has to blindly trust, like a government or a bank. We often talk about this property as decentralization (as in “we are decentralizing trust”). Thus, as you will see in this chapter, cryptocurrencies are designed to tolerate a certain number of malicious actors, and to allow people to verify that they function properly.
Cryptocurrencies are relatively new as the first experiment to be successful was Bitcoin, proposed in 2008 in the middle of a global financial crisis. While the crisis started in the US, it quickly spread to the rest of the world, eroding the trust people had in financial systems and providing a platform for more transparent initiatives like Bitcoin. At that time, many people started to realize that the status quo for financial transactions was inefficient, expensive to maintain, and opaque to most people. The rest is history, and I believe this book is the first book on cryptography to include a chapter on cryptocurrencies.
Imagine that you want to create a new digital currency. It’s actually not too involved to build something that works. You could set up a database on a dedicated server, which would be used to track users and their balances. With this, you provide an interface for people to query their balance or let them send payments, which would reduce their balance in the database and increase the balance in another row. Initially, you could also randomly attribute some of your made-up currency to your friends so that they can start transferring money to your system. But such a simple system has a number of flaws.
The system we just saw is a single point of failure. If you lose electricity, your users won’t be able to use the system. Worse, if some natural disaster unexpectedly destroys your server, everybody might permanently lose their balance. To tackle this issue, there exist well-known techniques that you can use to provide more resilience to your system. The field of distributed systems studies such techniques.
In this case, the usual solution used by most large applications is to replicate the content of your database in (somewhat) real time to other backup servers. These servers can then be distributed across various geographical locations, ready to be used as backup or even to take over if your main server goes down. This is called high availability. You now have a distributed database.
For large systems that serve lots of queries, it is often the case that these backup databases are not just sitting on the sideline waiting to be useful, but instead, they are used to provide reads to the state. It is difficult to have more than one database accept writes and updates because then you could have conflicts (the same way two people editing the same document can be dangerous). Thus, you often want a single database to act as leader and order all writes and updates to the database, while others can be used to read the state.
Replication of database content can be slow, and it is expected that some of your databases will lag behind the leader until they catch up. This is especially true if they are situated further away in the world or are experiencing network delays due to some reason. This lag becomes a problem when the replicated databases are used to read the state. (Imagine that you see a different account balance than your friend because you are both querying different servers.)
In these cases, applications are often written in order to tolerate this lag. This is referred to as eventual consistency because eventually the states of the databases become consistent. (Stronger consistency models exist, but they are usually slow and impractical.) Such systems also have other problems: if the main database crashes, which one gets to become the main database? Another problem is if the backup databases were lagging behind when the main database crashed, will we lose some of the latest changes?
This is where stronger algorithms—consensus algorithms (also referred to as log replication, state machine replication, or atomic broadcasts)—come into play when you need the whole system to agree (or come to a consensus) on some decision. Imagine that a consensus algorithm solves the solution of a group of people trying to agree on what pizza to order. It’s easy to see what the majority wants if everyone is in the same room. But if everyone is communicating through the network where messages can be delayed, dropped, intercepted, and modified, then a more complicated protocol is required.

Let’s see how consensus can be used to answer the previous two questions. The first question of which database gets to take over in the case of a crash is called leader election, and a consensus algorithm is often used to determine which will become the next leader. The second question is often solved by viewing database changes in two different steps: pending and committed. Changes to the database state are always pending at first and can only be set as committed if enough of the databases agree to commit it (this is where a consensus protocol can be used as well). Once committed, the update to the state cannot be lost easily as most of the database participanting have committed the change.
Some well-known consensus algorithms include Paxos (published by Lamport in 1989) and its subsequent simplification, Raft, (published by Ongaro and Ousterhout in 2013). You can use these algorithms in most distributed database systems to solve different problems. (For a great interactive explanation on Raft, check out https://thesecretlivesofdata.com/raft.)
Distributed systems (from an operational perspective) provide a resilient alternative to systems that act as a single point of failure. The consensus algorithms used by most distributed database systems do not tolerate faults well. As soon as machines start crashing, or start misbehaving due to hardware faults, or start getting disconnected from some of the other machines like network partitions, problems arise. Moreover, there’s no way to detect this from a user perspective, which is even more of an issue if servers become compromised.
If I query a server and it tells me that Alice has 5 billion dollars in her account, I just have to trust it. If the server includes in its response all the money transfers that she has received and sent since the beginning of time and sums it all up, I could verify that indeed it results with the 5 billion dollars she has in her account is correct. But what tells me the server didn’t lie to me? Perhaps when Bob asks a different server, it returns a completely different balance and/or history for Alice’s account. We call this a fork (two contradicting states presented as valid), a branch in history that should never have happened. And, thus, you can imagine that the compromise of one of the replicated databases can lead to pretty devastating consequences.
In chapter 9, I mentioned certificate transparency, a gossip protocol that aims at detecting such forks in the web public key infrastructure (PKI). The problem with money is that detection alone is not enough. You want to prevent forks from happening in the first place! In 1982, Lamport, the author of the Paxos consensus algorithm, introduced the idea of Byzantine fault-tolerant (BFT) consensus algorithms.
We imagine that several divisions of the Byzantine army are camped outside an enemy city, each division commanded by its own general. The generals can communicate with one another only by messenger. After observing the enemy, they must decide upon a common plan of action. However, some of the generals may be traitors, trying to prevent the loyal generals from reaching agreement.
—Lamport et al. (“The Byzantine Generals Problem,” 1982)
With his Byzantine analogy, Lamport started the field of BFT consensus algorithms, aiming at preventing bad consensus participants from creating different conflicting views of a system when agreeing on a decision. These BFT consensus algorithms highly resemble previous consensus algorithms like Paxos and Raft, except that the replicated databases (the participants of the protocol) do not blindly trust one another anymore. BFT protocols usually make heavy use of cryptography to authenticate messages and decisions, which in turn, can be used by others to cryptographically validate the decisions output by the consensus protocol.
These BFT consensus protocols are, thus, solutions to both our resilience and trust issues. The different replicated databases can run these BFT algorithms to agree on new system states (for example, user balances), while policing each other by verifying that the state transitions (transactions between users) are valid and have been agreed on by most of the participants. We say that the trust is now decentralized.
The first real-world BFT consensus algorithm invented was Practical BFT (PBFT), published in 1999. PBFT is a leader-based algorithm similar to Paxos and Raft, where one leader is in charge of making proposals while the rest attempt to agree on the proposals. Unfortunately, PBFT is quite complex, slow, and doesn’t scale well past a dozen participants. Today, most modern cryptocurrencies use more efficient variants of PBFT. For example, Diem, the cryptocurrency introduced by Facebook in 2019, is based on HotStuff, a PBFT-inspired protocol.
One limitation of these PBFT-based consensus algorithms is that they all require a known and fixed set of participants. More problematic, past a certain number of participants, they start breaking apart: communication complexity increases drastically, they become extremely slow, electing a leader becomes complicated, etc.
How does a cryptocurrency decide who the consensus participants are? There are several ways, but the two most common ways are
Proof of authority (PoA)—The consensus participants are decided in advance.
Proof of stake (PoS)—The consensus participants are picked dynamically, based on which has the most at stake (and, thus, is less incentivized to attack the protocol). In general, cryptocurrencies based on PoS elect participants based on the amount of digital currency they hold.
Having said that, not all consensus protocols are classical BFT consensus protocols. Bitcoin, for example, took a different approach when it proposed a consensus mechanism that had no known list of participants. This was quite a novel idea at the time, and Bitcoin achieved this by relaxing the constraints of classical BFT consensus protocols. As you will see later in this chapter, because of this approach, Bitcoin can fork, and this introduces its own sets of challenges.
Without participants, how do you even pick a leader? You could use a PoS system (for example, the Ouroboros consensus protocol does this). Instead, Bitcoin’s consensus relied on a probabilistic mechanism called proof of work (PoW). In Bitcoin, this translates to people attempting to find solutions to puzzles in order to become a participant and a leader. The puzzle is a cryptographic one as you will see later in this chapter.
Due to a lack of known participants, Bitcoin is called a permissionless network. In a permissionless network, you do not need extra permissions to participate in consensus; anyone can participate. This is in contrast to permissioned networks that have a fixed set of participants. I summarize some of these new concepts in figure 12.1.

Figure 12.1 A centralized network can be seen as a single point of failure, whereas a distributed and decentralized network are resilient to a number of servers shutting down or acting maliciously. A permissioned network has a known and fixed set of main actors, while in a permissionless network, anyone can participate.
Until recently, it was not known how to use classical BFT consensus protocols with a permissionless network, where anyone is allowed to join. Today, there exist many approaches using PoS to dynamically pick a smaller subset of the participants as consensus participants. One of the most notable ones is Algorand, published in 2017, which dynamically picks participants and leaders based on how much currency they hold.
Bitcoin also claims to be resistant to censorship because you cannot know in advance who will become the next leader and, therefore, cannot prevent the system from electing a new leader. It is less clear if this is possible in PoS systems where it might be easier to figure out the identities behind large sums of currency.
I should mention that not all BFT consensus protocols are leader-based. Some are leaderless, they do not work by having elected leaders decide on the next state transitions. Instead, everyone can propose changes, and the consensus protocol helps everyone agree on the next state. In 2019, Avalanche launched such a cryptocurrency that allowed anyone to propose changes and participate in consensus.
Finally, if you thought that consensus was necessary at all for a decentralized payment system, it’s not exactly right as well. Consensus-less protocols were proposed in 2018 in “AT2: Asynchronous Trustworthy Transfers” by Guerraoui, Kuznetsov, Monti, Pavlovic, and Seredinschi. With that in mind, I will not talk about consensus-less protocols in this chapter as they are a relatively new and haven’t been battle-tested yet. In the rest of this chapter, I will go over two different cryptocurrencies in order to demonstrate different aspects of the field:
Bitcoin—The most popular cryptocurrency based on PoW, introduced in 2008.
Diem—A cryptocurrency based on the BFT consensus protocol, announced by Facebook and a group of other companies in 2019.
On October 31, 2008, an anonymous researcher(s) published “Bitcoin: A Peer-to-Peer Electronic Cash System” under the pseudonym Satoshi Nakamoto. To this day, it remains unknown who Satoshi Nakamoto is. Not long after, “they” released the Bitcoin core client, a software that anyone can run in order to join and participate in the Bitcoin network. That was the only thing that Bitcoin needed: enough users to run the same software or at least the same algorithm. The first ever cryptocurrency was born—the bitcoin (or BTC).
Bitcoin is a true success story. The cryptocurrency has been running for more than a decade (at the time of this writing) and has allowed users from all around the world to undertake transactions using the digital currency. In 2010, Laszlo Hanyecz, a developer, bought two pizzas for 10,000 BTCs. As I am writing these lines (February 2021), a BTC is worth almost $57,000. Thus, one can already take away that cryptocurrencies can sometimes be extremely volatile.
Let’s dive deeper into the internals of Bitcoin, first looking at how Bitcoin handles user balances and transactions. As a user of Bitcoin, you directly deal with cryptography. You do not have a username and password to log into a website as with any bank; instead, you have an ECDSA (Elliptic Curve Digital Signature Algorithm) key pair that you generate yourself. A user’s balance is simply an amount of BTC associated with a public key, and as such, to receive BTCs, you simply share your public key with others.
To use your BTCs, you sign a transaction with your private key. A transaction pretty much says what you think it says, “I send X BTC to public key Y,” overlooking some details that I’ll explain later.
Note In chapter 7, I mentioned that Bitcoin uses the secp256k1 curve with ECDSA. The curve is not to be confused with NIST’s P-256 curve, which is known as secp256r1.
The safety of your funds is directly linked to the security your private key. And, as you know, key management is hard. In the past decade, key management issues in cryptocurrencies have led to the accidental loss (or theft) of keys worth millions of dollars. Be careful!
There exist different types of transactions in Bitcoin, and most of the transactions seen on the network actually hide the recipient’s public key by hashing it. In these cases, the hash of a public key is referred to as the address of an account. (For example, this is my Bitcoin address: bc1q8y6p4x3rp32dz80etpyffh6764ray9842egchy.) An address effectively hides the actual public key of the account until the account owner decides to spend the BTCs (in which case, the pre-image of the address needs to be revealed so that others can verify the signature). This makes addresses shorter in size and prevents someone from retrieving your private key in case ECDSA one day breaks.
The fact that different types of transactions exist is an interesting detail of Bitcoin. Transactions are not just payloads containing some information; they are actually short scripts written in a made-up and quite limited instruction set. When a transaction is processed, the script needs to be executed before the produced output can determine if the transaction is valid, and if it is, what steps need to be taken to modify the state of all the accounts.
Cryptocurrencies like Ethereum have pushed this scripting idea to the limit by allowing much more complex programs (so-called smart contracts) to run when a transaction is executed. There are a few things here that I didn’t touch on:
I will explain the second item in the next section. For now, let’s look at what is in a transaction.
A particularity of Bitcoin is that there is no real database of account balances. Instead, a user has pockets of BTCs that are available for them to spend and which are called Unspent Transaction Outputs (UTXOs). You can think of the concept of UTXOs as a large bowl, visible to everyone, and filled with coins that only their owners can spend. When a transaction spends some of the coins, the coins disappear from the bowl, and new ones appear for the payees of the same transaction. These new coins are just the outputs listed in the transaction.
To know how many BTCs you have in your account, you’d have to count all of the UTXOs that are assigned to your address. In other words, you’d have to count all of the money that was sent to you and that you haven’t spent yet. Figure 12.2 gives an example that illustrates how UTXOs are used in transactions.
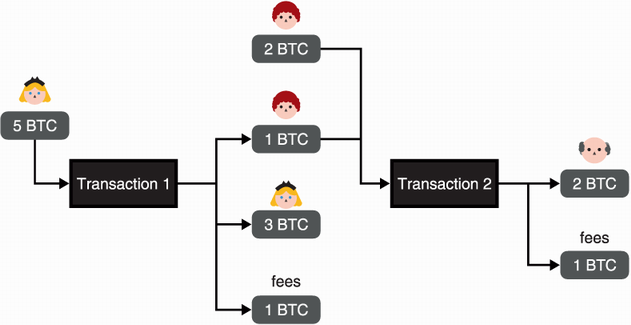
Figure 12.2 Transaction 1 is signed by Alice and transfers 1 BTC to Bob. Because it uses a UTXO of 5 BTCs, the transaction needs to also send back the change to Alice as well as reserve some of that change as fees. Transaction 2 is signed by Bob and combines two UTXOs to transfer 2 BTCs to Felix. (Note that in reality, fees are much lower.)
There’s now a chicken-and-egg question: where did the first UTXOs come from? That, I will answer in the next section.
You now understand what’s in a Bitcoin transaction and how you can manage your account or figure out someone’s balance. But who actually keeps track of all these transactions? The answer is everyone!
Indeed, using Bitcoin means that every transaction must be publicly shared and recorded in history. Bitcoin is an append-only ledger—a book of transactions where each page is connected to the previous one. I want to emphasize here that append-only means that you can’t go back and alter a page in the book. Note also that because every transaction is public, the only semblance of anonymity you get is that it might be hard to figure out who’s who (in other words, what public key is linked to what person in real life).
One can easily inspect any transaction that has happened since the inception of Bitcoin by downloading a Bitcoin client and using it to download the whole history. By doing this, you become part of the network and must re-execute every transaction according to the rules encoded in the Bitcoin client. Of course, Bitcoin’s history is pretty massive: at the time of this writing, it is around 300 GB, and it can take days, depending on your connection, to download the entire Bitcoin ledger. You can more easily inspect transactions by using an online service that does the heavy lifting for you (as long as you trust an online service). I give an example of these so-called blockchain explorers in figure 12.3.

Figure 12.3 A random transaction I chose to analyze on https://blockchain.com (http://mng.bz/n295). The transaction uses one input (of around 1.976 BTCs) and splits it in two outputs (of around 0.009 BTC and 1.967 BTCs). The difference between the total input amount and the total output amount is the transaction fee (not represented as an output). The other fields are the scripts written using Bitcoin’s scripting language in order to either spend the UTXOs in the inputs or to make the UTXOs in the outputs spendable.
Bitcoin is really just a list of all the transactions that have been processed since its inception (we call that the genesis) up until now. This should make you wonder: who is in charge of choosing and ordering transactions in this ledger?
In order to agree on an ordering of transactions, Bitcoin allows anyone (even you) to propose a list of transactions to be included in the next page of the ledger. This proposal containing a list of transactions is called a block in Bitcoin’s terms. But letting anyone propose a block is a recipe for disaster as there are a lot of participants in Bitcoin. Instead, we want just one person to make a proposal for the next block of transactions. To do this, Bitcoin makes everybody work on some probabilistic puzzle, and only allows the one who solves the puzzle first to propose their block. This is the proof of work (PoW) mechanism I talked about previously. Bitcoin’s PoW is based on finding a block that hashes to a digest smaller than some value. In other words, the block’s digest must have a binary representation starting with some given numbers of zeros.
In addition to the transactions you want to include, the block must contain the hash of the previous block. Hence the Bitcoin ledger is really a succession of blocks, where each block refers to the previous one, down to the very first block, the genesis block. This is what Bitcoin calls a blockchain. The beauty of the blockchain is that the slightest modification to a block would render the chain invalid as the block’s digest would also change and consequently break the reference the next block had to it.
Note that as a participant who is looking to propose the next block, you don’t have to change much in your block to derive a new hash from it. You can fix most of its content first (the transactions it includes, the hash of the block it extends, etc.) and then only modify a field (called the block’s nonce) to impact the block’s hash. You can treat this field as a counter, incrementing the value until you find a digest that fits the rules of the game, or you can generate a random value. I illustrate this idea of a blockchain in figure 12.4.

Figure 12.4 On https://andersbrownworth.com/blockchain/blockchain, one can interactively play with a toy blockchain. Each block includes its parent’s digest, and each block contains a random nonce that allows its digest to start with four 0s. Notice that this is true for the top blockchain, but the bottom one contains a block (number 2) that has been modified (its data was initially empty). As the modification changed the block’s digest, it is no longer authenticated by subsequent blocks.
All of this works because everyone is running the same protocol using the same rules. When you synchronize with the blockchain, you download every block from other peers and verify that:
Hashing each block indeed gives a digest that is smaller than some expected value.
Each block refers back to the previous block in the history.
Not everyone has to propose blocks, but you can if you want. If you do so, you are called a miner. This means that in order to get your transactions in the blockchain, you need the miners’ help (as figure 12.5 illustrates).

Figure 12.5 The Bitcoin network is a number of nodes (miners or not) that are interconnected. To submit a transaction, you must send it to a miner that can get it into the blockchain (by including it into a block). As you do not know which miner will be successful at mining a block, you must propagate your transaction through the network to reach as many miners as possible.
Miners do not work for free. If a miner finds a block, they collect:
A reward—A fixed number of BTCs will get created and sent to your address. In the beginning, miners would get 50 BTCs per block mined. But the reward value halves every 210,000 blocks and will eventually be reduced to 0, capping the total amount of BTCs that can be created to 21 million.
All the transaction fees contained in the block—This is why increasing the fees in your transactions allows you to get them accepted faster as miners tend to include transactions with higher fees in the blocks they mine.
This is how users of Bitcoin are incentivized in making the protocol move forward. A block always contains what is called a coinbase, which is the address that collects the reward and the fees. The miner usually sets the coinbase to their own address.
We can now answer the question we had at the beginning of the section: where did the first UTXOs come from? The answer is that all BTCs in history were, at some point or another, created as part of the block reward for miners.
Bitcoin distributes the task of choosing the next set of transactions to be processed via a PoW-based system. Your chance to mine a block is directly correlated to the amount of hashes you can compute, and thus, the amount of computation you can put produce. A lot of computation power nowadays is directed at mining blocks in Bitcoin or other PoW-based cryptocurrencies.
Note PoW can be seen as Bitcoin’s way of addressing sybil attacks, which are attacks that take advantage of the fact that you can create as many accounts as you want in a protocol, giving you an asymmetric edge to dishonest participants. In Bitcoin, the only way to obtain more power is really to buy more hardware to compute hashes, not to create more addresses in the network.
There is still one problem though: the difficulty of finding a hash that is lower than some value can’t be too easy. If it is, then the network will have too many participants mining a valid block at the same time. And, if this happens, which mined block is the legitimate next block in the chain? This is essentially what we call a fork.
To solve forks, Bitcoin has two mechanisms. The first is to maintain the hardness of PoW. If blocks get mined too quickly or too slowly, the Bitcoin algorithm that everyone is running dynamically adapts to the network conditions and increases or decreases the difficulty of the PoW. Simplified, miners have to find a block digest that has more or less zeros.
Note If the difficulty dictates that a block digest needs to start with a 0 byte, you are expected to try 28 different blocks (more specifically different nonces as explained previously) until you can find a valid digest. Raise this to 2 bytes, and you are now expected to try 216 different blocks. The time it takes for you to get there depends on the amount of power you have and whether you have specialized hardware to compute these hashes more rapidly. Currently, Bitcoin’s algorithm dynamically changes the difficulty so that a block is mined every 10 minutes.
Our second mechanism is to make sure everyone has the same way of going forward if a fork does happen. To do this, the rule is to follow the chain with the most amount of work. The 2008 Bitcoin paper stated, “the longest chain not only serves as proof of the sequence of events witnessed, but proof that it came from the largest pool of CPU power,” dictating that participants should honor what they see as the longest chain. The protocol was later updated to follow the chain with the highest cumulative amount of work, but this distinction does not matter too much here. I illustrate this in figure 12.6.
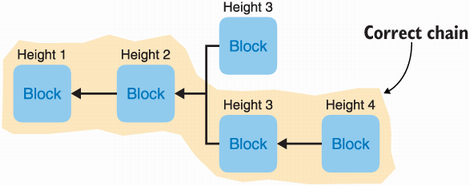
Figure 12.6 A fork in the blockchain: two miners publish a valid block at height 3 (meaning 3 blocks after genesis). Later, another miner mines a block at height 4 that points to the second block at height 3. As the second fork is now longer, it is the valid fork that miners should continue to extend. Note that arrows coming out of a block point to the parent block (the block they extend).
I said previously that the consensus algorithm of Bitcoin is not a BFT protocol. This is because the consensus algorithm allows such forks. Thus, if you are waiting for your transaction to be processed, you should absolutely not rely on simply observing your transaction being included in a block! The observed block could actually be a fork, and a losing one (to a longer fork) at that.
You need more assurance to decide when your transaction has been processed for real. Most wallets and exchange platforms wait for a number of confirmation blocks to be mined on top of your block. The more blocks on top of the one that includes your transaction, the less chance that chain will be reorganized into another, due to a longer existing fork.
The number of confirmation is typically set to 6 blocks, which makes the confirmation time for your transaction around an hour. That being said, Bitcoin still does not provide 100% assurance that a fork past 6 blocks would never happen. If the mining difficulty is well adjusted, then it should be fine, and we have reason to believe that this is true for Bitcoin.
Bitcoin’s PoW difficulty has increased gradually over time as cryptocurrency becomes more popular. The difficulty is now so high that most people cannot afford the hardware required to have a chance at mining a block. Today, most miners get together in what are called mining pools to distribute the work needed to mine a block. They then share the reward.
With block 632874 [. . .] the expected cumulative work in the Bitcoin blockchain surpassed 292 double-SHA256 hashes.
—Pieter Wuille (2020, http://mng.bz/aZNJ)
To understand why forks are disruptive, let’s imagine the following scenario. Alice buys a bottle of wine from you, and you’ve been waiting for her to send you the 5 BTCs she has in her account. Finally, you observe a new block at height 10 (meaning 10 blocks after genesis) that includes her transaction. Being cautious, you decide to wait for 6 more blocks to be added on top of that. After waiting for a while, you finally see a block at height 16 that extends the chain containing your block at height 10. You send the bottle of wine to Alice and call it a day. But this is not the end of the story.
Later, a block at height 30 appears out of nowhere, extending a different blockchain that branched out just a block before yours (at height 9). Because the new chain is longer, it ends up being accepted by everyone as the legitimate chain. The previous chain you were on (starting from your block at height 10) gets discarded, and participants in the network simply reorganize their chain to now point to the new longest one. And as you can guess, this new chain doesn’t has any block that includes Alice’s transaction. Instead, it includes a transaction moving all of her funds to another address, preventing you from republishing the original transaction that moved her funds to your address. Alice effectively double spent her money.
This is a 51% attack. The name comes from the amount of computation power Alice needed to perform the attack; she needed just a bit more than everyone else. (https://crypto51.app has an interesting table that lists the cost of performing a 51% attack on different cryptocurrencies based on PoW.) This is not just a theoretical attack! 51% attacks happen in the real world. For example, in 2018, an attacker managed to double-spend a number of funds in a 51% attack on the Vertcoin currency.
The attacker essentially rewrote part of the ledger’s history and then, using their dominant hashing power to produce the longest chain, convinced the rest of the miners to validate this new version of the blockchain. With that, he or she could commit the ultimate crypto crime: a double-spend of prior transactions, leaving earlier payees holding invalidated coins.
—Michael J. Casey (“Vertcoin’s Struggle Is Real: Why the Latest Crypto 51% Attack Matters,” 2018)
In 2019, the same thing happened to Ethereum Classic (a variant of Ethereum), causing losses of more than $1 million at the time with several reorganizations of more than 100 blocks of depth. In 2020, Bitcoin Gold (a variant of Bitcoin) also suffered from a 51% attack, removing 29 blocks from the cryptocurrency’s history and double-spending more than $70,000 in less than two days.
One last interesting aspect of Bitcoin that I want to talk about is how it compresses some of the information available. A block in Bitcoin actually does not contain any transactions! Transactions are shared separately, and instead, a block contains a single digest that authenticates a list of transactions. That digest could simply be the hash of all the transactions contained in the block, but it’s a bit more clever than that. Instead, the digest is the root of a Merkle tree.
What’s a Merkle tree? Simply put, it’s a tree (data structure) where internal nodes are hashes of their children. This might be a tad confusing, and a picture is worth a thousand words, so check out figure 12.7.
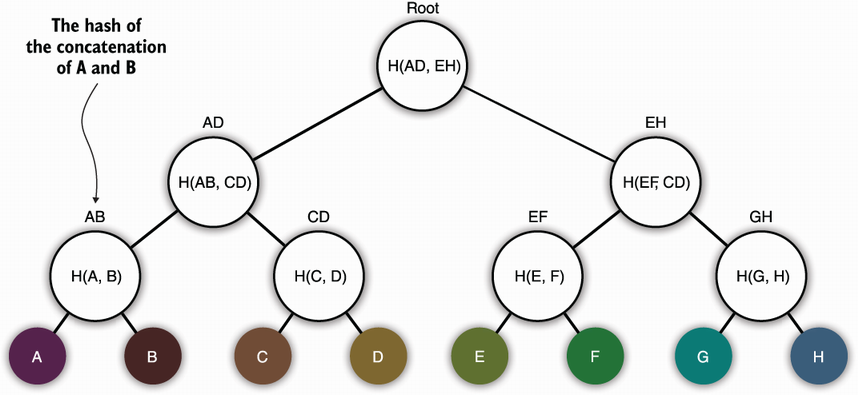
Figure 12.7 A Merkle tree, a data structure that authenticates the elements in its leaves. In the tree, an internal node is the hash of its children. The root hash can be used to authenticate the whole structure. In the diagram, H() represents a hash function, and the comma-separated inputs can be implemented as a concatenation (as long as there is no ambiguity).
Merkle trees are useful structures, and you will find them in all types of real world protocols. They can compress a large amount of data into a small, fixed-size value—the root of the tree. Not only that, you do not necessarily need all the leaves to reconstruct the root.
For example, imagine that you know the root of the Merkle tree due to its inclusion in a Bitcoin block, and you want to know if a transaction (a leaf in the tree) is included in the block. If it is in the tree, what I can do is to share with you the neighbor nodes in the path up to the root as a membership proof. (A proof that is logarithmic in the depth of the tree in size.) What’s left for you is to compute the internal nodes up to the root of the tree by hashing each pair in the path. It’s a bit complicated to explain this in writing, so I illustrate the proof in figure 12.8.

Figure 12.8 Knowing the root of a Merkle tree, one can verify that a leaf belongs to the tree by reconstructing the root hash from all the leaves. To do this, you would need all the leaves in the first place, which in our diagram is 8 digests (assuming leaves are the hashes of some object). There’s a more efficient way to construct a proof of membership if you don’t need all the other leaves: you only need the neighbor nodes in the path from the leaf to the root, which is 4 digests including your leaf. A verifier can then use these neighbor nodes to compute the hash of all the missing nodes in the path to the root until they reconstruct the root hash and see if it matches what they were expecting.
The reason for using Merkle trees in a block instead of listing all transactions directly is to lighten the information that needs to be downloaded in order to perform simple queries on the blockchain. For example, imagine that you want to check that your recent transaction is included in a block without having to download the whole history of the Bitcoin blockchain. What you can do is to only download the block headers, which are lighter as they do not contain the transactions, and once you have that, ask a peer to tell you which block included your transaction. If there is such a block, they should be able to provide you with a proof that your transaction is in the tree authenticated by the digest you have in the block header.
There’s a lot more to be said about Bitcoin, but there’s only so many pages left in this book. Instead, I will use the remaining space in this chapter to give you a tour of the field and to explain how the classical BFT consensus protocols work.
Bitcoin is the first successful cryptocurrency and has remained the cryptocurrency with the largest market share and value in spite of hundreds of other cryptocurrencies being created. What’s interesting is that Bitcoin had, and still has, many issues that other cryptocurrencies have attempted to tackle (and some with success). Even more interesting, the cryptocurrency field has made use of many cryptographic primitives that until now did not have many practical applications or did not even exist! So without further ado, the following sections list the issues that have been researched since the advent of Bitcoin.
Most people currently use cryptocurrencies as speculation vehicles. The price of Bitcoin obviously helps that story as it has shown that it can easily move thousands of dollars up or down in a single day. Some people claim that the stability will come over time, but the fact remains that Bitcoin is not usable as a currency nowadays. Other cryptocurrencies have experimented with the concept of stablecoin, by tying the price of their token to an existing fiat currency (like the US dollar).
You can measure the efficiency of a cryptocurrency in many ways. The throughput of a cryptocurrency is the number of transactions per second that it can process. Bitcoin’s throughput, for example, is quite low with only 7 transactions per second. On the other hand, finality is the time it takes for your transaction to be considered finalized once it is included in the blockchain. Due to forks, Bitcoin’s finality is never completely achieved. It is considered that at least one hour after a transaction is included in a new block, the probability of the transaction getting reverted becomes acceptable. Both numbers greatly impact the latency, which is the amount of time it takes for a transaction to be finalized from the point of view of the user. In Bitcoin, latency includes the creation of the transaction, the time it takes to propagate it through the network, the time it takes for it to get included in a block, and finally, the wait time for the block to be confirmed.
The solution to these speed issues can be solved by BFT protocols, which usually provide finality of mere seconds with an insurance that no forks are possible, as well as throughput in the order of thousands of transactions per second. Yet, this is sometimes still not enough, and different technologies are being explored. So-called layer 2 protocols attempt to provide additional solutions that can enact faster payments off-chain while saving progress periodically on the main blockchain (referred to as the layer 1 in comparison).
Another common problem with Bitcoin and other cryptocurrencies is that the size of the blockchain can quickly grow to impractical sizes. This creates usability issues when users who want to use the cryptocurrency (for example, to query their account’s balance) are expected to first download the entire chain in order to interact with the network. BFT-based cryptocurrencies that process a large number of transactions per second are expected to easily reach terabytes of data within months or even weeks. Several attempts exist for solving this.
One of the most interesting ones is Mina, which doesn’t require you to download the whole history of the blockchain in order to get to the latest state. Instead, Mina uses zero-knowledge proofs (ZKPs), mentioned in chapter 7 and that I’ll cover more in depth in chapter 15, to compress all the history into a fixed-size 11 KB proof. This is especially useful for lighter clients like mobile phones that usually have to trust third-party servers in order to query the blockchain.
Bitcoin provides pseudo-anonymity in that accounts are only tied to public keys. As long as nobody can tie a public key to a person, the associated account remains anonymous. Remember that all the transactions from and to that account are publicly available, and social graphs can still be created in order to understand who tends to trade more often with whom, and who owns how much of the currency.
There are many cryptocurrencies that attempt to solve these issues using ZKPs or other techniques. Zcash is one of the most well-known confidential cryptocurrencies as its transactions can encrypt the sender address, receiver address, and the amount being transacted. All of that using ZKPs!
Bitcoin has been criticized heavily for being too consuming in terms of electricity. Indeed, the University of Cambridge recently evaluated that all of the energy spent mining BTCs brings Bitcoin to the top 30 energy users in the world (if seen as a country), consuming more energy in a year than a country like Argentina (February 2021; https://cbeci.org/). BFT protocols on the other hand do not rely on PoW and so avoid this heavy overhead. This is most certainly why any modern cryptocurrency seems to avoid a consensus based on PoW, and even important PoW-based cryptocurrencies like Ethereum have announced plans to move towards greener consensus protocols. Before going to the next chapter, let’s take a look at these cryptocurrencies based on BFT consensus protocols.
Many modern cryptocurrencies have ditched the PoW aspect of Bitcoin for greener and more efficient consensus protocols. Most of these consensus protocols are based on classical BFT consensus protocols, which are mostly variants of the original PBFT protocol. In this last section, I will use Diem to illustrate such BFT protocols.
Diem (previously called Libra) is a digital currency initially announced by Facebook in 2019, and governed by the Diem Association, an organization of companies, universities, and nonprofits looking to push for an open and global payment network. One particularity of Diem is that it is backed by real money, using a reserve of fiat currencies. This allows the digital currency to be stable unlike its older cousin Bitcoin. To run the payment network in a secure and open manner, a BFT consensus protocol called DiemBFT is used, which is a variant of HotStuff. In this section, let’s see how DiemBFT works.
A BFT consensus protocol is meant to achieve two properties, even in the presence of a tolerated percentage of malicious participants. These properties include
Safety—No contradicting states can be agreed on, meaning that forks are not supposed to happen (or happen with a negligible probability).
Liveness—When people submit transactions, the state will eventually end up processing them. In other words, nobody can stop the protocol from doing its thing.
Note that a participant is generally seen as malicious (also called byzantine) if they do not behave according to the protocol. This could mean that they’re not doing anything, or that they’re not following the steps of the protocol in the correct order, or that they’re not respecting some mandatory rule meant to ensure that there is no fork, and so on.
It’s usually quite straightforward for BFT consensus protocols to achieve safety, while liveness is known to be more difficult. Indeed, there’s a well-known impossibility result from Fischer, Lync, and Paterson (“Impossibility of distributed consensus with one faulty process”) dating from 1985 and linked to BFT protocols that states that no deterministic consensus protocol can tolerate failures in an asynchronous network (where messages can take as much time as they want to arrive). Most BFT protocols avoid this impossibility result by considering the network somewhat synchronous (and indeed, no protocol is useful if your network goes down for a long period of time) or by introducing randomness in the algorithm.
For this reason, DiemBFT never forks, even under extreme network conditions. In addition, it always makes progress even when there’s network partitions where different parts of the network can’t reach other parts of the network, as long as the network ends up healing and stabilizing for a long enough period.
Diem runs in a permissioned setting where participants (called validators) are known in advance. The protocol advances in strictly increasing rounds (round 1, 2, 3, etc.), during which validators take turns to propose blocks of transactions. In each round
The validator that is chosen to lead (deterministically) collects a number of transactions, groups them into a new block extending the blockchain, then signs the block and sends it to all other validators.
Upon receiving the proposed block, other validators can vote to certify it by signing it and sending the signature to the leader of the next round.
If the leader of the next round receives enough votes for that block, they can bundle all of them in what is called a quorum certificate (QC), which certifies the block, and use the QC to propose a new block (in the next round) extending the now certified block.
Another way to look at this is that whereas in Bitcoin a block only contains the hash of the block it extends, in DiemBFT, a block also contains a number of signatures over that hash. (The number of signatures is important, but more on that later.)
Note that if validators do not see a proposal during a round (because the leader is AFK, for example), they can timeout and warn other validators that nothing happened. In this case, the next round is triggered and the proposer can extend whatever is the highest certified block that they have seen. I recap this in figure 12.9.
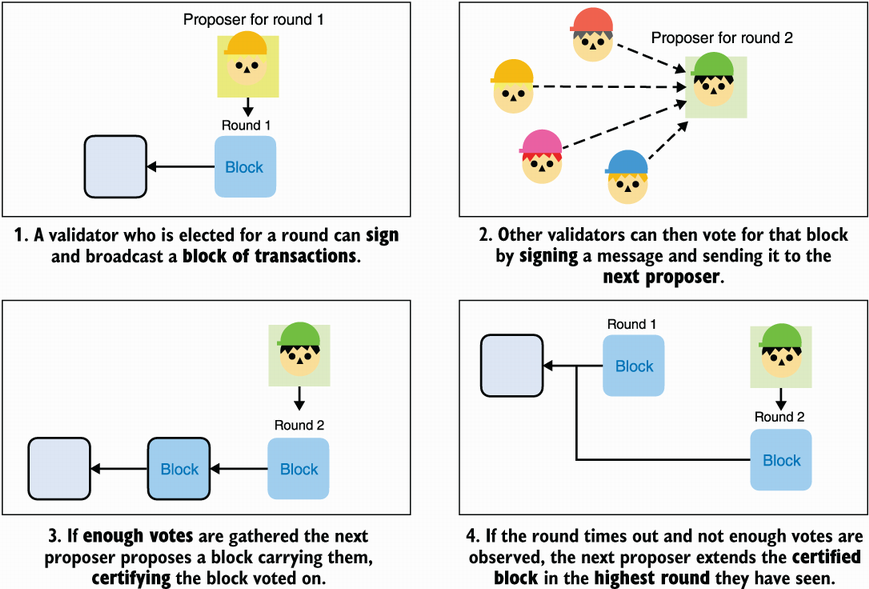
Figure 12.9 Each round of DiemBFT starts with the designated leader proposing a block that extends the last one they’ve seen. Other validators can then vote on this block by sending their vote to the next round’s leader. If the next round’s leader gathers enough votes to form a quorum certificate (QC), they can propose a new block containing the QC, effectively extending the previously seen block.
Let’s imagine that we want to be able to tolerate f malicious validators at most (even if they all collude), then DiemBFT says that there needs to be at least 3f + 1 validators to participate in the protocol (in other words, for f malicious validators there needs to be at least 2f + 1 honest validators). As long as this assumption is true, the protocol provides safety and liveness.
With that in mind, QCs can only be formed with a majority of honest validators’ votes, which is 2f + 1 signatures if there are 3f + 1 participants. These numbers can be a bit hard to visualize, so I show how they impact confidence in the votes we observe in figure 12.10.

Figure 12.10 In the DiemBFT protocol, at least two thirds of the validators must be honest for the protocol to be safe (it won’t fork) and live (it will make progress). In other words, the protocol can tolerate f dishonest validators if at least 2f + 1 validators are honest. A certified block has received at least 2f + 1 votes as it is the lowest number of votes that can represent a majority of honest validators.
Validators must follow two voting rules at all times, without which, they are considered byzantine:
They can’t vote in the past (for example, if you just finished voting in round 3, you can only vote in round 4 and above).
They can only vote for a block extending a block at their preferred round or higher.
What’s a preferred round? By default, it is 0, but if you vote for a block that extends a block that extends a block (and by that I mean you voted for a block that has a grandparent block), then that grandparent block’s round becomes your preferred round unless your previous preferred round was higher. Complicated? I know, that’s why I made figure 12.11.
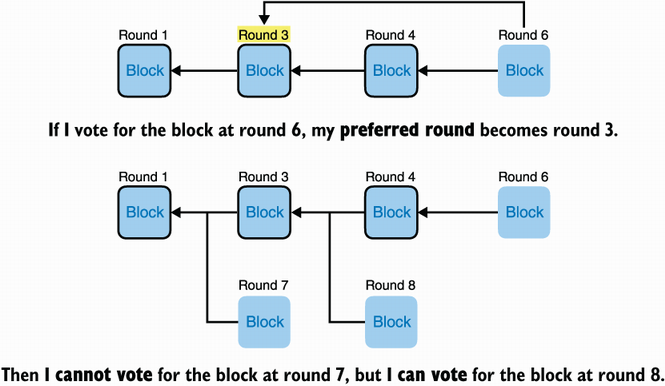
Figure 12.11 After voting for a block, a validator sets their preferred round to the round of the grandparent block if it is higher than their current preferred round. To vote on a block, its parent block must have a round greater or equal to the preferred round.
Note that blocks that are certified are not finalized yet, or as we also say, committed. Nobody should assume that the transactions contained in the pending blocks won’t be reverted. Blocks and the transactions they contain can only be considered finalized once the commit rule is triggered. The commit rule (illustrated in figure 12.12) says that a block and all the pending blocks it extends become committed if:
The block starts a chain of 3 blocks that are proposed in contiguous rounds (for example, in round 1, 2, and 3).

Figure 12.12 Three contiguous rounds (3, 4, 5) happen to have a chain of certified blocks. Any validator observing the certification of the last block in round 5 by the QC of round 9 can commit the first block of the chain at round 3, as well as all of its ancestors (here the block of round 1). Any contradicting branches (for example, the block of round 2) get dropped.
And this is all there is to the protocol at a high level. But, of course, once again, the devil is in the details.
While I encourage you to read the one-page safety proof on the DiemBFT paper, I want to use a couple pages here to give you an intuition on why it works. First, we notice that two different blocks cannot be certified during the same round. This is an important property, which I explain visually in figure 12.13.

Figure 12.13 Assuming that there can only be up to f malicious validators in a protocol of 3f + 1 validators, and that a quorum certificate is created from 2f + 1 signed votes, then there can only be one certified block per round. The diagram shows a proof by contradiction, a proof that this cannot be because then it would contradict our initial assumptions.
Using the property that only one block can get certified at a given round, we can simplify how we talk about blocks: block 3 is at round 3, block 6 is at round 6, and so on. Now, take a look at figure 12.14 and take a moment to figure out why a certified block, or two certified blocks, or three certified blocks at noncontiguous rounds cannot lead to a commit without risking a fork.
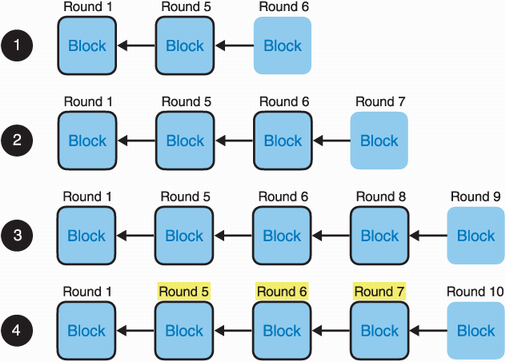
Figure 12.14 In all these scenarios, committing block 5 could lead to a fork. Only in scenario number 4 is committing block 5 safe. Can you tell why it is dangerous to commit block 5 in all scenarios but 4?
Did you manage to find out answers for all the scenarios? The short answer is that all scenarios, with the exception of the last one, leave room for a block to extend round 1. This late block effectively branches out and can be further extended according to the rules of the consensus protocol. If this happens, block 5 and other blocks extending it will get dropped as another earlier branch gets committed. For scenarios 1 and 2, this can be due to the proposer not seeing the previous blocks. In scenario 3, an earlier block could appear later than expected, perhaps due to network delays, or worse, due to a validator withholding it up to the right moment. I explain this further in figure 12.15.

Figure 12.15 Building on figure 12.14, all scenarios except the last one allow for a parallel chain that can eventually win and discard the branch of block 5. The last scenario has a chain of three certified blocks in contiguous rounds. This means that block 7 has had a majority of honest voters, who, in turn, updated their preferred round to round 5. After that, no block can branch out before block 5 and obtain a QC at the same time. The worst that can happen is that a block extends block 5 or block 6, which will eventually lead to the same outcome—block 5 is committed.
Cryptocurrencies are about decentralizing a payment network to avoid a single point of failure.
To have everyone agree on the state of a cryptocurrency, we can use consensus algorithms.
Byzantine fault-tolerant (BFT) consensus protocols were invented in 1982 and have evolved to become faster and simpler to understand.
BFT consensus protocols need a known and fixed set of participants to work (permissioned network). Such protocols can decide who is part of this participant set (proof of authority or PoA) or dynamically elect the participant set based on the amount of currency they hold (proof of stake or PoS).
Bitcoin’s consensus algorithm (the Nakamoto consensus) uses proof of work (PoW) to validate the correct chain and to allow anyone to participate (permissionless network).
Bitcoin’s PoW has participants (called miners) compute a lot of hashes in order to find some with specific prefixes. Successfully finding a valid digest allows a miner to decide on the next block of transaction and collect a reward as well as transaction fees.
Accounts in Bitcoin are simply ECDSA key pairs using the secp256k1 curve. A user knows how much BTCs their account holds by looking at all transaction outputs that have not yet been spent (UTXOs). A transaction is, thus, a signed message authorizing the movement of a number of older transaction outputs to new outputs, spendable to different public keys.
Bitcoin uses Merkle trees to compress the size of a block and allow verification of transaction inclusion to be small in size.
Stablecoins are cryptocurrencies that attempt to stabilize their values, most often by pegging their token to the value of a fiat currency like the US dollar.
Cryptocurrencies use so-called layer 2 protocols in order to decrease their latency by processing transactions off-chain and saving progress on-chain periodically.
Zero-knowledge proofs (ZKPs) are used in many different blockchain applications (for example, in Zcash to provide confidentiality and in Coda to compress the whole blockchain to a short proof of validity).
Diem is a stablecoin that uses a BFT consensus protocol called DiemBFT. It remains both safe (no forks) and live (progress is always made) as long as no more than f malicious participants exist out of 3f + 1 participants.
DiemBFT works by having rounds in which a participant proposes a block of transactions extending a previous block. Other participants can then vote for the block, potentially creating a quorum certificate (QC) if enough votes are gathered (2f + 1 ).
In DiemBFT, blocks and their transactions are finalized when the commit rule (a chain of 3 certified blocks at contiguous rounds) is triggered. When this happens, the first block of the chain and the blocks it extends are committed.