(S) of a set S, the Cartesian product S1 × S2 of two sets S1 and S2, maps ( = functions), and equivalence relations. In the first volume we generally gave preference to constructive arguments and avoided transfinite methods altogether.In the Introduction to Basic Algebra I (abbreviated throughout as “BAI”) we gave an account of the set theoretic concepts that were needed for that volume. These included the power set (S) of a set S, the Cartesian product S1 × S2 of two sets S1 and S2, maps ( = functions), and equivalence relations. In the first volume we generally gave preference to constructive arguments and avoided transfinite methods altogether.
The results that are presented in this volume require more powerful tools, particularly for the proofs of certain existence theorems. Many of these proofs will be based on a result, called Zorn’s lemma, whose usefulness for proving such existence theorems was first noted by Max Zorn. We shall require also some results on the arithmetic of cardinal numbers. All of this fits into the framework of the Zermelo–Fraenkel axiomatization of set theory, including the axiom of choice (the so-called ZFC set theory). Two excellent texts that can be used to fill in the details omitted in our discussion are P. R. Halmos’ Naive Set Theory and the more substantial Set Theory and the Continuum Hypothesis by P. J. Cohen.
Classical mathematics deals almost exclusively with structures based on sets. On the other hand, category theory—which will be introduced in Chapter 1—deals with collections of sets, such as all groups, that need to be treated differently from sets. Such collections are called classes. A brief indication of a suitable foundation for category theory is given in the last section of this Introduction.
0.1 ZORN’S LEMMA
We shall now formulate a maximum principle of set theory called Zorn’s lemma. We state this first for subsets of a given set. We recall that a set C of subsets of a set S (that is, a subset of the power set (S)) is called a chain if C is totally ordered by inclusion, that is, for any A, B ∈ C either A ⊂ B or B ⊂ A. A set T of subsets of S is called inductive if the union 
Aα of any chain C = {Aα} ⊂ T is a member of T. We can now state
ZORN’S LEMMA (First formulation). Let T be a non-vacuous set of subsets of a set S. Assume T is inductive. Then T contains a maximal element, that is, there exists an M ∈ T such that no A ∈ T properly contains M.
There is another formulation of Zorn’s lemma in terms of partially ordered sets (BAI, p. 456). Let P, ≥ be a partially ordered set. We call P, ≥ (totally or linearly) ordered if for every a, b ∈ P either a ≥ b or b ≥ a. We call P inductive if every non-vacuous subset C of P that is (totally) ordered by ≥ as defined in P has a least upper bound in P, that is, there exists a u ∈ P such that u ≥ a for every a ∈ C and if v ≥ a for every a ∈ C then v ≥ u. Then we have
ZORN’S LEMMA (Second formulation). Let P, ≥ be a partially ordered set that is inductive. Then P contains maximal elements, that is, there exists m ∈ P such that no a ∈ P satisfies m < a.
It is easily seen that the two formulations of Zorn’s lemma are equivalent, so there is no harm in referring to either as “Zorn’s lemma.” It can be shown that Zorn’s lemma is equivalent to the
AXIOM OF CHOICE. Let S be a set, (S)* the set of non-vacuous subsets of S. Then there exists a map f (a “choice function”) of (S)* into S such that f(A) ∈ A for every A ∈ (S)*.
This is equivalent also to the following: If {Aα} is a set of non-vacuous sets Aα, then the Cartesian product 
.
The statement that the axiom of choice implies Zorn’s lemma can be proved by an argument that was used by E. Zermelo to prove that every set can be well ordered (see Halmos, pp. 62–65). A set S is well ordered by an order relation ≥ if every non-vacuous subset of S has a least element. The well-ordering theorem is also equivalent to Zorn’s lemma and to the axiom of choice. We shall illustrate the use of Zorn’s lemma in the next section.
0.2 ARITHMETIC OF CARDINAL NUMBERS
Following Halmos, we shall first state the main results on cardinal arithmetic without defining cardinal numbers. We say that the sets A and B have the same cardinality and indicate this by |A| = |B| if there exists a bijective map of A onto B. We write |A| ≤ |B| if there is an injective map of A into B and |A| < |B| if |A| ≤ |B| and |A| ≠ |B|. Using these notations, the Schroder-Bernstein theorem (BAI, p. 25) can be stated as: |A| ≤ |B| and |B| ≤ |A| if and only if |A| = |B|. A set F is finite if |F| = |N| for some N = {0, 1, …, n– 1} and A is countably infinite if |A| = |ω| for ω = {0, 1, 2, …}. It follows from the axiom of choice that if A is infinite ( = not finite), then |ω| ≤ |A|. We also have Cantor’s theorem that for any A, |A| < |(A)|.
We write C = A 
B for sets A, B, C if C = A ∪ B and A ∩ B = ϕ. It is clear that if |A1| ≤ |A2| and |B1| ≤ |B2|, then |A1 B1| ≤ |A2 B2|. Let C = F ω where F is finite, say, F = {x0, …, xn – 1} where xi ≠ xj for i ≠ j. Then the map of C into ω such that xi 
i, k k + n for k ∈ ω is bijective. Hence |C| = |ω|. It follows from |ω| ≤ |A| for any infinite A that if C = F A, then |C| = |A|. For we can write A = D B where |D| = |ω|. Then we have a bijective map of F ∪ D onto D and we can extend this by the identity on B to obtain a bijective map of C onto A.
We can use the preceding result and Zorn’s lemma to prove the main result on “addition of cardinals,” which can be stated as: If A is infinite and C = A ∪ B where |B| = |A|, then |C| = |A|. This is clear if A is countable from the decomposition ω = {0, 2, 4, …} {1, 3, 5, …}. It is clear also that the result is equivalent to |A × 2| = |A| if 2 = {0, 1}, since |A × 2| = |A B|. We proceed to prove that |A × 2| = |A| for infinite A. Consider the set of pairs (X, f) where X is an infinite subset of A and f is a bijective map of X × 2 onto X. This set is not vacuous, since A contains countably infinite subsets X and for such an X we have bijective maps of X × 2 onto X. We order the set {(X, f)} by (X, f) ≤ (X', f') if X ⊂ X' and f' is an extension of f. It is clear that {(X, f)}, ≤ is an inductive partially ordered set. Hence, by Zorn’s lemma, we have a maximal (Y, g) in {(X, f)}. We claim that A – Y is finite. For, if A – Y is infinite, then this contains a countably infinite subset D, and g can be extended to a bijective map of (Y D) × 2 onto Y D contrary to the maximality of (Y, g). Thus A – Y is finite. Then
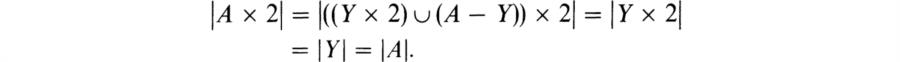
We can extend the last result slightly to
if B is infinite and |B| ≥ |A|. This follows from
The reader is undoubtedly familiar with the fact that |A × A| = |A| if A is countably infinite, which is obtained by enumerating ω × ω as
More generally we have |A × A| = |A| for any infinite A. The proof is similar to the one for addition. We consider the set of pairs (X, f) where X is an infinite subset of A and f is a bijective map of X × X onto X and we order the set {(X, f)} as before. By Zorn’s lemma, we have a maximal (Y, g) in this set. The result we wish to prove will follow if |Y| = |A|. Hence suppose |Y| < |A|. Then the relation A = Y (A – Y) and the result on addition imply that |A| = |A – Y|. Hence |A – Y| > |Y|. Then A – Y contains a subset Z such that |Z| = |Y|. Let W = Y ∪ Z, so W = Y Z and W × W is the disjoint union of the sets Y × Y, Y × Z, Z × Y, and Z × Z. We have
Hence we can extend g to a bijective map of W × W onto W. This contradicts the maximality of (Y, g). Hence |Y| = |A| and the proof is complete.
We also have the stronger result that if A ≠ ϕ and B is infinite and |B| ≥ |A|, then
This follows from
0.3 ORDINAL AND CARDINAL NUMBERS
In axiomatic set theory no distinction is made between sets and elements. One writes A ∈ B for “the set A is a member of the set B.” This must be distinguished from A ⊂ B, which reads “A is a subset of B.” (In the texts on set theory one finds A ⊆ B for our A ⊂ B and A ⊂ B for our A 
B.) One defines A ⊂ B to mean that C ∈ A ⇒ C ∈ B. One of the axioms of set theory is that given an arbitrary set C of sets, there is a set that is the union of the sets belonging to C, that is, for any set C there exists a set U such that A ∈ U if and only if there exists a B such that A ∈ B and B ∈ C. In particular, for any set A we can form the successor A+ = A ∪ {A} where {A} is the set having the single member A.
The process of forming successors gives a way of defining the set ω (= 
) of natural numbers. We define 0 = ϕ, 1 = ϕ+ = {ϕ}, 2 = l+, …, n + l = n+, … and we define ω to be the union of the set of natural numbers n. The natural number n and the set ω are ordinal numbers in a sense that we shall now define. First, we define a set S to be transitive if A ∈ S and B ∈ A ⇒ B ∈ S. This is equivalent to saying that every member of S is a subset. We can now give
DEFINITION 0.1. An ordinal is a set α that is well ordered by ∈ and is transitive.
The condition A ∈ A is excluded by the axioms of set theory. We write A ≤ B for A ∈ α, B ∈ α if A ∈ B or A = B. It is readily seen that every natural number n is an ordinal and the set ω of natural numbers is an ordinal. Also ω+,(ω+)+, … are ordinals. The union of these sets is also an ordinal. This is denoted as ω + ω or ω × 2.
We shall now state without proofs some of the main properties of ordinal numbers.
Two partially ordered sets Sl ≤1 and S2, ≤2 are said to be similar if there exists an order-preserving bijective map of S1 onto S2. The ordinals constitute a set of representatives for the similarity classes of well-ordered sets. For we have the following theorem: If S, ≤ is well ordered, then there exists a unique ordinal a and a unique bijective order-preserving map of S onto α. If α and β are ordinals, either α = β, α < β, or β < α. An ordinal a is called α successor if there exists an ordinal β such that α = β+. Otherwise, α is called a limit ordinal. Any non-vacuous set of ordinals has a least element.
DEFINITION 0.2. A cardinal number is an ordinal α such that if β is any ordinal such that the cardinality |β| = |α|, then α ≤ β.
A cardinal number is either finite or it is a limit ordinal. On the other hand, not every limit ordinal is a cardinal. For example ω + ω is not a cardinal. The smallest infinite cardinal is ω. Cardinals are often denoted by the Hebrew letter “aleph” 
with a subscript. In this notation one writes 
for ω.
Since any set can be well ordered, there exists a uniquely determined cardinal α such that |α| = |S| for any given set S. We shall now call α the cardinal number or cardinality of S and indicate this by |S| = α. The results that we obtained in the previous section yield the following formulas for cardinalities
if B is infinite and |B| ≥ |A|. Here, unlike in equation (1), |S| denotes the cardinal number of the set S. Similarly we have
if A is not vacuous and |B| is infinite and ≥ |A|.
0.4 SETS AND CLASSES
There is an axiomatization of set theory different from the ZF system that permits the discussion of collections of sets that may not themselves be sets. This is a system of axioms that is called the Gödel–Bernays (or GB) system. The primitive objects in this system are “classes” and “sets” or more precisely class variables and set variables together with a relation ∈. A characteristic feature of this system is that classes that are members of other classes are sets, that is, we have the axiom: Y ∈ X ⇒ Y is a set.
Intuitively classes may be thought of as collections of sets that are defined by certain properties. A part of the GB system is concerned with operations that can be performed on classes, corresponding to combinations of properties. A typical example is the intersection of classes, which is expressed by the following: For all X and Y there exists a Z such that u ∈ Z if and only if u ∈ X and u ∈ Y. We have given here the intuitive meaning of the axiom: ∀ X ∀ Y ∃ Z ∀ u (u ∈ Z ⇔ u ∈ X and u ∈ Y) where ∀ is read “for all” and ∃ is read “there exists.” Another example is that for every X there exists a Y such that u ∈ Y if and only if u ∉ X (∀ X ∃ Y ∀ u (u ∈ Y ⇔ ~ u ∈ X), where ~… is the negation of …). Other class formations correspond to unions, etc. We refer to Cohen’s book for a discussion of the ZF and the GB systems and their relations. We note here only that it can be shown that any theorem of ZF is a theorem of GB and every theorem of GB that refers only to sets is a theorem of ZF.
In the sequel we shall use classes in considering categories and in a few other places where we encounter classes and then show that they are sets by showing that they can be regarded as members of other classes. The familiar algebraic structures (groups, rings, fields, modules, etc.) will always be understood to be “small,” that is, to be based on sets.
Paul R. Halmos, Naive Set Theory, Springer, New York, 1960.
Paul J. Cohen, Set Theory and the Continuum Hypothesis, Addison-Wesley, Reading, Mass., 1966.