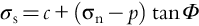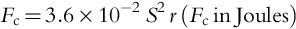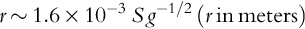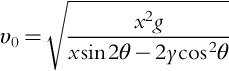Regolith and Dust: Movement and Transport
Abstract
The regolith found on the surfaces of all airless bodies is constantly in motion. From the subtle, global process of “soil creep” to the sudden and dramatic emplacement of impact ejecta, to the odd and counterintuitive levitation of dust, all particles are subject to displacement, locally, regionally, and globally. This complex weave of different processes is responsible for the formation of the features we see, and how those features change over time. The smaller asteroids can feature more extreme versions of these processes, with even tiny impactors resulting in global effects. Interparticle cohesion also plays an increasingly important role as objects become smaller, with the possibility that clumping of small, cohesive particles may mimic landforms that would otherwise be interpreted as due to intact rock.
Keywords
Regolith; Airless bodies; Dust; Movement; Transport; Cohesion
Introduction
The regolith found on the surfaces of all airless bodies is constantly in motion. From the subtle, global process of “soil creep” to the sudden and dramatic emplacement of impact ejecta, to the odd and counterintuitive levitation of dust, all particles are subject to displacement locally, regionally, and globally. This complex weave of different processes is responsible for the formation of the features we see, and how those features change over time.
We can separate the movement of regolith and dust into two regimes. The first regime is that which affects the larger particles and is dominated by gravity. In this regime, we see landslides and mass wasting, ejecta emplacement, creep, and slumping. The second regime is that which affects the smaller particles and is dominated by other forces such as electrostatic forces. In this regime we see electrostatic cohesion, levitation, and other phenomena that change the nature of creep and slumping, although cohesion or other “sticking” properties like internal friction can be a factor with larger particles on bodies with or without volatiles.
Cohesion
Before we consider processes that move material, we consider factors that keep material in place. Melosh in his book Surface Processes offers an excellent treatment of the nature of cohesion as it applies to the movement of regolith and to surface processes, and much of this chapter is inspired by his treatments.
Examining cases of stability under stress, we use an equation combining a summary of shear stress with pore pressure:
with terms defined as follows:
- σs = maximum sustainable shear stress
- c = cohesion
- σn = stress normal to the plane of shearing
- p = pore pressure
- Φ = angle of internal friction.
This equation, often called the Mohr-Coulomb failure criterion, was developed for civil engineering purposes.
Values that are available in the literature for the angle of internal friction in standard materials can range from basalt talus (45 degrees), through sand (33–43 degrees), to cold water ice (29 degrees). This means that loose materials are not “strengthless” such as, for instance, liquid water, which cannot support a slope of any height. Even in cases where there is no cohesion, internal friction must still be overcome by a finite shear stress for the material to start to move.
Cohesion in Microgravity
As noted earlier, gravity dominates the behavior of large particles while electrostatic cohesion dominates the behavior of smaller particles. The definition of “large” and “small” in this case is a function of gravity, and thus of object size. The van der Waals forces between particles are the main cause of cohesion that we consider here, and they operate at very short ranges—effectively only between particles in contact. Scheeres et al. (2010) find that the magnitude of the van der Waals forces at zero distance is:
where r is the average particle radius and S is the “cleanliness factor,” a measure of how much adsorbed material is on the molecules in question and increasing the distance between them. For a terrestrial environment, S ~ 0.1 due to adsorbed water. Perko et al. (2001) report S approaches the maximum value of 1 for sunlit lunar regolith, and it presumably is near that value on asteroidal regolith as well.
We can compare the strength of this force to the force of gravity, and to the weight of a particle. We find the particle radius at which the cohesive van der Waals force and the particle weight are equal is:
For the Moon, gravity is 1.6 m/s2, so r ~ 1 mm for S = 1. On the Earth, taking into account the smaller value of S, the critical radius is ~ 50 μm. On Deimos, the critical radius is 3 cm. On Itokawa, it's 16 cm. The consequences of the larger role of cohesion on smaller objects can be imagined by reconsidering what we experience on Earth.
It is likely we have all made piles of loose, dry, granular material, whether of sand, gravel, or something else. As noted earlier, when piled up, these materials do not form columns with vertical sides, but spread themselves out with slopes of particular angles. This is the angle of repose, discussed in more detail later. However, we have also likely all noted that some dry powders like flour, cocoa, or talcum powder can sustain vertical cliffs if they are created. In these cases, the particle sizes are small enough for cohesive van der Waals forces to be stronger than gravity, and we can note that individual particles of cocoa and talcum powder are typically ~ 10–30 μm in size, while sand is typically ~ 100 μm in size or larger (Chapter 7). This makes sense given the critical radius of 50 μm where cohesion and gravity are equal for particles on Earth: sand grains are too large for cohesion to dominate, while the opposite is true for the smaller cocoa and talcum powder grains.
Much larger particles on small body surfaces can act the way that those powders behave on Earth. This has led to supposition that some of the structures seen on the surface of Eros and interpreted as a sign of coherent rock could instead be composed of mm-sized particles held together by van der Waals forces, and that some of the cm-sized gravels seen on the surface of Itokawa could in principle be cohesive clumping of mm-sized grains (Scheeres et al., 2010). Cohesive forces are also thought to potentially play an important role in holding together small, rubble-pile asteroids that are being spun up by nongravitational forces (see Chapter 9).
Emplacement and Mixing of Impact Ejecta
The most obvious and dramatic movement of material on an airless body happens during an impact event (see Chapter 7 for the details of impact crater formation, and for explanation of impact “gardening”). Depending on impact energy, the results of an impact can move material all the way to the other side of the body. For larger airless worlds like the Moon, the material ejected from an impact crater is emplaced ballistically. Small worlds such as asteroids can have material launched well into space, only to re-encounter and re-impact the asteroid at some later time.
As noted previously, impact craters are formed through a process that resembles the explosion of a bomb—they are not “dug out” by the impactor, but rather are exploded outwards by the transfer and release of vast amounts of kinetic energy. When this happens, material is launched from the target area and follows a parabolic path, eventually leading back to the ground. In a technical sense, the material is launched into an orbit around the center of mass (Chapter 9), but because most of the orbit path is within the target body the ejected material doesn’t orbit for very long!
We define the launch velocity as v0, and note that material that reimpacts the surface also does so at v0 (ignoring effects of extreme shapes or topography).
The equation for the velocity is:
where x is the horizontal displacement, y is the vertical displacement, g is the surface gravity, and theta is the launch angle.
The material that originates closest to the center of the impact site is that which travels both the furthest and the fastest away from the impact event. The slowest-moving ejecta originates furthest from the center of impact. This ejecta will fall closer to the crater rim, while fast-moving ejecta will fall far out in a discontinuous ejecta blanket eventually formed around the crater. This situation forms a moving, inverted cone of material called a “debris curtain.” The debris curtain sweeps over the surface of the body, with the coarser debris near the base of the cone and the finer, more modified debris near the top.
Because of this, the material closer to the crater hits the ground more slowly, and with less of a horizontal component to its motion. This blankets the ground with minimal mixing between the original target regolith and soils. In contrast, the faster-moving material that is launched farthest from the crater hits the ground with more energy, and with a higher horizontal component. The result is greater disturbance and mixing with the regolith at the reimpact site. Such a fast-moving combination of material can move like a landslide debris flow, scouring the underlying surface, and “creating dunes, ridges and radial troughs” (Melosh, 2011).
Downslope Movement of Regolith
Even on bodies with very low gravity, the movement of material downslope to gravitational lows is a critical process. Such movement may be dramatic, as in the form of a landslide, or may be very slow and inexorable as in the form of regolith creep. Such movement might be triggered by a host of events: a nearby impact, seismic shaking, temperature cycling, and more. The ubiquitous nature of such regolith movement on all airless bodies makes it a key phenomenon with regards to soil movement. Here we begin with the subtle process of creep, to slumping, and then to landslides.
Regolith Creep
Creep is a result of a combination of processes slowly moving material down a slope. If there were no slopes, the processes may instead allow for a local and directionally balanced mixing. But because both gravity and topography exist on airless bodies, the movement of particles downhill is inevitable. Anything that disturbs the surface layer may serve as a catalyst for movement, and since coefficients of sliding friction are typically lower than for static friction, it typically takes less force to maintain motion than initiate it on planetary surfaces. There are several processes that could serve to initiate movement on airless bodies. Micrometeorite impacts are constantly sandblasting the surfaces of airless bodies (also see later). Temperature cycling can cause the expansion and contraction of materials. The gain or loss of volatiles can change the orientation and cohesion of particles. Other space-weathering processes also contribute in subtle ways to disturbing the surface, such as the emplacement of solar wind particles and alteration of basic minerals. In all cases, the existence of the slope causes a net asymmetry in the movement of the particles, resulting in downslope creep.
Creep is responsible for some tell-tale features such as hills with rounded tops, small, narrow terraces (called “terracettes”), and smooth, long ridges of debris at the bottoms of their slopes. Slopes of material formed by creep are usually convex—soft hill shapes, rather than straight or concave. Another tell-tale sign of creep is the general smoothing and filling of features such as impact craters. Smaller craters are rapidly and preferentially wiped out over time as creep takes its toll. Their rays and ejecta blankets are erased even faster than their rims.
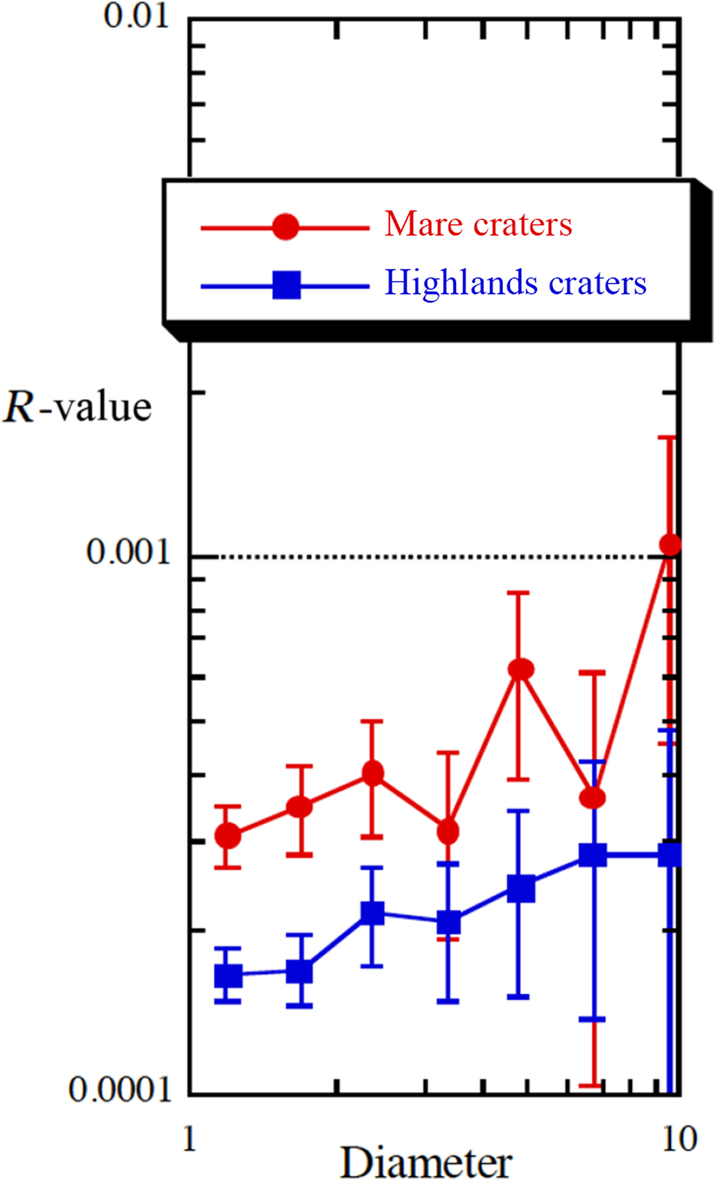
Optical maturity (as described in Chapter 4) can lend some insight into the results of downslope movement of ejecta. On the left of Fig. 8.1 is a Clementine visible light image of the surface of the Moon showing the expected clear boundary between the light highlands and the dark mare. On the right we see that that boundary is nearly invisible, as would be expected, because OMAT minimizes contrast due to mineralogical composition, and highlights contrast due to age. Again, as expected, the OMAT image reveals a large number of small, bright craters whose ejecta is optically immature, suggesting a very young age.

We would expect the highlands and the mare to have similar numbers of these very young craters, as both surfaces have been exposed to the same flux of small impactors for billions of years. However, we can see in the OMAT image that the bright ejecta from the small craters in the highlands has been preferentially wiped out. Statistics bear out the visual difference. Fig. 8.2 shows crater densities for these two groups. The mare region shows a higher density of craters. This is attributed to the creep and general downslope movement of material mixing and covering the bright, optically immature ejecta preferentially in the highlands, which has higher slopes on average than the mare.
Angle of Repose
As loose material moves, it can pile up or form debris slopes. The profile of slopes made of material that otherwise lacks any specific source of cohesion (c = 0 in the Mohr-Coloumb equation earlier) can be described by the “angle of repose.” This is the steepest angle with the surface of the body that a pile of loose material can assume. The angle is independent of the mass of the loose particles and independent from the gravity of the body. It relies strictly on internal friction. Loose material has no strength other than the internal friction between its constituent particles. The physical result of the equations is borne out through measurements of slopes on all forms of airless bodies from the Moon to asteroids, where such features vary only by a matter of degrees (Melosh, 2011; Fig. 8.3).
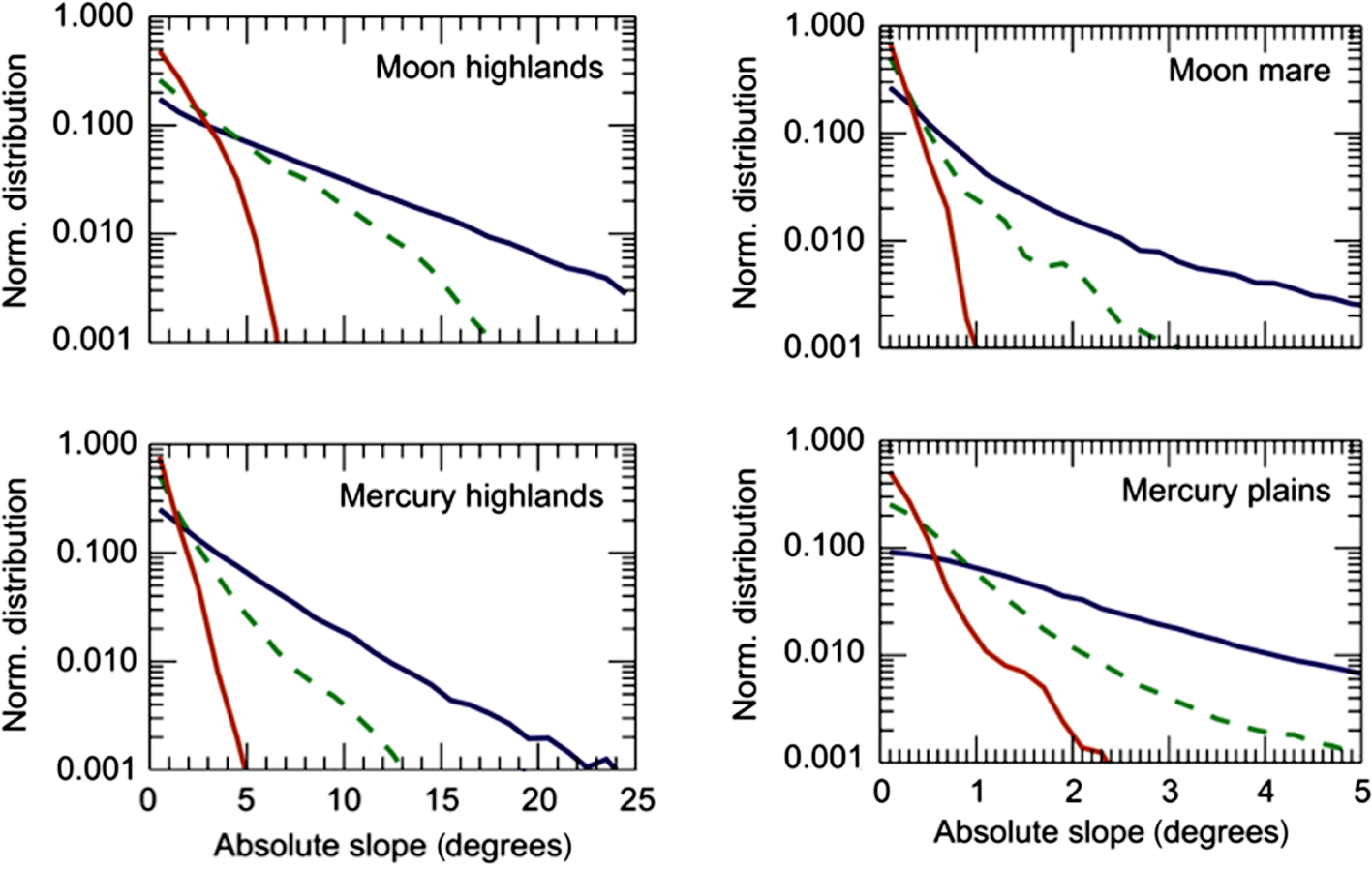
The slope measurements of unconsolidated debris on asteroids are dependent upon the shape model for the body and the direction of the local normal force of gravity. In this case, one sees the slopes are very consistent and less than the expected angle of repose (Fig. 8.4).

Note that on asteroids, slopes can appear to be counterintuitively steep. Nevertheless, the vast majority of slopes are less than about 30 degrees, even though they may appear steeper. This misconception is based on the shape of asteroids, which appear to have unusual topography in comparison to large, spherical bodies.
Slumping and Landslides
Slumping and other processes like landslides happen when a slope or cliff face suffers some form of failure, and suddenly slips downward. Cliffs can collapse in a variety of ways depending on catalysts like space weathering, shaking, preexisting faults or cracks, etc. We might see a coherent slab move down vertically, or an avalanche of a wedge-shaped mass of material (Fig. 8.5). Cliffs also fail slowly through smaller falls of rock or slow disintegration due to space weathering. These processes all produce falls or debris slopes of different kinds (Melosh, 2011).
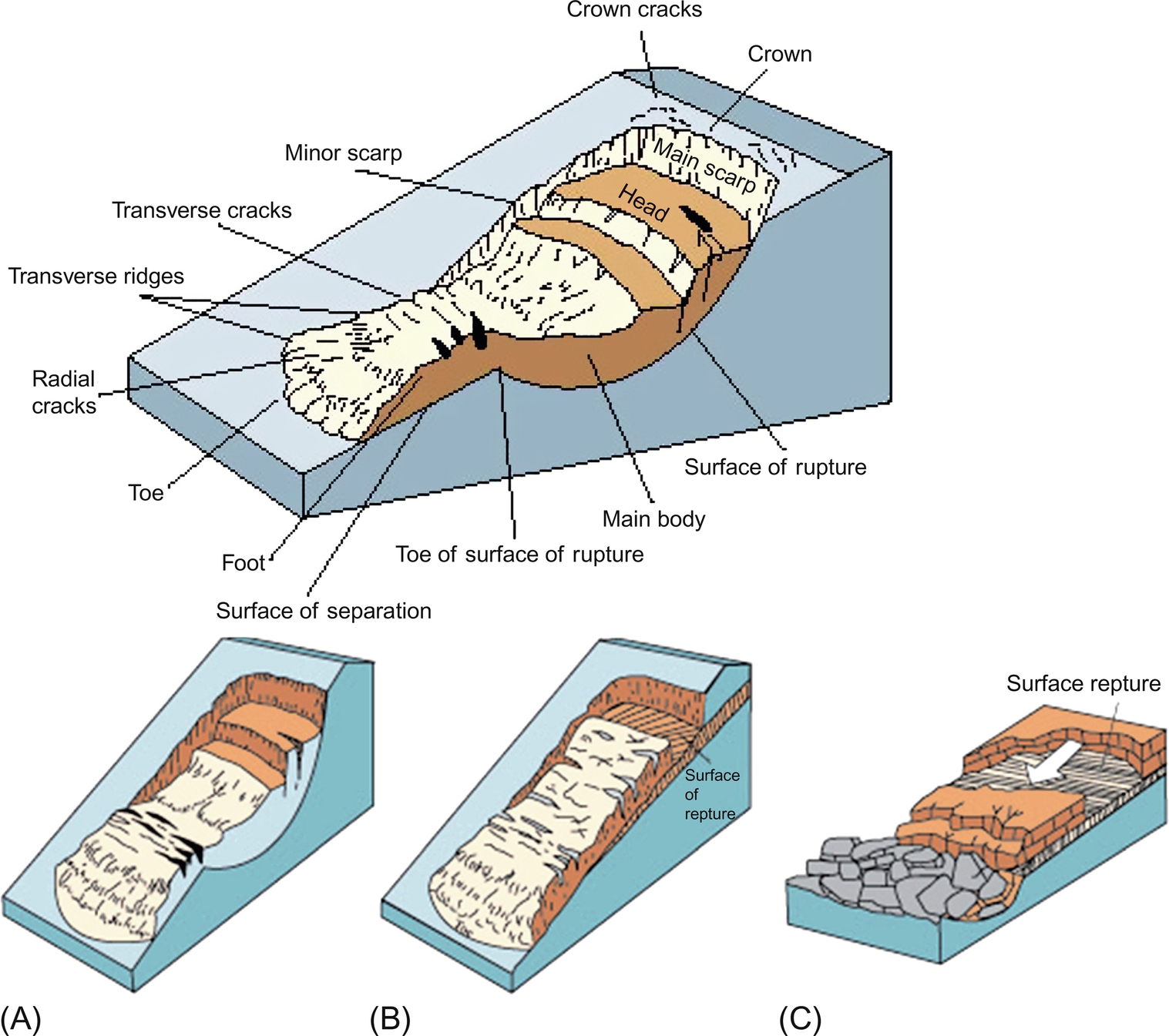
Slumping can happen on various time scales, and may result in a slice, terrace, or hummock of material that remains relatively close to the original location. A slump may include a slab of material slipping vertically, or a hemisphere of material essentially rotating as it slumps (Figs. 8.6–8.8). A rotational slump will have a raised scarp near its head. Materials with particularly low angles of internal friction are more susceptible to rotational slumping (Melosh, 2011).

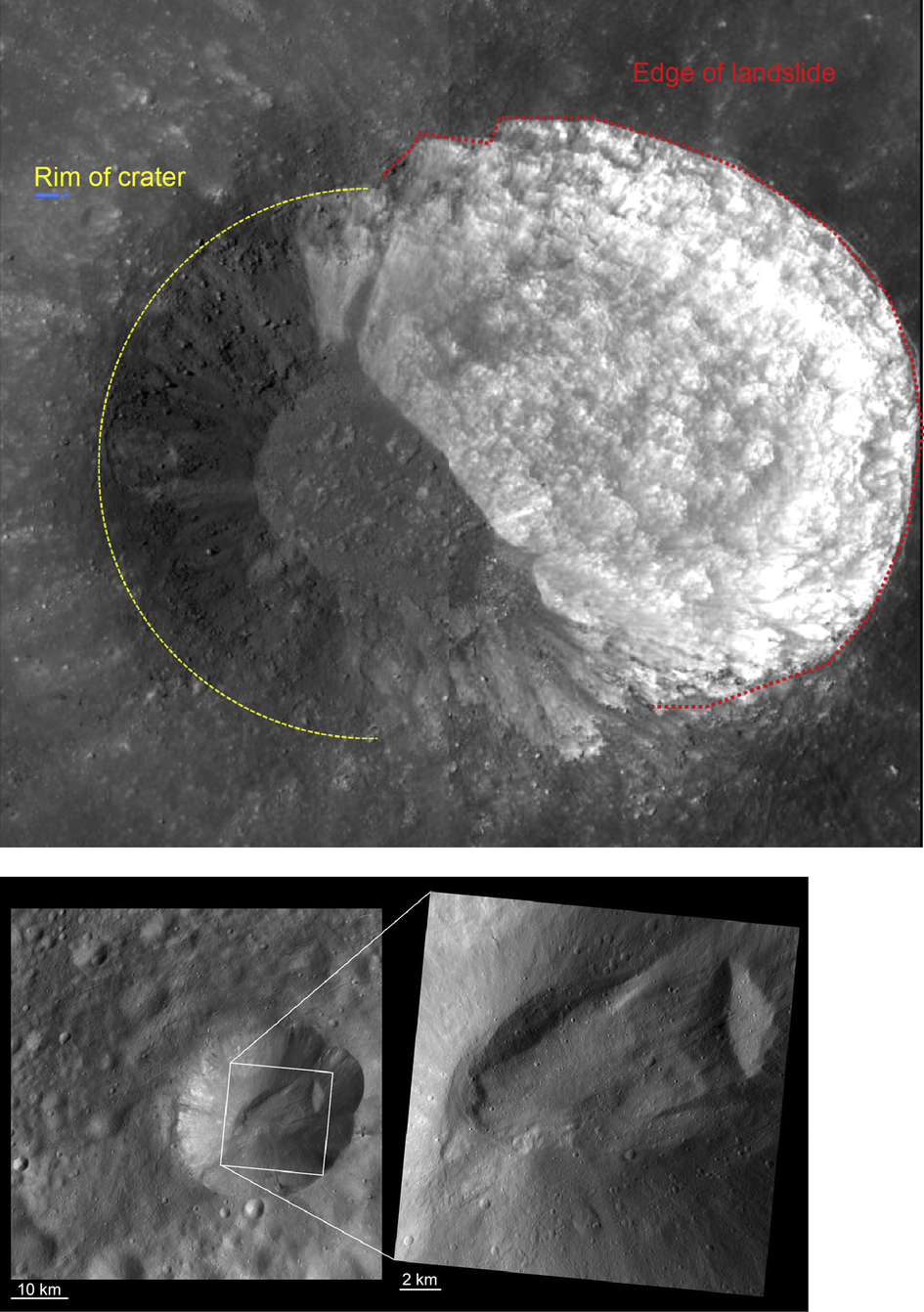

Slumps are a common feature of complex impact craters. Slumping is an important process in the postimpact modification of these craters. As noted in Fig. 8.6, parallel fractures can form in the crater rim, where blocks of material are slumping down to the interior of the crater.
Landslides are relatively dramatic events where a failure allows for a mass of material to move downslope some distance away from the point of origin. Landslides are a common feature on larger airless bodies.
Ceres, with its icy subsurface, has several different classes of landslides, including some that are not seen on the dry airless bodies. Schmidt et al. grouped cerean landslides into three classes: Type I, which are preferentially found at higher, colder latitudes on Ceres and appear like icy landslides on Earth; Type II, which appear like landslides on other objects; and Type III, which appear to involve liquid water, which may have been mobilized from the icy subsurface during impacts. While Ceres is unique in terms of being the only transitional ice-rock object visited by spacecraft, there are several other objects in the asteroid belt that could have similar landforms. Future spacecraft visits to those objects will be necessary to find them.
Most landslide-style movements do not happen at high speeds. But there are certain types that travel very quickly, and which travel extensive distances. Deposits from these “long-runout” landslides have been observed on airless worlds such as the Moon and even Phobos (Melosh, 2011). Such landslides require large volumes of material, but do not require steep slopes. They are enigmatic, and do not require fluid or gas. Such material movements may be mobilized through a process known as “acoustic fluidization” (discussed in the next section).
Seismic Shaking and Regolith Convection
Vibration has been used in industry to enhance the flow of granular materials. Melosh (1979, 1983, 1989) proposed the concept of “acoustic fluidization” to explain the physics of the transition from simple to complex lunar craters, though it also has application to mobility of long-runout landslides. The concept is that vibration or rhythmic shaking can cause material to flow like a fluid, and allow that material to achieve the viscosities needed to create lunar central peaks of the correct, observed heights (Melosh, 2015). Given the relative accessibility of terrestrial landslides to field geologists vs. lunar crater central peaks, much of the modeling and validation of the acoustic fluidization model can take place using these terrestrial analogs.
Impacts carry enough energy to shake the surrounding area. The size of that surrounding area depends upon the size of the impact, of course. The size of the object, in turn, determines whether the effects are near-global or very local. A 1-km crater on Mercury will not affect a very large fraction of its surface area, while a similar-sized crater on Eros will. The small impacts involved in the gardening process described in Chapter 7 can do more than simply mix material on smaller objects, but have also been implicated in the erasure of craters and other features on asteroids.
Richardson et al. (2005) looked at the detailed seismic effects on impacts on asteroids. They found that objects smaller than ~ 70–100 km could experience “global, surface-modifying” effects from a single impact—for larger objects to experience those effects would require a large enough impactor to disrupt the body. They also found that for Eros-sized asteroids, global effects could be induced by relatively small impactors: a 1-m impactor was calculated to be sufficiently large as to globally loft even cohesive material sitting on a 2 degrees slope. Such impacts were thought to occur on the timescale of centuries for an Eros-sized body in the main asteroid belt. More recent work by Garcia et al. (2015) focused on km-scale and smaller asteroids and found that earlier work may have underestimated the seismic effects of impacts on small bodies. They calculate that a 10-g impactor may loft material mm to cm off the surface for tens of seconds, depending on distance from the impact. Impacts of this mass (corresponding to ~ 1.5-cm impactors) occur on roughly yearly timescales for objects with a surface area of ~ 1 km2 (Richardson et al., 2005). This combination of frequent lofting of regolith and relatively shallow depths of small craters is thought to be responsible for erasing small craters on asteroid surfaces.
Seismic shaking also serves to sort the regolith of airless bodies. The sorting process is called the “Brazil Nut Effect” (BNE), after the experience of opening a can of mixed nuts to find them sorted, with the large Brazil nuts preferentially at or near the top of the can. In this case, smaller nuts can fit into spaces where larger nuts cannot. When shaken, smaller nuts tend to fall into those spaces and work their way to the bottom of the can, which given the limited volume, raises the larger nuts to the top. Asphaug et al. (2001) suggested this process might also happen on airless body surfaces, with smaller particles preferentially able to fall through voids, leaving larger particles and blocks at the surface. In particular, this has been investigated for smaller asteroids, which are thought to be rubble piles with the potential for significant void spaces throughout their volumes. Perera et al. (2016) found in simulations that the BNE was effective in bringing larger particles from the shallow subsurface to the surface, though it could not bring about similar sorting throughout the mass of an object: a body that is well mixed in terms of particle size remains well mixed at depth. Studies of the BNE have also shown that friction and boundary conditions play a role, and work is still underway to better simulate the conditions that would be found on airless bodies.
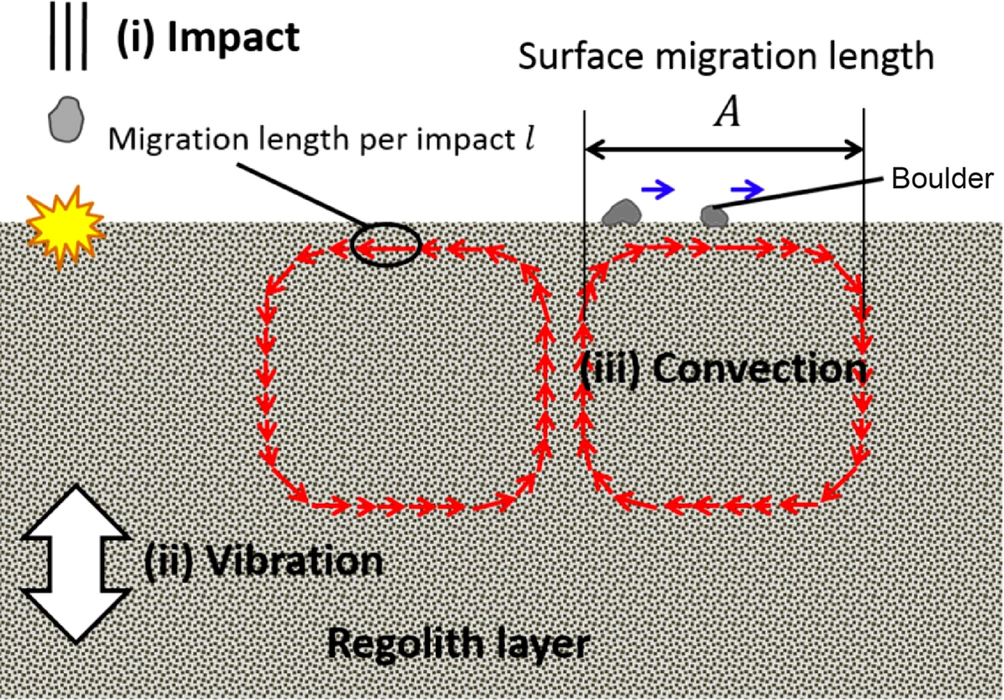
Granular convection is a general term for the process during which the BNE occurs. The causes for granular convection are still mysterious, but it is an experimentally well-established process that occurs when granular material (such as a regolith) is subjected to repetitive vibrations. In the laboratory these vibrations are continuous, but it is thought that the sporadic but unceasing micrometeorite impacts and long periods of time that are available can serve to create the needed vibrations and that granular convection may play a role in asteroid regolith gardening. In this scenario, the convection cells that are created bring material to the surface, and then move material laterally on the surface until reaching the end of the cell (Fig. 8.9). At that location, smaller particles move downward but larger particles remain stranded at the surface due to the BNE. Calculations by Yamada et al. (2016) show the conditions under which regolith convection can occur: for a 100-m object, impactors of ~ 0.9–2.5 m cause global convection while larger impactors disrupt the body and smaller ones do not cause convection. For 1-km objects, the global convection impactor size range is 5–30 m. For objects over 8 km, Yamada et al. calculate that only local convection is possible.
Asteroid Regolith “Ponds”
When NEAR Shoemaker began imaging Eros, it revealed many surprises. One of the greatest was that along with the boulders and craters that were expected images also revealed smooth deposits (Fig. 8.10). Their locations on Eros appeared to be nonrandom: over 90% of the identified ponded deposits are within 30 degrees of the equator, and most are at the ends of the Eros’ irregular shape (Sullivan et al., 2002; Dombard et al., 2010). Ponds can be over 200 m in size, but most are < 60 m across. This small size has led to concern that the apparent nonrandom location could be an observational artifact: while 60% of known ponds are found in the small surface area that was imaged with 2 m/pixel or better resolution, over 80% of Eros’ surface was not imaged to that resolution and therefore ponds may exist there but remain undiscovered (Roberts et al. 2014a). It also has been reported that another early observation, that of flat surfaces of ponded deposits, also may not hold up under increased scrutiny: Roberts et al. (2014b) find that fewer than half of candidate ponds have “clearly flat floors.”

It is generally agreed that ponds have spectrophotometric properties that differ from other parts of Eros, with bluer colors than typical areas on the asteroidal surface (Robinson et al. 2001). These colors suggest either very small grains or, somewhat paradoxically, relatively large ones compared to other parts of Eros. The highest-resolution images of Eros, including a small portion of a pond visible in the final prelanding images, are consistent with very fine grains. It is also noted that there is sufficient cohesion in ponded materials to support fairly high slopes, as seen by the existence of steep-sided collapse pits in the regolith (Fig. 8.11).

While the ponds on Eros were a huge surprise, two broad scenarios were quickly identified to explain their formation: (1) They are formed via mass wasting of material from crater walls during episodes of seismic shaking from impacts elsewhere on the body, or (2) They are full of material brought in from elsewhere on Eros by electrostatic levitation (see next section). The work of Roberts et al. suggests both processes may be operating in tandem and responsible for different ponds or “quasiponds.” A third possibility, that of in-place thermal disaggregation of boulders, has also been proposed in recent years (see discussion in Chapter 7).
Electrostatic Effects and Levitation
Regolith motion can also occur via other means. While Mercury's magnetic field globally protects its surface from the solar wind and the associated solar-generated interplanetary magnetic field (IMF), solar wind plasma interacts with the surfaces of airless bodies without magnetic fields, and there is evidence that these interactions can transport regolith grains.
The Physics of Dust Levitation
The solar wind is a plasma, with physics unlike the other processes we investigate in this book. As a plasma, it is charge-neutral on large spatial scales but protons, electrons, and alpha particles are not bound into atoms. Instead, each group of subatomic particles can come to its own group equilibrium and have a separate temperature, for instance. Also, because electrons, protons, and alpha particles have different charges, plasma interactions can become very complex when surfaces have generated a charge of their own.
Sunlit surfaces are subject to the photoelectric effect, which causes electrons to be emitted when electromagnetic radiation is incident upon them. This is sufficient to overcome any effects due to the solar wind plasma, and gives regolith grains an overall positive charge. On the night side of the object, the absence of the photoelectric effect means the situation is entirely controlled by plasma effects: the thermal speeds of the electrons are much higher than those of the positive ions, and as a result they are freer to move separately from the overall flow of the solar wind. The random motion of electrons allows them to reach the night side of the Moon and asteroids while protons cannot, which leads to a strong negative charge. This negative surface charge leads to the establishment of a Debye sheath (Stubbs et al., 2005), a region with enhanced concentrations of positive and neutral ions, with a thickness of tens of meters or more. The daytime surface potential has been calculated to be a few volts, while the nighttime potential can be − 100 V or more (Fig. 8.12).
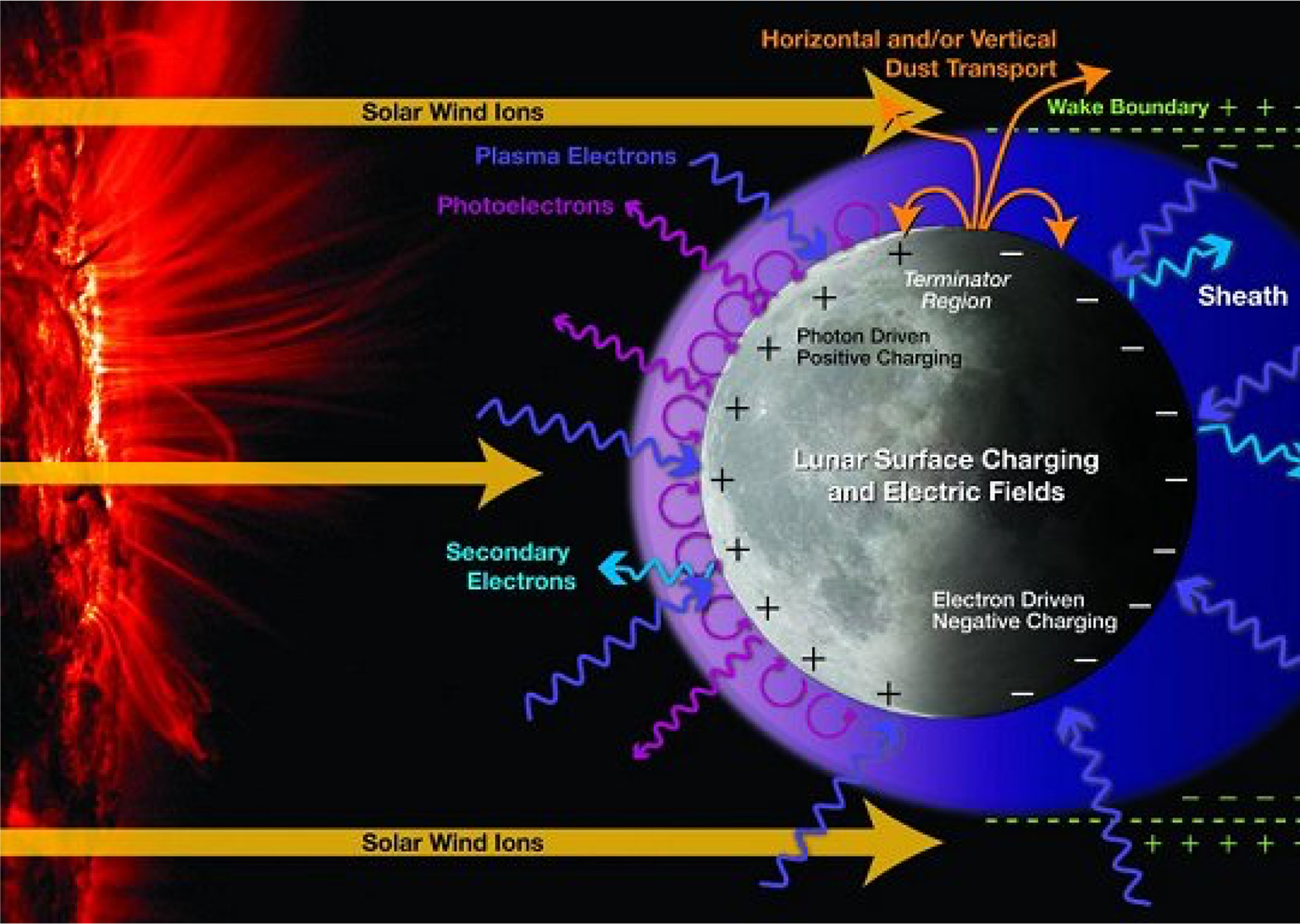
Given the change in the electrostatic environment between day and night, the strongest potential differences on airless bodies can be found at the terminator. The complicated plasma interactions around craters may also lead to enhanced electric potentials, as areas in full sunlight may be in close proximity to areas shaded by a block or other topography. Calculations by Criswell and De (1977) and Lee et al. confirmed by simulations done by Aplin et al. find that the field strength can be tens of kilovolts per meter at the terminator, or even higher on submeter spatial scales. More sophisticated models have been developed recently by Zimmerman et al. (2014).
Hartzell and Scheeres et al. estimated that fields of that strength could exert forces that are equal or greater than the surface gravity plus cohesion on ~ 100-m asteroids for regolith particles tens of cm in size. The stronger gravity of the Moon would keep more massive particles grounded but fields of that strength could still counteract gravity for lunar particles of ~ 10–100 μm. Aplin et al. developed a 3D model of the electrostatic environment of asteroids in support of an asteroid sample return proposal, and found the fields that were modeled to be present could not lift particles that large, concluding that electrostatic levitation was restricted to particles of 100–300 μm size on Itokawa.
Further calculations by Hartzell and Scheeres (2013) found that while electrostatic forces might be unlikely to loft particles from a position of rest at the surface, they could keep aloft particles lifted by other means (for instance, slow ejecta from a micrometeorite impact), and μm- to nm-sized particles could have stable hovering positions at ~ 10-m altitude in simulations of the Moon, Eros, and Itokawa. Depending on initial conditions, however, these hovering particles might eventually reimpact the surface or be ejected from the body entirely.
Very recent experimental work by Wang et al. and Zimmerman et al. suggests that even further charging of particles may be possible. The porosity found in regolith allows light to enter interparticle gaps and reach regolith grains that are not at the very surface of an airless body. The electrons emitted from these deeper grains via the photoelectric effect can, in turn, attach to grains that share these gaps. This increases the potential difference between the surface grains, which preferentially obtain a positive charge during the daytime, and the grains one or two particles deep, which preferentially obtain a negative charge at all times of the day. The experiments show that the resulting electrostatic force can eject surface particles at 10s of cm/s.
Lunar Observations
The recent attention given to electrostatic levitation of regolith particles via experiments, simulations, and calculations has been aimed in part at interpreting 50-year-old measurements. The lunar lander missions Surveyor 5, 6, and 7 all detected a glow along the horizon shortly after sunset (Fig. 8.13), which was interpreted as due to light scattering off of a layer of dust ~ 5 μm in size and roughly a meter or less above the lunar surface. Additional measurements were made by Apollo astronauts in lunar orbit who sketched areas of horizon glow and “twilight rays,” which have been explained by a combination of zodiacal dust (interplanetary dust also visible from dark sites on Earth) and crepuscular rays. However, the latter requires more dust at higher altitudes than the Surveyor observations of horizon glow. Glenar et al. argue that the Apollo measurements coincided with meteoroid showers on the Moon and that the excess dust could have been generated via impact and not typical.

A measurement of a horizon glow by the star trackers on the Clementine spacecraft suggested dust at altitudes of several tens of km, but this remains a preliminary measurement. Beyond the imaging and photographic evidence for dust levitation, there is evidence from a dust detector placed on the surface of the Moon by Apollo 17 astronauts, which registered an increase in events near sunrise and sunset. This has been interpreted as consistent with detections of electrically charged regolith grains moving at 100 m/s or less, with the timing of the detections suggesting a connection with the horizon glows and associated levitation process.
Levitation on Asteroids
Phobos, Deimos, and most if not all asteroids lack magnetic fields, and the processes that levitate particles on the Moon might be expected to also operate on their surfaces. To this point, however, we have had neither landers like the Surveyors nor orbiting humans in position to search for horizon glows. The reduced gravity of asteroids, as mentioned earlier, would allow larger particles to be lifted than on the Moon for similar conditions. It also should allow particles to be lifted with smaller electrostatic forces than are expected for the Moon. Interestingly, the escape speeds for 1-km asteroids are roughly 1 m/s (depending upon density), suggesting that the electrostatic forces could potentially not only loft regolith but eject it from an asteroid of that size or smaller.
The ponded deposits on Eros were first interpreted as created through dust transport via levitation, and these features remain the strongest candidates for evidence of this process on asteroids. Eros’ very high obliquity also provides long periods of light and darkness for most latitudes, though it is likely that charge equilibrium is reached relatively quickly. As noted, more recent work on the ponds of Eros by Roberts et al. favors seismic shaking as the primary source for ponded material, though electrostatic levitation remains a likely contributor.
Ponds similar to Eros are not seen on Itokawa, though this needn’t be inconsistent with electrostatic forces being important: the escape speed on Itokawa is sufficiently low that all fine material may have been lofted too quickly to be retained, for instance. It's also worth noting that the candidate pond locations on Eros are of similar size to Itokawa itself. No measurements of or constraints on dust levitation are available for Vesta or Ceres, though enigmatic “haze” has been imaged on the latter body. Vesta, with a basaltic composition like the Moon and abundant regolith, is a candidate for experiencing similar electrostatic processes, and measurements from a vestan equivalent to the Surveyor missions could allow a better understanding of dust levitation in general.
Summary
Once regolith is created, there are several processes that serve to move it. The constant rain of impactors can cause material to move as ejecta but can also create distant movement of material via seismic shaking. Regolith on slopes may steadily move to lower altitudes via creep or suddenly via slumps or landslides. Mixing within the regolith may occur via poorly understood granular convection, with larger particles preferentially finding their way to the surface at the expense of smaller particles. Plasma effects can also move particles, and are thought to create layers of levitating dust on the Moon and perhaps other airless bodies. The smaller asteroids can feature more extreme versions of these processes, with even tiny impactors resulting in global effects. Interparticle cohesion also plays an increasingly important role as objects become smaller, with the possibility that clumping of small, cohesive particles may mimic landforms that would otherwise be interpreted as due to intact rock.