9.1 Background and Objective of This Paper
One of the major tasks of the history of mathematics education is to clarify the current position of mathematics education by examining the viewpoints of past reforms, which include the transition of issues, objectives, and materials. One of the difficulties is the interpretation of curricular reform in the context of earlier periods. In particular, based on the Japanese interpretation of the new math movement,1 the secondary school curriculum was more oriented towards algebraic representation. Thus, current mathematics educators have never had a chance to study the mathematics that existed in the past. Historical mathematics before our times is, therefore, a kind of lost mathematics based on different conceptual frameworks, even though the technical terms look the same.
Reading and understanding historical textbooks gives the opportunity to relearn lost mathematics and recognize their viewpoint. The mathematics Clusters I and II textbooks from 1943 to 1944 (Grades 1 to 4, for 12- to 15-year-old students, Published from Secondary School Publisher)2 for secondary school,3 were a decisive achievement under the influence of the Klein movement4 in the Far East, since starting with these books preliminary calculus became introduced into the mathematics curriculum of Japanese secondary schools. Even though published in the middle of World War II, the textbooks were very well organized and applied the principle of mathematization. Thus, they are usually referred to as the mirror to reflect the curriculum reform that was oriented towards mathematical activity. Indeed, after World War II, Japanese curriculum reforms developed appropriate mathematical activities (beginning in 1947), mathematical thinking (beginning in 1951), and mathematization (after the war and again in 2017). For current educators, however, it is difficult to understand these textbooks within the original meaning of the reform because it is based on lost mathematics. However, what is that lost mathematics in Clusters I and II? Several mathematics education research papers in Japan have examined this question. However, due to their brevity, the papers mainly focused on historical issues in the development of textbooks but did not provide an opportunity for current readers to learn about the lost mathematics itself.

Van Schooten (1646), excerpted from pp. 1–3, 26, 28, and 30, and Cluster II (1943), Vol. 3 (Grade 3 for 14 year olds), excerpted from pp. 2, 3, 4, and 27
The textbooks in Fig. 9.1, published almost 300 years apart, cannot be directly connected. During those 300 years, historical processes were developed and revised for reorganizing mathematics in mathematics textbooks.5 In the end, the same tasks and sequences may emerge that were earlier based on Euclid. Thus, the sequence in Fig. 9.1 can be understood as being based on Euclid. However, Clusters I and II did not include Euclidean-geometric proofs even though they enhanced the demonstration and proving by students. Before Clusters I and II, geometrical proof and construction was employed in secondary school. To introduce content up until calculus, however, Clusters I and II used intuitive explanation with practical experiments using various instruments rather than exact proof.6
Even though the influence of Klein involves long historical processes, one piece of evidence of the missing link connecting Japan and Europe is Hans von Sanden’s Praktische Analysis (1914). This paper aims to illustrate the significance of this missing link in order to understand the historical development of the Clusters I and II mathematics textbooks. These books show the influence of the Klein movement on the integration of subjects up to calculus into the curricula of the Far East, especially in Japan, but not only there.7
9.2 The Influence of Klein on the Far East: The Case of Japan
During the Meiji period (1868–1912), leading Japanese mathematicians studied in Europe8 in countries such as UK, France, and Germany. Many of them studied in Germany and the Klein movement in Europe was well known since its earliest stage.
The state of mathematics in schools at that time was summarized at the Fifth International Congress of Mathematicians in Cambridge in 1912, when the Japanese sub-commission of the International Commission of the Teaching of Mathematics published the Report on the Teaching of Mathematics in Japan (see Fujisawa 1912/2017). In the attached Divisional Report II, after the preface of Fujisawa, Noriyuki Nishikawa, Professor at Tokyo Higher Normal School, already mentioned for the middle school the movement “to give the pupils elementary concept of function is most important as a direct aim in teaching of algebra” (Nishikawa 1912, p. 13). At that time, graphs and functions were recognized as content that bridged subjects such as arithmetic, algebra, and geometry. However, the curricular reform of 1911 only mentioned that they should be treated in teaching and not as a means of integration of subjects. The curriculum at that time was influenced by the first generation of mathematicians who had studied in Europe, such as Dairoku Kikuchi,9 who finally became the minister of education, and his colleague, Rikitaro Fujisawa.10 Fujisawa insisted in the independence of every sub-discipline in mathematics to keep their theoretical differences. In his context, he could not share the reform conception of integrating the sub-disciplines.
It was against this conservative situation that under the order of the Japanese Ministry of Education, Gaisaburo Mori translated Otto Behrendsen and Eduard Götting’s Lehrbuch der Mathematik nach Modernen Grundsätzen (1908, 1911) for secondary and high school teachers from German into Japanese in 1915–1916. To promote the reform movement throughout Japan, Motoji Kunieda and his colleagues at the Tokyo Higher Normal School established the Japan Society of Secondary School Mathematics11 in 1919. The society shared the reform movement at every annual meeting as a national issue. Secondary school teachers presented their research on curriculum innovation at these meetings and it was published in the society’s journal.
In 1921, Tsuruichi Hayashi, the first president of the society, translated Klein’s 1904–1905 lectures for secondary school mathematics as the first book (1907) of the University of Göttingen lecture series. Kinosuke Ogura supervised the translation of Leçons d’Algèbre Elémentaire by Bourlet (1909) in 1919 and translated Praktische Analysis by von Sanden (1914) in 1928. Before these translations, a limited number of mathematicians, teachers and students had read the original books. The reform’s intentions reached every secondary school teacher thanks to these Japanese editions. Hayashi recommended in his preface to Klein’s book (1907) that secondary school teachers read both books by Behrendsen and Götting and by Bourlet. Both books treat functions and calculus in their later chapters, which follows the goals of both textbooks. The book by Bourlet was dedicated to algebra. The book by Behrendsen and Götting treated geometry, algebra (including coordinates, graphs, and simple construction), trigonometry, calculus with functions for Gymnasium, and projection.12
While the book by Behrendsen and Götting was written for secondary schools (Gymnasium), the book by von Sanden (1914) was written for undergraduate students based on his experience at the University of Göttingen.13 It treated integration of algebra and geometry for calculus with graphs of functions, construction with geometry, and plotting points as the sets of numerical solutions. This paper discusses how von Sanden’s book influenced the integration of subjects up to calculus at secondary schools, comparing it with Hamley’s (1934) Relational and Functional Thinking in Mathematics.
9.3 Integration of Algebra and Geometry with Mechanical Instruments
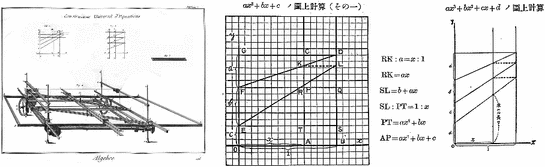
Mechanical instruments to draw the graph of polynomial functions, bridging geometry and algebra in Diderots’s Encyclopedia; cited in Vol. 19, of the Supplements (Diderot 1776): Equation, pp. 832–840 and in Vol. 33. Planches (Diderot 1777) Algebrae, p. 18, Constructeur Universel Equations, p. 14-E33-Nr. 33. The explanation on the right is from Kuroda (1927, p. 299) (Minoru Kuroda was the first mathematics educator who had the opportunity to study in Europe. This book was published posthumously in 1927 (he passed away in 1922) as a part of his collected publications. One third of the content was based on what he learned in Germany in 1910–1911 and in England and the US in 1912. The rest was his lectures at the open classes done by other teachers who promoted reform ideas and tentative plans for curricular reforms. His textbooks were mostly familiar textbooks that included the ideas of new movements within the limitation of the old curriculum. After he came back to Japan from abroad, he became a professor at the Tokyo Higher Normal School and wrote secondary school textbooks based on what he learned and what he experimented with at the affiliate secondary school of the Tokyo Higher Normal School.).
The influences of reform movements in Japan came not only from Germany but also from the UK and the US. Indeed, the Japanese respected John Perry, who began his professional career as a mathematician in Japan at the beginning of Meiji era. He became the president of the Physical Society of London in the early 20th century, and his works were also translated into Japanese. Perry also emphasized practical mathematics, even though he did not enhance the integration of the subjects including calculus using the function concept as Klein did. Experimental methods developed by Eliakin Hastings Moore in the US were also well known. Because the Japanese were able to practice their experimental research for several decades, reforms were achieved by the third generations, and thus, they also knew the work of Hamley14 (1934), which was also translated into Japanese by Aoki (1940).
Figure 9.2 shows an example for the integration of geometry and algebra for functions from Diderot (1776–1777) which is from Johann Andreas von Segner (1704–1777). He was born in Hungary, and in 1735 he became the first professor of mathematics at the newly founded University of Göttingen. This mechanism also appeared in von Sanden (1914). Kuroda (1927) explained the idea in the context of the reform movement proposed by Klein, which integrates geometry and algebra via graphs of functions.
9.4 Embedded German Praktische Analysis in the Japanese Textbook for Cluster I (1943)
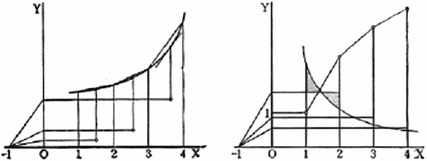
Drawing the derivative and the primitive function from the given graph in Mathematics Cluster I (1944), Vol. 4 (Grade 4 for 15-year-olds), p. 9
Figure 9.3 can also be seen in von Sanden (1914, pp. 97 and 103).15 According to the Japanese translators and editors, Ogura and Kondo (1928), Klein established the course for praktische Analysis at the University of Göttingen in 1904. Von Sanden became a lecturer at Göttingen and published the book based on his lecture courses. Ogura explained in the Japanese edition that Praktische Analysis was the best book in this area because of this origin. In addition to the English translation by Levy (1923), the Japanese edition was an adaptation by Ogura due to his addition of content and footnotes to make it more easily understood.16 Thus, various efforts have been made to adapt the ideas of von Sanden from university mathematics into Japanese secondary school mathematics.
9.5 The Influence of Klein: Germany or Origins from UK and US?
Klein has said that “for a thorough and fruitful treatment of the function concept, the fundamentals of mechanics may be taken as a necessary material.” With this opinion we are in full agreement. It is not clear whether Klein restricts the term “mechanics” to kinematics, or whether he also includes kinetics, which involves the concept of mass. In our course, we have confined our attention almost exclusively to kinematics, not because of any unwillingness to include kinetics, but because the space-time concept provides us with all the functional material we need. (p. 112)
Klein emphasized mechanics as the foundation of the treatment of the function concept. However, Hamley explained the space-time concept as an alternative to kinematics. Mechanics here was basically represented by geometry. Klein propagated the integration of algebra and geometry for teaching calculus. Hamley introduced the space-time concept, which can be represented by numbers and algebra without geometry. Even though the space-time concept is normally used for functions in algebra, according to Hamley’s claim, Fig. 9.3 could not be explained because it does not depend only on space-time. This is how we can affirm that Klein and von Sanden’s view is shown in Fig. 9.3.
Of course, we also recognize that space-time situations appear in the introduction of calculus in Cluster I. However, in the case of Cluster I, differentiation and integration are solved using Fig. 9.3 before introducing the algebraic operations of differentiation and integration.17 Before algebraic operations, the idea of the fundamental theorem of calculus is introduced, and space-time situations are solved by geometric operations as shown in Fig. 9.3. Additionally, in Cluster II, which is taught in parallel with Cluster I, before learning calculus, kinematics is applied as visualized in Fig. 9.1.
9.6 Conclusion
Due to the comparison between the books by von Sanden and Hamley, the integration of the sub-disciplines arithmetic, algebra, and geometry including calculus in Japanese school mathematics, which was originally proposed by Klein, is evidenced in Clusters I and II. We showed the book by von Sanden to be a missing link to the currently lost mathematics, which we never learn up to university in these days.

Mechanics and kinematics as a missing link for teaching the integration of the sub-disciplines including calculus
Figure 9.4 shows the basic framework for Clusters I and II. However, the era of the US occupation of Japan after WW II resulted geometry with constraction was reintroduced but the functions up to calculus were following space-time framework.18 There were two reasons. The first reason was the transforming of the school system from parallel to linear. The curriculum for secondary schools was divided into one part for new junior high and another for senior high schools, and student populations were redefined. Compulsory education ended with junior high schools, at 15 years old, with the curriculum reaching proofs in geometry and quadratic functions. Senior high schools were divided into schools depending on student achievement, from preparatory schools for the universities to various vocational schools. The second reason was the New Math. Algebraic mathematics including vectors and matrices were introduced, and construction and trigonometry in geometry became restricted. In this context, the direction from geometry to calculus in Fig. 9.4 by kinematics and mechanics becomes the missing link to understand Clusters I and II for our period.
Currently, technology such as dynamic geometry software enables anyone in the world to approach mechanisms and kinematics of Figs. 9.1, 9.2 and 9.3. For example, Isoda (2008) developed e-textbooks19 for Fig. 9.1 and engaged in lesson study to demonstrate their significance in mathematics education (see Bartolini Bussi et al. 2010). The objectives of lesson study with e-textbooks are firstly to demonstrate the close relationship between elementary geometry and mechanisms and recognize that elementary geometry provides the intuition for reasoning about mechanisms, and secondly, to recognize the difference between the mathematical systems for the solutions for the loci of the mechanism in Fig. 9.1 using elementary geometry, analytic geometry and vectors, and so on. Analytic geometry usually uses the conclusions of geometric reasoning in order to algebraically prove the equation for the algebraic solution; however, this is the adaptation of the conclusion of elementary geometry. From the perspective of elementary geometry, the ways of reasoning of analytic geometry include tautology.20 Mechanisms and kinematics provide intuition that is synchronized with elementary geometry which includes reasoning through the embedded figures of the theorem but is not always synchronized with reasoning using the form of algebra and calculus.
This paper concludes that the contents of the missing link between calculus and geometry was specified by kinematics and mechanics and that the link was one of the key ideas to be considered in the curricular integration of the subjects of arithmetic, algebra, and geometry for calculus and shows good evidence of what the Klein movement achieved in the Far East up until WW II. This paper also discussed how the Klein movement was introduced. However, it does not deeply describe how the Japanese worked on producing their own original adaptation through the decades until the production of the textbooks for Clusters I and II at the secondary level.
Acknowledgements
This research was supported by JSPS (KAKENHI-Kiban A) 26245082 and MEXT (KAKENHI-Tyousenteki Hoga) 16K13568. The author deeply acknowledges Dr. Gert Schubring at the University of Bielefeld and Dr. Michael Neubrand at the University of Oldenburg, who gave him fruitful suggestions, and Dr. Aira Yap and Mr. Guillermo Bautista at the University of the Philippines, who technically supported his English writing.

Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.