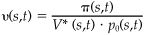
7This proof demonstrates the existence but not the uniqueness of the valuation mulipliers. Only if we have a complete market will we have unique valuation multipliers. In a complete market, for any t, we will be able to devise a self-financing strategy that pays off 1 in state s and 0 in states u∈S(t), u ≠ s. Not only that, we will be able to determine the minimum initial input, V*(s,t), into a self-financing strategy necessary to produce W(s,t) = 1, W(u,t) = 0 for u∈S(t), u ≠ s. The term V*(s,t) will be positive because of the no-arbitrage condition, and

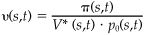
8Proposition 1 required the absence of arbitrage opportunities. In practice, e.g., if we generate prices via Monte Carlo, the process may not be exactly arbitrage-free. However, we can trick the process into being arbitrage-free by assuming that the original probabilities are the Martingale probabilities and adjusting the original prices appropriately To be exact, define δ_n(s,t) and adjusted prices :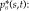

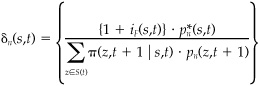
with

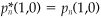
and

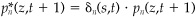
for z∈Ω(s,t).

With these adjusted prices, Eq. (8A.16) will hold using the original probabilities. Variations of this idea are used sometimes in options pricing theory.