Chapitre 7

Règles du jeu

« Mais que la Providence, ou bien que le Destin

Règle les affaires du monde… »

Jean DE LA FONTAINE

Nous abordons ici un sujet assez méconnu, peu orthodoxe dans ses méthodes sinon dans ses buts, qui se prolongera néanmoins au cours de quatre chapitres encore sans épuiser son pouvoir évocateur ni la force de ses enseignements. Ignoré par le mathématicien, voire méprisé, comme vil réseau de conventions arbitraires que dicteraient des bienséances obscures et prosaïques régnant sur l’expérimentation ; restreint, pour la plupart des physiciens eux-mêmes, à un simple garde-fou commode contre les erreurs de calcul – ce qui suppose déjà d’en reconnaître la validité – ; outil souple et inflexible à la fois, susceptible de s’adapter à de multiples problèmes, occupant même pour certains le noyau théorique de leur compréhension.

Unités et dimensions

« Chacune de ses formes a une allure particulière ; il y répond un bruit particulier. Le tout vit avec intensité comme un mécanisme compliqué, aussi précis que hasardeux. »

Francis PONGE

Je fus, il y a peu, sollicité par une jeune élève de lycée – « qui m’est chère » – à propos d’un problème de géométrie plane que proposait son manuel. Le programme de la classe de seconde – pensai-je in petto avec quelque suffisance – ne saurait m’embarrasser ! L’énoncé procédait d’un demi-cercle, dont le diamètre valait 4. – « Holà ! Quatre quoi ? » interroge le grand-père en fronçant un sourcil réprobateur – « Je ne sais pas, moi ! Quatre centimètres, ou quatre carreaux… » Appelé à témoin, le livre confirme, de tout le poids inhérent à la chose imprimée : 4, tout sec – « sec comme un coup de parapluie dans l’œil », disait l’humoriste ! – La figure « officielle » qui accompagne le texte dirait plutôt, à l’œil du physicien, 3 centimètres que 4 ; requis en tant qu’expert impartial, le double décimètre émet un verdict strict mais déconcertant : 3,2 centimètres.

Il faut se rendre à l’évidence : en mathématiques – celles, à tout le moins, qui s’enseignent aux novices à travers le « Journal officiel » du manuel scolaire –, en mathématiques un segment de droite se mesure par un nombre « sec », ou « pur » – sans unité, en tout cas –, qui par ailleurs n’a rien à voir avec la longueur réelle manifestée publiquement par la figure qui fait foi (on m’admoneste : je suis trop sévère, c’est tout de même un nombre positif qu’« ils » proposent…). On inculque pourtant à ces jeunes gens des notations codifiées par avance devant l’Éternité, précises et imposées, qui distinguent soigneusement – sous peine de sanctions sévères – un segment de droite [AB] de sa mesure AB, laquelle s’exprime, si nécessaire, par un nombre, comme ça, sans unités. 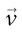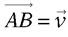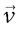C’est sans doute cette « généralité » qui permet, plus loin, de définir le module d’un vecteur générique images par la chaîne d’égalités (copiée directement dans le manuel) : images, et donc images. Si j’applique cette « définition » à une vitesse1 images, le module AB auquel j’aboutis – une longueur – se mesure en mètres – multiples ou sous-multiples – ; ne serait-il pas sain d’enseigner aux jeunes gens qu’il s’exprime en réalité en mètres par seconde ou kilomètres par heure ? La tête me tournait : la Première Guerre mondiale avait duré 7 et tué 500, le Mont-Blanc s’élevait à 10 000, la vitesse de la lumière valait 100 ou 1 000, et l’âge du capitaine 10…

Je me ressaisis : « J’en avais vu d’autres ! » Avalant ma salive physicienne, sans plus me récrier, je guidai l’adolescente docile et sensée – c’est en carreaux après tout, non en heures, qu’elle envisageait de mesurer le diamètre – vers le résultat final : y = 1 – x2 / 4 ; dans cette relation, x et y représentent les mesures de deux autres longueurs, définies dans l’énoncé. Ainsi, une aire (x2) – son quart – se retranche d’un nombre pur (1) pour s’égaler à une longueur (y) !… Mon instituteur campagnard, pleinement conscient, quant à lui, de la responsabilité lourde qui incombe aux pédagogues, affirmait avec une conviction communicative qu’« on ne peut ajouter des pommes et des vaches ».

 

En physique – dont le but, imprescriptible et inaliénable en même temps qu’obligé, consiste à décrire et comprendre la réalité –, en physique on affecte à toute grandeur des « dimensions ». On entend par dimensions physiques d’une grandeur, d’une quantité, d’une expression, les rapports (chiffrés) qu’elle entretient avec certaines de ces entités, en petit nombre, qui ont été choisies comme étalons – à savoir la longueur, la masse, le temps, l’intensité de courant électrique et la température. Par exemple, une vitesse – quelle que soit son origine et quel que soit l’objet qui la porte – présente les dimensions d’une longueur divisée par un temps ; on dit aussi qu’elle est « homogène » à ce quotient d’une longueur par un temps. Une accélération – celle d’un train qui démarre ou d’une fusée qui décolle, comme celle de la pesanteur sur Terre – reflète le taux temporel d’accroissement d’une vitesse, avec pour dimensions, par conséquent, celles d’une vitesse divisée par un temps, soit – pour « descendre » jusqu’aux étalons fondamentaux – celles du quotient d’une longueur par le carré d’un temps. La charge électrique s’obtient quant à elle par le produit d’une intensité de courant par un temps.

Lorsque, ayant affaire à une grandeur quelconque, on cherche ses dimensions physiques, on s’adresse à une formule – simple autant que possible – dont on sait qu’elle exprime cette grandeur ou la comporte, sous l’un ou l’autre de ses avatars. L’énergie, par exemple. On connaît l’expression (1 / 2) mv2 de l’énergie cinétique ; le demi ne fait rien à l’affaire – nombre pur –, de sorte qu’on se trouve en présence d’une masse multipliant le carré d’une longueur et que divise le carré d’un temps. Peut-être préférera-t-on analyser la formule W = F. d qui définit le travail W – une forme d’énergie – d’une force F le long d’un déplacement d (une longueur). Il y faut les dimensions de la force F, que l’on peut tirer sans coup férir de la loi de la dynamique classique (Newton) : F = ma, où a est une accélération. Une mise bout à bout aisée donne pour le travail-énergie mℓt–2 (la force) × ℓ (le déplacement), ce qui rejoint l’estimation précédente : mℓ2t–2 – masse, fois carré d’une longueur, par carré d’un temps.

C’est bien ! Personne, à ce que je vois, ne s’étonne que les deux calculs, d’inspiration fort différente, aboutissent au même résultat, ni que par ailleurs soient indispensables quelques connaissances en Physique. J’ai glissé sans crier gare la notation abrégée que nous utiliserons désormais : ℓ pour longueur, m pour masse (attention à l’homonymie avec « mètre »), t pour temps, i pour intensité, T pour température ; un exposant précédé du signe moins (t –2) vient du dénominateur (1 / t2).

Indissolublement liée aux dimensions physiques d’une grandeur, l’unité qui permet d’exprimer sa mesure : cm/s (centimètre par seconde) ou km/h (kilomètre à l’heure) pour la vitesse, m / s2 (mètre par seconde au carré) pour l’accélération, coulomb C ou ampère.seconde A.s pour la charge, joule J ou électron-Volt eV pour l’énergie… On voit déjà là que, malgré cette relation « indissoluble », on dispose dans chaque cas de plusieurs unités – ne serait-ce que par multiples et sous-multiples (centimètre ou kilomètre) – pour une seule et même dimension ; le choix entre elles est dicté par la commodité ou l’habitude…

Que l’on m’entende bien céans : insensé qui tenterait d’ajouter deux grandeurs, ou de retrancher l’une de l’autre, si elles ne présentaient pas les mêmes dimensions physiques ; en naîtrait un « monstr’ horrend’ inform’ ingens cui lumen ademptum2 ». Et si de mesures il s’agissait, les deux nombres s’ajouteraient ou se retrancheraient selon les règles « mathématiques » universelles et impassibles, mais ces opérations n’acquerraient de signification que si les dimensions physiques coïncidaient, et les unités – y compris les multiples et sous-multiples : on n’additionne pas « comme ça » 10 centimètres et 1 kilomètre.

L’atome d’hydrogène, fidèle archétype

« Mais ce champ ne se peut tellement moissonner

Que les derniers venus n’y trouvent à glaner. »

Jean DE LA FONTAINE

Le plus simple des atomes, celui qui occupe la première place dans la classification des éléments, est constitué d’un proton et d’un électron, seulement. Voyons à établir la liste – elle se révélera courte – des paramètres physiques pertinents susceptibles de figurer dans l’expression des grandeurs les plus patentes (rayon, énergie) de l’atome d’hydrogène.

L’électron propose aussitôt sa masse me et sa charge qe. Du proton, on retiendra aussi sa charge – exactement opposée à celle de l’électron – ; quant à sa masse, 1 840 fois supérieure à me, on pourra l’écarter en pratique : le proton sera considéré dans nos arguments, à une excellente approximation, comme immobile – de même que la Terre reste immuable sous l’action d’une balle de tennis. Aux charges nous aurons affaire ici uniquement en tant qu’agents de l’interaction – attraction – entre les deux particules, la force F que l’on connaît depuis Charles de Coulomb (1785) : à la distance r, F = (– qe × qe / 4πε0) / r2. La constante 1 / 4πε0 a été inventée sur le tard pour tirer l’électromagnétisme d’un inextricable nœud de conventions et d’unités disparates. Pour nous, il nous suffira de poser égale à e2 l’expression 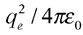images, qui se déplacerait en bloc dans les calculs – si nous envisagions d’y entrer – : 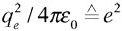images. Gardez le secret : nous revenons de la sorte à l’un des anneaux gluants et froids de l’effroyable entrelacs de vipères.

À me et e2 il faut adjoindre 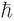images, la constante de Planck – ici canoniquement divisée par 2π –, signe héraldique que brandit en première évidence le blason de la mécanique quantique (« de gueules à besant d’or et chef d’azur à H barré d’argent »), car c’est à elle que ressortit – il est bientôt un siècle que nous l’avons appris – la structure de l’atome. Munis de ce viatique, recherchons l’expression qui pourrait convenir au rayon a0 de l’atome d’hydrogène : c’est ainsi qu’on le note, en le nommant « rayon de Bohr » – d’après Niels Bohr, qui le premier l’introduisit (1913). Sonnons donc « À l’analyse dimensionnelle ! » comme on fait « Au réveil ! » ou « Aux champs ! »…

Le rayon visé appartient à la catégorie « longueur ». Nous écrivons (e2)α meβћγ, et nous apprêtons à choisir les exposants α, β, γ – pas nécessairement positifs, pas nécessairement entiers – en sorte que le produit d’ensemble soit homogène à une longueur ℓ. La masse de l’électron parle d’elle-même : m. Pour e2 nous savons, de par la définition que nous en avons donnée, que e2 /  r2 désigne une force, laquelle – nous l’avons commenté ci-avant – répond aux dimensions de ma = mℓt–2 ; celles de e2 s’obtiennent donc en multipliant les précédentes par le carré de la distance r, soit par ℓ2 : e2 = mℓ3t–2. Nous nous comprenons, j’espère : le signe = ne sanctionne pas ici une véritable égalité, « mathématique » ou numérique, mais bien plutôt une similitude de dimensions physiques, signification qu’éclaire pleinement le contexte, et qu’iront précisant, s’il en était besoin, les maniements ultérieurs. Et ħ ? se demande-t-on alentour… « Et h-barre ? » répètent les échos. Rien de bien compliqué, malgré l’aura de mystère qui émane parfois encore de la mécanique quantique : la constante h – « pure », sans le dénominateur 2π – fut introduite par Max Planck (1900) afin que son produit hv par une fréquence v soit une énergie. Qu’importe ici son ordre de grandeur ! La fréquence v, en tant qu’inverse d’une période temporelle, s’avère homogène à 1 / t, ou t–1. Le retour à ħ le montre comme une énergie multipliée par un temps, c’est-à-dire – voir ci-dessus la double analyse de la grandeur énergie – ħ=mℓ2t−2 × t = mℓ2t−1.

Nous voici donc à pied d’œuvre. Pour « deviner » la formule en (e2)α meβћγ qui s’identifie au rayon a0, il nous faut résoudre l’équation aux dimensions (mℓ3t-2)α mβ (mℓt-1)γ = ℓ, avec pour inconnues les exposants α, β, γ. Prenons, dans l’ordre, les grandeurs de base m, puis ℓ, enfin t. La grandeur m ne figurant pas au second membre, il faut que, au premier, la somme des exposants qui l’affectent s’annule – car m0 = 1 – ; vient ainsi une première relation entre les inconnues : α + β + γ = 0. Une deuxième relation découlera de l’équilibrage de la grandeur ℓ, qui se trouve à la puissance 1 dans le membre de droite (on se rappellera que (ℓ3)α) = ℓ3α : 3α + 2γ = 1. Finalement, le temps t fournit, de même façon, – 2α – γ = 0.

Trois équations du premier degré à trois inconnues. Résolution d’autant plus aisée que les deux dernières équations ne contiennent pas β : 3α + 2γ = 1 et 2α + γ = 0 donneront α et γ, par quelque méthode simple – substitution ? combinaison ? – qu’on voudra bien mettre en œuvre : α = – 1 ; γ = 2. De la première provient alors β = – α – γ, qui aboutit à β = – 1.

Ce calcul simple implique alors une conséquence de haute signification physique : a0 = ħ2/ mee2. Précipitons-nous pour vérifier, pour…. Non ! Point de précipitation, ni de cette exaltation factice et immodérée des stades !… Nous avons pourtant marqué un essai d’anthologie : le rayon de Bohr a0 obéit précisément à cette expression ! Qu’il soit issu du modèle fruste originel (1913) ou de l’application rigoureuse de la Mécanique Quantique… Certes, dans ce dernier cas, on n’obtient pas vraiment le rayon d’une sphère qui engloberait l’atome, mais il n’en caractérise pas moins l’extension de la fonction d’onde qui décrit l’état de l’électron. Si l’on met des nombres dans cette formule (ħ = 1,05 × 10–34 J.s, me = 0,91 × 10–30 kg, qe = 1,6 × 10–19 C, 1 / 4πε0 = 9 × 109 SI – « système international3 »), on trouve a0 = 0,53 Å, avec l’ångström défini comme 1 Å = 10–10 m. Ainsi, par la vertu de notre formule « magique », les longueurs – rayons et distances – se mesurent, en Physique Atomique, à l’aune de l’ångström – disons par des nombres compris entre 1/10 et 10.

Halte-là ! Notre joie excède elle aussi la décence et se surfait ! Qui n’a vu le bât qui blesse, et où ? Notre raisonnement ne saurait avoir prise sur tel facteur sans dimension qui pourrait multiplier impunément l’expression tant louée. Quelle chance, la nôtre, que d’être tombés, sans savoir pourquoi, sur un cas où ce facteur vaut 1, tout simplement !

 

Voyons l’énergie du même atome d’hydrogène. Ce sera, à l’évidence, la plus immédiatement accessible, celle qu’il faut dépenser – au minimum – pour arracher l’électron au proton ; on la nomme « énergie d’ionisation ». Nous connaissons maintenant la musique du clairon. Nous reprenons (e2)α’ meβ’ћγ’, et recherchons quels exposants α’, β’, γ’ feront de cette expression une énergie. Équation aux dimensions : (mℓ3t-2)α’ mβ’(mℓ2t-1)γ’ = mℓ2t-2. « Projection » sur m : α' + β' + γ' = 1 ; sur l : 3α' + 2γ' = 2 ; sur t : – 2α' – γ' = – 2 donnent α' = 2 et γ' = – 2 ; d’où β' = –α' –  γ' + 1, soit β' = 1.

L’énergie E’ ainsi trouvée répond à la formule E' = mee4 / ħ2. Notre chance paraît moindre cette fois : l’énergie d’ionisation de l’atome d’hydrogène s’écrit E1 = mee4 / 2ħ2. Le facteur – celui qui nous échappe – vaut ici 1/2. Filant la métaphore sportive, nous dirons avoir incontestablement marqué un essai, mais avoir échoué – de peu : 1/2 – dans la transformation. Il n’en reste pas moins que l’ordre de grandeur des énergies atomiques tourne autour de la dizaine d’électronvolts. En effet, calculée numériquement à partir de l’expression mee4 / 2ħ2, l’énergie de liaison (ou d’ionisation) de l’atome d’hydrogène – que sa simplicité propulse au rang d’archétype – vaut EI = 13,6 eV (utiliser les données antérieures, et le facteur de conversion 1 eV = 1,6 × 10–19 J).

 

Mais je n’aurais pas dû présenter les deux calculs précédents ainsi que je l’ai fait – pour enfantins qu’ils soient –, comme s’ils visaient le simple but de résoudre quelque devinette élémentaire – dont la réponse figure en toutes lettres, par avance, sur les pages de garde de maint manuel ; je n’aurais pas dû laisser entendre qu’il s’agit là d’un jeu – fût-il jeu de ballon aux rebonds capricieux. « Au violon s’use l’archet / La pierre au jeu des ricochets » et apparaît à la réflexion, au tréfonds des choses et des idées, la véritable nature des enjeux : fondamentaux comme les énigmes du Sphinx de Thèbes, et comme elles vitaux pour la physique. Partis d’une collection de paramètres – ils n’étaient pas plus de trois – susceptibles de caractériser les principaux aspects du système étudié – choisi pour sa simplicité –, nous avons « découvert », c’est-à-dire trouvé et dévoilé en même temps, que ces paramètres s’agencent, de façon harmonieuse et unique, pour produire une longueur ; et d’une autre façon, tout aussi harmonieuse, pour faire sortir une énergie. Ou bien nous nous sommes lourdement trompés dans l’analyse physique préalable qui a dégagé les paramètres appropriés, ou bien toute longueur se doit, dans l’atome, de se conformer à l’expression ħ2 / mee2, et toute énergie à mee4 / ħ2. Le facteur inconnu, a priori arbitraire, qui multiplie l’une ou l’autre combinaison sans en altérer les dimensions physiques ? Il reste ici insignifiant : exactement 1 dans le premier cas, 1/2 dans le second. Invoquera-t-on la chance ? Que non pas ! on le constate systématiquement, dans ce type d’arguments dont nous donnerons bientôt d’autres exemples : ce facteur immotivé arrive chaque fois – lorsque le plein développement de la théorie vient à le révèler – proche de 1. On peut s’en étonner, comme d’un prodige. On peut estimer plutôt que ce fait même – un facteur capricieux mais d’ordre 1 – participe de l’analyse dimensionnelle : si le véritable rayon a0 de l’atome mesurait 100 ou 1 000 fois la longueur de base ħ2 / mee2, les dimensions physiques seraient respectées, mais un aspect important de l’atome d’hydrogène nous serait demeuré incompris, qui pourrait motiver de tels nombres.

2- « Monstre effroyable, difforme, gigantesque, à qui la lumière a été arrachée » (Virgile).