« Les houles, en roulant les images des cieux,
Mêlaient d’une façon solennelle et mystique
Les tout-puissants accords de leur riche musique
Aux couleurs du couchant reflété par mes yeux. »
Charles BAUDELAIRE
Équations aux dérivées partielles
Certaines grandeurs physiques – non des moindres ni des moins nombreuses – se répandent largement dans l’espace « ordinaire » à trois dimensions – leur valeur change d’un point à l’autre dudit espace – et elles évoluent au cours du temps – en chaque point leur valeur change d’un instant à l’autre. On les décrit, tout naturellement, par des fonctions de x, y, z – coordonnées cartésiennes du point courant – et du temps t. Nous écrirons génériquement, comme on fait traditionnellement en physique, u = u(x, y, z ;t), le symbole u désignant la grandeur particulière que nous souhaitons étudier.
Des exemples ? Le champ électrique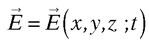 
et le champ magnétique 
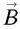, pour qui tient une formule analogue ; ce sont là fonctions à valeurs vectorielles, qui se déploient en trois composantes cartésiennes – lesquelles ne varient pas nécessairement de concert : Ex = Ex (x,y,z ;t), Ey = Ey (x,y,z ;t), Ez = Ez (x,y,z ;t), et de même Bx , By, Bz. Ce peut être aussi la densité volumique de charge électrique ρ = ρ (x,y,z ;t) – charge par unité de volume, au voisinage immédiat du point (x, y, z) et à l’instant t – ou la densité superficielle de courant 
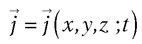– intensité de courant par unité de surface, à nouveau vectorielle. On peut dire que l’électromagnétisme vit tout entier dans et par le formalisme construit sur ces bases : « Dans les temps les plus noirs, il recevait la substance qui le fait vivre. » Mais, s’il y règne en seigneur incontesté – car de fondamentale extraction –, il n’est pas seul à l’arpenter avec rigueur, ce domaine avec grand soin balisé. L’acoustique elle aussi – pour donner un exemple – emprunte de bonne grâce ces sentiers parfois escarpés : le son consiste en de (légères) surpressions et dépressions qui se propagent dans l’espace en vibrant dans le temps, accompagnées du va-et-vient de (minces) tranches d’air ; c’est alors un p – pour « pression » – qui prendra la place de u, ou bien ce symbole u représentera le déplacement même, à l’instant t, de la parcelle centrée au point (x,y,z) de l’espace. On peut citer également la chaleur, qui diffuse à partir de ses sources pour affecter progressivement la température établie en les divers endroits.
Dès lors qu’une grandeur u se présente comme fonction de plusieurs variables – u = u (x,y,z ;t) – s’introduisent naturellement ses dérivées partielles, B, A – BA des manipulations mathématiques qui ont cours dans ce domaine à peine entrouvert ci-dessus. Le principe reste celui qui préside aux dérivations simples1. Mais il existe ici une dérivée par rapport à chaque variable. On y accède grâce à la convention que les autres variables sont maintenues constantes, c’est-à-dire traitées, au cours de l’opération de dérivation, comme inertes. Ainsi, la dérivée partielle de u par rapport à x, que l’on note – par consensus universel – avec des « d ronds », ∂u / ∂x, répond à la définition qui suit : limite, quand l’accroissement Δx tend vers zéro, du quotient Δu / Δx – l’accroissement Δu de la fonction, associé à Δx, étant calculé comme si y, z, et t étaient invariables.
Le présent chapitre et le suivant analysent – en se fondant à nouveau sur les préceptes de l’analyse dimensionnelle – deux « équations aux dérivées partielles », ainsi nommées car elles proposent, chacune d’elles, une relation entre les dérivées partielles – certaines parmi celles-ci – d’une grandeur physique représentée par une fonction des coordonnées d’espace et du temps. Ces équations ont été choisies ici – elles se sont imposées, devrais-je dire – comme décrivant et régissant deux phénomènes particulièrement importants – fondamentaux, devrais-je dire.
En cette noble terre signalée ci-avant réside à demeure – la parcourant sans trêve, inlassablement, en tous sens – une équation aux dérivées partielles que la Renommée a claironnée aux quatre horizons, et publiée aux quatre coins de l’univers physique :
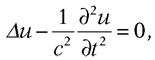
l’« équation de propagation » ou « équation d’onde ».
Diverses grandeurs – champ électrique ou champ magnétique, ou bien surpression ou déplacement acoustiques… – viennent à l’envi occuper la place (centrale) de u, fonction de x, y, z, t : la signification de ce symbole, u, se modifie du tout au tout au gré du phénomène que l’on décrit et, là même, selon l’aspect qu’on en veut privilégier. La quantité u change, l’équation demeure (« Passent les jours et passent les semaines… »). C’est sa structure, rigide, indéformable – si le signe moins était remplacé par plus, « toute la face de la terre aurait changé » –, qui véhicule le sens profond, tout le sens en vérité. C’est la Pythie. Ses oracles – nous en découvrirons bientôt la teneur essentielle – empruntent au langage mathématique sa rigueur. L’équation prophétesse elle-même, dès avant de se manifester à l’extérieur, s’édifie en termes de dérivées partielles secondes – à savoir dérivée chacune d’une première dérivée partielle – : ainsi de ∂2u / ∂t2, dérivée partielle par rapport au temps t de ∂u / ∂t ; ainsi de Δu, connu partout comme « le laplacien de u » – confusion à éviter avec l’accroissement de u – et défini selon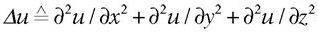 
. Quant au coefficient 1 / c2, il introduit une constante c qui figure au dénominateur par son carré – positif comme tout carré de nombre réel – et dont l’analyse dimensionnelle va aussitôt caractériser la nature physique.
Le laplacien Δu revêt pour dimensions, comme fait chacun de ses trois termes – qui ne saurait y manquer, par la règle primaire des pommes et des vaches –, celles de la grandeur u divisées par le carré d’une longueur : ils représentent en effet des longueurs – à l’instar des variables x, y, z, elles-mêmes – les accroissements Δx, Δy, Δz qui interviennent deux fois d’affilée, au dénominateur, dans les doubles dérivations du laplacien. Mais… les dimensions de u ?… Elles diffèrent radicalement, du champ électrique jusqu’à la pression acoustique ! Certes, mais elles apparaissent identiques dans tous les termes de l’équation, en sorte que seuls les dénominateurs doivent nous préoccuper ; on voit dans ceux du laplacien Δu le carré d’une longueur, qui se retrouve nécessairement dans c2 multipliant le carré d’un temps – venant de ∂2u / ∂t2 ; il s’en ensuit que le paramètre c ne peut faillir à son destin de vitesse. Effectivement, en électromagnétisme – la théorie reine –, les équations de propagation de l’un ou l’autre champ comportent pour vitesse c la combinaison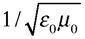 
des deux constantes fondamentales électrique ε0 et magnétique µ0, ce qui conduit à une valeur numérique très proche de 300 000 km/s. L’ordre de grandeur bondit – vers le bas – en Acoustique, et se diversifie : la vitesse du son avoisine 340 m/s dans l’air, 1 500 m/s dans l’eau, 5 km/s dans l’acier,…
Cette équation de propagation, qui semble simple à l’abord mais sitôt après énigmatique, recèle un phénomène à la fois curieux et fondamental, qui laisse pantelants de surprise le profane et le débutant ; tellement aisé à déduire, en vérité, qu’on en est doublement désarçonné.
Adoptons, pour le voir se manifester, une situation concrète et facile, où l’espace se restreint à une dimension : une corde tendue horizontalement (figure 1), dont les points seront repérés sur un axe Ox. Nous choisirons pour grandeur u le déplacement transversal – compté positivement vers le haut – des divers points, par rapport à leur position d’équilibre. Plus précisément (figure 2), u = u(x,t) mesurera l’écart vertical, à l’instant t, du point de la corde caractérisé par l’abscisse x.
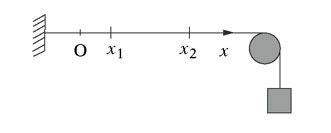
Figure 1
Si l’on se fixe tout d’abord une abscisse x0 – pour mieux comprendre – et qu’on observe le point particulier ainsi désigné sur la corde, la fonction de t qui s’écrit u(x0,t) retrace le mouvement vertical exécuté par ce point au cours du temps t ; ce mouvement diffère a priori d’un point de la corde à l’autre. Si maintenant, à l’inverse, on se fixe un instant t0, la fonction de x qui s’écrit u(x,t0) caractérise la distribution du décalage latéral des divers points, d’abscisse x, le long de la corde ; en somme, u(x,t0) dessine l’image photographique de la corde qui serait prise à cet instant t0.
Une analyse théorique un peu serrée – application de la loi fondamentale de Newton à un tronçon infinitésimal de la corde – avec introduction judicieuse de quelques approximations aboutit, pour u(x,t), à l’équation du dieu-soleil – ramenée à une dimension d’espace unique – : ∂2u / ∂x2 – (1 / c2)∂2u / ∂t2 = 0. La constante c qui se dégage de la démonstration s’exprime selon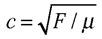 
à partir de la masse linéique (masse par unité de longueur) µ de la corde et de la force F qui la tend. Vérification des dimensions : F est homogène au produit d’une masse par une accélération, donc à mlt–2, et µ à ml –1 ; ainsi, F / µ s’affiche comme l2t–2 et sa racine carrée comme lt–1 – voilà bien une vitesse.
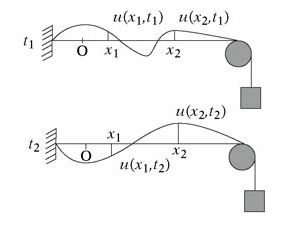
Figure 2
Propriété spécifique des solutions
À présent, que les âmes sensibles détournent les yeux : l’artiste va travailler sans filet !
Roulement prolongé de tambour, d’intensité progressivement croissante, jusqu’au seuil de l’insupportable. Interruption brutale, d’un coup, coïncidant avec l’extinction soudaine de l’éclairage : silence et ténèbres sous le chapiteau… Mais apparaît aussitôt la lumière d’un unique projecteur zénithal, qui imprime sur la piste un disque lumineux d’un mètre à peine de diamètre. L’« artiste » entre en scène dans ce rond éblouissant, qui ne le quittera plus dans ses évolutions, pour brusques et rapides et vastes qu’elles puissent être. Une voix caverneuse, emplissant l’espace, évoque avec respect et vénération la prêtresse de Delphes, tandis que se projette, sur un écran géant tendu par le travers de l’accès aux coulisses, l’équation magique que nous avons appris à connaître – sa version à une dimension : ∂2u / ∂x2 – (1 / c2)∂2u / ∂t2 = 0.
S’aidant d’un microphone dont de multiples haut-parleurs judicieusement disposés répercutent les accents solennels dans l’ensemble de la vaste tente, l’« artiste » s’adresse au public, fasciné, qui emplit les gradins. Il ponctue son discours, lent et persuasif, d’amples gestes de bras et de hochements de tête engageants. Il présente, en commençant, une variable homogène à une longueur baptisée ξ en l’honneur d’Apollon – la lettre ξ s’affiche, isolée, sur la toile de fond. Il sollicite avec insistance l’auditoire, demandant qu’on lui propose une fonction – quelconque, choisie sans contrainte – de cette variable unique, ξ. Sans se faire trop prier, les spectateurs relèvent le défi : on avance ici la fonction ξ2, on s’enhardit là jusqu’à l’exponentielle, on suggère encore, là-bas, le cosinus.
Procédant par ordre, l’« artiste » prend d’abord en main le carré ξ2 : « Je modifie légèrement cette fonction – sans l’altérer – pour l’adapter au problème concret de la corde tendue : ξ2 représentant le carré d’une longueur, je me permets de diviser par une autre longueur a constante pour obtenir globalement la dimension du déplacement u. Maintenant, que personne ne bouge !… Silence et recueillement, attention et expectative : « Agua y sombra, sombra y agua / por Jerez de la Frontera2. » De la fonction ξ2 / a, ainsi spontanément mise en avant, « En ferraillant je vais – hop ! – à l’improvisade », tirer une solution de l’équation de propagation. Le tour de passe-passe, exécuté devant les yeux ébahis de chacun et de tous, consiste à remplacer, d’un seul coup d’un seul, ξ par x – ct. Apparaît sur l’écran l’égalité u (x,t) = (x – ct)2 / a, flanquée des dérivées partielles pertinentes de cette fonction u (x,t) là – qu’a calculées in vivo un comparse mathématicien au chômage. Au premier ordre, ∂u / ∂x = 2(x – ct) / a et ∂u / ∂t = – 2c(x – ct) / a ; au second ordre, ∂2u / ∂x2 = 2 / a et ∂2u / ∂t2 = + 2c2 / a. Par conséquent, la combinaison ∂2u / ∂x2 – (1 / c2)∂2u / ∂t2 s’annule : u(x,t) = (x – ct)2 / a vérifie l’équation de propagation !
« “Bravo !” crie la foule en délire ; et de réclamer une autre représentation. »
La fonction exponentielle ne peut s’appliquer qu’à une variable sans dimension : nous prendrons ξ / a. En outre, nous affecterons à l’exponentielle, sans dimension elle-même, un multiplicateur A qui l’ajustera à la dimension voulue – une longueur. La « deuxième représentation » porte donc sur A exp (ξ / a). L’« artiste » lui fait aussitôt subir la transformation magique : u(x,t) = A exp (x – ct) / a. Sortant dans l’instant, des coulisses obscures à la projection lumineuse, les dérivées adéquates (je ne m’explique pas que, pour ces basses besognes, ait été engagé un mathématicien, au risque d’erreurs ; un physicien eût été plus fiable, dont c’est le lot quotidien) : au premier ordre, ∂u / ∂x = (A / a)exp(x – ct) / a et ∂u / ∂t = (–cA / a) exp(x – ct) / a ; au second ordre, ∂2u / ∂x2 = (A / a2)exp(x – ct) / a, et ∂2u / ∂t2 = (+ c2A / a2)exp(x – ct) / a. Et – ô miracle renouvelé ! – la combinaison fatidique des dérivées secondes s’annule à nouveau !
Le cosinus, traité au pas de charge, confirme la validité du procédé : A cosξ / a, aménagé en u(x,t) = A cos (x – ct) / a, conduit à ∂u / ∂x = – (A / a) sin (x – ct) / a et ∂u / ∂t = (+ cA / a) sin(x – ct) / a, puis à ∂2u / ∂x2 = – (A / a2) cos (x – ct) / a et ∂2u / ∂t2 = (– Ac2 / a2) cos (x – ct) / a. Encore gagné !
Mais voici que du premier rang, juste au-delà de la rambarde, partent des appels aigus et pressants : un enfant – un surdoué, peut-être –, juché sur son siège, interpelle l’« artiste » en brandissant au-dessus de sa tête un papier arraché à la hâte d’un agenda sans doute périmé, sur quoi est griffonné ce que donne à voir la figure 3, immédiatement reproduite, agrandie, pour être vue de tous. La fonction f(ξ) que voilà n’est pas définie par une formule analytique comme les précédentes, mais bien plutôt par sa représentation graphique, judicieusement choisie – comme nous serons amenés à le constater – : f(ξ) s’annule partout, excepté sur un intervalle (0,ξ0) restreint, où elle s’arrange néanmoins pour changer de signe ! Et le numéro reprend, selon le plan maintenant éprouvé. « Ne connaissant pas véritablement l’expression de f(ξ), j’émets l’hypothèse que les conditions dimensionnelles y sont respectées ; en particulier, les valeurs prises par cette fonction – la figure suggère de les nommer y – appartiennent comme celles de ξ à la classe des longueurs. J’applique alors, sans barguigner, mon tour de passe-passe : u(x,t) = f(x – ct), puis calcule du même élan les dérivées nécessaires : si l’on me permet de noter f’(ξ) et f’’(ξ) les dérivées première et seconde de la fonction f par rapport à son unique variable ξ, les règles – simples – de dérivation pour une fonction de fonction3 aboutissent à ∂u / ∂x = f’(x – ct) et ∂u / ∂t = – cf’(x – ct) comme dérivées premières ; on obtient les dérivées secondes en poussant d’un cran supplémentaire ces deux mêmes formules : ∂2u / ∂x2 = f’’(x – ct) et ∂2u / ∂t2 = (– c)2 f'’(x – ct). Ces résultats s’affichent en évidence sur l’écran. Quelques secondes de silence – l’« artiste » se tient coi, pointant seulement ses deux index vers ∂2u / ∂x2 et ∂2u / ∂t2 –, puis éclate un tonnerre d’applaudissements, ponctué de-ci de-là par des hurlements brefs dont on reconnaît seulement deux voyelles : « … a… o ! »
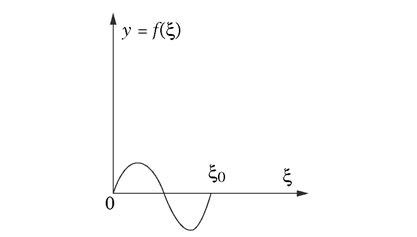
Figure 3
L’« artiste » salue de manière conventionnelle, fléchissant le cou (« Laissent pencher leur front et fléchissent le cou ») tout d’abord, puis se cassant en deux à la taille… s’y reprenant à plusieurs fois. Il sort, se courbant là aussi pour passer sous la vaste toile lumineuse – où persiste la source, indubitable mais prodigieuse, de son triomphe –, revient pour répondre à nouveau aux acclamations du public, qui prennent bientôt une forme rythmique impérieuse – les claquements des innombrables paumes se groupant en un seul et même battement coordonné. Fusent de toutes parts les cris de « Bis ! Bis ! ». À sa troisième fausse sortie, l’« artiste » lève à mi-hauteur ses deux mains disjointes, qu’il balance doucement en signe d’apaisement. Ayant obtenu le silence – présageant pour l’assistance la venue d’une répétition de l’exploit précédent –, l’« artiste » s’exprime d’une voix forte : « “Ce n’est pas une taille avantageuse, c’est / Mon âme que je cambre ainsi qu’en un corset.” Ce n’est pas une reprise du spectacle que je vais exécuter maintenant devant vous, mais bien plutôt son achèvement, son couronnement, son apothéose, que les succès antérieurs – merci de les avoir appréciés – préparent seulement, et rendent possible. Je vais exploiter, pour cette partie cruciale et ultime de la représentation, la même fonction f(ξ), mystérieuse mais générique : je reviens au diagramme qu’a soumis d’abord à ma perspicacité le jeune homme – enfant inspiré des dieux (figure 3). Je réitère le pas décisif qui a, sans coup férir ni artifice requérir, construit sur f(ξ) une solution u(x,t) = f(x – ct) de l’équation d’onde. Apparaîtra alors en pleine lumière l’origine sémantique de l’appellation “équation de propagation”. »
« Je m’attache, pour atteindre cet objectif, à interpréter sur la corde tendue horizontalement cette fonction de deux variables u(x,t) destinée à en décrire la forme et son évolution dans le temps : u(x,t) caractérise l’écart vertical, à l’instant t, du point d’abscisse x par rapport à sa position d’équilibre sur la droite horizontale. »
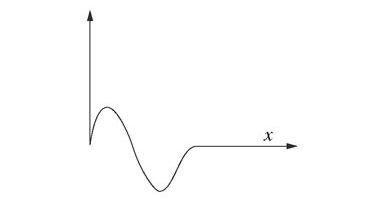
Figure 4
« Je demande en premier lieu : quel aspect présente la corde à l’instant initial t = 0 ? Le point repéré par x est déplacé verticalement de u(x,0) – par définition de u(x,t) et par choix de t = 0. Dans le cas présent, u(x,0) = f(x) – j’ai seulement remplacé t par zéro dans f(x – ct). Ainsi, au temps zéro, les points de la corde restent au repos, sauf toutefois ceux qui se situent entre x = 0 et x = ξ0 – rappelons-nous que ξ et x sont homogènes l’un à l’autre, comme longueurs –, lesquels reproduisent à l’identique le dessin que montre la figure 3. Autrement dit (figure 4), la photographie de la corde, prise à l’instant initial, révèle la forme de la représentation graphique de la fonction f. »
Sur le point de reprendre, les manifestations bruyantes d’approbation et d’admiration sont étouffées dans l’œuf par l’« artiste », d’un geste autoritaire de la main. « Maintenant, voici le summum, le faîte, le pinacle de ce temple que nous avons édifié pierre à pierre. Je pose la question : quelle forme développe la corde à un instant t0 ultérieur ? La réponse gît encore dans l’expression de u(x,t), prise en t = t0. Or, dans notre cas, u(x,t0) = f(x – ct0). L’interprétation de ce résultat s’appuie à nouveau sur le fait patent que la fonction f(ξ) prend des valeurs non nulles seulement entre ξ = 0 et ξ = ξ0. Ainsi, en l’occurrence présente, u(x,t0) reste nul partout en x, sauf entre x1 et x2, tels que x1 – ct0 = 0 et x2 – ct0 = ξ0 ; en d’autres termes, la corde n’est déformée qu’entre les abscisses x1 = ct0 et x2 = ξ0 + ct0. Il y a plus : la forme de la corde à t0 n’a pas changé (figure 5) – excepté un décalage horizontal de ct0 – par rapport à ce qu’elle était à l’instant initial t = 0. »
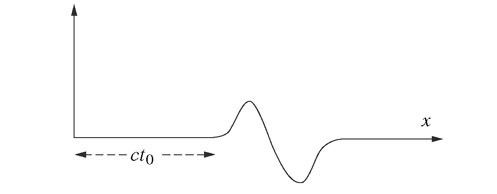
Figure 5
Si l’on imagine t0 d’abord tout proche de zéro, puis un peu postérieur, puis encore un peu ultérieur… alors jaillit soudain, évidence percutante, le concept de propagation, comme émerge de la brume une tour cathédrale (« Mais vous apparaissez, reine mystérieuse. / Cette pointe là-bas dans le moutonnement »). L’altération – brève ici pour mieux donner à voir – qui en perturbe l’horizontalité originelle court le long de la corde – conservant intact son dessin –, à la vitesse c, dans le sens des x croissants (ce serait en sens inverse si la même variable ξ avait été remplacée par x + ct dans la même fonction f). Qui ne s’extasierait devant ce phénomène, miracle naturel dévoilé par la mathématique physicienne, appuyée seulement ici sur l’analyse dimensionnelle ? N’est-ce pas elle qui permet et suggère d’ajouter ct à x ? Nul tronçon de la corde ne se déplace jamais dans la direction longitudinale : chaque point se contente d’obéir passivement, sans quitter sa place, pourrait-on dire, au va-et-vient transversal que lui prescrit à son passage l’ébranlement – « L’aliment idéal passe. » Et celui-ci, évident mais immatériel en soi, poursuit imperturbablement et obstinément son chemin filiforme de chanvre ou de métal, indifférent à la nature du support mais attentif aux lois universelles de la physique. À l’entrée d’un port de mer, la progression manifeste des vagues ni leur ressac n’entraînent contre les digues, où elles s’écrasent l’une après l’autre, la bouée solitaire et fiable au marin qui se soulève et retombe, à chaque ondulation, sans quitter l’emplacement significatif qu’on lui a de longtemps assigné.