Chapitre 18

Opérations de symétrie.
 Pseudo-scalaires
 et pseudo-vecteurs

« La terre jeune encore et vierge de désastres. »

Stéphane MALLARMÉ

Vrais vecteurs et pseudo-vecteurs

Considérons d’abord un vecteur géométrique 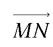, et construisons son symétrique par rapport à un point Ω (figure 1) ou par rapport à un plan π (figure 2). Nous n’envisageons ici que des symétries actives, car les symétries passives correspondantes transforment le trièdre de référence direct en un trièdre inverse, et nous sommes convenus au chapitre 16 de nous en tenir aux repères directs. On voit aussitôt que, dans une symétrie par rapport à un point Ω,

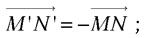
dans une symétrie par rapport à un plan π, la composante 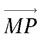parallèle à π reste inchangée, alors que la composante 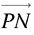perpendiculaire à π est changée en son opposée :

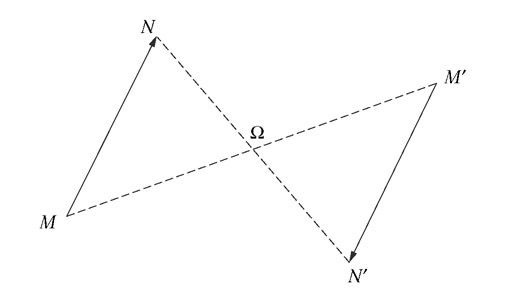
Figure 1

Les grandeurs vectorielles 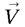qui se comportent, dans de telles symétries, comme les vecteurs géométriques sont appelées « vrais vecteurs », ou « vecteurs polaires » :

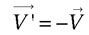dans une symétrie par rapport à un point ;

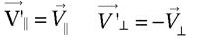dans une symétrie par rapport à un plan ( 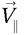et 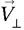désignent les composantes de 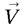respectivement parallèle et perpendiculaire au plan de symétrie).

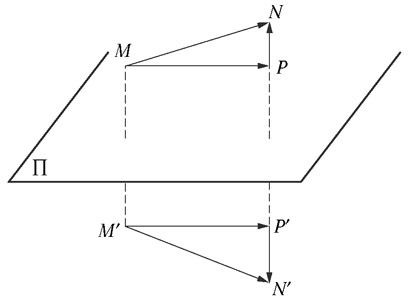
Figure 2

Mais, si l’on choisit deux vecteurs polaires 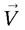et 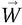, leur produit vectoriel 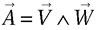se comporte, dans les symétries par rapport à un point ou un plan, de façon exactement opposée :

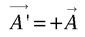dans une symétrie par rapport à un point ;

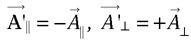dans une symétrie par rapport à un plan.

La première égalité coule de source : les changements de signe de 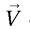et 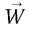se compensent. Quant aux relations venant en second, elles résultent des constatations suivantes. Les vecteurs 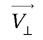et 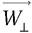, colinéaires puisque tous deux perpendiculaires au plan de symétrie, ne contribuent pas au produit vectoriel : . La composante perpendiculair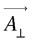e de est engendrée par les composantes de et parallèles au plan : . Quant à la composante , elle résulte des produits en quelque sorte « croisés » : .

On appelle « pseudo-vecteurs », ou « vecteurs axiaux », les grandeurs vectorielles se transformant selon ces formules.

 

Une vitesse, une force, un champ électrique… vecteurs polaires ; un moment cinétique, un vecteur vitesse angulaire, un champ magnétique… vecteurs axiaux. On comprend que le comportement, dans les symétries, d’un produit est caractérisé par le produit des changements de signes des deux grandeurs qui le construisent.

Examinons le comportement des champs électrique et magnétique par « parité » – ainsi nomme-t-on la réflexion par rapport à un point.

L’électromagnétisme classique – c’est-à-dire sans les photons – se fonde sur les champs électrique et magnétique , qui vérifient par postulat les quatre équations de Maxwell (1873) :

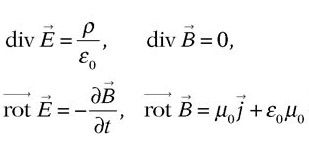
(ε₀ et µ₀, constantes universelles, harmonisent les dimensions et unités). Les « sources » ρ – densité volumique de charge – et 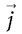– densité de courant électrique – sont connues comme un vrai scalaire (ρ) et un vrai vecteur .

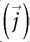On peut regrouper les opérateurs « divergence » et « rotationnel » en un opérateur de dérivation unique, appelé « nabla » et noté 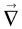 : c’est un opérateur vectoriel de composantes cartésiennes 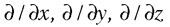– un « vrai » vecteur, par conséquent. Les équations de Maxwell s’écrivent alors

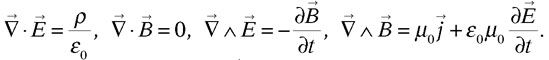
Le champ électrique 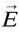, un vrai vecteur, change de signe par parité, comme fait 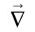. Ainsi 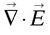, obtenu par le produit scalaire de deux vrais vecteurs, reste inchangé quant à lui, à l’instar de ρ au second membre. Mais , produit vectoriel de deux vrais vecteurs, se comporte en pseudo-vecteur – pas de changement de signe – ce qui doit donc être le cas pour 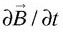et par suite pour 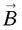(le temps t n’est pas affecté par la présente symétrie). 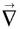Dans , le vecteur se transforme par parité en son opposé – vrai vecteur – mais 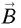ne change pas ; se comporte donc en vrai vecteur – changement de signe –, comme et .

La « force de Lorentz », qui agit sur une particule de charge q plongée dans un champ électromagnétique , s’écrit de son côté

( désigne la vitesse de la particule). Cette formule voit ses termes être tous remplacés par leur opposé dans la symétrie de parité : q vrai scalaire ; vrais vecteurs ; 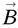vecteur axial.

Vrais scalaires et pseudo-scalaires

Les scalaires, invariants par rotation, se divisent eux aussi en deux catégories lorsqu’on envisage les opérations de symétrie par rapport à un point ou à un plan : les « vrais scalaires » gardent leur valeur, les « pseudo-scalaires » sont changés en leur opposé.

On montre sans difficulté que le produit scalaire de deux vecteurs polaires ou de deux vecteurs axiaux se comporte en vrai scalaire ; le produit scalaire d’un vecteur polaire et d’un vecteur axial, en pseudo-scalaire.