Notions probabilistes
élémentaires
« Inquiète, au milieu de leurs jeux ingénus,
De sentir s’agiter leurs chiffres inconnus
Dans l’urne de la destinée. »
Victor HUGO
Les techniques probabilistes sont fréquemment sollicitées en physique, dans des problèmes nombreux et variés, tant théoriques qu’expérimentaux. Plutôt que tenter une énumération, signalons ce fait remarquable que les probabilités participent du cœur même – au plus profond des postulats – de deux théories insignes par leur originalité et leur puissance prédictive : la mécanique statistique (voir chapitre 22) et la mécanique quantique (voir chapitre 23) – pour les citer dans l’ordre de leur apparition historique (1872 et 1930, respectivement).
Le présent chapitre se propose de décrire les notions élémentaires et fondamentales du « calcul des probabilités » tel que le pratiquent de façon effective, quotidiennement, voire pluriquotidiennement, des milliers et des centaines de physiciens œuvrant dans ce bas monde. Il existe certes, dans les sphères éthérées et altières où souffle le vent impérieux de l’axiomatique, il existe un édifice mathématique irréprochable qui revendique l’exclusivité sur le domaine des probabilités. Toutefois – incompréhension foncière entre les deux communautés, et plus radicalement incompatibilité entre les buts ultimes poursuivis – la gent physicienne, jusqu’à ses représentants les plus illustres, va son chemin aléatoire mais fermement fondé sans faire nullement appel à Kolmogorov ni à ses thuriféraires.
Notion de probabilité
« J’ai pris… — Lequel ? — Mais le plus simple, de beaucoup.
J’ai décidé d’être admirable, en tout, pour tout. »
Edmond ROSTAND
Notre démarche se veut ici résolument concrète et simple. Nous nous appuierons sur des situations claires et sur une argumentation élémentaire.
Pile ou face, archétype commode
Les probabilités se sont manifestées d’abord à propos des jeux de hasard. Il semble que le pionnier sur ce terrain fut Jérôme Cardan (1501-1576), suivi – après un siècle – par Blaise Pascal (1623-1662) et Pierre de Fermat (1601-1665), qui entretinrent une longue correspondance savante sur un problème concret surgi un jour dans un tripot. Et Pascal de s’émerveiller devant la « géométrie du hasard ».
Sans doute est-il superflu de détailler le déroulement et les règles du jeu de pile ou face, simple et familier, mais qui n’en révèle pas moins l’essence même de toute situation probabiliste.
Deux adversaires ont donc lié leur sort aux deux faces distinctes d’une pièce de monnaie que l’un ou l’autre jette en l’air. Ce ne serait pas de jeu si l’on pouvait déterminer par avance lequel des deux côtés de la pièce va finalement paraître. Rien de magique, pourtant, dans ce mouvement de montée puis redescente d’un corps rigide et connu ; les lois de la mécanique – newtonienne, cela va sans dire – devraient y suffire. Eh bien, non ! Cet espoir de rationalité s’avère illusoire : des modifications imperceptibles affectant les conditions de lancement ou l’angle de chute à la réception peuvent changer radicalement le résultat. L’information que l’on peut collecter avant ou pendant l’expérience se montre parfaitement insuffisante pour en prédire l’issue. Il s’avère dès lors plus simple et plus efficace de renoncer à obtenir cette prédiction par les lois analytiques qui régissent en principe le système, et d’invoquer le hasard. Pas aveuglément, cependant : les caractéristiques propres du hasard lui-même se feront jour et pourront offrir une compréhension, d’une espèce différente mais pertinente. On peut dès maintenant affirmer (voir ci-dessous pour plus de précision) que les chances de gagner des deux joueurs s’équilibrent exactement.
Par ailleurs, le lancement de la pièce peut être répété, sans limitation du nombre de fois, avec cette caractéristique remarquable que chaque nouveau lancement se déroule de façon totalement indépendante des précédents : le résultat qu’il s’apprête à donner ne saurait être influencé par ceux qui l’ont (éventuellement) précédé, tout aussi aléatoire que le premier ou l’un quelconque d’entre eux. On entend parfois, à ce sujet, le « bon sens » affirmer que si pile, par exemple, est déjà « sorti » 99 fois d’affilée, ses chances en sont amoindries lors du centième coup. Si l’on veut bien s’en tenir à une réflexion objective – sans invoquer une quelconque « fatalité » –, on se convaincra aisément que les lancements successifs ne dépendent pas les uns des autres, et l’on gardera cette conviction aussi inébranlable dans toutes les situations analogues.
Lorsque – ayant écarté tout trucage – nous proclamons l’égalité des chances des deux joueurs, nous n’entendons pas par là qu’il n’y aura ni gagnant ni perdant. Il y en aura dès le premier lancement de la pièce : il faut bien qu’il résulte en pile ou face – favorisant ainsi l’un ou l’autre. Mais un déséquilibre s’établira aussi, et persistera, dans la plupart des cas, après plusieurs essais : si l’on joue N fois de suite à pile ou face, on n’obtient pas exactement N / 2 piles et N / 2 faces – même si N est pair, même si N est grand. Ce n’est donc pas une simple égalité des gains qui rend manifeste l’égalité des chances des deux joueurs.
Pour concrétiser l’argument, avançons quelques nombres – sortis certes de quelque imagination, mais néanmoins parfaitement plausibles. Si par exemple on lance 100 fois la pièce (N = 100), il en résultera peut-être 42 piles (ou faces) et 58 faces (ou piles). Maintenant, si N atteint 10 000, on pourra compter 4 920 d’un côté contre 5 080 de l’autre. Les aperçus numériques que voilà sont destinés à suggérer les deux propriétés cardinales que voici. En premier lieu, l’écart à N / 2 croît, en règle générale, avec N (dans le premier exemple, 8 pour N = 100 ; dans le second, 80 pour N = 10 000) ; on comprendra ainsi que le désir de « se refaire », qui tenaille les perdants, s’apparente le plus souvent à un mirage fallacieux. Cependant – et cette seconde propriété se montre essentielle – l’écart relatif – soit l’écart divisé par N – décroît quand N croît : si 80 l’emporte nettement sur 8, en revanche 80/10 000 s’avère considérablement moindre que 8/ 100.
Exprimons de façon plus générale les deux tendances fondamentales qui se dégagent des nombres précédemment cités.
Désignons par N1 le nombre de fois qu’apparaît pile et par N2 celui où se montre face au cours de N(= N1 + N2) coups de pile ou face. Alors les proportions relatives N1 / N et N2 / N de piles et de faces s’égalisent lorsque N devient très grand : N1 ni N2 ne deviennent égaux à N / 2 – ni ne s’en rapprochent, en valeur absolue – mais N1 / N et N2 / N tendent tous deux vers 1/2 ; c’est dire que les écarts |N1 – N/2| et |N2 – N/2|, s’ils croissent avec N, croissent moins vite que N quand celui-ci devient grand.
Voilà un fait d’expérience marquant et significatif. Il ne concerne pas seulement le jeu de pile ou face ; on le retrouve, éventuellement formulé en termes différents mais inchangé quant à sa nature profonde et à son message, dans un vaste ensemble de situations analogues. C’est lui qui conduit à la notion de probabilité.
Généralisation – Définition des probabilités
Imaginons donc un processus expérimental vérifiant les deux caractéristiques cruciales du jeu de pile ou face, à savoir :
• Le résultat n’en est pas connu à l’avance avec certitude ; on sait seulement qu’il appartient nécessairement à un ensemble de résultats possibles – souvent appelés « événements » –, que nous noterons em, en les repérant par un indice m entier ; l’ensemble des résultats possibles peut donc s’écrire
{em ; m = 1,2,…}.
• Le processus peut être répété, dans les mêmes conditions, le nombre de reprises n’étant pas limité.
Prenons alors un événement particulier em, et soit Nm le nombre de fois qu’il s’est réalisé au cours de N expériences. On définit la probabilité Pm de em comme
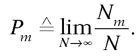
Soulignons – cf. la fin du paragraphe précédent – que cela ne signifie pas que Nm s’approche de NPm lorsque N devient grand.
Il ressort de la définition les bornes suivantes :
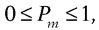
valables pour tout m. On dit « impossible » un événement de probabilité nulle, « certain » un événement de probabilité 1.
Ensemble continu d’événements
La notion de probabilité s’étend sans difficulté majeure à des situations où les événements possibles composent un ensemble continu. Il s’agira par exemple de repérer la position d’une particule (ponctuelle) sur un axe, ou dans l’espace : les événements seront caractérisés dans ce cas par l’abscisse x le long de l’axe ou le rayon-vecteur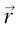 
dans l’espace. Il suffit alors de reprendre la définition des probabilités, en l’adaptant selon la technique habituelle de passage au continu (cf. chapitres 13 et 15).
Envisageons donc une « variable aléatoire » u réelle pouvant prendre a priori une valeur quelconque sur un intervalle (u1,u2) – fini ou infini. Comme aux paragraphes ci-dessus, une expérience déterminant u peut donner l’une de ces valeurs, sans qu’on sache à l’avance dire laquelle.
Fixons notre attention sur un espacement « infinitésimal » (u,u + du). Soit dN(u) le nombre (« infinitésimal ») de résultats qui, parmi un grand nombre N d’expériences, tombent entre u et u + du. La probabilité (« infinitésimale ») dP(u) associée aux événements qui se situent dans (u,u + du) est définie à la manière habituelle :
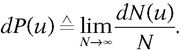
Sauf cas exceptionnels, la probabilité différentielle dP(u) se présente sous la forme
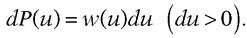
La fonction w(u) est appelée « densité de probabilité » ; partout positive ou nulle, elle présente pour dimensions physiques l’inverse de celles de la variable u – afin que la probabilité dP(u), produit de w(u) par du, reste sans dimensions.
Les deux lois de composition fondamentales
Lorsque sont connues les probabilités d’un (ou plusieurs) ensemble(s) d’événements, elles permettent souvent de calculer celles qui se rapportent à d’autres événements, éventuellement plus complexes, combinaisons des précédents. De ce « calcul des probabilités » nous nous contenterons de citer les deux piliers, lois simples qui se déduisent sans difficulté de la définition.
Envisageons deux événements e1 et e2, de probabilités respectives P1 et P2, et supposons qu’ils s’excluent l’un l’autre – c’est-à-dire que, si l’un d’eux se manifeste, il est certain que l’autre n’apparaît pas dans cette même expérience. Alors, la probabilité P(e1 ou e2) des cas où se présente soit e1 soit e2 s’obtient comme somme de P1 et P2 :
P(e1 ou e2) = P(e1) + P(e2) si e1 et e2 s’excluent.
Quelle est par exemple la probabilité d’obtenir un chiffre pair en jetant un dé ? La loi d’addition donne cette probabilité, P(2 ou 4 ou 6) comme la somme P(2) + P(4) + P(6). Si le dé n’est pas truqué, c’est trois termes égaux que l’on ajoute, valant chacun 1/6. D’où le résultat :
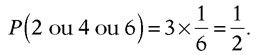
Dans un grand nombre N d’essais, soit N1 le nombre de résultats e1 et N2 le nombre de e2. Les événements e1 et e2 étant supposés incompatibles, aucune épreuve n’est comptée à la fois dans N1 et dans N2. Dans ces conditions, l’événement composé « e1 ou e2 » – c’est-à-dire « soit e1, soit e2 » – s’est produit dans (N1 + N2) occasions de ce lot de N tentatives. Par conséquent,
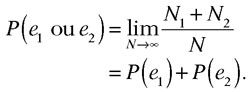
Si les deux événements ne s’excluent pas, la formule se généralise en
P(e1 ou e2) = P(e1) + P(e2) – P(e1 et e2).
En effet, une occurrence où coexistent e1 et e2 est recensée dans N1 et dans N2, et doit donc être retranchée de N1 + N2 si l’on s’en tient à « e1 ou e2 ».
Normalisation des probabilités
De la loi d’addition découle une conséquence importante et générale, une relation omniprésente dans les arguments et calculs de probabilités.
Supposons connus tous les résultats possibles em d’un processus, avec leurs probabilités Pm. Supposons que leur définition implique leur incompatibilité – ils s’excluent mutuellement. Dans ces conditions, tout essai donne pour résultat l’un des possibles – seulement l’un d’eux – ; aussi la probabilité d’obtenir e1, ou e2, ou e3,…, ou em,… vaut-elle 1 d’après la définition ; et la loi d’addition l’égale à la somme P1 + P2 + P3 + … + Pm + … On écrit, de façon plus compacte et plus élégante,
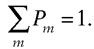
Ainsi , les probabilités associées aux six faces d’un dé se somment toujours à 1 – même pour un dé truqué. Attention : la sommation doit porter sur tous les événements envisageables, incompatibles entre eux.
Le contraire d’un événement quelconque, de probabilité P – on dit aussi son « complémentaire » –, se définit comme l’événement « e ne se produit pas ». La probabilité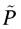 
de cet événement 
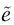contraire de e se calcule aisément à partir de la loi d’addition : il faut sommer toutes les probabilités Pm, à l’exception de celle de e. Si e occupe le rang m0 dans la liste des événements possibles,
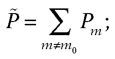
la relation de normalisation donne aussitôt la réponse :
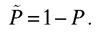
Dans le cas d’une pièce, l’événement contraire de pile ne peut être que face, et vice versa. Pour un dé, plus riche en possibilités, l’événement contraire du 6 regroupe les cinq autres faces :
1 – P(6) = P(1 ou 2 ou 3 ou 4 ou 5).
Envisageons maintenant deux processus distincts, P et P’, chacun d’eux nanti de son ensemble de résultats possibles, {em} et {e’m’} respectivement. Ces deux processus sont dits « statistiquement indépendants » – ou plus simplement « indépendants » – si le comportement de l’un n’influe en aucune manière sur l’autre : que le premier « sorte » l’événement e ne préjuge en rien du résultat e’ affiché par l’autre. Une pièce de monnaie et un dé constituent à l’évidence des systèmes indépendants, mais le sont aussi deux pièces séparées, et même deux lancements successifs d’une même pièce (le résultat du premier essai ne pèse en rien sur le résultat du suivant).
Dans une telle situation, la probabilité d’observer en concomitance deux événements, e et e’ – e venant du premier processus, e’ du second –, s’obtient comme produit des probabilités P(e) et P’(e’) des événements e et e’, chacun dans son cadre, P ou P’ :
P(e et e’) = P(e).P’(e’) si e et e’ sont indépendants.
Pour atteindre P(e et e’), on effectue un très grand nombre N d’expériences « doubles », observant simultanément un événement de P et un de P’ (s’il s’agit de deux pièces, on les jette en l’air N fois, toutes deux conjointement). Notons N(e) le nombre d’apparitions, parmi les N essais, de l’événement e de P, associé à un événement quelconque de P’, et N(e et e’) le nombre d’apparitions simultanées des deux événements e et e’. Il va sans dire que, d’après ces deux définitions, N(e et e’) contribue à N(e).
Raisonnons dans une situation où la probabilité P(e) ne s’annule pas. On peut dans ce cas choisir N (global) suffisamment grand pour que N(e) soit grand lui aussi (N(e) tend vers l’infini avec N). Alors N(e et e’) compte, parmi les N(e) expériences, celles où l’événement e’ accompagne e. L’hypothèse d’indépendance statistique permet d’affirmer que le rapport N(e et e’)/N(e) donne, à la limite des grands nombres, la probabilité P(e’) de l’événement e’ – puisque la présence, par ailleurs, de l’événement e ne l’influence pas – :
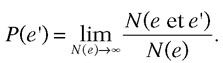
Insérons dans cette égalité le nombre total N d’épreuves :
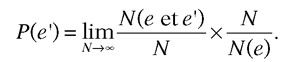
Apparaît ainsi le quotient de deux rapports ; N(e et e’) tend vers P(e et e’), et N(e)/N vers P(e). S’ensuit la « loi de multiplication ».
Le raisonnement suppose P(e) non nulle. Mais si P(e) = 0, l’événement e ne se montre jamais, de sorte que N(e) et N(e et e’) s’annulent tous deux. La relation de multiplication est trivialement vérifiée, sous la forme 0 = 0.
Dans les conditions générales où les processus P et P’ ne sont pas nécessairement indépendants, on définit la probabilité conditionnelle P(e' / e), probabilité que sorte e’ lorsque e sort par ailleurs :
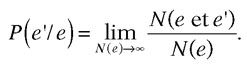
La « loi de multiplication » se généralise alors sous la forme
P(e et e’) = P(e) = P(e) × P(e’/e),
puisque P(e’) cède la place à P(e' / e). On revient à l’indépendance statistique si et seulement si
P(e' / e) = P(e’) : e et e’ indépendants.
Évaluation concrète des probabilités
Les deux lois qu’énonce le paragraphe antérieur, et le « calcul des probabilités » qu’elles fondent et qui les généralise, permettent d’évaluer les probabilités d’événements composés, à partir de celles d’événements plus simples.
Mais il faut à cela un commencement : dans chaque situation concrète, il faut se donner a priori les probabilités d’un ensemble d’événements particulièrement simples, qui se situent au cœur ou à la base du problème étudié. Ces « événements élémentaires » construisent, en se combinant, les diverses occurrences plus complexes qui peuvent apparaître dans le problème. Ainsi les probabilités des événements élémentaires peuvent-elles conduire, en suivant les combinaisons appropriées, jusqu’aux probabilités des circonstances les plus lointaines.
Méthodes d’évaluation
Revenons donc à notre modèle favori ; les événements élémentaires sont au nombre de deux seulement : pile ou face. Qu’est-ce qui nous a permis d’affirmer que les deux joueurs ont « autant de chances de gagner » – ce qui implique la probabilité 1/2 pour chacun des deux résultats possibles – ? C’est sans nul doute l’évidence qu’aucun des deux adversaires, et donc aucun des deux événements élémentaires, n’est initialement privilégié par rapport à l’autre – étant admise l’impossibilité d’une prédiction fondée sur les lois de la mécanique. Les deux événements possibles abordent l’épreuve symétriquement ; on est donc conduit à leur attribuer des probabilités égales.
Mais cela devient caduc si la pièce a été truquée de façon à favoriser l’une de ses deux faces. Plus d’équivalence entre les deux joueurs ou les deux événements élémentaires, donc plus d’équiprobabilité – « Plus d’amour, partant plus de joie. » L’absence de symétrie empêche toute évaluation théorique a priori des probabilités élémentaires.
On ne peut que les mesurer, en étudiant expérimentalement le comportement de la pièce pour appliquer la définition des probabilités. Dans le cas présent, on lance la pièce un grand nombre N de fois, et on compte les résultats « pile » (Np) et les résultats « face » (Nf = N – Np). Les rapports Np / N et Nf / N procurent une estimation – approchée, car N n’est certes pas infini – des probabilités Pp et Pf de pile et face. Celles-ci peuvent ensuite être utilisées dans des calculs de probabilités concernant des événements plus complexes. Il faut cependant s’assurer que c’est bien cette pièce-là qui intervient effectivement dans les expériences ultérieures : la substitution peut participer au trucage.
Généralisation
Deux procédés, essentiellement, permettent d’évaluer les probabilités élémentaires dans une situation physique donnée.
Le premier, le plus simple et le plus satisfaisant sur le plan intellectuel, s’applique seulement dans les cas de symétrie avérée entre les événements élémentaires : à ceux-ci sont alors affectées des probabilités toutes égales, que la condition de normalisation suffit à déterminer. Le postulat de la mécanique statistique d’équilibre est fondé sur un argument de ce type (voir chapitre 22).
Les probabilités jouent également un rôle de premier plan en mécanique quantique (voir chapitre 23), mais leurs valeurs pour les événements élémentaires diffèrent souvent entre elles. Elles sont néanmoins dictées par la théorie, ce qui les rattache au premier procédé.
Le second procédé, aussi universel que l’expérimentation, s’applique – seul à pouvoir le faire dans ces cas – lorsque les probabilités élémentaires ne découlent pas de considérations théoriques – on peut aussi le mettre en œuvre pour vérifier les conclusions théoriques dans les cas où il en existe. Il exige une étude statistique spécifique du système envisagé, destinée à mesurer les probabilités, en s’appuyant directement sur leur définition.
La réalité et les lois de la physique existent indépendamment de l’« observateur », c’est-à-dire de nous : ce présupposé est commun sans doute à tous les physiciens, quelles que soient par ailleurs leurs opinions ou croyances sur l’origine et la signification profonde de cette réalité extérieure.
Mais ce qui est en cause ici concerne la description de la nature. On qualifiera d’objective toute notion, grandeur ou propriété qui appartient de façon intrinsèque au système étudié, sur laquelle tous les observateurs s’accorderont nécessairement dès lors qu’ils seront convenus de sa définition. Sera subjective, en revanche, une notion, grandeur ou propriété qui fait intervenir l’observateur de façon irrémédiable, de sorte que son expression ou sa valeur peut varier irréductiblement d’un observateur à l’autre.
Il va sans dire que les théories physiques introduisent préférentiellement – uniquement, si possible – des concepts et outils objectifs. Mais les probabilités occupent de ce point de vue une place particulière. Plutôt que de caractéristiques intrinsèques d’un système physique, il s’agit à l’abord de pis-aller destinés à prendre en compte l’ignorance où nous laissent l’état du système et son évolution. La définition opératoire que nous avons proposée pour les probabilités n’exclut pas leur subjectivité : pourquoi l’expérience que nous entendons répéter à satiété peut-elle aboutir à plusieurs résultats différents, si ce n’est parce que l’observateur se montre incapable de prévoir lequel d’entre eux va sortir dans telle réalisation de ladite expérience ? La question peut légitimement se poser : les observateurs sont-ils tous logés à la même enseigne – objectivité –, ou certains se révèlent-ils plus malins que d’autres à évaluer les probabilités ?
Un exemple simple, emprunté encore à un jeu de hasard : on étale sur la table un jeu de cartes, dont les dos seulement apparaissent ; « la probabilité pour que telle carte pointée du doigt soit l’as de trèfle » s’évalue aussitôt. Il n’en reste pas moins que voilà une probabilité subjective : la disposition des cartes est parfaitement déterminée et immuable – et l’emplacement de l’as de trèfle fixé – dès leur répartition sur la table ; si l’on a recours aux probabilités, c’est que cette disposition n’est pas connue. Mais certes, un « observateur » astucieux saurait imaginer quelque moyen pour acquérir dans cette situation des informations décisives.
Examinons ensuite les probabilités associées à un jeu de dés. Lorsqu’on jette un dé, son état final – le nombre qu’il affiche – peut en principe être calculé, comme dans pile ou face, en appliquant les lois de la mécanique à partir de son état initial – position et orientation dans le cornet ou la main qui le lance, vitesse qui lui est imprimée, hauteur de la chute… Toute tentative pourtant de mettre en pratique ce « principe » est vouée à l’échec – chacun le sait pour avoir vainement espéré sortir un 6 en agissant sur le départ du dé. Les probabilités se révèlent dans ce cas vraiment objectives : les observateurs seront tous aussi malins – ou aussi naïfs – les uns que les autres – pourvu que soit écartée toute possibilité de prestidigitation. Cette situation découle de l’extrême sensibilité du système par rapport à d’infimes modifications dans les conditions initiales ou dans les influences extérieures : les états finals procédant d’états initiaux très proches diffèrent radicalement. Une telle instabilité du mouvement fait obstacle, en pratique, à toute prévision déterministe de l’état final et impose un traitement probabiliste objectif. On aura reconnu là les arguments qui ont déjà été avancés pour le jeu de pile ou face.
À cette question d’objectivité ou de subjectivité se rattache une remarque importante, que nous énoncerons encore dans un contexte ludique simple. Imaginons que nous ayons affaire à un dé truqué, construit de telle sorte que les probabilités d’apparition de ses six faces diffèrent entre elles. Elles n’en sont pas moins objectives, puisque inscrites dans le dé lui-même, et donc indépendantes de l’observateur. On peut les mesurer, en lançant le dé un très grand nombre de fois et en comptant, dans cette longue série d’épreuves, les fréquences selon lesquelles émergent les six faces. Mais que faire si la possibilité ou le temps manque pour mener à bien une telle série d’essais ? On doit se contenter alors de probabilités subjectives, différentes des précédentes – qui ne sont pas connues. Même si l’on sait pertinemment que le dé est falsifié, on ne sait pas comment, faute d’avoir pu exécuter les expériences nécessaires. Dans une telle situation, on doit choisir des probabilités subjectives égales pour les six faces ; si en effet on les choisissait différentes, on courrait le risque de s’éloigner davantage encore des probabilités objectives, inconnues mais effectives, car il se pourrait que l’on favorise subjectivement tel résultat qui est en réalité défavorisé objectivement.
Le rationnel peut-il parfois sembler irrationnel ?
« Le vrai peut quelquefois n’être pas vraisemblable. »
Nicolas BOILEAU