
The first mathematician to place his hand in the cookie jar was Jacob Bernoulli in 1713.
Okay, so it wasn’t a jar. And it wasn’t full of cookies.
It was an urn containing 5,000 pebbles, of which 3,000 were white and 2,000 black. (It was a big urn.)
Bernoulli imagined placing his hand in the urn and taking out a pebble at random. He had no way of knowing in advance whether it would be a white one or a black one. Random events are impossible to predict.
But, argued Bernoulli, if he took out a pebble at random, replaced it, took out another pebble, replaced it, took out another pebble, and so on, taking and replacing pebbles for a long enough time, he could guarantee that on average he would take out and replace about 3 white pebbles for every 2 black ones. In other words, because the ratio of white to black pebbles in the urn was 3 to 2, in the long run the total number of white pebbles taken out compared to the total number of black pebbles taken out would be approximately 3 to 2.
Bernoulli’s insight – that even though the outcome of a single random event is impossible to predict, the average outcome of that same event performed again and again and again may be extremely predictable (and approximately equal to the underlying probabilities) – is known as the law of large numbers. It is one of the foundational ideas of probability theory, the study of randomness, the mathematical field that underpins so much of modern life, from medicine to the financial markets, and from particle physics to weather forecasting.
Bernoulli’s pebble-picking thought experiment also created the template for puzzles in which common objects are plucked at random from urn-like receptacles, like cookies from a cookie jar.
101
BETTER THAN HALF A CHANCE
You are asked to place 100 cookies – 50 made with dark chocolate and 50 made with white chocolate – into two identical jars. Once you have completed this task you will be blindfolded, and you will have to open a jar randomly and take a single cookie from it.
When you are blindfolded, you will not be able to tell which jar is which, nor will you be able to tell the difference between cookies by touch or smell.
You hate white chocolate. How do you arrange the 100 cookies between the jars to have the best chance of choosing a dark chocolate one?
102
SINGLE WHITE PEBBLE
A bag contains a single white pebble and many black pebbles. You and a friend will take turns picking pebbles out of the bag, one at a time, choosing pebbles at random but not replacing them. The winner is the person who pulls out the white pebble.
To maximise your chance of winning, do you go first?
The advantage of going first is that you have a chance to win before your friend does. The disadvantage is that if you don’t get the white pebble on your first go, you are presenting your friend with a chance to win, and with one less black pebble in the bag your friend now has a better chance than you just had.
Randomness is a hard concept to wrap one’s head around. Indeed, probability is the area of basic maths most replete with seemingly paradoxical results, which is one reason why it is a rich source of recreational problems. Some of the best-known puzzles in maths are probability posers; and they are notorious because their answers are so counter-intuitive. In this chapter we will flip coins, roll dice and obsess over the gender of children. Your gut answers to many of the problems will invariably be wrong. Embrace the bewilderment.
Now back to extracting items from darkened receptacles.
103
THE JOY OF SOCKS
A sock drawer in a darkened room contains an equal number of red and blue socks. You are going to pick socks out at random. The minimum number of socks you need to pick to be sure of getting two of the same colour is the same as the minimum number of socks you need to pick to be sure of getting two of different colours. How many socks are in the drawer?
Next up, another sartorial stumper.
104
LOOSE CHANGE
I have 26 coins in my pocket. If I were to take out 20 coins from the pocket at random, I would have at least one 10p coin, at least two 20p coins, and at least five 50p coins. How much money is in my pocket?
Problems about selecting items often require you to count combinations. For example, how many ways are there of choosing from a group of two objects?
If the objects are A and B, we could choose: {nothing}, {A}, {B}, {A and B}. Total: four ways.
What about three objects?
If the objects are A, B and C we could choose: {nothing}, {A}, {B}, {C}, {A and B}, {A and C}, {B and C}, {A and B and C}. Total: eight ways.
To cut a long story short: if we have n objects, there are 2n different ways of choosing from them.
You may find this information helpful.
105
THE SACK OF SPUDS
A sack contains 11 potatoes with a combined weight of 2kg. Show that it is possible to take a number of potatoes out of the sack and divide them into two piles whose weights differ by less than 1g.
106
THE BAGS OF SWEETS
You have 15 plastic bags. How many sweets do you need in order to have a different number of sweets in each bag? Every bag must have at least one sweet.
The benefits of puzzles are many and varied. They can improve your powers of deduction, introduce you to interesting ideas and give you the pleasure of achievement.
They are also a ‘helpful ally’ in banishing ‘blasphemous’ and ‘unholy’ thoughts when lying awake at night, wrote Lewis Carroll, the God-fearing author of Alice’s Adventures in Wonderland.
Carroll, the pen name of Charles Dodgson, a maths don at Oxford University, celebrates puzzle solving as a remedy for self-loathing in Pillow Problems Thought Out During Sleepless Nights, a book of 72 recreational problems published in 1893. The book’s title is literal. Not only does Carroll divulge that he devised almost all the problems while tucked up in bed (think Victorian nightshirt and night-cap), he also specifies on precisely which sleepless night he thought out which problem.
In the dark hours of Thursday 8 September 1887, blood must have been pumping wildly around his brain, for that night he came up with the following brilliantly confounding teaser.
107
A STRATEGY FOR THE DISPLACEMENT OF IMPROPER THOUGHTS
A bag contains a single ball, which has a 50/50 chance of being white or black. A white ball is placed inside the bag so that there are now two balls in it. The bag is closed and shaken, and a ball is taken out, which is revealed to be white.
What is the chance that the ball remaining in the bag is also white?
In other words, you put a white ball in the bag and take a white ball out. The common sense, intuitive answer is 50 per cent, because nothing seems to have changed between the original state (mystery ball in bag, white ball outside bag) and the final state (mystery ball in bag, white ball outside bag). If the original ball in the bag had a 50 per cent chance of being white, then surely the ball left in the bag must also have a 50 per cent chance of being white? Not at all, I’m afraid. The answer is not 50 per cent.
In the second edition of Pillow Problems, Carroll made a retraction about his nocturnal musings. He rephrased the title, replacing ‘Sleepless Nights’ with ‘Wakeful Hours’ to ‘allay the anxiety of kind friends, who have written to me to express their sympathy in my broken-down state of health, believing that I am a sufferer from chronic “insomnia”, and that it is as a remedy for that exhausting malady that I have recommended mathematical calculation.’ He concludes: ‘I have never suffered from “insomnia” … [mathematical calculation is] a remedy for the harassing thoughts that are apt to invade a wholly-unoccupied mind.’ [His italics.]
At around the same time in Paris, a French mathematician was harassing his own mind with the conceptual difficulties inherent in basic probability. In his classic textbook from 1889, Calcul des Probabilités, Joseph Bertrand set the following problem. Like the Lewis Carroll problem, it involves a situation in which an object is randomly selected and its colour observed.
108
BERTRAND’S BOX PARADOX
In front of you are three identical boxes. One of them contains two black counters, one of them contains two white counters, and one of them contains a black counter and a white counter.
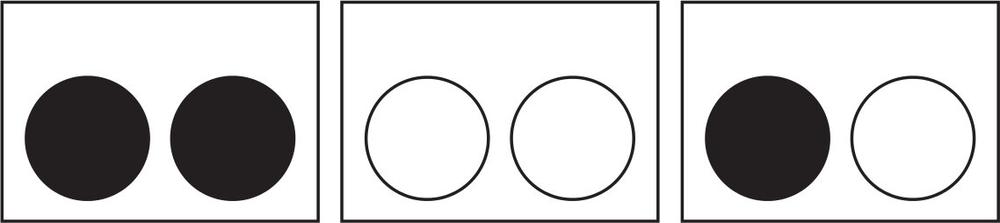
You choose a box at random, open it, and remove a counter at random without looking at the other counter in that box.
The counter you removed is black. What is the chance that the other counter in that box is also black?
If you have never seen this problem before, you will slip on the same banana skin that almost everyone else does.
The most common answer is 50 per cent. That is, most people think that if you remove a black counter from a box, half the time the counter left in the same box will be black, and half the time it will be white. The reasoning is as follows: if you choose randomly between the boxes and take out a black counter, you must have chosen from either the first or the third box. If you chose from the first box, the other counter is black, and if you chose from the third box the other counter is white. So the chances of a black counter are 1 in 2, or 50 per cent. Your task is to work out why this line of deduction is faulty.
The fact that the answer is not 50 per cent has led to this problem being known as Bertrand’s box paradox: the correct solution feels wrong, even though it is demonstrably true.
If you are still confused by the last two questions, the following discussion will be useful.
*
Paradoxes, puzzles and games have been at the heart of probability theory since its inception. In fact, the first ever mathematical analysis of randomness was written by an Italian professional gambler in the sixteenth century in order to understand the behaviour of dice.
Gerolamo Cardano – who also held down the jobs of mathematician, doctor and astrologer – played a gambling game, Sors, in which you throw two dice and add up the numbers on their faces. He saw that there were two ways to throw a 9 (the pairs 6, 3 and 5, 4), and two ways to throw a 10 (the pairs 6, 4 and 5, 5), yet somewhat curiously 9 was a more frequent throw than 10.
Total is 9
| Dice A | Dice B |
| 6 | 3 |
| 3 | 6 |
| 5 | 4 |
| 4 | 5 |
Total is 10
| Dice A | Dice B |
| 6 | 4 |
| 4 | 6 |
| 5 | 5 |
Cardano was the first person to realise that in a proper analysis of the problem, the dice must be considered separately, as illustrated here. When you roll two dice (A and B) there are four equally likely ways of getting 9, but only three of getting 10. Since there are more equally likely ways to get a 9 than a 10, when you roll two dice again and again, in the long run you will throw a 9 more often than you throw a 10.
The lesson from Cardano that will serve you well in this chapter is that when analysing a random event write out a table of all the equally likely outcomes – also called the ‘sample space’.
Roll with it.
109
THE DICE MAN DIET
In order to shed some pounds, you implement the following rule. Every day you will roll a die, and only if it rolls a 6 will you allow yourself pudding on that day.
You start on Monday, and roll the die.
On which day of the week are you most likely to eat your first pudding?
110
DIE! DIE! DIE!
You are given the chance to bet £100 on a number between 1 and 6.
Three dice are rolled. If your number doesn’t appear, you lose the stake. If your number appears once you win £100, if it appears twice you win £200 and if it appears on all three dice you win £300. (Like all betting games, if you win you also get your stake back.)
Is this bet in your favour or not?
Try to solve this problem using barely any calculations at all.
A dice throw is a very clear and understandable random event with six equally likely outcomes. Flipping a coin is a very clear and understandable random event with two equally likely outcomes.
111
THE PHONEY FLIPS
Here are two sequences of 30 coin flips. One I made by flipping an actual coin. The other I made up. Which sequence of heads and tails is most likely to be the one I made up?
[1] T T H T T T T T H H T H H T T H T H H T H H H H T H H H T T
[2] T T H T H H T T T H T H H H T H H T H H H T T H T H T T H T
In puzzle-land, giving birth supplants flipping coins as the model for a 50-50 random event. Just as a coin will land heads or tails, a child will be either a boy or a girl. Probability puzzles become much more colourful and evocative when discussing gender balance rather than comparing T’s and H’s. Indeed, one of the things that makes probability puzzles appealing is that they are usually stated using non-technical, everyday language.
In the following puzzles we ignore any global variation in gender ratios.
Assume that the chance of having a boy or a girl is the same and ignore the possibility of twins.
112
JUST FOUR KIDS
A couple plans on having four children. Is it more likely they will have two boys and two girls, or three of one sex and one of the other?
113
THE BIG FAMILY
The Browns are recently married and are planning a family. They are discussing how many children to have.
Mr Brown wants to stop as soon as they have two boys in a row, while Mrs Brown wants to stop as soon as they have a girl followed by a boy.
Which strategy is likely to result in a smaller family? In other words, once they start having children, when they get to the point that one of them wants to stop, is it more likely to be Mr Brown or Mrs Brown?
In 2010 I attended a conference of recreational mathematicians, puzzle designers and magicians in Atlanta. The biennial Gathering 4 Gardner is a celebration of the life and work of Martin Gardner (1914–2010), an American science writer whose most devoted readership comprised members of the above three groups.
One of the speakers, Gary Foshee, took to the stage to give his presentation. It consisted solely of the following words:
I have two children. One of them is a boy born on a Tuesday. What is the probability I have two boys?
Foshee left the stage to silence. The audience was bemused not only by the brevity of the talk but also by the seemingly arbitrary mention of the Tuesday.
What has Tuesday got to do with anything?
Later in the day I tracked Foshee down. He told me the answer: 13/27, a completely surprising, almost unbelievable result. And, of course, it’s all because he mentioned the day of the week.
I wrote about the Tuesday-boy problem later that year in New Scientist and on my own blog. Within weeks it had sent the internet into a frenzy of disbelief, indignation and debate. Why such a strange answer? Why does mentioning Tuesday make a difference? Mathematicians raced to give explanations and refutations. Some agreed with 13⁄27, while others argued over semantics or disputed ambiguities in the phrasing. It was my first experience of how fast a good puzzle – or at least a controversial one – can spread around the world.
We’ll get to the details of the solution shortly. But first let’s look at the Tuesday boy’s antecedents. The problem was a new spin on a doubleheader first posed by Martin Gardner in Scientific American in 1959, which itself generated a postbag of protests.
Mr Smith has two children. At least one of them is a boy. What is the probability that both children are boys?
Mr Jones has two children. The older child is a girl. What is the probability that both children are girls?
Read them quickly and you might think they are asking the same question, one about the chance of two sons and the other about the chance of two daughters. Not quite. The phrase ‘at least one of them’ opens up a world of confusion.
Mr Jones’s situation is uncontroversial and simple. If the older child is a girl, the only child of unknown gender is the younger child, who is either a boy or a girl. The probability that Mr Jones has two girls is 1 in 2, or 1/2.
Now to the troublesome Smiths. The phrase ‘at least one of them is a boy’ is to be taken mathematically, meaning that either one child is a boy, the other child is a boy, or both children are boys. In this case, there are three equally probable gender assignations of two siblings: boy-girl, girl-boy, and boy-boy. In one out of three of these cases both children are boys, so the probability is 1 in 3, or 1/3.
The puzzle is tantalizing. The two questions are almost identical, but have drastically different answers, one of which seems to go against common sense. If we know that Mr Smith has a son, but we don’t know whether this son is the older or the younger child, the chance of him having two sons is 1/3. But if we are told that the older (or indeed the younger) child is a son, the chance of him having two sons rises to 1/2. It seems paradoxical that specifying the birth order makes a difference, because we know with 100 per cent certainty that the boy is either the older or the younger.
Scientific American had barely hit the shops when the complaints started to come in. Readers pointed out that the Mr Smith question, as posed by Gardner, was ambiguous, since the given answer depended on how the information about his children was obtained. Gardner admitted the error and wrote a follow-up column about the perils of ambiguity in probability problems.
To make the Mr Smith question watertight we need to state that Mr Smith was chosen at random from the population of all families with exactly two children. If this is the case – and it is arguably how most people understand the question – then the probability that he has two boys is indeed 1/3. But imagine, on the other hand, if Mr Smith was chosen at random from the population of all two-children families and told to say ‘at least one is a boy’ if he has two boys, ‘at least one is a girl’ if he has two girls and if he has one of each to choose at random whether to say he has at least one boy or at least one girl. In this case, the probability he has two boys is 1/2. (The chance of having two boys is 1/4, the chance of two girls is 1/4 and the chance of one of each is 1/2. So the chance he has two boys is 1/4 + [1/2 x 1/2] = 1/2.)
The pitfalls of ambiguity mean that problems like this one must clearly state the process by which the available information is obtained. A further issue is plausibility. What are the real-life scenarios in which a parent of two children would meaningfully say ‘at least one of my children is a boy’ without specifying in any way which child is the boy? These next questions explore this issue.
Tread carefully, boys and girls.
114
PROBLEMS WITH SIBLINGS
For these questions assume that the parents are chosen at random from the population of families with exactly two children.
[1] Albert has two children. He is asked to complete the following form.
Of the following three choices, circle exactly one that is true for you:
My older child is a boy
My younger child is a boy
Neither child is a boy
If both are boys, flip a coin to decide which of the first two choices to circle.
Albert circles the first sentence (‘My older child is a boy’). What is the probability that both of his children are boys?
[2] A reporter sees Albert’s completed form, and writes in the newspaper:
Albert has exactly two children, the oldest of which is a son. Is a reader of the newspaper correct to deduce that the chance of Albert having two sons is 1 in 2?
[3] Beth has two children.
You: Can you think of one of your children?
Beth: OK, I have one in mind.
You: Is that child a girl?
Beth: Yes.
What do you estimate are the chances that Beth has two girls?
[4] All you know about Caleb is that he has two children, at least one of which is a girl. We can imagine asking him whether his older child is a girl, or whether his younger child is a girl, and we know his answer to at least one of these questions will be ‘Yes’. Does this insight alter the chances of him having two girls from 1 in 3 to 1 in 2?
[5] A year ago, I learned that Caleb has exactly two children. I asked him one of the following two questions: ‘Is your older child a girl?’ or ‘Is your younger child a girl?’ I know that his answer was ‘Yes’, but I can’t remember which question I asked! It’s a 50/50 chance I asked either question. What are the chances he has two girls?
These problems were set by the brothers Tom and Michael Starbird.
(Question to Mrs Starbird: You have two sons. At least one is a boy. What is the probability that both will become mathematicians?)
Tom is a veteran NASA scientist who has worked on many space missions and continues to help operate the Mars Curiosity rover, while Michael is a professor of mathematics at the University of Texas.
Michael also presents home-learning lecture courses. In the early 2000s, when he was preparing one on probability, the brothers came up with a twist on Gardner’s two-boy problem in which Mr Smith has two children, one of whom was a boy born on a Tuesday. Remarkably, once you mention the day of the week, the probability of Mr Smith having two boys is no longer 1⁄2 or 1⁄3 but somewhere in between. (Assuming that Mr Smith is randomly chosen from the population of all two-children families). The answer seems incomprehensible. How on Earth can knowing the day of the week make a difference to the probability that both children are boys, since the boy under discussion is equally likely to have been born on a Tuesday than he is likely to have been born on any other day?
The Starbirds did not realise quite how their Tuesday-boy problem would cause a trail of misery and irritation. ‘Many people resist the idea that apparent irrelevancies can have an impact on probabilities,’ says Michael. ‘People are so upset by it. Of course, surprises and counter-intuitive results are good, so I like people to be startled, but in this case the “aha” moment sometimes never comes.’
Tom says that two of his colleagues at the Jet Propulsion Laboratory reacted to the puzzle with ‘close to genuine anger. There is something about the puzzle that is seriously disconcerting to some people.’ He wonders if people get emotionally involved in this type of puzzle because it challenges their basic mathematical confidence – ‘there may be a subconscious aspect that is upsetting, along the lines of: if my intuition is so wrong for such an easy-to-state problem, am I making errors all the time in other areas?’
The solution to (and further discussion of) the Tuesday-boy problem is provided in the answer to the next question.
115
THE GIRL BORN IN AN EVEN YEAR
Doris has two children, at least one of whom is a girl born in an even-numbered year. What is the probability that both of her children are girls?
Assume that Doris is chosen at random from the population of two-child families and that babies are equally likely to be born in odd- or even-numbered years.
Here’s another puzzle about siblings that tricks our intuition. This time – you may be pleased to hear – their genders and birthdays are irrelevant.
116
THE TWYNNE TWINS
A class of 30 students – including the Twynne twins – lines up in single file in the lunch queue. The students select their positions randomly, that is, each student has an equal chance of being in any position. The line is single-file, so one of the Twynne twins will be ahead of the other in the queue. Call the Twynne twin nearer the front of the queue the ‘first’ twin in the queue.
If you had to bet that the first Twynne twin will be in a particular position in the line (as in, are they first, second, third…) which position would you pick as most likely? In other words, if the 30 students line up in a random order every lunchtime, where in the line would the first twin be most often?
Since the students select their positions randomly, in the long run each student will appear in every position roughly the same number of times. What’s counter-intuitive, however, is that the Twynne twin nearer the front of the queue is more likely to appear in one position than in any other.
The development of probability as a mathematical field led, in the nineteenth century, to the birth of modern statistics, the collection, analysis and interpretation of data. One important idea from statistics is the ‘average’ in a set of data. You may remember from school that the most common types of average are the mean (add up all the values and divide them by the number of terms), the median (the middle value if they are all listed in numerical order) and the mode (the most common value). Another familiar term when looking at data is the range, which is the difference between the highest and lowest values.
117
A JAB OF MMMR
Find two sets of five numbers for which the mean, median, mode and range are all 5. Use only whole numbers.
Averages often mislead. It all depends how you aggregate the data.
118
LIES AND STATISTICS
A headmaster is in charge of a junior school and an upper school. Across all pupils the median pupil, ranked by grade, gets a C in maths.
The headmaster introduces a new maths syllabus. The following year the median pupil’s score has reduced to grade D.
Can you devise a scenario in which the headmaster has in fact improved everyone’s grades?
The headmaster has all his pupils’ scores. Often, however, statisticians do not have all the data and must make estimates based on probabilities.
119
THE LONELINESS OF THE LONG-DISTANCE RUNNER
You know that there is a race on in your neighbourhood. You look out of your window and a runner passes by with the number 251 on their chest.
Given that the race organisers number the runners consecutively from 1, and that this runner is the only one you have seen, what is your best guess for how many runners are in the race? Take ‘best guess’ to mean the estimate that makes your observation the most likely.
Continuing our sporting interlude …
120
THE FIGHT CLUB
In order to become accepted into the prestigious Golden Cage Club, you need to win two cage fights in a row. You will fight three bouts in total. Your adversaries will be the fearsome Beast and the considerably less fearsome Mouse. In fact, you estimate that you only have a 2⁄5 chance of beating Beast, but a 9/10 chance of beating Mouse.
You can choose the order of your bouts from these two options:
Mouse, Beast, Mouse
Beast, Mouse, Beast
In order to have the greatest chance of winning entry into the Golden Cage Club, which option should you choose?
121
TYING THE GRASS AND TYING THE KNOT
In the rural Soviet Union, girls used to play the following game. One girl would take six blades of grass and put them in her hand like so.
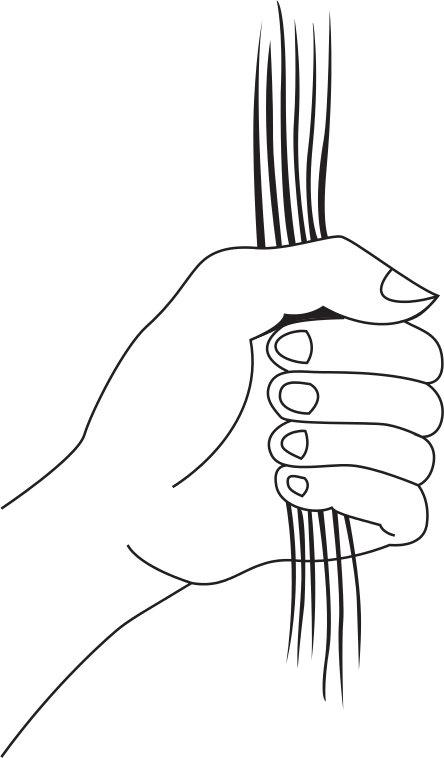
Another girl would tie the six top ends into three pairs, and then tie the six bottom ends into three pairs. When the fist was unclasped, if it revealed that the grass was joined in one big loop, it was said that the girl would marry within a year.
In this game, is it more likely than not that the girl will be told that she will marry within a year?
The search for love involves risk, luck, and probabilities. The following puzzle emerged as a problem about numbers on paper slips, but it would later became a problem about rings on fingers.
122
THE THREE SLIPS OF PAPER
Three numbers are chosen at random and written on three slips of paper. The numbers can be anything, including fractions and negative numbers. The slips are placed face down on a table. The objective of the game is to identify the slip with the highest number.
Your first move is to select a slip and turn it over. Once you see the number, you can nominate this slip as having the highest number. If you do, the game is over. However, you also have the opportunity to discard the first slip and turn over one of the remaining slips. As before, once you see the number on that slip, you can nominate it as being the highest. Or you can discard it, which means that you must choose the final slip, and nominate that as having the highest number.
The odds that the first slip you turn over has the highest number is 1 in 3, because you are randomly picking one option in three. What is the strategy, however, for the remaining slips that improves your odds of guessing the one with the highest number from 1 in 3?
A follow-up question: there are only two slips of paper. Each one has a number on it that was chosen at random. The slips are face down on a table. You are allowed to turn over only one of them, before stating your guess about which slip has the highest number.
Can you improve your odds from 1 in 2 of naming the slip with the highest number?
The answer to both these questions is yes, you can improve your odds with the right strategy. In the case of the problem with two slips only, it’s a stunning result, one of the most remarkable in this book. The values on the two slips can be any numbers at all. You only see one of them. Yet it is possible to guess which of the two is the biggest and have a greater than 50 per cent chance of being correct. Wow.
But what has all this got to do with marriage?
Like the Tuesday-boy problem, the roots of the slips of paper puzzle can be traced back to Martin Gardner and his Scientific American column, which ran monthly from 1959 to 1980. In 1960, he described a variation of the paper slip puzzle that allowed for as many slips as you like. The table now contains a multitude of face-down slips, each with a different random number on it. Again the aim is to name the highest number. You are allowed to turn over any one slip, but as soon as you do you must either choose it (and forgo seeing the others) or discard it. (The solution for that particular version is also in the back.)
Gardner suggested that this game models a woman’s search for a husband. Imagine a woman decides she will date, say, 10 men, each of different suitability, in a year, and imagine that she will indicate after each date whether he should propose. (One assumes that if she gives the okay he will propose, and she will say yes.) The men are the paper slips and the number is their ranking in terms of suitability. Clearly, the woman wants to marry the husband who ranks highest (i.e., she wants to choose the highest number). Once she has started dating, the following rules apply: if she allows someone to propose, she is not allowed to go on a date with the remaining men. And if she rejects a guy, then she cannot return to him later. This behaviour models having to either choose a slip and forgo seeing the others, or reject it and move on. Whether or not one agrees with Gardner’s simplifications – and even he took them with a pinch of salt – the puzzle has become known as the ‘marriage problem’. The field of maths involved here is called ‘optimal stopping’: in a process that could conceivably go on and on, based on what has happened in the past, when is it in your best interests to stop?
The following teaser also first appeared in Martin Gardner’s Scientific American column, in 1959. It was to become the most notorious probability puzzle of the last 50 years.
123
THE THREE PRISONERS
Three prisoners, A, B and C, are to be executed next week. In a moment of benevolence, the prison governor picks one at random to be pardoned. The governor visits the prisoners individually to tell them of her decision, but adds that she will not say which prisoner will be pardoned until the day of execution.
Prisoner A, who considers himself the smartest of the bunch, asks the governor the following question: ‘Since you won’t tell me who will be pardoned, could you instead tell me the name of a prisoner who will be executed? If B will be pardoned, give me C’s name. If C will be pardoned, give me B’s name. And if I am to be pardoned, flip a coin to decide whether to tell me B or C.’
The governor thinks about A’s request overnight. She reasons that telling A the name of a prisoner that will be executed is not giving away the name of the prisoner that will be pardoned, so she decides to comply with his demand. The following day she goes into A’s cell and tells him that B will be executed.
A is overjoyed. If B is definitely going to be executed, then either C or A will be pardoned, meaning that A’s chances of being pardoned have just increased from 1 in 3 to 1 in 2.
A tells C what happened. C is also overjoyed, since he too reasons that his chances of being pardoned have risen from 1 in 3 to 1 in 2.
Did both prisoners reason correctly? And if not, what are their odds of being pardoned?
This puzzle may feel familiar. At its core is Bertrand’s box paradox, which we discussed only a few pages ago.
It is also equivalent to a much more famous puzzle involving two horned, bearded ruminants, a car and a TV host.
The host is Monty Hall, who presented the US game show Let’s Make a Deal between 1963 and 1990. In the final segment of the show a prize was hidden behind one of three doors and the contestant had to choose the correct door to win it. (Let’s Make a Deal never caught on outside the US. A British version hosted by Mike Smith and Julian Clary ran for a single season in 1989.) Here’s the ‘Monty Hall problem’ in full.
You have made the final round on Let’s Make a Deal. In front of you are three doors. Behind one door is an expensive car; behind the other two doors are goats. Your aim is to choose the door with the car behind it.
The host, Monty Hall, says that once you have made your choice he will open one of the other doors to reveal a goat. (Since he knows where the car is, he can always do this. If the door you choose conceals the car, he will choose randomly between which of the other two doors to open).
The game begins and you pick door No. 1.
Monty Hall opens door No. 2, to reveal a goat.
He then offers you the option of sticking with door No. 1, or switching to door No. 3.
Is it in your advantage to make the switch?
The question was devised in 1975 by Steve Selvin, a young statistics professor at the University of California, for a lecture course he was giving on basic probability. The first time he asked it, all hell broke loose. ‘The class was divided into warring camps,’ he remembers. Do you stick or do you switch?
Perhaps the most common initial response is that it makes no difference to switch. If there are two doors left, and we know that the car has been randomly placed behind one of them, it’s intuitive to think that the odds of the car being behind either one are 1 in 2.
Wrong! The correct answer is to switch.
In fact, when you switch, you double your odds of getting the car. If you stick, your chances of winning the car are 1 in 3. There were three closed doors and you had a 1 in 3 chance of choosing correctly. Your odds don’t change when Monty Hall opens another door, because he was always going to open another door regardless of your choice.
If you switch, however, your chances of winning the car rise to 2 in 3. When you choose your first door, as I said in the previous paragraph, you have a 1 in 3 chance of choosing correctly. In other words, there is a 2 in 3 chance that the car is behind one of the other doors. When Monty Hall reveals that one of the doors you did not choose has a goat behind it, there is now only a single choice remaining for the ‘any other door’ option. Therefore, the probability that this remaining door is the one with the car behind it is 2 in 3.
If you are finding this confusing, or counter-intuitive, you are not alone. In 1990, the problem appeared in Marilyn vos Savant’s column in the large-circulation US magazine Parade. She said switch. Her article provoked a deluge of about 10,000 letters, almost all disagreeing with her. Almost a thousand of these letters came from people with a PhD after their names. The New York Times reported on the storm on its front page.
The Monty Hall problem requires careful thought. As does its sister puzzle …
124
THE MONTY FALL PROBLEM
You have made it to the final round of Let’s Make a Deal. In front of you are three doors. Behind one door is an expensive car; behind the other two doors are goats. Your aim is to choose the door with the car behind it.
The host, Monty Hall, says that once you have made your choice he will open one of the other doors to reveal a goat. (Since he knows where the car is, he can always do this. If the door you choose conceals the car, he will choose randomly between which of the other two doors to open.)
The game begins and you pick door No. 1.
Monty Hall walks to the doors, stumbles, falls flat on his face and accidentally, at random, opens one of the two doors that you didn’t pick. It’s door No. 2, which reveals a goat.
Monty Hall dusts himself off and gives you the option of sticking with door No. 1, or switching to door No. 3.
Is it in your advantage to make the switch?
Monty Hall’s fame has spawned many similar ‘stick or switch’ problems.
125
RUSSIAN ROULETTE
You are tied to a chair and your crazed captor decides to make you play Russian roulette. She picks up a revolver, opens the cylinder and shows you six chambers, all of which are empty.
She then puts two bullets in the revolver, each in a separate chamber. She closes the gun and spins the cylinder so you do not know which bullet is in which chamber.
She puts the gun to your head and pulls the trigger. Click. You got lucky.
‘I’m going to shoot again,’ she says. ‘Would you like me to pull the trigger now, or would you prefer me to spin the cylinder first?’
What’s your best course of action if the bullets are in adjacent chambers?
What’s your best course of action if the bullets are not in adjacent chambers?
Congratulations, you survived. You didn’t blow your brains out, although I hope they have been thoroughly massaged over the course of the book.
This chapter concerned probability, an area that underlies much of modern life – from finance to statistics to the frequencies of buses – and one in which it is easy to fall into traps. The more we are aware of how probability can mislead us, the better the decisions we will be able to make in real life. In fact, my aim in the whole of this book has been to present you with puzzles from which there is something to learn, whether a new concept, a clever strategy, or just a simple surprise. I have wanted to kindle creativity, encourage curiosity, hone powers of logical deduction, and share a sense of fun.
Most problems in life don’t come with a set of solutions. Thankfully, mine do. And here they are.