1 THE THREE RABBITS
2 DEAD OR ALIVE
See now the four lines. ‘Tally ho!’
We’ve touch’d the dogs, and away they go!
3 GOOD NEIGHBOURS
The rabbit was not harmed because it was already dead when the dog picked it up.
4 A FERTILE FAMILY
The single doe has more than 28 trillion descendants, which is about 300 times the estimated total number of humans that have ever lived.
Now to how we get there.
For the first six months of her life, the doe is not fertile. Let M(n) be the total number of does at the end of month n. We have
M(1) = M(2) = M(3) = M(4) = M(5) = M(6) = 1
Finally, at the end of the seventh month, she produces six kits, three of which are does, and she produces three more does per month until the end of the year. Note that we can write each monthly total in terms of the total of the previous month.
M(7) = 1 + 3 = 4
M(8) = M(7) + 3 = 7
M(9) = M(8) + 3 = 10
M(10) = M(9) + 3 = 13
M(11) = M(10) + 3 = 16
M(12) = M(11) + 3 = 19
In the second year, she will start to have grandchildren. In the first month of the second year, she adds another three does, and her first litter produces three each. That’s four batches of three added to the previous month’s total.
M(13) = M(12) + 4 x 3 = 31
In the second month of the second year, she adds another three does, and her first and second litters also produce another three. That’s seven batches of three.
M(14) = M(13) + 7 x 3 = 52
M(15) = M(14) + 10 x 3 = 82
M(16) = M(15) + 13 x 3 = 121
You may have spotted a pattern by now – the number of new does is the monthly total from six months previously, multiplied by 3. In other words:
M(14) = M(13) + 3 x M(8)
M(15) = M(14) + 3 x M(9)
M(16) = M(15) + 3 x M(10)
Rewritten as a formula we have M(n) = M(n – 1) + 3M(n – 6). The M(n – 1) part is the running total from the month before, and the 3M(n – 6) gives us three new does for every doe that was alive six months ago, which is necessary and sufficient for it to be fertile now. Since the life span of a rabbit is seven years, or 84 months, we want to know M(84).
Calculating this by hand will take too long. Put it in a computer and out will pop 14,340,818,086,651.
But this is not the answer, yet. We need to subtract 1 (the rabbit whose descendants we are trying to calculate) and multiply by 2, since for every doe born there is also a buck.
The final answer is 28,681,636,173,300 descendants.
A bunny bonanza!
5 A BUNCH OF HOPS
The rabbits were a clue. The answer is 55, the ninth term in the Fibonacci sequence.
Like many questions of this type, we embark on our solution by simplifying the problem and looking for a pattern. With only two lilies, there is only one way to get from the first to the last lily: a single jump of 1. With three lilies there are two ways: either two single jumps or a double jump; and with four there are three ways: three singles, a single followed by a double, or a double followed by a single.
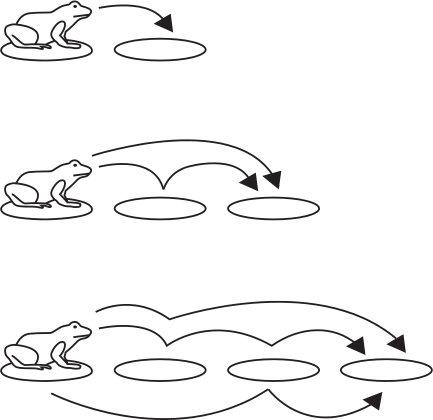
Now consider five lilies, as shown opposite. The frog’s first jump will be to either A or B. The total number of ways to get to the last lily is therefore the number of ways from A plus the number of ways from B, which is 2 + 3 = 5.
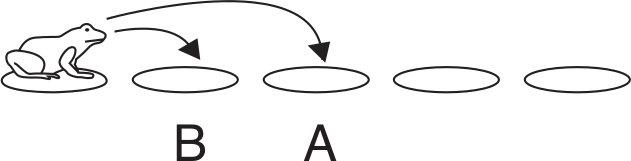
Continuing this line of thought, the number of ways to jump across six lilies is the number of ways to jump across four of them plus the number of ways to jump across five, which is 3 + 5 = 8. The answer for seven lilies is 5 + 8 = 13, for eight the answer is 8 + 13 = 21, for nine it’s 13 + 21 = 34, and for ten it’s 21 + 34 = 55.
This recursive process – starting with 1, 2 and 3, and generating the next term in a sequence by summing the last two terms – produces the Fibonacci sequence.
6 CROSSING THE DESERT
The four Bedouin tribesmen – let’s call them A, B, C and D – depart together, each loaded with five days’ worth of water.
At the end of the first day, they each have four days of water left. A gives a day’s worth of water to each of his three colleagues, leaving him with a single day’s worth of water.
On the second day A returns home (since he is a day away from there, and he has a day’s worth of water), while B, C and D carry on. At the end of the second day the three of them are now two days out, each with four days of water left. B gives a day’s worth of water to the other two, leaving him with two days’ worth of water, and the others at capacity with five days’ worth.
On the third day B now returns home (which he is able to do since he has two days’ worth of water, and the start is two days away) and C and D carry on, reaching a point three days away from the start, with both carrying four days’ worth of water. C now gives D a day’s worth of water.
On the fourth day, C returns home (which he is able to do since he has three days’ worth of water and home is three days away), while D finally reaches the camp, where he delivers the package. D has four days’ worth of water left, which is just what he needs to travel back home.
7 SAVE THE ANTELOPE
You set off with a full load of five gallons (that’s a full tank and four full canisters) and use a gallon to drive 100 miles. Call this point A. Fill the tank, leave the remaining three canisters by the side of the road, and return to base.
Set off again with five gallons and use a gallon to drive the 100 miles to A. Pick up a canister, fill the tank, and with a full load drive another 100 miles. Call this point B. Leave two canisters by the side of the road here. You have two canisters left, and this is enough to get you the 200 miles back to base.
So far you have taken 10 gallons from base, and have two canisters at A and two canisters at B. The petrol in these four canisters will let you drive for 400 miles, meaning that you only need another four gallons to do the round trip.
Set off for the final time with four gallons: one in the tank and three in canisters. Here is one way you can now split the journey: at A, fill the tank with one canister and take on the other. You now have a full load which will get you the 300 miles to the antelope and a further 200 miles back to B. Once you are back at B, take the two remaining canisters, which is just enough for the 200 miles home.
8 THE THIRTEEN CAMELS
The 17 camel puzzle is a lesson about how easily numbers can be used to mislead. The apparent contradiction comes from assuming that the fractions demanded by the father – 1⁄2, 1⁄3 and 1⁄9 – add up to 1. But they don’t. Written as fractions with lowest common denominator 18 they are 9⁄18, 6⁄18 and 2⁄18 which add up to 17⁄18. When the children are given 9, 6 and 2 camels they are not being given a half, a third and a ninth of the total inheritance, as the puzzle suggests. They each receive slightly more. What they do receive, however, is a number of camels that are in the proportions set out by the father – 1⁄2:1⁄3:1⁄9 – which when multiplied by 18 are the same as 9:6:2.
The 13 camel problem is a twist on the 17 camel problem in which the wise woman is a bit more provocative. Rather than loaning them a camel, she temporarily takes one away.
The woman hears the children’s gripe and says she can solve it if she can confiscate one of their camels. The children reluctantly agree, leaving them with only 12 camels left. She gives 6 to the eldest, which is half the total, and she gives 4 to the middle one, which is a third of the total.
That leaves only 2 camels, which she gives to the youngest child. To these camels she adds the one that she confiscated, meaning that the youngest now has 3 camels, a quarter of 12.
The three children thus receive 6, 4 and 3 camels each.
If you read the question carefully, the man does not say clearly that he wants his children to receive a half, a third and a quarter of the total number of camels. A fair interpretation is that he wants the children to have camels in the proportions 1⁄2:1⁄3:1⁄4, or 6⁄12:4⁄12:3⁄12, which is indeed the solution the wise woman presents.
9 CAMEL VS. HORSE
Ada says: ‘Get on the other person’s animal!’
10 THE ZIG-ZAGGING FLY
The simple way to solve this problem is not to think about the distance travelled, but about the time spent travelling. If two cyclists 20 miles apart are cycling at 10 miles an hour, they will meet in one hour. The fly, which is flying at 15 miles an hour, will therefore have travelled 15 miles.
11 THE ANTS ON A STICK
Carlos, our anty-hero, falls off last after exactly 100 seconds.
The arbitrary-sounding distances 38.5cm, 65.4cm and 90.8cm were a sign that you need to think laterally about this puzzle. No puzzle that passes as entertainment is going to require algebra or arithmetic with numbers like 38.5 and 65.4. (Of course, it would be possible to work out the answer by calculating the positions, but that would be messy.)
The piece of insight that makes this an elegant puzzle is this: think about what happens when two ants collide and both walk back the way they came. If you blur your eyes, this is equivalent to those two ants walking past each other. In other words, this puzzle can be treated as if six ants, each on their own track, are walking to the end of the stick. Another way to visualise it is this: imagine that each ant is carrying a leaf, and that on each collision they exchange leaves. The leaves will be moving at 1cm per second in a unique direction. The leaf that takes the longest to fall off the edge is the one that starts with Aggie. So, it will take 100 seconds – 1m at 1cm per second – until the last ant drops.
Now to the identity of the ant in question. Let’s continue thinking about the leaves. Four leaves will fall off the right side (because leaves only move in one direction, and four of them are moving to the right). The last leaf to fall off on the right side is the one that started on Aggie, and we can deduce that the ant carrying it at that point must be the ant that started fourth from the right. Stand up Carlos, that’s you. It has to be him because ants can’t walk past each other, so the order of the ants on the stick cannot change. The fact that we don’t know his position to start with is irrelevant.
12 THE SNAIL ON THE ELASTIC BAND
During the first second, the snail crawls 1cm.
In other words, the snail travels 1⁄100,000 of the length of the 1km-long elastic band.
The elastic band stretches instantly to 2km. During the following second, the snail travels another 1cm, which now represents 1⁄200,000 of the length of the elastic band. After the third second the length of the band is 3km, so the 1cm travelled by the snail represents 1⁄300,000 of the length of the elastic band. And so on.
If we add up all these fractions, we get the following term:
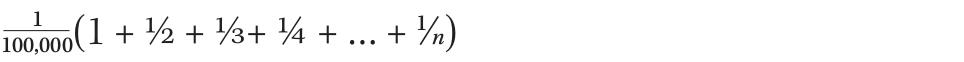
This number describes the snail’s progress after n seconds, expressed as a fraction of the total length of the elastic band.
If you got this far, congratulations. To finish this proof you need some background knowledge. The term in the brackets, (1 + 1⁄2 + 1⁄3 + 1⁄4 + … + 1⁄n), is also known as the ‘harmonic series’, and it gets bigger and bigger the more terms you add, eventually exceeding any finite number. (In my discussion of the jeep problem I mentioned the series 1 + 1⁄3 + 1⁄5 + …, which also increases beyond any finite number. If this series increases to infinity, so must the harmonic series. Proving the divergence of the harmonic series is not hard, and a proof can be found easily online.)
We know, therefore, that there exists a number N such that the term (1 + 1⁄2 + 1⁄3 + 1⁄4 + … + 1⁄N) exceeds 100,000. After N seconds the expression above describing the snail’s progress will be more than 1, which means that the snail will have reached the end of the elastic band. It will take a while! N seconds is longer than the age of the universe. And after N stretches, the elastic band will be so long it will not even fit in the universe.
13 ANIMALS THAT TURN HEADS
14 BANISHING BUGS FROM THE BED
The ceiling gutters need to be positioned outside the line of the bed, and the other way around.
15 THE DUMB PARROT
If we are told that the owner of the pet shop never lies, the problem must lie with either the customer or the bird. Here are four possible answers:
The bird is deaf. (She repeats every word she hears, but hears nothing.)
The bird will repeat every word she hears exactly a year after hearing it.
The bird is so intelligent she decided to ignore the owner because she deemed him too stupid.
The customer is lying.
16 CHAMELEON CAROUSEL
No, the chameleons will never all have the same colour.
Let the number of green, blue and red chameleons be G, B and R, and consider what happens when two chameleons meet. If green meets blue, both will become red. In other words, the total number of green lizards becomes G – 1, the total number of blue lizards becomes B – 1, and the total number of red lizards becomes R + 2.
Now consider what happens to the difference between the number of lizards of each colour when green meets blue – in other words, what happens to G – B, B – R and R – G:
G – B goes to G – 1 – (B – 1) = G – B
B – R goes to B – 1 – (R + 2) = B – R – 3
R – G goes to R + 2 – (G – 1) = R – G + 3
So, when green meets blue (and by extension when any two chameleons of different colours meet), either the difference between any two colours stays the same, or it increases or decreases by 3.
When all the chameleons in the colony are the same colour, the difference between any two colours (that’s G – B, B – R, and R – G) will be zero.
Now let’s enter the numbers given in the question: 13 green, 15 blue and 17 red. In other words, the difference between green and blue is 2, between blue and red it’s 2, and between red and green it’s 4. We know that when chameleons meet, the difference between any two colours either stays the same or changes by 3. We can deduce that it is impossible for the difference between any two colours to be 0, since you cannot get to 0 from either 2 or 4 simply by adding or subtracting 3.
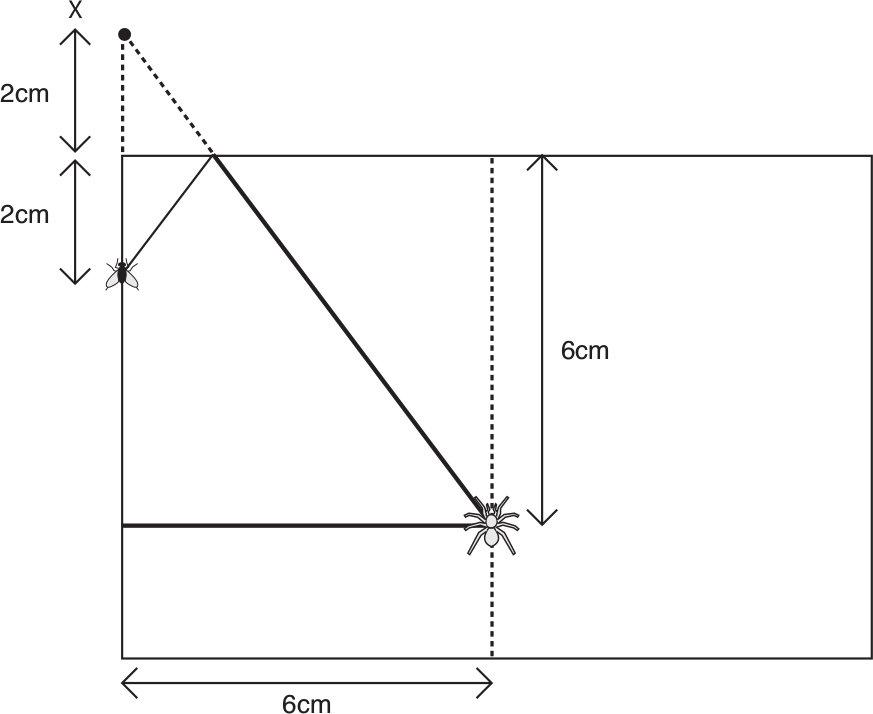
17 THE SPIDER AND THE FLY
Imagine the glass is made out of cardboard and unroll it, as shown below. From Heron’s theorem, the shortest path from the spider to the fly is the distance from the spider to X, where X is 2cm up the vertical from the horizontal edge of the cardboard. This distance is the hypotenuse of a right-angled triangle that has sides 6cm and 8cm. Using Pythagoras’ theorem for right-angled triangles (which states that the sum of the squares of the sides is equal to the square of the hypotenuse), we deduce that the distance in cm that the spider will travel is √(62 + 82) = √(36 + 64) = √100 = 10cm.
18 THE MEERKAT IN THE MIRROR
The vertical meerkat is looking at a vertical mirror, as illustrated here.
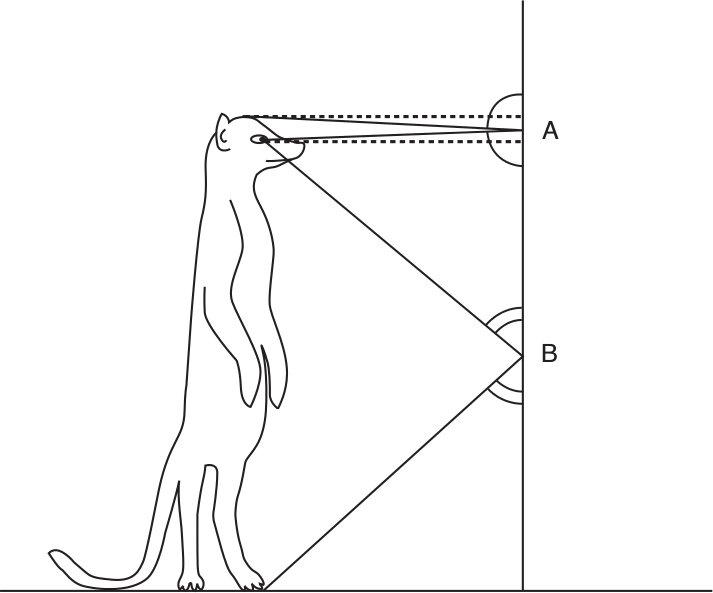
First we’re going to work out where the mirror must be hanging, and how long it is, so that the meerkat can see its reflection perfectly framed.
If the meerkat can see the top of its head, light from the top of its head must hit the mirror at a certain point and then rebound into its eyes. Let this point be A. Since the angles of incidence and reflection are equal, the height of A must be halfway between the height of the meerkat’s eyes and the height of its head.
Likewise, if the meerkat can see its toes, light from the toes must hit the mirror at a point and then rebound into its eyes. Let this point be B. The height of B must be half the height of the meerkat’s eyes from the ground.
If the meerkat’s reflection is perfectly framed, meaning that it can see no lower than its toes and no higher than its head, then the mirror must be positioned exactly between A and B. (Which means its length is equal to half the meerkat’s height.)
We’ve worked out the position of the mirror without knowing how far the meerkat is from the wall. Which means that the meerkat can be any distance from the wall, and it will see its reflection perfectly framed. When the meerkat steps back, points A and B stay where they are, meaning that the animal’s reflection neither magnifies nor shrinks with respect to the mirror: it stays perfectly framed. Because the angles of incidence and reflection of light are always equal, the angle from A to the meerkat’s eyes is always equal to the angle from A to the top of its head, even though the size of this angle will increase as the animal steps backwards. Likewise, the angle from B to the meerkat’s eyes is always equal to the angle from B to its toes, whatever the size of that angle.
19 CATCH THE CAT
Ten days.
Let’s begin with an explanation of the solution when there are only four doors. In the grid opposite, each row displays the possible positions of the cat on each day. The X marks the door I will open on each day.
On Day 1 the cat could be behind any door, so there are cats in every cell. I open the second door along. If the cat is there, game over. But if the cat is not there, I can eliminate the chance that the cat will be behind the first door on Day 2, since the only way the cat could be there is if it was behind the second door on Day 1. On Day 2, therefore, the cat can only be behind three possible doors.
On Day 2 I’ll open the third door along. If the cat is there, game over. If not, I can eliminate the chance that the cat will be behind the fourth door along on Day 3. I can also eliminate the chance that the cat will be behind the second door on Day 3, since to get there it would have had to have moved from either doors 1 or 3, both of which we know do not conceal a cat. We have reduced the choices to two. On Day 3 I open the third door. If the cat is there, game over. If the cat is not there, it must have been behind door 1, which means that by opening the second door on Day 4 I can guarantee that the cat is caught.
Once you work out the four-door solution, it’s not so tricky to add an extra door: you can bag the puss in six days by opening the doors 2, 3, 4, 4, 3, 2 in that order.
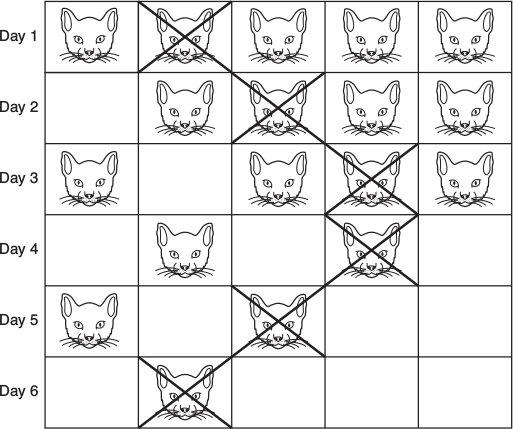
A pattern is developing: start at the second door along, then open the next door to the right on Day 2, and so on, until you get to the penultimate door. Then return. When there are seven doors, try them in this order: 2, 3, 4, 5, 6, 6, 5, 4, 3, 2. This will ensnare the furtive furry one.
If the number of doors is n, you can always catch the cat in (n – 2) x 2 days.
20 MAN SPITES DOG
The postman would do well to noisily circumnavigate the house, since if the dog is always straining at the leash to be as near to him as possible, it will end up winding its leash around the tree, thus reducing the effective length of the leash until the path is safe.
21 THE GERM JAR
Thirty minutes.
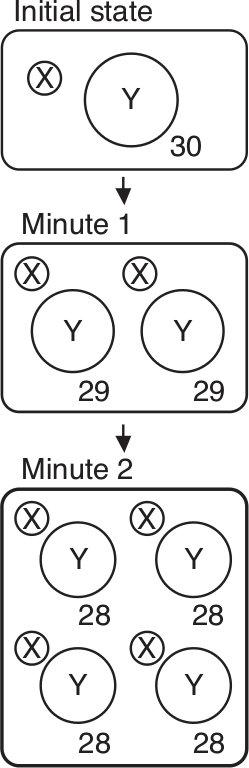
The initial state has a single X and 30 Ys. After one minute, an X will have eaten a Y and doubled, while all the remaining Ys will have doubled. In other words, the population of X is 2 while the population of Y is 2 x 29. A useful way to visualise this, illustrated right, splits the population into two: each half has a single X and 29 Ys. A minute later the population can be split in four batches, each with a single X and 28 Ys, and a minute after than into eight (or 23) batches, each with a single X and 27 Ys. At the end of the twenty-ninth minute there will be 229 batches, each containing a single X and a single Y. After 30 minutes there will be no Ys left at all.
22 THE FOX AND THE DUCK
The fox’s best strategy will always be to position itself on the shore as close to the duck as possible. Conversely, the duck’s best strategy is to position itself as far as possible from the fox.
We saw that if the duck heads in a straight line for the shore, the fox will catch it. So that plan is out.
But consider what happens when the duck travels in concentric circles around the centre of the lake. The fox will also travel in a circle round the lake, trying at all times to be at the closest point to the duck.
Whether or not the fox can keep up with the duck, however, depends on the size of the circle travelled by the duck. If the circular path is close to the edge of the lake, the fox will have no trouble marking the duck. However, if the circle is a small one at the centre of the lake, the duck will be able to go one full rotation faster than the fox can.
In fact, since the duck paddles at a quarter of the speed of the fox, both animals will take the same time to make a full rotation when the duck travels a quarter of the distance the fox does. This happens when the radius of the duck’s circle is r⁄4, a quarter of the radius of the lake. If the duck paddles in a concentric circle with a radius of less than r⁄4, the fox will not be able to keep up with it and will slowly lag behind.
Imagine now that the duck is travelling in a concentric circle with a radius just under r⁄4 (i.e. just under 0.25r). The fox will lag behind, and after a certain time the duck will be at the position on that circle that is opposite the position of the fox. At that moment the duck will be at a distance of just under 1.25r from the fox, and just over 0.75r from the opposite shore. If the duck makes a direct line to the shore now, it will have to travel this ‘just over 0.75r’ in the same time as the fox runs πr, or 3.14r. Since the fox is four times faster, the duck will make it if ‘just over 0.75r’ is less than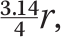 
which is about 0.78r. Which is possible. Let’s say the duck is travelling in a circle of, say, 0.24r. It will always be 0.76r from the shore, so if it starts for the shore when it’s opposite the position of the fox, it will reach land before the fox can catch it.
23 THE LOGICAL LIONS
If there are 10 lions, the sheep survives.
But if there are 11 of them, the sheep will die.
We solve this problem by seeing what happens when the pen has a single lion in it, and then increasing the number by one each time.
One lion, one sheep:
With a single lion in the pen, the sheep doesn’t stand a chance. The lion will gobble it up. Result: the sheep dies.
Two lions, one sheep:
Neither of the lions will risk eating the sheep, since if one of them did it would get drowsy and then be eaten by the other lion. Result: the sheep lives.
Three lions, one sheep:
One of the three lions will happily eat the sheep, because this lion knows that even though it will get drowsy, none of the other two lions will dare eat it. If one of the other lions did eat the sheep-eater, that lion would then get drowsy and be eaten by the last remaining lion. Result: the sheep dies.
Four lions, one sheep:
If one of the four lions eats the sheep, it will become drowsy and the situation becomes equivalent to the situation with three lions, only with the drowsy lion in place of the sheep. Since three lions/one sheep is a scenario in which the sheep dies, none of our four logical lions will eat the sheep. Result: the sheep lives.
You will hopefully see the pattern now. Whether or not a lion eats the sheep depends on the scenario in which there is one less lion. If the sheep in the scenario with one less lion lives, then the lion will eat the sheep, but if the sheep in the scenario with one less lion does not live, the lion will not eat the sheep.
In other words, the mortality of the sheep flips between alive and dead each time you increase the number of lions by 1. If there is an odd number of lions the sheep will live, and if there is an even number the sheep will die. Since the problem states 10 lions, the sheep will live.
24 TWO PIGS IN A BOX
The smaller, subordinate pig eats better. Strength is sometimes a weakness.
This paradoxical conclusion arises because the small pig quickly realises that when it does press the lever, all it is doing is feeding the big pig, since the big pig will be waiting by the bowl to eat up all the food. Once the big pig is by the bowl, the small pig will not be able to push it out of the way.
The small pig has no incentive to pull the lever, so it doesn’t. That job therefore falls to the big pig. When the big pig pulls the lever, the small pig will be waiting by the bowl and will eat as much as he can before the big pig arrives and pushes him out of the way. Since the big pig will get some food, he does have some incentive to press the lever, even though the small pig will often get most of what’s in the bowl.
25 TEN RATS AND ONE THOUSAND BOTTLES
Our method will be to feed each rat a mixture taken from different bottles, and to work out which is the poisoned bottle by noting which rats survive and which rats die by the end of the hour. The rats must be fed these mixtures simultaneously, so that after exactly an hour we can see the death toll and deduce which bottle has the poison.
We have 10 rats. After an hour they will be either alive or dead. There are exactly 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 = 210 = 1,024 possible combinations of 10 alive or dead rats, since there are 10 rats and every rat can be one of two things, alive or dead. The fact that there are 1,024 possible combinations and only 1,000 bottles means that we have more than enough combinations to specify individual bottles.
The question now becomes how to make each unique combination of live and dead rats refer to a unique bottle. The answer is that we use binary numbers – the number base in which only 0 and 1 are used. In the usual decimal number system, the digit furthest on the right is in the ‘units’ column, and then moving left we have the ‘tens’, the ‘hundreds’, the ‘thousands’, and so on, each one being 10 times the one before. In the binary system, the units column counts 1, but moving leftwards the columns count 2, 4, 8, 16, and so on, doubling each time, as shown below.
| Decimal | Binary |
|---|---|
| 1 | 1 |
| 2 | 10 |
| 3 | 11 |
| 4 | 100 |
| … | … |
| 998 | 1111100110 |
| 999 | 1111100111 |
| 1000 | 1111101000 |
Our first job is to order all the bottles in binary notation from 1 to 1111101000. We need them all in ten-digit form, so 1 is 0000000001, and 2 is 0000000010.
We also order the rats: we have a ‘units’ rat, a ‘twos’ rat, a ‘fours’ rat, an ‘eights’ rat, and so on up to a ‘five hundred and twelves’ rat.
Finally, we give the wine to the rats.
The units rat gets a cocktail that contains a sip from every bottle whose binary form has a 1 in the units column.
The twos rat gets a cocktail that contains a sip from every bottle whose binary form has a 1 in the twos column.
The fours rat gets a cocktail that contains a sip from every bottle whose binary form has a 1 in the fours column.
And so on.
If the units rat dies, we know that the binary representation of the poisoned bottle has a 1 in the units column.
If the units rat survives, we know that the binary representation of the poisoned bottle has a 0 in the units column.
If the twos rat dies, we know that the binary representation of the poisoned bottle has a 1 in the twos column.
If the twos rat survives, we know that the binary representation of the poisoned bottle has a 0 in the twos column. And so on.
In other words, in a ten-digit binary number that determines which bottle has the poison, the dead rats are the 1s and the live rats are the 0s. Voila!
The reason that not all the rats will die is because if they did they would have encoded the binary number 1111111111, which is 1,023 in decimal, and our bottles only go up to a thousand. (In fact, it is possible to ensure two rats survive. To do this we need to order the bottles in such a way that excludes the ten binary numbers with only one 0, as well as the binary number with all 1s.)