26 FIRE ISLAND
Take a piece of wood from a tree near the leading edge of the fire and light it. Carefully walk to a point on the eastern side of the island – say 100m from the coastline. Set the forest there alight. Make sure you stay to the west of this new fire, which, aided by the wind, will move eastward at 100m per hour. The fire will burn out once it reaches the coast, providing you with 100m of safe space – although be careful not to burn your feet in the ash. The items in your rucksack were red herrings, although the Bible might come in handy as a mat.
27 THE BROKEN STEERING WHEEL
It is possible to turn right by turning left.
28 WALK THE PLANK
To save the British, a = 1, b = 11.
To save the French, a = 9, b = 29.
In Bachet’s version of the Josephus problem, with 30 passengers, the mnemonic Mort, tu ne falliras pas, En me livrant le trépas!! encodes the solution with its vowels. If a = 1, e = 2, i = 3, o = 4, and u = 5, the order of the vowels reveals the order in which to position the passengers around a circle. Let’s call the 15 people you want to save Friends, and the 15 you want to drown Enemies. The first four vowels in the mnemonic are o, u, e and o (4, 5, 2 and 4), so you start the ordering around the circle with 4 Friends, then 5 Enemies, then 2 Friends, then 4 Enemies, and so on.
29 THE THREE BOXES
[1] The key is in the white box.
On the black and red boxes are statements that are opposites, which means that exactly one of them must be true. So the statement on the white box must be false, which means that the white box contains the key.
*
[2] The key is in the black box.
If the key is in the red box, then all three statements are true. If the key is in the white box, then all three statements are false. So the key must be in the black box, in which case two statements (on the black and white boxes) are true and one (on the red box) is false.
30 SAFE PASSAGE
Put the ring in the lock box, put a single padlock on it and send it. Your beloved will receive the box, put a second padlock on it and return it to you. You will then unlock your padlock and send the box back. Your beloved then opens the second padlock to retrieve the ring.
31 CRACK THE CODE
The code is 052. The fourth line eliminates 7, 3 and 8, meaning that the code must be composed from the set of digits 0, 1, 2, 4, 5, 6 and 9. The fifth line reveals that 0 is one of the numbers, and that it must be in either of the first two positions. The third line tells us that 0 must be in the first position, and that one of the other numbers is a 2 or a 6. The first line eliminates 6, since 6 cannot be correctly placed and in the first position, because we know that 0 is there. So 2 is the number in the third position. This leaves the middle position, which according to the second line must be 5. We eliminate 4 because if 4 was correct it would be correctly placed.
32 GUESS THE PASSWORD
Six guesses is the minimum.
If the digits in the password were independent of each other – that is, if they were allowed to be any digit from 0 to 9, irrespective of the digits in other positions – it would take 10 guesses to open the door because each position could be any of the 10 digits. (You are not going to be able to get a better strategy than typing in 0000000 at your first attempt, 1111111 at your second, 2222222 at your third, and so on until 9999999.) Yet because of the rule that no digit in the password appears twice, the digits are dependent on each other, since if a digit appears in one position it cannot appear in another position. The puzzle exploits this dependency.
The best strategy is as follows. Choose any six digits, say the digits between 0 and 5, and make six guesses that place each of these digits in the same six positions of the password. So, for example:
0123456
1234506
2345016
3450126
4501236
5012346
(I’ve put 6 as the final digit, but it can be anything you want.)
These guesses will open any password with a 0, 1, 2, 3, 4 or 5 in one of the first six positions. If the password does not have any of these digits in the first six positions, the first six positions must be made up of the other numbers: 6, 7, 8 or 9. However, since there are only four of these numbers, one or two of them would have to appear twice, contradicting the question. In other words, every 7-digit password with no repeated digits must have a 0, 1, 2, 3, 4 or 5 in one of the first six positions, and the above strategy works.
33 THE SPINNING SWITCHES
At the start, the buttons are in one of three possible combinations: both off, on and off, or off and on.
Our first move is to press both buttons together. If they were both off, now they are both on, and the door opens. If one was on and one was off, the overall picture stays the same. The one that was off is now on, and the one that was on is now off.
The wheel spins. The second move is to press a single button. Either both buttons will now be on, and the door will open, or they will both will be off, and the wheel will spin. When it comes to rest, our third and final move is to press both buttons together, opening the door.
For the harder version, I suggest building yourself a spinning wheel with four switches, and playing around with it. You’ll quickly figure out the pattern. In the absence of a spinning wheel, use four coins. Place them on the table in the four compass positions. Heads will represent ‘on’, and tails ‘off’. Pressing a button is now the same as turning a coin over.
Let the following abbreviations stand for the following moves:
E – we turn over every coin (or press every button)
O – we turn over any two opposite coins, such as, say, north and south. (Or we press two opposite buttons.)
A –we turn over any two adjacent coins, say, north and east. (Or we press two adjacent buttons). Assume that after each move the wheel spins round, unless the door is opened.
Our first seven moves are: EOEAEOE.
If the four coins are all heads in their initial positions (i.e. the buttons are all switched on), the door will open straight away. If the coins are all tails, an E will turn them all over, so the buttons will all be on and the door will open. The subsequent moves (OEAEOE) will open the door if exactly two coins are heads at the start. Here’s why:
If only two coins are showing heads at the start, either the heads are positioned opposite each other (say, north and south), or they are positioned adjacent to each other (say, north and east). Applying move E (as we did above) does not change the position of the coins – they are still either opposite or adjacent to each other.
If the heads are positioned opposite each other, a move O results in either four heads, or four tails. So either the door opens, or we apply E in next move and the door opens. If, on the other hand, the heads had been positioned adjacent to each other, turning over opposite coins leaves a situation in which, again, two heads are adjacent to each other. So, an O followed by an E does not change the situation. We then apply an A, turning over two adjacent coins. Either we now have four heads, in which case the door opens, or no heads, in which case the door will open if we turn all the coins over on the next turn. Alternatively, we are left with a situation in which we have two heads opposite each other. All we need to do again in that case is turn two opposite coins over; if that doesn’t work we can turn all the coins over again.
To complete the strategy, we need to find a way of opening the door if there is either one or three heads in the initial placement of the coins. If there was one or three heads at the start, there will still be one or three heads after the moves EOEAEOE have been applied. So for the eighth move, turn a single coin over. Either four coins will now be heads, in which case the door will open, or none of them will be heads, in which case we make our next move an E. Alternatively, exactly two coins will be heads, in which case we repeat the sequence (EOEAEOE) above.
34 PROTECT THE SAFE
The directors need to put three locks on the safe, and they need two keys for each lock, making a total of six keys.
If the locks are A, B and C, the keys need to be distributed as follows: one director has the keys for A and B, one those for B and C, and one those for A and C. In this way, no single director can open the door, but any combination of two directors can.
BONUS PROBLEM: THE AVERAGE SALARY
Let the three colleagues be Amy, Ben and Charlotte. Amy adds a constant to her salary, and tells Ben. Ben adds his salary to the total, and tells Charlotte. Charlotte adds her salary to the total and tells Amy. Amy now subtracts the constant from the total, and divides by three to get the average, which she tells the others.
35 THE SECRET NUMBER
The secret number puzzle involves similar thinking to that used in the average salary problem. You ask Lag to think up a number – let’s call it L – and he whispers it to you (without the other inmate hearing). You add your gang’s number to L, and tell the other inmate the total. The inmate subtracts his number from this total, and whispers it to Lag (so you don’t hear). You ask Lag whether or not it’s L. If he says yes, you and the inmate are in the same gang. If he says no, you are not in the same gang. You have therefore ascertained whether or not you are in the same gang without either of you having revealed the secret number.
36 REMOVING THE HANDCUFFS
One person (say, the person with the white string, as shown opposite) needs to thread their string through one of the loops that ties the other person’s string to their wrists, and then take it over that person’s hand:

37 THE REVERSIBLE TROUSERS
First, unpeel your trousers so that they’re inside out on the rope. (In other words, the trouser legs have been reversed once.) Next, grab the hem at the bottom of one trouser leg from the inside, pull it through that trouser leg and through the other leg. In other words, you are pushing one trouser leg through the other. This is a scrunch if you have skinny jeans! (Now the trousers have been turned inside out twice, so they are the right way round but with the legs pointing at your feet.) Turn the trousers inside out again by pulling each leg through itself (so that the trouser legs have been reversed a third time). The trousers can now be put on inside out, with the fly at the front.
38 MEGA AREA MAZE
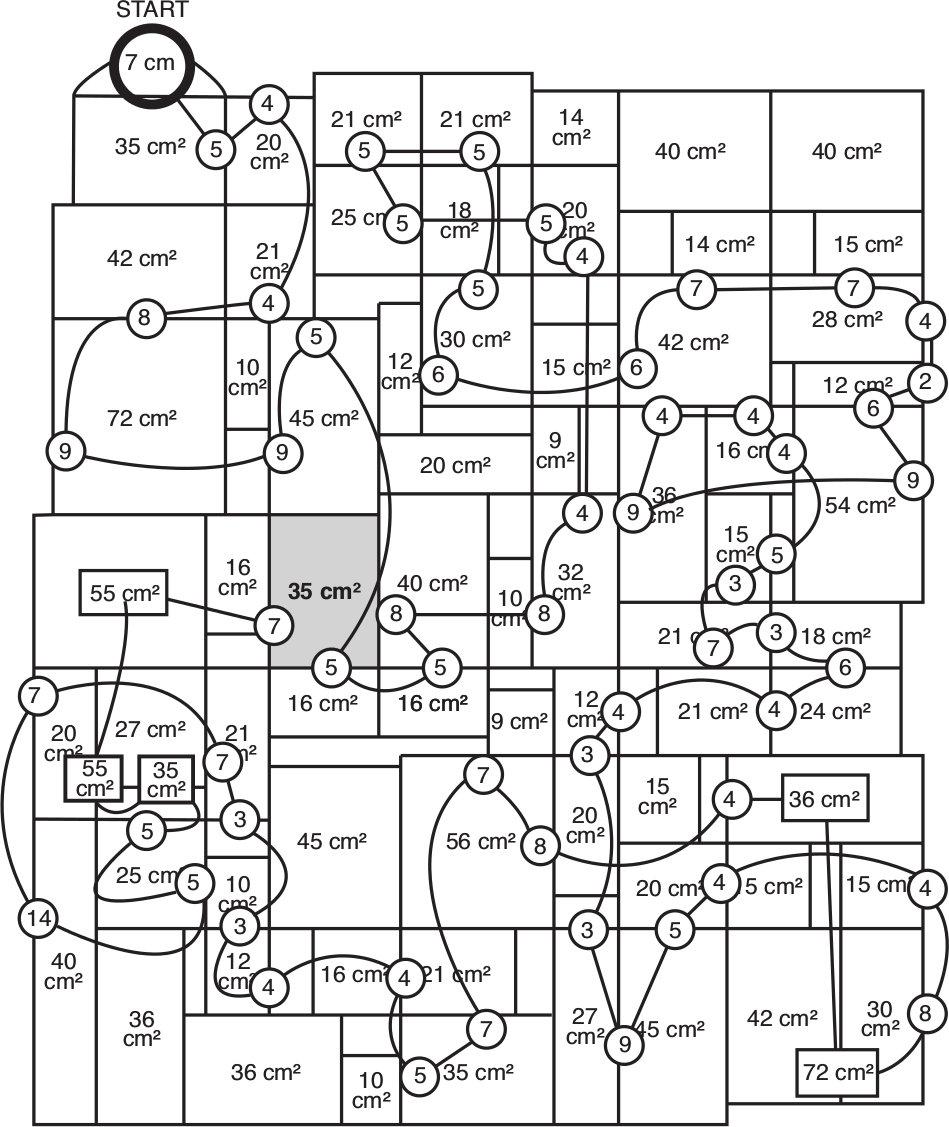
The path to the answer is revealed through the snake of numbers. In the text I explained the first steps: 7 → 5 → 4 → 4. If that rectangle has area 21cm2 and width 4cm, then the rectangle to its left with identical height and an area of 42cm2 must have width 8cm – and so on, until you reach the final area of 35cm2.
39 ARROW MAZE
Yes, you will get out of the grid.
We solve this problem not by considering this particular grid, but by considering every possible finite size of grid with every possible combination of arrow orientations. Whatever the grid size or arrow positions, you must eventually leave the grid.
Assume, for a moment, that you don’t get out of the grid. In this case, once you start, you continue moving around the cells for ever. But if you are moving, ad infinitum, around a finite number of cells, you must visit at least one of those cells an infinite number of times. Consider this cell. If you visit it an infinite number of times, you must also visit the four cells adjacent to it – that is, above it, below it, and to its left and right – an infinite number of times. Following on from that, you must also visit the cells adjacent to those four, and eventually all the cells in the grid, an infinite number of times.
You cannot visit the bottom right cell an infinite number of times. If the arrow is pointing down, as it is in this particular grid, then it will be pointing to the exit on your third visit and you will be able to leave the grid. If it is pointing in any other direction, you will also leave in at most three visits.
The assumption that you don’t get out of the grid must be false. Therefore, you do escape the grid.
40 THE TWENTY-FOUR GUARDS
Monday
| 4 | 1 | 4 |
| 1 | PRISON | 1 |
| 4 | 1 | 4 |
Tuesday
| 2 | 5 | 2 |
| 5 | PRISON | 5 |
| 2 | 5 | 2 |
Wednesday
| 1 | 7 | 1 |
| 7 | PRISON | 7 |
| 1 | 7 | 1 |
Thursday
| 9 | ||
| 9 | PRISON | 9 |
| 9 |
41 THE TWO ENVELOPES
Did you notice that there is a fire in the room? It pays to be observant in this type of lateral-thinking puzzle. A smart response is to take one of the envelopes and then throw it into the fire. (Making it look accidental, of course, and waiting until it has been fully consumed by the flames.) Tell the king that you would like to choose the one that fell in the fire. In other words, you do not want the one that is still on the table. The remaining one is opened, and it reveals the word DEATH. To keep his honour the king must accept that the other envelope contained the word PARDON.
42 THE MISSING NUMBER
You’re good at arithmetic, so I expect you to be able to sum the numbers from 1 to 100. The fast way to do this calculation is to realise that the sum is the same as (1 + 100) + (2 + 99) + (3 + 98) + … + (50 + 51). In other words, the sum of the first 100 numbers is 101 fifty times, or 101 × 50 = 5,050.
If you summed up all of the queen’s 99 numbers as she read them out, you could easily deduce the missing number, since the missing number would be equal to the difference between the sum you calculated and 5,050.
But adding 99 numbers is quite an effort, and it’s easy to make a mistake, even for the arithmetically gifted, especially once you start to hold three- or four-digit numbers in your head.
The clever insight here is to realise that you never need to count above 100. In other words, once you hit 100, rescale back to zero. For example 86 + 15 would be 1, rather than 101. (The mathematical term for this is ‘counting modulo 100’)
Since you are only keeping a number between 1 and 100 in your head, the summing is not so daunting. Once you get to the end, if the sum (modulo 100) is less than 50, this means the missing number is the difference between the total sum and 50. (This is because, had you not counted modulo 100, the total sum would be between 5,000 and 5,049 and, as stated above, the missing number is equal to the difference between the total sum and 5,050.) If the sum (modulo 100) is more than 50, the missing number is the difference between this number and 150. (This is because, had you not counted modulo 100, the total sum would be between 4,950 and 5,000, and the difference between this number and 5,050 is the same as the total [counted modulo 100] and 150.)
43 THE ONE HUNDRED CHALLENGE
Your strategy is always to say 11 minus the number your cellmate just said. That’s why after he started with 8, you replied with 3. Now he has just said 4, you must reply with 7, which will give a running total of 22. If you proceed in this way, you can guarantee that the running total each round will always be a multiple of 11. Eventually, the running total will be 99, when it will be your cellmate’s turn. He will therefore be the first to reach 100.
44 THE FORK IN THE ROAD
One solution is to point at a branch of the road and ask the local: ‘If I were to ask you if this branch leads to the airport, would you say yes?’ If it is the route to the airport, both truth-tellers and liars would say ‘yes’, because the liar is forced to lie about her response to the question ‘does this branch lead to the airport?’ If asked the direct question, she would lie and say ‘no, the branch does not lead to the airport’. But the way the question is stated means she must lie about saying no, so she would tell you that she would reply ‘yes’. Likewise, if it was not the route to the airport, both truth-tellers and liars would say ‘no’.
Another solution, which avoids embedding a question within a question, is to point at a road and ask: ‘Of the two statements “You are a liar” and “This branch leads to the airport”, is one and only one of them true?’ A truth-teller would say yes if the branch does lead to the airport, and no if not. A liar would also say yes if the branch leads to the airport, since in that case both statements would be true, making the correct answer to the question ‘no’. But since she is a liar she must say ‘yes’.
45 BISH AND BOSH
Look again at the first solution given to the previous problem: you point at a branch of road and ask ‘If I were to ask you if this route leads to the airport, would you say yes?’ Both liars and truth-tellers would say ‘yes’ if the branch did lead to the airport. Now imagine switching yes for no: you point at a branch of road and ask: ‘If I were to ask you if this branch leads to the airport, would you say no?’ In this case, both truth-tellers and liars would say ‘no’ if the branch leads to the airport. In other words, if you ask the question ‘If I were to ask you if this branch leads to the airport, would you say X?’, where X is either yes or no, a response of ‘X’ means that you have pointed at the airport branch. This insight leads to the answer to this problem.
Point at a branch and ask: ‘If I were to ask you if this route leads to the airport, would you say bish?’ If the response is ‘bish’ then the branch leads to the airport, and if it is ‘bosh’, it leads to the beach. Equally, you could ask: ‘If I were to ask you if this branch leads to the airport, would you say ‘bosh’?’ A response of ‘bosh’ means you will make your plane.
46 THE LAST REQUEST
An example of a successful question is:
‘Will you answer “no” and sentence me to death?’
In other words, you are asking whether both of these statements are true:
[1] The executioner will answer ‘no’.
[2] The executioner will sentence you to death.
The executioner cannot answer ‘yes’, since if he did he would be lying by contradicting the statement that he is answering ‘no’.
So the executioner must respond ‘no’. But if the answer is no then it is not true that both statements are true, so one of them must be false. Statement [1] cannot be false since we know it is true – he did answer ‘no’. So statement [2] is false. In other words the executioner will not sentence you to death. Your life is spared!
47 THE RED AND BLUE HATS
Let the prisoners be A and B. The question states that A sees B’s hat, and B sees A’s hat. If A’s guess is always the colour of B’s hat, and if B’s guess is always not the colour of A’s hat, then at least one guess will be correct.
We can see this in the table below, which lists all the possible colour combinations of the two hats. In each case, the correct guesses are in bold.
| A’s hat | B’s hat | A’s guess | B’s guess | Correct guesses |
|---|---|---|---|---|
| Red | Red | Red | Blue | 1 |
| Red | Blue | Blue | Blue | 1 |
| Blue | Red | Red | Red | 1 |
| Blue | Blue | Blue | Red | 1 |
For the three-player version in which at least one person must guess, and all guesses must be correct, the strategy is as follows:
If a player sees hats of two different colours, they stay silent.
If a player sees two hats of the same colour, they guess the opposite colour.
The eight possible combinations of hat colours on three players are RRB, RBR, BRR, BBR, BRB, RBB, BBB, RRR. Using the above strategy, the first six combinations will result in two players passing, and a third guessing their hat colour correctly. In the final two combinations, all three will guess incorrectly. In other words, in 6 of 8 equally likely arrangements of hat colours, at least one person is guessing and no one guesses wrongly, giving the prisoners a 75 per cent chance of survival.
To get a feel for why this works, think about the number of guesses made across all combinations of hat colours. A guess will be made 12 times. Six times the guess will be correct (once each in RRB, RBR, BRR, BBR, BRB and RBB), and six times the guess will be wrong (three times each in both BBB and RRR). The correct guesses, however, are spread across six combinations while the six incorrect ones are spread across just two combinations. It’s like you’re dividing up the good stuff across as many boxes as possible, while squeezing the bad stuff into the smallest number of boxes you can. The same approach works with more than three players, with even more impressive results. As mentioned in the main text, if you play this game with 16 prisoners, the odds of survival are more than 90 per cent.
48 THE MAJORITY REPORT
You should adopt this strategy:
[1] At the start of the recital, and whenever you see that the counter is at 0, commit the name you hear to memory and click once upwards, so the counter is on 1.
[2] When the counter is on 1 or greater, click upwards if the name you hear is the same as the one in your memory, but click downwards if the name you hear is not the one in your memory. In both cases keep the same name in your memory.
This strategy guarantees that the name in your memory after the list has been read out is the name that has been said more than half the time.
To get a feel for why the strategy works, let’s see what happens if the warden reads out the following list: A B C A B A A B A. She reads nine names in total, made up of three distinct names.
| Name read out | Counter | Name in memory |
|---|---|---|
| A | 1 | A |
| B | 0 | A |
| C | 1 | C |
| A | 0 | C |
| B | 1 | B |
| A | 0 | B |
| A | 1 | A |
| B | 0 | A |
| A | 1 | A |
The name in your memory at the end is A, which does indeed appear more than half the time.
49 THE ROOM WITH THE LAMP
Let’s begin with the situation with three prisoners, A, B and C. We also know that the lamp is off at the start.
The crucial element in the strategy, from which everything else follows, is that one prisoner will have a different role from all the others. Let’s call him the Counter, since his job will be to keep track of who has been in the room, and then to announce to the prison warden that everyone has visited it. The gist is that the regular prisoners will turn the lamp on, and that they will be tallied by the Counter, who will turn the lamp off.
Let’s say C is the Counter. The rules for him are:
If the lamp is off, do nothing.
If the lamp is on, turn it off.
While the rules for A and B are:
If this is the first time you’ve seen the lamp switched off, turn it on.
In all other cases, do nothing.
In this scenario, what happens is that the lamp is turned on at some stage by either A or B, after which C switches it off. Eventually either A or B will turn it back on again (if A switched it on first, then B will switch in on next, or vice versa). When C enters the room to see the lamp on for the second time he can be sure that both the other prisoners have been in the room, and he can holler at the top of his voice, ‘We have all visited the lamp room!’
This strategy can be extended to 23 prisoners. If the Counter follows the above rule, which is to turn the lamp off when he finds it on, and all the other prisoners follow A and B’s rules, which are to turn the lamp on the first time they find it off but otherwise to do nothing, then once the Counter has seen the lamp on 22 times he knows that everyone has visited the room.
Now let’s investigate what the prisoners need to do when they do not know the starting state of the lamp.
The above strategy won’t work, because the first time the Counter sees the lamp on he won’t be able to tell if it has been turned on by a prisoner, or if it is still in its original state.
Let’s say he enters the room when the lamp is on, and that this was its original state. The Counter will turn it off, as he must, but now for him to be sure that everyone has been in the room he must wait to see the lit lamp another 22 times. In other words, he must wait until he has turned the lamp off 23 times. However, the rule ‘wait until I see an on-lamp 23 times’ cannot be a solution to the problem, because if the lamp started in the ‘off’ state, it’s impossible for him to see the lamp lit 23 times.
The way around this problem is to keep the same rules for the Counter but to tweak the rules for the other prisoners by insisting that they turn the lamp on twice. The rules become:
If this is the first or second time you have seen the lamp off, turn it on.
In all other cases, do nothing.
The Counter can now be sure that once he has seen the lit lamp 44 times, everyone has been in the room.
If the lamp was off at the start, every other prisoner would have gone in twice. If the lamp was on at the start, every other prisoner would have gone in twice except for one, who would have gone in once. It’s possible that all the prisoners had been in the room before the Counter saw the 44th on switch, but he can only know for certain when he sees the ‘on’ switch that 44th time.
50 THE ONE HUNDRED DRAWERS
Before we get to the solution, here’s an introduction to the maths of permutations. It’s going to make the prisoners’ strategy much easier to understand. Let’s say we have 10 objects and we want to reorder them. One way to describe this reordering is in a table:
| Initial position | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| New position | 4 | 8 | 5 | 6 | 9 | 1 | 10 | 2 | 7 | 3 |
An easy way to understand the pattern described in the table is to represent it visually. In the table 1 → 4, 4 → 6 and 6 → 1. This forms a loop, or ‘permutation cycle’. The table can be illustrated thus:
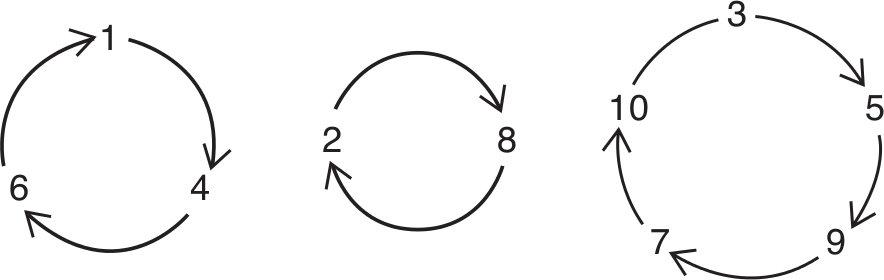
It’s plain to see that there are three cycles, one of length 3, one of length 2, and one of length 5. There are more than 3.6 million permutations of 10 objects, and they can contain cycles of length 1 to length 10.
Now back to the prisoners. The strategy that they must take is the following. First, they must number themselves from 1 to 100 – that is, they should order themselves into Prisoner 1, Prisoner 2, Prisoner 3, and so on.
They then must agree to abide by these rules when they enter the room:
[1] Each prisoner heads for the drawer with their number on it and opens it first. In other words, the first drawer that Prisoner 1 opens is drawer 1, the first drawer that Prisoner 2 opens is drawer 2, and so on.
[2] If a prisoner opens a drawer and it contains the name of another prisoner, say Prisoner k, the next drawer they open should be drawer k. In other words, if Prisoner 1 opens a drawer with Prisoner 32’s name in it, the next drawer he should open is drawer 32. If the drawer has Prisoner 67’s name in it, the next drawer he should open is drawer 67, and so on.
These two rules set each prisoner on a path that is equivalent to a permutation cycle.
Here’s why. Let’s imagine there are only 10 drawers and 10 prisoners. If the top row of the table on the left is relabelled ‘drawer number’ and the bottom row is relabelled ‘prisoner number’, the table now describes one possible arrangement of the prisoners’ names in the drawers. So, for example, in drawer 1 is the name of Prisoner 4, in drawer 2 is the name of Prisoner 8, and so on.
| Drawer number | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Prisoner number | 4 | 8 | 5 | 6 | 9 | 1 | 10 | 2 | 7 | 3 |
If Prisoner 1 abides by the rules in this strategy, he begins by opening drawer 1, in which he finds the name of Prisoner 4. So he opens drawer 4, in which he finds the name of Prisoner 6, so he opens drawer 6, in which he finds his own name. He has gone through the cycle 1 → 4 → 6 → 1, and has found his own name after opening three drawers.
We can see what happens to the other prisoners by following the cycles of this permutation (illustrated on the previous page.) Prisoners 4 and 6 will also find their names after three drawers, Prisoners 2 and 8 will find their names after two, and the others will find their names after five. In other words, the number of drawers a prisoner must open to find his own name is equal to the length of the permutation cycle he finds himself in. The strategy counts him round the cycle drawer by drawer, and he finds his name when he completes the cycle.
This observation is also true when we increase the number of drawers and prisoners to 100.
If there are 100 prisoners, and each prisoner can only open 50 drawers, every prisoner will find his own name if and only if all the permutation cycles have a length of at most 50. If the length of a cycle is longer than 50, a prisoner won’t be able to travel round it in only 50 drawer-openings.
The strategy works, therefore, if no permutation cycles are longer than 50. In other words, in order to work out the chances of freedom for all the prisoners – that is, of everyone finding their names – we need to calculate the chances of there being no permutation cycles longer than 50 in a random permutation of 100 objects. (In other words, we need to divide the number of permutations of 100 objects that have no permutation cycles longer than 50 by the total number of permutations of 100 objects.) The maths here is too technical for a book like this one, so you’ll need to trust me that the chances of there being no permutation cycles longer than 50 are just over 30 per cent.
The interesting behaviour of permutation cycles gives the prisoners an unexpectedly good chance of survival.

