
The ability to graph linear equations and functions is important in mathematics. In fact, graphing equations and solving equations are two of the most important concepts in mathematics. If you master these, all mathematical subjects will be much easier, even Calculus!
This chapter focuses on the visual representations of linear equations. You will learn how to graph lines from equations and write functions of graphed lines. You will also learn how to find the slope of a line and how to use a slope to interpret a graph.
Weather, such as temperature and the distance of a thunderstorm can be predicted using linear equations. You will learn about these applications and more in this chapter.

In Lesson 1.6, you graphed ordered pairs. This lesson will expand upon your knowledge of graphing ordered pairs to include vocabulary and naming of specific items related to ordered pairs.
An ordered pair is also called a coordinate. The ![]() value is called the ordinate and the
value is called the ordinate and the ![]() value is called the abscissa.
value is called the abscissa.
A two-dimensional (2-D) coordinate has the form ![]() .
.
The 2-D plane that is used to graph coordinates or equations is called a Cartesian plane or a coordinate plane. This 2-D plane is named after its creator, Rene Descartes. The Cartesian plane is separated into four quadrants by two axes. The horizontal axis is called the ![]() axis and the vertical axis is called the
axis and the vertical axis is called the ![]() axis. The quadrants are named using Roman Numerals. The image below illustrates the quadrant names.
axis. The quadrants are named using Roman Numerals. The image below illustrates the quadrant names.
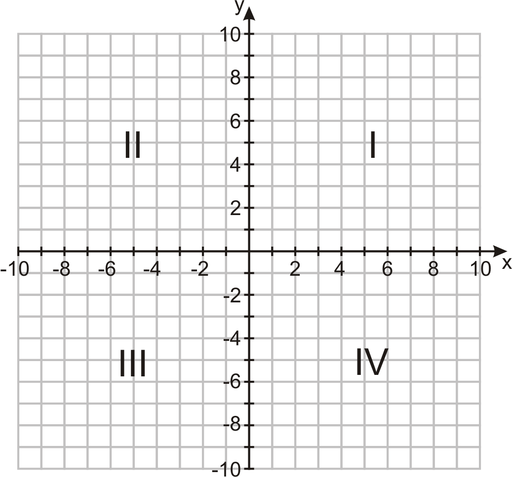
The first value of the ordered pair is the ![]() value. This value moves along the
value. This value moves along the ![]() axis (horizontally). The second value of the ordered pair is the
axis (horizontally). The second value of the ordered pair is the ![]() value. This value moves along the
value. This value moves along the ![]() axis (vertically). This ordered pair provides the direction of the coordinate.
axis (vertically). This ordered pair provides the direction of the coordinate.
Multimedia Link: For more information on the Cartesian plane and how to graph ordered pairs, visit Purple Math’s - http://www.purplemath.com/modules/plane.htm - website.
Example 1: Find the coordinates of points ![]() and
and ![]() .
.
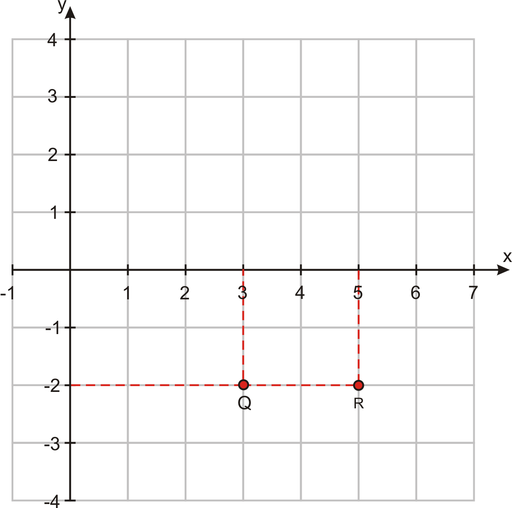
Solution: In order to get to ![]() , we move three units to the right, in the positive
, we move three units to the right, in the positive ![]() direction, then two units down, in the negative
direction, then two units down, in the negative ![]() direction. The
direction. The ![]() coordinate of
coordinate of ![]() is +3; the
is +3; the ![]() coordinate of
coordinate of ![]() is –2.
is –2.
![]()
The coordinates of ![]() are found in a similar way. The
are found in a similar way. The ![]() coordinate is +5 (five units in the positive
coordinate is +5 (five units in the positive ![]() direction). The
direction). The ![]() coordinate is –2 (two units in the negative
coordinate is –2 (two units in the negative ![]() direction).
direction).
![]()
Not all axes will be labeled for you. There will be many times you are required to label your own axes. Some problems may require you to graph only the first quadrant. Others need two or all four quadrants. The tic marks do not always count by ones. They can be marked in increments of 2, 5, or even ![]() . The axes do not even need to have the same increments! The Cartesian plane below shows an example of this.
. The axes do not even need to have the same increments! The Cartesian plane below shows an example of this.
The increments by which you count your axes should MAXIMIZE the clarity of the graph.
In Lesson 1.6, you learned the vocabulary words relation, function, domain, and range.
A relation is a set of ordered pairs.
A function is a relation in which every ![]() coordinate matches with exactly one
coordinate matches with exactly one ![]() coordinate.
coordinate.
The set of all possible ![]() coordinates is the domain.
coordinates is the domain.
The set of all possible ![]() coordinates is called the range.
coordinates is called the range.
If you kept track of the amount of money you earned for different hours of babysitting, you created a relation. You can graph the information in this table to visualize the relationship between these two variables.
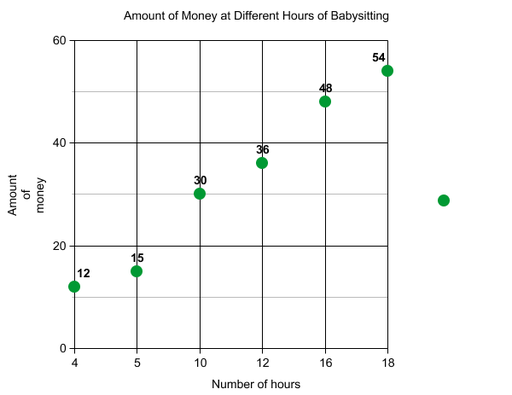
![]()
The domain of the situation would be all positive real numbers. You can babysit for a fractional amount of time but not a negative amount of time. The domain would also be all positive real numbers. You can earn fractional money, but not negative money.
If you read a book and can read twenty pages an hour, there is a relationship between how many hours you read and how many pages you read. You may even know that you could write the formula as either:

To graph this relation, you could make a chart. By picking values for the number of hours, you can determine the number of pages read. By graphing these coordinates, you can visualize the relation.
| Hours | Pages |
| 1 | 20 |
| 1.5 | 30 |
| 2 | 40 |
| 3.5 | 70 |
| 5 | 100 |
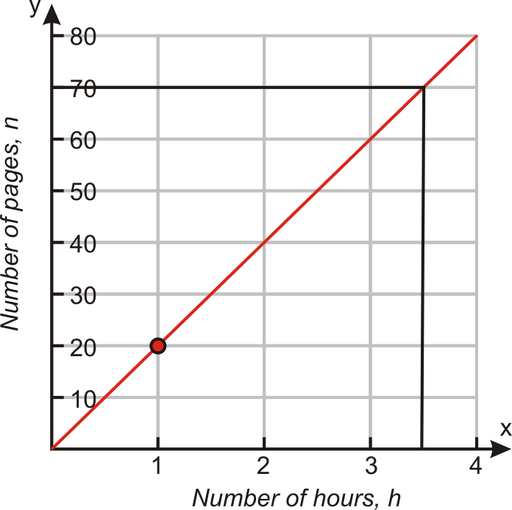
This relation appears to form a straight line. Therefore, the relationship between the total number of read pages and the number of hours can be called linear. The study of linear relationships is the focus of this chapter.
Sample explanations for some of the practice exercises below are available by viewing the following video. Note that there is not always a match between the number of the practice exercise in the video and the number of the practice exercise listed in the following exercise set. However, the practice exercise is the same in both.
Click here to watch the video on CK-12 Basic Algebra: The Coordinate Plane(6:50). Uploaded by khanacademy on 2010-04-03.
In questions 1 – 6, identify the coordinate of the given letter.

Graph the following ordered pairs on one Cartesian plane. Identify the quadrant in which each ordered pair is located.
In 15 – 22, using the directions given in each problem, find and graph the coordinates on a Cartesian plane.
| Year | % of Men Employed in the United States |
| 1973 | 75.5 |
| 1980 | 72.0 |
| 1986 | 71.0 |
| 1992 | 69.8 |
| 1997 | 71.3 |
| 2002 | 69.7 |
| 2005 | 69.6 |
| 2007 | 69.8 |
| 2009 | 64.5 |
Mixed Review
In Chapter 3, you learned how to solve equations in one variable. The answer was of the form variable = some number. In this lesson, you will learn how to solve equations with two variables. Below are several examples of two-variable equations:
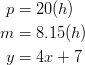
You have seen each of these equations in a previous lesson. Their solutions are not one value because there are two variables. The solutions to these equations are pairs of numbers. These pairs of numbers can be graphed in a Cartesian plane.
The solutions to an equation in two variables are sets of ordered pairs.
The solutions to a linear equation are the coordinates on the graphed line.
By making a table, you are finding the solutions to the equation with two variables.
Example: A taxi fare costs more the further you travel. Taxis usually charge a fee on top of the per-mile charge. In this case, the taxi charges $3 as a set fee and $0.80 per mile traveled. Find all the possible solutions to this equation.
Solution: Here is the equation linking the cost in dollars ![]() to hire a taxi and the distance traveled in miles
to hire a taxi and the distance traveled in miles ![]() :
: ![]() .
.
This is an equation in two variables. By creating a table, we can graph these ordered pairs to find the solutions.
|
|
|
| 0 | 3 |
| 10 | 11 |
| 20 | 19 |
| 30 | 27 |
| 40 | 35 |

The solutions to the taxi problem are located on the green line graphed above. To find any cab ride cost, you just need to find the ![]() ordinate of the desired
ordinate of the desired ![]() abscissa.
abscissa.
Multimedia Link: To see more simple examples of graphing linear equations by hand, view the video
Click here to watch the video on Khan Academy graphing lines(9:49).
.
The narrator of the video models graphing linear equations by using a table of values to plot points and then connecting those points with a line. This process reinforces the procedure of graphing lines by hand.
Not all graphs are slanted or oblique. Some are horizontal or vertical. Read through the next situation to see why.
Example: “Mad-cabs” have an unusual offer going on. They are charging $7.50 for a taxi ride of any length within the city limits. Graph the function that relates the cost of hiring the taxi ![]() to the length of the journey in miles
to the length of the journey in miles ![]() .
.
Solution: No matter the mileage, your cab fare will be $7.50. To see this visually, create a graph. You can also create a table to visualize the situation.
|
# of miles |
Cost |
| 0 | 7.50 |
| 10 | 7.50 |
| 15 | 7.50 |
| 25 | 7.50 |
| 60 | 7.50 |
Because the mileage can be anything, the equation should relate only to the restricted value, in this case, ![]() . The equation that represents this situation is:
. The equation that represents this situation is:
![]()
Whenever there is an equation of the form ![]() , the graph is a horizontal line that intercepts the
, the graph is a horizontal line that intercepts the ![]() axis at the value of the constant.
axis at the value of the constant.
Similarly, if there is an equation of the form ![]() , the graph is a vertical line that intercepts the
, the graph is a vertical line that intercepts the ![]() axis at the value of the constant. Notice that this is a relation but not a function because each
axis at the value of the constant. Notice that this is a relation but not a function because each ![]() value (there’s only one in this case) corresponds to many (actually an infinite number)
value (there’s only one in this case) corresponds to many (actually an infinite number) ![]() values.
values.
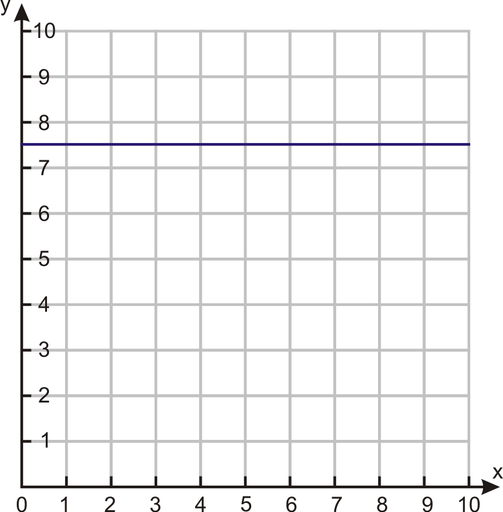
Example 1: Plot the following graphs.
(a) ![]()
(b) ![]()
(c) ![]()
(d) ![]()
Solution:
(a) ![]() is a horizontal line that crosses the
is a horizontal line that crosses the ![]() axis at 4.
axis at 4.
(b) ![]() is a horizontal line that crosses the
is a horizontal line that crosses the ![]() axis at –4.
axis at –4.
(c) ![]() is a vertical line that crosses the
is a vertical line that crosses the ![]() axis at 4.
axis at 4.
(d) ![]() is a vertical line that crosses the
is a vertical line that crosses the ![]() axis at –4.
axis at –4.
Analyzing linear graphs is a part of life – whether you are trying to decide to buy stock, figure out if your blog readership is increasing, or predict the temperature from a weather report. Although linear graphs can be quite complex, such as a six-month stock graph, many are very basic to analyze.
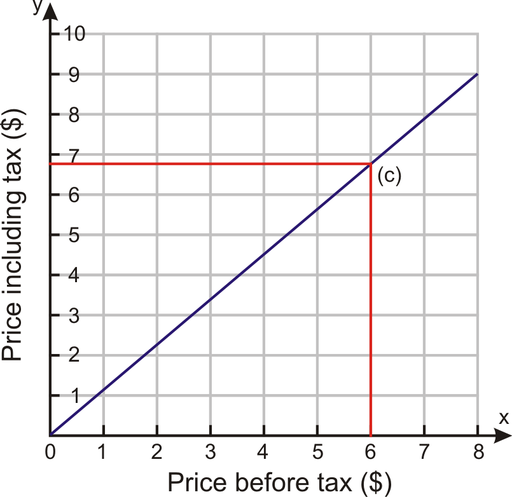
The graph below shows the solutions to the price before tax and the price after tax at a particular store. Determine the price after tax of a $6.00 item.
By finding the appropriate ![]() abscissa ($6.00), you can find the solution, the
abscissa ($6.00), you can find the solution, the ![]() ordinate (approximately $6.80). Therefore, the price after tax of a $6.00 item is approximately $6.80.
ordinate (approximately $6.80). Therefore, the price after tax of a $6.00 item is approximately $6.80.
The following graph shows the linear relationship between Celsius and Fahrenheit temperatures. Using the graph, convert ![]() to Celsius.
to Celsius.
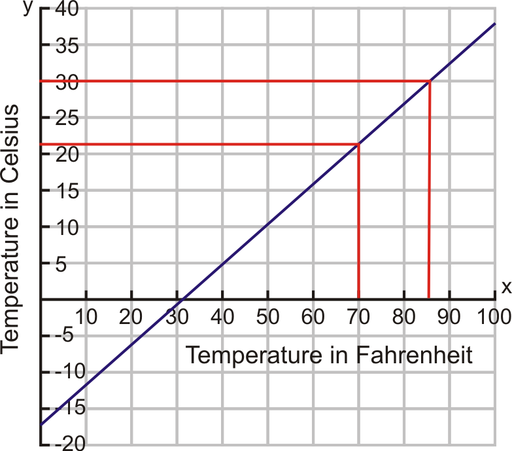
By finding the temperature of ![]() and locating its appropriate Celsius value, you can determine that
and locating its appropriate Celsius value, you can determine that ![]() .
.
Sample explanations for some of the practice exercises below are available by viewing the following video. Note that there is not always a match between the number of the practice exercise in the video and the number of the practice exercise listed in the following exercise set. However, the practice exercise is the same in both.
Click here to watch the video on CK-12 Basic Algebra: Graphs of Linear Equations(13:09). Uploaded by khanacademy on 2010-04-03.
Write the equations for the graphed lines pictured below.
Find the solutions to each equation by making a table and graphing the coordinates.
Mixed Review
As you may have seen in the previous lesson, graphing solutions to an equation of two variables can be time-consuming. Fortunately, there are several ways to make graphing solutions easier. This lesson will focus on graphing a line by finding its intercepts. Lesson 4.5 will show you how to graph a line using its slope and ![]() intercept.
intercept.
In geometry, there is a postulate that states, “Two points determine a line.” Therefore, to draw any line, all you need is two points. One way is to find its intercepts.
An intercept is the point at which a graphed equation crosses an axis.
The ![]() intercept is an ordered pair at which the line crosses the
intercept is an ordered pair at which the line crosses the ![]() axis (the horizontal axis). Its ordered pair has the form
axis (the horizontal axis). Its ordered pair has the form ![]() .
.
The ![]() intercept is an ordered pair at which the line crosses the
intercept is an ordered pair at which the line crosses the ![]() axis (the vertical axis). Its ordered pair has the form
axis (the vertical axis). Its ordered pair has the form ![]()
By finding the intercepts of an equation, you can quickly graph all the possible solutions to the equation.
Remember that the Substitution Property allows the replacement of a variable with a numerical value or another expression. You can use this property to help find the intercepts of an equation.
Example: Graph ![]() using its intercepts.
using its intercepts.
Solution: The ![]() intercept has an ordered pair
intercept has an ordered pair ![]() . Therefore, the
. Therefore, the ![]() coordinate has a value of zero. By substituting zero for the variable of
coordinate has a value of zero. By substituting zero for the variable of ![]() , the equation becomes:
, the equation becomes:
![]()
Continue solving for ![]() :
:
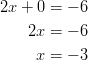
The ![]() intercept has an ordered pair of (–3, 0).
intercept has an ordered pair of (–3, 0).
Repeat the process to find the ![]() intercept. The ordered pair of the
intercept. The ordered pair of the ![]() intercept is
intercept is ![]() . Using substitution,
. Using substitution,
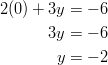
The ![]() intercept has the ordered pair (0, –2).
intercept has the ordered pair (0, –2).
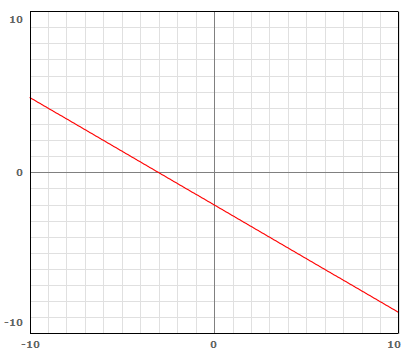
To graph the line formed by the solutions of the equation ![]() , graph the two intercepts and connect them with a straight line.
, graph the two intercepts and connect them with a straight line.
Example: Graph ![]() using its intercepts.
using its intercepts.
Solution: Determine the ![]() intercept by substituting zero for the variable
intercept by substituting zero for the variable ![]() .
.
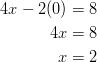
The ordered pair of the ![]() intercept is (2, 0). By repeating this process, you find the
intercept is (2, 0). By repeating this process, you find the ![]() intercept has the ordered pair (0, –4). Graph these two ordered pairs and connect with a line.
intercept has the ordered pair (0, –4). Graph these two ordered pairs and connect with a line.
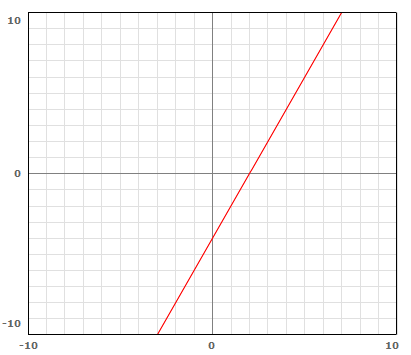
By finding an intercept, you are substituting the value of zero in for one of the variables.
To find the ![]() intercept, substitute zero for the
intercept, substitute zero for the ![]() -value.
-value.
To find the ![]() intercept, substitute zero for the
intercept, substitute zero for the ![]() -value.
-value.
A second method of finding the intercepts is called the Cover-Up Method. Using the Multiplication Property of Zero ![]() , you can “cover-up” the other variable and solve for the intercept you wish to find.
, you can “cover-up” the other variable and solve for the intercept you wish to find.
Example: Graph ![]() using its intercepts.
using its intercepts.
Solution: To solve for the ![]() intercept we set
intercept we set ![]() and cover up the
and cover up the ![]() term:
term:
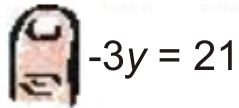
![]()
To solve for the ![]() intercept, cover up the
intercept, cover up the ![]() variable and solve for
variable and solve for ![]() :
:
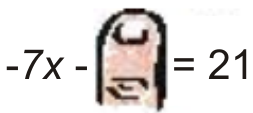
![]()
Now graph by first plotting the intercepts then drawing a line through these points.
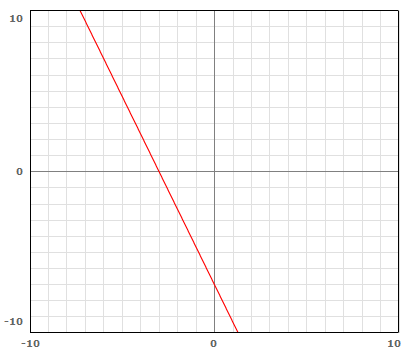
Example 1: Jose has $30 to spend on food for a class barbeque. Hot dogs cost $0.75 each (including the bun) and burgers cost $1.25 (including bun and salad). Plot a graph that shows all the combinations of hot dogs and burgers he could buy for the barbecue, spending exactly $30.
Solution: Begin by translating this sentence into an algebraic equation. Let ![]() the number of hot dogs and
the number of hot dogs and ![]() the number of burgers.
the number of burgers.
![]()
Find the intercepts of the graph. This example will use the Cover-Up Method. Feel free to use Substitution if you prefer.

![]()
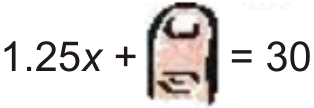
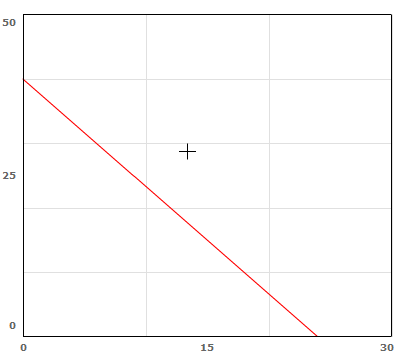
![]()
By graphing Jose’s situation, you can determine the combinations of hot dogs and burgers he can purchase for exactly $30.00.
Sample explanations for some of the practice exercises below are available by viewing the following video. Note that there is not always a match between the number of the practice exercise in the video and the number of the practice exercise listed in the following exercise set. However, the practice exercise is the same in both.
Click here to watch the video on CK-12 Basic Algebra: Graphing Using Intercepts(12:18). Uploaded by khanacademy on 2010-04-03.
Find the intercepts for the following equations using substitution.
Find the intercepts of the following equations using the Cover-Up Method.
In 13 – 24, use any method to find the intercepts and then graph the equation.
Mixed Review
Determine whether each ordered pair is a solution to the equation.
The pitch of a roof, the slant of a ladder against a wall, the incline of a road, and even your treadmill incline are all examples of slope.
The slope of a line measures its steepness (either negative or positive).
For example, if you have ever driven through a mountain range, you may have seen a sign stating, “10% incline.” The percent tells you how steep the incline is. You have probably seen this on a treadmill too. The incline on a treadmill measures how steep you are walking uphill. Below is a more formal definition of slope.
The slope of a line is the vertical change divided by the horizontal change.
In the figure below, a car is beginning to climb up a hill. The height of the hill is 3 meters and the length of the hill is 4 meters. Using the definition above, the slope of this hill can be written as ![]() . Because
. Because ![]() , we can say this hill has a 75% positive slope.
, we can say this hill has a 75% positive slope.
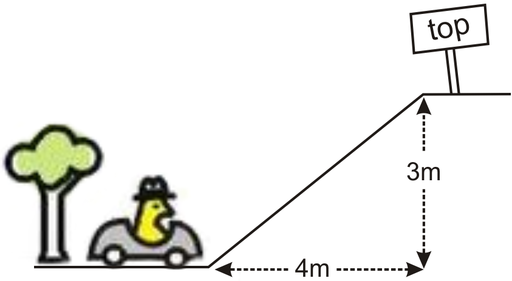
Similarly, if the car begins to descend down a hill, you can still determine the slope.
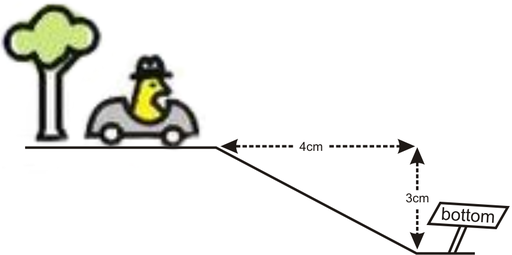
![]()
The slope in this instance is negative because the car is traveling downhill.
Another way to think of slope is: ![]() .
.
When graphing an equation, slope is a very powerful tool. It provides the directions on how to get from one ordered pair to another. To determine slope, it is helpful to draw a slope-triangle.
Using the following graph, choose two ordered pairs that have integer values such as (–3, 0) and (0, –2). Now draw in the slope triangle by connecting these two points as shown.
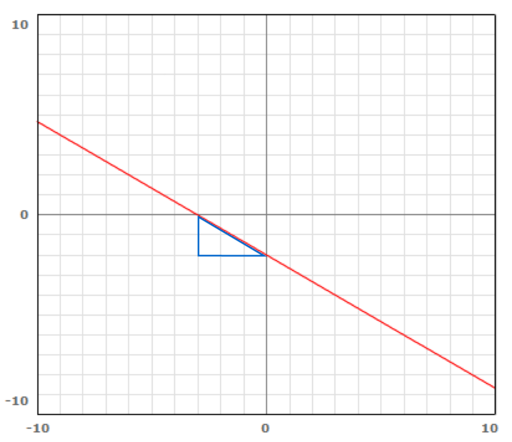
The vertical leg of the triangle represents the rise of the line and the horizontal leg of the triangle represents the run of the line. A third way to represent slope is:
![]()
Starting at the left-most coordinate, count the number of vertical units and horizontal units it took to get to the right-most coordinate.
![]()
Example 1: Find the slope of the line graphed below.
Solution: Begin by finding two pairs of ordered pairs with integer values: (1, 1) and (0, –2).
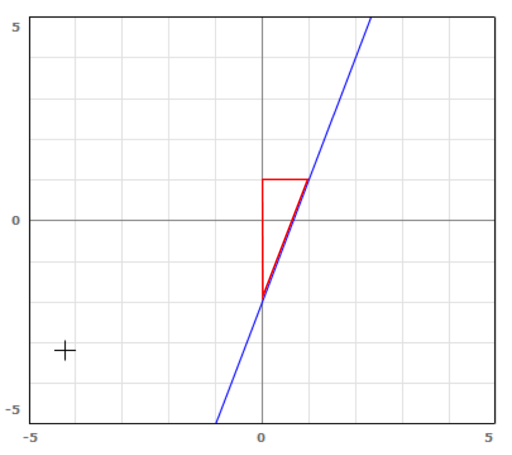
Draw in the slope triangle.
Count the number of vertical units to get from the left ordered pair to the right.
Count the number of horizontal units to get from the left ordered pair to the right.
![]()
A more algebraic way to determine a slope is by using a formula. The formula for slope is:
The slope between any two points ![]() and
and ![]() is:
is: ![]() .
.
![]() represents one of the two ordered pairs and
represents one of the two ordered pairs and ![]() represents the other. The following example helps show this formula.
represents the other. The following example helps show this formula.
Example 2: Using the slope formula, determine the slope of the equation graphed in Example 1.
Solution: Use the integer ordered pairs used to form the slope triangle: (1, 1) and (0, –2). Since (1, 1) is written first, it can be called ![]() . That means
. That means ![]()
Use the formula: ![]()
As you can see, the slope is the same regardless of the method you use. If the ordered pairs are fractional or spaced very far apart, it is easier to use the formula than to draw a slope triangle.
Slopes come in four different types: negative, zero, positive, and undefined. The first graph of this lesson had a negative slope. The second graph had a positive slope. Slopes with zero slopes are lines without any steepness, and undefined slopes cannot be computed.
Any line with a slope of zero will be a horizontal line with equation ![]() .
.
Any line with an undefined slope will be a vertical line with equation ![]() .
.
We will use the next two graphs to illustrate the previous definitions.
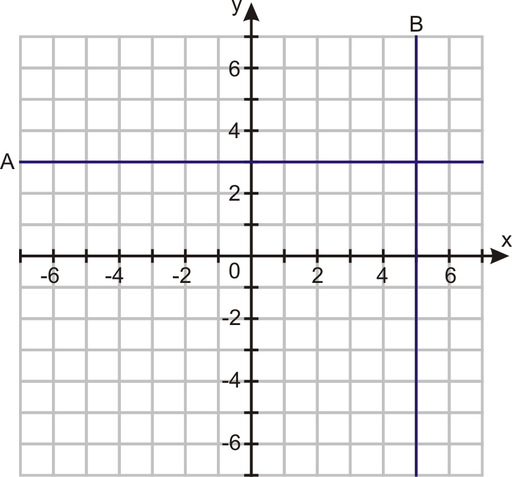
To determine the slope of line ![]() , you need to find two ordered pairs with integer values.
, you need to find two ordered pairs with integer values.
Sample: (–4, 3) and (1, 3). Choose one ordered pair to represent ![]() and the other to represent
and the other to represent ![]() .
.
Now apply the formula: ![]() .
.
To determine the slope of line ![]() , you need to find two ordered pairs on this line with integer values and apply the formula.
, you need to find two ordered pairs on this line with integer values and apply the formula.
Sample: (5, 1) and (5, –6)
![]()
It is impossible to divide by zero, so the slope of line ![]() cannot be determined and is called undefined.
cannot be determined and is called undefined.
When finding the slope of real-world situations, it is often referred to as rate of change. “Rate of change” means the same as “slope.” If you are asked to find the rate of change, use the slope formula or make a slope triangle.
Example 3: Andrea has a part-time job at the local grocery store. She saves for her vacation at a rate of $15 every week. Find her rate of change.
Solution: Begin by finding two ordered pairs. You can make a chart or use the Substitution Property to find two coordinates.
Sample: (2, 30) and (10, 150). Since (2, 30) is written first, it can be called ![]() . That means
. That means ![]() .
.
Use the formula: ![]() .
.
Andrea’s rate of change is $15/1 week.
Multimedia Link: For more information regarding rates of change, visit NCTM’s website for an interactive – http://standards.nctm.org/document/eexamples/chap6/6.2/part2.htm – rate of change activity.
Example 4: A candle has a starting length of 10 inches. Thirty minutes after lighting it, the length is 7 inches. Determine the rate of change in the length of the candle as it burns. Determine how long the candle takes to completely burn to nothing.
Solution: Begin by finding two ordered pairs. The candle begins at 10 inches in length. So at time “zero”, the length is 10 inches. The ordered pair representing this is (0, 10). 30 minutes later, the candle is 7 inches, so (30, 7). Since (0, 10) is written first, it can be called ![]() . That means
. That means ![]() .
.
Use the formula: ![]() .
.
The candle has a rate of change is –1 inch/10 minutes. To find the length of time it will take for the candle to burn out, you can create a graph, use guess and check, or solve an equation.
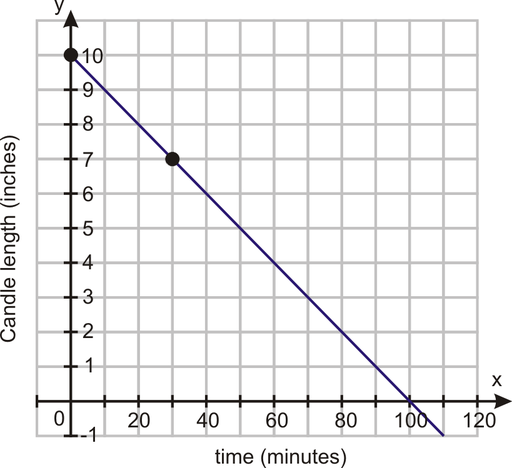
You can create a graph to help visualize the situation. By plotting the ordered pairs you were given and by drawing a straight line connecting them, you can estimate it will take 100 minutes for the candle to burn out.
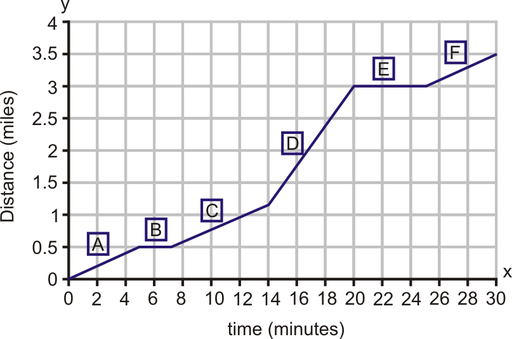
Example: Examine the following graph. It represents a journey made by a large delivery truck on a particular day. During the day, the truck made two deliveries, each one taking one hour. The driver also took a one-hour break for lunch. Identify what is happening at each stage of the journey (stages ![]() through
through ![]() ).
).
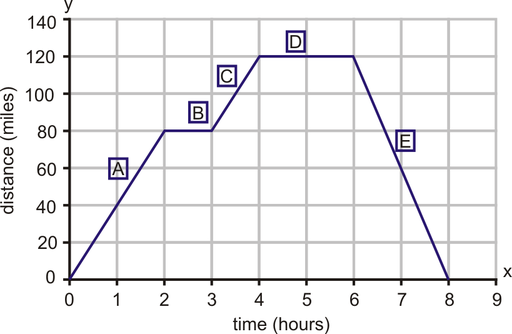
Truck’s Distance from Home by Time
Here is the driver's journey.
A. The truck sets off and travels 80 miles in 2 hours.
B. The truck covers no distance for 1 hour.
C. The truck covers ![]() miles in 1 hour.
miles in 1 hour.
D. The truck covers no distance for 2 hours.
E. The truck covers 120 miles in 2 hours.
Solution: To identify what is happening at each leg of the driver’s journey, you are being asked to find each rate of change.
The rate of change for line segment ![]() can be found using either the formula or the slope triangle. Using the slope triangle,
can be found using either the formula or the slope triangle. Using the slope triangle, ![]() and the
and the ![]() .
.
![]() .
.
Segments ![]() and
and ![]() are horizontal lines and each has a slope of zero.
are horizontal lines and each has a slope of zero.
The rate of change for line segment ![]() using the slope formula:
using the slope formula: ![]() .
.
The rate of change for line segment ![]() using the slope formula:
using the slope formula: ![]() . The truck is traveling at negative 60 mph. A better way to say this is that the truck is returning home at a rate of 60 mph.
. The truck is traveling at negative 60 mph. A better way to say this is that the truck is returning home at a rate of 60 mph.
Sample explanations for some of the practice exercises below are available by viewing the following video. Note that there is not always a match between the number of the practice exercise in the video and the number of the practice exercise listed in the following exercise set. However, the practice exercise is the same in both.
Click here to watch the video on CK-12 Basic Algebra: Slope and Rate of Change(13:42). Uploaded by khanacademy on 2010-04-04.
Using the graphed coordinates, find the slope of each line.
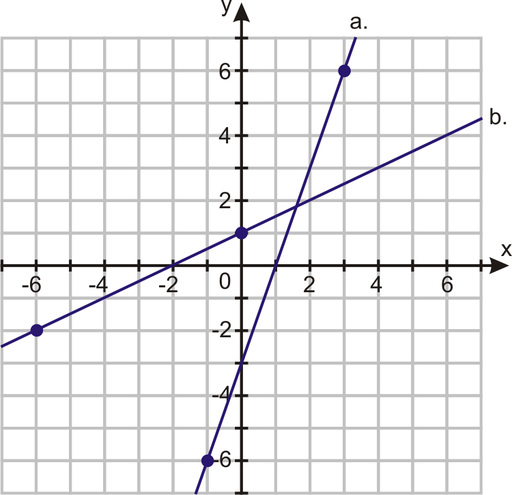
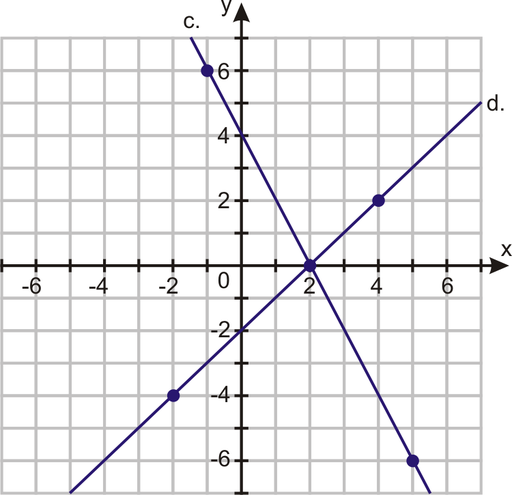
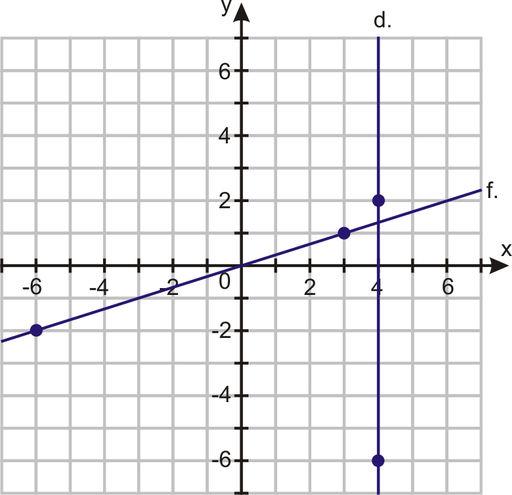
In 9 – 21, find the slope between the two given points.
Mixed Review
So far in this chapter, you have learned how to graph the solutions to an equation in two variables by making a table and by using its intercepts. The last lesson introduced the formulas for slope. This lesson will combine intercepts and slope into a new formula.
You have seen different forms of this formula several times in this chapter. Below are several examples.

The proper name given to each of these equations is slope-intercept form because each equation tells the slope and the ![]() intercept of the line.
intercept of the line.
The slope-intercept form of an equation is: ![]() intercept).
intercept).
![]() , where
, where ![]() and
and ![]() intercept
intercept
This equation makes it quite easy to graph the solutions to an equation of two variables because it gives you two necessary values:
Example 1: Determine the slope and the ![]() intercept of the first two equations in the opener of this lesson.
intercept of the first two equations in the opener of this lesson.
Solution: Using the definition of slope-intercept form; ![]() has a slope of 2 and a
has a slope of 2 and a ![]() intercept of
intercept of
(0, 5)
![]() has a slope of
has a slope of ![]() and a
and a ![]() intercept of (0, 11)
intercept of (0, 11)
Slope-intercept form applies to many equations, even those that do not look like the “standard” equation.
Example: Determine the slope and ![]() intercept of
intercept of ![]() .
.
Solution: At first glance, this does not look like the “standard” equation. However, we can substitute values for the slope and ![]() intercept.
intercept.
![]()
This means the slope is 7 and the ![]() intercept is 0.
intercept is 0.
Example: Determine the slope and ![]() intercept of
intercept of ![]() .
.
Solution: Using what you learned in the last lesson, the slope of every line of the form ![]() is zero because it is a horizontal line. Rewriting our original equation to fit slope-intercept form yields:
is zero because it is a horizontal line. Rewriting our original equation to fit slope-intercept form yields:
![]()
Therefore, the slope is zero and the ![]() intercept is (0, 5).
intercept is (0, 5).
You can also use a graph to determine the slope and ![]() intercept of a line.
intercept of a line.
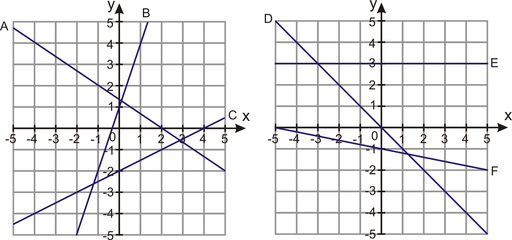
Example: Determine the slope and ![]() intercept of the lines graphed below.
intercept of the lines graphed below.
Solution: Beginning with line ![]() , you can easily see the graph crosses the
, you can easily see the graph crosses the ![]() axis (the
axis (the ![]() intercept) at (0, 5). From this point, find a second coordinate on the line crossing at a lattice point.
intercept) at (0, 5). From this point, find a second coordinate on the line crossing at a lattice point.
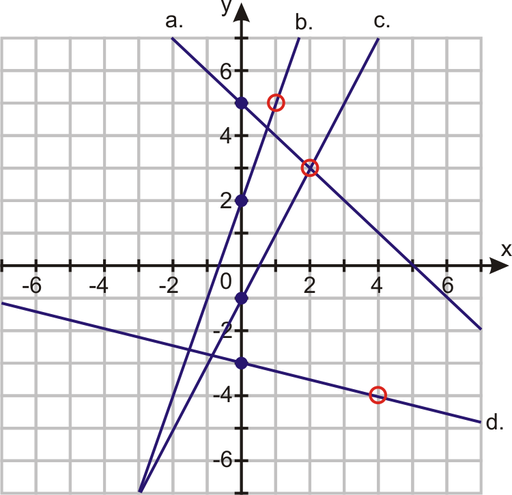
Line ![]() : The
: The ![]() intercept is (0, 5). The line also passes through (2, 3).
intercept is (0, 5). The line also passes through (2, 3).
![]()
Line ![]() : The
: The ![]() intercept is (0, 2). The line also passes through (1, 5).
intercept is (0, 2). The line also passes through (1, 5).
![]()
The remaining lines will be left for you in the Practice Set.
Once we know the slope and the ![]() intercept of an equation, it is quite easy to graph the solutions.
intercept of an equation, it is quite easy to graph the solutions.
Example: Graph the solutions to the equation ![]() .
.
Solution: The equation is in slope-intercept form. To graph the solutions to this equation, you should start at the ![]() intercept. Then, using the slope, find a second coordinate. Finally, draw a line through the ordered pairs.
intercept. Then, using the slope, find a second coordinate. Finally, draw a line through the ordered pairs.
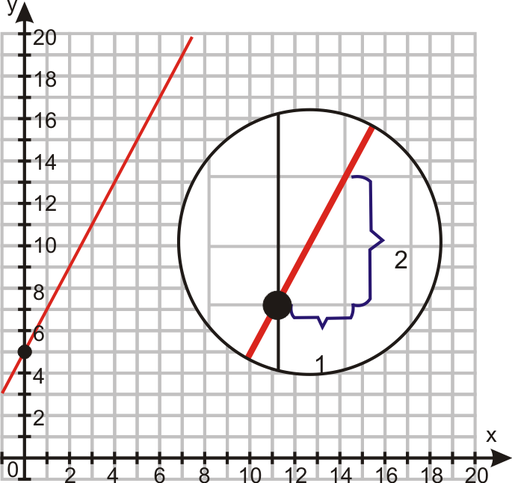
Example 2: Graph the equation ![]()
Solution: Using the definition of slope-intercept form, this equation has a ![]() intercept of (0, 5) and a slope of
intercept of (0, 5) and a slope of ![]() .
.
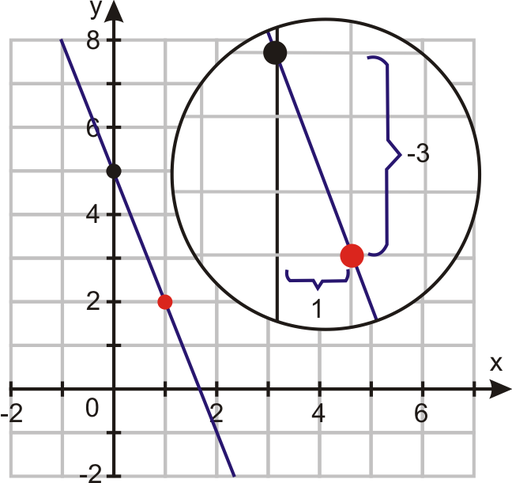
Parallel lines will never intersect, or cross. The only way for two lines never to cross is if the method of finding additional coordinates is the same.
Therefore, it's true that parallel lines have the same slope.
You will use this concept in Chapter 5 as well as in geometry.
Example 3: Determine the slope of any line parallel to ![]()
Solution: Because parallel lines have the same slope, the slope of any line parallel to ![]() must also be –3.
must also be –3.
Sample explanations for some of the practice exercises below are available by viewing the following video. Note that there is not always a match between the number of the practice exercise in the video and the number of the practice exercise listed in the following exercise set. However, the practice exercise is the same in both.
Click here to watch the video on CK-12 Basic Algebra: Graphs Using Slope-Intercept Form(11:11). Uploaded by khanacademy on 2010-04-05.
In 1 – 7, identify the slope and ![]() intercept for the equation.
intercept for the equation.
In 8 – 14, identify the slope of the following lines.
In 15 – 20, identify the slope and ![]() intercept for the following functions.
intercept for the following functions.
Plot the following functions on a graph.
In 30 – 37, state the slope of the line parallel to the line given.
Mixed Review
At the local farmer’s market, you saw someone purchase 5 pounds of strawberries and pay $12.50. You want to buy strawberries too, but you want only 2 pounds. How much would you expect to pay?

This situation is an example of a direct variation. You would expect that the strawberries are priced on a “per pound” basis, and that if you buy two-fifths of the amount of strawberries, you would pay two-fifths of $12.50 for your strawberries, or $5.00. Similarly, if you bought 10 pounds of strawberries (twice the amount), you would pay $25.00 (twice $12.50), and if you did not buy any strawberries you would pay nothing.
Direct Variation can be expressed as the equation ![]() , where
, where ![]() is called the constant of variation.
is called the constant of variation.
Direct variation occurs when:
Example: If ![]() varies directly with
varies directly with ![]() according to the relationship
according to the relationship ![]() , and
, and ![]() when
when ![]() , determine the constant of proportionality,
, determine the constant of proportionality, ![]() .
.
Solution: We can solve for the constant of proportionality using substitution.
Substitute ![]() and
and ![]() into the equation
into the equation ![]() .
.
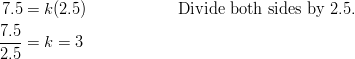
The constant of variation (or the constant of proportionality) is 3.
You can use this information to graph this direct variation situation. Remember that all direct variation situations cross the origin. You can plot the ordered pair (0, 0) and use the constant of variation as your slope.
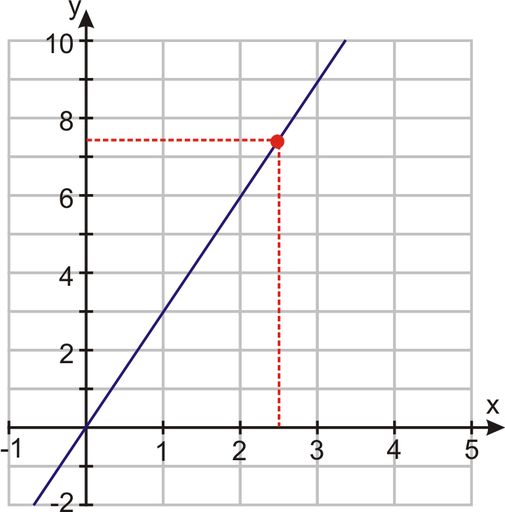
Example: Explain why each of the following equations are not examples of direct variation.

Solution: In equation 1, the variable is in the denominator of the fraction, violating the definition.
In equation 2, there is a ![]() intercept of –1, violating the definition.
intercept of –1, violating the definition.
In equation 3, there is also a ![]() intercept, violating the definition.
intercept, violating the definition.
Direct variation equations use the same phrase to give the reader a clue. The phrase is either “directly proportional” or “varies directly.”
Example: The area of a square varies directly as the square of its side.
Solution: The first variable you encounter is “area.” Think of this as your ![]() . Think the phrase “varies directly” means
. Think the phrase “varies directly” means ![]() . The second variable is “square of its side.” Call this letter
. The second variable is “square of its side.” Call this letter ![]() .
.
Now translate into an equation: ![]() .
.
You’ve written your first direct variation equation.
Example 2: The distance you travel is directly proportional to the time you have been traveling. Write this situation as a direct variation equation.
Solution: The first variable is distance; call it ![]() . The second variable is time you have been traveling, call it
. The second variable is time you have been traveling, call it ![]() . Apply the direct variation definition:
. Apply the direct variation definition:
![]()
Direct variation has numerous real-world examples. You have already seen three examples: the area of a square is directly proportional to its side length; the distance you travel varies directly as the time you have been driving; and the total cost is directly proportional to the number of pounds of strawberries you purchase.
Newton's Second Law
In 1687, Sir Isaac Newton published the famous Principea Mathematica. It contained his Second Law of Motion. This law is often written as: ![]() , where
, where ![]() the amount of force applied to an object with mass
the amount of force applied to an object with mass ![]() and
and ![]() acceleration.
acceleration.
Acceleration is given in the units meters/second![]() and force is given in units of Newtons.
and force is given in units of Newtons.
Example: If a 175 Newton force causes a heavily loaded shopping cart to accelerate down the aisle with an acceleration of ![]() , calculate:
, calculate:
(i) The mass of the shopping cart.
(ii) The force needed to accelerate the same cart at ![]() .
.
Solution: (i) This question is basically asking us to solve for the constant of proportionality. Let us compare the two formulas.
![]()
We see that the two equations have the same form. The variable ![]() is equal to force and
is equal to force and ![]() is equal to acceleration.
is equal to acceleration.
![]()
Now solve for ![]() , the constant of variation.
, the constant of variation.
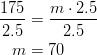
(ii) Now you know the constant of variation is 70. In this formula, 70 represents the mass. To find the force needed to move the cart at an accelerated rate of 6 meters/second, substitute 6 for ![]() and evaluate the equation.
and evaluate the equation.
When ![]() ,
, ![]() .
.
The force needed to accelerate the cart is 420 Newtons.
You can use the Cross Products Theorem of proportions to solve direct variation situations. Because the fraction ![]() is constant in a direct variation situation, you can create a proportion.
is constant in a direct variation situation, you can create a proportion.
Ohm’s Law states that the voltage ![]() is equal to the electrical current
is equal to the electrical current ![]() in amps times the resistance
in amps times the resistance ![]() in ohms. Translating this to an equation,
in ohms. Translating this to an equation, ![]() .
.
Suppose an electronics device passed a current of 1.3 amps at a voltage of 2.6 volts. What was the current when the voltage was increased to 12 volts?
Ohm’s Law matches with the definition of direct variation, so you can write a proportion. ![]() . Using the Cross Products Theorem, solve for
. Using the Cross Products Theorem, solve for ![]() .
. ![]() . Therefore, when the voltage was increased to 12 volts, the electronics device passed a current of 6 amps.
. Therefore, when the voltage was increased to 12 volts, the electronics device passed a current of 6 amps.
Sample explanations for some of the practice exercises below are available by viewing the following video. Note that there is not always a match between the number of the practice exercise in the video and the number of the practice exercise listed in the following exercise set. However, the practice exercise is the same in both.
Click here to watch the video on CK-12 Basic Algebra: Direct Variation Models(11:11).
Translate the following direct variation situations into equations. Choose appropriate letters to represent the varying quantities.
Explain why each equation is not an example of direct variation.
Graph the following direct variation equations.
In 20 – 24, determine the constant of variation in each exercise.
Mixed Review
So far, the term function has been used to describe many of the equations we have been graphing. The concept of a function is extremely important in mathematics. Not all equations are functions. To be a function, for each value of ![]() there is one and only one value for
there is one and only one value for ![]() .
.
Definition: A function is a relationship between two variables such that the input value has ONLY one unique output value.
Recall from Lesson 1.5 that a function rule replaces the variable ![]() with its function name, usually
with its function name, usually ![]() . Remember that these parentheses do not mean multiplication. They separate the function name from the independent variable,
. Remember that these parentheses do not mean multiplication. They separate the function name from the independent variable, ![]() .
.
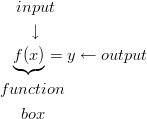
![]() is read “the function
is read “the function ![]() of
of ![]() ” or simply “
” or simply “![]() of
of ![]() .”
.”
If the function looks like this: ![]() , it would be read
, it would be read ![]() of
of ![]() equals 3 times
equals 3 times ![]() minus 1.
minus 1.
Function notation allows you to easily see the input value for the independent variable inside the parentheses.
Example: Consider the function ![]() .
.
Evaluate ![]() .
.
Solution: The value inside the parentheses is the value of the variable ![]() . Use the Substitution Property to evaluate the function for
. Use the Substitution Property to evaluate the function for ![]() .
.
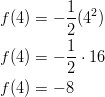
To use function notation, the equation must be written in terms of ![]() . This means that the
. This means that the ![]() variable must be isolated on one side of the equal sign.
variable must be isolated on one side of the equal sign.
Example: Rewrite ![]() using function notation.
using function notation.
Solution: The goal is to rearrange this equation so the equation looks like ![]() . Then replace
. Then replace ![]() with
with ![]() .
.
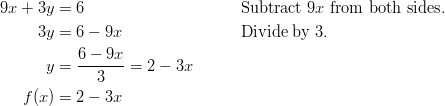
You can think of a function as a machine. You start with an input (some value), the machine performs the operations (it does the work), and your output is the answer. For example, ![]() takes some number,
takes some number, ![]() , multiplies it by 3 and adds 2. As a machine, it would look like this:
, multiplies it by 3 and adds 2. As a machine, it would look like this:

When you use the function machine to evaluate ![]() , the solution is
, the solution is ![]() .
.
Example 1: A function is defined as ![]() . Determine the following:
. Determine the following:
a) ![]()
b) ![]()
Solution:
a) Substitute ![]() into the function
into the function ![]() .
.
b) Substitute ![]() into the function
into the function ![]() .
.
You can see that the notation ![]() and
and ![]() are interchangeable. This means you can substitute the notation
are interchangeable. This means you can substitute the notation ![]() for
for ![]() and use all the concepts you have learned in this chapter.
and use all the concepts you have learned in this chapter.
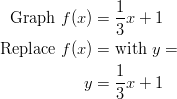
This equation is in slope-intercept form. You can now graph the function by graphing the ![]() intercept and then using the slope as a set of directions to find your second coordinate.
intercept and then using the slope as a set of directions to find your second coordinate.
Example: Graph ![]() .
.
Solution: The first step is to rewrite the single fraction as two separate fractions.
![]()
This equation is in slope-intercept form. The ![]() intercept is at the ordered pair (0,
intercept is at the ordered pair (0, ![]() ) and the slope is
) and the slope is ![]() . Beginning at the
. Beginning at the ![]() intercept and using the slope to find a second coordinate, you get the graph:
intercept and using the slope to find a second coordinate, you get the graph:

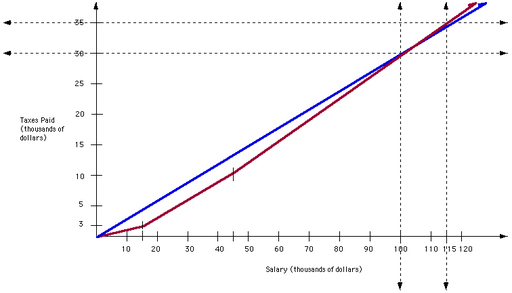
The previous graph, written by T. Barron and S. Katsberg from the University of Georgia http://jwilson.coe.uga.edu/emt668/EMAT6680.Folders/Barron/unit/Lesson%204/4.html, shows the relationship between the salary (in thousands of dollars) and the taxes paid (in thousands of dollars) in red. The blue function represents a direct variation situation in which the constant of variation (or the slope) is 0.30, or a 30% tax rate. This direct variation represents a flat tax of 30%.
The red line has three slopes. The first line from $0 to $15,000 has a slope of 0.20, or 20%. The second portion of the line from $15,000 to $45,000 has a slope of 0.25, or 25% tax rate. The slope of the line greater than $45,000 of salary is 0.35, or 35%.
Suppose you wanted to compare the amount of taxes you would pay if your salary was $60,000. If the blue line was ![]() and the red line was
and the red line was ![]() , then you would evaluate each function for
, then you would evaluate each function for ![]() .
.
Using the graph, ![]() and
and ![]() . Therefore, you would pay more taxes with the blue line tax rate than the red line tax rate. We will look at how to use graphs as a problem-solving strategy in the next lesson.
. Therefore, you would pay more taxes with the blue line tax rate than the red line tax rate. We will look at how to use graphs as a problem-solving strategy in the next lesson.
Sample explanations for some of the practice exercises below are available by viewing the following video. Note that there is not always a match between the number of the practice exercise in the video and the number of the practice exercise listed in the following exercise set. However, the practice exercise is the same in both.
Click here to watch the video on CK-12 Basic Algebra: Linear Function Graphs(11:49).
In 4 – 7, tell whether the graph is a function. Explain your reasoning.
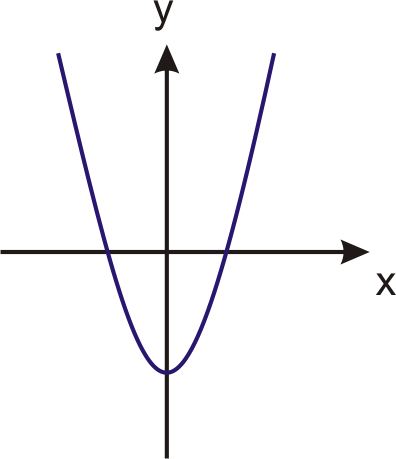
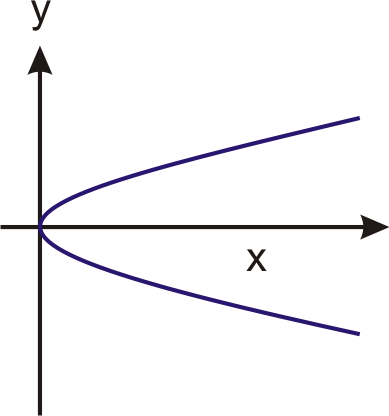
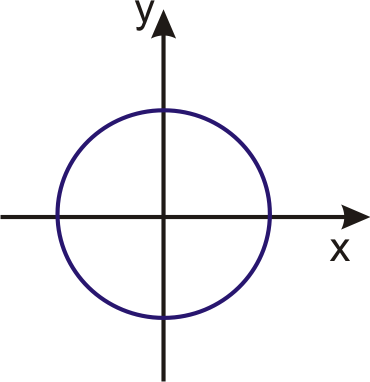
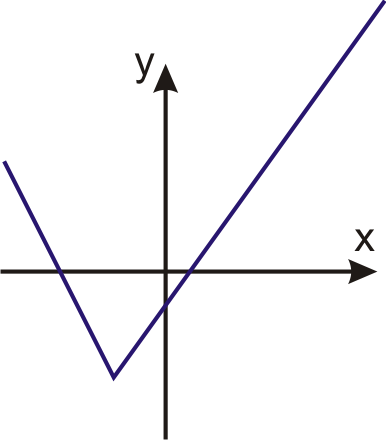
Rewrite each equation using function notation.
In 15 – 19, eevaluate ![]() , and
, and ![]() .
.
Mixed Review
Graphing is a very useful tool when analyzing a situation. This lesson will focus on using graphs to help solve linear situations that occur in real life.
Remember the 4-Step Problem-Solving Plan:
Example: A cell phone company is offering its costumers the following deal. You can buy a new cell phone for $60 and pay a monthly flat rate of $40 per month for unlimited calls. How much money will this deal cost you after 9 months?
Solution: Begin by translating the sentence into an algebraic equation.
![]()
Let ![]() the number of months and
the number of months and ![]() total cost. The equation becomes
total cost. The equation becomes
![]()
You could use guess and check or solve this equation. However, this lesson focuses on using a graph to problem-solve. This equation is in slope-intercept form. By graphing the line of this equation, you will find all the ordered pairs that are solutions to the cell phone problem.

Finding the cost at month 9, you can see the cost is approximately $425.00. To check if this is approximately correct, substitute 9 in for the variable ![]() .
.
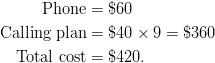
Our answer, $425.00 is approximately equal to the exact solution $420.00.
Example: Christine took one hour to read 22 pages of “Harry Potter and the Order of the Phoenix.” She has 100 pages left to read in order to finish the book. Assuming that she reads at a constant rate of pages per hour, how much time should she expect to spend reading in order to finish the book?

Solution: We do not have enough information to write an equation. We do not know the slope or the ![]() intercept. However, we have two points we can graph. We know that if Christine had never picked up the book, she would have read zero pages. So it takes Christine 0 hours to read 0 pages. We also know it took Christine one hour to read 22 pages. The two coordinates we can graph are (0, 0) and (1, 22).
intercept. However, we have two points we can graph. We know that if Christine had never picked up the book, she would have read zero pages. So it takes Christine 0 hours to read 0 pages. We also know it took Christine one hour to read 22 pages. The two coordinates we can graph are (0, 0) and (1, 22).

Using the graph and finding 100 pages, you can determine it will take Christine about 4.5 hours to read 100 pages.
You can also think of this as a direct variation situation and solve it by writing a proportion.
![]()
By using the Cross Products Theorem, you can find out ![]() . It will take Christine about 4.55 hours to read 100 pages, which is very close to your original estimate of 4.5 hours.
. It will take Christine about 4.55 hours to read 100 pages, which is very close to your original estimate of 4.5 hours.
Sample explanations for some of the practice exercises below are available by viewing the following video. Note that there is not always a match between the number of the practice exercise in the video and the number of the practice exercise listed in the following exercise set. However, the practice exercise is the same in both.
Click here to watch the video on CK-12 Basic Algebra: Word Problem Solving 4(10:05).
Mixed Review
Define the following words:
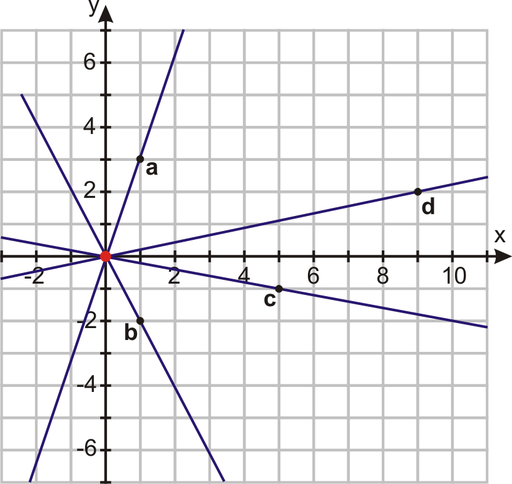
In 6 – 11, identify the coordinates using the graph below.

In 12 – 16, graph the following ordered pairs on one Cartesian Plane.
In 17 and 18, graph the function using the table.
|
|
|
| –2 | 7 |
| –1 | 9 |
| 0 | 11 |
| 1 | 13 |
| 2 | 15 |
In 19 – 24, graph the following lines on one set of axes.
In 25 – 28, find the intercepts of each equation.
In 29 – 34, graph each equation using its intercepts.
In 35 – 44, find the slope between the sets of points.
In 45 – 50, determine the rate of change.
In 51 – 55, identify the slope and the ![]() intercept of each equation.
intercept of each equation.
56 – 60, graph each equation.
In 61 – 63, decide whether the given lines are parallel.
In 64 – 70, evaluate the function for the indicated value.
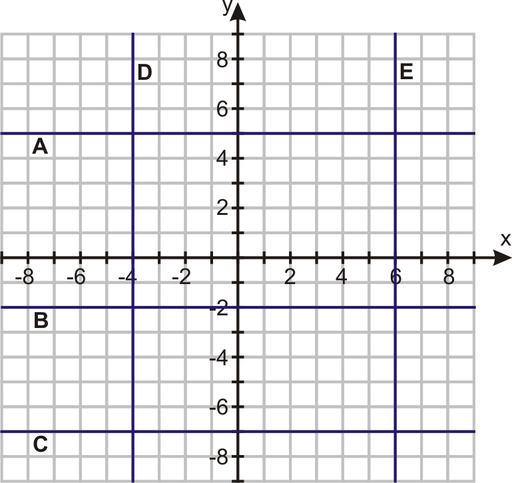
Give the location of the following ordered pairs using the graph below.
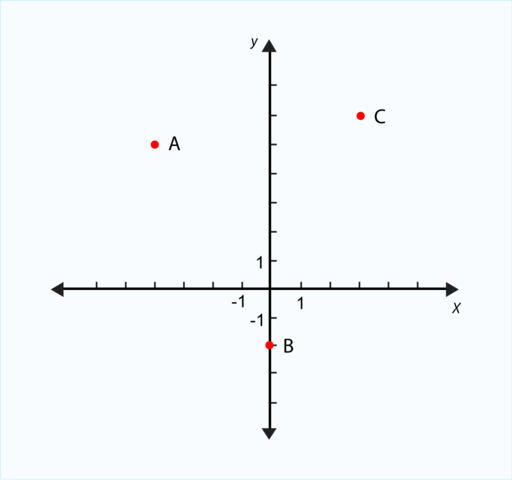
![]()
In the CK-12 Texas Instruments Algebra I FlexBook, there are graphing calculator activities designed to supplement the objectives for some of the lessons in this chapter. See http://www.ck12.org/flexr/chapter/9614.