FIGURE 1.1. Photo of Geller.
(Reprinted from German Language Wikipedia.)

Chapter 1
Sources of Error
Don’t think—use the computer.
Dyke (tongue in cheek) [1997].
We cannot help remarking that it is very surprising that research in an area that depends so heavily on statistical methods has not been carried out in close collaboration with professional statisticians, the panel remarked in its conclusions. From the report of an independent panel looking into “Climategate.”1
STATISTICAL PROCEDURES FOR HYPOTHESIS TESTING, ESTIMATION, AND MODEL building are only a part of the decision-making process. They should never be quoted as the sole basis for making a decision (yes, even those procedures that are based on a solid deductive mathematical foundation). As philosophers have known for centuries, extrapolation from a sample or samples to a larger, incompletely examined population must entail a leap of faith.
The sources of error in applying statistical procedures are legion and include all of the following:
But perhaps the most serious source of error lies in letting statistical procedures make decisions for you.
In this chapter, as throughout this text, we offer first a preventive prescription, followed by a list of common errors. If these prescriptions are followed carefully, you will be guided to the correct, proper, and effective use of statistics and avoid the pitfalls.
Statistical methods used for experimental design and analysis should be viewed in their rightful role as merely a part, albeit an essential part, of the decision-making procedure.
Here is a partial prescription for the error-free application of statistics.
Three concepts are fundamental to the design of experiments and surveys: variation, population, and sample. A thorough understanding of these concepts will prevent many errors in the collection and interpretation of data.
If there were no variation, if every observation were predictable, a mere repetition of what had gone before, there would be no need for statistics.
Variation is inherent in virtually all our observations. We would not expect outcomes of two consecutive spins of a roulette wheel to be identical. One result might be red, the other black. The outcome varies from spin to spin.
There are gamblers who watch and record the spins of a single roulette wheel hour after hour hoping to discern a pattern. A roulette wheel is, after all, a mechanical device and perhaps a pattern will emerge. But even those observers do not anticipate finding a pattern that is 100% predetermined. The outcomes are just too variable.
Anyone who spends time in a schoolroom, as a parent or as a child, can see the vast differences among individuals. This one is tall, that one short, though all are the same age. Half an aspirin and Dr. Good’s headache is gone, but his wife requires four times that dosage.
There is variability even among observations on deterministic formula-satisfying phenomena such as the position of a planet in space or the volume of gas at a given temperature and pressure. Position and volume satisfy Kepler’s Laws and Boyle’s Law, respectively (the latter over a limited range), but the observations we collect will depend upon the measuring instrument (which may be affected by the surrounding environment) and the observer. Cut a length of string and measure it three times. Do you record the same length each time?
In designing an experiment or survey we must always consider the possibility of errors arising from the measuring instrument and from the observer. It is one of the wonders of science that Kepler was able to formulate his laws at all given the relatively crude instruments at his disposal.
A phenomenon is said to be deterministic if given sufficient information regarding its origins, we can successfully make predictions regarding its future behavior. But we do not always have all the necessary information. Planetary motion falls into the deterministic category once one makes adjustments for all gravitational influences, the other planets as well as the sun.
Nineteenth century physicists held steadfast to the belief that all atomic phenomena could be explained in deterministic fashion. Slowly, it became evident that at the subatomic level many phenomena were inherently stochastic in nature, that is, one could only specify a probability distribution of possible outcomes, rather than fix on any particular outcome as certain.
Strangely, twenty-first century astrophysicists continue to reason in terms of deterministic models. They add parameter after parameter to the lambda cold-dark-matter model hoping to improve the goodness of fit of this model to astronomical observations. Yet, if the universe we observe is only one of many possible realizations of a stochastic process, goodness of fit offers absolutely no guarantee of the model’s applicability. (See, for example, Good, 2012.)
Chaotic phenomena differ from the strictly deterministic in that they are strongly dependent upon initial conditions. A random perturbation from an unexpected source (the proverbial butterfly’s wing) can result in an unexpected outcome. The growth of cell populations has been described in both deterministic (differential equations) and stochastic terms (birth and death process), but a chaotic model (difference-lag equations) is more accurate.
The population(s) of interest must be clearly defined before we begin to gather data.
From time to time, someone will ask us how to generate confidence intervals (see Chapter 8) for the statistics arising from a total census of a population. Our answer is no, we cannot help. Population statistics (mean, median, and thirtieth percentile) are not estimates. They are fixed values and will be known with 100% accuracy if two criteria are fulfilled:
Confidence intervals would be appropriate if the first criterion is violated, for then we are looking at a sample, not a population. And if the second criterion is violated, then we might want to talk about the confidence we have in our measurements.
Debates about the accuracy of the 2000 United States Census arose from doubts about the fulfillment of these criteria.2 “You didn’t count the homeless,” was one challenge. “You didn’t verify the answers,” was another. Whether we collect data for a sample or an entire population, both these challenges or their equivalents can and should be made.
Kepler’s “laws” of planetary movement are not testable by statistical means when applied to the original planets (Jupiter, Mars, Mercury, and Venus) for which they were formulated. But when we make statements such as “Planets that revolve around Alpha Centauri will also follow Kepler’s Laws,” then we begin to view our original population, the planets of our sun, as a sample of all possible planets in all possible solar systems.
A major problem with many studies is that the population of interest is not adequately defined before the sample is drawn. Do not make this mistake. A second major problem is that the sample proves to have been drawn from a different population than was originally envisioned. We consider these issues in the next section and again in Chapters 2, 6, and 7.
A sample is any (proper) subset of a population. Small samples may give a distorted view of the population. For example, if a minority group comprises 10% or less of a population, a jury of 12 persons selected at random from that population fails to contain any members of that minority at least 28% of the time.
As a sample grows larger, or as we combine more clusters within a single sample, the sample will grow to more closely resemble the population from which it is drawn.
How large a sample must be to obtain a sufficient degree of closeness will depend upon the manner in which the sample is chosen from the population.
Are the elements of the sample drawn at random, so that each unit in the population has an equal probability of being selected? Are the elements of the sample drawn independently of one another? If either of these criteria is not satisfied, then even a very large sample may bear little or no relation to the population from which it was drawn.
An obvious example is the use of recruits from a Marine boot camp as representatives of the population as a whole or even as representatives of all Marines. In fact, any group or cluster of individuals who live, work, study, or pray together may fail to be representative for any or all of the following reasons (Cummings and Koepsell, 2002):
A sample consisting of the first few animals to be removed from a cage will not satisfy these criteria either, because, depending on how we grab, we are more likely to select more active or more passive animals. Activity tends to be associated with higher levels of corticosteroids, and corticosteroids are associated with virtually every body function.
Sample bias is a danger in every research field. For example, Bothun [1998] documents the many factors that can bias sample selection in astronomical research.
To prevent sample bias in your studies, before you begin determine all the factors that can affect the study outcome (gender and lifestyle, for example). Subdivide the population into strata (males, females, city dwellers, farmers) and then draw separate samples from each stratum. Ideally, you would assign a random number to each member of the stratum and let a computer’s random number generator determine which members are to be included in the sample.
Being selected at random does not mean that an individual will be willing to participate in a public opinion poll or some other survey. But if survey results are to be representative of the population at large, then pollsters must find some way to interview nonresponders as well. This difficulty is exacerbated in long-term studies, as subjects fail to return for follow-up appointments and move without leaving a forwarding address. Again, if the sample results are to be representative, some way must be found to report on subsamples of the nonresponders and the dropouts.
Formulate and write down your hypotheses before you examine the data.
Patterns in data can suggest, but cannot confirm, hypotheses unless these hypotheses were formulated before the data were collected.
Everywhere we look, there are patterns. In fact, the harder we look the more patterns we see. Three rock stars die in a given year. Fold the United States twenty-dollar bill in just the right way and not only the Pentagon but the Twin Towers in flames are revealed.3 It is natural for us to want to attribute some underlying cause to these patterns, but those who have studied the laws of probability tell us that more often than not patterns are simply the result of random events.
Put another way, finding at least one cluster of events in time or in space has a greater probability than finding no clusters at all (equally spaced events).
How can we determine whether an observed association represents an underlying cause-and-effect relationship or is merely the result of chance? The answer lies in our research protocol. When we set out to test a specific hypothesis, the probability of a specific event is predetermined. But when we uncover an apparent association, one that may well have arisen purely by chance, we cannot be sure of the association’s validity until we conduct a second set of controlled trials.
In the International Study of Infarct Survival [1988], patients born under the Gemini or Libra astrological birth signs did not survive as long when their treatment included aspirin. By contrast, aspirin offered apparent beneficial effects (longer survival time) to study participants from all other astrological birth signs. Szydloa et al. [2010] report similar spurious correlations when hypothesis are formulated with the data in hand.
Except for those who guide their lives by the stars, there is no hidden meaning or conspiracy in this result. When we describe a test as significant at the 5% or one-in-20 level, we mean that one in 20 times we will get a significant result even though the hypothesis is true. That is, when we test to see if there are any differences in the baseline values of the control and treatment groups, if we have made 20 different measurements, we can expect to see at least one statistically significant difference; in fact, we will see this result almost two-thirds of the time. This difference will not represent a flaw in our design but simply chance at work. To avoid this undesirable result—that is, to avoid attributing statistical significance to an insignificant random event, a so-called Type I error—we must distinguish between the hypotheses with which we began the study and those which came to mind afterward. We must accept or reject our initial hypotheses at the original significance level while demanding additional corroborating evidence for those exceptional results (such as a dependence of an outcome on astrological sign) that are uncovered for the first time during the trials.
No reputable scientist would ever report results before successfully reproducing the experimental findings twice, once in the original laboratory and once in that of a colleague.4 The latter experiment can be particularly telling, as all too often some overlooked factor not controlled in the experiment—such as the quality of the laboratory water—proves responsible for the results observed initially. It is better to be found wrong in private, than in public. The only remedy is to attempt to replicate the findings with different sets of subjects, replicate, then replicate again.
Persi Diaconis [1978] spent some years investigating paranormal phenomena. His scientific inquiries included investigating the powers linked to Uri Geller, the man who claimed he could bend spoons with his mind. Diaconis was not surprised to find that the hidden “powers” of Geller were more or less those of the average nightclub magician, down to and including forcing a card and taking advantage of ad-hoc, post-hoc hypotheses (Figure 1.1).
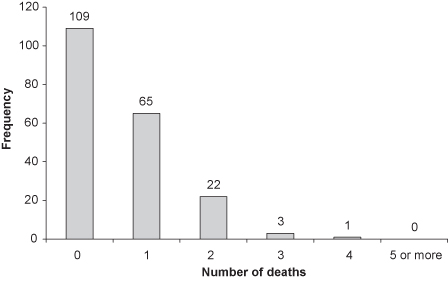
When three buses show up at your stop simultaneously, or three rock stars die in the same year, or a stand of cherry trees is found amid a forest of oaks, a good statistician remembers the Poisson distribution. This distribution applies to relatively rare events that occur independently of one another (see Figure 1.2). The calculations performed by Siméon-Denis Poisson reveal that if there is an average of one event per interval (in time or in space), whereas more than a third of the intervals will be empty, at least a quarter of the intervals are likely to include multiple events.
FIGURE 1.2. Frequency plot of the number of deaths in the Prussian army as a result of being kicked by a horse (there are 200 total observations).
Anyone who has played poker will concede that one out of every two hands contains “something” interesting. Do not allow naturally occurring results to fool you nor lead you to fool others by shouting, “Isn’t this incredible?”
TABLE 1.1. Probability of finding something interesting in a five-card hand
| Hand | Probability |
| Straight flush | 0.0000 |
| 4-of-a-kind | 0.0002 |
| Full house | 0.0014 |
| Flush | 0.0020 |
| Straight | 0.0039 |
| Three of a kind | 0.0211 |
| Two pairs | 0.0475 |
| Pair | 0.4226 |
| Total | 0.4988 |
The purpose of a recent set of clinical trials was to see if blood flow and distribution in the lower leg could be improved by carrying out a simple surgical procedure prior to the administration of standard prescription medicine.
The results were disappointing on the whole, but one of the marketing representatives noted that the long-term prognosis was excellent when a marked increase in blood flow was observed just after surgery. She suggested we calculate a p-value5 for a comparison of patients with an improved blood flow after surgery versus patients who had taken the prescription medicine alone.
Such a p-value is meaningless. Only one of the two samples of patients in question had been taken at random from the population (those patients who received the prescription medicine alone). The other sample (those patients who had increased blood flow following surgery) was determined after the fact. To extrapolate results from the samples in hand to a larger population, the samples must be taken at random from, and be representative of, that population.
The preliminary findings clearly called for an examination of surgical procedures and of patient characteristics that might help forecast successful surgery. But the generation of a p-value and the drawing of any final conclusions had to wait for clinical trials specifically designed for that purpose.
This does not mean that one should not report anomalies and other unexpected findings. Rather, one should not attempt to provide p-values or confidence intervals in support of them. Successful researchers engage in a cycle of theorizing and experimentation so that the results of one experiment become the basis for the hypotheses tested in the next.
A related, extremely common error whose correction we discuss at length in Chapters 13 and 15 is to use the same data to select variables for inclusion in a model and to assess their significance. Successful model builders develop their frameworks in a series of stages, validating each model against a second independent dataset before drawing conclusions.
One reason why many statistical models are incomplete is that they do not specify the sources of randomness generating variability among agents, i.e., they do not specify why otherwise observationally identical people make different choices and have different outcomes given the same choice.
—James J. Heckman
On the necessity for improvements in the use of statistics in research publications, see Altman [1982, 1991, 1994, 2000, 2002]; Cooper and Rosenthal [1980]; Dar, Serlin, and Omer [1994]; Gardner and Bond [1990]; George [1985]; Glantz [1980]; Goodman, Altman, and George [1998]; MacArthur and Jackson [1984]; Morris [1988]; Strasak et al. [2007]; Thorn et al. [1985]; and Tyson et al. [1983].
Brockman and Chowdhury [1997] discuss the costly errors that can result from treating chaotic phenomena as stochastic.
Notes
1 This is from an inquiry at the University of East Anglia headed by Lord Oxburgh. The inquiry was the result of emails from climate scientists being released to the public.
2 City of New York v. Department of Commerce, 822 F. Supp. 906 (E.D.N.Y, 1993). The arguments of four statistical experts who testified in the case may be found in Volume 34 of Jurimetrics, 1993, 64–115.
3 A website with pictures is located at http://www.foldmoney.com/.
4 Remember “cold fusion”? In 1989, two University of Utah professors told the newspapers they could fuse deuterium molecules in the laboratory, solving the world’s energy problems for years to come. Alas, neither those professors nor anyone else could replicate their findings, though true believers abound (see http://www.ncas.org/erab/intro.htm).
5 A p-value is the probability under the primary hypothesis of observing the set of observations we have in hand. We can calculate a p-value once we make a series of assumptions about how the data were gathered. These days, statistical software does the calculations, but it’s still up to us to validate the assumptions.