Chapter 2
Hypotheses: The Why of Your Research
All who drink of this treatment recover in a short time,
Except those whom it does not help, who all die,
It is obvious therefore, that it only fails in incurable cases.
—Galen (129–199)
IN THIS CHAPTER, AIMED AT BOTH RESEARCHERS WHO will analyze their own data as well as those researchers who will rely on others to assist them in the analysis, we review how to formulate a hypothesis that is testable by statistical means, the appropriate use of the null hypothesis, Neyman–Pearson theory, the two types of error, and the more general theory of decisions and losses.
Statistical methods used for experimental design and analysis should be viewed in their rightful role as merely a part, albeit an essential part, of the decision-making procedure:
A well-formulated hypothesis will be both quantifiable and testable, that is, involve measurable quantities or refer to items that may be assigned to mutually exclusive categories. It will specify the population to which the hypothesis will apply.
A well-formulated statistical hypothesis takes one of two forms:
Examples of well-formed statistical hypotheses include the following:
“All redheads are passionate” is not a well-formed statistical hypothesis, not merely because “passionate” is ill defined, but because the word “all” suggests there is no variability. The latter problem can be solved by quantifying the term “all” to, let’s say, 80%. If we specify “passionate” in quantitative terms to mean “has an orgasm more than 95% of the time consensual sex is performed,” then the hypothesis “80% of redheads have an orgasm more than 95% of the time consensual sex is performed” becomes testable.
Note that defining “passionate” to mean “has an orgasm every time consensual sex is performed” would not be provable as it too is a statement of the “all-or-none” variety. The same is true for a hypothesis such as “has an orgasm none of the times consensual sex is performed.” Similarly, qualitative assertions of the form “not all,” or “some” are not statistical in nature because these terms leave much room for subjective interpretation. How many do we mean by “some”? Five out of 100? Ten out of 100?
The statements, “Doris J. is passionate,” or “Both Good brothers are 5′10″ tall″ is equally not statistical in nature as they concern specific individuals rather than populations [Hagood, 1941]. Finally, note that until someone other than Thurber succeeds in locating unicorns, the hypothesis, “80% of unicorns are white” is not testable.
Formulate your hypotheses so they are quantifiable, testable, and statistical in nature.
The chief executive of a drug company may well express a desire to test whether “our antihypertensive drug can beat the competition.” The researcher, having done done preliminary reading of the literature, might want to test a preliminary hypothesis on the order of “For males over 40 suffering from chronic hypertension, there is a daily dose of our new drug that will lower diastolic blood pressure an average of 20 mm Hg.” But this hypothesis is imprecise. What if the necessary dose of the new drug required taking a tablet every hour? Or caused liver malfunction? Or even death? First, the researcher would need to conduct a set of clinical trials to determine the maximum tolerable dose (MTD). Subsequently, she could test the precise hypothesis, “a daily dose of one-third to one-fourth the MTD of our new drug will lower diastolic blood pressure an average of 20 mm Hg in males over 40 suffering from chronic hypertension.”
In a series of articles by Horwitz et al. [1998], a physician and his colleagues strongly criticize the statistical community for denying them (or so they perceive) the right to provide a statistical analysis for subgroups not contemplated in the original study protocol. For example, suppose that in a study of the health of Marine recruits, we notice that not one of the dozen or so women who received a vaccine contracted pneumonia. Are we free to provide a p-value for this result?
Statisticians Smith and Egger [1998] argue against hypothesis tests of subgroups chosen after the fact, suggesting that the results are often likely to be explained by the “play of chance.” Altman [1998; pp. 301–303], another statistician, concurs noting that, “… the observed treatment effect is expected to vary across subgroups of the data … simply through chance variation,” and that “doctors seem able to find a biologically plausible explanation for any finding.” This leads Horwitz et al. to the incorrect conclusion that Altman proposes that we “dispense with clinical biology (biologic evidence and pathophysiologic reasoning) as a basis for forming subgroups.” Neither Altman nor any other statistician would quarrel with Horwitz et al.’s assertion that physicians must investigate “how do we [physicians] do our best for a particular patient.”
Scientists can and should be encouraged to make subgroup analyses. Physicians and engineers should be encouraged to make decisions based upon them. Few would deny that in an emergency, coming up with workable, fast-acting solutions without complete information is better than finding the best possible solution.1 But, by the same token, statisticians should not be pressured to give their imprimatur to what, in statistical terms, is clearly an improper procedure, nor should statisticians mislabel suboptimal procedures as the best that can be done.2
We concur with Anscombe [1963] who writes, “… the concept of error probabilities of the first and second kinds … has no direct relevance to experimentation. … The formation of opinions, decisions concerning further experimentation, and other required actions, are not dictated … by the formal analysis of the experiment, but call for judgment and imagination. … It is unwise for the experimenter to view himself seriously as a decision-maker. … The experimenter pays the piper and calls the tune he likes best; but the music is broadcast so that others might listen. … ”
A Bill of Rights for Subgroup Analysis
p-values should not be computed for hypotheses based on “found data” as of necessity all hypotheses related to found data are after the fact. This rule does not apply if the observer first divides the data into sections. One part is studied and conclusions drawn; then the resultant hypotheses are tested on the remaining sections. Even then, the tests are valid only if the found data can be shown to be representative of the population at large.
A major research failing seems to be the exploration of uninteresting or even trivial questions. … In the 347 sampled articles in Ecology containing null hypotheses tests, we found few examples of null hypotheses that seemed biologically plausible.
—Anderson, Burnham, and Thompson [2000].
We do not perform an experiment to find out if two varieties of wheat or two drugs are equal. We know in advance, without spending a dollar on an experiment, that they are not equal.
—Deming [1975].
Test only relevant null hypotheses.
The null hypothesis has taken on an almost mythic role in contemporary statistics. Obsession with the null (more accurately spelled and pronounced nil), has been allowed to shape the direction of our research. We have let the tool use us instead of us using the tool.3
Virtually any quantifiable hypothesis can be converted into null form. There is no excuse and no need to be content with a meaningless nil.
For example, suppose we want to test that a given treatment will decrease the need for bed rest by at least three days. Previous trials have convinced us that the treatment will reduce the need for bed rest to some degree, so merely testing that the treatment has a positive effect would yield no new information. Instead, we would subtract three from each observation and then test the nil hypothesis that the mean value is zero.
We often will want to test that an effect is inconsequential, not zero but close to it, smaller than d, say, where d is the smallest biological, medical, physical, or socially relevant effect in our area of research. Again, we would subtract d from each observation before proceeding to test a null hypothesis.
The quote from Deming above is not quite correct as often we will wish to demonstrate that two drugs or two methods yield equivalent results. As shown in Chapter 5, we may test for equivalence using confidence intervals; a null hypothesis is not involved
To test that “80% of redheads are passionate,” we have two choices depending on how “passion” is measured. If “passion” is an all-or-none phenomena, then we can forget about trying to formulate a null hypothesis and instead test the binomial hypothesis that the probability p that a redhead is passionate is 80%. If “passion” can be measured on a seven-point scale and we define “passionate” as “passion” greater than or equal to 5, then our hypothesis becomes “the 20th percentile of redhead passion exceeds 5.” As in the first example above, we could convert this to a null hypothesis by subtracting five from each observation. But the effort is unnecessary as this problem, too, reduces to a test of a binomial parameter.
Formulate your alternative hypotheses at the same time you set forth the hypothesis that is of chief concern to you.
When the objective of our investigations is to arrive at some sort of conclusion, then we need not only have a single primary hypothesis in mind but one or more potential alternative hypotheses.
The cornerstone of modern hypothesis testing is the Neyman–Pearson lemma. To get a feeling for the working of this mathematical principle, suppose we are testing a new vaccine by administering it to half of our test subjects and giving a supposedly harmless placebo to each of the remainder. We proceed to follow these subjects over some fixed period and note which subjects, if any, contract the disease that the new vaccine is said to offer protection against.
We know in advance that the vaccine is unlikely to offer complete protection; indeed, some individuals may actually come down with the disease as a result of taking the vaccine. Many factors over which we have no control, such as the weather, may result in none of the subjects, even those who received only placebo, contracting the disease during the study period. All sorts of outcomes are possible.
The tests are being conducted in accordance with regulatory agency guidelines. Our primary hypothesis H is that the new vaccine can cut the number of infected individuals in half. From the regulatory agency’s perspective, the alternative hypothesis A1 is that the new vaccine offers no protection or, A2, no more protection than is provided by the best existing vaccine. Our task before the start of the experiment is to decide which outcomes will rule in favor of the alternative hypothesis A1 (or A2) and which in favor of the primary hypothesis H.
Note that neither a null nor a nil hypothesis is yet under consideration.
Because of the variation inherent in the disease process, each and every one of the possible outcomes could occur regardless of which of the hypotheses is true. Of course, some outcomes are more likely if A1 is true, for example, 50 cases of pneumonia in the placebo group and 48 in the vaccine group, and others are more likely if the primary hypothesis is true, for example, 38 cases of pneumonia in the placebo group and 20 in the vaccine group.
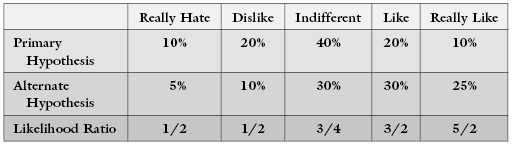
Following Neyman and Pearson, we order each of the possible outcomes in accordance with the ratio of its probability or likelihood when the primary hypothesis is true to its probability when the alternative hypothesis is true.4 When this likelihood ratio is large, we shall say the outcome rules in favor of the alternative hypothesis. Working downward from the outcomes with the highest values, we continue to add outcomes to the rejection region of the test—so-called because these are the outcomes for which we would reject the primary hypothesis—until the total probability of the rejection region under the primary hypothesis is equal to some predesignated significance level.5
In the following example, we would reject the primary hypothesis at the 10% level only if the test subject really liked a product.
To see that we have done the best we can do, suppose we replace one of the outcomes we assigned to the rejection region with one we did not. The probability that this new outcome would occur if the primary hypothesis is true must be less than or equal to the probability that the outcome it replaced would occur if the primary hypothesis is true. Otherwise, we would exceed the significance level.
Because of how we assigned outcome to the rejection region, the likelihood ratio of the new outcome is smaller than the likelihood ratio of the old outcome. Thus, the probability the new outcome would occur if the alternative hypothesis is true must be less than or equal to the probability that the outcome it replaced would occur if the alternative hypothesis is true. That is, by swapping outcomes we have reduced the power of our test. By following the method of Neyman and Pearson and maximizing the likelihood ratio, we obtain the most powerful test at a given significance level.
To take advantage of Neyman and Pearson’s finding, we need to have an alternative hypothesis or alternatives firmly in mind when we set up a test. Too often in published research, such alternative hypotheses remain unspecified or, worse, are specified only after the data are in hand. We must specify our alternatives before we commence an analysis, preferably at the same time we design our study.
Are our alternatives one-sided or two-sided? If we are comparing several populations at the same time, are their means ordered or unordered? The form of the alternative will determine the statistical procedures we use and the significance levels we obtain.
Decide beforehand whether you wish to test against a one-sided or a two-sided alternative.
Suppose on examining the cancer registry in a hospital, we uncover the following data that we put in the form of a 2 × 2 contingency table:
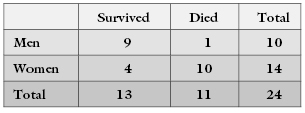
The 9 denotes the number of males who survived, the 1 denotes the number of males who died, and so forth. The four marginal totals or marginals are 10, 14, 13, and 11. The total number of men in the study is 10, whereas 14 denotes the total number of women, and so forth.
The marginals in this table are fixed because, indisputably, there are 11 dead bodies among the 24 persons in the study and 14 women. Suppose that before completing the table, we lost the subject IDs so that we could no longer identify which subject belonged in which category. Imagine you are given two sets of 24 labels. The first set has 14 labels with the word “woman” and 10 labels with the word “man.” The second set of labels has 11 labels with the word “dead” and 12 labels with the word “alive.” Under the null hypothesis, you are allowed to distribute the labels to subjects independently of one another. One label from each of the two sets per subject, please.
There are a total of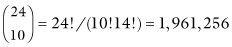 
ways you could hand out the labels; Table 2.1 illustrates two possible configurations. 
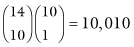of the assignments result in tables that are as extreme as our original table (that is, in which 90% of the men survive) and 
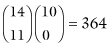in tables that are more extreme (100% of the men survive). This is a very small fraction of the total, (10,010 + 364)/(1,961,256) = 0.529%, so we conclude that a difference in survival rates of the two sexes as extreme as the difference we observed in our original table is very unlikely to have occurred by chance alone. We reject the hypothesis that the survival rates for the two sexes are the same and accept the alternative hypothesis that, in this instance at least, males are more likely to profit from treatment.
TABLE 2.1. In terms of the relative survival rates of the two sexes, the first of these tables is more extreme than our original table. The second is less extreme.
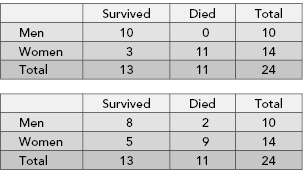
In the preceding example, we tested the hypothesis that survival rates do not depend on sex against the alternative that men diagnosed with cancer are likely to live longer than women similarly diagnosed. We rejected the null hypothesis because only a small fraction of the possible tables were as extreme as the one we observed initially. This is an example of a one-tailed test. But is it the correct test? Is this really the alternative hypothesis we would have proposed if we had not already seen the data? Wouldn’t we have been just as likely to reject the null hypothesis that men and women profit the same from treatment if we had observed a table of the following form?
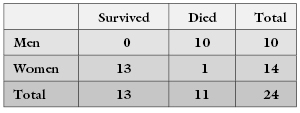
Of course, we would! In determining the significance level in the present example, we must add together the total number of tables that lie in either of the two extremes or tails of the permutation distribution.
The critical values and significance levels are quite different for one-tailed and two-tailed tests and, all too often, the wrong test has been employed in published work. McKinney et al. [1989] reviewed some 70-plus articles that appeared in six medical journals. In over half of these articles, Fisher’s exact test was applied improperly. Either a one-tailed test had been used when a two-tailed test was called for or the authors of the paper simply had not bothered to state which test they had used.
Of course, unless you are submitting the results of your analysis to a regulatory agency, no one will know whether you originally intended a one-tailed test or a two-tailed test and subsequently changed your mind. No one will know whether your hypothesis was conceived before you started or only after you had examined the data. All you have to do is lie. Just recognize that if you test an after-the-fact hypothesis without identifying it as such, you are guilty of scientific fraud.
When you design an experiment, decide at the same time whether you wish to test your hypothesis against a two-sided or a one-sided alternative. A two-sided alternative dictates a two-tailed test; a one-sided alternative dictates a one-tailed test.
As an example, suppose we decide to do a follow-on study of the cancer registry to confirm our original finding that men diagnosed as having tumors live significantly longer than women similarly diagnosed. In this follow-on study, we have a one-sided alternative. Thus, we would analyze the results using a one-tailed test rather than the two-tailed test we applied in the original study.
Determine beforehand whether your alternative hypotheses are ordered or unordered.
When testing qualities (number of germinating plants, crop weight, etc.) from k samples of plants taken from soils of different composition, it is often routine to use the F-ratio of the analysis of variance. For contingency tables, many routinely use the chi-square test to determine if the differences among samples are significant. But the F-ratio and the chi-square are what are termed omnibus tests, designed to be sensitive to all possible alternatives. As such, they are not particularly sensitive to ordered alternatives such “as more fertilizer equals more growth” or “more aspirin equals faster relief of headache.” Tests for such ordered responses at k distinct treatment levels should properly use the Pitman correlation described by Frank, Trzos, and Good [1978] when the data are measured on a metric scale (e.g., weight of the crop). Tests for ordered responses in 2 × C contingency tables (e.g., number of germinating plants) should use the trend test described by Berger, Permutt, and Ivanova [1998]. We revisit this topic in more detail in the next chapter.
When we determine a p-value as we did in the example above, we apply a set of algebraic methods and deductive logic to deduce the correct value. The deductive process is used to determine the appropriate size of resistor to use in an electric circuit, to determine the date of the next eclipse of the moon, and to establish the identity of the criminal (perhaps from the fact the dog did not bark on the night of the crime). Find the formula, plug in the values, turn the crank and out pops the result (or it does for Sherlock Holmes,6 at least).
When we assert that for a given population a percentage of samples will have a specific composition, this also is a deduction. But when we make an inductive generalization about a population based upon our analysis of a sample, we are on shakier ground. It is one thing to assert that if an observation comes from a normal distribution with mean zero, the probability is one-half that it is positive. It is quite another if, on observing that half the observations in the sample are positive, we assert that half of all the possible observations that might be drawn from that population will be positive also.
Newton’s Law of Gravitation provided an almost exact fit (apart from measurement error) to observed astronomical data for several centuries; consequently, there was general agreement that Newton’s generalization from observation was an accurate description of the real world. Later, as improvements in astronomical measuring instruments extended the range of the observable universe, scientists realized that Newton’s Law was only a generalization and not a property of the universe at all. Einstein’s Theory of Relativity gives a much closer fit to the data, a fit that has not been contradicted by any observations in the century since its formulation. But this still does not mean that relativity provides us with a complete, correct, and comprehensive view of the universe.
In our research efforts, the only statements we can make with God-like certainty are of the form “our conclusions fit the data.” The true nature of the real world is unknowable. We can speculate, but never conclude.
In our first advanced course in statistics, we read in the first chapter of Lehmann [1986] that the “optimal” statistical procedure would depend on the losses associated with the various possible decisions. But on day one of our venture into the real world of practical applications, we were taught to ignore this principle.
At that time, the only computationally feasible statistical procedures were based on losses that were proportional to the square of the difference between estimated and actual values. No matter that the losses really might be proportional to the absolute value of those differences, or the cube, or the maximum over a certain range. Our options were limited by our ability to compute.
Computer technology has made a series of major advances in the past half century. What forty years ago required days or weeks to calculate takes only milliseconds today. We can now pay serious attention to this long-neglected facet of decision theory: the losses associated with the varying types of decision.
Suppose we are investigating a new drug: We gather data, perform a statistical analysis, and draw a conclusion. If chance alone is at work yielding exceptional values and we opt in favor of the new drug, we have made an error. We also make an error if we decide there is no difference and the new drug really is better. These decisions and the effects of making them are summarized in Table 2.2.
TABLE 2.2. Decision making under uncertainty
| The Facts | Our Decision | |
| No Difference | No Difference | Drug is Better |
| Type I error: | ||
| Correct | Manufacturer wastes money developing ineffective drug. | |
| Drug is Better | Type II error: | |
| Manufacturer misses opportunity for profit. | Correct | |
| Public denied access to effective treatment. | ||
We distinguish the two types of error because they have quite different implications, as described in Table 2.2. As a second example, Fears, Tarone, and Chu [1977] use permutation methods to assess several standard screens for carcinogenicity. As shown in Table 2.3 their Type I error, a false positive, consists of labeling a relatively innocuous compound as carcinogenic. Such an action means economic loss for the manufacturer and the denial to the public of the compound’s benefits. Neither consequence is desirable. But a false negative, a Type II error, is much worse as it would mean exposing a large number of people to a potentially lethal compound.
TABLE 2.3. Decision making under uncertainty
| The Facts | Fears et al.’s Decision | |
| Not a Carcinogen | Compound a Carcinogen | |
| Not a Carcinogen | Type I error: | |
| Manufacturer misses opportunity for profit. | ||
| Public denied access to effective treatment. | ||
| Carcinogen | Type II error: | |
| Patients die; families suffer; | ||
| Manufacturer sued. | ||
What losses are associated with the decisions you will have to make? Specify them now before you begin.
The primary hypothesis/alternative hypothesis duality is inadequate in most real-life situations. Consider the pressing problems of global warming and depletion of the ozone layer. We could collect and analyze yet another set of data and then, just as is done today, make one of three possible decisions: reduce emissions, leave emission standards alone, or sit on our hands and wait for more data to come in. Each decision has consequences, as shown in Table 2.4.
TABLE 2.4. Results of a presidential decision under different underlying facts about the cause of hypothesized global warming
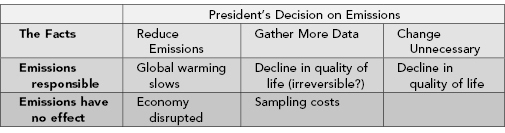
As noted at the beginning of this chapter, it is essential that we specify in advance the actions to be taken for each potential result. Always suspect are after-the-fact rationales that enable us to persist in a pattern of conduct despite evidence to the contrary. If no possible outcome of a study will be sufficient to change our mind, then we ought not undertake such a study in the first place.
Every research study involves multiple issues. Not only might we want to know whether a measurable, biologically (or medically, physically, or sociologically) significant effect takes place, but what the size of the effect is and the extent to which the effect varies from instance to instance. We would also want to know what factors, if any, will modify the size of the effect or its duration.
We may not be able to address all these issues with a single dataset. A preliminary experiment might tell us something about the possible existence of an effect, along with rough estimates of its size and variability. Hopefully, we glean enough information to come up with doses, environmental conditions, and sample sizes to apply in collecting and evaluating the next dataset. A list of possible decisions after the initial experiment includes “abandon this line of research,” “modify the environment and gather more data,” and “perform a large, tightly controlled, expensive set of trials.” Associated with each decision is a set of potential gains and losses. Common sense dictates we construct a table similar to Table 2.2 or 2.3 before we launch a study.
For example, in clinical trials of a drug we might begin with some animal experiments, then progress to Phase I clinical trials in which, with the emphasis on safety, we look for the maximum tolerable dose. Phase I trials generally involve only a small number of subjects and a one-time or short-term intervention. An extended period of several months may be used for follow-up purposes. If no adverse effects are observed, we might decide to pursue a Phase II set of trials in the clinic, in which our objective is to determine the minimum effective dose. Obviously, if the minimum effective dose is greater than the maximum tolerable dose, or if some dangerous side effects are observed that we did not observe in the first set of trials, we will abandon the drug and go on to some other research project. But if the signs are favorable, then and only then will we go to a set of Phase III trials involving a large number of subjects observed over an extended time period. Then, and only then, will we hope to get the answers to all our research questions.
Before you begin, list all the consequences of a study and all the actions you might take. Persist only if you can add to existing knowledge.
For more thorough accounts of decision theory, the interested reader is directed to Berger [1986], Blyth [1970], Cox [1958], DeGroot [1970], and Lehmann [1986]. For an applied perspective, see Clemen [1991], Berry [1995], and Sox, Blatt, Higgins, and Marton [1988].
Over 300 references warning of the misuse of null hypothesis testing can be accessed online at http://www.cnr.colostate.edu/∼anderson/thompson1.html. Alas, the majority of these warnings are ill informed, stressing errors that will not arise if you proceed as we recommend and place the emphasis on the why, not the what, of statistical procedures. Use statistics as a guide to decision making rather than a mandate.
Neyman and Pearson [1933] first formulated the problem of hypothesis testing in terms of two types of error. Extensions and analyses of their approach are given by Lehmann [1986] and Mayo [1996]. Their approach has not gone unchallenged, as seen in Berger [2003], Berger and Berry [1988], Berger and Selke [1987], Berkson [1942], Morrison and Henkel [1970], Savage [1972], Schmidt [1996], Seidenfeld [1979], and Sterne, Smith, and Cox [2001]. Hunter and Schmidt [1997] list and dismiss many of their objections.
Guthery, Lusk, and Peterson [2001] and Rozeboom [1960] are among those who have written about the inadequacy of the null hypothesis.
For more guidelines on formulating meaningful primary hypotheses, see Selike, Bayarri, and Berger [2001]. Clarity in hypothesis formulation is essential; ambiguity can only yield controversy; see, for example, Kaplan [2001].
Venn [1888] and Reichenbach [1949] are among those who have attempted to construct a mathematical bridge between what we observe and the reality that underlies our observations. Such efforts to the contrary, extrapolation from the sample to the population is not merely a matter of applying Sherlock Holmes-like deductive logic but entails a leap of faith. A careful reading of Locke [1700], Berkeley [1710], Hume [1748], and Lonergan [1992] is an essential prerequisite to the application of statistics.
See also Buchanan-Wollaston [1935], Cohen [1990], Copas [1997], and Lindley [2000].
Notes
1 Chiles [2001; p. 61].
2 One is reminded of the Dean, several of them in fact, who asked me to alter my grades.
“But that is something you can do as easily as I.” “Why Dr. Good, I would never dream of overruling one of my instructors.” See also Murder at Oklahoma by J. M. Bickham.
3 See, for example, Hertwig and Todd [2000].
4 When there are more than two hypotheses, the rejection region of the best statistical test (and the associated power and significance level) will be based upon the primary and alternative hypotheses that are the most difficult to distinguish from one another.
5 For convenience in calculating a rejection region, the primary and alternate hypotheses may be interchanged. Thus, the statistician who subsequently performs an analysis of the vaccine data may refer to testing the nil hypothesis A1 against the alternative H.
6 See “Silver Blaze” by A. Conan-Doyle, Strand Magazine, December 1892.