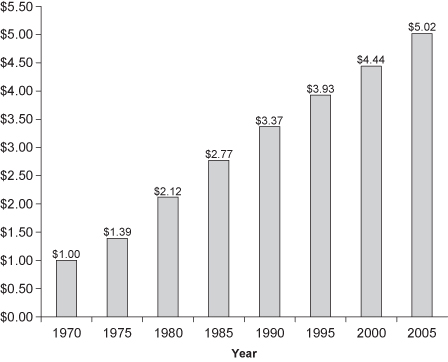
FIGURE 3.1. Equivalent purchasing powers over time using Consumer Price Index calculations. Each year shows the cost of the equivalent goods/services.
Chapter 3
Collecting Data
GIGO: Garbage in; Garbage out.
“Fancy statistical methods will not rescue garbage data.”
Course notes of Raymond J. Carroll [2001].
THE VAST MAJORITY OF ERRORS IN STATISTICS (and, not incidentally, in most human endeavors) arise from a reluctance (or even an inability) to plan. Some demon (or demonic manager) seems to be urging us to cross the street before we have had the opportunity to look both ways. Even on those rare occasions when we do design an experiment, we seem more obsessed with the mechanics than with the underlying concepts.
In this chapter, we review the fundamental concepts of experimental design, the choice of primary and secondary variables, the selection of measurement devices, the determination of sample size, the assumptions that underlie most statistical procedures along with the precautions necessary to ensure they are satisfied and that the data you collect will be representative of the population as a whole. We do not intend to replace a text on experiment or survey design, but to supplement one, providing examples and solutions that are often neglected in courses on the subject.
The first step in data collection is to have a clear, preferably written statement of your objectives. In accordance with Chapter 1, you will have defined the population or populations from which you intend to sample and have identified the characteristics of these populations you wish to investigate.
You developed one or more well-formulated hypotheses (the topic of Chapter 2) and have some idea of the risks you will incur should your analysis of the collected data prove to be erroneous. You will need to decide what you wish to observe and measure, and how you will go about observing it. We refer here not only to the primary variables or endpoints, but to the secondary variables or cofactors that may influence the former’s values. Indeed, it is essential that you be aware of all potential sources of variation.
Good practice is to draft the analysis section of your final report based on the conclusions you would like to make. What information do you need to justify these conclusions? All such information must be collected.
The next section is devoted to the choice of response variables and measuring devices, followed by sections on determining sample size and preventive steps to ensure your samples will be analyzable by statistical methods.
If you do not collect the values of cofactors, you will be unable to account for them later.
As whiplash injuries are a common consequence of rear-end collisions, there is an extensive literature on the subject. Any physician will tell you that the extent and duration of such injuries will depend upon the sex, age, and physical condition of the injured individual as well as any prior injuries the individual may have suffered. Yet we found article after article that failed to account for these factors; for example, Krafft, Kullgren, Ydenius, and Tingvall [2002], Kumar, Ferrari, and Narayan [2005], and Tencer, Sohail, and Kevin [2001] did not report the sex, age, or prior injuries of their test subjects.
Will you measure an endpoint such as death or a surrogate such as the presence of HIV antibodies? A good response variable takes values over a sufficiently large range so that they discriminate well [Bishop and Talbot, 2001].
The regression slope describing the change in systolic blood pressure (in mm Hg) per 100 mg of calcium intake is strongly influenced by the approach used for assessing the amount of calcium consumed (Cappuccio et al., 1995). The association is small and only marginally significant with diet histories (slope −0.01 (−0.003 to −0.016)) but large and highly significant when food frequency questionnaires are used (slope −0.15 (−0.11 to −0.19). With studies using 24 hour recall, an intermediate result emerges (slope −0.06 (−0.09 to −0.03). Diet histories assess patterns of usual intake over long periods of time and require an extensive interview with a nutritionist, whereas 24-hour recall and food frequency questionnaires are simpler methods that reflect current consumption (Block, 1982).
Before we initiate data collection, we must have a firm idea of what we will measure and how we will measure it. A good response variable
Collect exact values whenever possible.
A second fundamental principle is also applicable to both experiments and surveys: Collect exact values whenever possible. Worry about grouping them in intervals or discrete categories later.
A long-term study of buying patterns in New South Wales illustrates some of the problems caused by grouping prematurely. At the beginning of the study, the decision was made to group the incomes of survey subjects into categories—under $20,000, $20,000 to $30,000, and so forth. Six years of steady inflation later and the organizers of the study realized that all the categories had to be adjusted. An income of $21,000 at the start of the study would only purchase $18,000 worth of goods and housing at the end (see Figure 3.1). The problem was that those surveyed toward the end had filled out forms with exactly the same income categories. Had income been tabulated to the nearest dollar, it would have been easy to correct for increases in the cost of living and convert all responses to the same scale. But the study designers had not considered these issues. A precise and costly survey had been reduced to mere guesswork.
FIGURE 3.1. Equivalent purchasing powers over time using Consumer Price Index calculations. Each year shows the cost of the equivalent goods/services.

You can always group your results (and modify your groupings) after a study is completed. If after-the-fact grouping is a possibility, your design should state how the grouping will be determined; otherwise there will be the suspicion that you chose the grouping to obtain desired results.
Measuring devices differ widely both in what they measure and the precision with which they measure it. As noted in the next section of this chapter, the greater the precision with which measurements are made, the smaller the sample size required to reduce both Type I and Type II errors below specific levels.
All measuring devices have both linear and nonlinear ranges; the sensitivity, accuracy, and precision of the device are all suspect for both very small and very large values. Your measuring device ought be linear over the entire range of interest.
Before you rush out and purchase the most expensive and precise measuring instruments on the market, consider that the total cost C of an experimental procedure is S + nc, where n is the sample size and c is the cost per unit sampled.
The startup cost S includes the cost of the measuring device. c is made up of the cost of supplies and personnel costs. The latter includes not only the time spent on individual measurements but in preparing and calibrating the instrument for use.
Less obvious factors in the selection of a measuring instrument include impact on the subject, reliability (personnel costs continue even when an instrument is down), and reusability in future trials. For example, one of the advantages of the latest technology for blood analysis is that less blood needs to be drawn from patients. Less blood means happier subjects mean fewer withdrawals and a smaller initial sample size.
While no scientist would dream of performing an experiment without first mastering all the techniques involved, an amazing number will blunder into the execution of large-scale and costly surveys without a preliminary study of all the collateral issues a survey entails.
We know of one institute that mailed out some 20,000 questionnaires (didn’t the post office just raise its rates again?) before discovering that half the addresses were in error, and that the vast majority of the remainder were being discarded unopened before prospective participants had even read the sales pitch.
Fortunately, there are texts such as Bly [1990, 1996] that will tell you how to word a sales pitch and the optimal colors and graphics to use along with the wording. They will tell you what hooks to use on the envelope to ensure attention to the contents and what premiums to offer to increase participation.
There are other textbooks such as Converse and Presser [1986], Fowler and Fowler [1995], and Schroeder [1987] to assist you in wording questionnaires and in pretesting questions for ambiguity before you begin. We have only four paragraphs of caution to offer:
Recommended are Web-based surveys with initial solicitation by mail (letter or postcard) and e-mail. Not only are both costs and time to completion cut dramatically, but also the proportion of missing data and incomplete forms is substantially reduced. Moreover, Web-based surveys are easier to monitor and forms may be modified on the fly. Web-based entry also offers the possibility of displaying the individual’s prior responses during follow-up surveys.
Three other precautions can help ensure the success of your survey:
Determining optimal sample size is simplicity itself once we specify all of the following:
What could be easier?
Sample size must be determined for each experiment; there is no universally correct value. We need to understand and make use of the relationships among effect size, sample size, significance level, power, and the precision of our measuring instruments.
Increase the precision (and hold all other parameters fixed) and we can decrease the required number of observations. Decreases in any or all of the intrinsic and extrinsic sources of variation will also result in a decrease in the required number.
TABLE 3.1. Ingredients in a sample-size calculation
| Smallest Effect Size of Practical Interest | |
| Type I error (α) | Probability of falsely rejecting the hypothesis when it is true. |
| Type II error (1 − β[A]) | Probability of falsely accepting the hypothesis when an alternative hypothesis A is true. Depends on the alternative A. |
| Power = β[A] | Probability of correctly rejecting the hypothesis when an alternative hypothesis A is true. Depends on the alternative A. |
| Distribution functions | F[(x − μ)σ]; e.g., normal distribution |
| Location parameters | For both hypothesis and alternative hypothesis, μ1, μ2 |
| Scale parameters | For both hypothesis and alternative hypothesis, σ1, σ2 |
| Sample sizes | May be different for different groups in an experiment with more than one group. |
The smallest effect size of practical interest may be determined through consultation with one or more domain experts. The smaller this value, the greater the number of observations that will be required.
Permit a greater number of Type I or Type II errors (and hold all other parameters fixed) and we can decrease the required number of observations.
Explicit formula for power and sample size are available when the underlying observations are binomial, the results of a counting or Poisson process, time-to-event data, normally distributed, or ordinal with a limited number of discrete values (<7) and/or the expected proportion of cases at the boundaries is high (scoring 0 or 100). For the first four, several off-the-shelf computer programs including nQuery Advisor™, Pass 2005™, Power and Precision™, and StatX-act™ are available to do the calculations for us. For the ordinal data, use the method of Whitehead [1993].
During a year off from Berkeley’s graduate program to work as a statistical consultant, with a course from Erich Lehmann in testing hypotheses fresh under his belt, Phillip Good would begin by asking all clients for their values of α and β. When he received only blank looks in reply, he would ask them about the relative losses they assigned to Type I and Type II errors, but this only seemed to add to their confusion. Here are some guidelines for those left similarly to their own devices. Just remember this is all they are: guidelines, not universal truths. Strictly speaking, the significance level and power should be chosen so as to minimize the overall cost of any project, balancing the cost of sampling with the costs expected from Type I and Type II errors.
The environment in which you work should determine your significance level and power.
A manufacturer preparing to launch a new product line or a pharmaceutical company conducting a research for promising compounds typically adopt a three-way decision procedure: If the observed p-value is less than 1%, they go forward with the project. If the p-value is greater than 20%, they abandon it. And if the p-value lies in the gray area in between, they arrange for additional surveys or experiments.
A regulatory commission like the FDA that is charged with oversight responsibility must work at a fixed significance level, typically 5%. In the case of unwanted side effects, the FDA may also require a certain minimum power, usually 80% or better. The choice of a fixed significance level ensures consistency in both result and interpretation as the agency reviews the findings from literally thousands of tests.
If forced to pull numbers out of a hat, we would choose α = 20% for an initial trial and a sample size of 6 to 10. If we had some prior information in hand, we would choose α = 5% to 10% and β = 80% to 90%. If tests are to be performed on many different outcomes, lower significance levels of 2.5% or 1% may be desirable. (Remember that by chance alone, 1 in 20 results will be statistically significant at the 5% level.)
When using one of the commercially available programs to determine sample size, we also need to have some idea of the population proportion (for discrete counts) or the location (mean) and scale parameter (variance) (for continuous measurements), both when the primary hypothesis is true and when an alternative hypothesis is true. Since there may well be an infinity of alternatives in which we are interested, power calculations should be based on the worst case or boundary value. For example, if we are testing a binomial hypothesis p = 1/2 against the alternatives p ≥ 2/3, we would assume that p = 2/3.
A recommended rule of thumb is to specify as the alternative the smallest effect that is of practical significance.
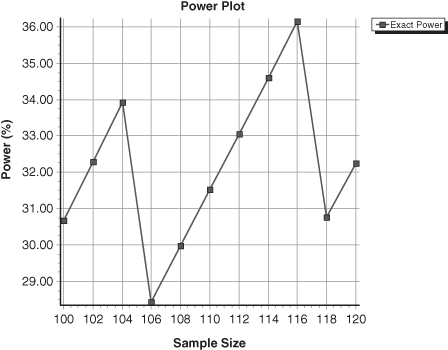
When determining sample size for data drawn from the binomial or any other discrete distribution, one should always display the power curve. The explanation lies in the saw-toothed nature of the curve [Chernick and Liu, 2002]; see Figure 3.2. As a result of inspecting the power curve by eye, you may come up with a less-expensive solution than your software.
FIGURE 3.2. Power as a Function of Sample Size. Test of the hypothesis that the prevalence in a population of a characteristic is 0.46 rather than 0.40.
If the data do not come from a well-tabulated distribution, then one might use a bootstrap to estimate the power and significance level.
In preliminary trials of a new device, test results of 7.0 were observed in 11 out of 12 cases and 3.3 in 1 out of 12 cases. Industry guidelines specified that any population with a mean test result greater than 5 would be acceptable. A worst-case or boundary-value scenario would include one in which the test result was 7.0, 3/7th of the time; 3.3, 3/7th of the time; and 4.1, 1/7th of the time.
The statistical procedure required us to reject if the sample mean of the test results were less than 6. To determine the probability of this event for various sample sizes, we took repeated samples with replacement from the two sets of test results. Some bootstrap samples consisted of all 7’s, some, taken from the worst-case distribution, only of 3’s. Most were a mixture. Table 3.2 illustrates the results; for example, in our trials, 23% of the bootstrap samples of size 3 from our starting sample of test results had medians less than 6.0. If we drew our bootstrap samples from the hypothetical worst-case population instead, then 84% had medians less than 6.
TABLE 3.2. Bootstrap estimates of Type I and Type II error
| Sample size | Test Mean < 6.0 | |
| α | Power | |
| 3 | 0.23 | 0.84 |
| 4 | 0.04 | 0.80 |
| 5 | 0.06 | 0.89 |
If you want to try your hand at duplicating these results, simply take the test values in the proportions observed, stick them in a hat, draw out bootstrap samples with replacement several hundred times, compute the sample means, and record the results. Or you could use the R or Stata bootstrap procedure, as we did.1
Determining sample size as we go (sequential sampling), rather than making use of a predetermined sample size, can have two major advantages:
When our experiments are destructive in nature (as in testing condoms) or may have an adverse effect upon the experimental subject (as in clinical trials), we prefer not to delay our decisions until some fixed sample size has been reached.
Figure 3.3 depicts a sequential trial of a new vaccine after eight patients who had received either the vaccine or an innocuous saline solution developed the disease. Each time a control patient came down with the disease, the jagged line was extended to the right. Each time a patient who had received the experimental vaccine came down with the disease, the jagged line was extended upward one notch. This experiment will continue until either of the following occurs:
FIGURE 3.3. Sequential Trial in Progress.
Reprinted from Good, Introduction to Statistics via Resampling Methods and R/SPlus, Copyright 2005, with the permission of John Wiley & Sons, Inc.
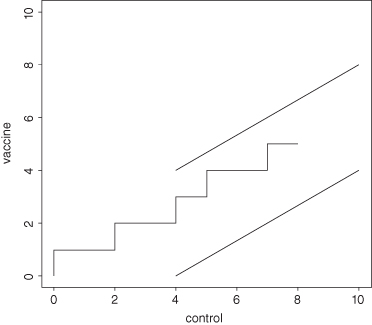
What Abraham Wald [1950] showed in his pioneering research was that, on average, the resulting sequential experiment would require many fewer observations whether or not the vaccine was effective than would a comparable experiment of fixed sample size.
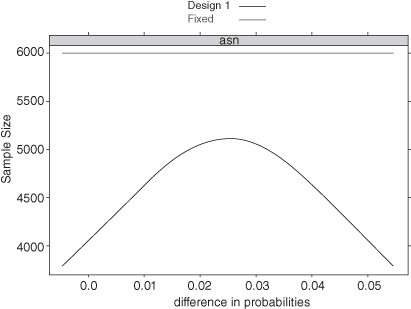
If the treatment is detrimental to the patient, we are likely to hit one of the lower boundaries early. If the treatment is far more efficacious than the control, we are likely to hit an upper boundary early. Even if the true difference is right in the middle between our two hypotheses—for example, because the treatment is only 2.5% better when the alternative hypothesis is that it is 5% better—we may stop early on occasion. Figure 3.4 shows the average sample size as a function of the difference in the probabilities of success for each treatment. When this difference is less than 0% or greater than 5%, we will need about 4000 observations on average before stopping. Even when the true difference is right in the middle, we will stop after about 5000 observations on average. In contrast, a fixed-sample design requires nearly 6000 observations for the same Type I error and power.
FIGURE 3.4. Average Sample Size as a Function of the Difference in Probability.
Reprinted from Good, Introduction to Statistics via Resampling Methods and R/SPlus, Copyright 2005, with the permission of John Wiley & Sons, Inc.
Warning: Simply performing a standard statistical test after each new observation as if the sample size were fixed will lead to inflated values of Type I error. The boundaries depicted in Figure 3.3 were obtained using formulas specific to sequential design. Not surprisingly, these formulas require us to know every one of the same factors we needed to determine the number of samples when the experiment is of fixed size.
A one-sided alternative (“Regular brushing with a fluoride toothpaste will reduce cavities”) requires a one-tailed or one-sided test. A two-sided alternative (“Which brand ought one buy?”) requires a two-tailed test. But it often can be difficult in practical situations to decide whether the real alternatives are one-sided or two-sided. Moyé [2000] provides a particularly horrifying illustration in his textbook Statistical Reasoning in Medicine (pp. 145–148) which, in turn, was extracted from Thomas Moore’s “Deadly Medicine” (pp. 203–204). It concerns a study of cardiac arrhythmia suppression, in which a widely used but untested therapy was at last tested in a series of controlled (randomized, double-blind) clinical trials [Greene et al., 1992].
The study had been set up as a sequential trial. At various checkpoints, the trial would be stopped if efficacy was demonstrated or if it became evident that the treatment was valueless. Though no preliminary studies had been made, the investigators did not plan for the possibility that the already widely used but untested treatment might be harmful. It was.
Fortunately, clinical trials have multiple endpoints, an invaluable resource, if the investigators choose to look at the data. In this case, a Data and Safety Monitoring Board (consisting of scientists not directly affiliated with the trial or the trial’s sponsors) noted that of 730 patients randomized to the active therapy, 56 died, whereas of the 725 patients randomized to placebo there were 22 deaths. They felt free to perform a two-sided test despite the fact that the original formulation of the problem was one-sided.
The relative ease with which a program like Stata or Power and Precision can produce a sample size may blind us to the fact that the number of subjects with which we begin a study may bear little or no relation to the number with which we conclude it.
A midsummer hailstorm, an early frost, or an insect infestation can lay waste to all or part of an agricultural experiment. In the National Institute of Aging’s first years of existence, a virus entirely wiped out a primate colony, destroying a multitude of experiments in progress.
Large-scale clinical trials and surveys have a further burden: the subjects themselves. Potential subjects can and do refuse to participate. (Do not forget to budget for a follow-up study, which is bound to be expensive, of responders versus nonresponders.) Worse, they may agree to participate initially, then drop out at the last minute (see Figure 3.5). They may move without a forwarding address before a scheduled follow-up, or may simply do not bother to show up for an appointment. Thirty percent of the patients who had received a life-saving cardiac procedure failed to follow up with their physician. (We cannot imagine not going in to see our surgeon after such a procedure, but then we guess we are not typical.)
FIGURE 3.5. A Typical Clinical Trial. Dropouts and non-compliant patients occur at every stage.
Reprinted from Good, The Manager’s Guide to Design and Conduct of Clinical Trials, Second Edition, Copyright 2006, with the permission of John Wiley & Sons, Inc.
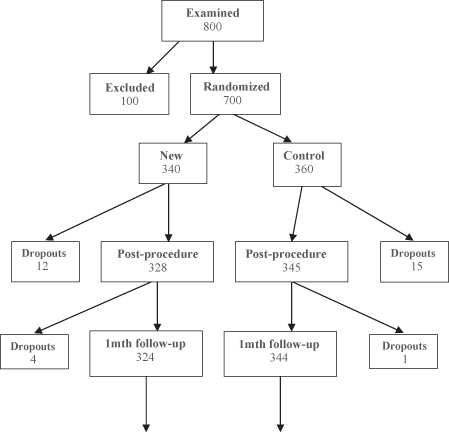
The key to a successful research program is to plan for such drop-outs in advance and to start the trials with some multiple of the number required to achieve a given power and significance level.
In a recent attempt to reduce epidemics at its training centers, the U.S. Navy vaccinated 50,000 recruits with an experimental vaccine and 50,000 others with a harmless saline solution. But at the halfway mark, with 50,000 inoculated and 50,000 to go, fewer than 500 had contracted the disease. The bottom line is, it is the sample you end with, not the sample you begin with, that determines the power of your tests.
An analysis of those who did not respond to a survey or a treatment can sometimes be as or more informative than the survey itself. See, for example, Mangel and Samaniego [1984] as well as the sections on the Behrens–Fisher problem and on the premature drawing of conclusions in Chapter 5. Be sure to incorporate in your sample design and in your budget provisions for sampling nonresponders.
Be sure you are sampling from the population as a whole rather than from an unrepresentative subset of the population. The most famous blunder along these lines was basing the forecast of Dewey over Truman in the 1948 U.S. presidential election on a telephone survey; those who owned a telephone and responded to the survey favored Dewey; those who voted did not.
An economic study may be flawed because we have overlooked the homeless. This was among the principal arguments the cities of New York and Los Angeles advanced against the use by the federal government of the 1990 and 2000 census to determine the basis for awarding monies to cities.2
An astrophysical study was flawed because of overlooking galaxies whose central surface brightness was very low.3 The FDA’s former policy of excluding women (those tender creatures) from clinical trials was just plain foolish.
Baggerly and Coombes [2009] examined several clinical trials in which patients were allocated to treatment arms on the basis of microarray-based signatures of drug sensitivity. Because the microarray studies often were poorly described or analyzed in error, the clinical trials results were rendered ambiguous.
In contributing to a plaintiff’s lawsuit following a rear-end collision, Good [2009] noted that while the plaintiff was in her fifties and had been injured previously; the studies relied on by the defendant’s biomechanical expert involved only much younger individuals with no prior history of injury.
Plaguing many surveys are the uncooperative and the nonresponder. Invariably, follow-up surveys of these groups show substantial differences from those who responded readily the first time around. These follow-up surveys are not inexpensive; compare the cost of mailing out a survey to telephoning or making face-to-face contact with a nonresponder. But if one does not make these calls, one may get a completely unrealistic picture of how the population as a whole would respond.
Most statistical procedures rely on two fundamental assumptions: that the observations are independent of one another and that they are identically distributed. If your methods of collection fail to honor these assumptions, then your analysis must fail also.
To ensure the independence of responses in a return-by-mail or return-by-Web survey, no more than one form per household should be accepted. If a comparison of the responses within a household is desired, then the members of the household should be interviewed separately, outside of each other’s hearing and with no opportunity to discuss the survey in between. People care what other people think and when asked about an emotionally charged topic may or may not tell the truth. In fact, they are unlikely to tell the truth if they feel that others may overhear or somehow learn of their responses.
To ensure independence of the observations in an experiment, determine in advance what constitutes the experimental unit.
In the majority of cases, the unit is obvious: one planet means one position in space, one container of gas means one volume and pressure to be recorded, one runner on one fixed racecourse means one elapsed time.
In a clinical trial, each individual patient corresponds to a single set of observations, or does she? Suppose we are testing the effects of a topical ointment on pink eye. Is each eye a separate experimental unit or each patient?
It is common in toxicology to examine a large number of slides, but regardless of how many are examined in the search for mutagenic and toxic effects, if all slides come from a single treated animal, then the total size of the sample is one.
We may be concerned with the possible effects a new drug might have on a pregnant woman and, as critically, on her children. In our preliminary tests, we will be working with mice. Is each fetus in the litter a separate experimental unit? or each mother?
If the mother is the one treated with the drug, then the mother is the experimental unit, not the fetus. A litter of six or seven corresponds only to a sample of size one.
As for the topical ointment, while more precise results might be obtained by treating only one eye with the new ointment and recording the subsequent difference in appearance between the treated and untreated eyes, each patient still yields only one observation, not two.
If you change measuring instruments during a study or change observers, then you will have introduced an additional source of variation and the resulting observations will not be identically distributed.
The same problems will arise if you discover during the course of a study (as is often the case) that a precise measuring instrument is no longer calibrated and readings have drifted. To forestall this, any measuring instrument should have been exposed to an extensive burn-in before the start of a set of experiments and should be recalibrated as frequently as the results of the burn-in or prestudy period dictate.
Similarly, one does not just mail out several thousands copies of a survey before performing an initial pilot study to weed out or correct ambiguous and misleading questions.
The following groups are unlikely to yield identically distributed observations: the first to respond to a survey, those who only respond after been offered an inducement, and nonresponders.
Statisticians have found three ways for coping with individual-to-individual and observer-to-observer variation:
Steps one and two are trickier than they appear at first glance. Do the phenomena under investigation depend upon the time of day, as with body temperature and the incidence of mitosis? Upon the day of the week, as with retail sales and the daily mail? Will the observations be affected by the sex of the observer? Primates (including you) and hunters (tigers, mountain lions, domestic cats, dogs, wolves, and so on) can readily detect the observer’s sex.4
Blocking may be mandatory as even a randomly selected sample may not be representative of the population as a whole. For example, if a minority comprises less than 10% of a population, then a jury of 12 persons selected at random from that population will fail to contain a single member of that minority at least 28% of the time.
Groups to be compared may differ in other important ways even before any intervention is applied. These baseline imbalances cannot be attributed to the interventions, but they can interfere with and overwhelm the comparison of the interventions.
One good after-the-fact solution is to break the sample itself into strata (men, women, Hispanics) and to extrapolate separately from each stratum to the corresponding subpopulation from which the stratum is drawn.
The size of the sample we take from each block or stratum need not and, in some instances should not, reflect the block’s proportion in the population. The latter exception arises when we wish to obtain separate estimates for each subpopulation. For example, suppose we are studying the health of Marine recruits and we wish to obtain separate estimates for male and female Marines as well as for Marines as a group. If we want to establish the incidence of a relatively rare disease, we will need to oversample female recruits to ensure that we obtain a sufficiently large number. To obtain a rate R for all Marines, we would then take the weighted average pFRF + pMRM of the separate rates for each gender, where the proportions pM and pF are those of males and females in the entire population of Marine recruits.
Fujita et al. [2000] compared the short-term effect of AAACa and CaCO3 on bone density in humans. But at the start of the experiment, the bone densities of the CaCO3 group were significantly greater than the bone densities of the AAACa group and the subjects were significantly younger. Thus, the reported changes in bone density could as easily be attributed to differences in age and initial bone density as to differences in the source of supplemental calcium. Clearly, the subjects ought to have been blocked by age and initial bone density before they were randomized to treatment.
In the next few sections on experimental design, we may well be preaching to the choir, for which we apologize. But there is no principle of experimental design, however obvious, however intuitive, that someone will not argue can be ignored in his or her special situation:
The statistician’s lot is not a happy one. The opposite sex ignores us because we are boring5 and managers hate us because all our suggestions seem to require an increase in the budget. But controls will save money in the end. Blinding is essential if our results are to have credence, and care in treatment allocation is mandatory if we are to avoid bias.
Permitting treatment allocation by either experimenter or subject will introduce bias. On the other hand, if a comparison of baseline values indicates too wide a difference between the various groups in terms of concomitant variables, then you will either need to rerandomize or to stratify the resulting analysis. Be proactive: stratify before you randomize, randomizing separately within each strata.
The efforts of Fujita et al. [2000] were doomed before they started as the placebo-treated group was significantly younger (6 subjects of 50 ± 5 years of age) than the group that had received the treatment of greatest interest (10 subjects of 60 ± 4 years of age).
On the other hand, the study employing case controls conducted by Roberts et al. [2007] could have been rescued had they simply included infant sex as one of the matching variables. For whereas 85% of the cases of interest were male, only 51% of the so-called matched case controls were of that sex.
To guard against the unexpected, as many or more patients should be assigned to the control regimen as are assigned to the experimental one. This sounds expensive and it is. But things happen. You get the flu. You get a headache or diarrhea. You have a series of colds that blend one into the other until you can not remember the last time you were well. So you blame your silicone implants. Or, if you are part of a clinical trial, you stop taking the drug. It is in these and similar instances that experimenters are grateful they have included controls. Because when the data are examined, experimenters learn that as many of the control patients came down with the flu as those who were on the active drug, and that women without implants had exactly the same incidence of colds and headaches as those who had implants.
Reflect on the consequences of not using controls. The first modern silicone implants (Dow Corning’s Silastic mammary prosthesis) were placed in 1962. In 1984, a jury awarded $2 million to a recipient who complained of problems resulting from the implants. Award after award followed, the largest being more than $7 million. A set of controlled randomized trials was finally initiated in 1994. The verdict: Silicon implants have no adverse effects on recipients. Tell this to the stockholders of bankrupt Dow Corning.
Use positive controls.
There is no point in conducting an experiment if you already know the answer.6 The use of a positive control is always to be preferred. A new antiinflammatory should be tested against aspirin or ibuprofen. And there can be no justification whatever for the use of placebo in the treatment of a life-threatening disease [Barbui et al., 2000; Djulbegovic et al., 2000].
Observers should be blinded to the treatment allocation.
Patients often feel better solely because they think they ought to feel better. A drug may not be effective if the patient is aware it is the old or less-favored remedy, nor is the patient likely to keep taking a drug on schedule if he or she feels the pill contains nothing of value. She is also less likely to report any improvement in her condition if she feels the doctor has done nothing for her. Vice versa, if a patient is informed she has the new treatment she may think it necessary to please the doctor by reporting some diminishment in symptoms. These sorts of behavioral phenomena are precisely the reason why clinical trials must include a control.
A double-blind study in which neither the physician nor the patient knows which treatment is received is preferable to a single-blind study in which only the patient is kept in the dark [Ederer, 1975; Chalmers, et al., 1983; Vickers, et al., 1997].
Even if a physician has no strong feelings one way or the other concerning a treatment, she may tend to be less conscientious about examining patients she knows belong to the control group. She may have other unconscious feelings that influence her work with the patients. Exactly the same caveats apply in work with animals and plants; units subjected to the existing, less-important treatment may be handled more carelessly and be less thoroughly examined.
We recommend that you employ two or even three individuals: one to administer the intervention, one to examine the experimental subject, and a third to observe and inspect collateral readings such as angiograms, laboratory findings, and x-rays that might reveal the treatment.
Without allocation concealment, selection bias can invalidate study results [Schultz, 1995; Schulz et al., 1995; Berger and Exner, 1999]. If an experimenter could predict the next treatment to be assigned, he might exercise an unconscious bias in the treatment of that patient; he might even defer enrollment of a patient he considers less desirable. In short, randomization alone, without allocation concealment, is insufficient to eliminate selection bias and ensure the internal validity of randomized clinical trials.
Lovell et al. [2000] describe a study in which four patients were randomized to the wrong stratum; in two cases, the treatment received was reversed. For an excruciatingly (and embarrassingly) detailed analysis of this experiment by an FDA regulator, see http://www.fda.gov/cder/biologics/review/etanimm052799r2.pdf.
Vance Berger and Costas Christophi offer the following guidelines for treatment allocation:
Berger [2005] notes that in unmasked trials (which are common when complementary and alternative medicines are studied), “the primary threat to allocation concealment is not the direct observation, but rather the prediction of future allocations based on the patterns in the allocation sequence that are created by the restrictions used on the randomization process.”
All the above caveats apply to these procedures as well. The use of an advanced statistical technique does not absolve its users from the need to exercise common sense. Observers must be kept blinded to the treatment received.
Do not be too clever. Factorial experiments make perfect sense when employed by chemical engineers, as do the Greco-Latin squares used by agronomists. But social scientists should stay well clear of employing them in areas that are less well understood than chemistry and agriculture.
Fukada [1993] reported, “Fifteen female rats were divided into three groups at the age of 12 months. Ten rats were ovariectimized and five of them were fed a diet containing 1% Ca as AAACa and the other five rats were fed a low-Ca diet containing 0.03% calcium. The remaining five rats were fed a control diet containing 1% Ca as CaCO3 as the control group.” Putting this description into an experimental design matrix yields the following nonsensical result:
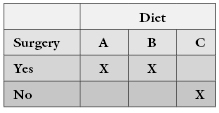
In the case of rare diseases and other rare events, it is tempting to begin with the data in hand, that is, the records of individuals known to have the disease rather than to draw a random and expensive sample from the population at large. There is a right way and a wrong way to conduct such studies.
The wrong way is to reason backward from effect to cause. Suppose that the majority of victims of pancreatic cancer are coffee drinkers. Does this mean that coffee causes pancreatic cancer? Not if the majority of individuals in the population in which the cases occurred are coffee drinkers also.
To be sure, suppose we create a set of case controls, matching each individual in the pancreatic data base with an individual in the population at large of identical race, sex, and age and with as many other near matching characteristics as the existing data can provide. We could then compare the incidence of coffee drinkers in the cancer database with the incidence in the matching group of case controls.
Good [2006] provides a series of anecdotes concerning the mythical Bumbling Pharmaceutical and Device Company that amply illustrate the results of inadequate planning. See also Andersen [1990] and Elwood [1998]. The opening chapters of Good [2001] contain numerous examples of courtroom challenges based on misleading or inappropriate samples. See also Copas and Li [1997] and the subsequent discussion.
Definitions and a further discussion of the interrelation among power and significance level may be found in Lehmann [1986], Casella and Berger [1990], and Good [2001]. You will also find discussions of optimal statistical procedures and their assumptions.
Lachin [1998], Lindley [1997], and Linnet [1999] offer guidance on sample size determination. Shuster [1993] provides sample size guidelines for clinical trials. A detailed analysis of bootstrap methodology is provided in Chapters 5 and 7 of this book.
Rosenberger and Lachin [2002] and Schulz and Grimes [2002] discuss randomization and blinding in clinical trials.
Recent developments in sequential design include group sequential designs, which involve testing not after every observation, as in a fully sequential design, but rather after groups of observations, for example, after every 6 months in a clinical trial. The design and analysis of such experiments is best done using specialized software such as S+SeqTrial from http://spotfire.tibco.com/products/s-plus/statistical-analysis-software.aspx. For further insight into the principles of experimental design, light on math and complex formulas but rich in insight, are the lessons of the masters: Fisher [1935, 1973] and Neyman [1952]. If formulas are what you desire, see Hurlbert [1984], Jennison and Turnbull [1999], Lachin [1998], Lindley [1997], Linnet [1999], Montgomery and Myers [1995], Rosenbaum [2002], Thompson and Seber [1996], and Toutenburg [2002].
Among the many excellent texts on survey design are Fink and Kosecoff [1988], Rea, Parker, and Shrader [1997], and Cochran [1977]. For tips on formulating survey questions, see Converse and Presser [1986], Fowler and Fowler [1995], and Schroeder [1987]. For tips on improving the response rate, see Bly [1990, 1996].
Notes
1 Chapters 5–8 provide more information on the bootstrap and its limitations.
2 City of New York v. Dept of Commerce, 822 F. Supp. 906 (E.D.N.Y., 1993).
3 Bothun [1998; p. 249]
4 The hair follicles of redheads—genuine, not dyed—are known to secrete a prostaglandin similar to an insect pheromone.
5 Dr. Good told his wife he was an author; it was the only way he could lure someone that attractive to his side. Dr. Hardin is still searching for an explanation for his own good fortune.
6 The exception being to satisfy a regulatory requirement.