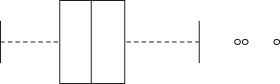
FIGURE 5.1. Boxplot of Heights of Sixth-Graders.
Chapter 5
Estimation
Can a man drown while crossing a stream with an average depth of six inches?
—W.I.E. Gates
ACCURATE, RELIABLE ESTIMATES ARE ESSENTIAL TO EFFECTIVE DECISION making. In this chapter, we review preventive measures and list the properties to look for in an estimation method. Several robust semiparametric estimators are considered along with one method of interval estimation, the bootstrap.
The vast majority of errors in estimation stem from a failure to measure what was wanted or what was intended. Misleading definitions, inaccurate measurements, errors in recording and transcription, and confounding variables plague results.
To prevent such errors, review your data collection protocols and procedure manuals before you begin, run several preliminary trials, record potential confounding variables, monitor data collection, and review the data as they are collected.
Before beginning to analyze data you have collected, establish the provenance of the data: Is it derived from a random sample? From a representative one?
Your first step should be to construct a summary of the data in both tabular and graphic form. Both should display the minimum, 25th percentile, median, mean, 75th percentile, and maximum of the data. This summary will usually suggest the estimators you will need.
Use a box plot rather than a stem-and-leaf diagram. The latter is an artifact of a time when people would analyze data by hand. Though stem-and leaf diagrams are relatively easy to manually construct for a small or moderate size dataset, a computer can generate a box plot like that shown in Figure 5.1 in a fraction of the time.
FIGURE 5.1. Boxplot of Heights of Sixth-Graders.
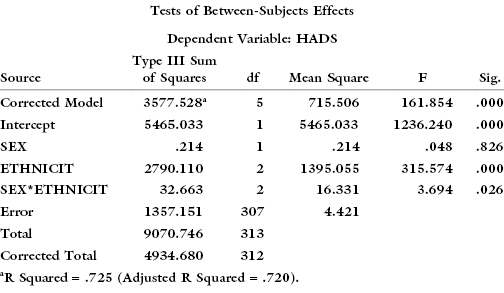
Do not be misled by aggregate statistics. David C. Howell reported the results of a study of depression as measured on the HADS (Hospital Anxiety and Depression Scale). The group statistics suggest major differences between the sexes:
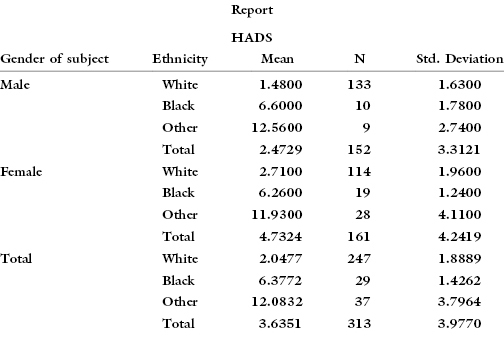
But a more thorough analysis of the data, taking both sex and ethnicity into consideration, yields quite a different picture:
The apparent difference between the sexes in the incidence of depression is merely an artifact of the difference in ethnic composition of the two samples:
Any method of estimation must be appropriate to the distribution of the data that is to be estimated. A frequent error in the astrophysical literature is to apply methods appropriate for data from a continuous distribution—such as the normal or multivariate normal distribution—to discrete data. Often, such data are comprised of counts of events (over space and/or time) that may well be more appropriately characterized by a Poisson distribution.
The data may have been drawn from several different distributions (as in data that is derived from both men and women). In such a case, it must be estimated by a finite mixture model that would estimate parameters from component distributions, or the data should be divided into two or more strata prior to being analyzed. Of course, the strata should also be appropriate for the data in hand.
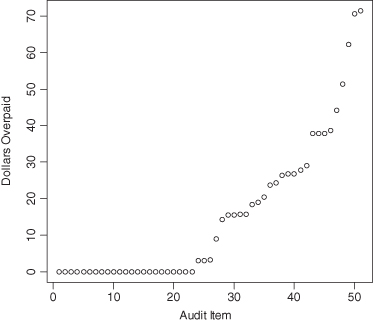
We are often given access to data arising from audits of submissions by Medicare practitioners. The distribution of one such sample is depicted in Figure 5.2. It can be seen that the sample divides into two populations: those without errors and those with. An appropriate method of analysis would consist of two stages. In the first, an attempt would be made to obtain a lower confidence bound for the proportion of errors. At the second stage, a lower confidence bound for the expected value of an error must be obtained.
FIGURE 5.2. Medicare Overpayments.
The method of maximum likelihood is by far the most popular technique for deriving estimators.
—Casella and Berger [1990, p. 289].
The proper starting point for the selection of the best method of estimation is with the objectives of our study: What is the purpose of our estimate? If our estimate is θ* and the actual value of the unknown parameter is θ, what losses will we be subject to? It is difficult to understand the popularity of the method of maximum likelihood and other estimation procedures that do not take these losses into consideration.
The majority of losses will be monotonically nondecreasing in nature, that is, the further apart the estimate θ* and the true value θ, the larger our losses are likely to be. Typical forms of the loss function are the absolute deviation |θ* – θ|, the square deviation (θ* − θ)2, and the jump, that is, no loss if |θ* − θ| < i, and a big loss otherwise. Or the loss function may resemble the square deviation but take the form of a step function increasing in discrete increments.
Desirable estimators share the following properties: impartial, consistent, efficient, robust, and minimum loss.
Estimation methods should be impartial. Decisions should not depend on the accidental and quite irrelevant labeling of the samples. Nor should decisions depend on the units in which the measurements are made.
Suppose we have collected data from two samples with the object of estimating the difference in location of the two populations involved. Suppose further that the first sample includes the values a, b, c, d, and e, the second sample the values f, g, h, i, j, and k, and our estimate of the difference is θ*. If the observations are completely reversed, that is, if the first sample includes the values f, g, h, i, j, and k and the second sample the values a, b, c, d, and e, our estimation procedure should declare the difference to be −θ*.
The units we use in our observations should not affect the resulting estimates. We should be able to take a set of measurements in feet, convert to inches, make our estimate, convert back to feet, and get absolutely the same result as if we had worked in feet throughout. Similarly, where we locate the zero point of our scale should not affect the conclusions.
Finally, if our observations are independent of the time of day, the season, and the day on which they were recorded (facts that ought to be verified before proceeding further), then our estimators should be independent of the order in which the observations were collected.
Estimators should be consistent, that is, the larger the sample, the greater the probability the resultant estimate will be close to the true population value.
One consistent estimator certainly is to be preferred to another if the first consistent estimator can provide the same degree of accuracy with fewer observations. To simplify comparisons, most statisticians focus on the asymptotic relative efficiency (ARE), defined as the limit with increasing sample size of the ratio of the number of observations required for each of two consistent statistical procedures to achieve the same degree of accuracy.
Estimators that are perfectly satisfactory for use with symmetric, normally distributed populations may not be as desirable when the data come from nonsymmetric or heavy-tailed populations, or when there is a substantial risk of contamination with extreme values.
When estimating measures of central location, one way to create a more robust estimator is to trim the sample of its minimum and maximum values (the procedure used when judging ice skating or gymnastics). As information is thrown away, trimmed estimators are less efficient.
In many instances, LAD (least absolute deviation) estimators are more robust than their LS counterparts.1 This finding is in line with our discussion of the F-statistic in the preceding chapter.
Many semiparametric estimators are not only robust but provide for high ARE with respect to their parametric counterparts.
As an example of a semiparametric estimator, suppose the {Xi} are independent identically distributed (i.i.d.) observations with distribution Pr{Xi ≤ x} = F[y − Δ] and we want to estimate the location parameter Δ without having to specify the form of the distribution F. If F is normal and the loss function is proportional to the square of the estimation error, then the arithmetic mean is optimal for estimating Δ. Suppose, on the other hand, that F is symmetric but more likely to include very large or very small values than a normal distribution. Whether the loss function is proportional to the absolute value or the square of the estimation error, the median, a semiparametric estimator, is to be preferred. The median has an ARE relative to the mean that ranges from 0.64 (if the observations really do come from a normal distribution) to values well in excess of 1 for distributions with higher proportions of very large and very small values (Lehmann, 1998, p. 242). Still, if the unknown distribution were “almost” normal, the mean would be far more preferable.
If we are uncertain whether F is symmetric, then our best choice is the Hodges–Lehmann estimator, defined as the median of the pairwise averages:
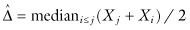
Its ARE relative to the mean is 0.97 when F is a normal distribution (Lehmann, 1998, p. 246). With little to lose with respect to the sample mean if F is near normal, and much to gain if F is not, the Hodges–Lehmann estimator is recommended.
Suppose m observations {Xi} and n observations {Yj} are i.i.d. with distributions Pr{Xi ≤ x} = F[x] and Pr{Yj ≤ y} = F[y − Δ], and we want to estimate the shift parameter Δ without having to specify the form of the distribution F. For a normal distribution F, the optimal estimator with least square losses is
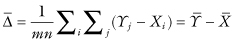
the arithmetic average of the mn differences Yj − Xi. Means are highly dependent on extreme values; a more robust estimator is given by
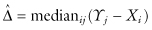
The accuracy of an estimate, that is, the degree to which it comes close to the true value of the estimated parameter, and the associated losses will vary from sample to sample. A minimum loss estimator is one that minimizes the losses when the losses are averaged over the set of all possible samples. Thus, its form depends upon all of the following: the loss function, the population from which the sample is drawn, and the population characteristic that is being estimated. An estimate that is optimal in one situation may only exacerbate losses in another.
Minimum loss estimators in the case of least-square losses are widely and well documented for a wide variety of cases. Linear regression with an LAD loss function is discussed in Chapter 12.
It is easy to envision situations in which we are less concerned with the average loss than with the maximum possible loss we may incur by using a particular estimation procedure. An estimate that minimizes the maximum possible loss is termed a mini–max estimator. Alas, few off-the-shelf mini–max solutions are available for practical cases, but see Pilz [1991] and Pinelis [1988].
The expected value of an unbiased estimator is the population characteristic being estimated. Thus, unbiased estimators are also consistent estimators.
Minimum variance estimators provide relatively consistent results from sample to sample. Although minimum variance is desirable, it may be of practical value only if the estimator is also unbiased. For example, 6 is a minimum variance estimator but offers few other advantages.
A plug-in estimator substitutes the sample statistic for the population statistic for example, the sample mean for the population mean, or the sample’s 20th percentile for the population’s 20th percentile. Plug-in estimators are consistent, but they are not always unbiased nor minimum loss.
Always choose an estimator that will minimize losses.
The popularity of the maximum likelihood estimator is hard to comprehend other than as a vehicle whereby an instructor can demonstrate knowledge of the calculus. This estimator may be completely unrelated to the loss function and has as its sole justification that it corresponds to that value of the parameter that makes the observations most probable—providing, that is, they are drawn from a specific predetermined (and unknown) distribution. The observations might have resulted from a thousand other a prior-possibilities.
A common and lamentable fallacy is that the maximum likelihood estimator has many desirable properties—that it is unbiased and minimizes the mean-squared error. But this is true only for the maximum likelihood estimator of the mean of a normal distribution.2
Statistics instructors would be well advised to avoid introducing maximum likelihood estimation and to focus instead on methods for obtaining minimum loss estimators for a wide variety of loss functions.
Brother Adel—who, I will hazard a guess, is a statistician—sent me a message criticizing my emails for being of varying lengths and not symmetrical like the hems of dresses in vogue this year. Adel says that in order for the lengths of my emails to be even, they must show evidence of natural distribution. According to him, natural distribution means that 95 percent of the data contained therein will center around the mean (taking into consideration of course the standard deviation), while the percentage of data outside the area of normal distribution on both sides of the mean does not exceed 2.5 percent in either direction, such that the sum total of standard deviation is 5 percent.
—Rajaa Alsanea in The Girls of Ryadh
Point estimates are seldom satisfactory in and of themselves. First, if the observations are continuous, the probability is zero that a point estimate will be correct and equal the estimated parameter. Second, we still require some estimate of the precision of the point estimate.
In this section, we consider one form of interval estimate derived from bootstrap measures of precision. A second form, derived from tests of hypotheses, will be considered in the next chapter.
A common error is to create a confidence interval of the form (estimate − k * standard error, estimate + k * standard error). This form is applicable only when an interval estimate is desired for the mean of a normally distributed random variable. Even then, k should be determined from tables of the Student’s t-distribution and not from tables of the normal distribution.
The bootstrap can help us obtain an interval estimate for any aspect of a distribution—a median, a variance, a percentile, or a correlation coefficient—if the observations are independent and all come from distributions with the same value of the parameter to be estimated. This interval provides us with an estimate of the precision of the corresponding point estimate.
From the original sample, we draw a random sample (with replacement); this random sample is called a bootstrap sample. The random sample is the same size as the original sample and is used to compute the sample statistic. We repeat this process a number of times, 1000 or so, always drawing samples with replacement from the original sample. The collection of computed statistics for the bootstrap samples serves as an empirical distribution of the sample statistic of interest, to which we compare the value of the sample statistic computed from the original sample.
For example, here are the heights of a group of 22 adolescents, measured in centimeters and ordered from shortest to tallest:
137.0 138.5 140.0 141.0 142.0 143.5 145.0 147.0 148.5
150.0 153.0 154.0 155.0 156.5 157.0 158.0 158.5 159.0
160.5 161.0 162.0 167.5
The median height lies somewhere between 153 and 154 centimeters. If we want to extend this result to the population, we need an estimate of the precision of this average.
Our first bootstrap sample, arranged in increasing order of magnitude for ease in reading, might look like this:
138.5 138.5 140.0 141.0 141.0 143.5 145.0 147.0 148.5 150.0 153.0
154.0 155.0 156.5 157.0 158.5 159.0 159.0 159.0 160.5 161.0 162.
Several of the values have been repeated, which is not surprising as we are sampling with replacement, treating the original sample as a stand-in for the much larger population from which the original sample was drawn. The minimum of this bootstrap sample is 138.5, higher than that of the original sample; the maximum at 162.0 is less than the original, whereas the median remains unchanged at 153.5.
137.0 138.5 138.5 141.0 141.0 142.0 143.5 145.0 145.0 147.0 148.5
148.5 150.0 150.0 153.0 155.0 158.0 158.5 160.5 160.5 161.0 167.5
In this second bootstrap sample, again we find repeated values; this time the minimum, maximum, and median are 137.0, 167.5, and 148.5, respectively.
The medians of fifty bootstrapped samples drawn from our sample ranged between 142.25 and 158.25 with a median of 152.75 (see Figure 5.3). These numbers provide an insight into what might have been had we sampled repeatedly from the original population.
We can improve on the interval estimate {142.25, 158.25} if we are willing to accept a small probability that the interval will fail to include the true value of the population median. We will take several hundred bootstrap samples instead of a mere 50, and use the 5th and 95th percentiles of the resulting bootstrap (empirical) distribution to establish the boundaries of a 90% confidence interval.
This method might be used equally well to obtain an interval estimate for any other population attribute: the mean and variance, the fifth percentile or the twenty-fifth, and the interquartile range. When several observations are made simultaneously on each subject, the bootstrap can be used to estimate covariances and correlations among the variables. The bootstrap is particularly valuable when trying to obtain an interval estimate for a ratio or for the mean and variance of a nonsymmetric distribution.
Unfortunately, such intervals have two deficiencies:
Two methods have been proposed to correct these deficiencies; let us consider each in turn.
The first is the Hall–Wilson [1991] corrections, in which the bootstrap estimate is Studentized. For the one-sample case, we want an interval estimate based on the distribution of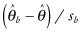 
, where 
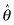and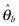 
are the estimates of the unknown parameter based on the original and bootstrap sample, respectively, and sb denotes the standard deviation of the bootstrap sample. An estimate 
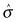of the population variance is required to transform the resultant interval into one about θ (see Carpenter and Bithell, 2000).
For the two-sample case, we want a confidence interval based on the distribution of
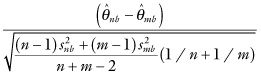
where n, m, and snb, smb denote the sample sizes and standard deviations, respectively, of the bootstrap samples. Applying the Hall–Wilson corrections, we obtain narrower interval estimates. Even though this interval estimate is narrower, it is still more likely to contain the true value of the unknown parameter.
The bias-corrected and accelerated BCa interval due to Efron and Tibshirani [1986] also represents a substantial improvement, though for samples under size 30 the properties of the interval are still suspect. The idea behind these intervals comes from the observation that percentile bootstrap intervals are most accurate when the estimate is symmetrically distributed about the true value of the parameter and the tails of the estimate’s distribution drop off rapidly to zero. The symmetric, bell-shaped normal distribution depicted in Figure 5.4 represents this ideal.
FIGURE 5.4. Bell-shaped symmetric curve of a normal distribution.
Suppose θ is the parameter we are trying to estimate,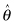 
is the estimate, and we establish a monotonically increasing transformation m such that m(θ) is normally distributed about 
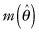. We could use this normal distribution to obtain an unbiased confidence interval, and then apply a back-transformation to obtain an almost-unbiased confidence interval.3 That we discovered and implemented a monotone transformation is what allows us to invert that function to transform the interval based on normality back to the original (possibly asymmetric and platykurtotic) distribution. Even with these modifications, we do not recommend the use of the nonparametric bootstrap with samples of fewer than 100 observations. Simulation studies suggest that with small sample sizes, the coverage is far from exact and the endpoints of the intervals vary widely from one set of bootstrap samples to the next. For example, Tu and Zhang [1992] report that with samples of size 50 taken from a normal distribution, the actual coverage of an interval estimate rated at 90% using the BCα bootstrap is 88%. When the samples are taken from a mixture of two normal distributions (a not uncommon situation with real-life datasets), the actual coverage is 86%. With samples of only 20 in number, the actual coverage is only 80%.
More serious than the disappointing coverage probabilities discussed is that the endpoints of the resulting interval estimates from the bootstrap may vary widely from one set of bootstrap samples to the next. For example, when Tu and Zhang drew samples of size 50 from a mixture of normal distributions, the average of the left limit of 1000 bootstrap samples taken from each of 1000 simulated datasets was 0.72 with a standard deviation of 0.16; the average and standard deviation of the right limit were 1.37 and 0.30, respectively.
Even when we know the form of the population distribution, the use of the parametric bootstrap to obtain interval estimates may prove advantageous either because the parametric bootstrap provides more accurate answers than textbook formulas or because no textbook formulas exist.
Suppose we know the observations that come from a normal distribution and want an interval estimate for the standard deviation. We would draw repeated bootstrap samples from a normal distribution the mean of which is the sample mean and the variance of which is the sample variance. As a practical matter, we would draw an element from a N(0,1) population, multiply by the sample standard deviation, then add the sample mean to obtain an element of our bootstrap sample. By computing the standard deviation of each bootstrap sample, an interval estimate for the standard deviation of the population may be constructed from the collection of statistics.
Of course, if the observations do not have a normal distribution, as would be the case with counts in a contingency table, treating the data as if they were from a normal distribution (see Tollenaar and Mooijaart, 2003) can only lead to disaster.
In many instances, we can obtain narrower interval estimates that have a greater probability of including the true value of the parameter by focusing on sufficient statistics, pivotal statistics, and admissible statistics.
A statistic T is sufficient for a parameter if the conditional distribution of the observations given this statistic T is independent of the parameter. If the observations in a sample are exchangeable, then the order statistics of the sample are sufficient; that is, if we know the order statistics x(1) ≤ x(2) ≤ … ≤ x(n), then we know as much about the unknown population distribution as we would if we had the original sample in hand. If the observations are on successive independent binomial trials that result in either success or failure, then the number of successes is sufficient to estimate the probability of success. The minimal sufficient statistic that reduces the observations to the fewest number of discrete values is always preferred.
A pivotal quantity is any function of the observations and the unknown parameter that has a probability distribution that does not depend on the parameter. The classic example is the Student’s t, whose distribution does not depend on the population mean or variance when the observations come from a normal distribution.
A decision procedure d based on a statistic T is admissible with respect to a given loss function L, providing there does not exist a second procedure d* whose use would result in smaller losses whatever the unknown population distribution.
The importance of admissible procedures is illustrated in an expected way by Stein’s paradox. The sample mean, which plays an invaluable role as an estimator of the population mean of a normal distribution for a single set of observations, proves to be inadmissible as an estimator when we have three or more independent sets of observations to work with. Specifically, if {Xij} are independent observations taken from four or more distinct normal distributions with means θi and variance 1, and losses are proportional to the square of the estimation error, then the estimators
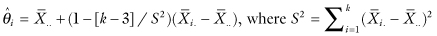
have smaller expected losses than the individual sample means, regardless of the actual values of the population means (see Efron and Morris, 1977).
Desirable estimators are impartial, consistent, efficient, robust, and minimum loss. Interval estimates are to be preferred to point estimates; they are less open to challenge for they convey information about the estimate’s precision.
Selecting more informative endpoints is the focus of Berger [2002] and Bland and Altman [1995].
Lehmann and Casella [1998] provide a detailed theory of point estimation.
Robust estimators are considered in Huber [1981], Maritz [1996], and Bickel et al. [1993]. Additional examples of both parametric and nonparametric bootstrap estimation procedures may be found in Efron and Tibshirani [1993]. Shao and Tu [1995; Section 4.4] provide a more extensive review of bootstrap estimation methods along with a summary of empirical comparisons.
Carroll and Ruppert [2000] show how to account for differences in variances between populations; this is a necessary step if one wants to take advantage of Stein–James–Efron–Morris estimators.
Bayes estimators are considered in Chapter 7.
Notes
1 See, for example, Yoo [2001].
2 It is also true in some cases for very large samples. How large the sample must be in each case will depend both upon the parameter being estimated and the distribution from which the observations are drawn.
3 Stata™ provides for bias-corrected intervals via its bstrap command. R and S-Plus both include BCa functions. A SAS macro is available at http://cuke.hort.ncsu.edu/cucurbit/wehner/software/pathsas/jackboot.txt.
