Chapter 6
Testing Hypotheses: Choosing a Test Statistic
Forget “large-sample” methods. In the real world of experiments, samples are so nearly always “small” that it is not worth making any distinction, and small-sample methods are no harder to apply.
—George Dyke [1997].
Statistical tests should be chosen before the data are analyzed, and the choice should be based on the study design and distribution of the data, not the results.
—Cara H. Olsen
LIFE CONSTANTLY FORCES US TO MAKE DECISIONS. IF life were not so uncertain, the “correct” choice always would be obvious. But life is not certain and the choice is not obvious. As always, proper application of statistical methods can help us to cope with uncertainty, but cannot eliminate it.
In the preceding chapter on estimation, our decision consisted of picking one value or one interval out of an unlimited number of possibilities. Each decision had associated with it a potential loss, an amount that increased as the difference between the correct decision and our decision increased.
In this chapter on hypothesis testing, our choices reduce to three possibilities:
Among the most common errors in (prematurely) published work is the failure to recognize that the last decision listed above is the correct one.
Before we can apply statistical methods properly, we need to establish all of the following:
Moreover, all these steps must be completed before the data are examined.
The first step allows us to select a testing procedure that maximizes the probability of detecting such alternatives. For example, if our primary hypothesis in a k-sample comparison is that the means of the k populations from which the samples are taken are the same, and the alternative is that we anticipate an ordered dose response, then the optimal test will be based on the correlation between the doses and the responses, and not the F-ratio of the between-sample and within-sample variances.
If we fail to complete step 2, we also risk selecting a less-powerful statistic. Suppose, once again, we are making a k-sample comparison of means. If our anticipated losses are proportional to the squares of the differences among the population means, then our test should be based on the F-ratio of the between-sample and within-sample variances. But if our anticipated losses are proportional to the absolute values of the differences among the population means, then our test should be based on the ratio of the between-sample and within-sample absolute deviations.
Several commercially available statistical packages automatically compute the p-values associated with several tests of the same hypothesis, for example, that of the Wilcoxon and the t-test. Rules 3 and 4 state the obvious. Rule 3 reminds us that the type of test to be employed will depend upon the type of data to be analyzed—binomial trials, categorical data, ordinal data, measurements, and time to events. Rule 4 reminds us that we are not free to pick and choose the p-value that best fits our preconceptions but must specify the test we employ before we look at the results.
Collectively, rules 1 through 5 dictate that we need always specify whether a test will be one-sided or two-sided before a test is performed and before the data are examined. Two notable contradictions of this collection of rules arose in interesting court cases.
In the first of these, the Commissioner of Food and Drugs had terminated provisional approval of a food coloring, Red No. 2. and the Certified Color Manufacturers sued.1
Included in the data submitted to the court was Table 6.1a; an analysis of this table by Fisher’s Exact Test reveals a statistically significant dose response to the dye. The response is significant, that is, if the court tests the null hypothesis that Red No. 2 does not affect cancer incidence against the one-sided alternative that high doses of Red No. 2 do induce cancer, at least in rats. The null hypothesis is rejected because only a small fraction of the tables with the marginals shown in Table 6.1a reveal a toxic effect as extreme as the one actually observed.
TABLE 6.1A. Rats fed Red No. 2
| Low dose | High Dose | |
| No cancer | 14 | 14 |
| Cancer | 0 | 7 |
The preceding is an example of a one-tailed test. Should it have been? What would your reaction have been if the results had taken the form shown in Table 6.1b, that is, that Red No. 2 prevented tumors, at least in rats?
TABLE 6.1B. Rats fed Red No. 2
| Low dose | High Dose | |
| No cancer | 7 | 21 |
| Cancer | 7 | 0 |
Should the court have guarded against this eventuality, that is, should they have performed a two-tailed test that would have rejected the null hypothesis if either extreme were observed? Probably not, but a Pennsylvania federal district court was misled into making just such a decision in Commonwealth of Pennsylvania et al v. Rizzo et al.2
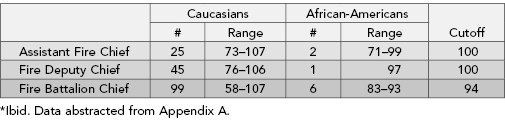
In the second illuminating example, African-American firemen sued the city of Philadelphia. The city’s procedures for determining which firemen would be promoted included a test that was alleged to be discriminatory against African-Americans. The results of the city promotion test are summarized in Table 6.2.
TABLE 6.2. Scores on department examinations
Given that the cutoff point always seems to be just above the African-American candidates’ highest score, these results look suspicious. Fisher’s Exact Test applied to the pass/fail results was only marginally significant at .0513; still the court ruled “we will not reject the result of plaintiffs’ study simply by mechanically lining it up with the 5% level.”3 Do you agree with this reasoning? We do.
Plaintiffs argued for the application of a one-tailed test, “Does a smaller proportion of African-American’s score at or above the cutoff?” but the defendants insisted that a two-tailed test is the correct comparison: “Are there differences in the proportions of African-American and Caucasian candidates scoring at or above the cutoff point?” The court agreed, in error, we feel, given the history of discrimination against African-Americans, to consider the two-tailed test as well as the one-tailed one (see Section 9.1 of Good, 2001).
Through a systematic literature search of articles published before March 2005, Morgan et al. [2007] identified genetic variants previously reported as significant susceptibility factors for atherosclerosis. They then designed and carried out a new separate set of trials. Given their knowledge gleaned from the literature review, one-tailed tests were appropriate. Instead two-tailed tests were performed leading to erroneous conclusions.
As noted in previous chapters, before any statistical test can be performed and a p-value or confidence interval be derived, we must first establish all of the following:
To these guidelines, we now add the following:
Every statistical procedure relies on certain assumptions for correctness. Errors in testing hypotheses come about either because the assumptions underlying the chosen test are not satisfied, or because the chosen test is less powerful than other competing procedures. We shall study each of these lapses in turn.
Virtually all statistical procedures rely on the assumption that the observations are independent.
Virtually all statistical procedures require that at least one of the following successively weaker assumptions be satisfied under the null hypothesis:
The first assumption is the strongest assumption. If it is true, the following two assumptions are also true. The first assumption must be true for a parametric test to provide an exact significance level. If the second assumption is true, the third assumption is also true. The second assumption must be true for a permutation test to provide an exact significance level.
The third assumption is the weakest. It must be true for a bootstrap test to provide an exact significance level asymptotically.
An immediate consequence of the first two assumptions is that if observations come from a multiparameter distribution, then all parameters, not just the one under test, must be the same for all observations under the null hypothesis. For example, a t-test comparing the means of two populations requires the variation of the two populations to be the same.
TABLE 6.3. Types of statistical tests of hypotheses
| Test Type | Definition | Example |
| Exact | Stated significance level is exact, not approximate | t-test when observations are i.i.d. normal; permutation test when observations are exchangeable. |
| Parametric | Obtains cutoff points from specific parametric distribution | t-test |
| Semiparametric Bootstrap | Obtains cutoff points from percentiles of bootstrap distribution of parameter | |
| Parametric Bootstrap | Obtains cutoff points from percentiles of parameterized bootstrap distribution of parameter | |
| Permutation | Obtains cutoff points from distribution of test statistic obtained by rearranging labels | Tests may be based upon the original observations, on ranks, on normal or Savage scores, or on U-statistics. |
For parametric tests and parametric bootstrap tests, under the null hypothesis, the observations must all come from a distribution of a specific form.
Let us now explore the implications of these assumptions in a variety of practical testing situations including comparing the means of two populations, comparing the variances of two populations, comparing the means of three or more populations, and testing for significance in two-factor and higher order experimental designs.
In each instance, before we choose4 a statistic, we check which assumptions are satisfied, which procedures are most robust to violation of these assumptions, and which are most powerful for a given significance level and sample size. To find the most powerful test, we determine which procedure requires the smallest sample size for given levels of Type I and Type II error.
With today’s high-speed desktop computers, a (computationally convenient) normal approximation is no longer an excusable shortcut when testing that the probability of success has a specific value; use binomial tables for exact, rather than approximate, inference. To avoid error, if sufficient data is available, test to see that the probability of success has not changed over time or from clinical site to clinical site.
When comparing proportions, two cases arise. If 0.1 < p < 0.9, use Fisher’s Exact Test. To avoid mistakes, test for a common odds ratio if several laboratories or clinical sites are involved. This procedure is described in the StatXact manual.
If p is close to zero, as it would be with a relatively rare event, a different approach is called for (see Lehmann, 1986, p. 151–154). Recently, Dr. Good had the opportunity to participate in the conduct of a very large-scale clinical study of a new vaccine. He had not been part of the design team, and when he read over the protocol, he was stunned to learn that the design called for inoculating and examining 100,000 patients! 50,000 with the experimental vaccine, and 50,000 controls with a harmless saline solution.
Why so many? The disease at which the vaccine was aimed was relatively rare. Suppose we could expect 0.8% or 400 of the controls to contract the disease, and 0.7% or 350 of those vaccinated to contract it. Put another way, if the vaccine were effective, we would expect 400 out of every 750 patients who contracted the disease to be controls, whereas if the vaccine were ineffective (and innocuous) we would expect 50% of the patients who contracted the disease to be controls.
In short, of the 100,000 subjects we had exposed to a potentially harmful vaccine, only 750 would provide information to use for testing the vaccine’s effectiveness.
The problem of comparing samples from two Poisson distributions boils down to testing the proportion of a single binomial. And the power of this test that started with 100,000 subjects is based on the outcomes of only 750.
But 750 was merely the expected value; it could not be guaranteed. In fact, less than a hundred of those inoculated—treated and control—contracted the disease. The result was a test with extremely low power. As always, the power of a test depends not on the number of subjects with which one starts a trial but the number with which one ends it.
The chi-square statistic that is so often employed in the analysis of contingency tables,
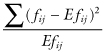
does not have the chi-square distribution. That distribution represents an asymptotic approximation of the statistic that is valid only with very large samples. To obtain exact tests of independence in a 2 × 2 table, use Fisher’s Exact Test.
Consider Table 6.4, in which we have recorded the results of a comparison of two drugs. It seems obvious that Drug B offers significant advantages over Drug A. Or does it? A chi-square analysis by parametric means in which the value of the chi-squared statistic is compared with a table of the chi-square distribution yields an erroneous p-value of 3%. But Fisher’s Exact Test yields a one-sided p-value of only 7%. The evidence of advantage is inconclusive and further experimentation is warranted.
TABLE 6.4. Comparison of two drugs
| Drug A | Drug B | |
| Response | 5 | 9 |
| No Response | 5 | 1 |
As in Fisher [1935], we determine the proportion of tables with the same marginals that are as or more extreme than our original table.
The problem lies in defining what is meant by “extreme.” The errors lie in failing to report how we arrived at our definition.
For example, in obtaining a two-tailed test for independence in a 2 × 2 contingency table, we can treat each table strictly in accordance with its probability under the multinomial distribution (Fisher’s method) or weight each table by the value of the Pearson chi-square statistic for that table.
To obtain exact tests of independence in a set of stratified 2 × 2 tables, first test for the equivalence of the odds ratios using the method of Mehta, Patel, and Gray [1985]. If the test for equivalence is satisfied, only then combine the data and use Fisher’s Exact Test.
In testing for differences in an R × C contingency table with unordered categories, possible test statistics include Freeman–Halton, chi-square, and the log-likelihood ratio ΣΣfij log[fijf../fi.f.j]. Regardless of which statistic is employed, one should calculate the exact significance levels of the test statistic by deriving its permutation distributions using the method of Mehta and Patel [1986].
The chief errors in practice lie in failing to report all of the following:
Chapter 13 contains a discussion of a final, not inconsiderable source of error: the neglect of confounding variables that may be responsible for creating an illusory association or concealing an association that actually exists.
In survival studies and reliability analyses, we follow each subject and/or experiment unit until either some event occurs or the experiment is terminated; the latter observation is referred to as censored. The principal sources of error are the following:
Lack of independence within a sample is often caused by the existence of an implicit factor in the data. For example, if we are measuring survival times for cancer patients, diet may be correlated with survival times. If we do not collect data on the implicit factor(s) (diet in this case), and the implicit factor has an effect on survival times, then we no longer have a sample from a single population. Rather, we have a sample that is a mixture drawn from several populations, one for each level of the implicit factor, each with a different survival distribution.
Implicit factors can also affect censoring times, by affecting the probability that a subject will be withdrawn from the study or lost to follow-up. For example, younger subjects may tend to move away (and be lost to follow-up) more frequently than older subjects, so that age (an implicit factor) is correlated with censoring. If the sample under study contains many younger people, the results of the study may be substantially biased because of the different patterns of censoring. This violates the assumption that the censored values and the noncensored values all come from the same survival distribution.
Stratification can be used to control for an implicit factor. For example, age groups (such as under 50, 51–60, 61–70, and 71 or older) can be used as strata to control for age. This is similar to using blocking in analysis of variance.
If the pattern of censoring is not independent of the survival times, then survival estimates may be too high (if subjects who are more ill tend to be withdrawn from the study), or too low (if subjects who will survive longer tend to drop out of the study and are lost to follow-up).
If a loss or withdrawal of one subject could increase the probability of loss or withdrawal of other subjects, this would also lead to lack of independence between censoring and the subjects.
Survival tests rely on independence between censoring times and survival times. If independence does not hold, the results may be inaccurate.
An implicit factor not accounted for by stratification may lead to a lack of independence between censoring times and observed survival times.
A study may end up with many censored values as a result of having large numbers of subjects withdrawn or lost to follow-up, or from having the study end while many subjects are still alive. Large numbers of censored values decrease the equivalent number of subjects exposed (at risk) at later times, reducing the effective sample sizes.
A high censoring rate may also indicate problems with the study: ending too soon (many subjects still alive at the end of the study), or a pattern in the censoring (many subjects withdrawn at the same time, younger patients being lost to follow-up sooner than older ones, etc.).
Survival tests perform better when the censoring is not too heavy, and, in particular, when the pattern of censoring is similar across the different groups.
A most powerful test for use when data are censored at one end only was developed by Good [1989, 1991, 1992]. It should be employed in the following situations:
Kaplan–Meier survival analysis (KMSA) is the appropriate starting point as Good’s test is not appropriate for use in clinical trials for which the times are commonly censored at both ends. KMSA can estimate survival functions even in the presence of censored cases and requires minimal assumptions.
If covariates other than time are thought to be important in determining duration to outcome, results reported by KMSA will represent misleading averages, obscuring important differences in groups formed by the covariates (e.g., men vs. women). Since this is often the case, methods that incorporate covariates, such as event-history models and Cox regression, may be preferred.
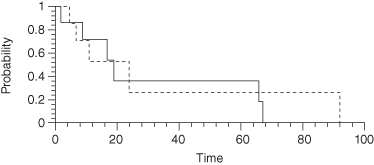
For small samples, the permutation distributions of the Gehan–Breslow, Mantel–Cox, and Tarone–Ware survival test statistics and not the chi-square distribution should be used to compute p-values. If the hazard or survival functions are not parallel, then none of the three tests (Gehan–Breslow, Mantel–Cox, or Tarone–Ware) will be particularly good at detecting differences between the survival functions. Before performing any of these tests, examine a Kaplan–Meier plot, plots of the life-table survival functions, and plots of the life-table hazard functions for each sample to see whether their graphs cross as in Figure 6.1.
FIGURE 6.1. Kaplan-Meier Plot Showing Crossing Survival Functions.
Buyse and Piedbois [1996] describe four further errors that can result in misleading treatment comparisons:
The most common test for comparing the means of two populations is based upon Student’s t. For Student’s t-test to provide significance levels that are exact rather than approximate, all the observations must be independent and, under the null hypothesis, all the observations must come from identical normal distributions.
Even if the distribution is not normal, the significance level of the t-test is almost exact for sample sizes greater than 12; for most of the distributions one encounters in practice,5 the significance level of the t-test is usually within a percent or so of the correct value for sample sizes between 6 and 12.
For testing against nonnormal alternatives, more powerful tests than the t-test exist. For example, a permutation test replacing the original observations with their normal scores is more powerful than the t-test [Lehmann, 1986, p. 321].
Permutation tests are derived by looking at the distribution of values the test statistic would take for each of the possible assignments of treatments to subjects. For example, if in an experiment two treatments were assigned at random to six subjects so that three subjects got one treatment and three the other, there would have been a total of 20 possible assignments of treatments to subjects.6 To determine a p-value, we compute for the data in hand each of the 20 possible values the test statistic might have taken. We then compare the actual value of the test statistic with these 20 values. If our test statistic corresponds to the most extreme value, we say that p = 1/20 = 0.05 (or 1/10 = 0.10 if this is a two-tailed permutation test).
Against specific normal alternatives, this two-sample permutation test provides a most powerful unbiased test of the distribution-free hypothesis that the centers of the two distributions are the same [Lehmann, 1986, p. 239]. For large samples, its power against normal alternatives is almost the same as Student’s t-test [Albers, Bickel, and van Zwet, 1976]. Against other distributions, by appropriate choice of the test statistic, its power can be superior [Lambert, 1985; Maritz, 1996]. Still, in almost every instance, Student’s-t remains the test of choice for the two-sample comparison of data derived from continuous measurements.
Results must be adjusted for baseline differences between the control and treatment groups for covariates that are strongly correlated with the outcomes, ρ > .5 [Pocock et al., 2002].
In many treatment comparisons, we are not so much interested in the final values as in how the final values differ from baseline. The correct comparison is thus between the two sets of differences. The two p-values that result from comparison of the within treatment before and after values are not of diagnostic value.
A test based on several variables simultaneously, a multivariate test, can be more powerful than a test based on a single variable alone, providing the additional variables are relevant. Adding variables that are unlikely to have value in discriminating among the alternative hypotheses simply because they are included in the dataset can only result in a loss of power.
Unfortunately, what works when making a comparison between two populations based on a single variable fails when we attempt a multivariate comparison. Unless the data are multivariate normal, Hötelling’s T2, the multivariate analog of Student’s t, will not provide tests with the desired significance level. Only samples far larger than those we are likely to afford in practice are likely to yield multi-variate results that are close to multivariate normal. Still, an exact significance level can be obtained in the multivariate case regardless of the underlying distribution by making use of the permutation distribution of Hötelling’s T2.
Let us suppose we had a series of multivariate observations on m control subjects and n subjects who had received a new treatment. Here is how we would construct a multivariate test for a possible treatment effect:
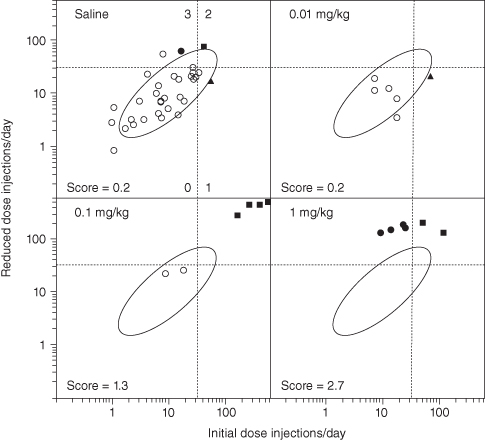
If only two or three variables are involved, a graph can sometimes be a more effective way of communicating results than a misleading p-value based on the parametric distribution of Hötelling’s T2. As an example, compare the graph in Weeks and Collins [1987] (Figure 6.2), with the analysis of the same data in Collins, Weeks, Cooper, Good, and Russell [1984].
FIGURE 6.2. Injection rates and scores for rats self-administering saline and morphine using the pneumatic syringe and new protocol. The ellipse is the 90% confidence limits for saline control rats based upon the assumption of a normal bivariate distribution of injection rates corresponding to the initial and reduced dose periods. The dashed lines represent the 90% confidence limits for saline self-administration for the initial and reduced doses individually. The scores for points falling in each quadrant formed by these lines are shown with the saline data. Open circles, score 0; solid triangles, score 1; solid squares, score 2; and solid circles, score 3. Note that injection rates are plotted to a logarithmic scale.
[Reproduced with kind permission of Springer Science + Business Media from J.R. Weeks and R.J. Collins, 1987.]
Alas, more and more individuals seem content to let their software do their thinking for them. It won’t.
Your first fundamental decision is to decide whether you are doing a one-tailed or a two-tailed test. If you are testing against a one-sided alternative, for example, no difference versus improvement, then you require a one-tailed or one-sided test. If you are doing a head-to-head comparison—which alternative is best?—then a two-tailed test is required.
Note that in a two-tailed test, the tails need not be equal in size but should be portioned out in accordance with the relative losses associated with the possible decisions [Moyé, 2000, pp. 152–157].
Second, you must decide whether your observations are paired (as would be the case when each individual serves as its own control) or unpaired, and use the paired or unpaired t-test.
A comparison of two experimental effects requires a statistical test on their difference, as described previously. But in practice, this comparison is often based on an incorrect procedure involving two separate tests in which researchers conclude that effects differ when one effect is significant (p < 0.05) but the other is not (p > 0.05). Nieuwenhuis, Forstmann, and Wagenmakers [2011] reviewed 513 behavioral, systems, and cognitive neuroscience articles in five top-ranking journals and found that 78 used the correct procedure and 79 used the incorrect procedure. Do not make the same mistake.
When the logic of a situation calls for demonstration of similarity rather than differences among responses to various treatments, then equivalence tests are often more relevant than tests with traditional no-effect null hypotheses [Anderson and Hauck, 1986; Dixon, 1998; pp. 257–301].
Two distributions F and G, such that G[x] = F[x − δ], are said to be equivalent providing |δ| < Δ, where Δ is the smallest difference of clinical significance. To test for equivalence, we obtain a confidence interval for δ, rejecting equivalence only if this interval contains values in excess of |Δ|. The width of a confidence interval decreases as the sample size increases; thus, a very large sample may be required to demonstrate equivalence just as a very large sample may be required to demonstrate a clinically significant effect.
Operationally, establishing equivalence can be accomplished with a pair of one-sided hypothesis tests:
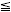−Δ versus H1: δ > −Δ
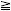Δ versus H1: δ < ΔIf we reject both of these hypotheses, then we establish that −Δ < δ < Δ, or, equivalently, that |δ| < Δ.
If the variances of the two populations are not the same, neither the t-test nor the permutation test will yield exact significance levels despite pronouncements to the contrary of numerous experts regarding the permutation tests.
Rule 1: If the underlying distribution is known, make use of it.
Some older textbooks recommend the use of an arcsine transformation when the data are drawn from a binomial distribution, and a square-root transformation when the data are drawn from a Poisson distribution. The resultant p-values are still only approximations and, in any event, lead to suboptimal tests.
The optimal test for comparing two binomial distributions is Fisher’s Exact Test and the optimal test for comparing two Poisson distributions is based on the binomial distribution (see, for example, Lehmann, 1986, Chapter 5, Section 5).
Rule 2: More important than comparing mean values can be determining why the variances of the populations are different.
There are numerous possible solutions for the Behrens–Fisher problem of unequal variances in the treatment groups. These include the following:
Hilton [1996] compared the power of the Wilcoxon test, O’Brien’s test, and the Smirnov test in the presence of both location shift and scale (variance) alternatives. As the relative influence of the difference in variances grows, the O’Brien test is most powerful. The Wilcoxon test loses power in the face of different variances. If the variance ratio is 4:1, the Wilcoxon test is not trustworthy.
One point is unequivocal. William Anderson writes,
The first issue is to understand why the variances are so different, and what does this mean to the patient. It may well be the case that a new treatment is not appropriate because of higher variance, even if the difference in means is favorable. This issue is important whether the difference was anticipated. Even if the regulatory agency does not raise the issue, I want to do so internally.
David Salsburg agrees:
If patients have been assigned at random to the various treatment groups, the existence of a significant difference in any parameter of the distribution suggests that there is a difference in treatment effect. The problem is not how to compare the means but how to determine what aspect of this difference is relevant to the purpose of the study.
Since the variances are significantly different, I can think of two situations where this might occur:
The preceding statistical methods are not applicable if the observations are interdependent. There are five cases in which, with some effort, analysis may still be possible: repeated measures, clusters, known or equal pairwise dependence, a moving average or autoregressive process,7 and group-randomized trials.
Repeated measures on a single subject can be dealt with in a variety of ways, including treating them as a single multivariate observation. Good [2001; Section 5.6] and Pesarin [2001; Chapter 11] review a variety of permutation tests for use when there are repeated measures.
Another alternative is to use one of the standard modeling approaches such as random- or mixed-effects models or generalized estimating equations (GEEs). See Chapter 13 for a full discussion.
Occasionally, data will have been gathered in clusters from families and other groups who share common values and work or leisure habits. If stratification is not appropriate, treat each cluster as if it were a single observation, replacing individual values with a summary statistic such as an arithmetic average [Mosteller & Tukey, 1977].
Cluster-by-cluster means are unlikely to be identically distributed, having variances, for example, that will depend on the number of individuals that make up the cluster. A permutation test based on these means would not be exact.
If there are a sufficiently large number of such clusters in each treatment group, the bootstrap, defined in Chapters 3 and 7, is the appropriate method of analysis. In this application, bootstrap samples are drawn on the clusters rather than the individual observations.
With the bootstrap, the sample acts as a surrogate for the population. Each time we draw a pair of bootstrap samples from the original sample, we compute the difference in means. After drawing a succession of such samples, we will have some idea of what the distribution of the difference in means would be were we to take repeated pairs of samples from the population itself.
As a general rule, resampling should reflect the null hypothesis, according to Young [1986] and Hall and Wilson [1991]. Thus, in contrast to the bootstrap procedure used in estimation (see Chapters 3 and 7), each pair of bootstrap samples should be drawn from the combined sample taken from the two treatment groups. Under the null hypothesis, this will not affect the results; under an alternative hypothesis, the two bootstrap sample means will be closer together than they would if drawn separately from the two populations. The difference in means between the two samples that were drawn originally should stand out as an extreme value.
Hall and Wilson [1991] also recommend that the bootstrap be applied only to statistics that, for very large samples, will have distributions that do not depend on any unknowns.8 In the present example, Hall and Wilson [1991] recommend the use of the t-statistic, rather than the simple difference of means, as leading to a test that is both closer to exact and more powerful.
Suppose we draw several hundred such bootstrap samples with replacement from the combined sample and compute the t-statistic each time. We would then compare the original value of the test statistic, Student’s t in this example, with the resulting bootstrap distribution to determine what decision to make.
If the covariances are the same for each pair of observations, then the permutation test described previously is an exact test if the observations are normally distributed [Lehmann, 1986], and is almost exact otherwise.
Even if the covariances are not equal, if the covariance matrix is nonsingular, we may use the inverse of this covariance matrix to transform the original (dependent) variables to independent (and, hence, exchangeable) variables. After this transformation, the assumptions are satisfied so that a permutation test can be applied. This result holds even if the variables are collinear. Let R denote the rank of the covariance matrix in the singular case. Then there exists a projection onto an R-dimensional subspace where R normal random variables are independent. So if we have an N dimensional (N > R) correlated and singular multivariate normal distribution, there exists a set of R linear combinations of the original N variables so that the R linear combinations are each univariate normal and independent.
The preceding is only of theoretical interest unless we have some independent source from which to obtain an estimate of the covariance matrix. If we use the data at hand to estimate the covariances, the estimates will be interdependent and so will the transformed observations.
These cases are best treated by the same methods and are subject to the caveats as described in Part 3 of this text.
Group randomized trials (GRTs) in public health research typically use a small number of randomized groups with a relatively large number of participants per group. Typically, some naturally occurring groups are targeted: work sites, schools, clinics, neighborhoods, even entire towns or states. A group can be assigned to either the intervention or control arm but not both; thus, the group is nested within the treatment. This contrasts with the approach used in multicenter clinical trials, in which individuals within groups (treatment centers) may be assigned to any treatment.
GRTs are characterized by a positive correlation of outcomes within a group and by the small number of groups. Feng et al. [2001] report a positive intraclass correlation (ICC) between the individuals’ target-behavior outcomes within the same group. This can be due in part to the differences in characteristics between groups, to the interaction between individuals within the same group, or (in the presence of interventions) to commonalities of the intervention experienced by an entire group.
The variance inflation factor (VIF) as a result of such commonalities is 1 + (n − 1)σ.
The sampling variance for the average responses in a group is VIF * σ2/n.
The sampling variance for the treatment average with k groups and n individuals per group is VIF * σ2/(nk).
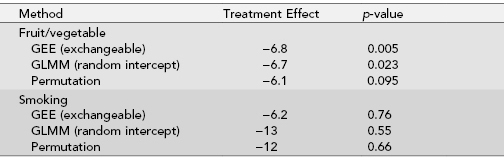
Problems arise. Although σ in GRTs is usually quite small, the VIFs could still be quite large because VIF is a function of the product of the correlation and group size n. Feng et al. [2001] report that in the Working Well Trial, while σ = 0.03 for daily number of fruit and vegetable servings and an average of 250 workers per work site, VIF = 8.5. In the presence of this deceivingly small ICC, an 8.5-fold increase in the number of participants is required to maintain the same statistical power as if there were no positive correlation. Ignoring the VIF in the analysis would lead to incorrect results.
To be appropriate, an analysis method of GRTs need acknowledge both the ICC and the relatively small number of groups. Three primary approaches are used:
Gail et al. [1996] demonstrate that in GRTs, the permutation test remains valid (exact or near exact in nominal levels) under almost all practical situations, including unbalanced group sizes, as long as the number of groups are equal between treatment arms or equal within each block if blocking is used.
The drawbacks of all three methods, including randomization-based inference if corrections are made for covariates, are the same as those for other methods of regression as detailed in Chapters 8 and 9.
TABLE 6.5. Comparison of different analysis methods for inference on treatment effect in the Working Well Trial (26 work sites with between 47 to 105 workers per site)
If the observations are interdependent and fall into none of the preceding categories, then the experiment is fatally flawed. Your efforts would be best expended on the design of a cleaner experiment. Or, as J. W. Tukey remarked on more than one occasion, “If a thing is not worth doing, it is not worth doing well.”
Most statistical software comes with built-in defaults, for example, a two-sided test at the 5% significance level. Even if altered, subsequent uses may default back to the previously used specifications. But what if these settings are not appropriate for your particular application? We know of one statistician who advised his company to take twice as many samples as necessary (at twice the investment in money and time) simply because he had allowed the software to make the settings. Always verify that the current default settings of your statistical software are appropriate before undertaking an analysis or a sample-size determination.
It is up to you and not your software to verify that all the necessary assumptions are satisfied. Just because your software yields a p-value does not mean that you performed the appropriate analysis.
Testing for the equality of the variances of two populations is a classic problem with many not-quite-exact, not-quite-robust, not-quite-powerful-enough solutions. Sukhatme [1958] lists four alternative approaches and adds a fifth of his own; Miller [1968] lists ten alternatives and compares four of these with a new test of his own; Conover, Johnson, and Johnson [1981] list and compare 56 tests; and Balakrishnan and Ma [1990] list and compare nine tests with one of their own.
None of these tests proves satisfactory in all circumstances, for each requires that two or more of the following four conditions be satisfied:
As an example, the first published solution to this classic testing problem is the z-test proposed by Welch [1937] based on the ratio of the two sample variances. If the observations are normally distributed, this ratio has the F-distribution, and the test whose critical values are determined by the F-distribution is uniformly most powerful among all unbiased tests [Lehmann, 1986, Section 5.3]. But with even small deviations from normality, significance levels based on the F-distribution are grossly in error [Lehmann, 1986, Section 5.4].
Box and Anderson [1955] propose a correction to the F-distribution for “almost” normal data, based on an asymptotic approximation to the permutation distribution of the F-ratio. Not surprisingly, their approximation is close to correct only for normally distributed data or for very large samples. The Box–Anderson statistic results in an error rate of 21%, twice the desired value of 10%, when two samples of size 15 are drawn from a gamma distribution with four degrees of freedom.
A more recent permutation test (Bailor, 1989) based on complete enumeration of the permutation distribution of the sample F-ratio is exact only when the location parameters of the two distributions are known or are known to be equal.
The test proposed by Miller [1968] yields conservative Type I errors, less than or equal to the declared error, unless the sample sizes are unequal. A 10% test with samples of size 12 and 8 taken from normal populations yielded Type I errors 14% of the time.
Fligner and Killeen [1976] propose a permutation test based on the sum of the absolute deviations from the combined sample mean. Their test may be appropriate when the medians of the two populations are equal, but can be virtually worthless otherwise, accepting the null hypothesis up to 100% of the time. In the first edition of this book, Good [2001] proposed a test based on permutations of the absolute deviations from the individual sample medians; this test yields discrete significance levels that oscillate about the desired significance level.
To compute the primitive bootstrap introduced by Efron [1979], we would take successive pairs of samples—one of n observations from the sampling distribution Fn which assigns mass 1/n to the values {Xi: i = 1, … , n}, and one of m observations from the sampling distribution Gm, which assigns mass 1/m to the values {Xj: j = n + 1, … , n + m}, and compute the ratio of the sample variances:
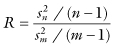
We would use the resultant bootstrap distribution to test the hypothesis that the variance of F equals the variance of G against the alternative that the variance of G is larger. Under this test, we reject the null hypothesis if the 100(1 − α) percentile is less than 1.
This primitive bootstrap and the associated confidence intervals are close to exact only for very large samples with hundreds of observations. More often the true coverage probability is larger than the desired value.
Two corrections yield vastly improved results. First, for unequal-sized samples, Efron [1982] suggests that more accurate confidence intervals can be obtained using the test statistic
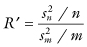
Second, applying the bias and acceleration corrections described in Chapter 3 to the bootstrap distribution of R′ yields almost exact intervals.
Lest we keep you in suspense, a distribution-free exact and more powerful test for comparing variances can be derived based on the permutation distribution of Aly’s statistic.
This statistic proposed by Aly[1990] is
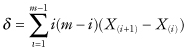
where X(1) ≤ X(2) ≤ … ≤ X(m) are the order statistics of the first sample.
Suppose, we have two sets of measurements, 121, 123, 126, 128.5, 129, and, in a second sample, 153, 154, 155, 156, 158. We replace these with the deviations z1i = X(i+1) − X(i) or 2, 3, 2.5, 0.5 for the first sample and z2i = 1, 1, 1, 2 for the second.
The original value of the test statistic is 8 + 18 + 15 + 2 = 43. Under the hypothesis of equal dispersions in the two populations, we can exchange labels between z1i and z2i for any or all of the values of i. One possible rearrangement of the labels on the deviations puts {2, 1, 1, 2} in the first sample, which yields a value of 8 + 6 + 6 + 8 = 28.
There are 24 = 16 rearrangements of the labels in all, of which only one {2, 3, 2.5, 2} yields a larger value of Aly’s statistic than the original observations. A one-sided test would have two out of 16 rearrangements as or more extreme than the original; a two-sided test would have four. In either case, we would accept the null hypothesis, though the wiser course would be to defer judgment until we have taken more observations.
If our second sample is larger than the first, we have to resample in two stages. First, we select a subset of m values at random without replacement from the n observations in the second, larger sample, and compute the order statistics and their differences. Last, we examine all possible values of Aly’s measure of dispersion for permutations of the combined sample as we did when the two samples were equal in size and compare Aly’s measure for the original observations with this distribution. We repeat this procedure several times to check for consistency.
Good [1994, p. 31] proposed a permutation test based on the sum of the absolute values of the deviations about the median. First, we compute the median for each sample; next, we replace each of the remaining observations by the square of its deviation about its sample median; last, in contrast to the test proposed by Brown and Forsythe [1974], we discard the redundant linearly dependent value from each sample.
Suppose the first sample contains the observations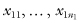 
whose median is M1; we begin by forming the deviates {
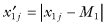} for j = 1, … n1. Similarly, we form the set of deviates {
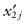} using the observations in the second sample and their median.
If there are an odd number of observations in the sample, then one of these deviates must be zero. We can not get any information out of a zero, so we throw it away. In the event of ties, should there be more than one zero, we still throw only one away. If there is an even number of observations in the sample, then two of these deviates (the two smallest ones) must be equal. We can not get any information out of the second one that we did not already get from the first, so we throw it away.
Our new test statistic SG is the sum of the remaining n1 − 1 deviations in the first sample, that is,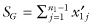 
.
We obtain the permutation distribution for SG and the cutoff point for the test by considering all possible rearrangements of the remaining deviations between the first and second samples.
To illustrate the application of this method, suppose the first sample consists of the measurements 121, 123, 126, 128.5, 129.1 and the second sample of the measurements 153, 154, 155, 156, 158. Thus, after eliminating the zero value,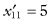 
, 
, 
, 
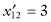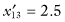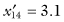, and SG = 13.6. For the second sample 
, 
, 
, 
.
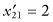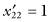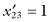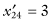In all, there are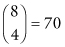 
arrangements of which only three yield values of the test statistic as or more extreme than our original value. Thus, our p-value is 3/70 = 0.043 and we conclude that the difference between the dispersions of the two manufacturing processes is statistically significant at the 5% level.
As there is still a weak dependency among the remaining deviates within each sample, they are only asymptotically exchangeable. Tests based on SG are alternately conservative and liberal according to Baker [1995] in part because of the discrete nature of the permutation distribution unless
The preceding test is easily generalized to the case of K samples from K populations. Such a test would be of value as a test for homoscedasticity as a preliminary to a K-sample analysis for a difference in means among test groups.
First, we create K sets of deviations about the sample medians and make use of the test statistic
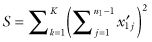
The choice of the square of the inner sum ensures that this statistic takes its largest value when the largest deviations are all together in one sample after relabeling.
To generate the permutation distribution of S, we again have two choices. We may consider all possible rearrangements of the sample labels over the K sets of deviations. Or, if the samples are equal in size, we may first order the deviations within each sample, group them according to rank, and then rearrange the labels within each ranking.
Again, this latter method is directly applicable only if the K samples are equal in size, and, again, this is unlikely to occur in practice. We will have to determine a confidence interval for the p-value for the second method via a bootstrap in which we first select samples from samples (without replacement) so that all samples are equal in size. While we would not recommend doing this test by hand, once programmed, it still takes less than a second on last year’s desktop.
Normality is a myth; there never has, and never will be a normal distribution.
—Geary [1947, p. 241]
Although the traditional one-way analysis of variance based on the F-ratio
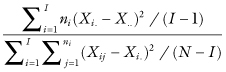
is highly robust, it has four major limitations:
A permutation test is preferred for the k-sample analysis [Good and Lunneborg, 2005]. These tests are distribution free (though the variances must be the same for all treatments). They are at least as powerful as the analysis of variance. And you can choose the test statistic that is optimal for a given alternative and loss function and not be limited by the availability of tables.
We take as our model Xij = αi + εjj, where i = 1, … I denotes the treatment, and j = 1, … , ni . We assume that the error terms {εjj} are independent and identically distributed.
We consider two loss functions: one in which the losses associated with overlooking a real treatment effect, a Type II error, are proportional to the sum of the squares of the treatment effects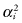 
(LS), and another in which the losses are proportional to the sum of the absolute values of the treatment effects, |αi| (LAD).
Our hypothesis, a null hypothesis, is that the differential treatment effects, the {αi}, are all zero. We will also consider two alternative hypotheses: KU that at least one of the differential treatment effects αi is not zero, and KO that exactly one of the differential treatment effects αi is not zero.
For testing against KU with the squared deviation loss function, Good [2002, p. 126] recommends the use of the statistic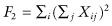 
which is equivalent to the F-ratio once terms that are invariant under permutations are eliminated.
We compared the parametric and permutation versions of this test when the data were drawn from a mixture of normal distributions. The difference between the two in power is exacerbated when the design is unbalanced. For example, the following experiment was simulated 4000 times:
Note that such mixtures are extremely common in experimental work. The parametric test in which the F-ratio is compared with an F-distribution had a power of 18%. The permutation test in which the F-ratio is compared with a permutation-distribution had a power of 31%.
For testing against KU with the absolute deviation loss function, Good [2002, p. 126] recommends the use of the statistic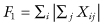 
.
For testing against K0, first denote by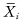 
the mean of the ith sample, and by 
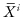the mean of all observations excluding those in the ith sample. A possible test statistic would be the maximum of the differences 
.
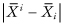A permutation test based on the original observations is appropriate only if one can assume that under the null hypothesis the observations are identically distributed in each of the populations from which the samples are drawn. If we cannot make this assumption, we will need to transform the observations, throwing away some of the information about them so that the distributions of the transformed observations are identical.
For example, for testing against K0, Lehmann [1999, p. 372] recommends the use of the Jonckheere–Terpstra statistic, the number of pairs in which an observation from one group is less than an observation from a higher-dose group. The penalty we pay for using this statistic and ignoring the actual values of the observations is a marked reduction in power for small samples, and a less pronounced loss for larger ones.
If there are just two samples, the test based on the Jonckheere–Terpstra statistic is identical with the Mann–Whitney test. For very large samples, with identically distributed observations in both samples, 100 observations would be needed with this test to obtain the same power as a permutation test based on the original values of 95 observations. This is not a price one would want to pay in human or animal experiments.
Student’s t and the analysis of variance are based on mathematics that requires the dependent variable to be measured on an interval or ratio scale so that its values can be meaningfully added and subtracted. But what does it mean if one subtracts the subjective data value “Indifferent” from the subjective data value “Highly preferable.” The mere fact that we have entered the data into the computer on a Likert scale, such as a “1” for “Highly preferable” and a “3” for “Indifferent” does not actually endow our preferences with those relative numeric values.
Unfortunately, the computer thinks it does and if asked to compute a mean preference will add the numbers it has stored and divide by the sample size. It will even compute a t statistic and a p-value if such is requested. But this does not mean that either is meaningful.
Of course, you are welcome to ascribe numeric values to subjective data, providing that you spell out exactly what you have done, and to realize that the values you ascribe may be quite different from the ones that some other investigator might attribute to precisely the same data.
Recent simulations reveal that the classic test based on Pearson correlation is almost distribution free [Good, 2009]. Still, too often we treat a test of the correlation between two variables X and Y as if it were a test of their independence. X and Y can have a zero correlation coefficient, yet be totally dependent (for example, Y = X2).
Even when the expected value of Y is independent of the expected value of X, the variance of Y might be directly proportional to the variance of X. Of course, if we had plotted the data, we would have spotted this right away.
Many variables exhibit circadian rhythms. Yet the correlation of such a variable with time when measured over the course of twenty-four hours would be zero. This is because correlation really means “linear correlation” and the behavior of diurnal rhythm is far from linear. Of course, this too would have been obvious had we drawn a graph rather than let the computer do the thinking for us.
Yet another, not uncommon, example would be when X is responsible for the size of a change in Y, but a third variable, not part of the study, determines the direction of the change.
The two principal weaknesses of the analysis of variance are as follows:
When we randomly assign subjects (or plots) to treatment, we may inadvertently assign all males, say, to one of the treatments. The result might be the illusion of a treatment effect that really arises from a sex effect. For example, the following table
suggests there exists a statistically significant difference between treatments.
But suppose, we were to analyze the same data correcting for sex and obtain the following:
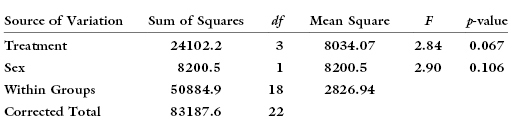
We longer observe a statistically significant difference between treatment groups.
As noted previously, one of the most common statistical errors is to assume that because an effect is not statistically significant it does not exist. One of the most common errors in using the analysis of variance is to assume that because a factor such as sex does not yield a significant p-value that we may eliminate it from the model. Had we done so in the above example, we would have observed a statistically significant difference among treatments that was actually due to the unequal distribution of the sexes amongst the various treatments.
The process of eliminating nonsignificant factors one by one from an analysis of variance means that we are performing a series of tests rather than a single test; thus, the actual significance level is larger than the declared significance level.
Further problems arise when one comes to interpret the output of three-way, four-way, and higher-order designs. Suppose a second- or higher-order interaction is statistically significant, how is this to be given a practical interpretation? Some authors suggest one write, “Factor C moderates the effect of Factor A on Factor B” as if this phrase actually had discernible meaning. Among the obvious alternative interpretations of a statistically significant higher order interaction are the following:
Still, it is clear there are situations in which higher-order interactions have real meaning. For example, plants require nitrogen, phosphorous, and potassium in sufficient concentrations to grow. Remove any one component and the others will prove inadequate to sustain growth—a clear-cut example of a higher-order interaction.
To avoid ambiguities, one need either treat multifactor experiments purely as pilot efforts and guides to further experimentation or to undertake such experiments only after one has gained a thorough understanding of interactions via one- and two-factor experiments. See the discussion in Chapter 13 on building a successful model.
On the plus side, the parametric analysis of variance is remarkably robust with respect to data from nonnormal distributions (Jagers, 1980). As with the k-sample comparison, it should be remembered that the tests for main effects in the analysis of variance are omnibus statistics offering all-round power against many alternatives but no particular advantage against any specific one of them.
Judicious use of contrasts can provide more powerful tests. For example, one can obtain a one-sided test of the row effect in a 2xCx … design by testing the contrast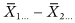 
or a test of an ordered row effect in an RxCx … design by testing the contrast ΣjajXj …, where Σaj = 0 and the aj are increasing in j. Note: These contrasts must be specified in advance of examining the data, Otherwise there will be a loss of power due to the need to correct for multiple tests.
Two additional caveats apply to the parametric ANOVA approach to the analysis of two-factor experimental design:
Alas, these same caveats apply to the permutation tests. Let us see why.
Imbalance in the design will result in the confounding of main effects with interactions. Consider the following two-factor model for crop yield:
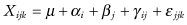
Now suppose that the observations in a two-factor experimental design are normally distributed as in the following diagram taken from Cornfield and Tukey [1956]:
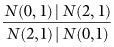
There are no main effects in this example—both row means and both column means have the same expectations, but there is a clear interaction represented by the two nonzero, off-diagonal elements.
If the design is balanced, with equal numbers per cell, the lack of significant main effects, and the presence of a significant interaction should and will be confirmed by our analysis. But suppose that the design is not in balance, that for every ten observations in the first column, we have only one observation in the second. Because of this imbalance, when we use the F-ratio or equivalent statistic to test for the main effect, we will uncover a false “row” effect that is actually due to the interaction between rows and columns. The main effect is confounded with the interaction.
If a design is unbalanced as in the preceding example, we cannot test for a “pure” main effect or a “pure” interaction. But we may be able to test for the combination of a main effect with an interaction by using the statistic that we would use to test for the main effect alone. This combined effect will not be confounded with the main effects of other unrelated factors.
Whether or not the design is balanced, the presence of an interaction may zero out a cofactor-specific main effect or make such an effect impossible to detect. More important, the presence of a significant interaction may render the concept of a single “main effect” meaningless. For example, suppose we decide to test the effect of fertilizer and sunlight on plant growth. With too little sunlight, a fertilizer would be completely ineffective. Its effects only appear when sufficient sunlight is present. Aspirin and Warfarin can both reduce the likelihood of repeated heart attacks when used alone; you do not want to mix them!
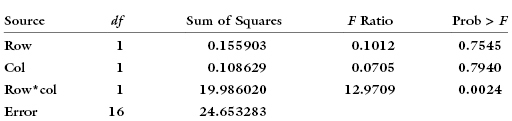
Gunter Hartel offers the following example: Using five observations per cell and random normals as indicated in Cornfield and Tukey’s diagram, a two-way ANOVA without interaction yields the following results:
Adding the interaction term yields:
Expanding the first row of the experiment to have 80 observations rather than 10, the main-effects-only table becomes:
But with the interaction term it is
The standard permutation tests for main effects and interactions in a multifactor experimental design are also correlated as the residuals (after subtracting main effects) and are not exchangeable even if the design is balanced [Lehmann & D’Abrera 1988]. To see this, suppose our model is Xijk = μ + αi + βj + γij + εijk, where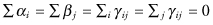 
.
Eliminating the main effects in the traditional manner, that is, setting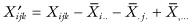 
, one obtains the test statistic
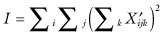
first derived by Still and White [1981]. A permutation test based on the statistic I will not be exact. For even if the error terms {εijk} are exchangeable, the residuals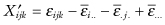 
are weakly correlated, the correlation depending on the subscripts.
The negative correlation between permutation test statistics works to their advantage only when just a single effect is present. Nonetheless, the literature is filled with references to permutation tests for the two-way and higher-order designs that produce misleading values. Included in this category are those permutation tests based on the ranks of the observations, for example, the Kruskall–Wallace test that may be found in many statistics software packages.
Salmaso [2002] developed exact distribution-free tests for analyzing factorial designs.
Good and Xie [2008] developed an exact distribution-free test for analyzing crossover designs.
Unbalanced designs with unequal numbers per cell may result from unanticipated losses during the conduct of an experiment or survey (or from an extremely poor initial design). There are two approaches to their analysis.
First, if we have a large number of observations and only a small number are missing, we might consider imputing values to the missing observations, recognizing that the results may be somewhat tainted.
Second, we might bootstrap along one of the following lines:
Violation of assumptions can affect not only the significance level of a test but the power of the test as well; see Tukey and MacLaughlin [1963] and Box and Tiao [1964]. For example, although the significance level of the t-test is robust to departures from normality, the power of the t-test is not. Thus, the two-sample permutation test may always be preferable.
If blocking including matched pairs was used in the original design then the same division into blocks should be employed in the analysis. Confounding factors such as sex, race, and diabetic condition can easily mask the effect we hoped to measure through the comparison of two samples. Similarly, an overall risk factor can be totally misleading [Gigerenzer, 2002]. Blocking reduces the differences between subjects so that differences between treatment groups stand out, if, that is, the appropriate analysis is used. Thus, paired data should always be analyzed with the paired t-test or its permutation equivalent, not with the group t-test.
To analyze a block design (for example, where we have sampled separately from whites, blacks, and Hispanics), the permutation test statistic is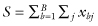 
,where xbj is the jth observation in the control sample in the bth block, and the rearranging of labels between control and treated samples takes place separately and independently within each of the B blocks [Good, 2001, p. 124].
Blocking can also be used after the fact if you suspect the existence of confounding variables and if you measured the values of these variables as you were gathering data.9
Always be sure your choice of statistic is optimal against the alternative hypotheses of interest for the appropriate loss function.
To avoid using an inferior, less sensitive, and possibly inaccurate statistical procedure, pay heed to another admonition from George Dyke [1997]: “The availability of ‘user-friendly’ statistical software has caused authors to become increasingly careless about the logic of interpreting their results, and to rely uncritically on computer output, often using the ‘default option’ when something a little different (usually, but not always, a little more complicated) is correct, or at least more appropriate.”
When we perform multiple tests in a study, there may not be journal room (nor interest) to report all the results, but we do need to report the total number of statistical tests performed so that readers can draw their own conclusions as to the significance of the results that are reported.
We may also wish to correct the reported significance levels by using one of the standard correction methods for independent tests (e.g., Bonferroni as described in Hsu, 1996 and Aickin and Gensler, 1996; for resampling methods, see Westfall and Young, 1993).
Several statistical packages—SAS is a particular offender—print out the results of several dependent tests performed on the same set of data, for example, the t-test and the Wilcoxon. We are not free to pick and choose. We must decide before we view the printout which test we will employ.
Let Wα denote the event that the Wilcoxon test rejects a hypothesis at the α significance level. Let Pα denote the event that a permutation test based on the original observations and applied to the same set of data rejects a hypothesis at the α significance level. Let Tα denote the event that a t-test applied to the same set of data rejects a hypothesis at the α significance level.
It is possible that Wα may be true when Pα and Tα are not, and so forth. As Pr{Wα or Pα or Tα|H} ≤ Pr{Wα|H} = α, we will have inflated the Type I error by picking and choosing after the fact which test to report. Vice versa, if our intent was to conceal a side effect by reporting the results were not significant, we will inflate the Type II error and deflate the power β of our test, by an after-the-fact choice as β = Pr{not (Wα and Pα and Tα)|K} ≤ Pr{Wα|K}.
To repeat, we are not free to pick and choose among tests; any such conduct is unethical. Both the comparison and the test statistic must be specified in advance of examining the data.
Clinical trials include substantial amounts of baseline data collected from each patient. Inevitably, subgroups exist for which a new treatment is more (or less) effective (or harmful) than for the trial as a whole. One has an ethical obligation to identify such subgroups.
But at the same time, one must guard against data dredging and placing post-hoc emphasis on the “most interesting” set of analyses across the many (many) potential subgroup analyses; p-values should not be given as they will depend on the total number of potential analyses, not merely on the actual number that were performed or reported. Results for subgroups may be factored in as part of a more-extensive Bayesian analysis; see Dixon and Simon [1991] and Simon [2002].
If the p-value you observe is greater than your predetermined significance level, this may mean any or all of the following:
If the p-value you observe is less than your predetermined significance level, this does not necessarily mean the effect you have detected is of practical significance; see, for example, the section on measuring equivalence. For this reason, as we discuss in Chapter 8, it is essential that you follow up any significant result by computing a confidence interval, so readers can judge for themselves whether the effect you have detected is of practical significance.
And do not forget that at the α percent significance level, α-percent of your tests will be statistically significant by chance alone.
Before you draw conclusions, be sure you have accounted for all missing data, interviewed nonresponders, and determined whether the data were missing at random or were specific to one or more subgroups.
During the Second World War, a group was studying planes returning from bombing Germany. They drew a rough diagram showing where the bullet holes were and recommended that those areas be reinforced. A statistician, Abraham Wald [1950],10 pointed out that essential data were missing from the sample they were studying. What about the planes that did not return from Germany?
When we think along these lines, we see that the two areas of the plane that had almost no bullet holes (where the wings and where the tail joined the fuselage) are crucial. Bullet holes in a plane are likely to be at random, occurring over the entire plane. Their absence in those two areas in returning bombers was diagnostic. Do the data missing from your experiments and surveys also have a story to tell?
Behold! human beings living in an underground den, which has a mouth open towards the light and reaching all along the den; here they have been from their childhood, and have their legs and necks chained so that they cannot move, and can only see before them, being prevented by the chains from turning round their heads. Above and behind them a fire is blazing at a distance, and between the fire and the prisoners there is a raised way; and you will see, if you look, a low wall built along the way, like the screen which marionette players have in front of them, over which they show the puppets.
And they see only their own shadows, or the shadows of one another, which the fire throws on the opposite wall of the cave.
To them, I said, the truth would be literally nothing but the shadows of the images.
—The Allegory of the Cave (Plato, The Republic, Book VII)
Never assign probabilities to the true state of nature, but only to the validity of your own predictions.
A p-value does not tell us the probability that a hypothesis is true, nor does a significance level apply to any specific sample; the latter is a characteristic of our testing in the long run. Likewise, if all assumptions are satisfied, a confidence interval will in the long run contain the true value of the parameter a certain percentage of the time. But we cannot say with certainty in any specific case that the parameter does or does not belong to that interval, Neyman [1961, 1977].
In our research efforts, the only statements we can make with God-like certainty are of the form “our conclusions fit the data.” The true nature of the real world is unknowable. We can speculate, but never conclude.
The gap between the sample and the population will always require a leap of faith, for we understand only insofar as we are capable of understanding [Lonergan, 1992]. See also the section on Deduction versus Induction in Chapter 2.
Know your objectives in testing. Know your data’s origins. Know the assumptions you feel comfortable with. Never assign probabilities to the true state of nature, but only to the validity of your own predictions. Collecting more and better data may be your best alternative.
For commentary on the use of wrong or inappropriate statistical methods, see Avram et al. [1985], Badrick and Flatman [1999], Berger et al. [2002], Bland and Altman [1995], Cherry [1998], Cox [1999], Dar, Serlin, and Omer [1994], Delucchi [1983], Elwood [1998], Felson, Cupples, and Meenan [1984], Fienberg [1990], Gore, Jones, and Rytter [1977], Lieberson [1985], MacArthur and Jackson [1984], McGuigan [1995], McKinney et al. [1989], Miller [1986], Padaki [1989], Welch and Gabbe [1996], Westgard and Hunt [1973], White [1979], and Yoccoz [1991].
Hunter and Schmidt [1997] emphasize why significance testing remains essential.
Guidelines for reviewers are provided by Altman [1998a], Bacchetti [2002], Finney [1997], Gardner, Machin and Campbell [1986], George [1985], Goodman, Altman and George [1998], International Committee of Medical Journal Editors [1997], Light and Pillemer [1984], Mulrow [1987], Murray [1988], Schor and Karten [1966], and Vaisrub [1985].
For additional comments on the effects of the violation of assumptions, see Box and Anderson [1955], Friedman [1937], Gastwirth and Rubin [1971], Glass, Peckham, and Sanders [1972], and Pettitt and Siskind [1981].
For the details of testing for equivalence, see Dixon [1998]. For a review of the appropriate corrections for multiple tests, see Tukey [1991].
For true tests of independence, see Romano [1990]. There are many tests for the various forms of dependence, such as quadrant dependence (Fisher’s Exact Test), trend (correlation), and serial correlation; see, for example, Maritz, 1996 and Manly [1997].
For procedures with which to analyze factorial and other multi-factor experimental designs, see Salmaso [2002] and Chapter 8 of Pesarin [2001].
Most of the problems with parametric tests reported here extend to and are compounded by multivariate analysis. For some solutions, see Chapter 9 of Good [2005], Chapter 6 of Pesarin [2001], and Pesarin [1990].
For a contrary view on adjustments of p-values in multiple comparisons, see Rothman [1990]. For a method for allocating Type I error among multiple hypotheses, see Moyé [2000].
Venn [1888] and Reichenbach [1949] are among those who have attempted to construct a mathematical bridge between what we observe and the reality that underlies our observations. To the contrary, extrapolation from the sample to the population is not a matter of applying Holmes-like deductive logic but entails a leap of faith. A careful reading of Locke [1700], Berkeley [1710], Hume [1748], and Lonergan [1992] is an essential prerequisite to the application of statistics.
For more on the contemporary view of induction, see Berger [2002] and Sterne, Smith, and Cox [2001]. The former notes yhat “Dramatic illustration of the non-frequentist nature of p-values can be seen from the applet available at www.stat.duke.edu/∼berger. The applet assumes one faces a series of situations involving normal data with unknown mean θ and known variance, and tests of the form H: θ = 0 versus K: θ ≠ 0. The applet simulates a long series of such tests, and records how often H is true for p-values in given ranges.”
Notes
1 Certified Color Manufacturers Association v. Mathews 543 F.2d 284 (1976 DC), Note 31.
2 466 F.Supp 1219 (E.D. PA 1979).
3 Id. at 1228–9.
4 Whether Republican or Democrat, Liberal or Conservative, male or female, we have the right to choose, and need not be limited by what our textbook, half-remembered teacher pronouncements, or software dictate.
5 Here and throughout this text, we deliberately ignore the many exceptional cases, the delight of the true mathematician, that one is unlikely to encounter in the real world.
6 Interested readers may want to verify this for themselves by writing out all the possible assignments of six items into two groups of three: 1 2 3/4 5 6, 1 2 4/3 5 6, and so forth.
7 For a discussion of these, see Brockwell and Davis [1987].
8 Such statistics are termed asymptotically pivotal.
9 This recommendation applies only to a test of efficacy for all groups (blocks) combined. p-values for subgroup analyses performed after the fact are still suspect; see Chapter 1.
10 This reference may be hard to obtain. Alternatively, see Mangel and Samaniego [1984].