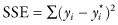, where yi and 
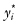denote the ith observed value and the corresponding value obtained from the model. The smaller this sum of squares, the better the fit.Chapter 15
Validation
[T]he simple idea of splitting a sample in two and then developing the hypothesis on the basis of one part and testing it on the remainder may perhaps be said to be one of the most seriously neglected ideas in statistics, if we measure the degree of neglect by the ratio of the number of cases where a method could give help to the number of cases where it is actually used.
—G. A. Barnard in discussion following Stone [1974, p. 133]
Validate your models before drawing conclusions.
ABSENT A DETAILED KNOWLEDGE OF CAUSAL MECHANISMS, THE results of a regression analysis are highly suspect. Freedman [1983] found highly significant correlations between totally independent variables. Gong [1986] resampled repeatedly from the data in hand and obtained a different set of significant variables each time.
A host of advertisements for new proprietary software claim an ability to uncover relationships previously hidden and to overcome the deficiencies of linear regression. But how can we determine whether or not such claims are true?
Good [2001; Chapter 10] reports on one such claim from the maker of PolyAnalyst™. He took the 400 records, each of 31 variables, PolyAnalyst provided in an example dataset, split the data in half at random, and obtained completely discordant results with the two halves, whether they were analyzed with PolyAnalyst, CART, or stepwise linear regression. This was yet another example of a spurious relationship that did not survive the validation process.
In this chapter, we review the various methods of validation and provide guidelines for their application.
Your choice of an appropriate methodology will depend upon your objectives and the stage of your investigation. Is the purpose of your model to predict whether there be an epidemic, to extrapolate—what might the climate have been like on the primitive Earth, or to elicit causal mechanisms—is development accelerating or decelerating? Which factors are responsible?
Are you still developing the model and selecting variables for inclusion, or are you in the process of estimating model coefficients?
There are three main approaches to validation:
Goodness of fit is no guarantee of predictive success. This is particularly true when an attempt is made to fit a deterministic model to a single realization of a stochastic process. Neyman and Scott [1952] showed that the distribution of galaxies in the observable universe could be accounted for by a two-stage Poisson process. At the initial stage, cluster centers come into existence so that their creation in nonoverlapping regions of time–space takes place independently of one another. At the second stage, the spatial distribution of galaxies about the cluster centers also follows a Poisson distribution.
Alas, our observations of the universe are based on a single realization of this two-stage process. Regardless, cosmologists, both astronomers and physicists, persist in validating their models on the basis of goodness of fit. See, for example, Bothun [1998], Springel et al. [2005] and Riess et al. [2007].
Independent verification is appropriate and preferable whatever the objectives of your model and whether selecting variables for inclusion or estimating model coefficients.
In soil, geologic, and economic studies, researchers often return to the original setting and take samples from points that have been by-passed on the original round; see, for example, Tsai et al. [2001].
In other studies, verification of the model’s form and the choice of variables are obtained by attempting to fit the same model in a similar but distinct context.
For example, having successfully predicted an epidemic at one army base, one would then wish to see if a similar model might be applied at a second and third almost but not quite identical base.
Stockton and Meko [1983] reconstructed regional-average precipitation to A.D. 1700 in the Great Plains of the United States with multiple linear regression models calibrated on the period 1933–1977. They validated the reconstruction by comparing the reconstructed regional percentage-of-normal precipitation with single-station precipitation for stations with records extending back as far as the 1870s. Lack of appreciable drop in correlation between these single-station records and the reconstruction from the calibration period to the earlier segment was taken as evidence for validation of the reconstructions.
Graumlich [1993] used a response-surface reconstruction method to reconstruct 1000 years of temperature and precipitation in the Sierra Nevada. The calibration climatic data were 62 years of observed precipitation and temperature (1928–1989) at Giant Forest/Grant Grove. The model was validated by comparing the predictions with the 1873–1927 segments of three climate stations 90 km to the west in the San Joaquin Valley. The climatic records of these stations were highly correlated with those at Giant Forest/Grant Grove. Significant correlation of these long-term station records with the 1873–1927 part of the reconstruction was accepted as evidence of validation.
Independent verification can help discriminate among several models that appear to provide equally good fits to the data. Independent verification can be used in conjunction with either of the two other validation methods. For example, an automobile manufacturer was trying to forecast parts sales. After correcting for seasonal effects and long-term growth within each region, ARIMA techniques were used.1 A series of best-fitting ARIMA models was derived, one model for each of the nine sales regions into which the sales territory had been divided. The nine models were quite different in nature. As the regional seasonal effects and long-term growth trends had been removed, a single ARIMA model applicable to all regions, albeit with differing coefficients, was more plausible. Accordingly, the ARIMA model that gave the best overall fit to all regions was utilized for prediction purposes.
Independent verification also can be obtained through the use of surrogate or proxy variables. For example, we may want to investigate past climates and test a model of the evolution of a regional or worldwide climate over time. We cannot go back directly to a period before direct measurements on temperature and rainfall were made, but we can observe the width of growth rings in long-lived trees or measure the amount of carbon dioxide in ice cores.
In 1929, Edwin Hubble conjectured that our universe was expanding at a constant rate h. The value of this constant can be determined in two ways:
The recession speed is easy to measure from the degree to which a distant object’s light is displaced toward the red end of the spectrum. Initially, the distance was measured from celestial objects within the Vegan supercluster of galaxies, the super-cluster to which our own Milky Way belongs. Various methods of measurement (Cepheid variables and Type II supernovae) yield an esimate for H close to 0.73 ± 0.07. Supernovae of Type Ia in galaxies far beyond the Vegan supercluster yield an average value for the Hubble constant of 0.58 ± 0.07.
The age of the universe is approximately the age of the Milky Way if one assumes that h = 0.85, and the standard model (Wm = 1, WL = 0) is satisfied only if h < 0.55.
Two explanations for the many discrepancies are available, both of which explain the postorbital-telescope discovery that though the Vegan supercluster is slowly collapsing on itself under the influence of gravity, the different superclusters of galaxies are flying apart at high speed:
Splitting the sample into two parts, one for estimating the model parameters, the other for verification, is particularly appropriate for validating time series models in which the emphasis is on prediction or reconstruction. If the observations form a time series, the more recent observations should be reserved for validation purposes. Otherwise, the data used for validation should be drawn at random from the entire sample.
Unfortunately, when we split the sample and use only a portion of it, the resulting estimates will be less precise.
Browne [1975] suggests that we pool rather than split the sample if
The proportion to be set aside for validation purposes will depend upon the loss function. If both the goodness-of-fit error in the calibration sample and the prediction error in the validation sample are based on mean-squared error, Picard and Berk [1990] report that we can minimize their sum by using between a quarter and a third of the sample for validation purposes.
A compromise proposed by Moiser [1951] is worth revisiting: the original sample is split in half and regression variables and coefficients are selected independently for each of the sub-samples. If they are more or less in agreement, then the two samples should be combined and the coefficients recalculated with greater precision.
A further proposal by Subrahmanyam [1972] to use weighted averages where there are differences strikes us as equivalent to painting over cracks left by the last earthquake. Such differences are a signal to probe deeper, to look into causal mechanisms, and to isolate influential observations which may, for reasons that need to be explored, be marching to a different drummer.
We saw in the report of Gail Gong [1986], reproduced in Chapter 13, that resampling methods such as the bootstrap may be used to validate our choice of variables to include in the model. As seen in Chapter 5, they may also be used to estimate the precision of our estimates.
But if we are to extrapolate successfully from our original sample to the population at large, then our original sample must bear a strong resemblance to that population. When only a single predictor variable is involved, a sample of 25 to 100 observations may suffice. But when we work with n variables simultaneously, sample sizes on the order of 25n to 100n may be required to adequately represent the full n-dimensional region.
Because of dependencies among the predictors, we can probably get by with several orders of magnitude fewer data points. But the fact remains that the sample size required for confidence in our validated predictions grows exponentially with the number of variables.
Five resampling techniques are in general use:
The correct choice among these methods in any given instance is still a matter of controversy (though any individual statistician will assure you that the matter is quite settled). See, for example, Wu [1986] and the discussion following, and Shao and Tu [1995].
Leave-one-out has the advantage of allowing us to study the influence of specific observations on the overall outcome.
Our own opinion is that if any of the above methods suggest that the model is unstable, the first step is to redefine the model over a more restricted range of the various variables. For example, with the data of Figure 11.3, we would advocate confining attention to observations for which the predictor (TNFAlpha) was less than 200.
If a more general model is desired, then many additional observations should be taken in underrepresented ranges. In the cited example, this would be values of TNFAlpha greater than 300.
Whatever method of validation is used, we need to have some measure of the success of the prediction procedure. One possibility is to use the sum of the losses in the calibration and the validation sample. Even this procedure contains an ambiguity that we need resolve. Are we more concerned with minimizing the expected loss, the average loss, or the maximum loss?
One measure of goodness of fit of the model is 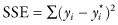, where yi and 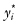denote the ith observed value and the corresponding value obtained from the model. The smaller this sum of squares, the better the fit.
If the observations are independent, then
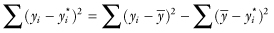
The first sum on the right hand side of the equation is the total sum of squares (SST). Most statistics software use as a measure of fit R2 = 1 − SSE/SST. The closer the value of R2 is to 1, the better.
The automated entry of predictors into the regression equation using R2 runs the risk of overfitting, as R2 is guaranteed to increase with each predictor entering the model. To compensate, one may use the adjusted R2:
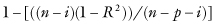
where n is the number of observations used in fitting the model, p is the number of estimated regression coefficients, and i is an indicator variable that is 1 if the model includes an intercept, and 0 otherwise.
The adjusted R2 has two major drawbacks according to Rencher and Pun [1980]:
A preferable method of guarding against overfitting the regression model, proposed by Wilks [1995], is to use validation as a guide for stopping the entry of additional predictors. Overfitting is judged to begin when entry of an additional predictor fails to reduce the prediction error in the validation sample.
Mielke et al. [1997] propose the following measure of predictive accuracy for use with either a mean-square-deviation or a mean-absolute-deviation loss function:
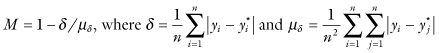
Whatever measure is used, the degree of uncertainty in your predictions should be reported. Error bars are commonly used for this purpose.
The prediction error is larger when the predictor data are far from their calibration-period means, and vice versa. For simple linear regression, the standard error of the estimate se and standard error of prediction sy* are related as follows:
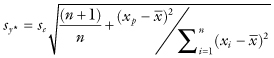
where n is the number of observations, xi is the ith value of the predictor in the calibration sample, and xp is the value of the predictor used for the prediction.
The relation between sy* and se is easily generalized to the multivariate case. In matrix terms, if Y = AX + E and y* = AXp, then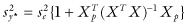 
.
This equation is only applicable if the vector of predictors lies inside the multivariate cluster of observations on which the model was based. An important question is how “different” can the predictor data be from the values observed in the calibration period before the predictions are considered invalid.
Time is a hidden dimension in most economic models. Many an airline has discovered to its detriment that today’s optimal price leads to half-filled planes and markedly reduced profits tomorrow. A careful reading of the Internet lets them know a competitor has slashed prices, but more advanced algorithms are needed to detect a slow shifting in tastes of prospective passengers. The public, tired of being treated no better than hogs2 turns to trains, personal automobiles, and teleconferencing.
An army base, used to a slow seasonal turnover in recruits, suddenly finds that all infirmary beds are occupied and the morning lineup for sick call stretches the length of a barracks.
To avoid a pound of cure
Most monitoring algorithms take the following form:
Almost always, a model developed on one set of data will fail to fit a second independent sample nearly as well. Mielke et al. [1996] investigated the effects of sample size, type of regression model, and noise-to-signal ratio on the decrease or shrinkage in fit from the calibration to the validation dataset.
For more on leave-one-out validation, see Michaelsen [1987], Weisberg [1985], and Barnston and van den Dool [1993]. Camstra and Boomsma [1992] and Shao and Tu [1995] review the application of resampling in regression.
Miller, Hui, and Tierney [1991] propose validation techniques for logistic regression models. Taylor [2000] recommends the bootstrap for validating financial models.
Watterson [1966] reviews the various measures of predictive accuracy.
Notes
1 For examples and discussion of autoregressive integrated moving average processes, see Brockwell and Davis [1987].
2 Or somewhat worse, because hogs generally have a higher percentage of fresh air to breathe.