

Solids are one of the three basic states of matter, the others being liquids and gases. (Sometimes plasmas, or ionized gases, are considered a fourth state of matter.) A solid forms from liquid or gas because the energy of atoms decreases when the atoms take up a relatively ordered, three-dimensional structure.
Solids exhibit certain characteristics that distinguish them from liquids and gases. All solids have, for example, the ability to resist forces applied either perpendicular or parallel to a surface (i.e., normal or shear loads, respectively). Such properties depend on the properties of the atoms that form the solid, on the way those atoms are arranged, and on the forces between them.
Solids are generally divided into three broad classes—crystalline, noncrystalline (amorphous), and quasicrystalline. Crystalline solids have a very high degree of order in a periodic atomic arrangement. Practically all metals and many other minerals, such as common table salt (sodium chloride), belong to this class. Noncrystalline solids are those in which atoms and molecules are not organized in a definite lattice pattern. They include glasses, plastics, and gels. Quasicrystalline solids display novel symmetries in which the atoms are arranged in quasiperiodic fashion—i.e., in patterns that do not repeat at regular intervals. They exhibit symmetries, such as fivefold symmetry, that are forbidden in ordinary crystals. Quasicrystal structures are common in alloys in which aluminum is combined with another metal, such as iron, cobalt, or nickel.
Some molecules may exist in the liquid crystal state, which is intermediate to the crystalline solid and liquid states. Liquid crystals flow like liquids yet display a certain degree of the symmetry characteristic of crystalline solids.
Four principal types of atomic bonds are found in crystalline solids: metallic, ionic, covalent, and molecular. Metals and their alloys are characterized in the main by their high electrical and thermal conductivity, which arise from the migration of free electrons; free electrons also influence how the atoms bond. Ionic crystals are aggregates of charged ions. These salts commonly exhibit ionic conductivity, which increases with temperature. Covalent crystals are hard, frequently brittle materials such as diamond, silicon, and silicon carbide. In the simpler, monatomic types (e.g., diamond), each atom is surrounded by a number of atoms equal to its valence. Molecular crystals are substances that have relatively weak intermolecular binding, such as dry ice (solidified carbon dioxide), solid forms of the rare gases (e.g., argon, krypton, and xenon), and crystals of numerous organic compounds.
Various alloys, salts, covalent crystals, and molecular crystals that are good electrical insulators at low temperature become conductors at elevated temperatures, conductivity increasing rapidly with temperature. Materials of this type are called semiconductors. Their electrical conductivity is generally low when compared with that of such metals as copper, silver, or aluminum.
The definition of a solid appears obvious; a solid is generally thought of as being hard and firm. Upon inspection, however, the definition becomes less straightforward. A cube of butter, for example, is hard after being stored in a refrigerator and is clearly a solid. After remaining on the kitchen counter for a day, the same cube becomes quite soft, and it is unclear if the butter should still be considered a solid. Many crystals behave like butter in that they are hard at low temperatures but soft at higher temperatures. They are called solids at all temperatures below their melting point. A possible definition of a solid is an object that retains its shape if left undisturbed. The pertinent issue is how long the object keeps its shape. A highly viscous fluid retains its shape for an hour but not a year. A solid must keep its shape longer than that.
The basic units of solids are either atoms or atoms that have combined into molecules. The electrons of an atom move in orbits that form a shell structure around the nucleus. The shells are filled in a systematic order, with each shell accommodating only a small number of electrons. Different atoms have different numbers of electrons, which are distributed in a characteristic electronic structure of filled and partially filled shells. The arrangement of an atom’s electrons determines its chemical properties. The properties of solids are usually predictable from the properties of their constituent atoms and molecules, and the different shell structures of atoms are therefore responsible for the diversity of solids.
All occupied shells of the argon (Ar) atom, for example, are filled, resulting in a spherical atomic shape. In solid argon the atoms are arranged according to the closest packing of these spheres. The iron (Fe) atom, in contrast, has one electron shell that is only partially filled, giving the atom a net magnetic moment. Thus, crystalline iron is a magnet. The covalent bond between two carbon (C) atoms is the strongest bond found in nature. This strong bond is responsible for making diamond the hardest solid.
A solid is crystalline if it has long-range order. Once the positions of an atom and its neighbours are known at one point, the place of each atom is known precisely throughout the crystal. Most liquids lack long-range order, although many have short-range order. Short range is defined as the first- or second-nearest neighbours of an atom. In many liquids the first-neighbour atoms are arranged in the same structure as in the corresponding solid phase. At distances that are many atoms away, however, the positions of the atoms become uncorrelated. These fluids, such as water, have short-range order but lack long-range order. Certain liquids may have short-range order in one direction and long-range order in another direction; these special substances are called liquid crystals. Solid crystals have both short-range order and long-range order.
Solids that have short-range order but lack long-range order are called amorphous. Almost any material can be made amorphous by rapid solidification from the melt (molten state). This condition is unstable, and the solid will crystallize in time. If the timescale for crystallization is years, then the amorphous state appears stable. Glasses are an example of amorphous solids. In crystalline silicon (Si) each atom is tetrahedrally bonded to four neighbours. In amorphous silicon (a-Si) the same short-range order exists, but the bond directions become changed at distances farther away from any atom. Amorphous silicon is a type of glass. Quasicrystals are another type of solid that lack long-range order.
Most solid materials found in nature exist in polycrystalline form rather than as a single crystal. They are actually composed of millions of grains (small crystals) packed together to fill all space. Each individual grain has a different orientation from its neighbours. Although long-range order exists within one grain, at the boundary between grains, the ordering changes direction. A typical piece of iron or copper (Cu) is polycrystalline. Single crystals of metals are soft and malleable, while polycrystalline metals are harder and stronger and are more useful industrially. Most polycrystalline materials can be made into large single crystals after extended heat treatment. In the past blacksmiths would heat a piece of metal to make it malleable: heat makes a few grains grow large by incorporating smaller ones. The smiths would bend the softened metal into shape and then pound it awhile; the pounding would make it polycrystalline again, increasing its strength.
Crystals are classified in general categories, such as insulators, metals, semiconductors, and molecular solids. A single crystal of an insulator is usually transparent and resembles a piece of glass. Metals are shiny unless they have rusted. Semiconductors are sometimes shiny and sometimes transparent but are never rusty. Many crystals can be classified as a single type of solid, while others have intermediate behaviour. Cadmium sulfide (CdS) can be prepared in pure form and is an excellent insulator; when impurities are added to cadmium sulfide, it becomes an interesting semiconductor. Bismuth (Bi) appears to be a metal, but the number of electrons available for electrical conduction is similar to that of semiconductors. In fact, bismuth is called a semimetal. Molecular solids are usually crystals formed from molecules or polymers. They can be insulating, semiconducting, or metallic, depending on the type of molecules in the crystal. New molecules are continuously being synthesized, and many are made into crystals. The number of different crystals is enormous.
Crystals can be grown under moderate conditions from all 92 naturally occurring elements except helium, and helium can be crystallized at low temperatures by using 25 atmospheres of pressure. Binary crystals are composed of two elements. There are thousands of binary crystals; some examples are sodium chloride (NaCl), alumina (Al2O3), and ice (H2O). Crystals can also be formed with three or more elements.
A basic concept in crystal structures is the unit cell. It is the smallest unit of volume that permits identical cells to be stacked together to fill all space. By repeating the pattern of the unit cell over and over in all directions, the entire crystal lattice can be constructed. A cube is the simplest example of a unit cell. Two other examples are the face-centred cubic lattice and the body-centred cubic lattice.
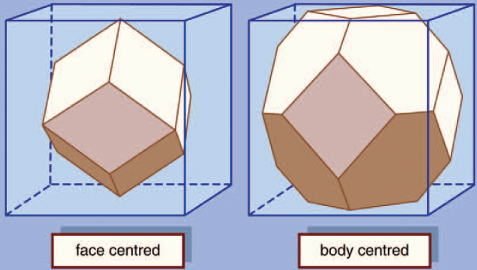
Unit cells for face-centred and body-centred cubic lattices. Copyright Encyclopædia Britannica; rendering for this edition by Rosen Educational Services
There are only a few different unit-cell shapes, so many different crystals share a single unit-cell type. An important characteristic of a unit cell is the number of atoms it contains. The total number of atoms in the entire crystal is the number in each cell multiplied by the number of unit cells. Copper and aluminum (Al) each have one atom per unit cell, while zinc (Zn) and sodium chloride have two. Most crystals have only a few atoms per unit cell, but there are some exceptions. Crystals of polymers, for example, have thousands of atoms in each unit cell.
The elements are found in a variety of crystal packing arrangements. The most common lattice structures for metals are those obtained by stacking the atomic spheres into the most compact arrangement. There are two such possible periodic arrangements. In each, the first layer has the atoms packed into a plane-triangular lattice in which every atom has six immediate neighbours. The second layer has the same plane-triangular structure; the atoms sit in the holes formed by the first layer. The first layer has two equivalent sets of holes, but the atoms of the second layer can occupy only one set. The third layer, labeled C, has the same structure, but there are two choices for selecting the holes that the atoms will occupy. The third layer can be placed over the atoms of the first layer, generating an alternate layer sequence ABABAB…, which is called the hexagonal closest-packed (hcp) structure. Cadmium and zinc crystallize with this structure.
The second possibility is to place the atoms of the third layer over those of neither of the first two but instead over the set of holes in the first layer that remains unoccupied. The fourth layer is placed over the first, and so there is a three-layer repetition ABCABCABC…, which is called the face-centred cubic (fcc), or cubic-closest-packed, lattice. Copper, silver (Ag), and gold (Au) crystallize in fcc lattices. In the hcp and the fcc structures the spheres fill 74 percent of the volume, which represents the closest possible packing of spheres. Each atom has 12 neighbours. The number of atoms in a unit cell is two for hcp structures and one for fcc. There are 32 metals that have the hcp lattice and 26 with the fcc. Another possible arrangement is the body-centred cubic (bcc) lattice, in which each atom has eight neighbours arranged at the corners of a cube. For example, the cesium chloride (CsCl) structure is a cubic arrangement. If all atoms in this structure are of the same species, it is a bcc lattice. The spheres occupy 68 percent of the volume. There are 23 metals with the bcc arrangement. The sum of these three numbers (32 + 26 + 23) exceeds the number of elements that form metals (63), since some elements are found in two or three of these structures.
Stacking of spheres in closest-packed arrangements. Copyright Encyclopædia Britannica; rendering for this edition by Rosen Educational Services
The fcc structure is also found for crystals of the rare gas solids neon (Ne), argon (Ar), krypton (Kr), and xenon (Xe). Their melting temperatures at atmospheric pressure are: Ne, 24.6 K (–248.5 °C, or –415.4 °F); Ar, 83.8 K (–189.4 °C, or –308.8 °F); Kr, 115.8 K (–157.4 °C, or –251.2 °F); and Xe, 161.4 K (–111.8 °C, or –169.2 °F).
The elements in the fourth row of the periodic table—carbon, silicon, germanium (Ge), and α-tin (α-Sn)—prefer covalent bonding. Carbon has several possible crystal structures. Each atom in the covalent bond has four first-neighbours, which are at the corners of a tetrahedron. This arrangement is called the diamond lattice. There are two atoms in a unit cell, which is fcc. Large crystals of diamond are valuable gemstones. The crystal has other interesting properties; it has the highest sound velocity of any solid and is the best conductor of heat. Besides diamond, the other common form of carbon is graphite, which is a layered material. Each carbon atom has three coplanar near neighbours, forming an arrangement called the honeycomb lattice. Three-dimensional graphite crystals are obtained by stacking similar layers.
Another form of crystalline carbon is based on a molecule with 60 carbon atoms called buckminsterfullerene (C60). The molecular shape is spherical. Each carbon is bonded to three neighbours, as in graphite, and the spherical shape is achieved by a mixture of 12 rings with five sides and 20 rings with six sides. Similar structures were first visualized by the American architect R. Buckminster Fuller for geodesic domes. The C60 molecules, also called buckyballs, are quite strong and almost incompressible. Crystals are formed such that the balls are arranged in an fcc lattice with a one-nanometre spacing between the centres of adjacent balls. The similar C70 molecule has the shape of a rugby ball; C70 molecules also form an fcc crystal when stacked together. The solid fullerenes form molecular crystals, with weak binding—provided by van der Waals interactions—between the molecules.
Many elements form diatomic gases: hydrogen (H), oxygen (O), nitrogen (N), fluorine (F), chlorine (Cl), bromine (Br), and iodine (I). When cooled to low temperature, they form solids of diatomic molecules. Nitrogen has the hcp structure, while oxygen has a more complex structure.
The most interesting crystal structures are those of elements that are neither metallic, covalent, nor diatomic. Although boron (B) and sulfur (S) have several different crystal structures, each has one arrangement in which it is usually found. Twelve boron atoms form a molecule in the shape of an icosahedron. Crystals are formed by stacking the molecules. The β-rhombohedral structure of boron has seven of these icosahedral molecules in each unit cell, giving a total of 84 atoms. Molecules of sulfur are usually arranged in rings; the most common ring has eight atoms. The typical structure is α-sulfur, which has 16 molecules per unit cell, or 128 atoms. In the common crystals of selenium (Se) and tellurium (Te), the atoms are arranged in helical chains, which stack like cordwood. However, selenium also makes eight-atom rings, similar to sulfur, and forms crystals from them. Sulfur also makes helical chains, similar to selenium, and stacks them together into crystals.
The icosahedral arrangement of a boron molecule. Copyright Encyclopædia Britannica; rendering for this edition by Rosen Educational Services
Binary crystals are found in many structures. Some pairs of elements form more than one structure. At room temperature, cadmium sulfide may crystallize either in the zinc blende or wurtzite structure. Alumina also has two possible structures at room temperature, α-alumina (corundum) and β-alumina. Other binary crystals exhibit different structures at different temperatures. Among the most complex crystals are those of silicon dioxide (SiO2), which has seven different structures at various temperatures and pressures; the most common of these structures is quartz. Some pairs of elements form several different crystals in which the ions have different chemical valences. Cadmium (Cd) and phosphorus (P) form the crystals Cd3P2, CdP2, CdP4, Cd7P10, and Cd6P7. Only in the first case are the ions assigned the expected chemical valences of Cd2+ and P3-.
Among the binary crystals, the easiest structures to visualize are those with equal numbers of the two types of atoms. The structure of sodium chloride is based on a cube. To construct the lattice, the sodium and chlorine atoms are placed on alternate corners of a cube, and the structure is repeated. The structure of the sodium atoms alone, or the chlorine atoms alone, is fcc and defines the unit cell. The sodium chloride structure thus is made up of two interpenetrating fcc lattices. The cesium chloride lattice is based on the bcc structure; every other atom is cesium or chlorine. In this case, the unit cell is a cube. The third important structure for AB (binary) lattices is zinc blende. It is based on the diamond structure, where every other atom is A or B. Many binary semiconductors have this structure, including those with one atom from the third (boron, aluminum, gallium [Ga], or indium [In]) and one from the fifth (nitrogen, phosphorus, arsenic [As], or antimony [Sb]) column of the periodic table (GaAs, InP, etc.). Most of the chalcogenides (O, S, Se, Te) of cadmium and zinc (CdTe, ZnSe, ZnTe, etc.) also have the zinc blende structure. The mineral zinc blende is ZnS; its unit cell is also fcc. The wurtzite structure is based on the hcp lattice, where every other atom is A or B. These four structures comprise most of the binary crystals with equal numbers of cations and anions.
Crystal structures. There is an equal number of the two types of ions in the unit cell of the (A) cesium chloride, (B) sodium chloride, and (D) zinc blende arrangements. The diamond arrangement is shown in (C). If both atoms are identical in (A), the structure is body-centred cubic. Copyright Encyclopædia Britannica; rendering for this edition by Rosen Educational Services
The fullerene molecule forms binary crystals Mx C60 with alkali atoms, where M is potassium (K), rubidium (Rb), or cesium (Cs). The fullerene molecules retain their spherical shape, and the alkali atoms sit between them. The subscript x can take on several values. A compound with x = 6 (e.g., K6C60) is an insulator with the fullerenes in a bcc structure. The case x = 4 is an insulator with the body-centred tetragonal structure, while the case x = 3 is a metal with the fullerenes in an fcc structure. K3C60, Rb3C60, and Cs3C60 are superconductors at low temperatures.
Alloys are solid mixtures of atoms with metallic properties. The definition includes both amorphous and crystalline solids. Although many pairs of elements will mix together as solids, many pairs will not. Almost all chemical entities can be mixed in liquid form. But cooling a liquid to form a solid often results in phase separation; a polycrystalline material is obtained in which each grain is purely one atom or the other. Extremely rapid cooling can produce an amorphous alloy. Some pairs of elements form alloys that are metallic crystals. They have useful properties that differ from those exhibited by the pure elements. For example, alloying makes a metal stronger; for this reason alloys of gold, rather than the pure metal, are used in jewelry.
Atoms tend to form crystalline alloys when they are of similar size. The sizes of atoms are not easy to define, however, because atoms are not rigid objects with sharp boundaries. The outer part of an atom is composed of electrons in bound orbits; the average number of electrons decreases gradually with increasing distance from the nucleus. There is no point that can be assigned as the precise radius of the atom. Scientists have discovered, however, that each atom in a solid has a characteristic radius that determines its preferred separation from neighbouring atoms. For most types of atom this radius is constant, even in different solids. An empirical radius is assigned to each atom for bonding considerations, which leads to the concept of atomic size. Atoms readily make crystalline alloys when the radii of the two types of atoms agree to within roughly 15 percent.
Two kinds of ordering are found in crystalline alloys. Most alloys at low temperature are binary crystals with perfect ordering. An example is the alloy of copper and zinc. Copper is fcc, whereas zinc is hcp. A 50-percent-zinc–50-percent-copper alloy has a different structure—β-brass. At low temperatures it has the cesium chloride structure: a bcc lattice with alternating atoms of copper and zinc and a cubic unit cell. If the temperature is raised above 470 °C (878 °F), however, a phase transition to another crystalline state occurs. The ordering at high temperature is also bcc, but now each site has equal probability of having a copper or zinc atom. The two types of atoms randomly occupy each site, but there is still long-range order. At all temperatures, thousands of atoms away from a site, the location of the atom site can be predicted with certainty. At temperatures below 470 °C one also knows whether that site will be occupied by a copper or zinc atom, while above 470 °C there is an equal likelihood of finding either atom. The high-temperature phase is crystalline but disordered. The disorder phase is obtained through a partial melting, not into a liquid state but into a less ordered one. This behaviour is typical of metal alloys. Other common alloys are steel, an alloy of iron and carbon; stainless steel, an alloy of iron, nickel (Ni), and chromium (Cr); pewter and solder, alloys of tin and lead (Pb); and britannia metal, an alloy of tin, antimony, and copper.
A crystal is never perfect; a variety of imperfections can mar the ordering. A defect is a small imperfection affecting a few atoms. The simplest type of defect is a missing atom and is called a vacancy. Since all atoms occupy space, extra atoms cannot be located at the lattice sites of other atoms, but they can be found between them; such atoms are called interstitials. Thermal vibrations may cause an atom to leave its original crystal site and move into a nearby interstitial site, creating a vacancy-interstitial pair. Vacancies and interstitials are the types of defects found in a pure crystal. In another defect, called an impurity, an atom is present that is different from the host crystal atoms. Impurities may either occupy interstitial spaces or substitute for a host atom in its lattice site.
There is no sharp distinction between an alloy and a crystal with many impurities. An alloy results when a sufficient number of impurities are added that are soluble in the host metal. However, most elements are not soluble in most crystals. Crystals generally can tolerate a few impurities per million host atoms. If too many impurities of the insoluble variety are added, they coalesce to form their own small crystallite. These inclusions are called precipitates and constitute a large defect.
Germanium is a common impurity in silicon. It prefers the same tetrahedral bonding as silicon and readily substitutes for silicon atoms. Similarly, silicon is a common impurity in germanium. No large crystal can be made without impurities; the purest large crystal ever grown was made of germanium. It had about 1010 impurities in each cubic centimetre of material, which is less than one impurity for each trillion atoms.
Impurities often make crystals more useful. In the absence of impurities, α-alumina is colourless. Iron and titanium impurities impart to it a blue colour, and the resulting gem-quality mineral is known as sapphire. Chromium impurities are responsible for the red colour characteristic of rubies, the other gem of α-alumina. Pure semiconductors rarely conduct electricity well at room temperatures. Their ability to conduct electricity is caused by impurities. Such impurities are deliberately added to silicon in the manufacture of integrated circuits. In fluorescent lamps the visible light is emitted by impurities in the phosphors (luminescent materials).
Other imperfections in crystals involve many atoms. Twinning is a special type of grain boundary defect, in which a crystal is joined to its mirror image. Another kind of imperfection is a dislocation, which is a line defect that may run the length of the crystal. One of the many types of dislocations is due to an extra plane of atoms that is inserted somewhere in the crystal structure. Another type is called an edge dislocation. This line defect occurs when there is a missing row of atoms. In the figure the crystal arrangement is perfect on the top and on the bottom. The defect is the row of atoms missing from region b. This mistake runs in a line that is perpendicular to the page and places a strain on region a.
Crystalline lattice defect. An edge dislocation occurs when there is a missing row of atoms as shown in region b. Region a is strained. Copyright Encyclopædia Britannica; rendering for this edition by Rosen Educational Services
Dislocations are formed when a crystal is grown, and great care must be taken to produce a crystal free of them. Dislocations are stable and will exist for years. They relieve mechanical stress. If one presses on a crystal, it will accommodate the induced stress by growing dislocations at the surface, which gradually move inward. Dislocations make a crystal mechanically harder. When a metal bar is cold-worked by rolling or hammering, dislocations and grain boundaries are introduced; this causes the hardening.
Crystal structures are determined by scattering experiments using a portion of the crystal as the target. A beam of particles is sent toward the target, and upon impact some of the particles scatter from the crystal and ricochet in various directions. A measurement of the scattered particles provides raw data, which is then computer-processed to give a picture of the atomic arrangements. The positions are then inferred from the computer-analyzed data.
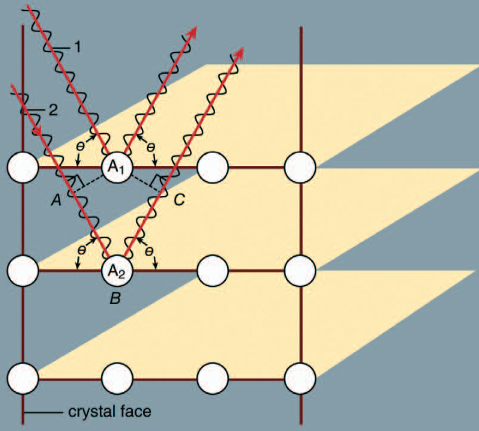
Incident rays (1 and 2) at angle θ on the planes of atoms in a crystal. Rays reinforce if their difference in path length (AB + BC) is an integer times the wavelength of the X ray. Copyright Encyclopædia Britannica; rendering for this edition by Rosen Educational Services
Max von Laue first suggested in 1912 that this measurement could be done using X rays, which are electromagnetic radiation of very high frequency. High frequencies are needed because these waves have a short wavelength. Von Laue realized that atoms have a spacing of only a few angstroms (1 angstrom [Å] is 10-10 metre, or 3.94 × 10-9 inch). In order to measure atomic arrangements, the particles scattering from the target must also have a wavelength of a few angstroms. X rays are required when the beam consists of electromagnetic radiation. The X rays only scatter in certain directions, and there are many X rays associated with each direction. The scattered particles appear in spots corresponding to locations where the scattering from each identical atom produces an outgoing wave that has all the wavelengths in phase. The scattering from an atom A2 further in the crystal has a longer path than that from atom A1. If this additional path has a length (AB + BC) that is an exact multiple of the wavelength, then the two outgoing waves are in phase and reinforce each other. If the scattering angle is changed slightly, the waves no longer add coherently and begin to cancel one another. Combining the scattered radiation from all the atoms in the crystal causes all the outgoing waves to add coherently in certain directions and produce a strong signal in the scattered wave. If the extra path length (AB + BC) is five wavelengths, for example, the spot appears in one place. If it is six wavelengths, the spot is elsewhere. Thus, the different spots correspond to the different multiples of the wavelength of the X ray. The measurement produces two types of information: the directions of the spots and their intensity. This information is insufficient to deduce the exact crystal structure, however, as there is no algorithm by which the computer can go directly from the data to the structure. The crystallographer must propose various structures and compute how they would scatter the X rays. The theoretical results are compared with the measured one, and the theoretical arrangement is chosen that best fits the data. Although this procedure is fast when there are only a few atoms in a unit cell, it may take months or years for complex structures. Some protein molecules, for instance, have hundreds of atoms. Crystals of the proteins are grown, and X rays are used to measure the structure. The goal is to determine how the atoms are arranged in the protein, rather than how the proteins are arranged in the crystal.
Beams of neutrons may also be used to measure crystal structure. The beam of neutrons is obtained by drilling a hole in the side of a nuclear reactor. The energetic neutrons created in nuclear fission escape through the hole. The motion of elementary particles is governed by quantum, or wave, mechanics. Each neutron has a wavelength that depends on its momentum. The scattering directions are determined by the wavelength, as is the case with X rays. The wavelengths for neutrons from a reactor are suitable for measuring crystal structures.
X rays and neutrons provide the basis for two competing technologies in crystallography. Although they are similar in principle, the two methods have some differences. X rays scatter from the electrons in the atoms so that more electrons result in more scattering. X rays easily detect atoms of high atomic number, which have many electrons, but cannot readily locate atoms with few electrons. In hydrogen-bonded crystals, X rays do not detect the protons at all. Neutrons, on the other hand, scatter from the atomic nucleus. They scatter readily from protons and are excellent for determining the structure of hydrogen-bonded solids. One drawback to this method is that some nuclei absorb neutrons completely, and there is little scattering from these targets.
Beams of electrons can also be used to measure crystal structure, because energetic electrons have a wavelength that is suitable for such measurements. The problem with electrons is that they scatter strongly from atoms. Proper interpretation of the experimental results requires that an electron scatter only from one atom and leave the crystal without scattering again. Low-energy electrons scatter many times, and the interpretation must reflect this. Low-energy electron diffraction (LEED) is a technique in which a beam of electrons is directed toward the surface. The scattered electrons that reflect backward from the surface are measured. They scatter many times before leaving backward but mainly leave in a few directions that appear as “spots” in the measurements. An analysis of the varied spots gives information on the crystalline arrangement. Because the electrons are scattered strongly by the atoms in the first few layers of the surface, the measurement gives only the arrangements of atoms in these layers. It is assumed that the same structure is repeated throughout the crystal. Another scattering experiment involves electrons of extremely high energy. The scattering rate decreases as the energy of the electron increases, so that very energetic electrons usually scatter only once. Various electron microscopes are constructed on this principle.
The properties of a solid can usually be predicted from the valence and bonding preferences of its constituent atoms. Four main bonding types are discussed here: ionic, covalent, metallic, and molecular. Hydrogen-bonded solids, such as ice, make up another category that is important in a few crystals. There are many examples of solids that have a single bonding type, while other solids have a mixture of types, such as covalent and metallic or covalent and ionic.
Sodium chloride exhibits ionic bonding. The sodium atom has a single electron in its outermost shell, while chlorine needs one electron to fill its outer shell. Sodium donates one electron to chlorine, forming a sodium ion (Na+) and a chlorine ion (Cl-). Each ion thus attains a closed outer shell of electrons and takes on a spherical shape. In addition to having filled shells and a spherical shape, the ions of an ionic solid have integer valence. An ion with positive valence is called a cation. In an ionic solid the cations are surrounded by ions with negative valence, called anions. Similarly, each anion is surrounded by cations. Since opposite charges attract, the preferred bonding occurs when each ion has as many neighbours as possible, consistent with the ion radii. Six or eight nearest neighbours are typical; the number depends on the size of the ions and not on the bond angles. The alkali halide crystals are binaries of the AH type, where A is an alkali ion (lithium [Li], sodium, potassium, rubidium, or cesium) and H is a halide ion (fluorine, chlorine, bromine, or iodine). The crystals have ionic bonding, and each ion has six or eight neighbours. Metal ions in the alkaline earth series (magnesium [Mg], calcium [Ca], barium [Ba], and strontium [Sr]) have two electrons in their outer shells and form divalent cations in ionic crystals. The chalcogenides (oxygen, sulfur, selenium, and tellurium) need two electrons to fill their outer p-shell. (Electron shells are divided into subshells, designated as s, p, d, f, g, and so forth. Each subshell is divided further into orbitals.) Two electrons are transferred from the cations to the anions, leaving each with a closed shell. The alkaline earth chalcogenides form ionic binary crystals such as barium oxide (BaO), calcium sulfide (CaS), barium selenide (BaSe), or strontium oxide (SrO). They have the same structure as sodium chloride, with each atom having six neighbours. Oxygen can be combined with various cations to form a large number of ionically bonded solids.
Silicon, carbon, germanium, and a few other elements form covalently bonded solids. In these elements there are four electrons in the outer sp-shell, which is half filled. (The sp-shell is a hybrid formed from one s and one p subshell.) In the covalent bond an atom shares one valence (outer-shell) electron with each of its four nearest neighbour atoms. The bonds are highly directional and prefer a tetrahedral arrangement. A covalent bond is formed by two electrons—one from each atom—located in orbitals between the ions. Insulators, in contrast, have all their electrons within shells inside the atoms.
The perpetual spin of an electron is an important aspect of the covalent bond. From a vantage point above the spinning particle, counterclockwise rotation is designated spin-up, while clockwise rotation is spin-down. A fundamental law of quantum physics is the Pauli exclusion principle, which states that no two electrons can occupy the same point in space at the same time with the same direction of spin. In a covalent bond two electrons occupy the same small volume of space (i.e., the same orbital) at all times, so they must have opposite spin: one up and one down. The exclusion principle is then satisfied, and the resulting bond is strong.
In graphite the carbon atoms are arranged in parallel sheets, and each atom has only three near neighbours. The covalent bonds between adjacent carbons within each layer are quite strong and are called σ bonds. The fourth valence electron in carbon has its orbital perpendicular to the plane. This orbital bonds weakly with the similar orbitals on all three neighbours, forming π bonds. The four bonds for each carbon atom in the graphite structure are not arranged in a tetrahedron; three are in a plane. The planar arrangement results in strong bonding, although not as strong as the bonding in the diamond configuration. The bonding between layers is quite weak and arises from the van der Waals interaction; there is much slippage parallel to the layers. Diamond and graphite form an interesting contrast: diamond is the hardest material in nature and is used as an abrasive, while graphite is used as a lubricant.
Besides the elemental semiconductors, such as silicon and germanium, some binary crystals are covalently bonded. Gallium has three electrons in the outer shell, while arsenic lacks three. Gallium arsenide (GaAs) could be formed as an insulator by transferring three electrons from gallium to arsenic; however, this does not occur. Instead, the bonding is more covalent, and gallium arsenide is a covalent semiconductor. The outer shells of the gallium atoms contribute three electrons, and those of the arsenic atoms contribute five, providing the eight electrons needed for four covalent bonds. The centres of the bonds are not at the midpoint between the ions but are shifted slightly toward the arsenic. Such bonding is typical of the III–V semiconductors—i.e., those consisting of one element from the third column of the periodic table and one from the fifth column. Elements from the third column (boron, aluminum, gallium, and indium) contribute three electrons, while the fifth-column elements (nitrogen, phosphorus, arsenic, and antimony) contribute five electrons. All III–V semiconductors are covalently bonded and typically have the zinc blende structure with four neighbours per atom. Most common semiconductors favour this arrangement.
The factor that determines whether a binary crystal will act as an insulator or a semiconductor is the valence of its constituent atoms. Ions that donate or accept one or two valence electrons form insulators. Those that have three to five valence electrons tend to have covalent bonds and form semiconductors. There are exceptions to these rules, however, as is the case with the IV–VI semiconductors such as lead sulfide. Heavier elements from the fourth column of the periodic table (germanium, tin, and lead) combine with the chalcogenides from the sixth row to form good binary semiconductors such as germanium telluride (GeTe) or tin sulfide (SnS). They have the sodium chloride structure, where each atom has six neighbours. Although not tetrahedrally bonded, they are good semiconductors.
Filled atomic shells with d-orbitals have an important role in covalent bonding. Electrons in atomic orbits have angular momentum (L), which is quantized in integer (n) multiples of Planck’s constant h: L = nh. Electron orbitals with n = 0 are called s-states, with n = 1 are p-states, and with n = 2 are d-states. Silver and copper ions have one valence electron outside their closed shells. The outermost filled shell is a d-state and affects the bonding. Eight binary crystals are formed from the copper and silver halides. Three (AgF, AgCl, AgBr) have the sodium chloride structure with six neighbours. The other five (AgI, CuF, CuCl, CuBr, CuI) have the zinc blende structure with four neighbours. The bonding in this group of solids is on the borderline between covalent and ionic, since the crystals prefer both types of bonds. The alkali metal halides exhibit somewhat different behaviour. The alkali metals are also monovalent cations, but their halides are strictly ionic. The difference in bonding between the alkali metals on the one hand and silver and copper on the other hand is that silver and copper have filled d-shells while the alkalis have filled p-shells. Since the d-shells are filled, they do not covalently bond. This group of electrons is, however, highly polarizable, which influences the bonding of the valence electrons. Similar behaviour is found for zinc and cadmium, which have two valence electrons outside a filled d-shell. They form binary crystals with the chalcogenides, which have tetrahedral bonding. In this case the covalent bonding seems to be preferred over the ionic bond. In contrast, the alkaline earth chalcogenides, which are also divalent, have outer p-shells and are ionic. The zinc and cadmium chalcogenides are covalent, as the outer d-shell electrons of the two cations favour covalent bonding.
Metallic bonds fall into two categories. The first is the case in which the valence electrons are from the sp-shells of the metal ions; this bonding is quite weak. In the second category the valence electrons are from partially filled d-shells, and this bonding is quite strong. The d-bonds dominate when both types of bonding are present.
The simple metals are bonded with sp-electrons. The electrons of these metal atoms are in filled atomic shells except for a few electrons that are in unfilled sp-shells. The electrons from the unfilled shells are detached from the metal ion and are free to wander throughout the crystal. They are called conduction electrons, since they are responsible for the electrical conductivity of metals. Although the conduction electrons may roam anywhere in the crystal, they are distributed uniformly throughout the entire solid. Any large imbalance of charge is prevented by the strong electrical attraction between the negative electrons and the positive ions, plus the strong repulsion between electrons. The phrase electron correlation describes the correlated movements of the electrons; the motion of each electron depends on the positions of neighbouring electrons. Electrons have strong short-range order with one another. Correlation ensures that each unit cell in the crystal has, on the average, the number of electrons needed to cancel the positive charge of the cation so that the unit cell is electrically neutral.
Cohesive energy is the energy gained by arranging the atoms in a crystalline state, as compared with the gas state. Insulators and semiconductors have large cohesive energies; these solids are bound together strongly and have good mechanical strength. Metals with electrons in sp-bonds have very small cohesive energies. This type of metallic bond is weak; the crystals are barely held together. Single crystals of simple metals such as sodium are mechanically weak. At room temperature the crystals have the mechanical consistency of warm butter. Special care must be used in handling these crystals, because they are easily distorted. Metals such as magnesium or aluminum must be alloyed or polycrystalline to have any mechanical strength. Although the simple metals are found in a variety of structures, most are in one of the three closest-packed structures: fcc, bcc, and hcp. Theoretical calculations show that the cohesive energy of a given metal is almost the same in each of the different crystal arrangements; therefore, crystal arrangements are unimportant in metals bound with electrons from sp-shells.
A different type of metallic bonding is found in transition metals, which are metals whose atoms are characterized by unfilled d-shells. The d-orbitals are more tightly bound to an ion than the sp-orbitals. Electrons in d-shells do not wander away from the ion. The d-orbitals form a covalent bond with the d-orbitals on the neighbouring atoms. The bonding of d-orbitals does not occur in a tetrahedral arrangement but has a different directional preference. In metals the bonds from d-orbitals are not completely filled with electrons. This situation is different from the tetrahedral bonds in semiconductors, which are filled with eight electrons. In transition metals the covalent bonds formed with the d-electrons are much stronger than the weak bonds made with the sp-electrons of simple metals. The cohesive energy is much larger in transition metals. Titanium, iron, and tungsten, for example, have exceptional mechanical strength. Crystal arrangements are important in the behaviour of the transition metals and occur in the close-packed fcc, bcc, or hcp arrangements.
The Dutch physicist Johannes D. van der Waals first proposed the force that binds molecular solids. Any two atoms or molecules have a force of attraction (F) that varies according to the inverse seventh power of the distance R between the centres of the atoms or molecules: F = –C/R7, where C is a constant. The force, known as the van der Waals force, declines rapidly with the distance R and is quite weak. If the atoms or molecules have a net charge, there is a strong force whose strength varies according to Coulomb’s law as the inverse second power of the separation distance: F = –C′/R2, where C′ is a constant. This force provides the binding in ionic crystals and some of the binding in metals. Coulomb’s law does not apply to atoms or molecules without a net charge. Molecules with a dipole moment, such as water, have a strong attractive force owing to the interactions between the dipoles. For atoms and molecules with neither net charges nor dipole moments, the van der Waals force provides the crystal binding. The force of gravity also acts between neutral atoms and molecules, but it is far too weak to bind molecules into crystals.
The van der Waals force is caused by quantum fluctuations. Two neighbouring atoms that are each fluctuating can lower their joint energy by correlating their fluctuations. The van der Waals force arises from correlations in their dipole fluctuations. Electrons bound in atomic orbits are in constant motion around the nucleus, and the distribution of charges in the atom changes constantly as the electrons move, owing to quantum fluctuations. One fluctuation might produce a momentary electric dipole moment (i.e., a separation of charges) on an atom if a majority of its electrons are on one side of the nucleus. The dipole moment creates an electric field on a neighbouring atom; this field will induce a dipole moment on the second atom. The two dipoles attract one another via the van der Waals interaction. Since the force depends on the inverse seventh power of the distance, it declines rapidly with increasing distance. Atoms have a typical radius of one to three angstroms. The van der Waals force binds atoms and molecules within a few angstroms of each other; beyond that distance the force is negligible. Although weak, the van der Waals force is always present and is important in cases where the other forces are absent.
Hydrogen is rarely found as a single atom. Instead it forms diatomic molecules (H2), which are gaseous at room temperature. At lower temperatures the hydrogen becomes a liquid and at about 20 K turns into a solid. The molecule retains its identity in the liquid and solid states. The solid exists as a molecular crystal of covalently bound H2 molecules. The molecules attract one another by van der Waals forces, which provide the crystal binding. Helium, the second element in the periodic table, has two electrons, which constitute a filled atomic shell. In its liquid and solid states, the helium atoms are bound together by van der Waals forces. In fact, all the rare gases (helium, neon, argon, krypton, and xenon) are molecular crystals with the binding provided by van der Waals forces.
Many organic molecules form crystals where the molecules are bound by van der Waals forces. In methane (CH4), a central carbon makes a covalent bond with each hydrogen atom, forming a tetrahedron. In crystalline methane the molecules are arranged in the fcc structure. Benzene (C6H6) has the carbon atoms in a hexagonal ring; each carbon has three coplanar σ bonds, as in graphite, where two bonds are with neighbouring carbon atoms and the third bond is with a hydrogen atom. Crystalline benzene has four molecules per unit cell in a complex arrangement. Fullerene and the rare gas atoms are spherical, and the crystalline arrangement corresponds to the closest packing of spheres. Most organic molecules, however, are not spherical and display irregular shapes. For odd-shaped molecules, the van der Waals interaction depends on the rotational orientation of the two molecules. In order to maximize the force, the molecules in the crystal have unusual arrangements, as in the case of benzene.
Hydrogen bonding is important in a few crystals, notably in ice. With its lone electron, a hydrogen atom usually forms a single covalent bond with an electronegative atom. In the hydrogen bond the atom is ionized to a proton. The proton sits between two anions and joins them. Hydrogen bonding occurs with only the most electronegative ions: nitrogen, oxygen, and fluorine. In water the hydrogen links pairs of oxygen ions. Water is found in many different crystal structures, but they all have the feature that the hydrogen atoms sit between pairs of oxygen. Another hydrogen-bonded solid is hydrogen fluoride (HF), in which the hydrogen atom (proton) links pairs of fluorines.
The earliest crystal grower was nature. Many excellent crystals of minerals formed in the geologic past are found in mines and caves throughout the world. Most precious and semiprecious stones are well-formed crystals. Early efforts to produce synthetic crystals were concentrated on making gems. Synthetic ruby was grown by the French scientist Marc Antoine Augustin Gaudin in 1873. Since about 1950 scientists have learned to grow in the laboratory crystals of quality equal or superior to those found in nature. New techniques for growth are continually being developed, and crystals with three or more atoms per unit cell are continually being discovered.
Crystals can be grown from a vapour when the molecules of the gas attach themselves to a surface and move into the crystal arrangement. Several important conditions must be met for this to occur. At constant temperature and equilibrium conditions, the average number of molecules in the gas and solid states is constant; molecules leave the gas and attach to the surface at the same rate that they leave the surface to become gas molecules. For crystals to grow, the gas-solid chemical system must be in a nonequilibrium state such that there are too many gaseous molecules for the conditions of pressure and temperature. This state is called supersaturation. Molecules are more prone to leave the gas than to rejoin it, so they become deposited on the surface of the container. Supersaturation can be induced by maintaining the crystal at a lower temperature than the gas. A critical stage in the growth of a crystal is seeding, in which a small piece of crystal of the proper structure and orientation, called a seed, is introduced into the container. The gas molecules find the seed a more favourable surface than the walls and preferentially deposit there. Once the molecule is on the surface of the seed, it wanders around this surface to find the preferred site for attachment. Growth proceeds one molecule at a time and one layer at a time. The process is slow; it takes days to grow a small crystal. Crystals are grown at temperatures well below the melting point to reduce the density of defects. The advantage of vapour growth is that very pure crystals can be grown by this method, while the disadvantage is that it is slow.
Most clouds in the atmosphere are ice crystals that form by vapour growth from water molecules. Most raindrops are crystals as they begin descending but thaw during their fall to Earth. Seeding for rain—accomplished by dropping silver iodide crystals from airplanes—is known to induce precipitation. In the laboratory, vapour growth is usually accomplished by flowing a supersaturated gas over a seed crystal. Quite often a chemical reaction at the surface is needed to deposit the atoms. Crystals of silicon can be grown by flowing chlorosilane (SiCl4) and hydrogen (H2) over a seed crystal of silicon. Hydrogen acts as the buffer gas by controlling the temperature and rate of flow. The molecules dissociate on the surface in a chemical reaction that forms hydrogen chloride (HCl) molecules. Hydrogen chloride molecules leave the surface, while silicon atoms remain to grow into a crystal. Binary crystals such as gallium arsenide (GaAs) are grown by a similar method. One process employs gallium chloride (GaCl) as the gallium carrier. Arsenic is provided by molecules such as arsenous chloride (AsCl3), arsine (AsH3), or As4 (yellow arsenic). These molecules, with hydrogen as the buffer gas, grow crystals of gallium arsenide while forming gas molecules such as gallium trichloride (GaCl3) and hydrogen chloride. Trimethylgallium, (CH3)3Ga, is another molecule that can be used to deliver gallium to the surface.
Large single crystals may be grown from solution. In this technique the seed crystal is immersed in a solvent that contains typically about 10–30 percent of the desired solute. The choice of solvent usually depends on the solubility of the solute. The temperature and pH (a measure of acidity or basicity) of the solution must be well controlled. The method is faster than vapour growth, because there is a higher concentration of molecules at the surface in a liquid as compared to a gas, but it is still relatively slow.
This method is the most basic. A gas is cooled until it becomes a liquid, which is then cooled further until it becomes a solid. Polycrystalline solids are typically produced by this method unless special techniques are employed. In any case, the temperature must be controlled carefully. Large crystals can be grown rapidly from the liquid elements using a popular method invented in 1918 by the Polish scientist Jan Czochralski and called crystal pulling. One attaches a seed crystal to the bottom of a vertical arm such that the seed is barely in contact with the material at the surface of the melt. The arm is raised slowly, and a crystal grows underneath at the interface between the crystal and the melt. Usually the crystal is rotated slowly, so that inhomogeneities in the liquid are not replicated in the crystal. Large-diameter crystals of silicon are grown in this way for use as computer chips. Based on measurements of the weight of the crystal during the pulling process, computer-controlled apparatuses can vary the pulling rate to produce any desired diameter.
Crystal pulling using the Czochralski method. A schematic view of a modern apparatus. Copyright Encyclopædia Britannica; rendering for this edition by Rosen Educational Services
Crystal pulling is the least expensive way to grow large amounts of pure crystal. The original seed is on the right tip. Binary crystals can also be pulled; for example, synthetic sapphire crystals can be pulled from molten alumina. Special care is required to grow binary and other multicomponent crystals; the temperature must be precisely controlled because such crystals may be grown only at a single, extremely high temperature. The melt has a tendency to be inhomogeneous, since the two liquids may try to separate by gravity.
The Bridgman method (named after the American scientist Percy Williams Bridgman) is also widely used for growing large single crystals. The molten material is put into a crucible, often of silica, which has a cylindrical shape with a conical lower end. Heaters maintain the molten state. As the crucible is slowly lowered into a cooler region, a crystal starts growing in the conical tip. The crucible is lowered at a rate that matches the growth of the crystal, so that the interface between crystal and melt is always at the same temperature. The rate of moving the crucible depends on the temperature and the material. When done successfully, the entire molten material in the crucible grows into a single large crystal. One disadvantage of the method is that excess impurities are pushed out of the crystal during growth. A layer of impurities grows at the interface between melt and solid as this surface moves up the melt, and the impurities become concentrated in the higher part of the crystal.
Epitaxy is the technique of growing a crystal, layer by layer, on the atomically flat surface of another crystal. In homoepitaxy a crystal is grown on a substrate of the same material. Silicon layers of different impurity content, for example, are grown on silicon substrates in the manufacture of computer chips. Heteroepitaxy, on the other hand, is the growth of one crystal on the substrate of another. Silicon substrates are often used since they are readily available in atomically smooth form. Many different semiconductor crystals can be grown on silicon, such as gallium arsenide, germanium, cadmium telluride (CdTe), and lead telluride (PbTe). Any flat substrate can be used for epitaxy, however, and insulators such as rock salt (NaCl) and magnesium oxide (MgO) are also used.
Molecular-beam epitaxy, commonly abbreviated as MBE, is a form of vapour growth. The field began when the American scientist John Read Arthur reported in 1968 that gallium arsenide could be grown by sending a beam of gallium atoms and arsenic molecules toward the flat surface of a crystal of the molecule. The amount of gas molecules can be controlled to grow just one layer, or just two, or any desired amount. This method is slow, since molecular beams have low densities of atoms. Chemical vapour deposition (CVD) is another form of epitaxy that makes use of the vapour growth technique. Also known as vapour-phase epitaxy (VPE), it is much faster than MBE since the atoms are delivered in a flowing gas rather than in a molecular beam. Synthetic diamonds are grown by CVD. Rapid growth occurs when methane (CH4) is mixed with atomic hydrogen gas, which serves as a catalyst. Methane dissociates on a heated surface of diamond. The carbon remains on the surface, and the hydrogen leaves as a molecule. Growth rates are several micrometres (1 micrometre is equal to 0.00004 inch) per hour. At that rate, a stone 1 cm (0.4 inch) thick is grown in 18 weeks. CVD diamonds are of poor quality as gemstones but are important electronic materials. Because hydrogen is found in nature as a molecule rather than as a single atom, making atomic hydrogen gas is the major expense in growing CVD diamonds. Liquid-phase epitaxy (LPE) uses the solution method to grow crystals on a substrate. The substrate is placed in a solution with a saturated concentration of solute. This technique is used to grow many crystals employed in modern electronics and optoelectronic devices, such as gallium arsenide, gallium aluminum arsenide, and gallium phosphide.
An important concern in successful epitaxy is matching lattice distances. If the spacing between atoms in the substrate is close to that of the top crystal, then that crystal will grow well; a small difference in lattice distance can be accommodated as the top crystal grows. When the lattice distances are different, however, the top crystal becomes deformed, since structural defects such as dislocations appear. Although few crystals share the same lattice distance, a number of examples are known. Aluminum arsenide and gallium arsenide have the same crystal structure and the same lattice parameters to within 0.1 percent; they grow excellent crystals on one another. Such materials, known as superlattices, have a repeated structure of n layers of GaAs, m layers of AlAs, n layers of GaAs, m layers of AlAs, and so forth. Superlattices represent artificially created structures that are thermodynamically stable; they have many applications in the modern electronics industry. Another lattice-matched epitaxial system is mercury telluride (HgTe) and cadmium telluride (CdTe). These two semiconductors form a continuous semiconductor alloy CdxHg1 – x Te, where x is any number between 0 and 1. This alloy is used as a detector of infrared radiation and is incorporated in particular in night-vision goggles.
At slow rates of crystal growth, the interface between melt and solid remains planar, and growth occurs uniformly across the surface. At faster rates of crystal growth, instabilities are more likely to occur; this leads to dendritic growth. Solidification releases excess energy in the form of heat at the interface between solid and melt. At slow growth rates, the heat leaves the surface by diffusion. Rapid growth creates more heat, which is dissipated by convection (liquid flow) when diffusion is too slow. Convection breaks the planar symmetry so that crystal growth develops along columns, or “fingers,” rather than along planes. Each crystal has certain directions in which growth is fastest, and dendrites grow in these directions. As the columns grow larger, their surfaces become flatter and more unstable. This feather or tree structure is characteristic of dendritic growth. Snowflakes are an example of crystals that result from dendritic growth.
Liquid crystals blend the structures and properties of the normally disparate liquid and crystalline solid states. Liquids can flow, for example, while solids cannot, and crystalline solids possess special symmetry properties that liquids lack. Ordinary solids melt into ordinary liquids as the temperature increases—e.g., ice melts into liquid water. Some solids actually melt twice or more as temperature rises. Between the crystalline solid at low temperatures and the ordinary liquid state at high temperatures lies an intermediate state, the liquid crystal. Liquid crystals share with liquids the ability to flow but also display symmetries inherited from crystalline solids. The resulting combination of liquid and solid properties allows important applications of liquid crystals in the displays of such devices as wristwatches, calculators, portable computers, and flat-screen televisions.
Crystals exhibit special symmetries when they slide in certain directions or rotate through certain angles. These symmetries can be compared to those encountered when walking in a straight line through empty space. Regardless of the direction or distance of each step, the view remains the same, as there are no landmarks by which to measure one’s progress. This is called continuous translational symmetry because all positions look identical. A crystal lattice breaks the continuous translational symmetry of free space; starting at one molecule there is a finite distance to travel before reaching the next. Some translational symmetry is present, however, because, by moving the proper distance in the proper direction, one is guaranteed to locate additional molecules on repeated excursions. This property is called discrete translational periodicity. Real, three-dimensional crystals display translational periodicity in three independent directions.
Rotational symmetries can be considered in a similar fashion. From one point in empty space, the view is the same regardless of which direction one looks. There is continuous rotational symmetry—namely, the symmetry of a perfect sphere. In a crystal, however, the distance to the nearest molecule from any given molecule depends on the direction taken. Furthermore, the molecules themselves may have shapes that are less symmetric than a sphere. A crystal possesses a certain discrete set of angles of rotation that leave the appearance unchanged. The continuous rotational symmetry of empty space is broken, and only a discrete symmetry exists. Broken rotational symmetry influences many important properties of crystals. Their resistance to compression, for example, may vary according to the direction along which one squeezes the crystal. Transparent crystals, such as quartz, may exhibit an optical property known as birefringence. When a light ray passes through a birefringent crystal, it is bent, or refracted, at an angle depending on the direction of the light and also its polarization, so that the single ray is broken up into two polarized rays. This is why one sees a double image when looking through such crystals.
Arrangements of molecules. Copyright Encyclopædia Britannica; rendering for this edition by Rosen Educational Services
In a liquid, all the molecules sit in random positions with random orientations. This does not mean that there is less symmetry than in the crystal, however. All positions are actually equivalent to one another, and likewise all orientations are equivalent, because in a liquid the molecules are in constant motion. At one instant the molecules in the liquid may occupy specific positions and orientations, but a moment later the molecules will move to previously empty points in space. Likewise, at one instant a molecule points in one direction, and the next instant it points in another. Liquids share the homogeneity and isotropy of empty space; they have continuous translational and rotational symmetries. No form of matter has greater symmetry.
As a general rule, molecules solidify into crystal lattices with low symmetry at low temperatures. Both translational and rotational symmetries are discrete. At high temperatures, after melting, liquids have high symmetry. Translational and rotational symmetries are continuous. High temperatures provide molecules with the energy needed for motion. The mobility disorders the crystal and raises its symmetry. Low temperatures limit motion and the possible molecular arrangements. As a result, molecules remain relatively immobile in low-energy, low-symmetry configurations.
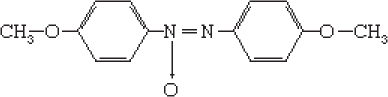
Liquid crystals, sometimes called mesophases, occupy the middle ground between crystalline solids and ordinary liquids with regard to symmetry, energy, and properties. Not all molecules have liquid crystal phases. Water molecules, for example, melt directly from solid crystalline ice into liquid water. The most widely studied liquid-crystal-forming molecules are elongated, rodlike molecules, rather like grains of rice in shape (but far smaller in size). A popular example is the molecule p-azoxyanisole (PAA):
Typical liquid crystal structures include the smectic and the nematic (this nomenclature was invented in the 1920s by the French scientist Georges Friedel). The smectic phase differs from the solid phase in that translational symmetry is discrete in one direction and continuous in the remaining two.
In the nematic phase all translational symmetries are continuous. The molecule positions are disordered in all directions. Their orientations are all alike, however, so that the rotational symmetry remains discrete. The orientation of the long axis of a nematic molecule is called its director.
It was noted earlier that, as temperature decreases, matter tends to evolve from highly disordered states with continuous symmetries toward ordered states with discrete symmetries. This can occur through a sequence of symmetry-breaking phase transitions. As a substance in the liquid state is reduced in temperature, rotational symmetry breaking creates the nematic liquid crystal state in which molecules are aligned along a common axis. Their directors are all nearly parallel. At lower temperatures continuous translational symmetries break into discrete symmetries. There are three independent directions for translational symmetry. When continuous translational symmetry is broken along only one direction, the smectic liquid crystal is obtained. At temperatures sufficiently low to break continuous translational symmetry in all directions, the ordinary crystal is formed.
The mechanism by which liquid crystalline order is favoured can be illustrated through an analogy between molecules and grains of rice. Collisions of molecules require energy, so the greater the energy, the greater the tolerance for collisions. If rice grains are poured into a pan, they fall at random positions and orientations and tend to jam up against their neighbours. This is similar to the liquid state. After the pan is shaken to allow the rice grains to readjust their positions, the neighbouring grains tend to line up. The alignment is not perfect across the sample owing to defects, which also can occur in nematic liquid crystals. When all grains align, they have greater freedom to move before hitting a neighbour than they have when they are disordered. This produces the nematic phase. The freedom to move is primarily in the direction of molecular alignment, as sideways motion quickly results in collision with a neighbour. Layering the grains enhances sideways motion. This produces the smectic phase. In the smectic phase some molecules have ample free volume to move in, while others are tightly packed. The lowest-energy arrangement shares the free volume equitably among molecules. Each molecular environment matches all others, and the structure is a crystal.
There is a great variety of liquid crystalline structures known in addition to those described so far. Continuous in-plane rotational symmetry, present within smectic-A layers, is broken in the hexatic-B phase, but a proliferation of dislocations maintains continuous translational symmetry within its layers. A similar relationship holds between smectic-C and smectic-F. Crystal-B and crystal-G have molecular positions on regular crystal lattice sites, with long axes of molecules (directors) aligned, but allow rotation of molecules about their directors. These are the so-called plastic crystals. There also are crystals in the discotic phase, consisting of disk-shaped molecules, and the columnar phases, in which translational symmetry is broken in not one but two spatial directions, leaving liquidlike order only along columns. In general, crystals in the isotropic liquid and nematic phases are expected at high temperatures, while many of the other phases mentioned here are expected at low temperatures.
Liquid-crystal-forming compounds are widespread and quite diverse. Soap can form a type of smectic known as a lamellar phase, also called neat soap. In this case it is important to recognize that soap molecules have a dual chemical nature. One end of the molecule (the hydrocarbon tail) is attracted to oil, while the other end (the polar head) attaches itself to water. When soap is placed in water, the hydrocarbon tails cluster together, while the polar heads adjoin the water. Small numbers of soap molecules form spherical or rodlike micelles, which float freely in the water, while concentrated solutions create bilayers, which stack along some direction just like smectic layers. Indeed, the name smectic is derived from the Greek word for soap. The slippery feeling caused by soap reflects the ease with which the layers slide across one another.
Many biological materials form liquid crystals. Myelin, a fatty material extracted from nerve cells, was the first intensively studied liquid crystal. The tobacco mosaic virus, with its rodlike shape, forms a nematic phase. In cholesterol the nematic phase is modified to a cholesteric phase characterized by continuous rotation of the direction of molecular alignment. An intrinsic twist of the cholesterol molecule, rather like the twist of the threads of a screw, causes this rotation. Since the molecular orientation rotates steadily, there is a characteristic distance after which the orientation repeats itself. This distance is frequently comparable to the wavelength of visible light, so brilliant colour effects result from the diffraction of light by these materials.
Perhaps the first description of a liquid crystal occurred in the story The Narrative of Arthur Gordon Pym, by Edgar Allan Poe:
I am at a loss to give a distinct idea of the nature of this liquid, and cannot do so without many words. Although it flowed with rapidity in all declivities where common water would do so, yet never, except when falling in a cascade, had it the customary appearance of limpidity…. At first sight, and especially in cases where little declivity was found, it bore resemblance, as regards consistency, to a thick infusion of gum Arabic in common water. But this was only the least remarkable of its extraordinary qualities. It was not colourless, nor was it of any one uniform colour—presenting to the eye, as it flowed, every possible shade of purple, like the hues of a changeable silk…. Upon collecting a basinful, and allowing it to settle thoroughly, we perceived that the whole mass of liquid was made up of a number of distinct veins, each of a distinct hue; that these veins did not commingle; and that their cohesion was perfect in regard to their own particles among themselves, and imperfect in regard to neighbouring veins. Upon passing the blade of a knife athwart the veins, the water closed over it immediately, as with us, and also, in withdrawing it, all traces of the passage of the knife were instantly obliterated. If, however, the blade was passed down accurately between two veins, a perfect separation was effected, which the power of cohesion did not immediately rectify.
The liquid described in this passage is human blood. In its usual state within the human body, blood is an ordinary disordered isotropic fluid. The disklike shape of red blood cells, however, favours liquid crystallinity at certain concentrations and temperatures.
An understanding of the principal technological applications of liquid crystals requires a knowledge of their optical properties. In particular, liquid crystals alter the polarization of light passing through them.
Light waves are actually waves in electric and magnetic fields. The direction of the electric field is the polarization of the light wave. A polarizing filter selects a single component of polarized light to pass through while absorbing all other components of incoming waves. If a second polarizing filter is placed above the first but with its polarization axis rotated by 90°, no light can pass through because the polarization passed by the first filter is precisely the polarization blocked by the second filter. When optically active materials, such as liquid crystals, are placed between polarizing filters crossed in this manner, some light may get through, because the intervening material changes the polarization of the light. If the nematic director is not aligned with either of the polarizing filters, polarized light passing through the first filter becomes partially polarized along the nematic director. This component of light in turn possesses a component aligned with the top polarizing filter, so a fraction of the incoming light passes through the entire assembly. The amount of light passing through is largest when the nematic director is positioned at a 45° angle from both filters. The light is fully blocked when the director lies parallel to one filter or the other.

Spatial variation of the director causing threadlike images. Copyright Encyclopædia Britannica; rendering for this edition by Rosen Educational Services
During the last decades of the 19th century, pioneering investigators of liquid crystals, such as the German physicist Otto Lehmann and the Austrian botanist Friedrich Reinitzer, equipped ordinary microscopes with pairs of polarizing filters to obtain images of nematic and smectic phases. Spatial variation in the alignment of the nematic director causes spatial variation in light intensity. Since the nematic is defined by having all directors nearly parallel to one another, the images arise from defects in the nematic structure. The directors may rotate or bend around defect lines. The resulting threadlike images inspired the name nematic, which is based on the Greek word for thread. The layered smectic structure causes layering of defects.
Nonuniformity in director alignment may be induced artificially. The surfaces of a glass container can be coated with a material that, when rubbed in the proper direction, forces the director to lie perpendicular or parallel to the wall adjacent to a nematic liquid crystal. The orientation forced by one wall need not be consistent with that forced by another wall; this situation causes the director orientation to vary in between the walls. The nematic must compromise its preference for all directors to be parallel to one another with the inconsistent orienting forces of the container walls. In doing so, the liquid crystal may take on a twisted alignment across the container. Electric or magnetic fields provide an alternate means of influencing the orientation of the nematic directors. Molecules may prefer to align so that their director is, say, parallel to an applied electric field.
Optical behaviour and orienting fields underlie the important contemporary use of liquid crystals as optoelectronic displays. Consider, for example, the twisted-nematic cell. The polarizer surfaces are coated and rubbed so that the nematic will align with the polarizing axis. The two polarizers are crossed, forcing the nematic to rotate between them. The rotation is slow and smooth, assuming a 90° twist across the cell. Light passing through the first polarizer is aligned with the bottom of the nematic layer. As the nematic twists, it rotates the polarization of the light so that, as the light leaves the top of the nematic layer, its polarization is rotated by 90° from that at the bottom. The new polarization is just right for passing through the top filter, and so light travels unhindered through the assembly.

A twisted-nematic cell. (A) The assembly is transparent to light in the absence of an electric field. (B) An applied field destroys the twist of the nematic, rendering the assembly opaque. Copyright Encyclopædia Britannica; rendering for this edition by Rosen Educational Services
If an electric field is applied in the direction of light propagation, the liquid crystal directors align with the orienting field, so they are no longer parallel to the light passing though the bottom polarizer. They are no longer capable of rotating this polarization through the 90° needed to allow the light to emerge from the top polarizer. Although this assembly is transparent when no field is applied, it becomes opaque when the field is present. A grid of such assemblies placed side by side may be used to display images. If one turns on the electric field attached to the parts of the grid that lie where the image is to appear, these points will turn black while the remaining points of the grid stay white. The resulting patchwork of dark and light creates the image on the display. In a wristwatch, calculator, or computer these may be simply numbers or letters, and in a television the images may be detailed pictures. Switching the electric fields on or off will cause the picture to move, just as ordinary television pictures display an ever-changing stream of electrically encoded images.