CHAPTER 5

MÖBIUS TRANSFORMATIONS

             23. THE GROUP PROPERTY OF MOBIUS TRANSFORMATIONS

It follows from Theorems 4.3 and 4.4 that the rational function of order 1, i. e., the fractional linear transformation or Möbius transformation

is the only rational function which maps the extended plane onto itself in a one-to-one fashion. Here, we assume that the quantity ad — bc, called the determinant of the function L(z), is nonzero, since otherwise L(z) is identically equal to a constant mapping the extended plane into a single point. As we know from Sec. 17, the mapping w = L(z) is conformal at all points of the extended plane. This mapping (or its various special cases) plays an important role in a variety of problems encountered in the theory of functions of a complex variable, and it therefore merits a detailed study (to which we devote the present chapter).

Let denote the set of all Möbius transformations. Two such transformations

are regarded as identical if and only if L₁(z) = L₂(z) for all z.

THEOREM 5.1 A necessary and sufficient condition for the two Möbius transformations (5.1) to be identical is that

Proof. The sufficiency of the condition is obvious. To prove the necessity, suppose L₁(z) ≡ L₂(z). Then, in particular,

which means that¹

Substituting

into the second of the equations (5.3), we obtain

or

But q ≠ p, since otherwise

contrary to hypothesis, and therefore

Together with (5.3), this implies (5.2), as required.

Remark. A Möbius transformation is not characterized by the value of its determinant, since the determinant is multiplied by λ² when the coefficients change as described by (5.2). It can only be asserted that the determinant remains nonzero under any substitution (5.2).

The transformation

which obviously belongs to the set , is called the unit transformation (or the identity transformation). By the inverse of a given transformation

we mean the transformation which assigns to each w its inverse image z under the transformation (5.4). Thus the transformation

(whose coefficients are unique only to within a multiplicative constant, as in Theorem 5.1) is the inverse of the transformation (5.4), We denote the inverse of the transformation L by L^–1.

Given two arbitrary Möbius transformations

we define the product of L₁ and L₂ as the result of first carrying out one transformation and then carrying out the other. There are two possible products corresponding to the two orders in which the transformations can be carried out. One product, written L₁ L₂(z), equals

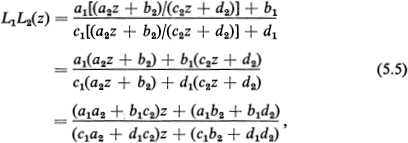
and the other, written L₁L₂(z), is obtained from (5.5) by permuting the indices 1 and 2. Moreover, since

each of the transformations L₁L₂(z) and L₂L₁(z) belongs to the set . In general L₁L₂(z) ≠ L₂L₁(z), but obviously

and

for any L(z) ∈ .

Example. If

then

Multiplication of transformations, as just defined, is an associative operation, i.e.,

To see this, we merely write z₃ = L₃(z), and then both sides of (5.6) reduce at once to L₁L₂(z₃). This associative property generalizes immediately to the product of an arbitrary number of transformations, and makes it unnecessary to use parentheses when writing products. For example, we have

Thus we have shown that the set of Möbius transformations has the following properties:²

1. is closed under multiplication, i.e., if L₁∈ , L₂ ∈ , then L₁L₂∈ , L₂L₁∈ .

2. Multiplication is associative.

3. There is an element U ∈ such that LU = UL = L for any L ∈ .

4. For each L ∈ , there is an element L^–1 ∈ such that LL^–1 = L^–1L = U.

In algebraic language, these four properties are summarized by saying that is a group of transformations³.

Problem. Prove that the Möbius transformations of the special form

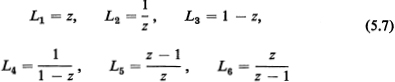
form a group.

Comment. This fact is summarized by saying that the transformations (5.7) are a subgroup of .⁴

24. THE CIRCLE-PRESERVING PROPERTY OF MÖBIUS TRANSFORMATIONS

We now prove that any Möbius transformation carries a straight line or a circle into another straight line or circle. We call this the circle-preserving property, since a straight lines can be regarded as a limiting case of a circle (corresponding to infinite radius). The entire linear transformation L(z) = αz + β(α ≠ 0) is obviously circle-preserving, since the mapping w = L(z) is just a shift (if α = 1), or a shift combined with a rotation and a uniform magnification (if α ≠ 1).

LEMMA. The transformation

is circle-preserving.

Proof. The equation of any straight line or circle in the z-plane can be written in the form

where we have a straight line if A = 0 and at least one of the numbers B, C is nonzero, and a circle if A ≠ 0 and B² + C² — AD > 0. Since

where = x — iy is the complex conjugate of z = x + iy, we can rewrite (5.9) as

where E = B + iC. It is easy to see that equation (5.10), where A and D are real and E is complex, is the equation of a straight line if and only if A = 0, E ≠ 0, and the equation of a circle if and only if A ≠ 0, E – AD > 0.

We now find the image of the curve with equation (5.10) under the transformation (5.8). Replacing z by 1/w in (5.10), we obtain

or

Equation (5.11) has the same form as equation (5.10), with D, and A substituted for A, E and D, respectively. It follows that (5.11) is the equation of a straight line if D = 0, since then either A = 0 and E ≠ 0 if (5.10) is the equation of a straight line, or else A ≠ 0 and E — AD = E > 0 (so that E ≠ 0 again) if (5.10) is the equation of a circle. Moreover, (5.11) is the equation of a circle if D ≠ 0, since then either A ≠ 0 and E — AD > 0 if (5.10) is the equation of a circle, or else A = 0 and E ≠ 0 (so that E — AD = E > 0 again) if (5.10) is the equation of a straight line.

THEOREM 5.2. Every Möbius transformation

is circle-preserving.

Proof. If c = 0, (5.12) reduces to an entire linear transformation and hence is circle-preserving. If c ≠ 0, (5.12) can be written in the form

Setting

we can write L(z) as a product

of three transformations which are all circle-preserving (use the lemma). It follows that L itself is circle-preserving.

COROLLARY. Let δ = —d/c be the pole of the (rational) function (5.12). Then (5.12) transforms every straight line or circle which passes through δ into a straight line, and every other straight line or circle into a circle.

Proof. If the circle or straight line passes through δ, its image under (5.12) contains the point at infinity, and hence must be a straight line, since it cannot be a circle (no circle contains ∞). Similarly, if the circle or straight line does not pass through δ, its image does not contain the point at infinity, and hence must be a circle, since it cannot be a straight line (every straight line contains ∞).

Remark. Let w = L(z) be any Möbius transformation, let γ be a straight line or circle in the z-plane, and let Γ = L(γ) be the image of γ in the w-plane (Γ is itself a straight line or a circle). The two domains G₁ and G₂ with boundary γ are either two half-planes or the interior and exterior of a circle. Let L(G₁) and L(G₂) be the images of these two domains under the mapping w = L(z). We now show that L(G₁) and L(G₂) are the two domains whose common boundary is the curve Γ.

First suppose z₁ ∈ G_l, z₂ ∈ G₂, and let w₁ = L(z₁), w₂ = L(z₂). Then w₁ ∉ Γ, w₂ ∉ Γ, since z₁ ∉ γ, z₂ ∉ Γ, and hence w₁ and w₂ must belong to the union of the two (disjoint) domains into which Γ divides the extended w-plane. If w₁ and w₂ both belong to one of these two domains, we can join w₁ to w₂ by a line segment or circular arc Δ which does not intersect Γ (see Figure 5.1). The inverse image of Δ in the z-plane must be a line segment or circular arc δ, which joins z₁ to z₂ and does not intersect γ. But the existence of δ contradicts the assumption that z₁ and z₂ belong to different domains G₁ and G₂. Therefore, if z₁ and z₂ belong to different domains with boundary γ, their images w₁ and w₂ must belong to different domains with boundary Γ.

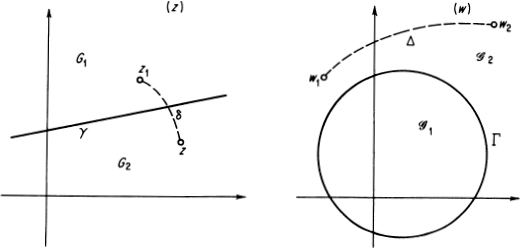
FIGURE 5.1

We now denote the domains containing w₁ and w₂ by and , respectively. If z is an arbitrary point in G₁ then, since z and z₂ belong to different domains and G₁ and G₂. their images w and w₂ belong to different domains and . But w₂ ∈ , and hence w ∈ , i.e., L(z) ∈ if z ∈ G₁. Similarly, L(z) ∈ if z ∈ G₂, and hence

Conversely, let w be an arbitrary point in . Then w must be the image of a point z in G₁ or G₂. But z ∈ G₂ implies w ∈ , contrary to hypothesis, and hence z ∈ G_l, i.e., ⊂ L(G₁). Similarly, we find that ⊂ L(G₂). It follows by comparison with (5.13) that

i.e., the two domains with boundary Γ are just the images of the two domains G₁ and G₂, as asserted. Moreover, to determine which of the two domains with boundary Γ is actually the image of a given domain G₁ with boundary γ, it is sufficient to locate the image w₁ of any point z₁ ∈ G₁, for then the domain containing w₁ is the image of G₁.

Problem. Find the images of the following domains under the indicated Möbius transformations:

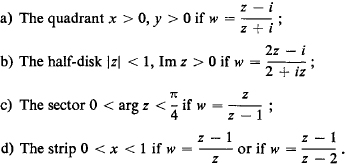
25. FIXED POINTS OF A MÖBIUS TRANSFORMATION. INVARIANCE OF THE CROSS RATIO

By a fixed point of a transformation or mapping w = f(z), we mean a point which is carried into itself by the transformation. Obviously, every such point is a solution of the equation

Moreover, every point of the z-plane is trivially a fixed point of the unit transformation U(z) = z.

THEOREM 5.3. Every Möbius transformation different from the unit transformation has two fixed points, which in certain cases coalesce into a single fixed point.

Proof. First let c = 0 (d ≠ 0), so that L(z) reduces to the entire linear transformation

Then, since L(∞) = ∞, one fixed point is the point at infinity. If α ≠ 1, there is another fixed point determined from the equation

i. e., the point β/(1 — α), but if α = 1, β ≠ 0, there is no finite fixed point. Moreover, if α ≠ 1, β ≠ 0, the finite fixed point β/(1 — α) approaches ∞ as α → 1. Therefore, in the case of the transformation

the point at infinity can be regarded as two fixed points which have coalesced.

Now let c ≠ 0, so that

i. e., the point at infinity is not a fixed point5. Similarly, the pole δ = –d/c of the transformation is not a fixed point, since

Assuming that z ≠ ∞ and z ≠ δ, we solve the equation

or

obtaining

If (a — d)² + 4bc ≠ 0, we obtain two different finite fixed points; if (a — d)² + 4bc = 0, these two points coalesce to form a single finite fixed point (a — d)/2c.

COROLLARY. The only Möbius transformation with more than two fixed points is the unit transformation U(z) = z, for which all points are fixed points.

THEOREM 5.4. A sufficient condition for two Möbius transformations L(z) and ∧(z) to be identical is that the equation

hold for three distinct points z₁, z₂ and z₃. In particular, there cannot exist two distinct Möbius transformations taking three given values w₁, w₂, w₃ at three given distinct points z₁, z₂, z₃.

Proof. It follows from

that

and hence

Therefore the transformation ∧^–1L has three distinct fixed points, which, according to the corollary, implies

where U is the unit transformation. Multiplying both sides of (5.14) by ∧ from the left, we obtain

which implies

as asserted.

We now set about determining the (unique) Möbius transformation w = L(z) carrying the points z₁, z₂, z₃ into the points w₁, w₂, w₃. First we consider the problem of finding the special Möbius transformation w = ∧(z) carrying three finite points z_l, z₂, z₃ into the points 0, ∞, 1. Since the function

vanishes for z = z₁ and becomes infinite for z = z₂ if and only if z₁ is a zero of the numerator and z₂ is a zero of the denominator, it follows that

But w must equal 1 for z = z₃, i.e.,

which implies⁶

Therefore the Möbius transformation carrying z₁, z₂, z₃ into 0, ∞, 1 is

Next we determine the more general Möbius transformation w = L(z) satisfying

where w₁, w₂, w₃ are three arbitrary (but distinct) finite points. As we have just seen, the transformation

carries the points w_l, w₂, w₃ into the points 0, ∞, 1. Therefore the transformation ∧₁L carries the points z₁, z₂, z₃ into the points 0, ∞, 1, so that

Multiplying both sides of the equation

by ∧^–1₁ from the left, we obtain

This solves the problem, since the functions ∧(z) and ∧₁(z), and hence ∧^–1₁(z), are known [cf. (5.17) and (5.16)]. However, it is more convenient to use (5.18) directly, after writing w = L(z). The result is

or

which expresses the Möbius transformation w = L(z) in implicit form.

Remark. In finding the Möbius transformation carrying the points z₁, z₂, z₃ into the points w₁, w₂, w₃, it was assumed that all six points are finite. However, the case of infinite points is easily handled. For example, the transformation carrying the points ∞, z₂, z₃ into the points 0, ∞, 1 has the form

which can be found by inspection or by writing (5.15) in the form

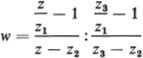
and then taking the limit as z₁ → ∞. Therefore (5.19) is replaced by

where it is assumed that the points w₁, w₂, w₃ are finite. Similarly, the transformation carrying the points z₁, ∞, z₃ into the points 0, ∞, 1 has the form

and hence we have

instead of (5.19). Finally, the transformation carrying the points z₁, z₂, ∞ into the points 0, ∞, 1 has the form

and hence we have

instead of (5.19).

In just the same way, we have to replace the left-hand side of (5.19) by

depending on whether w₁ = ∞, w₂ = ∞ or w₃ = ∞. As a result, we arrive at the following mnemonic rule: If z_k = ∞ or w_l = ∞ (k, l = 1, 2, 3), the differences involving z_k or w_l have to be replaced by 1. The reader can easily verify this rule by taking the appropriate limits (as z_k → ∞ or w_l → ∞) in equation (5.19).

Equation (5.19) implies an important general property of Möbius transformations. If a, b, c and d are arbitrary distinct finite complex numbers, then the ratio

denoted by (a, b, c, d), is called the cross ratio (or anharmonic ratio) of the four numbers (or points) a, b, c and d. If one of the four points a, b, c, d is the point at infinity, we define the cross ratio as the limit of the cross ratio of four finite points, three of which coincide with the three given finite points, as the fourth point approaches infinity. Thus, according to this definition, we have

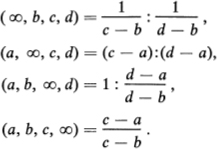
Now let w = L(z) be an arbitrary Möbius transformation, and let A, B, C, D be the points into which L(z) maps four arbitrary (but distinct) points a, b, c, d. Since the points A, B and D are the images of the points a, b and d, it follows from (5.19) that the relation between z and w = L(z) is given by

where differences involving the point at infinity have to be replaced by 1. Moreover, since the point C is the image of the point c, we have

(where again differences involving the point at infinity have to be replaced by 1), or equivalently

In other words, the cross ratio of any four distinct points is invariant under a Möbius transformation.

Problem 1. Prove that every Möbius transformation w = L(z) with a single finite fixed point z₀ satisfies a relation of the canonical form

Problem 2. Prove that every Möbius transformation w = L(z) with two distinct finite fixed points z₁ and z₂ satisfies a relation of the canonical form

Problem 3. Suppose the Möbius transformation L(z) has two distinct finite fixed points z₁ and z₂. Prove that

Hint. Use the preceding problem.

Problem 4.Find the Möbius transformation which carries the points – 1, i, 1 + i into the points

a) 0, 2i, 1 – i; b) i, ∞, 1.

Ans.

Problem 5. Find the Möbius transformation which carries the points —1, ∞, i into the points

a) i, 1, 1 + i; b) ∞, i, 1; c) 0, ∞, 1.

Ans.

Problem 6. Find the Möbius transformation such that

a) The points 1 and i are fixed, but the point 0 goes into the point – 1;

b) The points and 2 are fixed, but the point goes into ∞;

c) The point i is the only fixed point and the point 1 goes into ∞.

26. MAPPING OF A CIRCLE ONTO A CIRCLE7

Using the circle-preserving property of Möbius transformations and the possibility of mapping any given triple of distinct points z₁, z₂, z₃ into any other given triple of distinct points w₁, w₂, w₃, we obtain the following basic

THEOREM5.5. Let γ and Γ be any two straight lines or circles, and let z₁, z₂, z₃ and w₁, w₂, w₃ be any two triples of distinct points belonging to γ and Γ, respectively. Then there exists a Möbius transformation w = L(z) mapping γ onto Γ in such a way that

Proof. Construct the Möbius transformation w = L(z) satisfying the conditions (5.20), which according to Theorem 5.4 and the subsequent construction, exists and is unique. According to Theorem 5.2, w = L(z) maps the straight line or circle γ onto another straight line or circle Γ*. But since γ goes through the points z₁, z₂ and z₃, Γ* must go through the points w₁, w₂ and w₃. Moreover, since two different straight lines or circles cannot be drawn through the same three points, Γ* must coincide with Γ, as asserted.

Remark. Again consider two arbitrary straight lines or circles γ and Γ (which may coincide). Let G be one of the two domains with boundary γ, and let be one of the two domains with boundary Γ, so that G is either a half-plane, the interior of a circle or the exterior of a circle, and the same is true of . We now show how to map G onto . Choose an arbitrary triple of distinct points z₁, z₂, z₃ on γ, and suppose an observer moving along γ in the direction from z₁ to z₃ through z₂ finds the domain G on his left, say. Next choose a triple of distinct points w₁, w₂, w₃ on Γ such that an observer moving along Γ in the direction from w₁ to w₃ through w₂ finds the domain on his left, but let w₁, w₂, w₃ be otherwise arbitrary. As in Theorem 5.5, we form the Möbius transformation w = L(z) which satisfies the conditions (5.20) and hence maps γ onto Γ. Then w = L(z) also maps G onto , i.e., = L(G). In fact, if δ is a segment of the normal to the curve γ drawn from the point z₂ and pointing into the interior of G, so that an observer at z₂ facing in the direction established on γ finds δ on his left, then, since the mapping w = L(z) is conformal, an observer at w₂ facing in the direction established on Γ will also find the image Δ = L(δ), which is a line segment or circular arc, on his left (see Figure 5.2.)⁸ Therefore Δ ∩ ≠ 0 and hence contains images of certain points belonging to G (i.e., points of the segment δ). But, according to the remark on pp. 94–96, L(G) is one of the two domains with boundary Γ = L(γ), in fact just the domain containing the image of any point in G. In other words = L(G), as asserted.

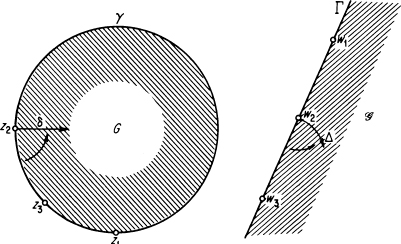
FIGURE 5.2

Example. Find a conformal mapping of the upper half plane Im z > 0 onto the interior of the unit circle.

To solve this problem, we choose z₁ = — 1, z₂ = 0, z₃ = 1, say, so that the upper half-plane is on the left of an observer moving along the real axis in the direction from z₁ to z₃ through z₂. We also choose three points w₁, w₂, w₃ on the unit circle, such that the interior of the circle is on the left of an observer moving along the circle in the direction from w₁ to w₃ through w₂. For simplicity, let w₁ = 1, w₂ = i, w₃ = — 1. Then the desired Möbius transformation satisfies the conditions L(z_k) = w_k, k = 1, 2, 3 and can be represented in the form

or

where we have used (5.19).

Problem. Find the Möbius transformation w = L(z) mapping the upper half-plane Im z > 0 onto itself and satisfying the conditions w(0) = 1, w(l) = 2, w(2) = ∞.

27. SYMMETRY TRANSFORMATIONS

Let z₁ and z₂ be two points which are symmetric with respect to a given straight line γ, i.e., such that γ is the perpendicular bisector of the line segment joining z₁ and z₂. By definition, the straight line passing through z₁ and z₂ is orthogonal to γ. Moreover, the center of any circle δ passing through z₁ and z₂ lies on γ, and hence δ is also orthogonal to γ. It is easy to see that the converse is true as well, i.e., if every straight line or circle passing through a pair of points z₁ and z₂ is orthogonal to a given straight line γ, then z₁ and z₂ are symmetric with respect to γ. Generalizing the concept of symmetry with respect to a straight line, we introduce the following definition: Two points z₁ and z₂ are symmetric with respect to a given circle γ if and only if every straight line or circle passing through z₁ and z₂ is orthogonal to γ.

THEOREM 5.6. Let z₁ and z₂ be any two points symmetric with respect to a given straight line or circle γ, and let w = L(z) be any Möbius transformation. Then the points w₁ = L(z₁) and w₂ = L(z₂) are symmetric with respect to the straight line or circle Γ = L(γ)⁹.

Proof. We have to show that an arbitrary straight line or circle Δ passing through w₁ and w₂ is orthogonal to Γ. Let z = L^–1(w) be the inverse of the transformation w = L(z). Clearly, L^–1 is also a Möbius transformation, and

Moreover, δ = L^–1(Δ) is a straight line or circle passing through z₁ and z₂. Since z₁ and z₂ are symmetric with respect to γ, by hypothesis, it follows that δ is orthogonal to γ. But then, since the mapping w = L(z) is conformal, Δ = L(δ) is orthogonal to Γ, and the proof is complete.

COROLLARY. There is only one point z₂ symmetric to a given point z₁ with respect to a given straight line or circle γ.

Proof. If γ is a straight line, the statement is obvious. Thus let γ be a circle, and suppose that besides z₂, there is another point z′₂ ≠ z₂ symmetric to z₁ with respect to γ. Choosing a Möbius transformation w = L(z) mapping γ onto a straight line Γ, we find that w₂ = L(z₂) and w′₂ = L(z′₂) are two distinct points symmetric with respect to Γ, which is impossible.

Remark. Suppose w = L(z) maps a straight line or circle γ onto a circle Γ with center w₁, and let z₁ be the inverse image of w₁. Then the point z₂ symmetric to z₁ with respect to γ must be mapped into the point at infinity. To see this, we note that w₂ = ∞ is symmetric to w₁ with respect to the circle Γ, since any straight line or circle passing through 0 and ∞, i.e., any straight line passing through the center of Γ, is orthogonal to Γ. The uniqueness of w₂ follows from the corollary.

Let γ be an arbitrary straight line or circle. A transformation of the extended plane into itself, which carries each point z into the point z* symmetric to z with respect to γ is called a symmetry transformation with respect to γ or a reflection in γ. In the case where γ is a circle, the transformation is also called an inversion in γ. We now derive analytical expressions for symmetry transformations.

First let γ be a straight line with an assigned direction, and consider reflection in γ. The straight line γ is completely characterized by one of its points a and by the unit vector

pointing in the direction of γ. Suppose we carry out the entire linear transformation

which obviously maps the real axis onto γ, since (5.21) corresponds to a shift by the vector a (carrying the origin of coordinates into the point a), followed by a rotation through the angle θ about the point a. Since the inverse transformation w = L^–1(z) maps γ onto the real axis, it maps every pair of points z and z* symmetric with respect to γ into a pair of points w and w* symmetric with respect to the real axis. But the points w and w* are represented by two conjugate complex numbers, i.e.,

Therefore z — a = τt, and

Eliminating t from (5.23), we obtain

According to (5.24), reflection in a straight line γ going through a point a at an angle θ with the real axis can be accomplished by first constructing the vector which is the reflection of the vector z — a the real axis, and then rotating through the angle 2θ about the point a.

Next let γ be a circle, and consider inversion in γ. Let R (0 < R < ∞) be the radius and a the center of γ. We begin by finding a Möbius transformation which maps γ onto the real axis. The simplest approach is to choose the transformation

which maps the three points w₁ = — 1, w₂ = 0, w₃ = 1 of the real axis into the points z₁ = a — iR, z₂ = a + R, z₃ = a + iR of the circle γ. The inverse transformation w = L^–1(z) maps γ onto the real axis, and maps every pair of points z and z* symmetric with respect to γ into a pair of points w and w* symmetric with respect to the real axis. As before, the points w and w* are represented by two conjugate complex numbers (5.22). Therefore

and

Multiplying the two equations (5.25), we obtain

or

In particular, it follows from (5.26) that

and

Therefore the points z and z* lie on the same ray emanating from the center of γ, and the product of their distances from the center of γ equals the square of the radius of γ. These two conditions, equivalent to formula (5.26), determine the position of one of the points z, z* with respect to the other, and completely characterize the operation of inversion in the circle γ with equation |z — a| = R.

Remark. We note that any symmetry transformation reduces to consecutive application of a linear transformation (entire or fractional), followed by reflection in the real axis. In fact, according to (5.24), reflection in a straight line can be represented in the form

while, according to (5.26), reflection in a circle can be represented in the form

Since any Möbius transformation is conformal and circle-preserving, and since reflection in the real axis has the same properties, except that while preserving the magnitudes of angles it reverses the directions in which they are measured, we see that the most general symmetry transformation is a conformal mapping of the second kind (see p. 57) which is also circle- preserving.

Problem 1. Find the point symmetric to the point 2 + i with respect to

a) The circle |z| = 1; b) The circle |z — i| = 3.

Problem 2. Invert each of the following curves in the unit circle:

g) The boundary of the triangle with nonzero vertices z₁, z₂, z₃.

28. EXAMPLES

We now give two examples illustrating the use of the symmetry-preserving property of Möbius transformations.

Example 1. Find a conformal mapping of the upper half plane ∏ _U: Im z > 0 onto the disk K: |w| < R, such that a given point α ∈ ∏ _U is mapped into the center of K.10

Any such mapping

provided it exists, vanishes for z = α, and hence α is the zero of L(z). But the point symmetric to α with respect to the real axis must be mapped into the point symmetric to the center w = 0 of K with respect to the boundary of K, i.e., the circle C: |w| = R. Therefore must be mapped into the point at infinity (see the remark on p. 105), so that L() = ∞ and is the pole of L(z). It follows that L(z) has the form

where λ is a nonzero complex number.

We now show that (5.27) maps ∏_U onto K, with z = α going into w = 0, if we choose |λ| = R. Since L(α) = 0 for any λ, by construction, it is sufficient to show that (5.27) maps the real axis onto the circle C. If z = x is an arbitrary real number, then x — α and x — are complex conjugates, and hence

Therefore (5.27) maps the real axis into C. But since any three distinct points of the real axis are mapped into three distinct points of C, it follows from Theorem 5.5 that the real axis is mapped onto C.

In (5.27) the argument of λ is left unspecified. The geometric reason for this indeterminacy is clear: Going from one value of λ to another in (5.27), while keeping |λ| = R fixed, is equivalent to changing the arguments of all points w by the same quantity, i.e., to rotating the disk K about its center w = 0. Such a rotation transforms K into itself while leaving its center fixed, and hence does not violate the conditions of the problem. Thus, if the problem is to have a unique solution, we must impose an extra condition on L(z). For example, we might require either that

1. A given point x = x₀ of the real axis should go into the point w = R of the circle C, or that

2. The derivative L′(α) should be a positive real number. (Geometrically, this means that the mapping does not change the slopes of tangents to curves passing through the point α.)

Imposing condition 1, we find from (5.27) that

so that

and hence

Moreover, we still have

as required. Imposing condition 2, with we have

so that λ/i is a positive real number. But, on the other hand, |λ| must equal R. Therefore λ = iR, and

Example 2. Find a conformal mapping of the disk K: |z| < R onto itself such that a given point α ∈ K is mapped into the center of K.

Any such mapping

provided it exists, vanishes for z = α, and hence α is the zero of L(z). But the point α* symmetric to α with respect to the boundary of K, i.e., the circle C: |z| = R, must be mapped into a point symmetric to the center w = 0 of K with respect to C. Therefore α* must be mapped into the point at infinity, so that L(α*) = ∞ and α* is the pole of L(z). It follows that L(z) has the form

[cf. (5.27)], where λ is a nonzero complex number. According to (5.26), the point α* symmetric to α with respect to C is

and hence (5.28) becomes

We now show that (5.29) maps K onto K, with z = α going into w = 0, if we choose |μ| = R². Since L(α) = 0 for any μ, by construction, it is sufficient to show that (5.29) maps the circle C:|z| = R onto itself. If

is an arbitrary point of C, where

then

and hence

Therefore (5.29) maps C into C, and hence onto C, by the same argument as before. This example is considered further in Probs. 4–6.

Problem 1. Map the upper half-plane Im z > 0 onto the unit disk |w| < 1 in such a way that

a) w(i) = 0, arg w′(i) = –π/2;

b) w(2i) = 0, arg w′(2i) = 0;

c) w(α) = 0, arg w′(α) = θ (Im α > 0).

Problem 2. Map the disk |z| < 2 onto the half-plane Re w > 0 in such a way that w(0) = 1, arg w′(0) = π/2.

Problem 3. Map the disk |z – 4i| < 2 onto the half-plane v > u in such a way that the center of the disk goes into the point –4, while the point 2i on the circumference of the disk goes into the origin.

Problem 4. In formula (5.29), the argument of μ is left unspecified. If the problem is to have a unique solution, we must impose an extra condition on L(z). Find the form of the mapping (5.29) if

a) A given point a on the circle C: |z| = R goes into the point w = R on C;

b) The derivative L′(α) is a positive real number.

Comment. Cf. the corresponding conditions on p. 108 for the mapping (5.27).

Problem 5. Find the Möbius transformation w = L(z) mapping the unit disk |z| < 1 onto itself in such a way that

Problem 6. Find the Möbius transformation mapping the unit disk |z| < 1 onto itself in such a way that two given points z₁ and z₂ of the disk go into the points ±α (|α| < 1). Find the expression for α in terms of z₁ and z₂.

---

1 Here we allow p or q to take the improper value ∞

² Henceforth, for simplicity, we shall often omit the argument z, writing L₁ instead of L₁(z), U instead of U(z), etc.

³ See e.g., G. Birkhoff and S. MacLane, op. cit., Chap. 6, Sec. 2.

⁴ See e.g., G. Birkhoff and S. MacLane, op. cit., Chap. 6, Sec. 7.

⁵ Therefore, in the class of Möbius transformations, an entire linear transformation is characterized by the fact that at least one of its fixed points is the point at infinity.

⁶ By x:y is meant the ratio of x to y, i.e., the quantity x/y.

⁷ As usual, a straight line is regarded as a limiting case of a circle (cf. p. 93).

⁸ Note that the assertion that the observer at z₂ finds G on his left is equivalent to the assertion that in order to enter G along the segment δ at the point z₂, the observer must make a “left turn,” i.e., a counterclockwise rotation through 90°. But w = L(z) has a nonzero derivative at z₂, and hence is a conformal mapping of the first kind which preserves not only angles but also the directions in which they are measured (recall p. 57). Therefore, in order to enter along the arc Δ at the point w₂, the observer at w₂ must also make a left turn and hence finds on his left.

⁹ It is in this sense that Möbius transformations are said to be symmetry-preserving.

¹⁰ In expressions like Π_U: Im z > 0 and K:|w| < R, the colon means “defined by the condition.”