Chapter 2
Proto-mathematics
Most of the history of mathematics is inferred from documents written down by scholars, starting about 4000 years ago. Before that time, and in more recent times among certain groups, mathematical ideas were being used, but not written down. In the present chapter, we shall explore this proto-mathematics, the kinds of mathematical thinking that people naturally engage in while going about the practical business of daily life. This inquiry assumes that there is a mode of thought called mathematizing that is intrinsic to human nature and therefore common to different cultures. The simplest assumption is that counting and common shapes such as squares and circles have the same meaning to everyone. Our inquiry will make use of three sources:
We shall examine these sources as they relate to the four basic ingredients of mathematics listed in the preceding chapter.
2.1 Number
There is ample evidence of counting from all three of the sources listed above.
2.1.1 Animals' Use of Numbers
It is not clear just how high animals and birds can count, but they certainly have the ability to distinguish not merely patterns, but actual numbers. The counting abilities of birds were studied in a series of experiments conducted in the 1930s and 1940s by O. Koehler (1889–1974) at the University of Freiburg. Koehler (1937) kept the trainer isolated from the bird. In the final tests, after the birds had been trained, the birds were filmed automatically, with no human beings present. Koehler found that parrots and ravens could learn to compare the number of dots, up to 6, on the lid of a hopper with a “key” pattern in order to determine which hopper contained food. They could make the comparison no matter how the dots were arranged, thereby demonstrating an ability to take account of the number of dots rather than the pattern.
2.1.2 Young Children's Use of Numbers
Preschool children also learn to count and use small numbers. The results of many studies have been summarized by Karen Fuson (1988). A few of the results from observation of children at play and at lessons were as follows:
One can thus observe in children the capacity to recognize groups of two or three without performing any conscious numerical process. This observation suggests that these numbers are primitive, while larger numbers are a conscious creation.
The V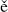 stonice wolf bone. Copyright © Illustrated London News, October 2, 1937. Courtesy of the Mary Evans Picture Library.
stonice wolf bone. Copyright © Illustrated London News, October 2, 1937. Courtesy of the Mary Evans Picture Library.

2.1.3 Archaeological Evidence of Counting
Animal bones containing notches have been found in Africa and Europe, suggesting that some sort of counting procedure was being carried on at a very early date, although what exactly was being counted remains unknown. One such bone, the radius bone of a wolf, was discovered at V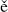 stonice (Moravia) in 1937. This bone is marked with two series of notches, grouped by fives, the first series containing five groups and the second six. Its discoverer, Karel Absolon (1887–1960), believed the bone to be about 30,000 years old, and modern tests on artifacts from the site appear to confirm this dating. The people who produced this bone were clearly a step above mere survival, since a human portrait carved in ivory was found in the same settlement, along with a variety of sophisticated tools. Because of the grouping by fives, it seems likely that this bone was being used to count something. Even if the groupings are meant to be purely decorative, they point to a use of numbers and counting for a practical or artistic purpose.
stonice (Moravia) in 1937. This bone is marked with two series of notches, grouped by fives, the first series containing five groups and the second six. Its discoverer, Karel Absolon (1887–1960), believed the bone to be about 30,000 years old, and modern tests on artifacts from the site appear to confirm this dating. The people who produced this bone were clearly a step above mere survival, since a human portrait carved in ivory was found in the same settlement, along with a variety of sophisticated tools. Because of the grouping by fives, it seems likely that this bone was being used to count something. Even if the groupings are meant to be purely decorative, they point to a use of numbers and counting for a practical or artistic purpose.
2.2 Shape
Spatial relations are also used by animals, and the gradual mastery of these phenomena by children has been charted by psychologists. In addition, many crafts, both ancient and modern show how these relations are used for both practical and decorative purposes.
2.2.1 Perception of Shape by Animals
Obviously, the ability to perceive shape is of value to an animal in determining what is or is not food, what is a predator, and so forth; and in fact the ability of animals to perceive space has been very well documented. One of the most fascinating examples is the ability of certain species of bees to communicate the direction and distance of sources of plant nectar by performing a dance inside the beehive. The pioneer in this work was Karl von Frisch (1886–1982), and his work has been continued by James L. Gould and Carol Grant Gould (1995). The experiments of von Frisch left many interpretations open and were challenged by other specialists. The Goulds performed more delicately designed experiments which confirmed the bee language by deliberately misleading the bees about the food source. The bee will traverse a circle alternately clockwise and counterclockwise if the source is nearby. If it is farther away, the alternate traversals will spread out, resulting in a figure eight, and the dance will incorporate sounds and waggling. By moving food sources, the Goulds were able to determine the precision with which this communication takes place (about 25%). Still more intriguing is the fact that the direction of the food source is indicated by the direction of the axis of the figure eight, oriented relative to the sun if there is light and relative to the vertical if there is no light.
As another example, in his famous experiments on conditioned reflexes using dogs as subjects the Russian scientist Pavlov (1849–1936) taught dogs to distinguish ellipses of very small eccentricity from circles. He began by projecting a circle of light on the wall each time he fed the dog. Eventually the dog came to expect food (as shown by salivation) every time it saw the circle. When the dog was conditioned, Pavlov began to show the dog an ellipse in which one axis was twice as long as the other. The dog soon learned not to expect food when shown the ellipse. At this point the malicious scientist began making the ellipse less eccentric and found, with fiendish precision, that when the axes were nearly equal (in a ratio of 8:9, to be exact) the poor dog had a nervous breakdown (Pavlov, 1928, p. 122).
2.2.2 Children's Concepts of Space
The most famous work on the development of mathematical concepts in children is due to Jean Piaget (1896–1980) of the University of Geneva, who wrote several books on the subject, some of which have been translated into English. Piaget divided the development of the child's ability to perceive space into three periods: a first period (up to about 4 months of age) consisting of pure reflexes and culminating in the development of primary habits, a second period (up to about one year) beginning with the manipulation of objects and culminating in purposeful manipulation, and a third period in which the child conducts experiments and becomes able to comprehend new situations. He categorized the primitive spatial properties of objects as proximity, separation, order, enclosure, and continuity. These elements are present in greater or less degree in any spatial perception. In the baby they come together at the age of about 2 months to provide recognition of faces. The human brain seems to have some special “wiring” for recognizing faces.1
The interesting thing about these concepts is that mathematicians recognize them as belonging to the subject of topology, an advanced branch of geometry that developed in the late nineteenth and early twentieth centuries. It is an interesting paradox that the human ability to perceive shape depends on synthesizing topological concepts; this progression reverses the pedagogical and historical ordering between geometry and topology. Piaget pointed out that children can make topological distinctions (often by running their hands over models) before they can make geometric distinctions. Discussing the perceptions of a group of 3-to-5-year-olds, Piaget and Inhelder (1967) stated that the children had no trouble distinguishing between open and closed figures, surfaces with and without holes, intertwined rings and separate rings, and so forth, whereas the seemingly simpler relationships of geometry—distinguishing a square from an ellipse, for example—were not mastered until later.
2.2.3 Geometry in Arts and Crafts
Weaving and knitting are two excellent examples of activities in which the spatial and numerical aspects of the world are combined. Even the sophisticated idea of a rectangular coordinate system is implicit in the placing of different-colored threads at intervals when weaving a carpet or blanket so that a pattern appears in the finished result.
Marcia Ascher (1991) has assembled many examples of rather sophisticated mathematics connected with arts and crafts. The Bushoong people of Zaire make part of their living by supplying embroidered cloth, articles of clothing, and works of art to others in the economy of the Kuba chiefdom. As a consequence of this work, perhaps as preparation for it, Bushoong children amuse themselves by tracing figures on the ground. The rule of the game is that a figure must be traced without repeating any strokes and without lifting the finger from the sand. In graph theory, this problem is known as the unicursal tracing problem. It was analyzed by the Swiss mathematician Leonhard Euler (1707–1783) in the eighteenth century in connection with the famous Königsberg bridge problem. According to Ascher, in 1905 some Bushoong children challenged the ethnologist Emil Torday (1875–1931) to trace a complicated figure without lifting his finger from the sand. Torday did not know how to do this, but he did collect several examples of such figures. The Bushoong children seem to learn intuitively what Euler proved mathematically: A unicursal tracing of a connected graph is possible if there are at most two vertices where an odd number of edges meet. The Bushoong children become very adept at finding such a tracing, even for figures as complicated as that shown in Fig. 2.1.
Figure 2.1 A graph for which a unicursal tracing is possible.

Examples of intricate geometric patterns susceptible to mathematical analysis are abundant throughout human history. A recent example is the book of Belcastro and Yackel (2008), which gives detailed analyses of the connections between mathematics and needlework.
2.3 Symbols
Visual symbolism seems to be a peculiarly human mode of thought, not observable in animals, and one learned by children only through teaching. Artifacts from archaeological sites are sometimes interpreted as representations of divinities, but generally ancient paintings and statues tend to represent physical objects, with certain distortions in size that reflect their relative importance to the artist, or the artist's employer, in the case of Egyptian paintings that show the pharaoh much larger than anyone else.
We tend to think of symbolism as arising in algebra, since that is the subject in which we first become aware of it as a concept. The thing itself, however, is implanted in our minds much earlier, when we learn to talk. Human languages, in which sounds correspond to concepts and the temporal order or inflection of those sounds maps some relation between the concepts they signify, exemplify the process of abstraction and analogy, essential elements in mathematical reasoning.
Once numbers have been represented symbolically, the next logical step would seem to be to introduce symbols for arithmetic operations or for combining the number symbols in other ways. This step may not be necessary for rapid computation, since mechanical devices such as counting rods, pebbles, counting boards, and the like can be used as analog computers. The symbolic ability of the human mind is shown when pebbles or tally marks are used to represent objects in the mind of the calculator. The operations performed using these methods can rise to a high level of sophistication without the need for any written computations. An example of the use of an automatic counting device is given by Ascher (1997) in a discussion of a system of divination used by the Malagasy of Madagascar, in which four piles of seeds are arranged in a column and the seeds removed from each pile two at a time until only one or two seeds remain. Each set of seeds in the resulting column can be interpreted as “odd” or “even.” After this procedure is performed four times, the four columns and four rows that result are combined in different pairs using the ordinary rules for adding odds and evens to generate eight more columns of four numbers. The accuracy of the generation is checked by certain mathematical consequences of the method used. If the results are satisfactory, the 16 sets of four odds and evens are used as an oracle for making decisions and ascribing causes to such events as illnesses.
Divination seems to fulfill a nearly universal human desire to feel in control of the powerful forces that threaten human happiness and prosperity. It manifests itself in a variety of ways, as just shown by the example of the Malagasy. We could also cite large parts of the Jewish Kabbalah, the mysticism of the Pythagoreans, and many others, down to the geometric logic of Ramon Lull (1232–1316), who was himself steeped in the Kabbalah. The variety of oracles that people have consulted for advice about the conduct of their lives—tarot cards, crystal balls, astrology, the entrails of animals and birds, palmistry, and the like—seems endless. For the purposes of this book, however, we shall be interested only in those aspects of divination that involve mathematics, such as magic squares. Whether or not a person believes that divination reveals hidden truth about the universe—the author does not—it remains a prominent form of human behavior over the centuries and deserves to be studied for that reason alone. But it is time to return to more prosaic matters.
The primary mathematical example of symbolism is the writing of positive integers. Some systems, like those of ancient Egypt, Greece, and Rome, are adequate for recording numbers, but comparatively cumbersome in computation. Just imagine trying to multiply XLI by CCCIV! [However, Detlefsen et al. (1975) demonstrate that this task is not as difficult as it might seem.] Even to use a 28 × 19 table of dates of Easter compiled in Russia some centuries ago, the calculators had to introduce simplifications to accommodate the fact that dividing a four-digit number by a two-digit number was beyond the skill of many of the users of the table.
The earliest mathematical texts discuss arithmetical operations using everyday words that were probably emptied of their usual meaning, thereby becoming abstract symbols capable of representing a variety of objects. Students had to learn to generalize from a particular example to the abstract case, and many problems that refer to specific objects probably became archetypes for completely abstract reasoning, just as we use such expressions as “putting the cart before the horse” and “comparing apples and oranges” to refer to situations having no connection at all with horse-and-buggy travel or the appraisal of fruit. For example, problems of the type “If 3 bananas cost 75 cents, how much do 7 bananas cost?” occur in the work of Brahmagupta from 1300 years ago. Brahmagupta named the three data numbers argument (3), fruit (75), and requisition (7). His rule for getting the answer was to multiply the fruit by the requisition and divide by the argument, a rule now known as the Rule of Three. As another example, cuneiform tablets from Mesopotamia that are several thousand years old contain general problems that we would now solve using quadratic equations. These problems are stated as variants of the problem of finding the length and width of a rectangle whose area and perimeter are known. The mathematician and historian of mathematics B. L. van der Waerden (1903–1996) claimed that the words for length and width were being used in a completely abstract sense in these problems. They had become abstract symbols, rather than words denoting concrete objects.
In algebra, symbolism seems to have occurred for the first time in the work of the (probably third-or fourth-century) Greek mathematician Diophantus of Alexandria, who introduced the symbol ς for an unknown number. A document from India, the Bakshali manuscript, which may have been written within a century of the work of Diophantus, also introduces an abstract symbol for an unknown number. Symbolism developed gradually in modern algebra. Originally, the Arabic word for thing was used to represent the unknown in a problem. This word, and its Italian translation cosa, was eventually replaced by the familiar x most often used today. In this way an entire word was gradually pared down to a single letter that could be manipulated graphically.
2.4 Mathematical Reasoning
Inferences made by animals and young children that appear to fit the “if A, then B” pattern are usually traceable to conditioning. When people or animals experience B after A, they rather quickly come to expect B any time that A happens, especially if the first experience had powerful emotional connections.
2.4.1 Animal Reasoning
Logic is concerned with getting conclusions that are as reliable as the premises. From a behavioral point of view, the human tendency to make inferences based on logic is probably hardwired and expressed as the same mechanism by which habits are formed. This same mechanism probably accounts for the metaphysical notion of cause. If A implies B, one feels that in some sense A causes B to be true. The dogs in Pavlov's experiments, described above, were given total reinforcement as they learned geometry and came to make associations based on the constant conjunction of a given shape and a given reward or lack of reward. In the real world, however, we frequently encounter a weaker type of cause, where A is usually, but not always, followed by B. For example, lightning is always followed by thunder; but if the lightning is very distant, the thunder will not be heard. The analog of this weaker kind of cause in conditioning is partial reinforcement. A classical example is a famous experiment of Skinner (1948), who put hungry pigeons in a cage and attached a food hopper to the cage with an automatic timer to permit access to the food at regular intervals. The pigeons at first engaged in aimless activity when not being fed, but tended to repeat whatever activity they happened to be doing when the food arrived, as if they made an association between the activity and the arrival of food. Naturally, the more they repeated a given activity, the more likely that activity was to be reinforced by the arrival of food. Since they were always hungry, it was not long before they were engaged full time in an activity that they apparently considered an infallible food producer. This activity varied from one bird to another. One pigeon thrust its head into an upper corner of the cage; another made long sweeping movements with its head; another tossed its head back; yet another made pecking motions toward the floor of the cage.
The difficulties that people, even mathematicians, have in understanding and applying probability can be seen in this example. For example, the human body has some capacity to heal itself. Like the automatic timer that eventually provided food to the pigeons, the human immune system often overcomes the disease. Yet sick people, like hungry pigeons, try various methods of alleviating their misery. The consequence is a wide variety of nostrums said to cure a cold or arthritis. One of the triumphs of modern mathematical statistics is the establishment of reliable systems of inference to replace the inferences that Skinner called “superstitious.”
Modern logic has purged the concept of implication of all connection with the notion of cause. The statement “If Abraham Lincoln was the first President of the United States, then 2 + 2 = 4” is considered a true implication, even though Lincoln was not the first President and in any case his being such would have no causal connection with the truth of the statement “2 + 2 = 4.” In standard logic the statement “If A is true, then B is true” is equivalent to the statement “Either B is true, or A is false, or both.” Absolute truth or falsehood is not available in relation to the observed world, however. As a result, science must deal with propositions of the form “If A is true, then B is highly probable.” One cannot infer from this statement that “If B is false, then A is highly improbable.” For example, an American citizen, taken at random, is probably not a U. S. Senator. It does not follow that if a person is a U. S. Senator, that person is probably not an American citizen.
Since we cannot trace the development of mathematical reasoning through the sources we have been using, we look instead at ancient documents and at the modern school curriculum to see how it arose. Taking the latter first, we note that students generally learn all of arithmetic and the rules for manipulating algebraic expressions by rote. Any justification of these rules is purely experimental. Logic enters the curriculum, along with proof, in the study of geometry. This sequence is not historical and may leave the impression that mathematics was an empirical science until the time of Euclid (ca. 300 BCE). But the ancient documents give us good reason to believe that some facts were deduced from simpler considerations at a very early stage. The main reason for thinking so is that the conclusions reached by some ancient authors are not visually obvious.
2.4.2 Visual Reasoning
As an example, it is immediately obvious that a diagonal divides a rectangle into two congruent triangles. If through any point on the diagonal we draw two lines parallel to the sides, these two lines will divide the rectangle into four rectangles. The diagonal divides two of these smaller rectangles into pairs of congruent triangles, just as it does the whole rectangle, thus yielding three pairs of congruent triangles, one large pair and two smaller pairs. It then follows (see Fig. 2.2) that the two remaining rectangles must have equal area, even though their shapes are different and to the eye they do not appear to be equal. Each of these rectangles is obtained by subtracting the two smaller triangles from the large triangle in which they are contained. When we find an ancient author mentioning that these two rectangles of different shape are equal, as if it were a well-known fact, we can be confident that this knowledge does not rest on an experimental or inductive foundation. Rather, it is the result of a combination of numerical and spatial reasoning.
Figure 2.2 (a) The diagonal AC divides the rectangle ABCD into congruent triangles ABC and CDA. (b) When the congruent pairs (AEI, IGA) and (IHC, CFI) are subtracted from the congruent pair (ABC, CDA), the remainders (rectangles EBHI and GIFD) must be equal.
Ancient authors often state what they know without saying how they know it. As the example just cited shows, we can be confident that the basis was not always induction or experiment. Perminov (1997) points out that solutions of complicated geometric problems which can be shown to be correct are stated without proof by the writers of the very earliest mathematical documents, such as the Rhind papyrus from Egypt and cuneiform tablets from Mesopotamia. The facts that an author presents not merely a solution but a sequence of steps leading to that solution and that this solution can now be reconstructed justify the conclusion that the result was arrived at through mathematical reasoning, even though the author does not write out the details. This observation is particularly important in evaluating the mathematical achievements of the Mesopotamian, Egyptian, Hindu, and Chinese mathematicians, who did not write out formal proofs in the Greek sense. Since they often got results that agree with modern geometry, they must have used some form of visual reasoning such as we have presented here.
Problems and Questions
Mathematical Problems
2.1. Find a unicursal tracing of the graph shown in Fig. 2.1.
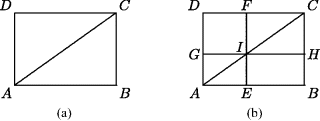
2.2. Perminov (1997, p. 183) presents the following example of tacit mathematical reasoning from an early cuneiform tablet. Given a right triangle ACB divided into a smaller right triangle DEB and a trapezoid ACED by the line DE parallel to the leg AC, such that EC has length 20, EB has length 30, and the trapezoid ACED has area 320, what are the lengths AC and DE? (See Fig. 2.3b.) The author of the tablet very confidently computes these lengths by the following sequence of operations: (1) 320 ÷ 20 = 16; (2) 30 · 2 = 60; (3) 60 + 20 = 80; (4) 320 ÷ 80 = 4; (5) 16 + 4 = 20 = AC; (6) 16 − 4 = 12 = DE. As Perminov points out, to present this computation with any confidence, you would have to know exactly what you are doing. What was this anonymous author doing?
Figure 2.3 (a) Line DE divides triangle ABC into triangle DEB and trapezoid ACED. (b) Line FGIH bisects line AD. Rectangle FCEI has the same area as trapezoid ACED, and rectangle JCED equals rectangle MDKL.
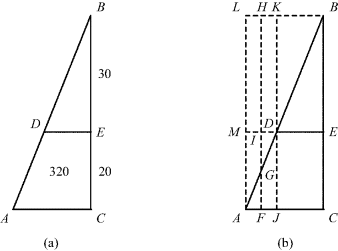
To find out, fill in the reasoning in the following sketch. The author's first computation shows that a rectangle of height 20 and base 16 would have exactly the same area as the trapezoid. Hence if we draw the vertical line FH through the midpoint G of AD, and complete the resulting rectangles as in Fig. 2.3, rectangle FCEI will have area 320. Since AF = MI = FJ = DI, it now suffices to find this common length, which we will call x; for AC = CF + FA = 16 + x and DE = EI − DI = 16 − x. By the principle demonstrated in Fig. 2.2, JCED has the same area as DKLM, so that DKLM + FJDI = DKLM + 20x. Explain why DKLM = 30 · 2 · x, and hence why 320 = (30 · 2 + 20) · x.
Could this procedure have been obtained experimentally?
2.3. A now-famous example of mathematical blunders committed by mathematicians (not statisticians, however) occurred a few decades ago. At the time, a very popular television show in the United States was called Let's Make a Deal. On that show, the contestant was often offered the chance to keep his or her current winnings or to trade them for a chance at some other unknown prize. In the case in question the contestant had chosen one of three boxes, knowing that only one of them contained a prize of any value, but not knowing the contents of any of them. For ease of exposition, let us call the boxes A, B, and C and assume that the contestant chose box A.
The emcee of the program was about to offer the contestant a chance to trade for another prize, but in order to make the program more interesting, he had box B opened, in order to show that it was empty. Keep in mind that the emcee knew where the prize was and would not have opened box B if the prize had been there. Just as the emcee was about to offer a new deal, the contestant asked to exchange the chosen box (A) for the unopened box (C) on stage. The problem posed to the reader is: Was this a good strategy? To decide, analyze 300 hypothetical games, in which the prize is in box A in 100 cases, in box B in 100 cases (in these cases, of course, the emcee will open box C to show that it is empty), and in box C in the other 100 cases. First assume that in all 300 games the contestant retains box A. Then assume that in all 300 games the contestant exchanges box A for the unopened box on stage. By which strategy does the contestant win more games?
2.4. Explain why the following analysis of the game described in the preceding question leads to an erroneous result. Consider all the situations in which the contestant has chosen box A and the emcee has shown box B to be empty. Imagine 100 games in which the prize is in box A and 100 games in which it is in box C. Suppose the contestant retains box A in all 200 games; then 100 will be won and 100 lost. Likewise, if the contestant switches to box C in all 200 games, then 100 will be won and 100 lost. Hence there is no advantage to switching boxes.
2.5. The fallacy discussed in the last two exercises is not in the mathematics, but rather in its application to the real world. The question involves what is known as conditional probability. Mathematically, the probability of event E, given that event F has occurred, is defined as the probability that E and F both occur, divided by the probability of F. The many mathematicians who analyzed the game erroneously proceeded by taking E as the event “The prize is in box C” and F as the event “Box B is empty.” Given that box B has a 2/3 probability of being empty and the event “E and F” is the same as event E, which has a probability of 1/3, one can then compute that the probability of E given F is (1/3)/(2/3) = 1/2. Hence the contestant seems to have a 50% probability of winning as soon as the emcee opens Box B, revealing it to be empty.
Surely this conclusion cannot be correct, since the contestant's probability of having chosen the box with the prize is only 1/3 and the emcee can always open an empty box on stage. Replace event F with the more precise event “The emcee has shown that box B is empty” and redo the computation. Notice that the emcee is going to show that either box B or box C is empty and that the two outcomes are equally likely. Hence the probability of this new event F is 1/2. Thus, even though the mathematics of conditional probability is quite simple, it can be a subtle problem to describe just what event has occurred. Conclusion: To reason correctly in cases of conditional probability, one must be very clear in describing the event that has occurred.
2.6. Reinforcing the conclusion of the preceding question, exhibit the fallacy in the following “proof” that lotteries are all dishonest.
Proof. The probability of winning a lottery is less than one chance in 1,000,000 (= 10−6). Since all lottery drawings are independent of one another, the probability of winning a lottery five times is less than (10−6)5 = 10−30. But this probability is far smaller than the probability of any conceivable event. Any scientist would disbelieve a report that such an event had actually been observed to happen. Since the lottery has been won five times in the past year, it must be that winning it is not a random event; that is, the lottery is fixed.
What is the event that has to occur here? Is it “Person A (specified in advance) wins the lottery,” or is it “At least one person in this population (of, say, 30 million people) wins the lottery”? What is the difference between those two probabilities? (The same fallacy occurs in the probabilistic arguments purporting to prove that evolution cannot occur, based on the rarity of mutations.)
Questions for Reflection
2.7. At what point do you find it necessary to count in order to say how large a collection is? Can you look at a word such as tendentious and see immediately how many letters it has? The American writer Henry Thoreau (1817–1863) was said to have the ability to pick up exactly one dozen pencils out of a pile. Try as an experiment to determine the largest number of pencils you can pick up out of a pile without counting. The point of this exercise is to see where direct perception needs to be replaced by counting.
2.8. How confidently can we make inferences about the development of mathematics from the study of animals, children, and archaeological sites?
2.9. One aspect of symbolism that has played a large role in human history is the mystical identification of things that exhibit analogous relations. The divination practiced by the Malagasy is one example, and there are hundreds of others: astrology, alchemy, numerology, tarot cards, palm reading, and the like, down to the many odd beliefs in the effects of different foods based on their color and shape. Even if we dismiss the validity of such divination, is there any value for science in the development of these subjects?
Note
1. And for “seeing” faces on the moon, in clouds, and on burnt pieces of toast!