Chapter 10
Fifth-Century Greek Geometry
It is easy to surmise what problems the pre-Euclidean geometers must have worked on. One has only to look at the propositions in Euclid's Elements, which was, as its name implies, an elementary textbook of geometry and number theory, summarizing in systematic fashion what had gone before. It was certainly not the most advanced mathematics of its day, since its basic geometric tools are lines (what we now call line segments), circles, planes, and spheres. The conic sections, which were known before Euclid, and on which Euclid himself wrote a treatise, are not mentioned in it. As we have said, later commentators ascribed this geometry to the Pythagoreans. The historical problem is to trace a line of development from the basic facts Thales is said to have known to the elaborate systematic treatise of Euclid three centuries later. For guidance, we have the statements of the commentators, but they provide only a few points of light. To get a more comprehensive picture, we need to use our imaginations and conjecture one. It may not be correct, but at least it provides some coherence to the narrative and can be modified or rejected if it is incompatible with hard historical facts. The reader is hereby warned that we are about to write such a scenario and will therefore adopt a skeptical attitude toward it.
10.1 “Pythagorean” Geometry
Proclus mentions two topics of geometry as being Pythagorean in origin. One is the theorem that the sum of the angles of a triangle is two right angles (Book 1, Proposition 32). Since this statement is equivalent to Euclid's parallel postulate, it is not clear what the discovery amounted to or how it was made.
10.1.1 Transformation and Application of Areas
The other topic mentioned by Proclus is a portion of Euclid's Book 6 that is not generally taught any more, called application of areas.
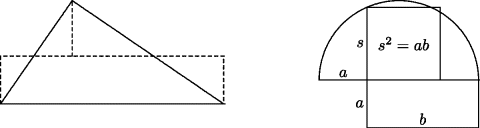
That topic had to be preceded by the simpler topic of transformation of areas. In his Nine Symposium Books,1 Plutarch called the transformation of areas “one of the most geometrical” problems. He thought solving it was a greater achievement than discovering the Pythagorean theorem and said that Pythagoras was led to make a sacrifice when he solved the problem. The basic idea is to convert a figure having one shape to another shape while preserving its area, as in Fig. 10.1. To describe the problem in a different way: Given two geometric figures A and B, construct a third figure C the same size as A and the same shape as B. One can imagine many reasons why this problem would be attractive. If one could find, for example, a square equal to any given figure, then comparing sizes would be simple, merely a matter of converting all areas into squares and comparing the lengths of their sides. But why stop at that point? Why not consider the general problem of converting any shape into any other? For polygons this problem was solved very early, and the solution appears in Proposition 25 of Euclid's Book 6, which shows how to construct a polygon of prescribed shape equal in area to another polygon of possibly different shape.
Figure 10.1 Left: turning a triangle into a rectangle. Right: turning a rectangle into a square (s2 = ab).
The problem of application of areas is one degree more complicated than simply transforming an area from one shape to another. There are two such problems, both involving a given straight line segment AB and a planar polygon Γ. The first problem is to construct a parallelogram equal to Γ on part of the line segment AB in such a way that the parallelogram needed to fill up a parallelogram on the entire base, called the defect, will have a prescribed shape. This is the problem of application with defect, and the solution is given in Proposition 28 of Book 6. The second application problem is to construct a parallelogram equal to Γ on a base that is an extension of the line AB in such a way that the portion of the parallelogram extending beyond AB (the excess) will have a prescribed shape. This is the problem of application with excess, and the solution is Proposition 29 of Book 6.
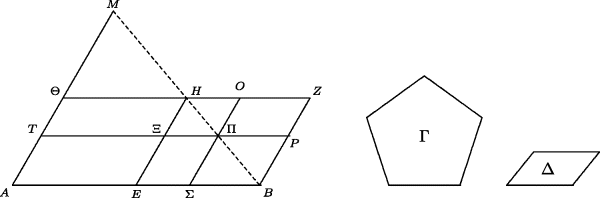
The construction for application with defect is shown in Fig. 10.2. This problem does not have a solution for all given lines and areas, since the largest parallelogram that can be formed under these conditions is the one whose base is half of the given line (Book 6, Proposition 26). Assuming that the given polygon Γ is smaller than this parallelogram, let AB be the given line, Γ the given polygonal region, and Δ the given parallelogram shape. The dashed line from B makes the same angle with AB that the diagonal of the parallelogram Δ makes with its base. The line AM is drawn to make the same angle as the corresponding sides of Δ. Then any parallelogram having its sides along AB and AM and opposite corner Π from A on the dashed line will automatically generate a “defect” that is similar to Δ. The remaining problem is to choose Π so that AΣΠT has the same area as Γ. That is achieved by constructing the parallelogram HΞΠO similar to Δ and equal to the difference between AEHΘ, where H is the midpoint of MB and Γ. Constructing HΞΠO is the simpler transformation-of-area problem.
Figure 10.2 Application with defect. Euclid, Book 6, Proposition 28. Line AB, plane region Γ, and parallelogram Δ are given. Then parallelogram AΣΠT is constructed on part of line AB so as to be equal to Γ, while the defect ΣBPΠ is similar to Δ.
Besides these two problems, there is a much simpler problem of pure application, that is, finding the proper altitude for a parallelogram on the base AB so that the area is Γ. The Greek word for application is parabol
. Proclus cites Eudemus in asserting that the solution of the application problems was an ancient discovery of the Pythagoreans and that they gave these problems the names ellipse (application with defect) and hyperbola (application with excess), names that were later transferred to the conic curves by Apollonius. This version of events was also reported by Pappus. We shall see the reason for the transfer below.
Although most of Euclid's theorems have obvious interest from the point of view of anyone curious about the world, the application problems raise a small mystery. Why were the Pythagoreans interested in them? Were they merely a refinement of the transformation problems? Why would anyone be interested in applying an area so as to have a defect or excess of a certain shape? Without restriction on the shape of the defect or excess, the application problem does not have a unique solution. Were the additional conditions imposed simply to make the problem determinate? Some historians have speculated that there was a further motive.
In the particular case when the excess or defect is a square, these problems amount to finding two unknown lengths given their sum and product (application with defect) or given their difference and product (application with excess). In modern terms, these two problems amount to quadratic equations. (Pure application amounts to a linear equation.) Several prominent historians in the mid-twentieth century endorsed the view that Euclid's Book 2 was merely a translation into geometric language of the computational techniques found on the cuneiform tablets. And indeed, both do correspond mathematically to what we nowadays write as linear and quadratic equations. But neither the cuneiform writers nor Euclid had any concept corresponding to our word equation. Therefore neither of them was doing algebra as we understand it, and there is no reason to think that the Greek geometers were translating Mesopotamian techniques into geometric language. This hypothesis of “geometric algebra” was severely attacked by Unguru (1975/76), and no longer has many defenders.
Some historians have argued that this “geometric algebra” was a natural response to the discovery of incommensurable magnitudes, which will be discussed below, indeed a logically necessary response. On this point, however, many others disagree. Gray, for example, says that, while the discovery of incommensurables did point out a contradiction in a naive approach to ratios, “it did not provoke a foundational crisis.” Nor did it force the Pythagoreans to recast algebra as geometry. In fact, it is premature to speak of equations or algebra in connection with the Greeks at this point. They had figurate numbers, among which were square numbers. At the most, we can admit that they may have looked for the side of a square equal to a certain multiple of another square. Such a problem can be considered without thinking about equations at all. Gray (1989, p. 16) concludes that “[r]ather than turning from algebra to geometry,. . .the Greeks were already committed to geometry.”
The problem of incommensurables just mentioned was one of three challenges that one can easily imagine the early geometers having to face, once they set off down the road of a systematic, logical development of the subject to replace the isolated results achieved during the earlier period in which the main problem was to get a numerical value for an area or volume. We shall see that one of these three challenges could be ignored as far as mathematics itself was concerned, but the other two were genuine stimuli to further work and proved very fruitful, extending the Euclidean approach, which was based on two-and three-dimensional figures generated by straight lines and circles, to the limits of its potential. (After that, except for the revival of some metrical methods that had not formed part of the Euclidean canon, Greek geometry declined for lack of new material.) Let us now look at these three problems as they may have arisen. In this chapter, we shall merely state the problems. The partial solutions found to them will form most of the subject matter of the next chapter.
10.2 Challenge No. 1: Unsolved Problems
Supposing that the techniques of transformation and application of areas were known to the fifth-century geometers, we can easily guess what problems they would have been trying to solve. There are three natural directions in which the plane geometry of lines and circles could be extended.
The three problems just listed were mentioned by later commentators as an important challenge to all geometers. To solve them, geometers had to enlarge their set of basic objects beyond lines and planes. They were rather conservative in doing so, first invoking familiar surfaces such as cones and cylinders, which could be generated by moving lines on circles, and intersecting them with planes so as to get the conic sections that we know as the ellipse, parabola, and hyperbola. These curves made it possible to solve two of the three problems (trisecting the angle and doubling the cube). Later, a number of more sophisticated curves were invented, among them spirals, and the quadratrix. This last curve got its name from its use in squaring the circle. Although it is not certain that the fifth-century geometers had a program like the one described above, it is known that all three of these problems were worked on in antiquity. Solving these problems was certainly a desirable goal, but that solution could take its time. Mathematical problems only become more interesting when they remain unsolved for an extended period. Not solving them in no way threatened the achievements already gained.
10.3 Challenge No. 2: The Paradoxes of Zeno of Elea
Although we have some idea of the geometric results proved by the early Greek geometers, our knowledge of their interpretation of these results is murkier. How did they conceive of geometric entities such as points, lines, planes, and solids? Were these objects physically real or merely ideas? What properties did they have? Some light is shed on this question by the philosophical critics, one of whom has become famous for the paradoxes he invented.
As mentioned, in the Pythagorean philosophy, the universe was said to have been generated by numbers and motion. That these concepts needed to be sharpened up became clear from critics of a naive view of geometry. We now know that the basic problem is the incompatibility between discrete modes of thought and continua. (As we shall see below, the third challenge—that of incommensurable pairs of lines—arises precisely because lines are continuous.) It turns out to be more difficult to think about continuous media than one might imagine.
These paradoxes are ascribed to the philosopher Zeno of Elea. Zeno died around 430 BCE, and we do not have any of his works to rely on, only expositions of them by other writers. Aristotle, in particular, says that Zeno gave four puzzles about motion, which he called the Dichotomy (division), the Achilles, the Arrow, and the Stadium. Here is a summary of these arguments in modern language, based on Book 6 of Aristotle's Physics.
Even today, we think of a line as “made of” points, but Zeno's paradoxes seem to show that space cannot be “made of” points in the same way that a building can be made of bricks. For assuredly the number of points in a line segment cannot be finite. If it were, since points are indivisible (atoms in the original Greek sense of the word), the line would not be infinitely divisible as the dichotomy and Achilles paradoxes showed that it must be; moreover, the stadium paradox would show that the number of points in a line equals its double. There must therefore be an infinity of points in a line. But then each of these points must take up no space; for if each point occupied some space, an infinite number of them would occupy an infinite length.2 But if points occupy no space, how can the arrow, whose tip is at a single point at each instant of time, move through a positive quantity of space? A continuum whose elements are points was needed for geometry, yet it could not be thought of as being made up of points in the way that discrete collections are made up of individuals.
This challenge, while it no doubt provided brain-breaking puzzles for mathematicians for a long time, can nevertheless be ignored by those who have no metaphysical bent and are concerned only with deriving one statement from another by logical deduction. Geometers had no acute need to solve the problems posed by Zeno, even though they pointed up difficulties with the interpretation of mathematical concepts. Like the unsolved construction problems listed above, leaving them unanswered posed no threat to the formal creation of geometry.
10.4 Challenge No. 3: Irrational Numbers and Incommensurable Lines
The difficulties pointed out by Zeno affected the intuitive side of geometry and its interpretation. We would call them metaphysical puzzles rather than mathematical puzzles nowadays. The challenge they posed, which involved elucidating the nature of a continuum, was not satisfactorily met until the late nineteenth and early twentieth century. (Some say not even then!) There was, however, a challenge that came from within the formal system of geometry. To the modern mathematician, this second challenge in dealing with the concept of a continuum is much more pertinent and interesting than the paradoxes of Zeno. That challenge is the problem of incommensurables, which led ultimately to the concept of a real number.
The existence of incommensurables throws doubt on certain oversimplified proofs of proportion. When two lines or areas are commensurable, one can describe their ratio as, say, 5 : 7, meaning that there is a common measure such that the first object is five times this measure and the second is seven times it. A proportion such as a : b : : c : d, then, is the statement that ratios a : b and c : d are both represented by the same pair of numbers. Almost certainly, the legendary aphorism of Pythagoras, that “all is number,” refers to this use of integers to define the ratio of two objects.3 It was therefore problematic when pairs of lines were discovered that had no common measure, and whose ratio could therefore not be expressed in this way. As the concept of incommensurable pairs of lines is intimately bound up with what we now call irrational numbers (and were not considered numbers at all by the Greeks working in the Euclidean tradition), we shall look at these two phenomena together and compare them.
The absence of a place-value system of writing numbers forced the Greek mathematicians to create a way around the problem that other societies have dealt with through rational approximations. Place-value notation provides approximate square roots in practical form, even when the expansion does not terminate. We already mentioned, in Chapter 5, a cuneiform tablet from Iraq (YBC 7289 from the Yale Babylonian Collection) showing a square with its diagonals drawn and the sexagesimal number 1;24,51,10, which gives the length of the diagonal of a square of side 1 to great precision. This rational sexagesimal number surely represents the irrational “number”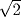 
.
The word number is placed in inverted commas here because the meaning of the square root of 2 is not easy to define. One quickly gets into a vicious circle when trying to formulate its definition. The difficulty came in a clash of geometry and arithmetic, the two fundamental modes of mathematical thinking. From the arithmetical point of view the problem is minimal. If numbers must be what we now call positive rational numbers, then some of them are squares and some are not, just as some integers are triangular, square, pentagonal, and so forth, while others are not. No one would be disturbed by this fact. Since the Greeks had no place-value system to suggest an infinite process leading to an exact square root, they might not have speculated deeply on the implications of this arithmetical distinction in geometry. In other words, they, like their predecessors, had no reason to think about what we call infinitely precise real numbers. They did, however, speculate on both the numerical and geometric aspects of the problem, as we shall now see.
Just when the problem of irrationals and incommensurables arose cannot be specified very exactly. Probably it was in the early fourth century BCE, and certainly before 350 BCE. Since the problem has both numerical and geometric aspects, we begin with the numerical problem.
10.4.1 The Arithmetical Origin of Irrationals
In Plato's dialogue Theatetus, the title character reports that a certain Theodorus proved that the integers 2, 3, 5, and so on, up to 17 have no (rational) square roots, except of course the obvious integers 1, 4, and 9; and he says that for some reason, Theodorus got stuck at that point. On that basis the students decided to classify numbers as equilateral and oblong. The former class consists of the squares of rational numbers, for example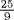 
, and the latter are all other positive rational numbers, such as 
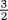, which cannot be written as a product of two equal factors.
One cannot help wondering why Theodorus got stuck at 17 after proving that the numbers 3, 5, 6, 7, 8, 10, 11, 12, 13, 14, and 15 have no square roots. What might the difficulty have been? The square root of 17 is irrational, and the proof commonly given nowadays to show the irrationality of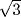 
, for example, based on the unique prime factorization of integers, works just as well for 17 as for any other nonsquare integer. If Theodorus had our proof, he wouldn't have gotten stuck doing 17, and he wouldn't have bothered to do so many special cases, since the proofs are all the same. Therefore, we must assume that he was using some other method.
An ingenious conjecture as to Theodorus' method was provided by the late Wilbur Knorr (1945–1997) in his book (1975). Knorr suggested that the proof was based on the elementary distinction between even and odd. To see how such a proof works, suppose that 7 is an equilateral number in the sense mentioned by Theatetus. Then there must exist two integers m and n such that m2 = 7n2. We can assume that both integers are odd, since if both are even, we can divide them both by 2, and it is impossible for one of them to be odd and the other even. (The fact that the square of one of them equals seven times the square of the other would imply that an odd integer equals an even integer if this were the case.) Now it is well known that the square of an odd integer is always 1 larger than a multiple of 8. The supposition that the one square is seven times the other then implies that an integer 1 larger than a multiple of 8 equals an integer 7 larger than a multiple of 8, which is clearly impossible.
This same argument shows that none of the odd numbers 3, 5, 7, 11, 13, and 15 can be the square of a rational number. With a slight modification, it can also be made to show that none of the numbers 2, 6, 8, 10, 12, and 14 is the square of a rational number, although no argument is needed in the case of 8 and 12, since it is already known that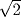 
and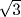 
are irrational. Notice that the argument fails, as it must, for 9: A number 9 larger than a multiple of 8 is also 1 larger than a multiple of 8. However, it also breaks down for 17 and for the same reason: A number 17 larger than a multiple of 8 is also 1 larger than a multiple of 8. Thus, even though it is true that 17 is not the square of a rational number, the argument just given, based on what we would call arithmetic modulo 8, cannot be used to prove this fact. In this way the conjectured method of proof would explain why Theodorus got stuck at 17.
Theodorus thus proved not only that there was no integer whose square is, say, 11 (which is a simple matter of ruling out the few possible candidates), but also that there was not even any rational number having this property; that is, 11 is not the square of anything the Greeks recognized as a number.
10.4.2 The Geometric Origin of Irrationals
A second, “geometric” theory of the origin of irrational numbers comes from geometry and seems less plausible. If we apply the Euclidean algorithm to the side and diagonal of the regular pentagon in Fig. 10.3, we find that the diagonal AD and the CD get replaced by lines equal, respectively, to CD (which equals CF, the bisector of angle ACD, which in turn equals AF) and DF, and these are the diagonal and side of a smaller pentagon since ∠ACD = 2 ∠ FCD. Thus, no matter how many times we apply the procedure of the Euclidean algorithm, the result will always be a pair consisting of the side and diagonal of a pentagon. Therefore, in this case the Euclidean algorithm will never produce an equal pair of lines. We know, however, that it must produce an equal pair if a common measure exists. We conclude that no common measure can exist for the side and diagonal of a pentagon. The same is true for the side and diagonal of a square, although the algorithm requires two applications in order to cycle. The absence of a common measure for the side and diagonal of a square is the exact geometric equivalent of the arithmetic fact that there is no rational number whose square is 2. In other words, incommensurable magnitudes and irrational numbers (as we think of them—again, they were not numbers to the Greeks) are two different ways of looking at the same phenomenon.
Figure 10.3 Diagonal and side of a regular pentagon. If a unit is chosen that divides the side into equal parts, it cannot divide the diagonal into equal parts, and vice versa.
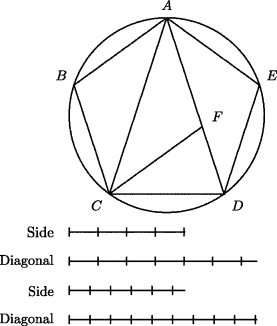
The argument just presented was originally given by von Fritz (1945). Knorr (1975, pp. 22–36) argued against this approach, however, pointing out that the simple arithmetic relation d2 = 2s2 satisfied by the diagonal and side of a square can be used in several ways to show that d and s could not both be integers, no matter what length is chosen as unit. Knorr preferred a reconstruction closer to the argument given in Plato's Meno, in which the problem of doubling a square is discussed. Knorr pointed out that when discussing irrationals, Plato and Aristotle always invoke the side and diagonal of a square, never the pentagon or the related problem of dividing a line in mean and extreme ratio, which they certainly knew about.
10.4.3 Consequences of the Discovery
Whatever the argument used may have been, the Greeks somehow discovered the existence of incommensurable pairs of line segments before the time of Plato. If indeed Pythagorean metaphysics was what it appears to be, this discovery must have been disturbing: Number, it seems, is not adequate to explain all of nature. As mentioned in Chapter 8, a legend arose that the Pythagoreans attempted to keep secret the discovery of this paradox. However, scholars believe that the discovery of incommensurables came near the end of the fifth century BCE, when the original Pythagorean group was already defunct.
The existence of incommensurables throws doubt on certain oversimplified proofs of geometric proportion, as we shall now show. This theory of proportion is extremely important in geometry if we are to have such theorems as Proposition 2 of Book 12 of Euclid's Elements, which says that circles are proportional (in area) to the squares on their diameters. Even the simplest constructions, such as the construction of a square equal in area to a given rectangle or the application problems mentioned above, may require the concept of proportionality of lines. Because of the importance of the theory of proportion for geometry, the discovery of incommensurables made it imperative to give a definition of proportion without relying on a common measure to define a ratio.
To see why the discovery of incommensurables created a problem, although perhaps not a scandal, consider the following conjectured early proof of a fundamental result in the theory of proportion: the proposition that two triangles having equal altitudes have areas proportional to their bases. This assertion is half of Proposition 1 of Book 6 of Euclid's Elements. Let ABC and ACD in Fig. 10.4 be two triangles having the same altitude. Euclid draws them as having a common side, but that is only for convenience. This positioning causes no loss in generality because of the proposition that any two triangles of equal altitude and equal base are equal, proved as Proposition 38 of Book 1.
Figure 10.4 A fundamental theorem in the theory of proportion. Proposition 1 of Book 6 of the Elements.
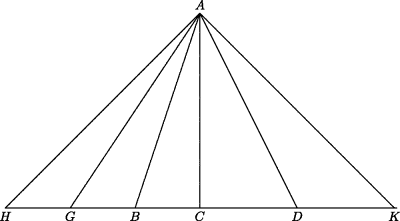
Suppose that the ratio of the bases BC : CD is 2 : 3, that is, 3BC = 2CD. Extend BD leftward to H so that BC = BG = GH, producing triangle AHC, which is three times triangle ABC. Then extend CD rightward to K so that CD = DK, yielding triangle ACK equal to two times triangle ACD. But then, since GC = 3BC = 2CD = CK, triangles AGC and ACK are equal. Since AGC = 3ABC and ACK = 2ACD, it follows that ABC : ACD = 2 : 3. We, like Euclid, have no way of actually drawing an unspecified number of copies of a line, and so we are forced to illustrate the argument using specific numbers (2 and 3 in the present case) while expecting the reader to understand that the argument is completely general.
An alternative proof could be achieved by finding a common measure of BC and CD, namely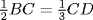 
. Then, dividing the two bases into parts of this length, one would have divided ABC into two triangles and divided ACD into three triangles, and all five of the smaller triangles would be equal. But both of these arguments fail if no integers m and n can be found such that mBC = nCD, or (equivalently) no common measure of BC and CD exists. This proof needs to be shored up, but how is that to be done? We shall see in the next chapter.
Like Gray (quoted above), Knorr (1975) argued that the discovery of irrationals was not a major “scandal,” and that it was not responsible for the “geometric algebra” in Book 2 of Euclid. While arguing that incommensurability forced some modifications in the way of thinking about physical magnitudes, he said (p. 41):
It is thus thoroughly obvious that, far from being in a state of paralysis, fifth-and fourth-century geometers proceeded with their studies of similar figures as if they were still unaware of the foundational consequences of the existence of incommensurable lines.
Problems and Questions
Mathematical Problems
10.1 The problem of application with defect discussed above requires constructing a parallelogram of a given shape that is equal to the difference of two other parallelograms of the same shape. Show how to do this using the Pythagorean theorem. (Assume the given shape is square, if it makes the problem easier. In fact, as we shall see in Chapter 13, Euclid shows in Book VI of the Elements that the Pythagorean theorem works just as well for similar parallelograms as it does for squares. It should be noted that Euclid elegantly shortens this construction, as he so often does.)
10.2 Assuming that there are two square integers whose ratio is 5, derive a contradiction using the principle that underlies Knorr's conjecture. (If the integers are relatively prime, then both must be odd. Use that fact and the fact that the square of any odd number is one unit larger than a multiple of 8 to derive a contradiction.)
10.3 The ratio of the diagonal of a pentagon to its side has been called the Golden Ratio for many centuries. It is usually denoted Φ, and its exact value is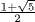 
. Use the fact that 
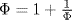to show that the Euclidean algorithm applied to find a common measure of Φ and 1 will go on forever producing a quotient of 1, but never terminate. (Keep substituting the entire right-hand side of this equation for the Φ that occurs there in the denominator.)
Historical Questions
10.4 What achievements do Proclus and Plutarch ascribe to the Pythagoreans?
10.5 Summarize the four Zeno paradoxes, as reported by Aristotle.
10.6 What were the three classical problems of geometry worked on during the fifth and fourth centuries BCE ?
Questions for Reflection
10.7 What motive could the early Greek geometers have had for studying the problems of transformation and application of areas?
10.8 How do you know that there “exists” a number whose square is 2? In what sense do we know what this number is?
10.9 How do you resolve the paradoxes of Zeno?
Notes
1. The book is commonly known as Convivial Questions. The Greek word sympósion means literally drinking together.
2. Keep in mind that a line, to the Greeks, was what we now call a line segment. It was not infinitely long.
3. Since no writings of Pythagoras or his immediate followers survive, it is not possible to find this aphorism stated so concisely anywhere. In his Metaphysics, Bekker 985b, Aristotle says that the Pythagoreans “supposed the elements of numbers to be the elements of all things.”