Chapter 13

Euclid of Alexandria

In many ways, the third century BCE looks like the high-water mark of Greek geometry. This century saw the creation of sublime mathematics in the treatises of Euclid, Archimedes, and Apollonius. It is very tempting to regard Greek geometry as essentially finished after Apollonius, to see everything that came before as leading up to these creations and everything that came after as “polishing up.” And indeed, although there were some bright spots afterward and some interesting innovations, none had the scope or the profundity of the work done by these three geometers.

The first of the three major figures from this period is Euclid, who is world famous for his Elements, which we have in essence already discussed. This work is so famous, and it dominated all teaching in geometry throughout much of the world for so long that the man and his work have essentially merged. For centuries, people did not say that they were studying geometry, but instead that they were studying Euclid. This one work has eclipsed both Euclid's other books and his biography. He did write other books, two of which still exist, named the Data and Optics. Other works are ascribed to him by Pappus, including Phænomena, Loci, Conics, and Porisms. Pappus quotes theorems from some of these works.

Euclid is defined for us as the author of the Elements. Apart from his writings, we know only that he worked at Alexandria in Egypt after the establishment of the Library there. He was traditionally thought to have flourished about 300 BCE, but, as mentioned in Chapter 8, Alexander Jones argued in favor of a later date. The quotations from ancient authors supporting the traditional date are of doubtful authenticity, and they may be interpolations by later editors. In a possibly spurious passage in Book 7 of his Synagg (Collection), Pappus gives a brief description of Euclid as the most modest of men, a man who was precise but not boastful, like (he implies) Apollonius, whom he disparages.

13.1 The Elements

The earliest existing manuscripts of the Elements date to the ninth century CE, nearly 1200 years after the book was originally written. These manuscripts have passed by many editors, and some passages seem to have been added by hands other than Euclid's, especially Theon of Alexandria. Theon was probably not interested in preserving an ancient artifact unchanged; he was more likely trying to produce a good, usable treatise on geometry. Some manuscripts have 15 books, but the last two have since been declared spurious by the experts, so that the currently standard edition has 13 books, the last of which looks suspiciously less formal than the first 12, leading some to doubt that Euclid wrote it. For the few bits of evidence that exist concerning the original text, we once again have the dry Egyptian climate to thank, which preserved a few fragments of papyrus. The best example comes from an 1896 excavation at Oxyrhynchus, about 100 km upstream from Cairo, which turned up the fragment of Book 2, Proposition 5, by good fortune, a key proposition from that book (see photo). As mentioned, there are also a few ostraca containing propositions from the Elements.

The Oxyrhynchus fragment. Courtesy of the Penn Museum, image #142655.

Leaving aside the question of which parts were actually written by Euclid, we shall give a summary of the contents, which we have seen coming together in the work of the fifth and fourth-century mathematicians.

13.1.1 Book 1

The contents of the first book of the Elements are covered in the standard geometry courses given in high schools. This material involves the elementary geometric constructions of copying angles and line segments, drawing squares, and the like and the basic properties of parallelograms, culminating in the Pythagorean theorem (Proposition 47) and its converse (Proposition 48). In addition, these properties are applied to the problem of transformation of area, leading to the construction of a parallelogram with a given base angle and having an area equal to that of any given polygon (Proposition 45). There the matter rests until the end of Book 2, where it is shown (Proposition 14) how to construct a square equal to any given polygon.

13.1.2 Book 2

The second book contains geometric constructions needed to solve problems that may involve quadratic incommensurables without resorting to the Eudoxan theory of proportion. For example, a fundamental result is Proposition 5: If a straight line is cut into equal and unequal segments, the rectangle contained by the unequal segments of the whole together with the square on the straight line between the points of the section is equal to the square on the half. This proposition is easily seen using Fig. 13.1, in terms of which it asserts that (A + B) + D = 2A + C + D; that is, B = A + C. It is used as a “polarization” technique, in the form A + B = (2A + C + D) − D, where A + B is a rectangle, 2A + C + D is the square on the average of its length and width, and D is the square on half of the difference between the length and width.

Figure 13.1 Book 2, Proposition 5: Expression of a rectangle as the difference of two squares.

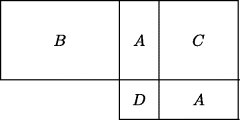
Here for the first time, the polarization identity and the Pythagorean theorem are combined to express a rectangle as the difference of two squares which in turn is the square on a known line, thus implicitly showing how to transform a rectangle into a square. As we have said, the key ingredients were known in ancient Mesopotamia, but not combined in this way.

Geometric Algebra.

We have already mentioned the once-popular interpretation of Book 2 as geometric expressions of what we regard as algebraic identities. It is understandable that people were tempted to think of these propositions in this way. The proposition just stated says 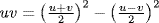. That fact, interpreted numerically, occurs as a fundamental tool in the cuneiform tablets. For if the unequal segments of the line are regarded as two unknown quantities, then half of the original line segment is their average, and the straight line between the points (that is, the segment between the midpoint of the whole segment and the point dividing the whole segment into unequal parts) is what we called earlier the semidifference. Thus, this proposition says that the square of the average equals the product plus the square of the semidifference. Recall that that result was fundamental for solving the important problems of finding two numbers, given their sum and product or their difference and product. On the other hand, in most cases, even in the cuneiform tablets, those two numbers were still the length and width of a rectangle. Thus, who can say whether this proposition was thought of separately from plane geometry? In Euclid, most of the geometric constructions that depend on this proposition (the problems of application with defect and excess) do not appear until Book 6. These application problems could have been solved in Book 2 in the case when the excess or defect is a square. Instead, these special cases were passed over and the more general results, which depend on the Eudoxan theory of proportion to cover the incommensurable cases, were included in Book 6.

Book 2 also contains the construction of what came to be known as the Section, that is, the division of a line in mean and extreme ratio so that the whole is to one part as that part is to the other. But Euclid is not ready to prove that version yet, since he doesn't have the theory of proportion. Instead, he gives what must have been the original form of this proposition (Proposition 11): Cut a line so that the rectangle on the whole and one of the parts equals the square on the other part. One way of doing it is shown in Fig. 13.2.

Figure 13.2 Line AB is given with midpoint C, and ABDL is a square. The circular arc 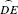is centered at C and the semicircle 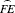is centered at B. Then AE : AB : : AB : BF : : BF : AF. Also, the rectangle AFNL equals the square FBKM, that is, the rectangle on the whole and the segment AF equals the square on the complementary segment FB.

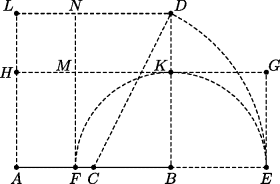
After it is established that four lines are proportional when the rectangle on the means equals the rectangle on the extremes (Proposition 16, Book 6), it becomes possible to convert this construction into the construction of the Section (Proposition 30, Book 6).

13.1.3 Books 3 and 4

The next two books take up topics familiar from high-school geometry: (a) circles, tangents, and secants and (b) inscribed and circumscribed polygons. Book 4 shows how to inscribe a regular pentagon in a circle (Proposition 11—this construction requires the construction given in Proposition 11 of Book 2 and shown in Fig. 13.2) and how to circumscribe a regular pentagon about a circle (Proposition 12), and then it reverses the figures and shows how to get the circles given the pentagon (Propositions 13 and 14). After the easy construction of a regular hexagon (Proposition 15), Euclid finishes off Book 4 with the construction of a regular pentakaidecagon (15-sided polygon, Proposition 16).

13.1.4 Books 5 and 6

The Eudoxan theory of geometric proportion is expounded in Book 5, which contains the construction of the mean proportional between two lines (Proposition 13 of Book 5). In Proposition 16 of Book 6, Euclid proves the all-important result that if four lines (line segments, as we would say) are in proportion, then the rectangle on the means equals the rectangle on the extremes. This theory is applied to solve the problems of application with defect and excess. A special case of the latter, in which it is required to construct a rectangle on a given line having area equal to the square on the line and with a square excess is the very famous Section (Proposition 30). Euclid phrases the problem as follows: Divide a line into mean and extreme ratio. This means to find a point on the line so that the whole line is to one part as that part is to the second part. The Pythagorean theorem is then generalized to cover not merely the squares on the sides of a right triangle, but any similar polygons on those sides (Proposition 31). The book finishes with the well-known statement that central and inscribed angles in a circle are proportional to the arcs they subtend.

13.1.5 Books 7–9

Euclid's exposition of Greek number theory in Books 7–9 was discussed in Chapter 9. Here, since irrationals cannot occur, the notion of proportion is redefined to eliminate the need for the Eudoxan technique.

13.1.6 Book 10

The tenth book is evidently placed so as to be an extension of the rational theory of proportion in the number-theory books to a more detailed study of the situation when incommensurable lines arise that can be handled with no techniques beyond square roots, what we would call quadratic irrationals. This book occupies fully one-fourth of the entire length of the Elements. For its sheer bulk, one would be inclined to consider it the most important of all the 13 books, yet its 115 propositions are among the least studied of all, principally because of their technical nature. The irrationals constructed in this book by taking square roots are needed in the theory developed in Book 13 for inscribing regular solids in a sphere (that is, finding the lengths of their sides knowing the radius of the sphere). The book begins with the operating principle of the method of exhaustion, also known as the principle of Archimedes. That is, if a quantity is continually cut in half, it will eventually become smaller than any preassigned quantity of the same type. The way to demonstrate incommensurability through the Euclidean algorithm then follows as Proposition 2: If, when the smaller of two given quantities is continually subtracted from the larger, that which is left never divides evenly the one before it, the quantities are incommensurable. We used this method of showing that the side and diagonal of a regular pentagon are incommensurable in Chapter 9.

13.1.7 Books 11–13

The basic concepts of solid geometry, namely planes, parallelepipeds, and pyramids, are introduced in Book 11. The theory of proportion for these solid figures and the regular solids (cube, tetrahedron, octahedron, dodecahedron, icosahedron) is developed in Book 12, which contains the theorem that circles are proportional to the squares on their diameters (Proposition 2). This result, as mentioned in Chapter 11, is needed to make Hippocrates' quadrature of a lune rigorous.

Book 12 continues the development of solid geometry by establishing the usual proportions and volume relations for solid figures; for example, a triangular prism can be divided by planes into three equal pyramids (Proposition 7), a cone is one-third of a cylinder on the same base, and similar cones and cylinders are proportional to the cubes of their linear dimensions, ending with the proof that spheres are proportional to the cubes on their diameters (Proposition 18). Archimedes (or someone who edited his works) credited these theorems to Eudoxus.

Book 13, the last book of the Elements, is devoted to the construction of the regular solids and the relation between their sides, diagonals, and apothems and the radius of the sphere in which they are inscribed. The last proposition (Proposition 18) sets out the sides of these regular solids and their ratios to one another. An informal discussion following this proposition concludes that there can be only five regular solids.

13.2 The Data

Euclid's Elements assume a certain familiarity with the principles of geometric reasoning, principles that are explained in more detail in the Data. The Greek name of this work (Dedoména) means [Things That] Have Been Given, just as Data does in Latin. The title is a good description of the contents, which discuss the conditions that determine various geometric objects uniquely. The propositions in this book can be interpreted in various ways. Some can be looked at as uniqueness theorems. For example (Proposition 53), if the shapes—that is, the angles and ratios of the sides—are given for two polygons, and the ratio of the areas of the polygons is given, then the ratio of any side of one to any side of the other is given. Here, being given means being uniquely determined. Uniqueness is needed in proofs and constructions so that one can be sure that the result will be the same no matter what choices are made. It is an issue that arises frequently in modern mathematics, where operations on sets are defined by choosing representatives of the sets; when that is done, it is necessary to verify that the operation is well-defined, that is, independent of the choice made. An example of this need has already been cited in the previous chapter in connection with the definition of a composite ratio. In geometry we frequently say, “Let ABC be a triangle having the given properties and having such-and-such a property,” such as being located in a particular position. In such cases we need to be sure that the additional condition does not restrict the generality of the argument. In still another sense, this same proposition may guarantee that an explicit construction is possible, thereby removing the necessity of including it in the exposition of a theorem.

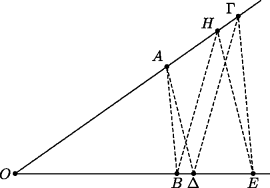
Other propositions assert that certain properties are invariant. For example (Proposition 81), when four lines A, B, Γ, and Δ are given, and the line H is such that Δ : E = A : H, where E is the fourth proportional to A, B, and Γ, then Δ : Γ = B : H. This proposition, illustrated in Fig. 13.3, is trivial to prove in modern notation. It also follows from Proposition 16 of Book 6 of the Elements, since AE = BΓ = ΔH, that is, A : B : : Γ : E and Delta : E : : AH. This proposition is a lemma that can be useful in working out locus problems, which require finding a curve on which a point must lie if it satisfies certain prescribed conditions. Finally, a modern mathematician might interpret the assertion that an object is “given” as saying that the object “exists” and can be meaningfully talked about. To Euclid, that existence would mean that the object was explicitly constructible. (However, note that in two-dimensional figures, Euclid was inclined to gloss over these details, as in the proof of Proposition 2 of Book 12, exhibited in Chapter 12.)

Figure 13.3 Proposition 81 of Euclid's Data.

Problems and Questions

Mathematical Problems

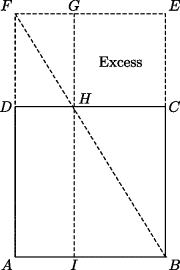
13.1 Show how the construction of the Section (Fig. 13.3) can be interpreted as a problem in application with square excess. (See Fig. 13.4.)

Figure 13.4 The Section as a problem in application with square excess. Rectangle BEGI, which is applied to the extension of BC, equals square ABCD by Proposition 5 of Book 2. The “excess” CEGH is a square by the construction of the Section.

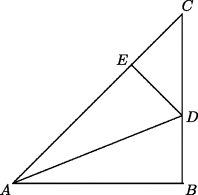
13.2 Use an argument similar to the argument in Chapter 9 showing that the side and diagonal of a pentagon are incommensurable to show that the side and diagonal of a square are incommensurable. That is, show that the Euclidean algorithm, when applied to the diagonal and side of a square, requires only two steps to produce the side and diagonal of a smaller square and hence can never produce an equal pair. [Hint: In Fig. 13.5, AB = BC, angle ABC is a right angle, AD is the bisector of angle CAB, and DE is drawn perpendicular to AC. Prove that BD = DE, DE = EC, and AB = AE. Then show that the Euclidean algorithm starting with the pair (AC, AB) leads first to the pair (AB, EC) = (BC, BD) and then to the pair (CD, BD) = (CD, DE), and these last two are the diagonal and side of a square.]

Figure 13.5 Diagonal and side of a square.

13.3 The problem of constructing a rectangle of prescribed area on part of a given base a in such a way that the defect is a square is equivalent, when formulated as a problem about the lengths of the sides, to the problem of finding two numbers given their sum and product (the two numbers are the lengths of the sides of the rectangle). Stated in algebraic language, this problem asks for two numbers u and (interpreted as lengths), such that 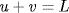and uv = A, where L is the given length and A the given area. Show that this is equivalent to solving the quadratic equation x² + A = Lx. [Hint: If u and are the roots of this equation, then 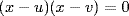when x is a root.] Since the largest rectangle that can be constructed on part of a line L so as to leave a square defect has area L²/4 (the square on half of the line), the inequality L² ≥ 4A must hold. What does this condition say in terms of the algebra. [Hint: Look at the quadratic formula for solving the equation x² − Lx + A = 0.]

Historical Questions

13.4 Was the Elements an exposition of the most advanced mathematics of its time?

13.5 What does Euclid have to say in the Elements about the problems of squaring the circle, doubling the cube, and trisecting the angle?

13.6 Why does Euclid give two definitions of ratio and proportion, one in Book 6, the other in Book 7?

Questions for Reflection

13.7 If you were editing the Elements, how would you separate it into major parts. Which books belong in each?

13.8 Proposition 14 of Book 2 of Euclid shows how to construct a square equal in area to a rectangle. Since this construction is logically equivalent to constructing the mean proportional between two line segments, why does Euclid wait until Book 6, Proposition 13 to give the construction of the mean proportional?

13.9 Reflecting on the “geometric algebra” hypothesis, consider the plausibility of the following pseudo-syllogism: Mathematician A proved result B. Result B is logically equivalent to result C. Therefore mathematician A proved result C. Is this valid reasoning from the point of view of history? From the point of view of heritage? (Refer to Chapter 1 for an explanation of the difference between the two.)