Chapter 20
From the Vedas to Aryabhata I
A unique feature of arithmetic in ancient India, pointed out by Plofker (2009, pp. 14–15), is the existence of names for very large powers of 10, going beyond any conceivable practical social or commercial need. One early poem, the Valmiki Ramayana, from about 500 BCE, explains the numeration system in the course of recounting the size of an army. The description uses special words for 107, 1012, 1017, and many other denominations, all the way up to 1055. An important part of the place-value notation we now use is the zero symbol for an empty place, which may have been invented in India before 200 BCE. [Plofker (2009, p. 16) notes that while the concept of an empty place can be found in early documents, there is no clear “paper trail” to the first mathematical documents where it is known to occur, and (Plofker 2009, p. 48) it may not have been part of the early place-value decimal system, which was being used by the third century CE.]
20.1 Problems from the Sulva Sutras
We now examine some mathematical problems posed in the Vedas. These problems were sometimes connected with the construction of altars. Our source for most of this material is the book of Srinivasiengar (1967).
20.1.1 Arithmetic
Some of the arithmetic content of the Sulva Sutras consists of rules for finding Pythagorean triples of integers, such as (3, 4, 5), (5, 12, 13), (8, 15, 17), and (12, 35, 37). It is not certain what practical use these arithmetic rules had. The best conjecture is that they were part of religious ritual. A Hindu home was required to have three fires burning at three different altars. The three altars were to be of different shapes, but all three were to have the same area. These conditions led to certain Diophantine-type problems, a particular case of which is the generation of Pythagorean triples, so as to make one square integer equal to the sum of two others.
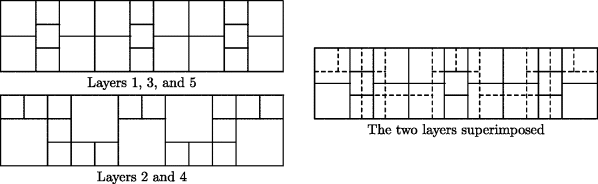
One class of mathematical problems associated with altar building involves an altar of prescribed area having several layers. In one problem from the Bodhayana Sutra the altar is to have five layers of bricks, each layer containing 21 bricks. Now one cannot simply divide a pile of 105 identical bricks into five layers and pile them up. Such a structure would not be stable. It is necessary to stagger the edges of the bricks. Thus, so that the outside of the altar will not be jagged, it is necessary to have at least two different sizes of bricks. The problem is to decide how many different sizes of bricks will be needed and how to arrange them. Assuming an area of one square unit—actually the unit is one square vyayam, a little over 6 square meters—the author suggests using three kinds of square bricks, of areas 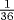 ,
, 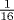 , and
, and 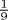 square unit. The first, third, and fifth layers are to have 9 of the first kind and 12 of the second. The second and fourth layers get 16 of the first kind and 5 of the third. One way to arrange these layers so as to stagger the gaps in successive layers is shown in Fig. 20.1.
square unit. The first, third, and fifth layers are to have 9 of the first kind and 12 of the second. The second and fourth layers get 16 of the first kind and 5 of the third. One way to arrange these layers so as to stagger the gaps in successive layers is shown in Fig. 20.1.
Figure 20.1 Construction of a brick altar with the same number of bricks and the same area in each of five layers.
20.1.2 Geometry
The geometric content of the Sulva Sutras encompasses some of the transformation-of-area constructions such as we have seen in Euclid's Elements. The Pythagorean theorem is given, along with constructions for finding the side of a square equal to a rectangle, or the sum or difference of two other squares. The quadrature of a rectangle resembles the one found in Proposition 5 of Book 2 of Euclid rather than Euclid's construction of the mean proportional in Book 6, which is equivalent to it.
The Pythagorean theorem is not given a name, but is stated as the fact that “the diagonal of a rectangle produces both [areas] which its length and breadth produce separately.” It is interesting that the problem of doubling a square, which might have led to the discovery of this theorem, produces a figure in the shape of one of the altars discussed in the Vedas. Is it merely a coincidence that the problem of doubling the cube was said by the Greeks to have been inspired by an attempt to double the size of an altar?
The Hindu method of constructing of a square equal to a given rectangle (see Fig. 20.2) is as follows. Let ABCD be the given rectangle, with AD longer than AB. Mark point E on AD so that AE = AB, and mark F on BC so that BF = AB. Draw EF, obtaining the square ABFE. Let G be the midpoint of ED and let H be the midpoint of FC. Draw GH and extend it to K so that GK = AG. Extend AB to L so that AL = GK = AG. Draw KL, obtaining the square ALKG. Extend EF to meet LK at M. Then the rectangle ABCD equals the square ALKG minus the square HKMF, since the rectangle CDGH equals the rectangle BLMF. Next choose P on BH so that PL = KL. (This point can be located by drawing a circle with L as center and LK as radius, as shown in Fig. 20.2.) Draw the line from P perpendicular to LK meeting LK at Q. Then the square on LQ is the square on LP minus the square on PQ. But since PQ = HK and LP = LK, it follows that the square on LQ is precisely equal to the rectangle ABCD.
Figure 20.2 Quadrature of the rectangle in the Sulva Sutras.
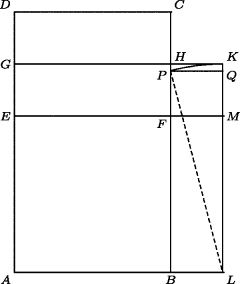
To construct a square equal to a multiple of a given square, say seven times as large as a square of side a, the Katyayana Sutra says to construct an isosceles triangle of base 6a and two sides equal to 4a. The altitude, which is the perpendicular bisector of the base, will have length 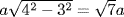 , and hence will be the side of a square 7 times the original square.
, and hence will be the side of a square 7 times the original square.
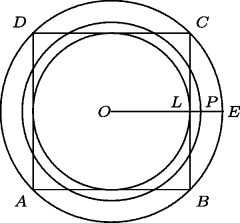
The requirement of three altars of equal areas but different shapes would explain the interest in transformation of areas. Among other transformation of area problems, the authors of the Vedas considered the relative sizes of squares and circles. The Bodhayana Sutra states the problem of constructing a circle equal to a given square. The following approximate construction is given as the solution.
Let ABCD be the square (see Fig. 20.3). From the center O of the square draw a circle with radius equal to OC. Let L be the midpoint of side BC, and let the radius through L meet the circle in the point E. Choose a point P on LE one-third of the way from L to E. The point P will lie on the circle with center at O equal to the square ABCD. In other words, the radius of a circle equal to a given square is one-third the radius of the circle circumscribed about the square, plus two-thirds the radius of the circle inscribed in it. In contrast to the polygonal transformations just discussed, which were exact, this result is only approximate. In our terms, this construction gives a value for two-dimensional π of  , which is about 3.088.
, which is about 3.088.
Figure 20.3 Rounding a square.
20.1.3 Square Roots
The geometry of rectangles and right triangles leads naturally to the problem of handling numerical square roots, and accordingly the Sulva Sutras discuss a way of approximating them. The Apastamba, Bodhayana, and Katyayana Sulva Sutras (Plofker, 2009, p. 21) give the expression
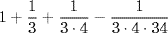
for the diagonal of a square of side 1 (that is, 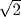 ). If this series represents successive approximations to
). If this series represents successive approximations to 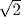 , these approximations are 1,
, these approximations are 1, 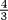 ,
, 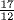 ,
, 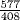 . The Mesopotamian approximation conjectured in Chapter 3 gives 1, 2,
. The Mesopotamian approximation conjectured in Chapter 3 gives 1, 2, 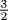 ,
, 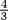 ,
, 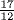 ,
, 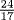 , . . . . One conjecture as to the origin of the present approximation is that it comes from the approximate equation
, . . . . One conjecture as to the origin of the present approximation is that it comes from the approximate equation
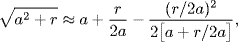
with 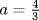 and
and 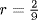 . This approximation may be the source of similar rule given by the twelfth-century Moroccan mathematician Abu Bakr al-Hassar.
. This approximation may be the source of similar rule given by the twelfth-century Moroccan mathematician Abu Bakr al-Hassar.
In the early seventh century, the mathematician Bhaskara I (ca. 600–ca. 680) expressed the opinion that the ratio of the circumference of a circle to its diameter cannot be exactly expressed. In Greek terms, the two are incommensurable; in our terms, π is irrational. By the late fourteenth century, the mathematician Madhava (ca. 1350–ca. 1425) gave a rule that expresses this ratio as an infinite series:
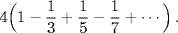
This same series was given some 300 years later by Leibniz (Plofker, 2009, pp. 140, 224).
In the treatment of what we call irrational numbers, we see an instance in which the Greek insistence on logical correctness was a hindrance. The Greeks did not regard 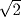 as a number, since they could not express it exactly as a ratio and they knew that they could not. The Hindus may or may not have known of the impossibility of a rational expression for this number (they certainly knew that they did not have any rational expression for it); but, undeterred by the incompleteness of their knowledge, they proceeded to make what use they could of this number. This same “reckless” spirit served them well in the use of infinity and the invention of zero and negative numbers. They saw the usefulness of such numbers and either chose to live with or did not notice certain difficulties of a metaphysical character.
as a number, since they could not express it exactly as a ratio and they knew that they could not. The Hindus may or may not have known of the impossibility of a rational expression for this number (they certainly knew that they did not have any rational expression for it); but, undeterred by the incompleteness of their knowledge, they proceeded to make what use they could of this number. This same “reckless” spirit served them well in the use of infinity and the invention of zero and negative numbers. They saw the usefulness of such numbers and either chose to live with or did not notice certain difficulties of a metaphysical character.
20.1.4 Jain Mathematics: The Infinite
Like Greek mathematics, Hindu mathematics has a prominent metaphysical component. This metaphysical aspect manifests itself in various ways—for example, in handling the infinite. Where the Greeks had regarded all reasoning as finite and accepted only a potential infinity, as shown by the method of exhaustion, the Hindus accepted an actual infinity and classified different kinds of infinities. This part of Hindu mathematics is particularly noticeable with the Jains. They classified numbers as enumerable, unenumerable, and infinite, and space as one-dimensional, two-dimensional, three-dimensional, and infinitely infinite. The first unenumerable number is the most unusual of these concepts. It is a finite number, but one can never describe it explicitly. The idea is to progress through the finite numbers 2, 3, 4, . . . in one's imagination until the “first unenumerable” number is reached. We can define it implicitly as the first positive integer that cannot be named. Does this mean the first number that no one ever will name (in the whole of human history), or the first number that in principle could not be named? The reader is invited to speculate.
20.1.5 Jain Mathematics: Combinatorics
The metaphysics of the Hindus, and especially the Jains, based on a classification of sentient beings according to the number of senses possessed, led them to a mathematical topic not discussed by the Greeks. The Hindus called it vikalpa, and we know it as combinatorics. The Sanskrit word kalpa has many meanings, among which are possible, feasible, and ordered. The prefix vi- corresponds roughly to the English prefix dis-, so that vikalpa may mean distribution in the sense of arrangement. The occurrence of the word in the present context probably derives from the Kalpa Sutras, a set of Jain verses.
Given that there are five senses and animals are to be classified according to the senses they possess, how many different classes will there be? A typical question might be, How many groups of three can be formed from a set of five elements? We know the answer, as did the early Jain mathematicians. In the Bhagabati Sutra, written about 300 BCE, the author asks how many philosophical systems can be formed by taking a certain number of doctrines from a given list of basic doctrines. After giving the answers for 2, 3, 4, etc., the author says that enumerable, unenumerable, and infinite numbers of things can be discussed, and, “as the number of combinations are formed, all of them must be worked out.”
The general process for computing combinatorial coefficients was known to the Hindus at an early date. Combinatorial questions seemed to arise everywhere for the Hindus, not only in the examples just given but also in a much earlier work on medicine that poses the problem of the number of different flavors that can be made by choosing subsets of six basic flavors (bitter, sour, salty, astringent, sweet, hot). The author gives the answer as 6 + 15 + 20 + 15 + 6 + 1, that is, 63. We recognize here the combinatorial coefficients that give the subsets of various sizes that can be formed from six elements. The author did not count the possibility of no flavor at all.
Combinatorics also arose with the Hindus in the study of literature in the third century BCE, when Pingala gave a rule for finding the number of different words that could be formed from a given number of letters. This rule was written very obscurely, but a commentator named Halayudha in the tenth century CE explained it as follows. First draw a square. Below it and starting from the middle of the lower side, draw two squares. Then draw three squares below these, and so on. Write the number 1 in the middle of the top square and inside the first and last squares of each row. Inside every other square the number to be written is the sum of the numbers in the two squares above it and overlapping it. This description of what we know as Pascal's triangle was thus given in India 300 years before it was published in China and 700 years before Pascal. Moreover, it purports to be only a clarification of a rule invented 1200 years earlier! Its Sanskrit name is Meru Prastara (Fig. 20.4), which means the Mount Meru staircase.1 The inspiration for the study of this figure was quite different in China and India. In China, it came about in connection with the extraction of roots and the solution of equations, whereas in India the inspiration was directly from the area of combinatorics.
Figure 20.4 The Meru Prastara.
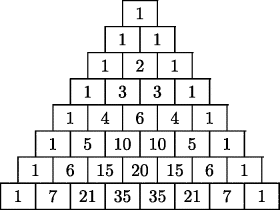
According to Srinivasiengar (1967, p. 25), by the year 300 BCE Jain mathematicians understood certain cases of the laws of exponents. They could make sense of an expression like 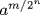 , interpreting it as extracting the square root n times and then raising the result to the power m. The notation used was of course not ours. The power
, interpreting it as extracting the square root n times and then raising the result to the power m. The notation used was of course not ours. The power 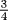 , for example, was described as “the cube of the second square root.” That the laws of exponents were understood for these special values is attested by such statements as “the second square root multiplied by the third square root, or the cube of the third square root,” indicating an understanding of the equality
, for example, was described as “the cube of the second square root.” That the laws of exponents were understood for these special values is attested by such statements as “the second square root multiplied by the third square root, or the cube of the third square root,” indicating an understanding of the equality 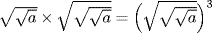 , which we would write in exponential notation as
, which we would write in exponential notation as
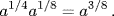
20.1.6 The Bakshali Manuscript
Some symbolic algebra can be found in the Bakshali manuscript. The symbol  is used to denote an unknown quantity. One of the problems in the manuscript is written as follows, using modern number symbols and a transliteration of the Sanskrit into the Latin alphabet:
is used to denote an unknown quantity. One of the problems in the manuscript is written as follows, using modern number symbols and a transliteration of the Sanskrit into the Latin alphabet:
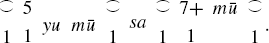
This symbolism can be translated as follows: “A certain thing is increased by 5 and the square root is taken, giving [another] thing; and the thing is decreased by 7 and the square root is taken, giving [yet another] thing.” In other words, we are looking for a number x such that x + 5 and x − 7 are both perfect squares. This problem is remarkably like certain problems in Diophantus. For example, Problem 11 of Book 2 of Diophantus' Arithmetica is to add the same number to two given numbers so as to make each of them a square. If the two given numbers are 5 and −7, this is exactly the problem stated here; Diophantus, however, did not use negative numbers.
The Bakshali manuscript also contains problems in linear equations, of the sort that has had a long history in elementary mathematics texts. For example, three persons possess seven thoroughbred horses, nine draft horses, and 10 camels, respectively. Each gives one animal to each of the others. The three are then equally wealthy. Find the (relative) prices of the three animals. Before leaping blindly into the set of two linear equations in three unknowns that this problem prescribes, we should take time to note that the problem can be solved by imagining the experiment actually performed. Suppose that these donations have been made and the three people are now equally wealthy. They will remain equally wealthy if each gives away one thoroughbred horse, one draft horse, and one camel. It follows that four thoroughbred horses, six draft horses, and seven camels are all of equal value. The problem has thereby been solved, and no actual algebra has been performed. Srinivasiengar (1967, p. 39) gives the solution using symbols for the unknown values of the animals, but does not assert that the solution is given this way in the manuscript itself.
20.2 Aryabhata I: Geometry and Trigonometry
Chapter 2 of Aryabhata's Aryabhatiya (Clark, 1930, pp. 21–50) is called Ganitapada (Mathematics). In Stanza 6 of this chapter, Aryabhata gives the correct rule for area of a triangle, but declares that the volume of a tetrahedron is half the product of the altitude and the area of the base. He says in Stanza 7 that the area of a circle is half the diameter times half the circumference, which is correct, and shows that he knew that one-and two-dimensional π were the same number. But he goes on to say that the volume of a sphere is the area of a great circle times its own square root. This would be correct only if three-dimensional π equaled 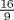 , very far from the truth! Plofker (2009, p. 126) discusses a suggested reinterpretation of this rule as applying to the surface area of the sphere rather than its volume and concludes that it will not do. In a way, this inaccurate result is surprising, since Aryabhata knew a very good approximation to one-dimensional π. In Stanza 10 he writes:
, very far from the truth! Plofker (2009, p. 126) discusses a suggested reinterpretation of this rule as applying to the surface area of the sphere rather than its volume and concludes that it will not do. In a way, this inaccurate result is surprising, since Aryabhata knew a very good approximation to one-dimensional π. In Stanza 10 he writes:
Add 4 to 100, multiply by 8, and add 62,000. The result is approximately the circumference of a circle of which the diameter is 20,000.
This procedure gives a value of one-dimensional π equal to 3.1416, which exceeds the true value by less than 0.01%.
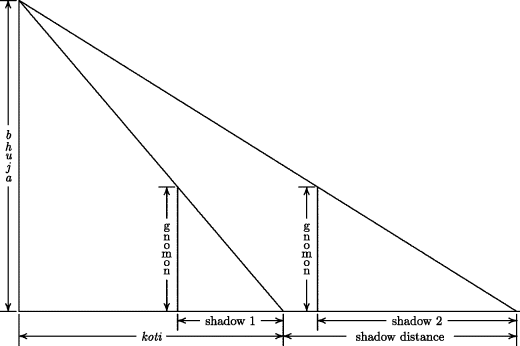
Aryabhata also knew a method of surveying by sighting along the tops of two poles of equal height called gnomons. This same method was practiced in China. Whether this common method is a case of transmission or independent discovery is not clear. The rule given is illustrated by Fig. 20.5.
The distance between the ends of the two shadows multiplied by the length of the shadow and divided by the difference in length of the two shadows give the koti. The koti multiplied by the length of the gnomon and divided by the length of the shadow gives the length of the bhuja. [Clark, 1930, p. 32]
Figure 20.5 Aryabhata's method of surveying.
20.2.1 Trigonometry
The inclusion of this method of surveying in the Aryabhatiya presents us with a small puzzle. As a method of surveying, it is not efficient. It would seem to make more sense to measure angles rather than using only right angles and measuring more lines. But angles are really not involved here. It is possible to have a clear picture of two mutually perpendicular lines without thinking “right angle.” The notion of angles in general as a species of mathematical objects—the figures formed by intersecting lines, which can be measured, added, and subtracted—appears to be a Greek innovation in the sixth and fifth centuries BCE, and it seems to occur only in plane geometry, not spherical, where arcs are used instead. Its origins may be in stonemasonry and carpentry, where regular polygons have to be fitted together. Astronomy probably also made some contribution. Since Aryabhata I was one of the pioneers of this trigonometry and was primarily an astronomer, it seems slightly inconsistent that he recommended this method of surveying. Perhaps the explanation is that measuring the sky and measuring the earth belong to different categories.
The earliest form of trigonometry was a table of correspondences between arcs and their chords. We know exactly how such a table was originally constructed, since we have already looked at Ptolemy's treatise on astronomy, written around 150 CE. Although this table fulfilled its purpose in astronomy, the chord is a cumbersome tool to use in studying plane geometry. For example, it was well known that in any triangle, the angle opposite the larger of two sides will be larger than the angle opposite the smaller side. But what is the exact, quantitative relation between the two sides and the two angles? The ratio of the sides has no simple relationship to the ratio of the angles or to the chords those angles subtend as central angles in a circle. But the sides are directly proportional to the chords of twice those central angles. In fact, as we have seen, Ptolemy was constantly working with the chord of twice an angle when he applied Menelaus' theorem to solve spherical triangles. But he never used half of the chord of a doubled angle.
It was the Hindu astronomers who discovered that trigonometry is simpler if you use half of the chord of a doubled angle. Those half-chords are now called sines. In Fig. 20.6 the arc 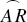 can be measured by either line AB or AR. Ptolemy chose AR and was led to the complications already mentioned. The Hindus preferred AB. We shall see that the Chinese word (xian) for the hypotenuse of a right triangle means bowstring. The Hindus used the Sanskrit term for a bowstring (jya or jiva) to mean the sine. The reason for the colorful language is obvious from Fig. 20.6.
can be measured by either line AB or AR. Ptolemy chose AR and was led to the complications already mentioned. The Hindus preferred AB. We shall see that the Chinese word (xian) for the hypotenuse of a right triangle means bowstring. The Hindus used the Sanskrit term for a bowstring (jya or jiva) to mean the sine. The reason for the colorful language is obvious from Fig. 20.6.
Figure 20.6 The “bowstring” diagram. The sine of the arc 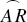 is the line AB. The tabular value of the sine is the number of minutes in an arc of the same length as AB.
is the line AB. The tabular value of the sine is the number of minutes in an arc of the same length as AB.
To all appearances, then, trigonometry began to assume its modern form among the Hindus some 1500 years ago. A few reservations are needed, however. First, for the Hindu mathematicians the sine was not, as it is to us, a ratio. It was a length, and that physical dimension had to be taken into account in all computations. Second, the only Hindu concept corresponding approximately to our trigonometric functions were those of sine and cosine. The tangent, secant, cotangent, and cosecant were not included until much later. Third, the use of trigonometry was restricted to astronomy. As already pointed out, surveying, which is the other natural place to use trigonometry, did not depend on angle measurement.
Aryabhata used the sine function developed in the Surya Siddhanta, giving a table for computing its values at intervals of 225′ (3 45′) of arc from 0
45′) of arc from 0 to 90
to 90 degrees and expressing these values in units of 1′ of arc, rounded to the nearest integer, so that the sine of 90
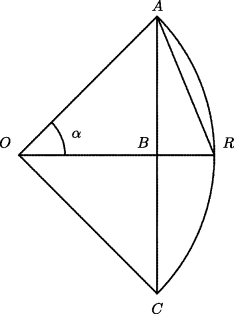
degrees and expressing these values in units of 1′ of arc, rounded to the nearest integer, so that the sine of 90 , which is the radius of the circle, is 3438. In our terms, that number is, to the nearest integer, the number of minutes in one radian of arc, since the length of a one-radian arc is equal to the radius. The value is rounded up from 3437.75, however, and the use of that value in computations will yield better agreement with Aryabhata's table. His sine of a given angle is 3438 times the number that we would call its sine.
, which is the radius of the circle, is 3438. In our terms, that number is, to the nearest integer, the number of minutes in one radian of arc, since the length of a one-radian arc is equal to the radius. The value is rounded up from 3437.75, however, and the use of that value in computations will yield better agreement with Aryabhata's table. His sine of a given angle is 3438 times the number that we would call its sine.
Thus, the number 3438 is an artifact of the units chosen for the arcs and their sines. Since the unit of length for a sine is 1′, the fact that the arc is closely approximated by the chord for small angles means that sin (θ) ≈ θ for small arcs θ. This approximation holds within the limits of precision of the table up to 6 of arc when the arcs are also expressed in minutes, as Aryabhata does.
of arc when the arcs are also expressed in minutes, as Aryabhata does.
The  interval between entries suggests that the tables were computed independently of Ptolemy's work. If the Hindu astronomers had read Ptolemy, their tables of sines could easily have been constructed from his table of chords, and with more precision than is actually found. Almost certainly, this interval was reached by starting with an angle of 30
interval between entries suggests that the tables were computed independently of Ptolemy's work. If the Hindu astronomers had read Ptolemy, their tables of sines could easily have been constructed from his table of chords, and with more precision than is actually found. Almost certainly, this interval was reached by starting with an angle of 30 , whose sine was known to be half of the radius, then applying the formula for the sine of half an angle to get successively the sines of 15
, whose sine was known to be half of the radius, then applying the formula for the sine of half an angle to get successively the sines of 15 , 7
, 7 30′, and finally 3
30′, and finally 3 45′, which is 225′. Arybhata's table is actually a list of the differences of 24 successive sines at intervals of 225 minutes. Since one minute of arc is a very small quantity relative to the radius, these 24 values of the sine provide sufficient precision for the observational technology available at the time. Notice, however, that to calculate the sine of half of an angle θ one would have to carry out a computation equivalent to evaluating the cumbersome formula
45′, which is 225′. Arybhata's table is actually a list of the differences of 24 successive sines at intervals of 225 minutes. Since one minute of arc is a very small quantity relative to the radius, these 24 values of the sine provide sufficient precision for the observational technology available at the time. Notice, however, that to calculate the sine of half of an angle θ one would have to carry out a computation equivalent to evaluating the cumbersome formula
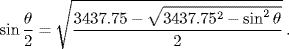
It is therefore understandable that Aryabhata did not refine his table further. Aryabhata's list of sine differences is the following:
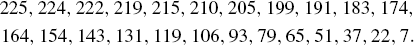
A comparison with a computer-generated table for the same differences reveals that Aryabhata's table is accurate, except that the sixth entry should be 211 instead of 210 and the eighth should be 198 instead of 199. But an error of only half of one percent is not critical, given the limited precision of Aryabhata's observations. It has been believed that this table of sine differences was computed by a recursive procedure, which can be described in our terms as follows (Clark, 1930, p. 29). Starting with d1 = 225,
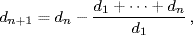
where each term is rounded to the nearest integer after being calculated from this formula. Plofker (2009, p. 128), however, says that this interpretation of the text of the Aryabhatiya did not appear in any commentary until the fifteenth century; it is therefore not certain that this procedure is exactly what he meant. Moreover, a computer following this recursive instruction will generate a table that diverges from the one shown (see Problem 20.2).
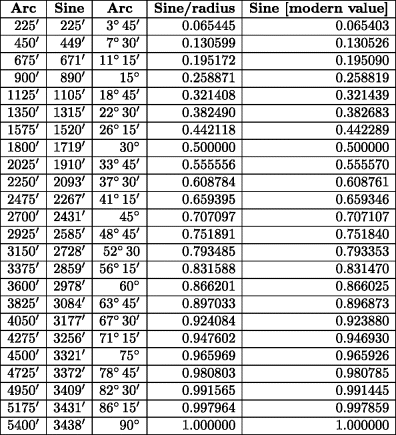
Figure 20.7 shows a table of sine values that can be constructed on the basis of this table of differences. The first two columns give the arcs and their sines as implied by Aryabhata's table of differences. The third column converts Aryabhata's minutes to degrees and minutes. The fourth column gives the ratio of Aryabhata's sine to the radius (3438), which is what is nowadays called the sine. The last column gives the modern value of this sine and shows that it agrees up to three decimal places with the value in the fourth column. For use in the next chapter, we note that the sum of all of Aryabhata's sines is 54, 233′.
Figure 20.7 Aryabhata's table of sines (first two columns) and their modern equivalents (last three columns).
Aryabhata applied the sine function to determine the altitude of the sun at a given hour of the day. The procedure is illustrated in Fig. 20.8 for an observer located at O in the northern hemisphere on a day in spring or summer. This figure shows a portion of the celestial sphere. The arc RETSWV is the portion of the great circle in which the observer's horizontal plane intersects the sphere. The sun will rise for this observer at the point R and set at the point V. The arc is slightly larger than a semicircle, since we are assuming a day in spring or summer. The chord RV runs from east to west. The sun will move along the small circle RHV at a uniform rate, and the plane of this circle is parallel to the equatorial circle EMW. (At the equinox, the day-circle RV coincides with the equatorial circle EW.) Aryabhata gave the correct formula for finding the radius of this day-circle in terms of the elevation of the sun above the celestial equator and the radius of the celestial sphere. That radius is the sine of the co-declination of the sun. Although Aryabhata had the concept of co-latitude, which served him in places where we would use the cosine function, for some reason he did not use the analogous concept of co-declination. As a result, he had to subtract the square of the sine of the declination from the square of the radius of the celestial sphere and then take the square root.
Figure 20.8 Finding the sun's elevation at a given hour.
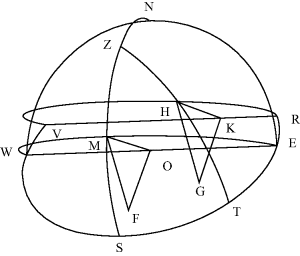
The point Z is the observer's zenith, M is the point on the celestial equator that is due south to the observer, and S is the point due south on the horizon, so that the arc 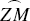 is the observer's terrestrial latitude, and the two arcs
is the observer's terrestrial latitude, and the two arcs 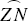 and
and 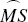 are both equal to the observer's co-latitude. The point H is the location of the sun at a given time, MF and HG are the projections of M and H respectively on the horizontal plane, and K is the projection of H on the chord RV. Finally, the great-circle arc HT, which runs through Z, is the altitude of the sun. The problem is to determine its sine HG in terms of lengths that can be measured.
are both equal to the observer's co-latitude. The point H is the location of the sun at a given time, MF and HG are the projections of M and H respectively on the horizontal plane, and K is the projection of H on the chord RV. Finally, the great-circle arc HT, which runs through Z, is the altitude of the sun. The problem is to determine its sine HG in terms of lengths that can be measured.
Because their sides are parallel lines, the triangles MOF and HKG are similar, so that MO : HK = MF : HG. Hence we get
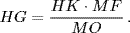
In this relation, MF is the sine of MS, that is, the sine of the observer's co-latitude, and MO is the radius of the celestial sphere. The line HK is, in a loose sense, the sine of the arc 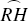 , which is proportional to the time elapsed since sunrise. It is perpendicular to the chord RV and would be a genuine sine if RV were the diameter of its circle. As it is, that relation holds only at the equinoxes. It is not certain whether Aryabhata meant his formula to apply only on the equinox, or whether he intended to use the word sine in this slightly inaccurate sense. Because the radius of the sun's small circle is never less than 90% of the radius of the celestial sphere, probably no observable inaccuracy results from taking HK to be a sine. In any case, that is the way Aryabhata phrased the matter:
, which is proportional to the time elapsed since sunrise. It is perpendicular to the chord RV and would be a genuine sine if RV were the diameter of its circle. As it is, that relation holds only at the equinoxes. It is not certain whether Aryabhata meant his formula to apply only on the equinox, or whether he intended to use the word sine in this slightly inaccurate sense. Because the radius of the sun's small circle is never less than 90% of the radius of the celestial sphere, probably no observable inaccuracy results from taking HK to be a sine. In any case, that is the way Aryabhata phrased the matter:
The sine of the sun at any given point from the horizon on its day-circle multiplied by the sine of the co-latitude and divided by the radius is the [sine of the altitude of the sun] when any given part of the day has elapsed or remains. [Clark, 1930, p. 72]
20.2.2 The Kuttaka
Verses 32 and 33 of the Aryabhatiya contain a method known as the kuttaka (pulverizer) for solving problems related the “Chinese remainder theorem,” which will be discussed in Chapter 22. Since the process was described more clearly by Brahmagupta, we reserve our discussion of it for the next chapter.
Problems and Questions
Mathematical Problems
20.1. Show that Aryabhata's list of sine differences can be interpreted in our language as the table whose nth entry is
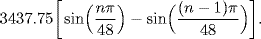
Here the angles are written in radian measure. Use a computer to generate this table for n = 1,. . ., 24, and compare the result with Aryabhata's table.
20.2. If the recursive procedure said to have been used by Aryabhata is followed faithfully (as a computer can do), the result is the following sequence.
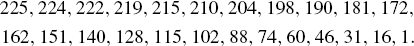
Compare this list with Aryabhata's list, and note the systematic divergence. These differences should be approximately 225 times the cosine of the appropriate angle. That is, dn ≈ 225 · cos (225(n + 0.5) minutes). What does that fact suggest about the source of the systematic errors in the recursive procedure described by Aryabhata?
20.3. Use Aryabhata's rule to compute the altitude of the sun above the horizon in London (latitude 51 32′) at 10:00 am (local solar time) on the vernal equinox. Assume that the sun rises at 6:00 am on that day and sets at 6:00 pm.
32′) at 10:00 am (local solar time) on the vernal equinox. Assume that the sun rises at 6:00 am on that day and sets at 6:00 pm.
Historical Questions
20.4. Describe three kinds of geometric problems considered in the Sulva Sutras.
20.5. How does the trigonometry used by Aryabhata I differ from what had been developed by Ptolemy four centuries earlier?
20.6. Which geometric formulas given by Aryabhata I are accurate from the point of view of Euclidean geometry, and which are inaccurate?
Questions for Reflection
20.7. Consider the problem posed by the Jain concept of the first unenumerable number. If this number is defined as the first number that no one ever will name, then in some sense it certainly exists (why?). But it will never be explicitly known to anyone, since, by definition, explicitly knowing a number means being able to name it. If it is defined as the first number that cannot even theoretically be named, another problem arises. Are there finite integers that cannot even theoretically be named? If there are, in what sense do they “exist”?
20.8. Compare the conjecture given in the text as to the origin of the approximation for 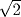 with the following, due to a later commentator of 1500 CE. Assume that each side of the square is 12 units long. Then the diagonal has length
with the following, due to a later commentator of 1500 CE. Assume that each side of the square is 12 units long. Then the diagonal has length 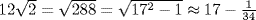 [since
[since 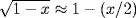 ]. It follows that
]. It follows that 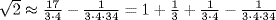 . Which explanation seems more probable to you? Does either imply the other?
. Which explanation seems more probable to you? Does either imply the other?
20.9. Besides the sine function, we also use the tangent and secant and their cofunctions. What is the origin of the words tangent and secant (in Latin), and why are they applied to the objects of trigonometry?
Note
1. In Hindu mythology, Mount Meru plays a role similar to that of Mount Olympus in Greek mythology. One Sanskrit dictionary gives this mathematical phrase as a separate entry.